Mathematics is not a careful march down a well-cleared highway, but a journey into a strange wilderness, where the explorers often get lost. Rigour should be a signal to the historian that the maps have been made, and the real explorers have gone elsewhere.
W.S. Anglin
‘Since I first met Fermat’s Last Theorem as a child it’s been my greatest passion,’ recalls Andrew Wiles, in a hesitant voice which conveys the emotion he feels about the problem. ‘I’d found this problem which had been unsolved for three hundred years. I don’t think many of my schoolfriends caught the mathematics bug, so I didn’t discuss it with my contemporaries. But I did have a teacher who had done research in mathematics and he gave me a book about number theory that gave me some clues about how to start tackling it. To begin with I worked on the assumption that Fermat didn’t know very much more mathematics than I would have known. I tried to find his lost solution by using the kind of methods he might have used.’
Wiles was a child full of innocence and ambition, who saw an opportunity to succeed where generations of mathematicians had failed. To others this might have seemed like a foolhardy dream but young Andrew was right in thinking that he, a twentieth-century schoolboy, knew as much mathematics as Pierre de Fermat, a genius of the seventeenth century. Perhaps in his naïvety he would stumble upon a proof which other more sophisticated minds had missed.
Despite his enthusiasm every calculation resulted in a dead end. Having racked his brains and sifted through his schoolbooks he was achieving nothing. After a year of failure he changed his strategy and decided that he might be able to learn something from the mistakes of other more eminent mathematicians. ‘Fermat’s Last Theorem has this incredible romantic history to it. Many people have thought about it, and the more that great mathematicians in the past have tried and failed to solve the problem, the more of a challenge and the more of a mystery it’s become. Many mathematicians had tried it in so many different ways in the eighteenth and nineteenth centuries, and so as a teenager I decided that I ought to study those methods and try to understand what they’d been doing.’
Young Wiles examined the approaches of everyone who had ever made a serious attempt to prove Fermat’s Last Theorem. He began by studying the work of the most prolific mathematician in history and the first one to make a breakthrough in the battle against Fermat.
Creating mathematics is a painful and mysterious experience. Often the object of the proof is clear, but the route is shrouded in fog, and the mathematician stumbles through a calculation, terrified that each step might be taking the argument in completely the wrong direction. Additionally there is the fear that no route exists. A mathematician may believe that a statement is true, and spend years trying to prove that it is indeed true, when all along it is actually false. The mathematician has effectively been attempting to prove the impossible.
In the entire history of the subject only a handful of mathematicians appear to have avoided the self-doubt which intimidates their colleagues. Perhaps the most notable example of such a mathematician was the eighteenth-century genius Leonhard Euler, and it was he who made the first breakthrough towards proving Fermat’s Last Theorem. Euler had such an incredible intuition and vast memory that it was said he could map out the entire bulk of a calculation in his head without having to put pen to paper. Across Europe he was referred to as ‘analysis incarnate’, and the French academician François Arago said, ‘Euler calculated without apparent effort as men breathe, or as eagles sustain themselves in the wind.’
Leonhard Euler was born in Basle in 1707, the son of a Calvinist pastor, Paul Euler. Although the young Euler showed a prodigious talent for mathematics, his father was determined that he should study theology and pursue a career in the Church. Leonhard dutifully obeyed and studied theology and Hebrew at the University of Basle.
Fortunately for Euler the town of Basle was also home to the eminent Bernoulli clan. The Bernoullis could easily claim to be the most mathematical of families, creating eight of Europe’s most outstanding minds within only three generations – some have said that the Bernoulli family was to mathematics what the Bach family was to music. Their fame spread beyond the mathematical community and one particular legend typifies the profile of the family. Daniel Bernoulli was once travelling across Europe and had struck up a conversation with a stranger. After a while he modestly introduced himself: ‘I am Daniel Bernoulli.’ ‘And I,’ said his companion sarcastically, ‘am Isaac Newton.’ Daniel fondly recalled this incident on several occasions, considering it the most sincere tribute he had ever received.
Daniel and Nikolaus Bernoulli were close friends of Leonhard Euler, and they realised that the most brilliant of mathematicians was being turned into the most mediocre of theologians. They appealed to Paul Euler and requested that Leonhard be allowed to forsake the cloth in favour of numbers. Euler senior had in the past been taught mathematics by Bernoulli senior, Jakob, and had a tremendous respect for the family. Reluctantly he accepted that his son had been born to calculate, not preach.
Leonhard Euler soon left Switzerland for the palaces of Berlin and St Petersburg, where he was to spend the bulk of his creative years. During the era of Fermat, mathematicians were considered amateur number-jugglers, but by the eighteenth century they were treated as professional problem-solvers. The culture of numbers had changed dramatically, and this was partly a consequence of Sir Isaac Newton and his scientific calculations.
Newton believed that mathematicians were wasting their time teasing each other with pointless riddles. Instead he would apply mathematics to the physical world and calculate everything from the orbits of the planets to the trajectories of cannon-balls. By the time Newton died, in 1727, Europe had undergone a scientific revolution, and in the same year Euler published his first paper. Although the paper contained elegant and innovative mathematics, it was primarily aimed at describing a solution to a technical problem regarding the masting of ships.
The European powers were not interested in using mathematics to explore esoteric and abstract concepts; instead they wanted to exploit mathematics to solve practical problems, and they competed to employ the best minds. Euler began his career with the Czars, before being invited to the Berlin Academy by Frederick the Great of Prussia. Eventually he returned to Russia, under the rule of Catherine the Great, where he spent his final years. During his career he tackled a multitude of problems, ranging from navigation to finance, and from acoustics to irrigation. The practical world of problem-solving did not dull Euler’s mathematical ability. Instead tackling each new task would inspire him to create innovative and ingenious mathematics. His single-minded passion drove him to write several papers in a single day, and it is said that between the first and second calls for dinner he would attempt to dash off a complete calculation worthy of publication. Not a moment was wasted and even when he was cradling an infant in one hand Euler would be outlining a proof with the other.
One of Euler’s greatest achievements was the development of the algorithmic method. The point of Euler’s algorithms was to tackle apparently impossible problems. One such problem was predicting the phases of the moon far into the future with high accuracy – information which could be used to draw up vital navigation tables. Newton had already shown that it is relatively easy to predict the orbit of one body around another, but in the case of the moon the situation is not so simple. The moon orbits the earth, but there is a third body, the sun, which complicates matters enormously. While the earth and moon attract each other, the sun perturbs the position of the earth and has a knock-on effect on the orbit of the moon. Equations could be used to pin down the effect of any two of the bodies, but eighteenth-century mathematicians could not incorporate the third body into their calculations. Even today it is impossible to predict the exact solution to the so-called ‘three-body problem’.
Euler realised that mariners did not need to know the phase of the moon with absolute accuracy, only with enough precision to locate their own position to within a few nautical miles. Consequently Euler developed a recipe for generating an imperfect but sufficiently accurate solution. The recipe, known as an algorithm, worked by first obtaining a rough-and-ready result, which could then be fed back into the algorithm to generate a more refined result. This refined result could then be fed back into the algorithm to generate an even more accurate result, and so on. A hundred or so iterations later Euler was able to provide a position for the moon which was accurate enough for the purposes of the navy. He gave his algorithm to the British Admiralty and in return they rewarded him with a prize of £300.
Euler earned a reputation for being able to solve any problem which was posed, a talent which seemed to extend even beyond the realm of science. During his stint at the court of Catherine the Great he encountered the great French philosopher Denis Diderot. Diderot was a committed atheist and would spend his days converting the Russians to atheism. This infuriated Catherine, who asked Euler to put a stop to the efforts of the godless Frenchman.
Euler gave the matter some thought and claimed that he had an algebraic proof for the existence of God. Catherine the Great invited Euler and Diderot to the palace and gathered together her courtiers to listen to the theological debate. Euler stood before the audience and announced:
![]()
With no great understanding of algebra, Diderot was unable to argue against the greatest mathematician in Europe and was left speechless. Humiliated, he left St Petersburg and returned to Paris. In his absence, Euler continued to enjoy his return to theological study and published several other mock proofs concerning the nature of God and the human spirit.
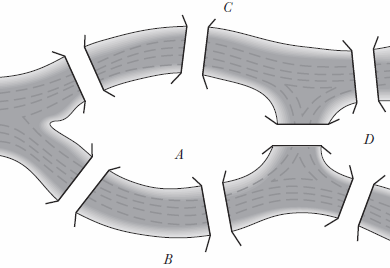
Figure 5. The River Pregel divides the town of Königsberg into four seperate parts, A, B, C and D. Seven bridges connect the various parts of the town, and a local riddle asked if it was possible to make a journey such that each bridge is crossed once and only once.
A more valid problem which also appealed to Euler’s whimsical nature concerned the Prussian city of Königsberg, now known as the Russian city of Kaliningrad. The city is built on the banks of the river Pregel and consists of four separate quarters connected by seven bridges. Figure 5 shows the layout of the city. Some of the more curious residents of Königsberg wondered if it was possible to plot a journey across all seven bridges without having to stroll across any bridge more than once. The citizens of Königsberg tried various routes but each one ended in failure. Euler also failed to find a successful route, but he was successful in explaining why making such a journey was impossible.
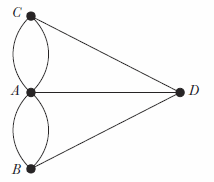
Figure 6. A simplified representation of the bridges of Königsberg
Euler began with a plan of the city, and from it he generated a simplified representation in which the sections of land were reduced to points and bridges were replaced by lines, as shown in Figure 6. He then argued that, in general, in order to make a successful journey (i.e. crossing all bridges only once) a point should be connected to an even number of lines. This is because in the middle of a journey when the traveller passes through a land mass, he or she must enter via one bridge and then leave via a different bridge. There are only two exceptions to this rule – when a traveller either begins or ends the journey. At the start of the journey the traveller leaves a land mass and requires only a single bridge to exit, and at the end of the journey the traveller arrives at a land mass and requires only a single bridge to enter. If the journey begins and ends in different locations, then these two land masses are allowed to have an odd number of bridges. But if the journey begins and ends in the same place, then this point, like all the other points, must have an even number of bridges.
So, in general, Euler concluded that, for any network of bridges, it is only possible to make a complete journey crossing each bridge only once if all the landmasses have an even number of bridges, or exactly two land masses have an odd number of bridges. In the case of Königsberg there are four land masses in total and all of them are connected to an odd number of bridges – three points have three bridges, and one has five bridges. Euler had been able to explain why it was impossible to cross each one of Königsberg’s bridges once and only once, and furthermore he had generated a rule which could be applied to any network of bridges in any city in the world. The argument is beautifully simple, and was perhaps just the sort of logical problem that Euler dashed off before dinner.
The Königsberg bridge puzzle is a so-called network problem in applied mathematics, but it inspired Euler to consider more abstract networks. He went on to discover a fundamental truth about all networks, the so-called network formula, which he could prove with just a handful of logical steps. The network formula shows an eternal relationship between the three properties which describe any network:
![]()
where
V = the number of vertices (intersections) in the network,
L = the number of lines in the network,
R = the number of regions (enclosed areas) in the network.
Euler claimed that for any network one could add the number of vertices and regions and subtract the number of lines and the total would always be 1. For example, all the networks in Figure 7 obey the rule.

Figure 7. All conceivable networks obey Euler’s network formula.
It is possible to imagine testing this formula on a whole series of networks and if it turned out to be true on each occasion it would be tempting to assume that the formula is true for all networks. Although this might be enough evidence for a scientific theory, it is inadequate to justify a mathematical theorem. The only way to show that the formula works for every possible network is to construct a foolproof argument, which is exactly what Euler did.
Euler began by considering the simplest network of all, i.e. a single vertex as shown in Figure 8. For this network the formula is clearly true: there is one vertex, and no lines or regions, and therefore
![]()
Euler then considered what would happen if he added something to this simplest of all networks. Any extension to the single vertex requires the addition of a line. The line can either connect the existing vertex to itself, or it can connect the existing vertex to a new vertex.
First, let us look at connecting the vertex to itself with this additional line. As shown in Figure 8, when the line is added, this also results in a new region. Therefore the network formula remains true because the extra region (+1) cancels the extra line (–1). If further lines are added in this way the network formula will still remain true because each new line will create a new region.

Figure 8. Euler proved his network formula by showing that it was true for the simplest network, and then demonstrating that the formula would remain true whatever extensions were added to the single vertex.
Second, let us look at using the line to connect the original vertex to a new vertex, as shown in Figure 8. Once again the network formula remains true because the extra vertex (+1) cancels the extra line (–1). If further lines are added in this way, the network formula will still remain true because each new line will create a new vertex.
This was all that Euler required for his proof. He argued that the network formula was true for the simplest of all networks, the single vertex. Furthermore, all other networks, no matter how complicated, can be constructed from the simplest network by adding lines one at a time. Each time a new line is added the network formula will remain true because either a new vertex or a new region will always be added and this will have a compensating effect. Euler had developed a simple but powerful strategy. He proved that the formula is true for the most basic network, a single vertex, and then he demonstrated that any operation which complicated the network would continue to conserve the validity of the formula. Therefore the formula is true for the infinity of all possible networks.
When Euler first encountered Fermat’s Last Theorem, he must have hoped that he could solve it by adopting a similar strategy. The Last Theorem and the network formula come from very different areas of mathematics but they have one thing in common, which is that both say something about an infinite number of objects. The network formula says that for the infinite number of networks that exist the number of vertices and regions less the number of lines always equals 1. Fermat’s Last Theorem claims that for an infinite number of equations there are no whole number solutions. Recall that Fermat stated that there are no whole number solutions to the following equation:
![]()
This equation represents an infinite set of equations:

Euler wondered if he could prove that one of the equations had no solutions and then extrapolate the result to all the remaining equations, in the same way he had proved his network formula for all networks by generalising it from the simplest case, the single vertex.
Euler’s task was given a head start when he discovered a clue hidden in Fermat’s jottings. Although Fermat never wrote down a proof for the Last Theorem, he did cryptically describe a proof for the specific case n = 4 elsewhere in his copy of the Arithmetica and incorporated it into the proof of a completely different problem. Even though this is the most complete calculation he ever committed to paper, the details are still sketchy and vague, and Fermat concludes the proof by saying that lack of time and paper prevent him from giving a fuller explanation. Despite the lack of detail in Fermat’s scribbles, they clearly illustrate a particular form of proof by contradiction known as the method of infinite descent.
In order to prove that there were no solutions to the equation x4 + y4 = z4, Fermat began by assuming that there was a hypothetical solution
![]()
By examining the properties of (X1, r1, Z1), Fermat could demonstrate that if this hypothetical solution did exist then there would have to be a smaller solution (X2, r2, Z2). Then, by examining this new solution, Fermat could show there would be an even smaller solution (X3, r3, Z3), and so on.
Fermat had discovered a descending staircase of solutions, which theoretically would continue forever, generating ever-smaller numbers. However, x, y and z must be whole numbers, and so the never-ending staircase is impossible because there must be a smallest possible solution. This contradiction proves that the initial assumption that there is a solution (X1, r1, Z1) must be false. Using the method of infinite descent Fermat had demonstrated that it is forbidden for the equation with n = 4 to have any solutions, because otherwise the consequences would be absurd.
Euler tried to use this as a starting point for constructing a general proof for all the other equations. As well as building up to n = infinity, he would also have to build down to n = 3 and it was this single downward step which he attempted first. On 4 August 1753 Euler announced in a letter to the Prussian mathematician Christian Goldbach that he had adapted Fermat’s method of infinite descent and successfully proved the case for n = 3. After a hundred years this was the first time anybody had succeeded in making any progress towards meeting Fermat’s challenge.
In order to extend Fermat’s proof from n = 4 to cover the case n = 3 Euler had to incorporate the bizarre concept of a so-called imaginary number, an entity which had been discovered by European mathematicians in the sixteenth century. It is strange to think of new numbers being ‘discovered’, but this is mainly because we are so familiar with the numbers we commonly use that we forget that there was a time when some of these numbers were not known. Negative numbers, fractions and irrational numbers all had to be discovered and the motivation in each case was to answer otherwise unanswerable questions.
The history of numbers begins with the simple counting numbers (1,2,3, …) otherwise known as natural numbers. These numbers are perfectly satisfactory for adding together simple whole quantities, such as sheep or gold coins, to achieve a total number which is also a whole quantity. As well as addition, the other simple operation of multiplication also acts upon whole numbers to generate other whole numbers. However, the operation of division throws up an awkward problem. While 8 divided by 2 equals 4, we find that 2 divided by 8 equals ¼. The result of the latter division is not a whole number but a fraction.
Division is a simple operation performed on natural numbers which requires us to look beyond the natural numbers in order to obtain the answer. It is unthinkable for mathematicians not, in theory at least, to be able to answer every single question, and this necessity is called completeness. There are certain questions concerning natural numbers which would be unanswerable without resorting to fractions. Mathematicians express this by saying that fractions are necessary for completeness.
It is this need for completeness which led the Hindus to discover negative numbers. The Hindus noticed that, while 3 subtracted from 5 was obviously 2, subtracting 5 from 3 was not such a simple matter. The answer was beyond the natural counting numbers, and could only be accommodated by introducing the concept of negative numbers. Some mathematicians did not accept this extension into abstraction and referred to negative numbers as ‘absurd’ or ‘fictitious’. While an accountant could hold one gold coin, or even half a gold coin, it was impossible to hold a negative coin.
The Greeks also had a yearning for completeness and this led them to discover irrational numbers. In Chapter 2 the question arose, What number is the square root of two, √2? The Greeks knew that this number was roughly equal to 7⁄7, but when they tried to discover the exact fraction they found that it did not exist. Here was a number which could never be represented as a fraction, but this new type of number was necessary in order to answer a simple question, What is the square root of two? The demand for completeness meant that yet another colony was added to the empire of numbers.
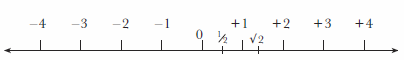
Figure 9. All numbers can be positioned along the number line, which extends to infinity in both directions.
By the Renaissance, mathematicians assumed that they had discovered all the numbers in the universe. All numbers could be thought of as lying on a number line, an infinitely long line with zero at the centre, as shown in Figure 9. The whole numbers were spaced equally along the number line, with the positive numbers on the right of zero extending to positive infinity and the negative numbers on the left of zero extending to negative infinity. The fractions occupied the spaces between the whole numbers, and the irrational numbers were interspersed between the fractions.
The number line suggested that completeness had apparently been achieved. All the numbers seemed to be in place, ready to answer all mathematical questions – in any case, there was no more room on the number line for any new numbers. Then during the sixteenth century there were renewed rumblings of disquiet. The Italian mathematician Rafaello Bombelli was studying the square roots of various numbers when he stumbled upon an unanswerable question.
The problem began by asking, What is the square root of one, √1? The obvious answer is 1, because 1 × 1 = 1. The less obvious answer is –1. A negative number multiplied by another negative number generates a positive number. This means –1 × –1 = +1. So, the square root of +1 is both +1 and –1. This abundance of answers is fine, but then the question arises, What is the square root of negative one, √–1? The problem seems to be intractable. The solution cannot be +1 or –1, because the square of both these numbers is +1. However, there are no other obvious candidates. At the same time completeness demands that we must be able to answer the question.
The solution for Bombelli was to create a new number, i, called an imaginary number, which was simply defined as the solution to the question, What is the square root of negative one? This might seem like a cowardly solution to the problem, but it was no different to the way in which negative numbers were introduced. Faced with an otherwise unanswerable question the Hindus merely defined –1 as the solution to the question, What is zero subtract one? It is easier to accept the concept of –1 only because we have experience of the analogous concept of ‘debt’, whereas we have nothing in the real world to underpin the concept of an imaginary number. The seventeenth-century German mathematician Gottfried Leibniz elegantly described the strange nature of the imaginary number: ‘The imaginary number is a fine and wonderful recourse of the divine spirit, almost an amphibian between being and non-being.’
Once we have defined i as being the square root of –1, then 2i must exist, because this would be the sum of i plus i (as well as being the square root of –4). Similarly i⁄2 must exist because this is the result of dividing i by 2. By performing simple operations it is possible to achieve an imaginary equivalent of every so-called real number. There are imaginary counting numbers, imaginary negative numbers, imaginary fractions and imaginary irrationals.

Figure 10. The introduction of an axis for imaginary numbers turns the number line into a number plane. Any combination of real and imaginary numbers has a position on the number plane.
The problem which now arises is that all these imaginary numbers have no natural position along the real number line. Mathematicians resolve this crisis by creating a separate imaginary number line which is perpendicular to the real one, and which crosses at zero, as shown in Figure 10. Numbers are now no longer restricted to a one-dimensional line, but rather they occupy a two-dimensional plane. While pure imaginary or pure real numbers are restricted to their respective lines, combinations of real and imaginary numbers (e.g. 1 + 2i), called complex numbers, live on the so-called number plane.
What is particularly remarkable is that complex numbers can be used to solve any conceivable equation. For example, in order to calculate √(3 + 4i), mathematicians do not have to resort to inventing a new type of number – the answer turns out to be 2 + i, another complex number. In other words the imaginary numbers appear to be the final element required to make mathematics complete.
Although the square roots of negative numbers have been referred to as imaginary numbers, mathematicians consider i no more abstract than a negative number or any counting number. In addition, physicists discovered that imaginary numbers provide the best language for describing some real-world phenomena. With a few minor manipulations imaginary numbers turn out to be the ideal way to analyse the natural swinging motion of objects such as pendula. This motion, technically called a sinusoidal oscillation, is found throughout nature, and so imaginary numbers have become an integral part of many physical calculations. Nowadays electrical engineers conjure up i to analyse oscillating currents, and theoretical physicists calculate the consequences of oscillating quantum mechanical wave functions by summoning up the powers of imaginary numbers.
Pure mathematicians have also exploited imaginary numbers, using them to find answers to previously impenetrable problems. Imaginary numbers literally add a new dimension to mathematics, and Euler hoped to exploit this extra degree of freedom to attack Fermat’s Last Theorem.
In the past other mathematicians had tried to adapt Fermat’s method of infinite descent to work for cases other than n = 4, but in every case attempts to stretch the proof only led to gaps in the logic. However, Euler showed that by incorporating the imaginary number, i, into his proof he could plug holes in the proof, and force the method of infinite descent to work for the case n = 3.
It was a tremendous achievement, but one which he could not repeat for other cases of Fermat’s Last Theorem. Unfortunately Euler’s endeavours to make the argument work for the cases up to infinity all ended in failure. The man who created more mathematics than anybody else in history was humbled by Fermat’s challenge. His only consolation was that he had made the first breakthrough in the world’s hardest problem.
Undaunted by this failure Euler continued to create brilliant mathematics until the day he died, an achievement made all the more remarkable by the fact that during the final years of his career he was totally blind. His loss of sight began in 1735 when the Academy in Paris offered a prize for the solution to an astronomical problem. The problem was so awkward that the mathematical community asked the Academy to allow them several months in which to come up with an answer, but for Euler this was unnecessary. He became obsessed with the task, worked continually for three days and duly won the prize. However, poor working conditions combined with intense stress cost Euler, then still only in his twenties, the sight of one eye. This is apparent in many portraits of Euler.
On the advice of Jean Le Rond d’Alembert, Euler was replaced by Joseph-Louis Lagrange as mathematician to the court of Frederick the Great, who later commented: ‘To your care and recommendation am I indebted for having replaced a half-blind mathematician with a mathematician with both eyes, which will especially please the anatomical members of my Academy.’ Euler returned to Russia where Catherine the Great welcomed back her ‘mathematical cyclops’.
The loss of one eye was only a minor handicap – in fact Euler claimed that ‘now I will have less distraction’. Forty years later, at the age of sixty, his situation worsened considerably, when a cataract in Euler’s good eye meant he was destined to become completely blind. He was determined not to give in and began to practise writing with his fading eye closed in order to perfect his technique before the onset of darkness. Within weeks he was blind. The rehearsal paid off for a while, but a few months later Euler’s script became illegible, whereupon his son Albert acted as his amanuensis.
Euler continued to produce mathematics for the next seventeen years and, if anything, he was more productive than ever. His immense intellect allowed him to juggle concepts without having to commit them to paper, and his phenomenal memory allowed him to use his own brain as a mental library. Colleagues suggested that the onset of blindness appeared to expand the horizons of his imagination. It is worth noting that Euler’s computations of lunar positions were completed during his period of blindness. For the emperors of Europe this was the most prized of mathematical achievements, a problem that had confounded the greatest mathematicians in Europe, including Newton.
In 1776 an operation was performed to remove the cataract, and for a few days Euler’s sight seemed to have been restored. Then infection set in and Euler was plunged back into darkness. Undaunted he continued to work until, on 18 September 1783, he suffered a fatal stroke. In the words of the mathematician-philosopher the Marquis de Condorcet, ‘Euler ceased to live and calculate.’
A century after Fermat’s death there existed proofs for only two specific cases of the Last Theorem. Fermat had given mathematicians a head start by providing them with the proof that there were no solutions to the equation
![]()
Euler had adapted the proof to show that there were no solutions to
![]()
After Euler’s breakthrough it was still necessary to prove that there were no whole number solutions to an infinity of equations:
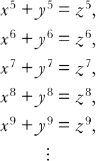
Although mathematicians were making embarrassingly slow progress, the situation was not quite as bad as it might seem at first sight. The proof for the case n = 4 also proves the cases n = 8, 12, 16, 20, …. The reason is that any number which can be written as an 8th (or a 12th, 16th, 20th, …) power can also be rewritten as a 4th power. For instance, the number 256 is equal to 28, but it is also equal to 44. Therefore any proof which works for the 4th power will also work for the 8th power and for any other power that is a multiple of 4. Using the same principle, Euler’s proof for the case n = 3 automatically proves the cases n = 6, 9, 12, 15, …
Suddenly, the numbers are tumbling and Fermat looks vulnerable. The proof for the case n = 3 is particularly significant because the number 3 is an example of a prime number. As explained earlier, a prime number has the special property of not being the multiple of any whole number except for 1 and itself. Other prime numbers are 5, 7, 11, 13, …. All the remaining numbers are multiples of the primes, and are referred to as non-primes, or composite numbers.
Number theorists consider prime numbers to be the most important numbers of all because they are the atoms of mathematics. Prime numbers are the numerical building blocks because all other numbers can be created by multiplying combinations of the prime numbers. This seems to lead to a remarkable breakthrough. To prove Fermat’s Last Theorem for all values of n, one merely has to prove it for the prime values of n. All other cases are merely multiples of the prime cases and would be proved implicitly.
Intuitively this enormously simplifies the problem, because you can ignore those equations which involve a value of n that is not a prime number. The number of equations remaining is now vastly reduced. For example, for the values of n up to 20, there are only six values which need to be proved:
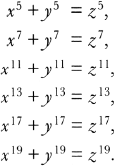
If one can prove Fermat’s Last Theorem for just the prime values of n, then the theorem is proved for all values of n. If one considers all whole numbers, then it is obvious that there are infinitely many. If one considers just the prime numbers, which are only a small fraction of all the whole numbers, then surely the problem is much simpler?
Intuition would suggest that if you begin with an infinite quantity and then remove the bulk of it, then you would expect to be left with something finite. Unfortunately intuition is not the arbiter of truth in mathematics, but rather logic. In fact, it is possible to prove that the list of primes is never-ending. Therefore, despite being able to ignore the vast majority of equations relating to non-prime values of n, the remaining equations relating to prime values of n are still infinite in number.
The proof that there is an infinity of primes dates all the way back to Euclid, and is one of the classic arguments of mathematics. Initially Euclid assumes that there is a finite list of known prime numbers, and then shows that there must exist an infinite number of additions to this list. There are N prime numbers in Euclid’s finite list, which are labelled P1, P2, P3, …,PN. Euclid can then generate a new number QA such that
![]()
This new number QA is either prime or not prime. If it is prime then we have succeeded in generating a new, bigger prime number, and therefore our original list of primes was not complete. On the other hand, if QA is not prime, then it must be perfectly divisible by a prime. This prime cannot be one of the known primes because dividing QA by any of the known primes will inevitably lead to a remainder of 1. Therefore there must be some new prime, which we can call PN + 1.
We have now arrived at the stage where either QA is a new prime or we have another new prime PN+1. Either way we have added to our original list of primes. We can now repeat the process, including our new prime (PN+1 or QA) in our list, and generate some new number QB. Either this new number will be yet another new prime, or there will have to be some other new prime PN+2 that is not on our list of known primes. The upshot of the argument is that, however long our list of prime numbers, it is always possible to find a new one. Therefore the list of primes is never-ending and infinite.
But how can something which is undeniably smaller than an infinite quantity also be infinite? The German mathematician David Hilbert once said: ‘The infinite! No other question has ever moved so profoundly the spirit of man; no other idea has so fruitfully stimulated his intellect; yet no other concept stands in greater need of clarification than that of the infinite.’ To resolve the paradox of the infinite it is necessary to define what is meant by infinity. Georg Cantor, who worked alongside Hilbert, defined infinity as the size of the never-ending list of counting numbers (1, 2, 3, 4, …). Consequently anything which is comparable in size is equally infinite.
By this definition the number of even counting numbers, which would intuitively appear to be smaller, is also infinite. It is easy to demonstrate that the quantity of counting numbers and the quantity of even numbers are comparable because we can pair off each counting number with a corresponding even number:

If every member of the counting numbers list can be matched up with a member of the even numbers list then the two lists must be the same size. This method of comparison leads to some surprising conclusions, including the fact that there are an infinite number of primes. Although Cantor was the first person to tackle infinity in a formal way, he was initially heavily criticised by the mathematical community for his radical definition. Towards the end of his career the attacks became increasingly personal and this resulted in Cantor suffering mental illness and severe depression. Eventually, after his death, his ideas became widely accepted as the only consistent, accurate and powerful definition of infinity. As a tribute Hilbert said: ‘No one shall drive us from the paradise Cantor has created for us.’
Hilbert went on to create an example of infinity, known as Hilbert’s Hotel, which clearly illustrates its strange qualities. This hypothetical hotel has the desirable attribute of having an infinite number of rooms. One day a new guest arrives and is disappointed to learn that, despite the hotel’s infinite size, all the rooms are occupied. Hilbert, the clerk, thinks for a while and then reassures the new arrival that he will find an empty room. He asks all his current guests to move to the next room, so that the guest in room 1 moves to room 2, the guest in room 2 moves to room 3, and so on. Everybody who was in the hotel still has a room, which allows the new arrival to slip into the vacant room 1. This shows that infinity plus one equals infinity.
The following night Hilbert has to deal with a much greater problem. The hotel is still full when an infinitely large coach arrives with an infinite number of new guests. Hilbert remains unperturbed and rubs his hands at the thought of infinitely more hotel bills. He asks all his current guests to move to the room which is double the number of their current room. So the guest in room 1 moves to room 2, the guest in room 2 moves to room 4, and so on. Everybody who was in the hotel still has a room and yet an infinite number of rooms, all the odd ones, have been vacated for the new arrivals. This shows that double infinity is still infinity.
Hilbert’s Hotel seems to suggest that all infinities are as large as each other, because various infinities seem to be able to squeeze into the same infinite hotel – the infinity of even numbers can be matched up and compared with the infinity of all counting numbers. However, some infinities are indeed bigger than others. For example, any attempt to pair every rational number with every irrational number ends in failure, and in fact it can be proved that the infinite set of irrational numbers is larger than the infinite set of rational numbers. Mathematicians have had to develop a whole system of nomenclature to deal with the varying scales of infinity and conjuring with these concepts is one of today’s hottest topics.
Although the infinity of primes dashed hopes for an early proof of Fermat’s Last Theorem, a countless supply of prime numbers does have more positive implications in other areas such as espionage and the evolution of insects. Before returning to the quest for a proof of Fermat’s Last Theorem it is worth briefly investigating the uses and abuses of primes.
Prime number theory is one of the few areas of pure mathematics that has found a direct application in the real world, namely in cryptography. Cryptography involves scrambling secret messages so that they can only be unscrambled by the receiver and not by anybody else who might intercept them. The scrambling process requires the use of a secret key, and traditionally unscrambling the message simply requires the receiver to apply the key in reverse. With this procedure the key is the weakest link in the chain of security. First, the receiver and the sender must agree on the details of the key and the exchange of this information is a risky process. If the enemy can intercept the key being exchanged, then they can unscramble all subsequent messages. Second, the keys must be regularly changed in order to maintain security, and each time this happens there is a risk of the new key being intercepted.
The problem of the key revolves around the fact that applying it one way will scramble the message, and applying it in reverse unscrambles the message – unscrambling a message is almost as easy as scrambling it. However, experience tells us that there are many everyday situations when unscrambling is far harder than scrambling – it is relatively easy to scramble an egg, but to unscramble it is far harder.
In the 1970s Whitfield Diffie and Martin Hellman came up with the idea of looking for a mathematical process which was easy to perform in one direction but incredibly difficult to perform in the opposite direction. Such a process would provide a perfect key. For example, I could have my own two-part key, and publish the scrambling half of it in a public directory. Then anybody could send me scrambled messages, but only I would know the unscrambling half of the key. Although everyone would have knowledge of the scrambling part of the key, it bears no relation to the unscrambling part of the key.
In 1977 Ronald Rivest, Adi Shamir and Leonard Adleman, a team of mathematicians and computer scientists at the Massachusetts Institute of Technology, realised that prime numbers were the ideal basis for an easy-scramble/hard-unscramble process. In order to make my own personal key I would take two huge prime numbers, each one containing up to 80 digits, and then multiply them together to achieve an even larger non-prime number. In order to scramble messages all that is required is knowledge of the large non-prime number, whereas to unscramble the message you would need to know the two original prime numbers which were multiplied together, known as the prime factors. I can now publish the large non-prime number, the scrambling half of the key, and keep the two prime factors, the unscrambling half of the key, to myself. Importantly, even though everybody knows the large non-prime number, they would have immense difficulty in working out the two prime factors.
Taking a simpler example, I could hand out the non-prime number 589, which would enable everyone to scramble messages to me. I would keep the two prime factors of 589 secret, so that only I could unscramble the messages. If others could work out the two prime factors then they too could unscramble my messages, but even with this small number it is not obvious what the two prime factors are. In this case it would only take a few minutes on a desktop computer to figure out that the prime factors are actually 31 and 19 (31 × 19 = 589), and so my key would not remain secure for very long.
However, in reality the non-prime number which I would publish would have over a hundred digits, which makes the task of finding its prime factors effectively impossible. Even if the world’s most powerful computers were used to split this huge non-prime number (the scrambling key) into its two prime factors (the unscrambling key) it would take several years to achieve the answer. Therefore, to foil foreign spies, I merely have to change my key on an annual basis. Once a year I announce my new giant non-prime number, and anybody who wants to try and unscramble my messages would then have to start all over again trying to compute the two prime factors.
As well as finding a role in espionage, prime numbers also appear in the natural world. The periodical cicadas, most notably Magicicada septendecim, have the longest life-cycle of any insect. Their unique life-cycle begins underground, where the nymphs patiently suck the juice from the roots of trees. Then, after 17 years of waiting the adult cicadas emerge from the ground, swarm in vast numbers and temporarily swamp the landscape. Within a few weeks they mate, lay their eggs and die.
The question which puzzled biologists was, Why is the cicada’s life-cycle so long? And is there any significance to the life-cycle being a prime number of years? Another species, Magicicada tredecim, swarms every 13 years, implying that life-cycles lasting a prime number of years offer some evolutionary advantage.
One theory suggests that the cicada has a parasite which also goes through a lengthy life-cycle and which the cicada is trying to avoid. If the parasite has a life-cycle of, say, 2 years then the cicada wants to avoid a life-cycle which is divisible by 2, otherwise the parasite and the cicada will regularly coincide. Similarly, if the parasite has a life-cycle of 3 years then the cicada wants to avoid a life-cycle which is divisible by 3, otherwise the parasite and the cicada will once again regularly coincide. Ultimately, to avoid meeting its parasite the cicadas’ best strategy is to have a long life-cycle lasting a prime number of years. Because nothing will divide into 17, Magicicada septendecim will rarely meet its parasite. If the parasite has a 2-year life-cycle they will only meet every 34 years, and if it has a longer life-cycle, say 16 years, then they will only meet every 272 (16 × 17) years.
In order to fight back, the parasite only has two life-cycles which will increase the frequency of coincidences – the annual cycle and the same 17-year cycle as the cicada. However, the parasite is unlikely to survive reappearing 17 years in a row, because for the first 16 appearances there will be no cicadas for it to parasitise. On the other hand, in order to reach the 17-year life-cycle, the generations of parasites would first have to evolve through the 16-year life-cycle. This would mean at some stage of evolution the parasite and cicada would not coincide for 272 years! In either case the cicadas long prime life-cycle protects it.
This might explain why the alleged parasite has never been found! In the race to keep up with the cicada, the parasite probably kept extending its life-cycle until it hit the 16-year hurdle. Then it failed to coincide for 272 years, by which time the lack of coinciding with cicadas had driven it to extinction. The result is a cicada with a 17-year life cycle, which it no longer needs because its parasite no longer exists.
By the beginning of the nineteenth century, Fermat’s Last Theorem had already established itself as the most notorious problem in number theory. Since Euler’s breakthrough there had been no further progress, but a dramatic announcement by a young Frenchwoman was to reinvigorate the pursuit of Fermat’s lost proof. Sophie Germain lived in an era of chauvinism and prejudice, and in order to conduct her research she was forced to assume a false identity, study in terrible conditions and work in intellectual isolation.
Over the centuries women have been discouraged from studying mathematics, but despite the discrimination there have been several female mathematicians who fought against the establishment and indelibly forged their names in the annals of mathematics. The first woman known to have made an impact on the subject was Theano in the sixth century BC, who began as one of Pythagoras’ students before becoming one of his foremost disciples and eventually marrying him. Pythagoras is known as the ‘feminist philosopher’ because he actively encouraged women scholars, Theano being just one of the twenty-eight sisters in the Pythagorean Brotherhood.
In later centuries the likes of Socrates and Plato would continue to invite women into their schools, but it was not until the fourth century AD that a woman mathematician founded her own influential school. Hypatia, the daughter of a mathematics professor at the University of Alexandria, was famous for giving the most popular discourses in the known world and for being the greatest of problem-solvers. Mathematicians who had been stuck for months on a particular problem would write to her seeking a solution, and Hypatia rarely disappointed her admirers. She was obsessed by mathematics and the process of logical proof, and when asked why she never married she replied that she was wedded to the truth. Ultimately her devotion to the cause of rationalism caused her downfall, when Cyril, the patriarch of Alexandria, began to oppress philosophers, scientists and mathematicians, whom he called heretics. The historian Edward Gibbon provided a vivid account of what happened after Cyril had plotted against Hypatia and turned the masses against her:
On a fatal day, in the holy season of Lent, Hypatia was torn from her chariot, stripped naked, dragged to the church, and inhumanely butchered by the hands of Peter the Reader and a troop of savage and merciless fanatics; her flesh was scraped from her bones with sharp oyster-shells, and her quivering limbs were delivered to the flames.
Soon after the death of Hypatia mathematics entered a period of stagnation and it was not until after the Renaissance that another woman made her name as a mathematician. Maria Agnesi was born in Milan in 1718 and, like Hypatia, was the daughter of a mathematician. She was acknowledged to be one of the finest mathematicians in Europe, particularly famous for her treatises on the tangents to curves. In Italian, curves were called versiera, a word derived from the Latin vertere, ‘to turn’, but it was also an abbreviation for avversiera, or ‘wife of the Devil’. A curve studied by Agnesi (versiera Agnesi) was mistranslated into English as the ‘witch of Agnesi’, and in time the mathematician herself was referred to by the same title.
Although mathematicians across Europe acknowledged Agnesi’s ability, many academic institutions, in particular the French Academy, refused to give her a research post. Institutionalised discrimination against women continued right through to the twentieth century, when Emmy Noether, described by Einstein as ‘the most significant creative mathematical genius thus far produced since the higher education of women began’, was denied a lectureship at the University of Göttingen. The majority of the faculty argued: ‘How can it be allowed that a woman become a Privatdozent? Having become a Privatdozent, she can then become a professor and a member of the University Senate …. What will our soldiers think when they return to the University and find that they are expected to learn at the feet of a woman?’ Her friend and mentor David Hilbert replied: ‘Meine Herren, I do not see that the sex of the candidate is an argument against her admission as a Privatdozent. After all, the Senate is not a bathhouse.’
Later her colleague Edmund Landau was asked whether Noether was indeed a great woman mathematician, to which he replied: ‘I can testify that she is a great mathematician, but that she is a woman, I cannot swear.’
In addition to suffering discrimination Noether had much else in common with other women mathematicians through the centuries, such as the fact that she too was the daughter of a mathematics professor. Many mathematicians, of both genders, are from mathematical families, giving rise to light-hearted rumours of a mathematical gene, but in the case of women the percentage is particularly high. The probable explanation is that most women with potential were never exposed to the subject or encouraged to pursue it, whereas those born to professors could hardly avoid being immersed in the numbers. Furthermore, Noether, like Hypatia, Agnesi and most other women mathematicians, never married, largely because it was not socially acceptable for women to pursue such careers and there were few men who were prepared to wed brides with such controversial backgrounds. The great Russian mathematician Sonya Kovalevsky is an exception to this rule, inasmuch as she arranged a marriage of convenience to Vladimir Kovalevsky, a man who was agreeable to a platonic relationship. For both parties the marriage allowed them to escape their families and concentrate on their researches, and in Sonya’s case travelling alone around Europe was much easier once she was a respectable married woman.
Of all the European countries France displayed the most chauvinistic attitude towards educated women, declaring that mathematics was unsuitable for women and beyond their mental capacity. Although the salons of Paris dominated the mathematical world for most of the eighteenth and nineteenth centuries, only one woman managed to escape the constraints of French society and establish herself as a great number theorist. Sophie Germain revolutionised the study of Fermat’s Last Theorem and made a contribution greater than any of the men who had gone before her.
Sophie Germain was born on 1 April 1776, the daughter of a merchant, Ambroise-François Germain. Outside of her work, her life was to be dominated by the turmoils of the French Revolution – the year she discovered her love of numbers the Bastille was stormed, and her study of calculus was shadowed by the Reign of Terror. Although her father was financially successful, Sophie’s family were not members of the aristocracy.
Although ladies of Germain’s social background were not actively encouraged to study mathematics, they were expected to have sufficient knowledge of the subject in order to be able to discuss the topic should it arise during polite conversation. To this end a series of textbooks were written to help young women get to grips with the latest developments in mathematics and science. Francesco Algarotti was the author of Sir Isaac Newton’s Philosophy Explain’d for the Use of Ladies. Because Algarotti believed that women were only interested in romance, he attempted to explain Newton’s discoveries through the flirtatious dialogue between a Marquise and her interlocutor. For example, the interlocutor outlines the inverse square law of gravitational attraction, whereupon the Marquise gives her own interpretation on this fundamental law of physics: ‘I cannot help thinking … that this proportion in the squares of the distances of places … is observed even in love. Thus after eight days’ absence love becomes sixty-four times less than it was the first day.’
Not surprisingly this gallant genre of books was not responsible for inspiring Sophie Germain’s interest in mathematics. The event that changed her life occurred one day when she was browsing in her father’s library and chanced upon Jean-Etienne Montucla’s book History of Mathematics. The chapter that caught her imagination was Montucla’s essay on the life of Archimedes. His account of Archimedes’ discoveries was undoubtedly interesting, but what particularly kindled her fascination was the story surrounding his death. Archimedes had spent his life at Syracuse, studying mathematics in relative tranquillity, but when he was in his late seventies the peace was shattered by the invading Roman army. Legend has it that during the invasion Archimedes was so engrossed in the study of a geometric figure in the sand that he failed to respond to the questioning of a Roman soldier. As a result he was speared to death.
Germain concluded that if somebody could be so consumed by a geometric problem that it could lead to their death, then mathematics must be the most captivating subject in the world. She immediately set about teaching herself the basics of number theory and calculus, and soon she was working late into the night, studying the works of Euler and Newton. This sudden interest in such an unfeminine subject worried her parents. A friend of the family, Count Guglielmo Libri-Carrucci dalla Sommaja, told how Sophie’s father confiscated her candles and clothes and removed any heating in order to discourage her from studying. Only a few years later in Britain, the young mathematician Mary Somerville would also have her candles confiscated by her father who maintained that ‘we must put a stop to this, or we shall have Mary in a strait-jacket one of these days’.
In Germain’s case she responded by maintaining a secret cache of candles and wrapping herself in bed-clothes. Libri-Carrucci wrote that the winter nights were so cold that the ink froze in the inkwell but Sophie continued regardless. She was described by some people as shy and awkward, but she was also immensely determined and eventually her parents relented and gave Sophie their blessing. Germain never married and throughout her career her father funded her research. For many years Germain continued to study alone because there were no mathematicians in the family who could introduce her to the latest ideas and her tutors refused to take her seriously.
Then, in 1794, the Ecole Polytechnique opened in Paris. It was founded as an academy of excellence to train mathematicians and scientists for the nation. This would have been an ideal place for Germain to develop her mathematical skills except for the fact that it was an institution reserved only for men. Her natural shyness prevented her from confronting the academy’s governing body, so instead she resorted to covertly studying at the Ecole by assuming the identity of a former student at the academy, Monsieur Antoine-August Le Blanc. The academy’s administration was unaware that the real Monsieur Le Blanc had left Paris and continued to print lecture notes and problems for him. Germain managed to obtain what was intended for Le Blanc and each week she would submit answers to the problems under her new pseudonym. Everything was going to plan until a couple of months later when the supervisor of the course, Joseph-Louis Lagrange, could no longer ignore the brilliance of Monsieur Le Blanc’s answer sheets. Not only were Monsieur Le Blanc’s solutions marvellously ingenious, but they showed a remarkable transformation in a student who had previously been notorious for his abysmal calculations. Lagrange, who was one of the finest mathematicians of the nineteenth century, requested a meeting with the reformed student and Germain was forced to reveal her true identity. Lagrange was astonished and pleased to meet the young woman and became her mentor and friend. At last Sophie Germain had a teacher who could inspire her, and with whom she could be open about her skills and ambitions.
Germain grew in confidence and she moved from solving problems in her coursework to studying unexplored areas of mathematics. Most importantly she became interested in number theory and inevitably she came to hear of Fermat’s Last Theorem. She worked on the problem for several years, eventually reaching the stage where she believed she had made an important breakthrough. She needed to discuss her ideas with a fellow number theorist and decided that she would go straight to the top and consult the greatest number theorist in the world, the German mathematician Carl Friedrich Gauss.
Gauss is acknowledged as being one of the most brilliant mathematicians who has ever lived. While E.T. Bell referred to Fermat as the ‘Prince of Amateurs’, he called Gauss the ‘Prince of Mathematicians’. Germain had first encountered his work through studying his masterpiece Disquisitiones arithmeticae, the most important and wide-ranging treatise since Euclid’s Elements. Gauss’s work influenced every area of mathematics, but strangely enough he never published anything on Fermat’s Last Theorem. In one letter he even displayed contempt for the problem. His friend the German astronomer Heinrich Olbers had written to Gauss encouraging him to compete for a prize which had been offered by the Paris Academy for a solution to Fermat’s challenge: ‘It seems to me, dear Gauss, that you should get busy about this.’ Two weeks later Gauss replied, ‘I am very much obliged for your news concerning the Paris prize. But I confess that Fermat’s Last Theorem as an isolated proposition has very little interest for me, for I could easily lay down a multitude of such propositions, which one could neither prove nor disprove.’ Gauss was entitled to his opinion, but Fermat had clearly stated that a proof existed and even the subsequent failed attempts to find the proof had generated innovative new techniques, such as proof by ‘infinite descent’ and the use of imaginary numbers. Perhaps in the past Gauss had tried and failed to make any impact on the problem, and his response to Olbers was merely a case of intellectual sour grapes. Nonetheless, when he received Germain’s letters he was sufficiently impressed by her breakthrough that he temporarily forgot his ambivalence towards Fermat’s Last Theorem.
Seventy-five years earlier Euler had published his proof for the case n = 3, and ever since mathematicians had been trying in vain to prove other individual cases. However, Germain adopted a new strategy and described to Gauss a so-called general approach to the problem. In other words, her immediate goal was not to prove one particular case, but to say something about many cases at once. In her letter to Gauss she outlined a calculation which focused on a particular type of prime number p such that (2p + 1) is also prime. Germain’s list of primes includes 5, because 11 (2 × 5 + 1) is also prime; but it does not include 13, because 27 (2 × 13 + 1) is not prime.
For values of n equal to these Germain primes, she used an elegant argument to show that there were probably no solutions to the equation xn + yn = zn. By ‘probably’ Germain meant that it was unlikely that any solutions existed, because if there was a solution then either x, y or z would be a multiple of n, and this would put a very tight restriction on any solutions. Her colleagues examined her list of primes one by one trying to prove that x, y or z could not be a multiple of n, thereby showing that for that particular value of n there could be no solutions.
In 1825 her method claimed its first complete success thanks to Gustav Lejeune-Dirichlet and Adrien-Marie Legendre, two mathematicians a generation apart. Legendre was a man in his seventies who had lived through the political turmoil of the French Revolution. His failure to support the government candidate for the Institut National led to the stopping of his pension, and by the time he made his contribution to Fermat’s Last Theorem he was destitute. On the other hand, Dirichlet was an ambitious young number theorist who had only just turned twenty. Both of them independently were able to prove that the case n = 5 has no solutions, but they based their proofs on, and owed their success to, Sophie Germain.
Fourteen years later the French made another breakthrough. Gabriel Lamé made some further ingenious additions to Germain’s method and proved the case for the prime n = 7. Germain had shown numbers theorists how to destroy an entire section of prime cases and now it was up to the combined efforts of her colleagues to continue proving Fermat’s Last Theorem one case at a time.
Germain’s work on Fermat’s Last Theorem was to be her greatest contribution to mathematics but initially she was not credited for her breakthrough. When Germain wrote to Gauss she was still in her twenties, and although she had gained a reputation in Paris she feared that the great man would not take her seriously because of her gender. In order to protect herself Germain resorted once again to her pseudonym, signing her letters as Monsieur Le Blanc.
Her fear and respect for Gauss is shown in one of her letters to him: ‘Unfortunately, the depth of my intellect does not equal the voracity of my appetite, and I feel a kind of temerity in troubling a man of genius when I have no other claim to his attention than an admiration necessarily shared by all his readers.’ Gauss, unaware of his correspondent’s true identity, attempted to put Germain at ease and replied: ‘I am delighted that arithmetic has found in you so able a friend.’
Germain’s contribution may have been forever wrongly attributed to the mysterious Monsieur Le Blanc were it not for the Emperor Napoleon. In 1806 Napoleon was invading Prussia and the French army was storming through one German city after another. Germain feared that the fate that befell Archimedes might also take the life of her other great hero Gauss, so she sent a message to her friend General Joseph-Marie Pernety, who was in charge of the advancing forces. She asked him to guarantee Gauss’s safety, and as a result the general took special care of the German mathematician, explaining to him that he owed his life to Mademoiselle Germain. Gauss was grateful but surprised, for he had never heard of Sophie Germain.
The game was up. In Germain’s next letter to Gauss she reluctantly revealed her true identity. Far from being angry at the deception, Gauss wrote back to her with delight:
But how to describe to you my admiration and astonishment at seeing my esteemed correspondent Monsieur Le Blanc metamorphose himself into this illustrious personage who gives such a brilliant example of what I would find it difficult to believe. A taste for the abstract sciences in general and above all the mysteries of numbers is excessively rare: one is not astonished at it: the enchanting charms of this sublime science reveal themselves only to those who have the courage to go deeply into it. But when a person of the sex which, according to our customs and prejudices, must encounter infinitely more difficulties than men to familiarise herself with these thorny researches, succeeds nevertheless in surmounting these obstacles and penetrating the most obscure parts of them, then without doubt she must have the noblest courage, quite extraordinary talents and superior genius. Indeed nothing could prove to me in so flattering and less equivocal manner that the attractions of this science, which has enriched my life with so many joys, are not chimerical, as the predilection with which you have honoured it.
Sophie Germain’s correspondence with Carl Gauss inspired much of her work, but in 1808 the relationship ended abruptly. Gauss had been appointed professor of astronomy at the University of Göttingen, his interest shifted from number theory to more applied mathematics, and he no longer bothered to return Germain’s letters. Without her mentor her confidence began to wane, and within a year she abandoned pure mathematics.
Although she made no further contributions to proving Fermat’s Last Theorem, she did embark on an eventful career as a physicist, a discipline in which she would again excel only to be confronted by the prejudices of the establishment. Her most important contribution to the subject was ‘Memoir on the vibrations of elastic plates’, a brilliantly insightful paper which laid the foundations for the modern theory of elasticity. As a result of this research and her work on Fermat’s Last Theorem she received a medal from the Institut de France, and became the first woman who was not a wife of a member to attend lectures at the Academy of Sciences. Then towards the end of her life she re-established her relationship with Carl Gauss, who convinced the University of Göttingen to award her an honorary degree. Tragically, before the university could bestow the honour upon her, Sophie Germain died of breast cancer.
All things considered she was probably the most profoundly intellectual woman that France has ever produced. And yet, strange as it may seem, when the state official came to make out the death certificate of this eminent associate and co-worker of the most illustrious members of the French Academy of Science, he designated her as a rentière-annuitant (a single woman with no profession) – not as a mathématicienne. Nor is this all. When the Eiffel Tower was erected, in which the engineers were obliged to give special attention to the elasticity of the materials used, there were inscribed on this lofty structure the names of seventy-two savants. But one will not find in this list the name of that daughter of genius, whose researches contributed so much towards establishing the theory of the elasticity of metals – Sophie Germain. Was she excluded from this list for the same reason that Agnesi was ineligible for membership in the French Academy – because she was a woman? It would seem so. If such, indeed, was the case, more is the shame for those who were responsible for such ingratitude towards one who had deserved so well of science, and who by her achievements had won an enviable place in the hall of fame.
H.J. Mozans, 1913
After the breakthrough of Sophie Germain the French Academy of Sciences offered a series of prizes, including a gold medal and 3,000 Francs to the mathematician who could finally put to rest the mystery of Fermat’s Last Theorem. As well as the prestige of proving Fermat’s Last Theorem there was now an immensely valuable reward attached to the challenge. The salons of Paris were full of rumours as to who was adopting which strategy and how close they were to announcing a result. Then, on 1 March 1847, the Academy held its most dramatic meeting ever.
The proceedings describe how Gabriel Lamé, who had proved the case n = 7 some years earlier, took the podium in front of the most eminent mathematicians of the age and proclaimed that he was on the verge of proving Fermat’s Last Theorem. He admitted that his proof was still incomplete, but he outlined his method and predicted with relish that he would in the coming weeks publish a complete proof in the Academy’s journal.
The entire audience was stunned, but as soon as Lamé left the floor Augustin Louis Cauchy, another of Paris’s finest mathematicians, asked for permission to speak. Cauchy announced to the Academy that he had been working along similar lines to Lamé, and that he too was about to publish a complete proof.
Both Cauchy and Lamé realised that time was of the essence. Whoever would be first to submit a complete proof would receive the most prestigious and valuable prize in mathematics. Although neither of them had a complete proof, the two rivals were keen to somehow stake a claim and so just three weeks after they had made their announcements they deposited sealed envelopes at the Academy. This was a common practice at the time which enabled mathematicians to go on record without revealing the exact details of their work. If a dispute should later arise regarding the originality of ideas, then a sealed envelope would provide the evidence needed to establish priority.
The anticipation built up throughout April as Cauchy and Lamé published tantalising but vague details of their proof in the proceedings of the Academy. Although the entire mathematical community was desperate to see the proof completed, many of them secretly hoped that it would be Lamé and not Cauchy who would win the race. By all accounts Cauchy was a self-righteous creature, a religious bigot and extremely unpopular with his colleagues. He was only tolerated at the Academy because of his brilliance.
Then, on 24 May, an announcement was made which put an end to the speculation. It was neither Cauchy nor Lamé who addressed the Academy but rather Joseph Liouville. Liouville shocked the entire audience by reading out the contents of a letter from the German mathematician Ernst Kummer.
Kummer was a number theorist of the highest order, but for much of his career a fierce patriotism fired by a hatred of Napoleon deflected him from his true calling. When Kummer was an infant the French army invaded his home town of Sorau, bringing with them an epidemic of typhus. Kummer’s father was the town physician and within weeks he was taken by the disease. Traumatised by the experience Kummer swore to do his utmost to defend his country from further attack, and as soon as he left university he applied his intellect to the problem of plotting the trajectories of cannon-balls. Ultimately he taught the laws of ballistics at Berlin’s war college.
In parallel with his military career Kummer actively pursued pure mathematical research and had been fully aware of the ongoing saga at the French Academy. He had read through the proceedings and analysed the few details that Cauchy and Lamé had dared to reveal. To Kummer it was obvious that the two Frenchmen were heading towards the same logical dead end, and he outlined his reasons in the letter which he sent to Liouville.
According to Kummer the fundamental problem was that the proofs of both Cauchy and Lamé relied on using a property of numbers known as unique factorisation. Unique factorisation states that there is only one possible combination of primes which will multiply together to give any particular number. For instance, the only combination of primes which will build the number 18 is as follows:
![]()
Similarly, the following numbers are uniquely factorised in the following ways:
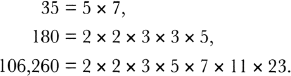
Unique factorisation was discovered back in the fourth century BC by Euclid, who proved that it is true for all counting numbers and described the proof in Book IX of his Elements. The fact that unique factorisation is true for all counting numbers is a vital element in many other proofs and is nowadays called the fundamental theorem of arithmetic.
At first sight there should have been no reason why Cauchy and Lamé should not rely on unique factorisation, as had hundreds of mathematicians before them. Unfortunately both of their proofs involved imaginary numbers. Although unique factorisation is true for real numbers, Kummer pointed out that it might not necessarily hold true when imaginary numbers are introduced. According to him this was a fatal flaw.
For example, if we restrict ourselves to real numbers then the number 12 can only be factorised into 2 × 2 × 3. However, if we allow imaginary numbers into our proof then 12 can also be factorised in the following way:
![]()
Here (1 + √–11) is a complex number, a combination of a real and an imaginary number. Although the process of multiplication is more convoluted than for ordinary numbers, the existence of complex numbers does lead to additional ways to factorise 12. Another way to factorise 12 is (2 + √–8) × (2 – √–8). There is no longer a unique factorisation but rather a choice of factorisations.
This loss of unique factorisation severely damaged the proofs of Cauchy and Lamé, but it did not necessarily destroy them completely. The proofs were supposed to show that there were no solutions to the equation xn + yn = zn, where n represents any number greater than 2. As discussed earlier in this chapter, the proof only had to work for the prime values of n. Kummer showed that by employing extra techniques it was possible to restore unique factorisation for various values of n. For example, the problem of unique factorisation could be circumvented for all prime numbers up to and including n = 31. However, the prime number n = 37 could not be dealt with so easily. Among the other primes less than 100, two others, n = 59 and 67, were also awkward cases. These so-called irregular primes, which are sprinkled throughout the remaining prime numbers, were now the stumbling block to a complete proof.
Kummer pointed out that there was no known mathematics which could tackle all these irregular primes in one fell swoop. However, he did believe that, by carefully tailoring techniques to each individual irregular prime, they could be dealt with one by one. Developing these customised techniques would be a slow and painful exercise, and worse still the number of irregular primes is still infinite. Disposing of them individually would occupy the world’s community of mathematicians until the end of time.
Kummer’s letter had a devastating effect on Lamé. With hindsight the assumption of unique factorisation was at best over-optimistic and at worst foolhardy. Lamé realised that had he been more open about his work he might have spotted the error sooner, and he wrote to his colleague Dirichlet in Berlin: ‘If only you had been in Paris, or I had been in Berlin, all of this would not have happened.’
While Lamé felt humiliated, Cauchy refused to accept defeat. He felt that compared to Lamé’s proof his own approach was less reliant on unique factorisation, and until Kummer’s analysis had been fully checked there was the possibility that it was flawed. For several weeks he continued to publish articles on the subject, but by the end of the summer he too fell silent.
Kummer had demonstrated that a complete proof of Fermat’s Last Theorem was beyond the current mathematical approaches. It was a brilliant piece of mathematical logic, but a massive blow to an entire generation of mathematicians who had hoped that they might solve the world’s hardest mathematical problem.
The situation was summarised by Cauchy, who in 1857 wrote the Academy’s closing report on their prize for Fermat’s Last Theorem:
Report on the competition for the Grand Prize in mathematical sciences. Already set in the competition for 1853 and prorogued to 1856.
Eleven memoirs have been presented to the secretary. But none has solved the proposed question. Thus, after many times being put forward for a prize, the question remains at the point where Monsieur Kummer left it. However, the mathematical sciences should congratulate themselves for the works which were undertaken by the geometers, with their desire to solve the question, specially by Monsieur Kummer; and the Commissaries think that the Academy would make an honorable and useful decision if, by withdrawing the question from the competition, it would adjugate the medal to Monsieur Kummer, for his beautiful researches on the complex numbers composed of roots of unity and integers.
For over two centuries every attempt to rediscover the proof of Fermat’s Last Theorem had ended in failure. Throughout his teenage years Andrew Wiles had studied the work of Euler, Germain, Cauchy, Lamé and finally Kummer. He hoped he could learn by their mistakes, but by the time he was an undergraduate at the University of Oxford he confronted the same brick wall that faced Kummer.
Some of Wiles’s contemporaries were beginning to suspect that the problem might be impossible. Perhaps Fermat had deceived himself and therefore the reason why nobody had rediscovered Fermat’s proof was that no such proof existed. Despite this scepticism Wiles continued to search for a proof. He was inspired by the knowledge that there had been several cases in the past of proofs which had eventually been discovered only after centuries of effort. And in some of those cases the flash of insight which solved the problem did not rely on new mathematics; rather it was a proof which could have been done long ago.

Figure 11. In these diagrams every dot is connected to every other dot by straight lines. Is it possible to construct a diagram such that every line has at least three dots on it?
One example of a problem which evaded solution for decades is the dot conjecture. The challenge involves a series of dots which are all connected to each other by straight lines, such as the dot diagrams shown in Figure 11. The conjecture claims that it is impossible to draw a dot diagram such that every line has at least three dots on it (excluding the diagram where all the dots are on the same line). Certainly by experimenting with a few diagrams this appears to be true. For example, Figure 11(a) has five dots connected by six lines. Four of the lines do not have three dots on them and so clearly this arrangement does not satisfy the requirement that all lines have three dots. By adding an extra dot and the associated line, as in Figure 11(b), the number of lines which do not have three dots is reduced to just three. However, trying to adapt the diagram further so that all the lines have three dots appears to be impossible. Of course, this does not prove that no such diagram exists.
Generations of mathematicians tried and failed to find a proof of the apparently straightforward dot conjecture. What made the conjecture even more infuriating was that when a proof was eventually discovered, it involved only a minimal amount of mathematical knowledge mixed with a little extra cunning. The proof is outlined in Appendix 6.
There was a possibility that all the techniques required to prove Fermat’s Last Theorem were available, and that the only missing ingredient was ingenuity. Wiles was not prepared to give up: finding a proof of the Last Theorem had turned from being a childhood fascination in to a fully fledged obsession. Having learnt all there was to learn about the mathematics of the nineteenth century, Wiles decided to arm himself with techniques of the twentieth century.