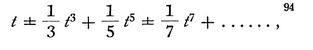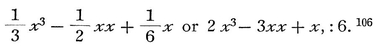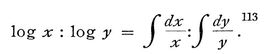III.

“HISTORIA ET ORIGO CALCULI DIFFERENTIALIS.”

§2.

HISTORY AND ORIGIN OF THE DIFFERENTIAL CALCULUS.

It is an extremely useful thing to have knowledge of the true origins of memorable discoveries, especially those that have been found not by accident but by dint of meditation. It is not so much that thereby history may attribute to each man his own discoveries and that others should be encouraged to earn like commendation, as that the art of making discoveries should be extended by considering noteworthy examples of it.

Among the most renowned discoveries of the times must be considered that of a new kind of mathematical analysis, known by the name of the differential calculus; and of this, even if the essentials are at the present time considered to be sufficiently demonstrated, nevertheless the origin and the method of the discovery are not yet known to the world at large. Its author invented it nearly forty years ago, and nine years later (nearly thirty years ago) published it in a concise form; and from that time it has not only been frequently made known in memoirs,43 but also has been a method of general employment; while many splendid discoveries have been made by its assistance, such as have been included in the Acta Eruditorum, Leipsic, and also such as have been published in the memoirs of the Royal Academy of Sciences; so that it would seem that a new aspect has been given to mathematical knowledge arising out of its discovery.

Now there never existed any uncertainty as to the name of the true inventor, until recently, in 1712, certain upstarts, either in ignorance of the literature of the times gone by, or through envy, or with some slight hope of gaining notoriety by the discussion, or lastly from obsequious flattery, have set up a rival to him; and by their praise of this rival, the author has suffered no small disparagement in the matter, for the former has been credited with having known far more than is to be found in the subject under discussion. Moreover, in this they acted with considerable shrewdness, in that they put off starting the dispute until those who knew the circumstances, Huygens, Wallis, Tschirnhaus, and others, on whose testimony they could have been refuted, were all dead.⁴⁴ Indeed this is one good reason why contemporary prescripts should be introduced as a matter of law; for without any fault or deceit on the part of the responsible party, attacks may be deferred until the evidence with which he might be able to safeguard himself against his opponent had ceased to exist. Moreover, they have changed the whole point of the issue, for in their screed, in which under the title of Commercium Epistolicum D. Johannis Collinsii (1712) they have set forth their opinion in such a manner as to give a dubious credit to Leibniz, they have said very little about the calculus; instead, every other page is made up of what they call infinite series. Such things were first given as discoveries by Nicolaus Mercator⁴⁵ of Holstein, who obtained them by the process of division, and Newton gave the more general form by extraction of roots.⁴⁶ This is certainly a useful discovery, for by it arithmetical approximations are reduced to an analytical reckoning; but it has nothing at all to do with the differential calculus. Moreover, even in this they make use of fallacious reasoning; for whenever this rival works out a quadrature by the addition of the parts by which a figure is gradually increased,⁴⁷ at once they hail it as the use of the differential calculus (as for instance on page 15 of the Commercium). By the selfsame argument, Kepler (in his Stereometria Doliorum) ,⁴⁸ Cavalieri, Fermat, Huygens, and Wallis used the differential calculus; and indeed, of those who dealt with “indivisibles” or the “infinitely small,” who did not use it? But Huygens, who as a matter of fact had some knowledge of the method of fluxions as far as they are known and used, had the fairness to acknowledge that a new light was shed upon geometry by this calculus, and that knowledge of things beyond the province of that science was wonderfully advanced by its use.

Now it certainly never entered the mind of any one else before Leibniz to institute the notation peculiar to the new calculus by which the imagination is freed from a perpetual reference to diagrams, as was made by Vieta and Descartes in their ordinary or Apollonian geometry; moreover, the more advanced parts pertaining to Archimedean geometry, and to lines which were called “mechanical” ⁴⁹ by Descartes, were excluded by the latter in his calculus. But now by the calculus of Leibniz the whole of geometry is subjected to analytical computation, and those transcendent lines that Descartes called mechanical are also reduced to equations chosen to suit them, by considering the differences dx, ddx, etc., and the sums that are the inverses of these differences, as functions of the x’s; and this, by merely introducing the calculus, whereas before this no other functions were admissible but x, xx, x³, √x, etc., that is to say, powers and roots.⁵⁰ Hence it is easy to see that those who expressed these differences by 0, as did Fermat, Descartes, and even that rival, in his Principia published in 16—,⁵¹ were by that very fact an extremely long way off from the differential calculus; for in this way neither gradation of the differences nor the differential functions of the several quantities can possibly be made out.

There does not exist anywhere the slightest trace of these methods having been practised by any one before Leibniz.⁵² With precisely the same amount of justice as his opponents display in now assigning such discoveries to Newton, any one could equally well assign the geometry of Descartes to Apollonius, who, although he possessed the essential idea of the calculus, yet did not possess the calculus.

For this reason also the new discoveries that were made by the help of the differential calculus were hidden from the followers of Newton’s method, nor could they produce anything of real value nor even avoid inaccuracies until they learned the calculus of Leibniz, as is found in the investigation of the catenary as made by David Gregory.⁵³ But these contentious persons have dared to misuse the name of the English Royal Society, which body took pains to have it made known that no really definite decision was come to by them; and this is only what is worthy of their reputation for fair dealing, in that one of the two parties was not heard, indeed my friend himself did not know that the Royal Society had undertaken an inquiry into the matter. Else the names of those to whom it had entrusted the report would have been communicated to him,⁵⁴ so that they might either be objected to, or equipped for their task. He indeed, astounded not by their arguments but by the fictions that pervaded their attack on his good faith, considered such things unworthy of a reply, knowing as he did that it would be useless to defend his case before those who were unacquainted with this subject (i. e., the great majority of readers) ; also feeling that those who were skilled in the matter under discussion would readily perceive the injustice of the charge.⁵⁵ To this was added the reason that he was absent from home when these reports were circulated by his opponents, and returning home after an interval of two years and being occupied with other business, it was then too late to find and consult the remains of his own past correspondence from which he might refresh his memory about matters that had happened so long ago as forty years previously. For transcripts of very many of the letters once written by him had not been kept; besides those that Wallis found in England and published with his consent in the third volume of his works, Leibniz himself had not very many.

Nevertheless, he did not lack for friends to look after his fair name; and indeed a certain mathematician, one of the first rank of our time⁵⁶ well skilled in this branch of learning and perfectly unbiased, whose good-will the opposite party had tried in vain to obtain, plainly stated, giving reasons of his own finding, and let it be known, not altogether with strict justice, that he considered that not only had that rival not invented the calculus, but that in addition he did not understand it to any great extent.⁵⁷ Another friend of the inventor⁵⁸ published these and other things as well in a short pamphlet, in order to check their base contentions. However it was of greater service to make known the manner and reasoning by which the discoverer arrived at this new kind of calculus; for this indeed has been unknown up till now, even to those perchance, who would like to share in this discovery. Indeed he himself had decided to explain it, and to give an account of the course of his researches in analysis partly from memory and partly from extant writings and remains of old manuscripts, and in this manner to illustrate in due form in a little book the history of this higher learning and the method of its discovery. But since at the time this was found to be impossible owing to the necessities of other business, he allowed this short statement of part of what there was to tell upon the matter to be published in the meantime by a friend who knew all about it,⁵⁹ so that in some measure public curiosity should be satisfied.

The author of this new analysis, in the first flower of his youth, added to the study of history and jurisprudence other more profound reflections for which he had a natural inclination. Among the latter he took a keen delight in the properties and combinations of numbers; indeed, in 1666 he published an essay, De Arte Combinatoria, afterward reprinted without his sanction. Also, while still a boy, when studying logic he perceived that the ultimate analysis of truths that depended on reasoning reduced to two things, definitions and identical truths, and that these alone of the essentials were primitive and undemonstrable. When it was stated in contradiction that identical truths were useless and nugatory, he gave illustrative proofs to the contrary. Among these he gave a demonstration that that mighty axiom, “The whole is greater than its part,” could be proved by a syllogism of which the major term was a definition and the minor term an identity.⁶⁰ For if one of two things is equal to a part of another the former is called the less, and the later the greater; and this is to be taken as the definition. Now, if to this definition there be added the following identical and undemonstrable axiom, “Every thing possessed of magnitude is equal to itself,” i. e., A = A, then we have the syllogism:

Whatever is equal to a part of another, is less than that other:

(by the definition)

 

But the part is equal to a part of the whole:

(i. e., to itself, by identity)

 

Hence the part is less than the whole.

Q. E. D.

As an immediate consequence of this he observed that from the identity A = A, or at any rate from its equivalent, A − A = 0, as may be seen at a glance by straightforward reduction, the following very pretty property of differences arises, namely:

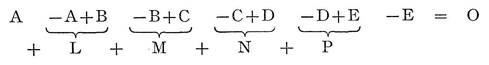
If now A, B, C, D, E are supposed to be quantities that continually increase in magnitude, and the differences between successive terms are denoted by L, M, N, P, it will then follow that

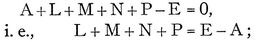
that is, the sums of the differences between successive terms, no matter how great their number, will be equal to the difference between the terms at the beginning and the end of the series.⁶¹ For example, in place of A, B, C, D, E, let us take the squares, 0, 1, 4, 9, 16, 25, and instead of the differences given above, the odd numbers, 1, 3, 5, 7, 9, will be disclosed; thus

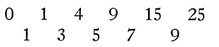
From which is evident that

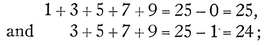
and the same will hold good whatever the number of terms or the differences may be, or whatever numbers are taken as the first and last terms. Delighted by this easy, elegant theorem, our young friend considered a large number of numerical series, and also proceeded to the second differences or differences of the differences,⁶² the third differences or the differences between the differences of the differences, and so on. He also observed that for the natural numbers, i. e., the numbers in order proceeding from 0, the second differences vanished, as also did the third differences for the squares, the fourth differences for the cubes, the fifth for the biquadrates, the sixth for the surdesolids,⁶³ and so on; also that the first differences for the natural numbers were constant and equal to 1; the second differences for the square, 1.2, or 2; the third for the cubes, 1.2.3, or 6; the fourth for the biquadrates, 1.2.3.4, or 24; the fifth for the surdesolids, 1.2.3.4.5, or 120, and so on. These things it is admitted had been previously noted by others, but they were new to him, and by their easiness and elegance were in themselves an inducement to further advances. But especially he considered what he called “combinatory numbers,” such as are usually tabulated as in the margin. Here a preceding series, either horizontal or vertical, always contains the first differences of the series immediately following it, the second differences of the one next after that, the third differences of the third, and so on. Also, each series, either horizontal or vertical contains the sums of the series immediately preceding it, the sums of the sums or the second sums of the series next before that, the third sums of the third, and so on. But, to give something not yet common knowledge, he also brought to light certain general theorems on differences and sums, such as the following. In the series, a, b, c, d, e, etc., where the terms continually decrease without limit we have

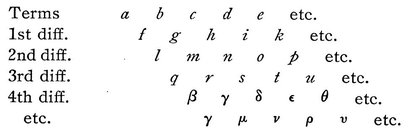
Taking a as the first term, and ω as the last, he found

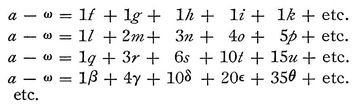
Again we have⁶⁴

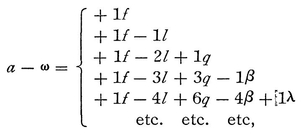
Hence, adopting a notation invented by him at a later date, and denoting any term of the series generally by y (in which case a = y as well), we may call the first difference dy, the second ddy, the third d³y, the fourth d⁴y; and calling any term of another of the series x, we may denote the sum of its terms by f x, the sum of their sums or their second sum by ∫ ∫ x, the third sum by ∫³x, and the fourth sum by ∫⁴x. Hence, supposing that

1 + 1 + 1 + 1 + 1 + etc. = x,

or that x represents the natural numbers, for which dx = 1, then

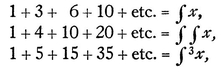
and so on. Finally it follows that

y − ω = dy . x − ddy. ∫x + d³y. ∫ ∫x − d⁴y. ∫³x + etc.;

and this is equal to y, if we suppose that the series is continued to infinity, or that ω becomes zero. Hence also follows the sum of the series itself, and we have

∫ y = yx − dy. ∫x + ddy. ∫ ∫x − d³y. ∫^3x + etc.⁶⁵

These two like theorems possess the uncommon property that they are equally true in either differential calculus, the numerical or the infinitesimal; of the distinction between them we will speak later.⁶⁶

However, the application of numerical truths to geometry, as well as the consideration of infinite series, was at that time at all events unknown to our young friend, and he was content with the satisfaction of having observed such things in series of numbers. Nor did he then, except for the most ordinary practical rules, know anything about geometry;⁶⁷ he had scarcely even considered Euclid with anything like proper attention, being fully occupied with other studies. However, by chance he came across the delightful contemplation of curves by Leotaud, in which the author deals with the quadrature of lunules, and Cavalieri’s geometry of indivisibles;⁶⁸ having given these some slight consideration, he was delighted with the facility of their methods. However, at the time he was in no mind to go fully into these more profound parts of mathematics; although just afterwards he gave attention to the study of physics and practical mechanics, as may be understood from his essay that he published on the Hypothesis of Physics.⁶⁹

He then became a member of the Revision Council⁷⁰ of the Most Noble the Elector of Mainz; later, having obtained permission from this Most Gracious and Puissant Prince (for he had taken our young friend into his personal service when he was about to leave⁷¹ and go further afield) to continue his travels, he set out for Paris in the year 1672. There he became acquainted with that genius, Christiaan Huygens, to whose example and precepts he always declared that he owed his introduction to higher mathematics. At that time it so happened that Huygens was engaged on his work with regard to the pendulum. When Huygens brought our young friend a copy of this work as a present and in the course of conversation discussed the nature of the center of gravity, which our young friend did not know very much about, the former explained to him shortly what sort of thing it was and how it could be investigated. ⁷² This roused our young friend from his lethargy, for he looked upon it as something of a disgrace that he should be ignorant of such matters.⁷³

Now it was impossible for him to find time for such studies just then; for almost immediately, at the close of the year, he crossed the Channel to England in the suite of the envoy from Mainz, and stayed there for a few weeks with the envoy. Having been introduced by Henry Oldenburg, at that time secretary to the Royal Society, he was elected a member of that illustrious body. He did hot however at that time discuss geometry with any one (in truth at that time he was quite one of the common herd as regards this subject) ; he did not on the other hand neglect chemistry, consulting that excellent man, Robert Boyle, on several occasions. He also came across Pell accidentally, and he described to him certain of his own observations on numbers; and Pell told him that they were not new, but that it had been recently made known by Nicolaus Mercator, in his Hyperbolae Quadratura, that the differences of the powers of the natural numbers, when taken continuously, finally vanished; this made Leibniz obtain the work of Nicolaus Mercator.⁷⁴ At that time he did not become acquainted with Collins; and, although he conversed with Oldenburg on literary matters, on physics and mechanics, he did not exchange with him even one little word on higher geomery, much less on the series of Newton. Indeed, that he was almost a stranger to these subjects, except perhaps in the properties of numbers, even that he had not paid very much attention to them, is shown well enough by the letters which he exchanged with Oldenburg, which have been lately published by his opponents. The same fact will appear clearly from those which they say have been preserved in England; but they suppressed them,⁷⁵ I firmly believe, because it would be quite clear from them that up to then there had been no correspondence between him and Oldenburg on matters geometrical. Nevertheless, they would have it credited (not indeed with the slightest evidence brought forward in favor of the supposition) that certain results obtained by Collins, Gregory and Newton, which were in the possession of Oldenburg, were communicated by him to Leibniz.

On his return from England to France in the year 1673,⁷⁶ having meanwhile satisfactorily performed his work for the Most Noble Elector of Mainz, he still by his favor remained in the service of Mainz; but his time being left more free, at the instigation of Huygens he began to work at Cartesian analysis (which aforetime had been beyond him),⁷⁷ and in order to obtain an insight into the geometry of quadratures he consulted the Synopsis Geometriae of Honoratus Fabri, Gregory St. Vincent, and a little book by Dettonville (i. e., Pascal).⁷⁸ Later on from one example given by Dettonville, a light suddenly burst upon him, which strange to say Pascal himself had not perceived in it. For when he proves the theorem of Archimedes for measuring the surface of a sphere or parts of it, he used a method in which the whole surface of the solid formed by a rotation round any axis can be reduced to an equivalent plane figure. From it our young friend made out for himself the following general theorem.⁷⁹

Portions of a straight line normal to a curve, intercepted between the curve and an axis, when taken in order and applied at right angles to the axis give rise to a figure equivalent to the moment of the curve about the axis.⁸⁰

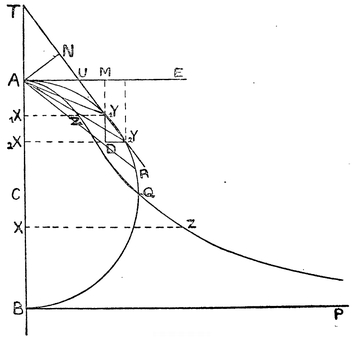
When he showed this to Huygens the latter praised him highly and confessed to him that by the help of this very theorem he had found the surface of parabolic conoids and others of the same sort, stated without proof many years before in his work on the pendulum clock. Our young friend, stimulated by this and pondering on the fertility of this point of view, since previously he had considered infinitely small things such as the intervals between the ordinates in the method of Cavalieri and such only, studied the triangle ₁Y D ₂Y, which he called the Characteristic Triangle,⁸¹ whose sides D₁Y, D₂Y are respectively equal to ₁X ₂X, ₂Z,⁸² parts of the coordinates or coabscissae AX, AZ, and its third side ₁Y ₂Y a part of the tangent TV, produced if necessary.

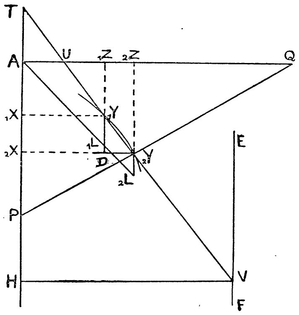
Fig. 3.

Even though this triangle is indefinite (being infinitely small), yet he perceived that it was always possible to find definite triangles similar to it. For, suppose that AXX, AZZ are two straight lines at right angles, and AX, AZ the coabscissae, YX, YZ the coordinates, TUV the tangent, PYQ the perpendicular, XT, ZU the subtangents, XP, ZQ the subnormals ; and lastly let EF be drawn parallel to the axis AX ; let the tangent TY meet EF in V, and from V draw VH perpendicular to the axis. Then the triangles ₁YD ₂Y, TXY, YZU, TAU, YXP, QZY, QAP, THV, and as many more of the sort as you like, are all similar. For example, from the similar triangles ₁YD ₂Y, ₂Y ₂XP, we have P ₂Y.₁YD = ₂Y ₂X.₂Y ₁Y; that is, the rectangle contained by the perpendicular P ₂Y and ₁YD (or the element of the axis, ₁X ₂X) is equal to the rectangle contained by the ordinate ₂Y ₂X and the element of the curve, ₁Y ₂Y, that is, to the moment of the element of the curve about the axis. Hence the whole moment of the curve is obtained by forming the sum of these perpendiculars to the axis.

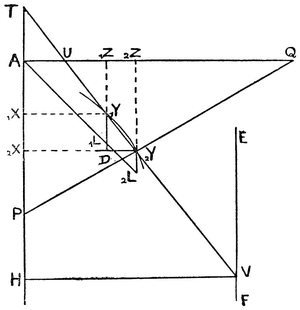
Also, on account of the similar triangles ₁YD ₂Y, THV, we have ₁Y ₂Y :₂YD = TV : VH, or VH.₁Y ₂Y=TV.₂YD; that is, the rectangle contained by the constant length VH and the element of the curve, ₁Y ₂Y, is equal to the rectangle contained by TV and ₂YD, or the element of the coabscissa, ₁Z ₂Z. Hence the plane figure produced by applying the lines TV in order at right angles to AZ is equal to the rectangle contained by the curve when straightened out and the constant length HV.

Again, from the similar triangles ₁YD ₂Y, ₂Y ₂XP, we have ₁YD : D ₂Y = ₂Y ₂X : ₂XP, and thus ₂XP ₁YD = ₂Y ₂X.D ₂Y, or the sum of the subnormals ₂XP, taken in order and applied to the axis, either to ₁YD or to ₁X ₂X, will be equal to the sum of the products of the ordinates ₂Y ₂X and their elements, ₂YD, taken in order. But straight lines that continually increase from zero, when each is multiplied by its element of increase, form altogether a triangle. Let then AZ always be equal to ZL, then we get the right-angled triangle AZL, which is half the square on AZ; and thus the figure that is produced by taking the subnormals in order and applying them perpendicular to the axis will be always equal to half the square on the ordinate. Thus, to find the area of a given figure, another figure is sought such that its subnormals are respectively equal to the ordinates of the given figure, and then this second figure is the quadratrix of the given one; and thus from this extremely elegant consideration we obtain the reduction of the areas of surfaces described by rotation⁸³ to plane quadratures, as well as the rectification of curves; at the same time we can reduce these quadratures of figures to an inverse problem of tangents. From these results,⁸⁴ our young friend wrote down a large collection of theorems (among which in truth there were many that were lacking in elegance) of two kinds. For in some of them only definite magnitudes were dealt with, after the manner not only of Cavalieri, Fermat, Honoratus Fabri, but also of Gregory St. Vincent, Guldinus, and Dettonville; others truly depended on infinitely small magnitudes, and advanced to a much greater extent. But later our young friend did not not trouble to go on with these matters, when he noticed that the same method had been brought into use and perfected by not only Huygens, Wallis, Van Huraet, and Neil, but also by James Gregory and Barrow. However it did not seem to me to be altogether useless to explain at this juncture, as is plain from what I have given,⁸⁵ the steps by which he attained to greater things, and also the manner in which, as if led by the hand, those who are at present but beginners⁸⁶ with regard to the more abstruse parts of geometry may hope to rise to greater heights.

Now Leibniz worked these things out at Paris in the year 1673 and part of 1674. But in the year 1674 (so much it is possible to state definitely), he came upon the well-known arithmetical tetragonism ;⁸⁷ and it will be worth while to explain how this was accomplished. He once happened to have occasion to break up an area into triangles formed by a number of straight lines meeting in a point, and he perceived that something new could be readily obtained from it.⁸⁸

Fig. 4.

In Fig. 4, let any number of straight lines, AY, be drawn to the curve AYR, and let any axis AC be drawn, and AE, a normal or coaxis to it; and let the tangent at Y to the curve cut them in T and U. From A draw AN perpendicular to the tangent; then

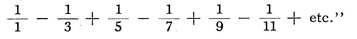
it is plain that the elementary triangle A ₁Y ₂Y is equal to half the rectangle contained by the element of the curve ₁Y ₂Y and AN. Now draw the characteristic triangle mentioned above, ₁YD ₂Y, of which the hypotenuse is a portion of the tangent or the element of the arc, and the sides are parallel to the axis and the coaxis. It is then plain from the similar triangles ANU, ₁YD ₂Y, that ₁Y ₂Y : ₁YD = AU : AN, or AU . ₁YD or AU . ₁X ₂X is equal to AN.₁Y ₂Y, and this, as has been already shown, is equal to double the triangle A₁Y ₂Y. Thus if every AU is supposed to be transferred to XY, and taken in it as AZ,⁸⁹ then the trilinear space AXZA so formed will be equal to twice the segment AY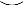A,⁹⁰ included between the straight line AY and the arc AY. In this way are obtained what he called the figures of segments or the proportionals of a segment. A similar method holds good for the case in which the point is not taken on the curve, and in this manner he obtained the proportional trilinear figures for sectors cut off by lines meeting in the point; and even when the straight lines had their extremities not in a line but in a curve (which one after the other they touched), none the less on that account were useful theorems made out.⁹¹ But this is not a fit occasion to follow out such matters; it is sufficient for our purpose to consider the figures of segments, and that too only for the circle. In this case, if the point A is taken at the beginning of the quadrant AYQ, the curve AZQZ will cut the circle at Q, the other end of the quadrant, and thence descending will be asymptotic to the base BP (drawn at right angles to the diameter at its other end B) ; and, although extending to infinity, the whole figure, included between the diameter AB, the base BP...., and the curve AZQZ. . . . asymptotic to it, will be equal to the circle on AB as diameter.

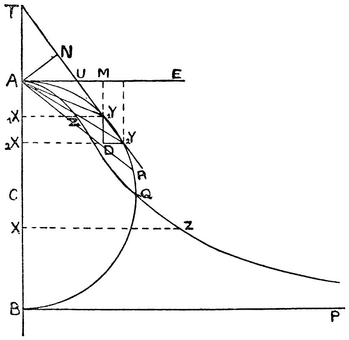
But to come to the matter under discussion, take the radius as unity, put AX or UZ = x, and AU or AZ = z, then we have x = 2zz:, 1 + zz;⁹² and the sum of all the x’s applied to AU, which at the present time we call f x dz, is the trilinear figure AUZA, which is the complement of the trilinear figure AXZA, and this has been shown to be double the circular segment.

The author obtained the same result by the method of transmutations, of which he sent an account to England.⁹³ It is required to form the sum of all the ordinates 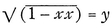; suppose y = ± 1 xz, from which x = 2z:, 1 + zz, and y = ± zz 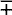1, :, zz + 1; and thus again all that remains to be done is the summation of rationals.

This seemed to him to be a new and elegant method, as it did to Newton also, but it must be acknowledged that it is not of universal application. Moreover it is evident that in this way the arc may be obtained from the sine, and other things of the same kind, but indirectly. So when later he heard that these things had been derived in a direct manner by Newton with the help of root-extractions,⁹⁴ he was desirous of getting a knowledge of the matter.

From the above it was at once apparent that, using the method by which Nicolaus Mercator had given the arithmetical tetragonism of the hyperbola by means of an infinite series, that of the circle might also be given, though not so symmetrically, by dividing by 1 + zz, in the same way that the former had divided by 1 + z. The author, however, soon found a general theorem for the area of any central conic. Namely, the sector included by the arc of a conic section, starting from the vertex, and two straight lines joining its ends to the center, is equal to the rectangle contained by the semi-transverse axis and a straight line of length

⁹⁵

where t is the portion of the tangent at the vertex intercepted between the vertex and the tangent at the other extremity of the arc, and unity is the square on the semi-conjugate axis or the rectangle contained by the halves of the latus-rectum and the transverse axis, and ± is to be taken to mean + for the hyperbola and – for the circle or the ellipse. Hence if the square of the diameter is taken to be unity, then the area of the circle is

When our friend showed this to Huygens, together with a proof of it, the latter praised it very highly, and when he returned the dissertation said, in the letter that accompanied it, that it would be a discovery always to be remembered among mathematicians, and that in it the hope was born that at some time it might be possible that the general solution should be obtained either by exhibiting its true value or by proving the impossibility of expressing it in recognized numbers.⁹⁶ There is no doubt that neither he nor the discoverer, nor yet any one else in Paris, had heard anything at all by report concerning the expression of the area of a circle by means of an infinite series of rationals (such as afterward it became known had been worked out by Newton and Gregory). Certainly Huygens did not, as is evident from the short letter from him that I give herewith.⁹⁷. . . Thus Huygens believed that it was now proved for the first time that the area of a circle was exactly equal to a series of rational quantities. Leibniz (relying on the opinion of Huygens, who was well versed in such matters), believed the same thing and so wrote those two letters to Oldenburg in 1674, which his opponents have published, in which he announces it as a new discovery;⁹⁸ indeed he went so far as to say that he, before all others, had found the magnitude of the circle expressed as a series of rational numbers, as had already been done in the case of the hyperbola.⁹⁹ Now, if Oldenburg had already communicated to him during his stay in London the series of Newton and Gregory,¹⁰⁰ it would have been the height of impudence for him to have dared to write in this way to Oldenburg ; and either forgetfulness or collusion on the part of Oldenburg in not charging him with the deceit. For these opponents publish the reply of Oldenburg, in which he merely points out (he says “I do not wish you to be unaware. . . . ”) that similar series had been noted by Gregory and Newton; and these things also he communicated in the year following in a letter (which they publish) written in the month of April.¹⁰¹ From which it can be seen that they are blinded with envy or shameless with spite who dare to pretend that Oldenburg had already communicated those things to him in the preceding year. Yet there may be some blindness in their spite, because they do not see that they publish things by which their lying statements are refuted, nor that it would have been far better to have suppressed these letters between him and Oldenburg, as they have done in the case of others, either wholly or in part. Besides, from this time onwards he begins to correspond with Oldenburg about geometry; that is, from the time when he, who up till then had been but a beginner in this subject, first found out anything that he considered worthy to be communicated; and former letters written from Paris on March 30, April 26, May 24, and June 8, in the year 1673, which they say they have at hand but suppress, together with the replies of Oldenburg, must undoubtedly have dealt with other matters and have nothing in them to render those fictitious communications from Oldenburg the more deserving of belief. Again, when our young friend heard that Newton and Gregory had discovered their series by the extraction of roots,¹⁰² he acknowledged that this was new to him, nor at first did he understand it very much; and he confessed as much quite frankly and asked for information on certain points, especially for the case in which reciprocal series were sought, by means of which from one infinite series the root was extracted by means of another infinite series. And from this also it is evident that what his opponents assert, that Oldenburg communicated the writings of Newton to him, is false; for if that were the truth, there would have been no need to ask for further information. On the other hand, when he began to develop his differential calculus, he was convinced that the new method was much more universal for finding infinite series without root-extractions, and adapted not only for ordinary quantities but for transcendent quantities as well, by assuming that the series required was given; and he used this method to complete his short essay on the arithmetical quadrature; in this he also included other series that he had discovered, such as an expression for the arc in terms of the sine or the complement of the sine, and conversely he showed how, by this same method, to find the sine or cosine when the arc was given.¹⁰³ This too is the reason why later he stood in no need of other methods than his own; and finally, he published his own new way of obtaining series in the Acta Eruditorum. Moreover, as it was at this time, just after he had published the essay on the Arithmetical Quadrature in Paris, that he was recalled to Germany, having perfected the technique of the new calculus he paid less attention to the former methods.

 

Now it is to be shown how, little by little, our friend arrived at the new kind of notation that he called the differential calculus. In the year 1672, while conversing with Huygens on the properties of numbers, the latter propounded to him this problem :¹⁰⁴

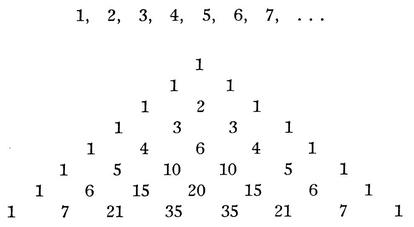
To find the sum of a decreasing series of fractions, of which the numerators are all unity and the denominators are the triangular numbers; of which he said that he had found the sum among the contributions of Hudde on the estimation of probability. Leibniz found the sum to be 2, which agreed with that given by Huygens. While doing this he found the sums of a number of arithmetical series of the same kind in which the numbers are any combinatory numbers whatever, and communicated the results to Oldenburg in February 1673, as his opponents have stated. When later he saw the Arithmetical Triangle of Pascal, he formed on the same plan his own Harmonic Triangle.¹⁰⁵

Arithmetical Triangle

in which the fundamental series is an arithmetical progression

Harmonic Triangle

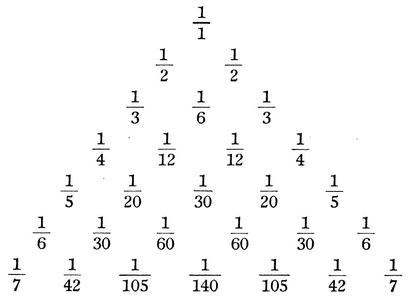
in which the fundamental series is a harmonical progression ; where, if the denominators of any series descending obliquely to infinity or of any parallel finite series, are each divided by the term that corresponds in the first series, the combinatory numbers are produced, namely those that are contained in the arithmetical triangle. Moreover this property is common to either triangle, namely, that the oblique series are the sum- and difference-series of one another. In the Arithmetical Triangle any given series is the sum-series of the series that immediately precedes it, and the difference-series of the one that follows it; in the Harmonic Triangle, on the other hand, each series is the sum-series of the series following it, and the difference-series of the series that precedes it. From which it follows that

and so on.

Now he had found out these things before he had turned to Cartesian analysis; but when he had had his thoughts directed to this, he considered that any term of a series could in most cases be denoted by some general notation, by which it might be referred to some simple series. For instance, if the general term of the series of natural numbers is denoted by x, then the general term of the series of squares would be x², that of the cubes would be x³, and so on. Any triangular number, such as 0, 1, 3, 6, 10, would be

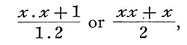
any pyramidal number, such as 0, 1, 4, 10, 20, etc., would be

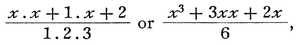
and so on.

From this it was possible to obtain the difference-series of a given series, and in some cases its sum as well, when it was expressed numerically. For instance, the square is xx, the next greater square is xx+2x+1, and the difference of these is 2x+1; i. e., the series of odd numbers is the difference-series for the series of squares. For, if x is 0, 1, 2, 3, 4, etc., then 2x+1 is 1, 3, 5, 7, 9. In the same way the difference between x³ and x³ + 3xx + 3x + 1 is 3xx + 3x+ 1, and thus the latter is the general term of the difference-series for the series of cubes. Further, if the value of the general term can thus be expressed by means of a variable x so that the variable does not enter into a denominator or an exponent, he perceived that he could always find the sum-series of the given series. For instance, to find the sum of the squares, since it is plain that the variable cannot be raised to a higher degree than the cube, he supposed its general term z to be

z = lx³ + mxx + nx, where dz has to be xx;

we have dz = l d(x³) + m d (xx) + n, (where dx is taken = 1) ; now d(x³) = 3xx + 3x + 1, and d(xx) = 2x + 1, as already found; hence

dz = 3lxx + 3lx + l + 2mx + m + n xx;¹⁰⁶

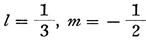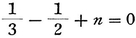therefore , and , or 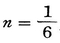; and the general term of the sum-series for the squares is

¹⁰⁷

As an example, if it is desired to find the sum of the first nine or ten squares, i. e., from 1 to 81 or from 1 to 100, take for x the values 10 or 11, the numbers next greater than the root of the last square, and 2x² − 3xx + x,:6 will be 2000 − 300 + 10, : 6 = 285, or 2.1331-3.121+11,: 6= 385. Nor is it much more difficult with this formula to sum the first 100 or 1000 squares. The same method holds good for any powers of the natural numbers or for expressions which are made up from such powers, so that it is always possible to sum as many terms as we please of such series by a formula. But our friend saw that it was not always easy to proceed in the same way when the variable entered into the denominator, as it was not always possible to find the sum of a numerical series; however, on following up this same analytical method, he found in general, and published the result in the Acta Eruditorum, that a sum-series could always be found, or the matter be reduced to finding the sum of a number of fractional terms such as 1/x, 1/xx, 1/x³, etc, which at any rate, if the number of terms taken is finite, can be summed, though hardly in a short way (as by a formula) ; but if it is a question of an infinite number of terms, then terms such as 1/x cannot be summed at all, because the total of an infinite number of terms of such a series is an infinite quantity, but that of an infinite number of terms such as 1/xx, 1/x³, etc., make a finite quantity, which nevertheless could not up till now be summed, except by taking quadratures. So, in the year 1682, in the month of February, he noted in the Acta Eruditorum that if the numbers 1.3, 3.5, 5.7, 7.9, 9.11, etc., or 3, 15, 35, 63, 99, etc., are taken, and from them is formed the series of fractions

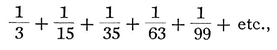
then the sum of this series continued to infinity is nothing else but ½; while, if every other fraction is left out, 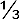+ + 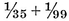etc. expresses the magnitude of a semicircle of which the square on the diameter is represented by 1.¹⁰⁸

Thus, suppose x = 1, 2, 3, etc.¹⁰⁹ Then the general term of

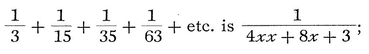
it is required to find the general term of the sum-series.

Let us try whether it can have the form e/(bx+c), the reasoning being very simple; then we shall have

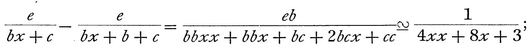
hence, equating coefficients in these two formulas, we have

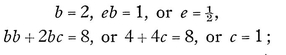
and finally we should have also bc + cc = 3, which is the case. Hence the general term of the sum-series is (1:2)/(2x+1) or 1/(4x+2), and these numbers of the form 4x+2 are the doubles of the odd numbers. Finally he gave a method for applying the differential calculus to numerical series when the variable entered into the exponent, as in a geometrical progression, where, taking any radix b the term is b^x, where x stands for a natural number. The terms of the differential series will be b^x+1 − b^x, or b^x(b − 1); and from this it is plain that the differential series of the given geometrical series is also a geometrical series proportional to the given series. Thus the sum of a geometrical series may be obtained.

But our young friend quickly observed that the differential calculus could be employed with diagrams in an even more wonderfully simple manner than it was with numbers, because with diagrams the differences were not comparable with the things which differed; and as often as they were connected together by addition or subtraction, being incomparable with one another, the less vanished in comparison with the greater; and thus irrationals could be differentiated no less easily than surds, and also, by the aid of logarithms, so could exponentials. Moreover, he observed that the infinitely small lines occurring in diagrams were nothing else but the momentaneous differences of the variable lines. Also, in the same way as quantities hitherto considered by analytical mathematicians had their functions such as powers and roots, so also such quantities as were variable had new functions, namely, differences. Also, that as hitherto we had x, xx, x³, etc., y, yy, y³, etc., so now it was possible to have dx, ddx, d³x, etc., dy, ddy, d³y, and so forth. In the same way, that it was possible to express curves, which Descartes had excluded as being “mechanical,” by equations of position, and to apply the calculus to them and thus to free the mind from a perpetual reference to diagrams. In the applications of the differential calculus to geometry, differentiations of the first degree were equivalent to nothing else but the finding of tangents, differentiations of the second degree to the finding of osculating circles (the use of which was-introduced by our friend) ; and that it was possible to go on in the same fashion. Nor were these things only of service for tangents and quadratures, but for all kinds of problems and theorems in whch the differences were intermingled with integral terms (as that brilliant mathematician Bernoulli called them), such as are used in physico-mechanical problems.

Thus it follows generally that if any series of numbers or lines of a figure have a property that depends on two, three or more consecutive terms, it can be expressed by an equation involving differences of the first, second, third, or higher degree. Moreover, he discovered general theorems for any degree of the differences, just as we have had theorems of any degree, and he made out the remarkable analogy between powers and differences published in the Miscellania Berolinensia.

If his rival had known of these matters, he would not have used dots to denote the degrees of the differences,¹¹⁰ which are useless for expressing the general degree of the differences, but would have used the symbol d given by our friend or something similar, for then d^e can express the degree of the difference in general. Besides everything which was once referred to figures, can now be expressed by the calculus.

For 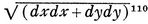¹¹¹ is the element of the arc of a curve, ydx is the element of its area; and from that it is immediately evident that ∫y dx and ∫x dy are the complements of one another, since d(xy) = x dy + y dx, or conversely, xy = ∫x dy+ ∫y dx, however these figures vary from time to time; and from this, since xyz = ∫xy dz + ∫xz dy + ∫yz dx, three solids are also given that are complementary, every two to the third. Nor is there any need for him to have known those theorems which we deduced above from the characteristic triangle; for example, the moment of a curve about the axis is sufficiently expressed by 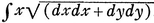. Also what Gregory St. Vincent has concerning ductus, what he or

Fig. 5.

Pascal had concerning ungulae and cunei,¹¹² every one of these is immediately deduced from a calculus such as this. Thus Leibniz saw with delight those discoveries that he had applauded in others obtained by himself, and thereupon he left off studying them at all closely, because all of them were contained in a calculus such as his.

For example, the moment of the figure AXYA (Fig. 5) about the axis is 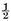∫ yy dx, the moment of the figure about the tangent at the vertex is ∫ xy dx, the moment of the complementary trilinear figure AZYA about the tangent at the vertex is 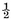∫ xx dy. Now these two last moments taken together yield the moment of the circumscribed rectangle AXYZ about the tangent at the vertex, and are complementary to one another.

However, the calculus also shows this without reference to any figure, for 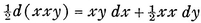; so that now there is need for no greater number of the fine theorems of celebrated men for Archimedean geometry, than at most those given by Euclid in his Book II or elsewhere, for ordinary geometry.

It was good to find that thereafter the calculus of transcendent quantities should reduce to ordinary quantities, and Huygens¹¹³ was especially pleased with this. Thus, if it is found that

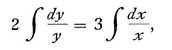
then from this we get yy = x³, and this too from the nature of logarithms combined with the differential calculus, the former also being derived from the same calculus. For let x^m = y, then mx^m—1 dx = dy. Hence, dividing each side by equal things, we have

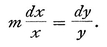
Again, from the equation, m log x = log y, we have

¹¹⁴

By this the exponential calculus is rendered practicable as well. For let y^x = z, then x log y = log z, dx log y + x dy : y = dz : z.

In this way we free the exponents from the variable, or at other times we may transpose the variable exponent with advantage under the circumstances. Lastly, those things that were once held in high esteem are thus made a mere child’s-play.

Now of all this calculus not the slightest trace existed in all the writings of his rival before the principles of the calculus were published by our friend ;¹¹⁵ nor indeed anything at all that Huygens or Barrow had not accomplished in the same way, in the cases where they dealt with the same problems.

But how great was the extent of the assistance afforded by the use of this calculus was candidly acknowledged by Huygens ; and this his opponents suppress as much as ever they can, and straightway go on with other matters, not mentioning the real differential calculus in the whole of their report. Instead, they adhere to a large extent to infinite series, the method for which no one denies that his rival brought out in advance of all others. For those things which he said enigmatically, and explained at a much later date, are all they talk about, namely, fluxions and fluents, i. e., finite quantities and their infinitely small elements; but as to how one can be derived from the other they offer not the slightest suggestion. Moreover, while he considers nascent or evanescent ratios, leading straight away from the differential calculus to the method of exhaustions, which is widely different from it (although it certainly also has its own uses), he proceeds not by means of the infinitely small, but by ordinary quantities, though these latter do finally become the former.

Since therefore his opponents, neither from the Commercium Epistolicum that they have published, nor from any other source, brought forward the slightest bit of evidence whereby it might be established that his rival used the differential calculus before it was published by our friend; therefore all the accusations that were brought against him by these persons may be treated with contempt as beside the question. They have used the dodge of the pettifogging advocate¹¹⁶ to divert the attention of the judges from the matter on trial to other things, namely to infinite series. But even in these they could bring forward nothing that could impugn the honesty of our friend, for he plainly acknowledged the manner in which he had made progress in them; and in truth in these also, he finally attained to something higher and more general.

SUPPLEMENT.

Barrow, Lectiones Geometricae, Lect. XII, Prop. 117^{, 118, 119}.

[Page 105, First Edition, 1670.]

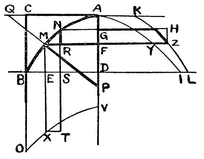
Fig. 6.

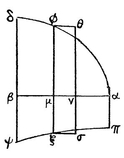
Fig. 7.

General foreword. We will now proceed with the matter in hand; and, in order that we may save time and words, it is to be observed everywhere in what now follows that AB is some curved line, such as we shall draw, of which the axis is AD; to this axis all the straight lines BD, CA, MF, NG are applied perpendicular; the arc MN is indefinitely small; the straight line αβ = arc AB, the straight line αµ = arc AM, and µν = arc MN ; also lines applied to αβ are perpendicular to it. On this understanding:

NOTE. In the above figure, I have “lined in” the part of the diagram (which serves for about ten theorems) especially used for the first two theorems. If this is compared with Leibniz’s figure on p. 15, further comment is needless.