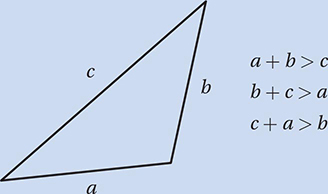
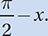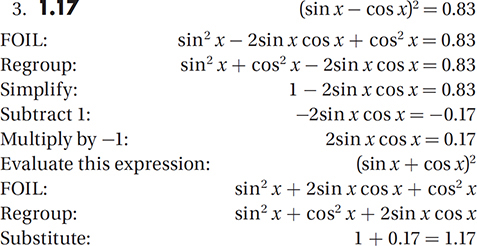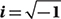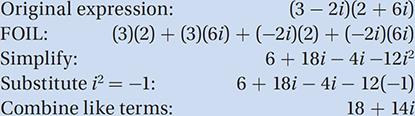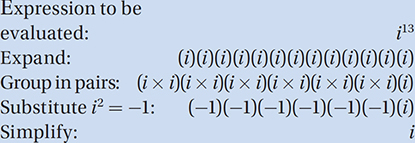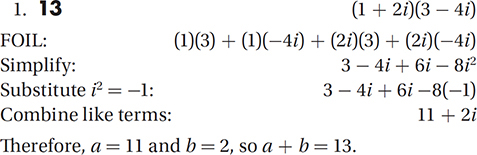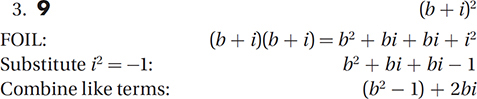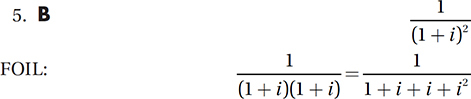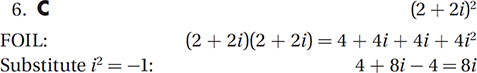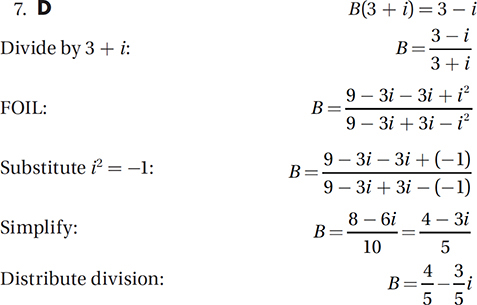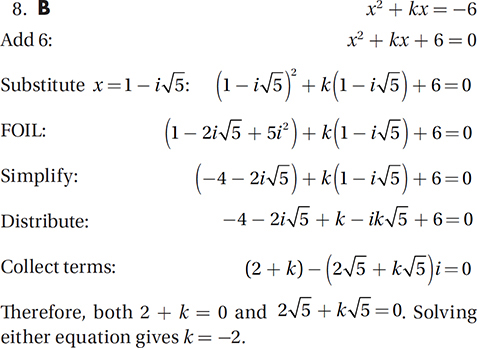CHAPTER 10
1. Understanding Geometric Relationships
2. Understanding Basic Trigonometry
3. Understanding Complex Numbers

The SAT Math: Additional Topics
What other special topics are included on the SAT Math test?
About 10% (6 out of 58 points) of the SAT Math questions are “Additional Topics” questions. These include topics like
• analyzing triangles using the Pythagorean Theorem
• graphing circles and other figures in the xy-plane
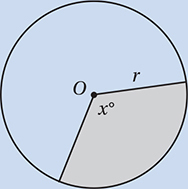
• analyzing areas, circumferences, chords, and sectors of circles
• measuring angles and arcs in radians
• working with area and volume and their formulas
• using the theorems of congruence and similarity
• working with basic trigonometric relationships including cofunction identities
• calculating with imaginary and complex numbers
Why are these topics important?
These topics from geometry, trigonometry, and advanced analysis are crucial to work in engineering, physics, architecture, and even design. Although they are not essential to every college major, they do provide tools for understanding and analyzing advanced concepts across the curriculum.
Sound intimidating? It’s not.
Some of you have already spent some time in math class studying these topics. If not, the three skills described in these 12 lessons will give you the knowledge and practice you need to master them.
Skill 1: Understanding Geometric Relationships
Lesson 1: Intersecting and parallel lines
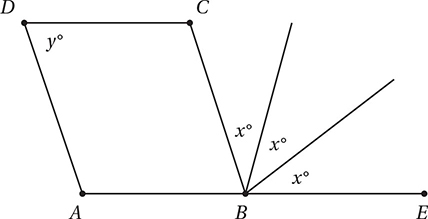
In the figure above, ABCD is a parallelogram, and point B lies on 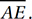 If x = 40, what is the value of y ?
If x = 40, what is the value of y ?
A) 40
B) 50
C) 60
D) 70
(Medium) Since ABCD is a parallelogram, we can take advantage of the Parallel Lines Theorem.
First, let’s mark up the diagram with what we know from the Parallel Lines Theorem.
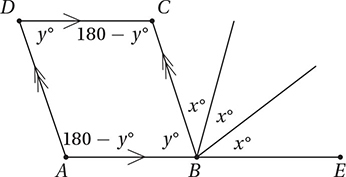
Since the pairs of opposite sides are parallel, the consecutive angles in the parallelogram must be supplementary (that is, have a sum of 180°). Notice that these pairs of consecutive angles form “U”s or “C”s as mentioned in the previous Helpful Tip. This implies that opposite angles are congruent in a parallelogram.
Therefore, the correct answer is (C).
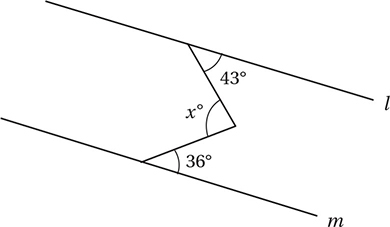
In the figure above, lines l and m are parallel. What is the value of x?
A) 43
B) 79
C) 86
D) 101
(Hard) Although our diagram includes parallel lines, it doesn’t seem to show any of the parallel line “letter pairs” that we discussed above, because no line directly connects the parallel lines. We can fix this problem by drawing an extra line that’s parallel to l and m through the vertex of the angle.
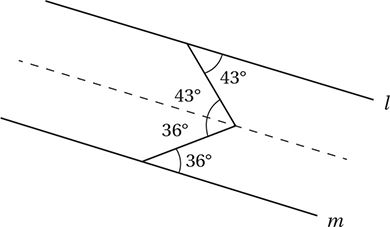
Now we have two “Z” pairs of angles (otherwise known as “alternate interior” pairs) that show that the middle angle is actually the sum of two smaller angles of 36° and 43°, and therefore, x = 36 + 43 = 79, and the correct answer is (B).
Lesson 2: Triangles
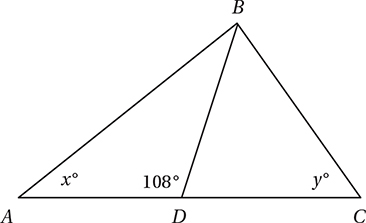
In the figure above, if AD = DB = DC, what is the value of x + y ?
A) 72
B) 90
C) 96
D) 108
(Medium) Since angle ADB and angle BDC are supplementary and AD = DB = DC, we can take advantage of the Isosceles Triangle Theorem to mark up the diagram.
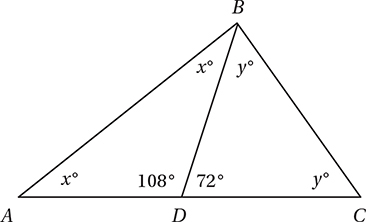
Now let’s look at triangle ABC. Since its interior angles must have a sum of 180°, x + x + y + y = 180, and therefore, 2x + 2y = 180 and x + y = 90. So the correct answer is (B). Notice that this fact is independent of the measures of the other two (108° and 72°) angles. As long as AD = DB = DC, this relationship will hold. We can see these angle relationships if we notice that these three segments could all be radii of a circle centered at D.
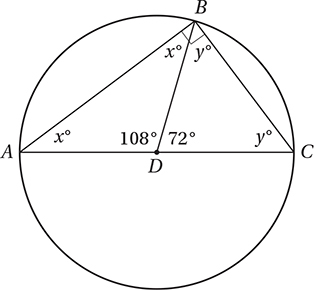
You may remember from studying geometry that any “inscribed” angle (an angle inside a circle with a vertex on the circle) intercepts an arc on the circle that is twice its measure. Since angle ABC is an inscribed angle that intercepts a 180° arc, it must have a measure of 90° and therefore, x + y = 90.
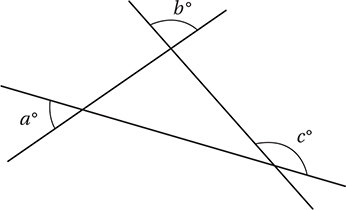
The figure above shows three intersecting lines. What is the value of c in terms of a and b ?
A) 180 – a – b
B) 180 – a + b
C) 90 + b – a
D) a + b
(Easy) First, we should notice that two of the angles are “vertical” to two interior angles of the triangle, and the other is an exterior angle.
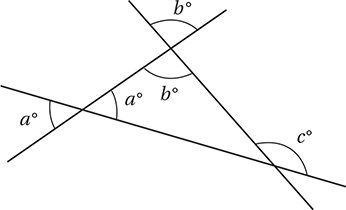
Since the c° angle is an exterior angle to the triangle, the Exterior Angle Theorem tells us that c = a + b, so the correct answer is (D).
Alternately, we could just choose reasonable values for a and b, like a = 50 and b = 90, and then analyze the diagram in terms of these values. This would imply that the interior angles of the triangle are 50°, 90°, and 40°, and c° would then be the measure of the supplement of 40°, which is 140°. If we then plug these values for a and b into all of the choices, the only one that yields 140 is D.
Lesson 3: The xy-plane
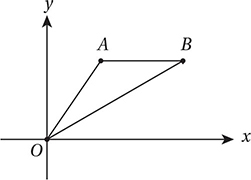
Note: Figure not drawn to scale.
In the xy-plane above, points A and B lie on the graph of the line y = 6. If OB has a slope of  and AB = 5, what is the slope of
and AB = 5, what is the slope of  ?
?

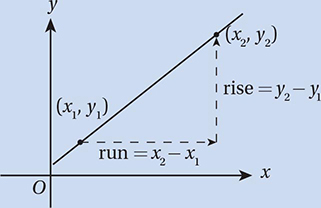
(Medium-hard) To analyze this diagram, we must recall the definition of slope from Chapter 7, Lesson 5.
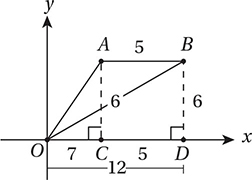
First, let’s drop two perpendicular segments from A and B to points C and D, respectively, on the x-axis. Since A and B lie on the line y = 6, they are both 6 units from the x-axis, and so AC = BD = 6. Then, since the slope of OB is ½, BD/OD = ½, and therefore, OD = 12. Since AB = 5, CD = 5 also, and therefore, OC = 12 – 5 = 7. (Don’t worry that 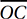 looks shorter than
looks shorter than 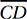 in the diagram. Remember, the figure is not drawn to scale!) This gives us everything we need to find the slope of
in the diagram. Remember, the figure is not drawn to scale!) This gives us everything we need to find the slope of 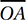 , which connects (0, 0) to (7, 6). By the slope formula from Chapter 7, Lesson 5, slope = (6 – 0)/(7 – 0) = 6/7 = 0.857.
, which connects (0, 0) to (7, 6). By the slope formula from Chapter 7, Lesson 5, slope = (6 – 0)/(7 – 0) = 6/7 = 0.857.
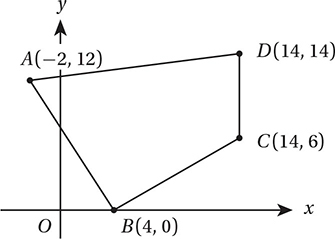
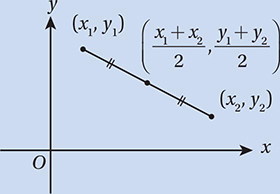
In the figure above, point M (not shown) is the midpoint of  and point N (not shown) is the midpoint of
and point N (not shown) is the midpoint of  What is the slope of
What is the slope of  ?
?

(Medium) To find the midpoint of a segment, we just need to take the average of the endpoints. Point M, the midpoint of 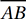 , therefore has coordinates
, therefore has coordinates 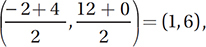 and point N, the midpoint of
and point N, the midpoint of 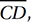 has coordinates
has coordinates 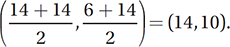 By the Slope Formula, then, the slope of
By the Slope Formula, then, the slope of 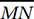 is
is 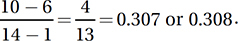
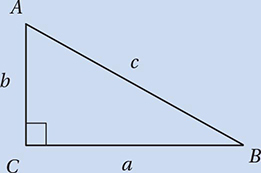
Lesson 4: The Pythagorean Theorem and the Distance Formula
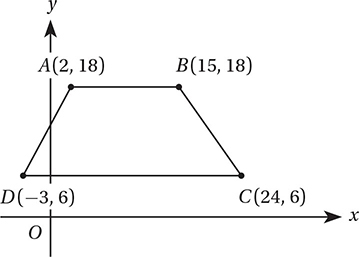
What is the perimeter of quadrilateral ABCD in the figure above?

(Medium) The perimeter of a figure is the distance around its edges. It’s easy to find the lengths of 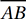 and
and 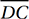 because they are horizontal. The length of a horizontal segment is just the difference between the x-coordinates of its endpoints. The length of
because they are horizontal. The length of a horizontal segment is just the difference between the x-coordinates of its endpoints. The length of 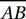 is 15 – 2 = 13, and the length of
is 15 – 2 = 13, and the length of 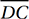 is 24 – (–3) = 27. To find the lengths of
is 24 – (–3) = 27. To find the lengths of 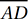 and
and 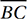 , we can drop two vertical lines from points A and B to the bottom edge. This shows that
, we can drop two vertical lines from points A and B to the bottom edge. This shows that 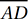 and
and 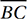 are hypotenuses of two right triangles as shown in the figure below.
are hypotenuses of two right triangles as shown in the figure below.
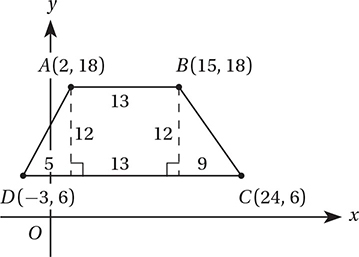
(Take a minute to confirm the lengths of all the segments for yourself.) With this information, we can find AD and BC by the Pythagorean Theorem.
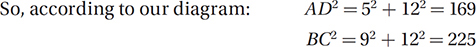
Notice that triangle on the left is a 5-12-13 special right triangle, and the triangle on the right is a 3-4-5 special right triangle. Noticing these relationships provides a shortcut to using the Pythagorean Theorem.

Therefore, the perimeter of ABCD is 13 + 15 + 27 + 13 = 68.
The Distance Formula
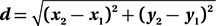
We can generalize the technique we used in the previous problem to find the distance between any two points in the xy-plane. Just think of this distance as the length of the hypotenuse of a right triangle, as in the figure below. In other words, the Pythagorean Theorem and the Distance Formula are one and the same.

The 3-D Distance Formula
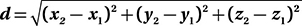
If we need to find the distance between two points in three-dimensional xyz-space, we just need to use a modified version of the distance formula that includes the extra z-dimension. You can see where this formula comes from if you imagine trying to find the length of the longest diagonal through a rectangular box.
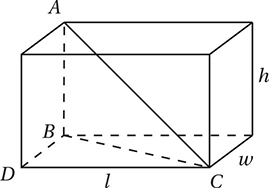
The length of this diagonal, AC, is also the hypotenuse of right triangle ABC, and so its length is given by the Pythagorean Theorem.

Exercise Set 1: Geometry (No Calculator)
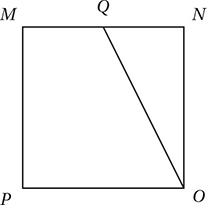
In the figure above, MNOP is a square and Q is the midpoint of  what is the area of square MNOP ?
what is the area of square MNOP ?

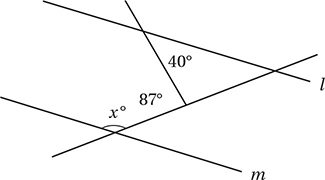

Lines l and m are parallel in the figure above. What is the value of x ?
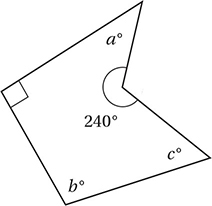

In the figure above, what is the value of a + b + c ?
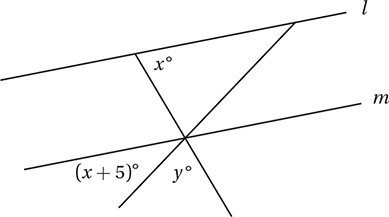
Lines l and m are parallel in the figure above. Which of the following expresses the value of y in terms of x ?
A) 95 – 2x
B) 165 – 2x
C) 175 – 2x
D) 185 – 2x
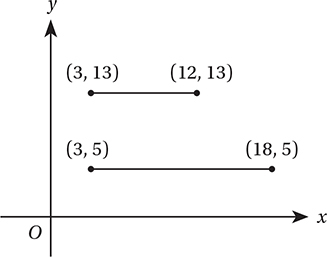
In the figure above, what is the distance between the midpoints (not shown) of the two line segments?
A) 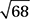
B) 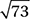
C) 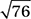
D) 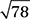
What is the perimeter of an equilateral triangle inscribed in a circle with circumference 24π ?
A) 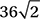
B) 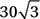
C) 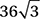
D) 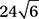
Exercise Set 1: Geometry (Calculator)
Questions 7–9 are based on the figure below.
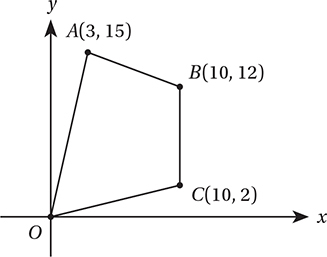
Note: Figure not drawn to scale.
In the figure above, what is the perimeter of quadrilateral ABCO, to the nearest integer?

In the figure above, what is the area, in square units, of ABCO ?

In the figure above, point K (not shown) is the midpoint of 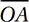 , and point M (not shown) is the midpoint of
, and point M (not shown) is the midpoint of 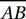 . What is the slope of
. What is the slope of 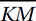 ?
?

In the xy-plane, point H has coordinates (2, 1) and point J has coordinates (11, 13). If 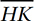 is parallel to the x-axis and
is parallel to the x-axis and 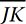 is parallel to the y-axis, what it the perimeter of triangle HJK ?
is parallel to the y-axis, what it the perimeter of triangle HJK ?

Note: Figure not drawn to scale.
In the figure above, what is the value of x ?
A) 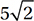
B) 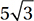
C) 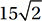
D) 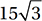

Questions 12–15 are based on the information below.
In the xy-plane, ABCD is a square. Point A has coordinates (–1, 2) and point B has coordinates (3, 5).
Which of the following could be the coordinates of C ?
A) (0, 9)
B) (6, 0)
C) (2, –2)
D) (–4, 6)
What is the area of square ABCD ?
A) 25
B) 28
C) 30
D) 32
What is the slope of 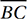 ?
?
A) 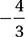
B) 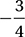
C) 
D) 
What is the distance between C and the midpoint of 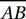 ?
?
A) 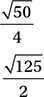
B) 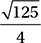
C) 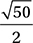
D) 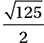
EXERCISE SET 1: GEOMETRY ANSWER KEY
No Calculator
1. 16/9 or 1.77 or 1.78 If we define x as the length of 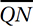 , then the length of one side of the square is 2x, and so the area of square MNOP is (2x)(2x) = 4x2. To find this value, we can apply the Pythagorean Theorem to right triangle QNO:
, then the length of one side of the square is 2x, and so the area of square MNOP is (2x)(2x) = 4x2. To find this value, we can apply the Pythagorean Theorem to right triangle QNO:
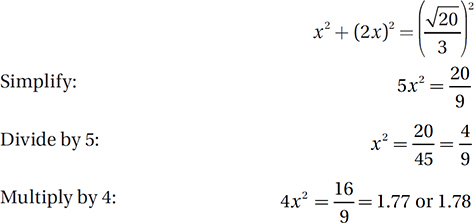
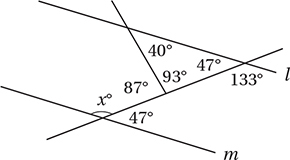
2. 133 The key is to notice simple relationships between angles until we get around to x.
3. 210 Draw three lines as shown:
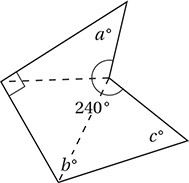
Since the polygon divides into 3 triangles, the sum of its internal angles is (3)(180°) = 540°. Therefore a + b + c + 240 + 90 = 540, and so a + b + c = 210.
4. C Using the Crossed Lines Theorem and the Parallel Lines Theorem, we can mark up the diagram like this:
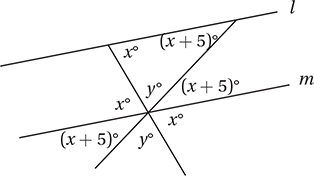
This shows that x + y + x + 5 = 180, and so y = 175 – 2x.
5. B The midpoint of the top segment is  and the midpoint of the bottom segment is
and the midpoint of the bottom segment is 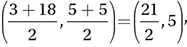 therefore, the distance between them is
therefore, the distance between them is 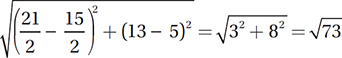
6. C To solve this problem we must draw a diagram and find the relationship between the radius of the circle and the sides of the triangle. By the Isosceles Triangle Theorem, if all three sides of a triangle are congruent, then all three angles must be congruent. Since these angles also must have a sum of 180°, they must each be 60°. If we draw the bisectors of each of these angles, we divide the triangle into six smaller triangles. These smaller triangles are congruent 30°-60°-90 °triangles, as shown here:
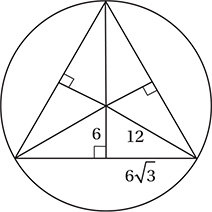
Since the circumference of the circle (2πr) is 24π, its radius is 12. Since each of the hypotenuses of our right triangles is also a radius of the circle, we can find all of the sides of these triangles using the 30°-60°-90° relationships. Each side of the equilateral triangle is therefore 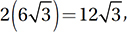 , and its perimeter is therefore
, and its perimeter is therefore 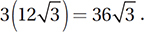
Calculator
7. 43 Using the distance formula, we can calculate the lengths of each segment. 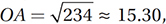
 BC = 10, and
BC = 10, and 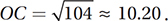 Therefore, the perimeter is approximately 15.30 + 7.61 + 10 + 10.20 = 43.11, which rounds to 43.
Therefore, the perimeter is approximately 15.30 + 7.61 + 10 + 10.20 = 43.11, which rounds to 43.
8. 107 Since we do not have a formula that directly calculates the area of such an odd-shaped quadrilateral, we must analyze its area in terms of simpler shapes. The simplest way to do this is by drawing a box around it. This turns the area of interest into a rectangle minus three right triangles, all of which have areas that can be easily calculated.
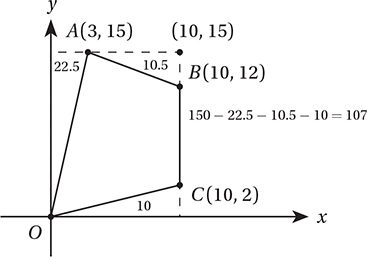
9. 6/5 or 1.2 The midpoint of 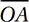 is (1.5, 7.5) and the midpoint of
is (1.5, 7.5) and the midpoint of 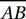 is (6.5, 13.5); therefore, the slope of the segment between them is 6/5.
is (6.5, 13.5); therefore, the slope of the segment between them is 6/5.
10. 36 If point K is on the same horizontal line as (2, 1), it must have a y-coordinate of 1, and if it is on the same vertical line as (11, 13), it must have an x-coordinate of 11. Therefore, K is the point (11, 1), and so HK = 9, JK = 12, and 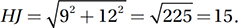 Notice that it is a 3-4-5 triangle!
Notice that it is a 3-4-5 triangle!
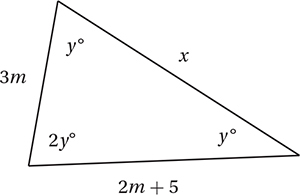
11. C Since the sum of the interior angles of any triangle is 180°, y + y + 2y = 4y = 180, and therefore y = 45. Therefore, this is a 45°-45°-90° right triangle. Since two angles are equal, the two opposite sides must also be equal, so 3m = 2m + 5 and so m = 5 and the two legs each have measure 15. Using the Pythagorean Theorem or the 45°-45°-90 ° shortcut, we can see that 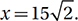
12. A The key to questions 12 through 15 is a good diagram in the xy-plane that represents the given information:
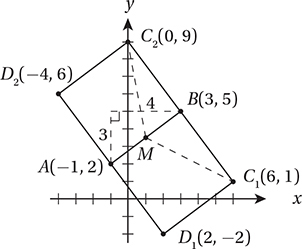
If ABCD is a square, then the points A, B, C, and D must appear in that order around the square. Notice that to get from point A to point B, we must move 4 units to the right and 3 units up. This means that, in order to get to point C along a perpendicular of the same length, we must go either 3 units right and 4 units down, or 3 units left and 4 units up. This puts us either at (6, 1) or (0, 9).
13. A The diagram shows that AB is the length of the hypotenuse of a right triangle with legs 3 and 4. You should recognize this as the special 3-4-5 right triangle. If AB = 5, then the area of the square is 52 = 25.
14. A Notice that the slope of 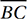 is the same regardless of which option we choose for C. In either case, the slope formula tells us that the slope is –4/3.
is the same regardless of which option we choose for C. In either case, the slope formula tells us that the slope is –4/3.
15. D The midpoint of 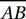 (point M above) is (1, 3.5). We can use the distance formula to find the distance between this point and either of the possible locations of C. (Notice that the distance is the same either way.) Alternately, we might notice that MC is the hypotenuse of a right triangle with legs 5 and 2.5. Either way, we get a value of
(point M above) is (1, 3.5). We can use the distance formula to find the distance between this point and either of the possible locations of C. (Notice that the distance is the same either way.) Alternately, we might notice that MC is the hypotenuse of a right triangle with legs 5 and 2.5. Either way, we get a value of 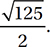
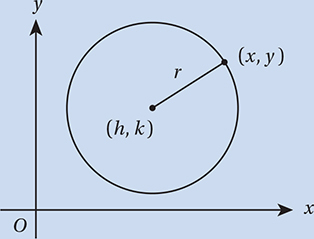
Lesson 5: Circles
Which of the following equations represents a circle in the xy-plane that passes through the point (1, 5) and has a center of (3, 2) ?
A) (x – 3)2 + (y – 2)2 = 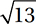
B) (x – 3)2 + (y – 2)2 = 13
C) (x – 1)2 + (y – 5)2 = 13
D) (x – 3)2 + (y – 2)2 = 25
(Easy) Since our circle has a center at (3, 2), its equation must have the form (x – 3)2 + (y – 2)2 = r2, which eliminates choice (C). To find r, the radius, we simply have to find the distance between the center and any point on the circle. By the distance formula, this is 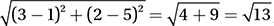 , and therefore,
, and therefore, 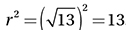 . The correct answer is (B). If you chose (A), keep in mind that the equation for a circle has r2 on the right side, not r.
. The correct answer is (B). If you chose (A), keep in mind that the equation for a circle has r2 on the right side, not r.
What is the area, in square centimeters, of a circle with circumference of 16π centimeters?
A) 8π
B) 16π
C) 32π
D) 64π

So the correct answer is (D).
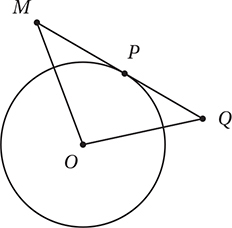
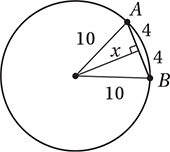
In the figure above,  is tangent to the circle at point P,
is tangent to the circle at point P, 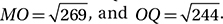 If the circle has an area of 100π, what is the area of triangle MOQ ?
If the circle has an area of 100π, what is the area of triangle MOQ ?

(Hard) The first thing we should do is draw radius  . Since this is a radius to the point of tangency, it is perpendicular to the tangent. We should also write in the given measures.
. Since this is a radius to the point of tangency, it is perpendicular to the tangent. We should also write in the given measures.
Notice that 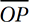 is the height of triangle MOQ if
is the height of triangle MOQ if 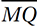 is taken as its base. If we can find the length of base
is taken as its base. If we can find the length of base 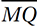 , we can simply use the triangle angle formula
, we can simply use the triangle angle formula 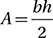 .
.
To find MQ, we can use the Pythagorean Theorem to find MP and PQ and just add them together.

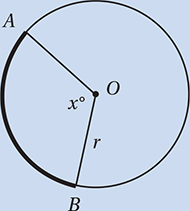
Lesson 6: Radians, chords, arcs, and sectors
What is the degree measure of an angle that measures 4.5 radians?
A) 4.5π°
B) 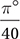
C) 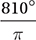
D) 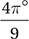
(Medium) Although many students will get this question wrong, it is very simple if you know how to convert radians to degrees. All we need to do to convert any radian measure to a degree measure is to multiply it by the conversion factor 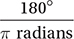 (as explained below).
(as explained below).
Therefore, 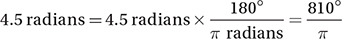 , and the correct answer is (C).
, and the correct answer is (C).
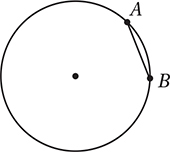
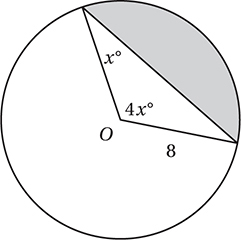
The circle above has an area of 100π square centimeters. If chord  is 8 centimeters long, how far, in centimeters, is
is 8 centimeters long, how far, in centimeters, is  from the center of the circle?
from the center of the circle?
A) 6
B) 8
C) 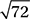
D) 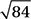
(Medium) First, let’s draw three extra line segments:
Since πr2 = 100π, r = 10. If we draw a perpendicular from the center to the chord, the length of this segment is the distance from the center to the chord. This segment also bisects the chord, dividing it into two equal segments of 4 centimeters each. This allows us to use the Pythagorean Theorem to find this distance: 42 + x2 = 102

Therefore, the correct answer is (D).
Note: Figure not drawn to scale.
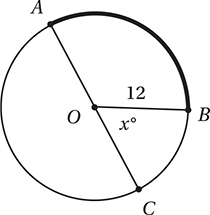
In the figure above, AC is a diameter of the circle with center O, OB = 12, and the length of arc AB is 7π. What is the value of x ?
A) 60
B) 72
C) 75
D) 78
(Medium) Since the circle has a radius of 12, its circumference is 2π(12) = 24π. Since AC is a diameter, then the measure of arc AC is half the circumference, or 12π. If the length of arc AB is 7π, then the length of arc BC is 12π – 7π = 5π. Since the central angle of x° is the same fraction of 360° as its arc BC is to the
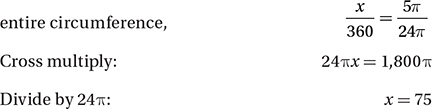
Therefore, the correct answer is (C).
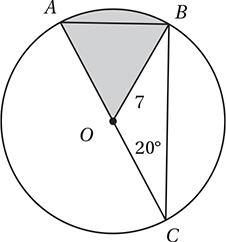
Note: Figure not drawn to scale.
In the figure above, AC is a diameter of the circle with center O, OB = 7, and the measure of ACB is 20°. What is the area of the shaded sector?
A) 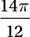
B) 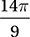
C) 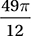
D) 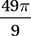
(Medium-Hard) Since 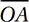 ,
, 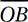 , and
, and 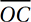 are all radii, triangles AOB and BOC are isosceles. Therefore, we can analyze the diagram with the Isosceles Triangle Theorem and the Angle Sum Theorem:
are all radii, triangles AOB and BOC are isosceles. Therefore, we can analyze the diagram with the Isosceles Triangle Theorem and the Angle Sum Theorem:
Since the central angle of the sector is 40°, the area of the sector is 40°/360° = 1/9 the area of the circle. Since the area of the circle is π(7)2 = 49π, the area of the sector is 49π/9 square units. Therefore, the correct answer is (D).
Lesson 7: Areas and volumes
Reference Information
Every SAT Math section will include the following Reference Information. Take some time to familiarize yourself with these area and volume formulas.
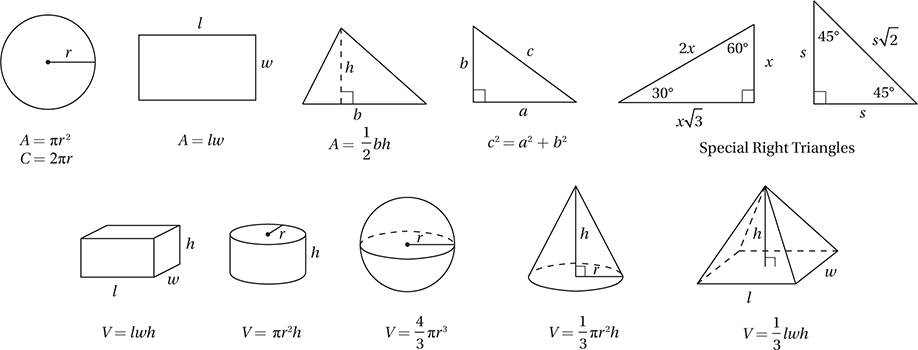
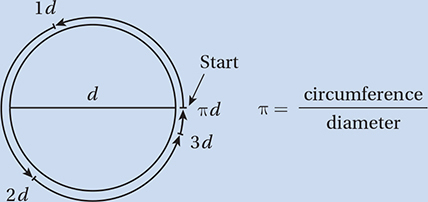
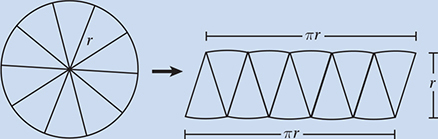
The number of degrees of arc in a circle is 360.
The number of radians of arc in a circle is 2.
The sum of the measures in degrees of the angles of a triangle is 180.
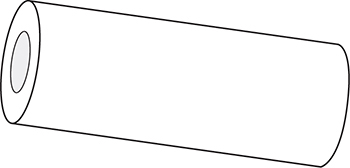
The figure above shows a wooden cylindrical tube with a length of 10 centimeters and a diameter of 4 centimeters with a cylindrical hole with a diameter of 2 centimeters that extends 40% of the length of the tube. The tube is closed on the end opposite to the hole. The density of the wood is 4.2 grams per cubic centimeter. What is the mass of this tube, to the nearest gram? (Recall that mass = density × volume)
A) 151 grams
B) 343 grams
C) 468 grams
D) 475 grams
(Medium) To find the mass of the tube, we must multiply its density by its volume. To find its volume, we must subtract the volume of cylindrical hole from the volume of the wooden cylinder. The large cylinder has a radius of 2 (remember, the diameter is 4 and so the radius is 4 ÷ 2 = 2) and a length of 10, so its volume is π(2)2(10) = 40π. The cylindrical hole has a radius of 1 (because its diameter is 2) and a length of (0.40)(10) = 4, so the volume of the hole is π(1)2(4) = 4π. Therefore the total volume of the closed tube is 40π – 4π = 36π ≈ 113.1. Since the mass is equal to the volume times the density, its mass is (113.1)(4.2) = 475 grams, so the correct answer is (D).
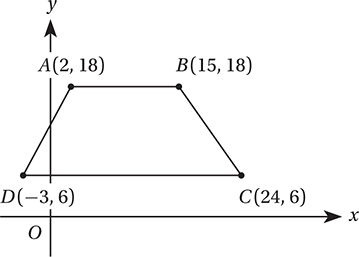
What is the area, in square units, of quadrilateral ABCD above?

(Medium) You might remember this figure from Lesson 4, in which we found its perimeter. Now we are asked to find its area. Unfortunately, we are not given any formula for calculating the area of this kind of quadrilateral. (You might remember that its technical name is a trapezoid, but in fact we don’t need to know anything special about trapezoids to solve this problem.) In such situations, it helps to remember the Strange Area Rule.
In this case, we can look at this area in two different ways: as a rectangle plus two right triangles, or as a bigger rectangle minus two right triangles:
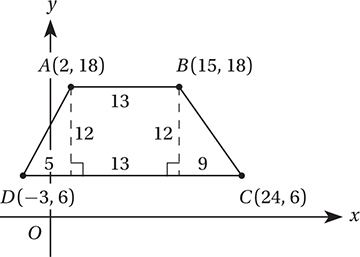
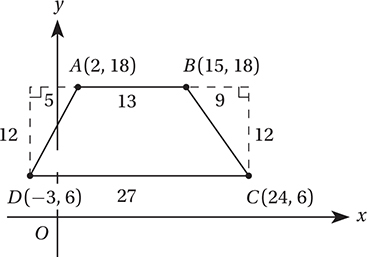
We should get the same result from either method. With the first method, the area of the trapezoid is the area of the rectangle plus the areas of two right triangles. This gives us a total area of (12)(13) + (1/2)(5)(12) + (1/2)(9)(12) = 156 + 30 + 54 = 240. With the second method, the area of the trapezoid is the area of the large rectangle minus the areas of the two right triangles. This gives us a total area of (12)(27) – (1/2)(5)(12) – (1/2)(9)(12) = 324 – 30 – 54 = 240. Bingo!
Lesson 8: Similar figures
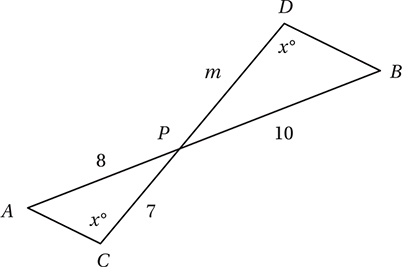
In the figure above, 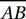 and
and 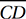 are line segments that intersect at point P. What is the value of m?
are line segments that intersect at point P. What is the value of m?

(Medium) The key to this question is noticing that the two triangles are similar. That is, that they are the same shape, although they may be different sizes.
AA (Angle-Angle) Similarity Theorem
If two triangles have two pairs of congruent corresponding angles, then (1) the remaining pair of corresponding angles must be congruent, and (2) the triangles must be similar.
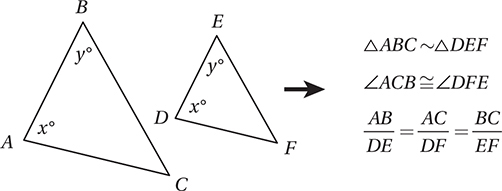
SAS (Side-Angle-Side) Similarity Theorem
If two triangles have two pairs of proportional corresponding sides, and the corresponding angles between those sides are also congruent, then the triangles must be similar.
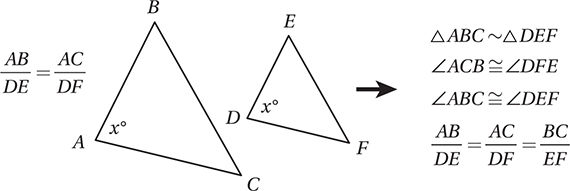
Perimeters, Areas, and Volumes of Similar Figures
If two polygons are similar with corresponding sides in ratio of a:b, then the corresponding perimeters of those figures have a ratio of a:b and their corresponding areas have a ratio of a2:b2. If two solids have corresponding lengths in a ratio of a:b, then their volumes have a ratio of a3:b3.
Coming back to our diagram, if 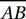 and
and 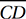 intersect at point P, the Crossed Lines Theorem tells us that ∠APC and ∠BPD must be congruent, and so, by the AA Theorem, ΔAPC ∼ ΔBPD. Therefore, the corresponding sides are proportional:
intersect at point P, the Crossed Lines Theorem tells us that ∠APC and ∠BPD must be congruent, and so, by the AA Theorem, ΔAPC ∼ ΔBPD. Therefore, the corresponding sides are proportional:

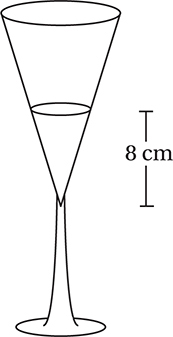
The figure above shows a fluted glass filled with water to a height of 8 centimeters. The interior of the glass is a right cone. If the water in the glass has a volume of 64 milliliters, how many more milliliters of water must be added so that the water reaches a height of 12 centimeters? (1 milliliter = 1 cubic centimeter)

(Hard) Many students will make this problem harder by trying to use the cone volume formula 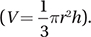 This is messy and unnecessary. Instead, notice that the original volume of water and the final volume of water are similar cones. Since the heights of these cones are in a ratio of 12:8, or 3:2, each length in the larger cone is 1.5 times the corresponding length in the smaller cone. By the theorem on the previous page, this means that the volume of the larger cone is (1.5)3 = 3.375 times the volume of the smaller one, which is 3.375(64) = 216 milliliters, which means we must add 216 – 64 = 152 more milliliters of water.
This is messy and unnecessary. Instead, notice that the original volume of water and the final volume of water are similar cones. Since the heights of these cones are in a ratio of 12:8, or 3:2, each length in the larger cone is 1.5 times the corresponding length in the smaller cone. By the theorem on the previous page, this means that the volume of the larger cone is (1.5)3 = 3.375 times the volume of the smaller one, which is 3.375(64) = 216 milliliters, which means we must add 216 – 64 = 152 more milliliters of water.
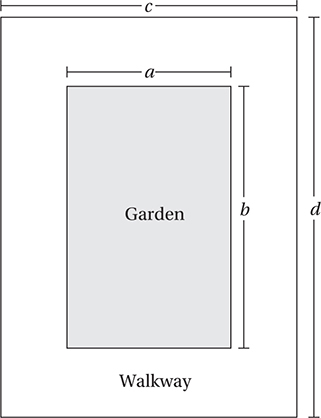
The figure above shows a scale drawing of a rectangular garden surrounded by a walkway that is 6 feet wide. If the ratio of a to b is 5:8, and the ratio of c to d is 3:4, what is the area of the garden (not including the walkway), in square feet?

(Hard) Since the ratio of the width of the garden to its length is 5 to 8, let’s call the width of the garden 5x and the length of the garden 8x, where all lengths are in feet. Now, since the walkway is 6 feet wide all around, c = 5x + 6 + 6 = 5x + 12 feet, and d = 8x + 6 + 6 = 8x + 12 feet. Since we are given the ratio of these two lengths, we can set up an equation and solve.

Recall that the length and width of the garden are 5x and 8x, so the dimensions are 5(3) = 15 feet and 8(3) = 24 feet, and so the area of the garden is (15)(24) = 360 square feet.
Exercise Set 2: Geometry (No Calculator)
A cereal company sells oatmeal in two sizes of cylindrical containers. The radius of the larger container is twice that of the smaller, and the height of the larger container is 50% greater than the smaller. If the smaller container holds 10 ounces of oatmeal, how many ounces can the larger container hold?

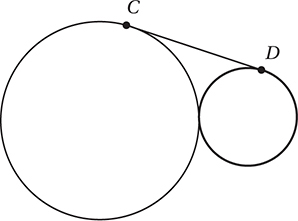
Note: Figure not drawn to scale.
In the figure above,  is tangent to both circles, which are tangent to each other. If the smaller circle has a circumference of 4π and the larger circle has a circumference of 16π, what is the length of
is tangent to both circles, which are tangent to each other. If the smaller circle has a circumference of 4π and the larger circle has a circumference of 16π, what is the length of  ?
?

What is the area, in square inches, of a circle with diameter 6π2 inches?
A) 9π4
B) 9π5
C) 36π4
D) 36π5
What is the length of the longest line segment that connects two vertices of a rectangular box that is 6 units wide, 4 units long, and 2 units tall?
A) 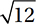
B) 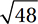
C) 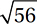
D) 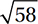
Which of the following equations represents a circle in the xy-plane that intersects the x-axis at (3, 0) and (9, 0) ?
A) (x – 6)2 + (y – 4)2 = 25
B) (x – 3)2 + (y – 9)2 = 25
C) (x – 6)2 + (y – 4)2 = 36
D) (x – 3)2 + (y – 9)2 = 36
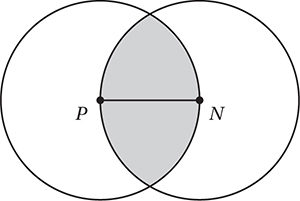
In the figure above, P and N are the centers of the circles and PN = 6. What is the area of the shaded region?
A) 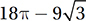
B) 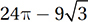
C) 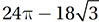
D) 
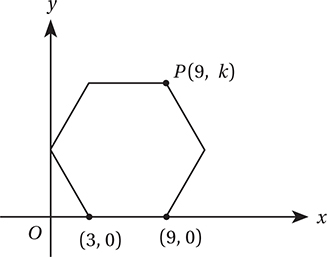
The diagram above shows a hexagon with all sides congruent and all angles congruent. What is the value of k ?
A) 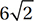
B) 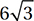
C) 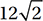
D) 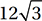
Exercise Set 2: Geometry (Calculator)
What is the area, in square units, of the quadrilateral above?

What is the degree measure, to the nearest whole degree, of an angle that measures 5.6 radians?

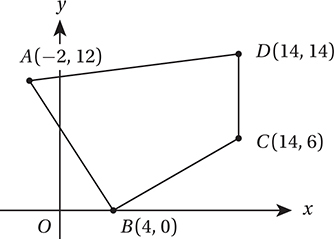
In the figure above, arc  has a length of 11.5. To the nearest integer, what is the value of x ?
has a length of 11.5. To the nearest integer, what is the value of x ?

The Great Pyramid in Giza, Egypt, has a height of 140 meters and a volume of 2.6 million cubic meters. If a scale model of the Great Pyramid is to be built that is 2 meters high, what will be the volume, in cubic meters, of this model?

Which of the following equations defines a circle that is tangent to the y-axis?
A) (x – 2)2 + (y + 3)2 = 2
B) (x – 2)2 + (y + 3)2 = 3
C) (x – 2)2 + (y + 3)2 = 4
D) (x – 2)2 + (y + 3)2 = 9

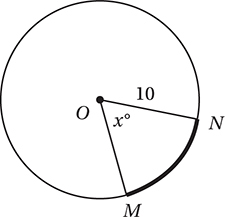
Questions 13 and 14 refer to the diagram below.
The figure above shows two rectangles that share a common vertex, and  is a line segment that passes through C.
is a line segment that passes through C.
What is the ratio of the area of rectangle ABCD to the area of rectangle AEFG ?
A) 3:5
B) 9:25
C) 5:8
D) 25:64
If CD = 9, what is the perimeter of rectangle AEFG ?
A) 67.2
B) 72.6
C) 76.2
D) 78.6

Point O is the center of the circle above. What is the area of the shaded region?
EXERCISE SET 2: GEOMETRY ANSWER KEY
No Calculator
1. 60 If the smaller cylinder has a radius of r and a height of h, its volume is πr2h. The larger cylinder therefore must have a radius of 2r and a height of 1.5h, and a volume of π(2r)2(1.5h) = 6πr2h. Since this is 6 times the volume of the smaller cylinder, it must hold 10 × 6 = 60 ounces of oatmeal.
2. 8 First, let’s draw the radii to the points of tangency, the segment joining the centers, and the segment from the center of the smaller circle that is perpendicular to the radius of the larger circle. Since the tangent segment is perpendicular to the radii, these segments form a rectangle and a right triangle.
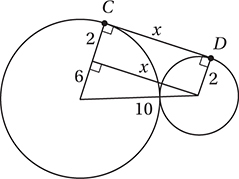
Since the circumference of the smaller circle is 4π, its radius is 2, and since the circumference of the larger circle is 16π, its radius is 8. The hypotenuse of the right triangle is the sum of the two radii: 2 + 8 = 10. One of the legs of the right triangle is the difference of the two radii: 8 – 2 = 6.

4. C From the 3-D Distance Formula back in Lesson 4, the length of the diagonal is 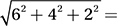
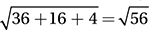
5. A All of the equations are clearly equations of circles, so our only task is to verify that one of these equations is satisfied by both point (3, 0) and point (9, 0). Simply by plugging these coordinates into the equations, we can verify that only the equation in (A) is true for both points: (3 – 6)2 + (0 – 4)2 = 25 and (9 – 6)2 + (0 – 4)2 = 25.
6. C In this problem, we have to take advantage of the Strange Area Rule from Lesson 7. First we should draw the segments from P and N to the points of intersection. Since each of these segments is a radius, they have equal measure (6), and form two equilateral 60°-60°-60° triangles.
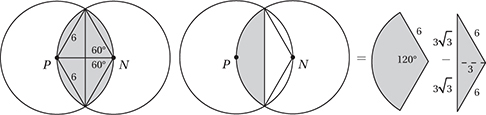
The shaded region is composed of two circle “segments,” each of which is a sector minus a triangle, as shown in the figure above. The sector, since it has a 120° central angle, has an area 1/3 of the whole circle, or (1/3) (π(6)2) = 12π and the triangle has area 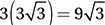 . Therefore, the shaded region has an area of
. Therefore, the shaded region has an area of 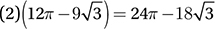 .
.
7. B Each side of the hexagon has length 9 – 3 = 6. Each interior angle of a regular hexagon has measure (6 – 2)(180°)/6 = 120°, so the segments shown form two 30°-60°-90° triangles with lengths shown below.
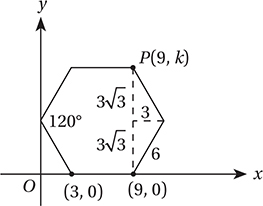
Therefore, 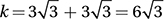 .
.
Calculator
8. 142 First, let’s draw a rectangle around the figure as shown.
This shows that the area we want is the area of the rectangle minus the areas of the three triangles: (16)(14) – (1/2)(2)(16) – (1/2)(12)(6) – (1/2)(10)(6) = 224 – 16 – 36 – 30 = 142.
9. 321 To convert any angle from radians to degrees, we just multiply by the conversion factor (180°)/(π radians). 5.6 × 180°/π = 320.86 ≈ 321°.
10. 66 In a circle with radius 10, and arc of length 11.5 has a radian measure of 11.5/10 = 1.15 radians. In degrees, this equals 1.15 × 180°/π = 65.89° ≈ 66°.
11. 7.58 If two similar solids have sides in ratio of a:b, then their volumes are in a ratio of a3:b3. The ratio of the heights is 140:2 = 70:1, so the ratio of volumes is 703:13 = 343,000:1. This means that the volume of the model is 2,600,000 ÷ 343,000 ≈ 7.58 cubic meters.
12. C As a quick sketch will verify, in order for a circle to be tangent to the y-axis, its radius must equal the absolute value of the x-coordinate of its center. Since the center of each square is (2, –3), the radius must be 2. The only circle with a radius of 2 is (C).
13. D By the AA Theorem, triangle ACD is similar to triangle AFG, and so rectangle ABCD is similar to rectangle AEFG. The ratio of the corresponding sides is equal to the ratio of their diagonals, which is 15:24 = 5:8. Therefore, the ratio of their areas is 52:82 = 25:64.
14. A If CD = 9, we can find AD by the Pythagorean Theorem. (AD)2 + (CD)2 = (AC)2

15. A The two radii and the chord form an isosceles triangle.

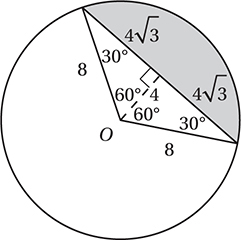
As we saw in question 6, this portion of the circle is called a “segment,” and we find its area by taking the area of the sector minus the area of the triangle. The sector has area (120/360)(π82) = 64π/3, and the triangle has area 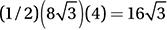 , so the segment has an area of
, so the segment has an area of 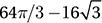 .
.
Skill 2: Understanding Basic Trigonometry
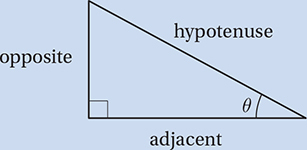
Lesson 9: The basic trigonometric functions
Which of these is equivalent to 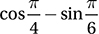 ?
?
(No calculator)
A) 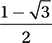
B) 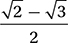
C) 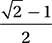
D) 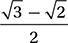
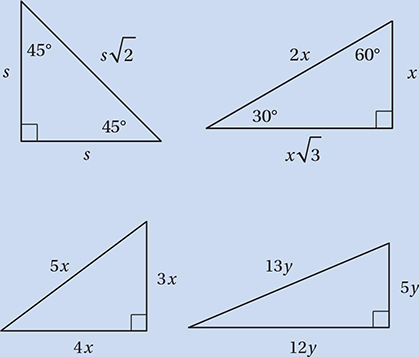
(Medium-hard) First, you may find it useful to convert the angles to degree measures using the conversion factor (180°/π radians). This gives us π/4 radians = 45° and π/6 radians 30°. We should recognize these as angles in two Special Right Triangles:
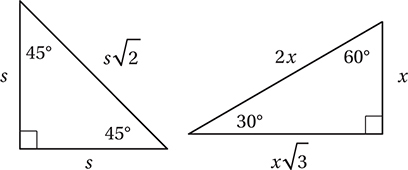
Using the definitions for sine and cosine above, these triangles show us that 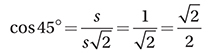 and
and 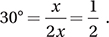 Therefore,
Therefore, 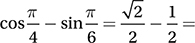
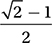 and the correct answer is (C).
and the correct answer is (C).
If sin x = a and sin z = –a, where x and z are in radians, and 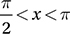 , which of the following could be the value of z in terms of x ?
, which of the following could be the value of z in terms of x ?
A) π – x
B) x – π
C) 2π + x
D) 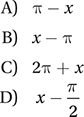
(Hard) The statement 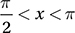 indicates that x is an angle in quadrant II, where the sine (the y-value of the points on the unit circle) is positive. Let’s draw this situation on the unit circle so we can visualize it. (We don’t want to confuse the angles called x and y in the problem with the x-coordinates and y-coordinates in the xy-plane. For this reason, let’s label the terminal rays for the angles “angle x” and “angle z.”) Recall that the sine of any angle is the y-coordinate of the point on the unit circle that corresponds to that angle. If sin x = a, then a is the y-coordinate of the point on the unit circle that corresponds to “angle x,” as shown in the diagram. If sin z = –a, then –a is the y-coordinate of the point on the unit circle that corresponds to “angle z.” There are two possible locations for “angle z” as shown in the diagram.
indicates that x is an angle in quadrant II, where the sine (the y-value of the points on the unit circle) is positive. Let’s draw this situation on the unit circle so we can visualize it. (We don’t want to confuse the angles called x and y in the problem with the x-coordinates and y-coordinates in the xy-plane. For this reason, let’s label the terminal rays for the angles “angle x” and “angle z.”) Recall that the sine of any angle is the y-coordinate of the point on the unit circle that corresponds to that angle. If sin x = a, then a is the y-coordinate of the point on the unit circle that corresponds to “angle x,” as shown in the diagram. If sin z = –a, then –a is the y-coordinate of the point on the unit circle that corresponds to “angle z.” There are two possible locations for “angle z” as shown in the diagram.
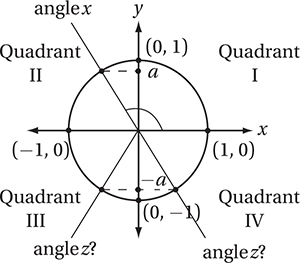
At this point, it may be easiest to simply pick a value for “angle x” that is between π/2 (≈ 1.57) and π (≈ 3.14), such as x = 2. Since sin 2 ≈ 0.909 (remember to put your calculator into “radian mode”), a = 0.909. Now we just need to find which angle among the choices has a sine of – 0.909.
A) sin(π – 2) = 0.909
B) sin(2 – π) = – 0.909
C) sin(2π + 2) = 0.909
D) sin(2 – π/2) = 0.416
Therefore, the correct answer is (B).
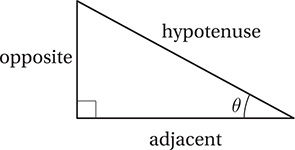
The Pythagorean Identity
sin2 x + cos2 x = 1 for all values of x
An identity is an algebraic equation that is true for all values of the unknown, and not just for particular values. We can prove the Pythagorean Identity by just applying the Pythagorean Theorem to our right triangle and thinking about the trigonometric ratios.
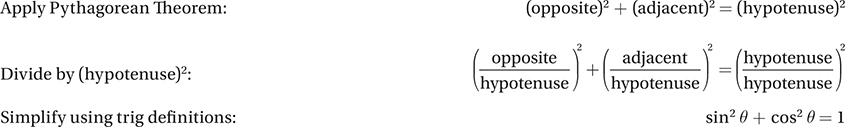
If b is an angle measure such that sin 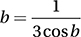 , what is the value of (sin b – cos b)2?
, what is the value of (sin b – cos b)2?

(Medium) The expression we are trying to evaluate includes squared trigonometric ratios, so we will probably have to take advantage of the Pythagorean Identity.
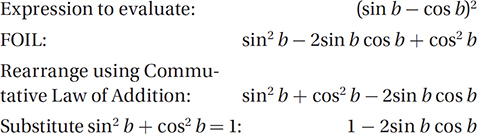
Now we’ll have to find the value of sin b cos b, which we can find with the given equation.
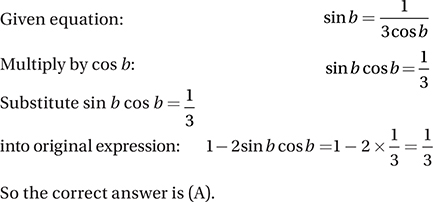
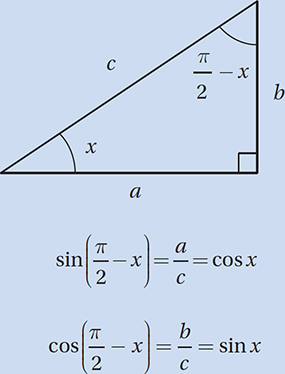
Lesson 10: The trigonometry of complementary angles
If 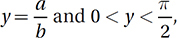 which of the following is equal to
which of the following is equal to 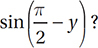
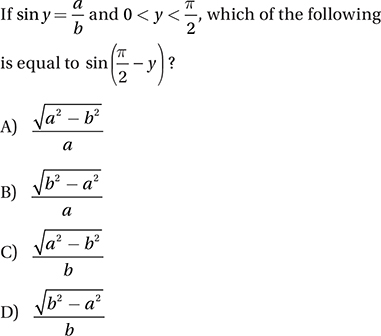
(Medium-hard) Let’s start by drawing a picture of this situation. Since y is the measure of an acute angle, we can imagine it as the interior angle of a right triangle. Since its sine is equal to a/b, we can say that the opposite side has measure a and the hypotenuse has measure b.
Now we can find the length of the remaining leg (let’s call it k) in terms of a and b using the Pythagorean Theorem:k2 + a2 = b2

Also, we know that the other acute angle has a measure of 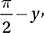 so let’s complete the picture:
so let’s complete the picture:
Now, finding the value of 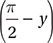 is just a matter of using the definition of sine: SOH.
is just a matter of using the definition of sine: SOH.
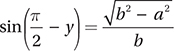
So the correct answer is (D).
Exercise Set 3: Trigonometry (No Calculator)
What is the greatest possible value of f if 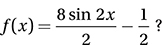

If cos , what is the value of
, what is the value of 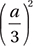 ?
?

If (sin x – cos x)2 = 0.83, what is the value of (sin x + cos x)2 ?

Which of the following is equivalent to 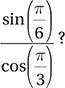
A) 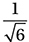
B) 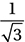
C) 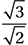
D) 1
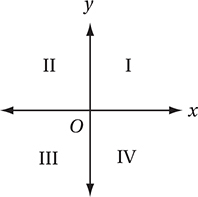
If sin θ < 0 and sin θ cos θ < 0, then θ must be in which quadrant of the figure above?
A) I
B) II
C) III
D) IV
If sin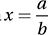 and
and 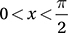 , which of the following expressions is equal to
, which of the following expressions is equal to 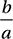 ?
?
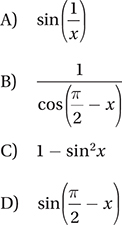
If sin b = a, which of the following could be the value of cos (b + π) ?
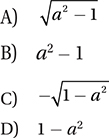
If 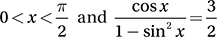 , what is the value of
, what is the value of
cos x ?
A) 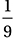
B) 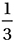
C) 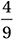
D) 
EXERCISE SET 3: TRIGONOMETRY ANSWER KEY
No Calculator
1. 7/2 or 3.5 The discussion in Lesson 9 about the definition of the sine function and the unit circle made it clear that the value of the sine function ranges from –1 to 1. Therefore, the maximum value of 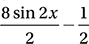 is
is 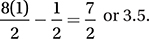
2. 1/36 or .027 or .028 An radian measure of π/3 is equivalent to 60°. If you haven’t memorized the fact that cos(60°) = ½ you, can derive it from the Reference Information at the beginning of every SAT Math section, which includes the 30°-60°-90° special right triangle. Since a = ½, (a/3)2 = (1/6)2 = 1/36.
4. D sin(π/6) = ½ and cos(π/3) = ½, so sin(π/6)/cos(π/3) = 1.
5. D If sin θ < 0, then θ must be either in quadrant III or in quadrant IV. (Remember that sine corresponds to the y-coordinates on the unit circle, so it is negative in those quadrants where the y-coordinates are negative.) If sin θ cos θ < 0, then cos θ must be positive (because a negative times a positive is a negative). Since cos θ is only positive in quadrants I and IV (because cosine corresponds to the x-coordinates on the unit circle), θ must be in quadrant IV.
6. B First, notice that a/b and b/a are reciprocals. Next, we can use the identity in Lesson 10 that 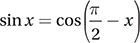 to see that choice (B) is just the reciprocal of sin x. Alternately, we can just choose a value of x, like x = 1, and evaluate sin 1 = 0.841. The correct answer is the expression that gives a value equal to the reciprocal of 0.841, which is 1/0.841 = 1.19. Plugging in x = 1 gives (A) 0.841, (B) 1.19, (C) 0.292, (D) 0.540.
to see that choice (B) is just the reciprocal of sin x. Alternately, we can just choose a value of x, like x = 1, and evaluate sin 1 = 0.841. The correct answer is the expression that gives a value equal to the reciprocal of 0.841, which is 1/0.841 = 1.19. Plugging in x = 1 gives (A) 0.841, (B) 1.19, (C) 0.292, (D) 0.540.
7. C Recall from the Pythagorean Identity that 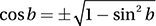 . Substituting sin b = a gives
. Substituting sin b = a gives 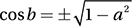 . The angle b + π is the reflection of angle b through the origin, so cos(b + π) is the opposite of cos b, which means that cos
. The angle b + π is the reflection of angle b through the origin, so cos(b + π) is the opposite of cos b, which means that cos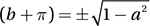 .
.
8. D Recall from the Pythagorean Identity that cos2 x = 1 – sin2 x.
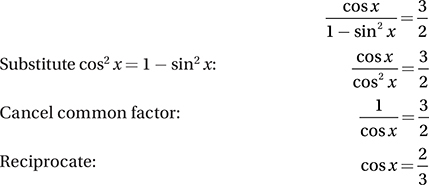
Skill 3: Understanding Complex Numbers
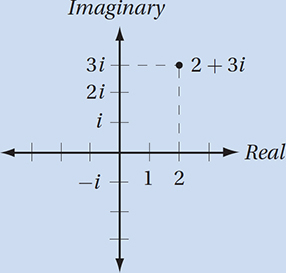
Lesson 11: Understanding the imaginary number i and the complex plane
Given that 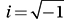 , which of the following is equal to
, which of the following is equal to 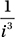 ?
?
A) i
B) –i
C) 1
D) –1
(Medium-hard) To answer this question, we just need to know the basic exponent rules and the definition of i.

Lesson 12: Adding, multiplying, dividing, and simplifying complex numbers
If 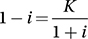 , where i =
, where i = 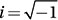 which of the following is equal to K2 ?
which of the following is equal to K2 ?
A) 2i
B) 4i
C) 4 + i
D) 4

Therefore, the correct answer is (D).
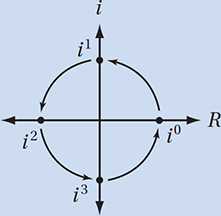
Which of the following is NOT equal to i6 – i2 ?
A) i5 – i
B) i4
C) 2i3 + 2i
D) 1 + i6
(Medium) Here, we have to use our knowledge about powers of i. Since i6 = (i × i)(i × i)(i × i) = (–1)(–1)(–1) = –1, and i2 = –1, the given expression, i6 – i2, is equal to (–1) – (–1) = 0. Simplifying each choice gives us
A) i5 – i = i – i = 0
B) i4 = 1
C) 2i3 + 2i = –2i + 2i = 0
D) 1 + i6 = 1 + (–1) = 0
Therefore, the correct answer is (B).
Exercise Set 4: Complex Numbers (No Calculator)
If a + bi = (1 + 2i)(3 – 4i), where a and b are constants and 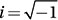 , what is the value of a + b ?
, what is the value of a + b ?

If 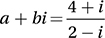 , where a and b are constants and
, where a and b are constants and 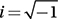 , what is the value of a ?
, what is the value of a ?

For what value of b does (b + i)2 = 80 + 18i ?

The solutions of the equation x2 – 2x + 15 = 0 are 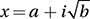 and
and 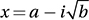 , where a and b are positive numbers. What is the value of a + b ?
, where a and b are positive numbers. What is the value of a + b ?

Given that 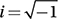 , which of the following is equal to
, which of the following is equal to 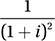 ?
?
A) 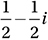
B) 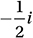
C) 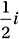
D) 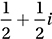
Which of the following expressions is equal to (2 + 2i)2 ?
A) 0
B) 4i
C) 8i
D) 4 – 4i
If B(3 + i) = 3 – i, what is the value of B ?
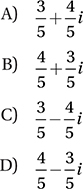
x2 + kx = –6
If one of the solutions to the equation above is 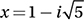 , what is the value of k ?
, what is the value of k ?
A) –4
B) –2
C) 2
D) 4
If im = –i, which of the following CANNOT be the value of m ?
A) 15
B) 18
C) 19
D) 27
EXERCISE SET 4: COMPLEX NUMBERS ANSWER KEY
No Calculator
Since this must equal 80 + 18i, we can find b by solving either b2 – 1 = 80 or 2b = 18. The solution to both equations is b = 9.
4. 15 The equation we are given is a quadratic equation in which a = 1, b = –2, and c = 15. Therefore, we can use the quadratic formula:
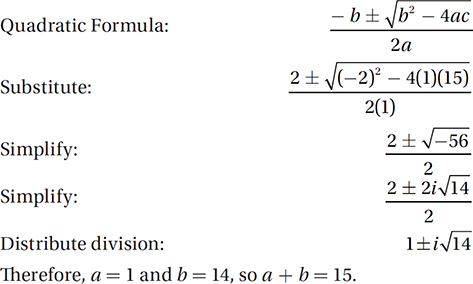
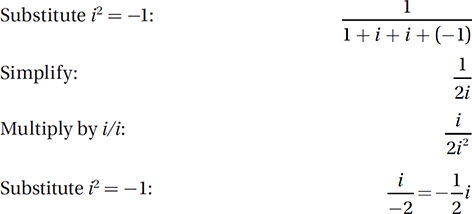
9. B As we discussed in Lesson 10, the powers of i are “cyclical,” and im = –i if and only if m is 3 more than a multiple of 4. The only number among the choices that is not 3 more than a multiple of 4 is (B) 18.
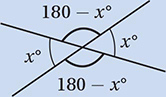
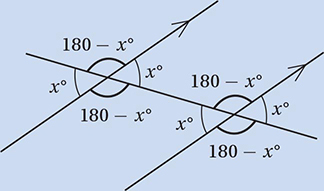
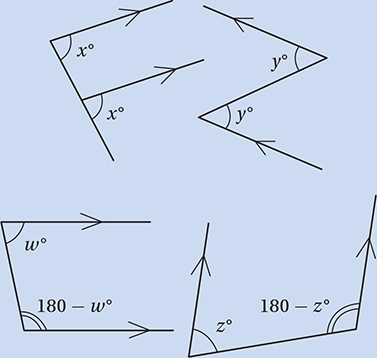
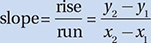

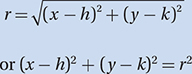
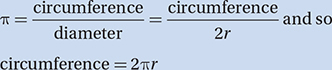
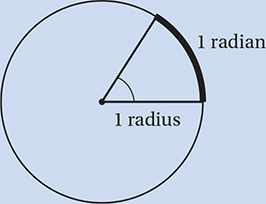
 as a conversion factor to convert a degree measure to radians, and
as a conversion factor to convert a degree measure to radians, and  as a conversion factor to convert a radian measure to degrees.
as a conversion factor to convert a radian measure to degrees.

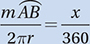

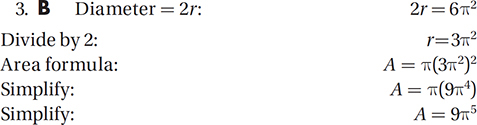

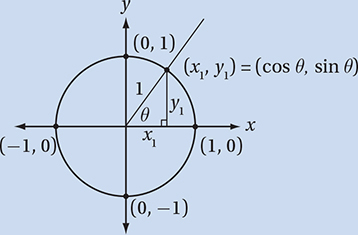

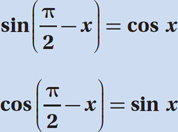
 ). So, if one of the angles has a radian measure of x, the other has a measure of
). So, if one of the angles has a radian measure of x, the other has a measure of