The Alpha and the Omega of Risk
At bottom no one believes in his own death,… in the unconscious every one of us is convinced of his own immortality.
The relationship between human beings and the risks of their world is both ancient and complex.2 It is the stuff of myth and literature as well as philosophy and science. Wars, plagues, famines, floods, and earthquakes mark many of the turning points of the Hebrew Bible, and Greek mythology provides a generous reservoir of risk-related metaphors: Achilles’ heel, the Sword of Damocles, Pandora’s box, the Lernean Hydra, etc. In modern times, epic disasters—such as the Titanic, Pearl Harbor, Apollo 13, and Chernobyl—have assumed their own roles in our collective psychology.
Today, problems of risk form the basis for insurance and other financial services industries and are studied rigorously by scholarly researchers. But regardless of how these problems are formulated and analyzed, I would argue that they all flow from the same source: the specter of mortality. Like a serpent coiled around the trunk and branches of the Tree of Life, the risk of death squeezes at every aspect of human existence.
Downside Risk Versus Upside Risk
In recent decades, we have come to believe that the course of biological evolution on Earth was changed dramatically by chance encounters between our planet and approaching asteroids or comets. Instructively, these cataclysmic impacts—leading, among other things, to the extinction of the dinosaurs and the ascendancy of the mammals—point up one important aspect of risk: although the word generally has negative connotations because of its association with destruction, it also can suggest positive, albeit uncertain, developments. Like the Hindu god Shiva, whose destructive nature paves the way for creation and growth, risks have their positive side.
The asymmetry between the positive and negative aspects of risk arises because random change is more likely to damage than to enhance the carefully wrought equilibrium of the status quo, especially in the short run. This is nowhere clearer than in evolutionary biology, where for every salutary genetic mutation there are countless lethal deviations. Nevertheless, whether we see risk as primarily negative or as a balance between negative and positive potentials is largely a matter of perspective. If I assume that a human being’s life on Earth should be unending, then clearly I will see any degree of mortality risk as negative. However, if I view each human being as entitled to only the expected lifetime given by the actuary’s mortality table, then I will acknowledge a reasonable balance between negative outcomes (early deaths) and positive outcomes (late deaths).
When embedded in the financial products of modern economic markets, risks naturally assume a degree of symmetry by way of the pricing mechanism. Although an office building, taken as an isolated entity, is exposed primarily to the pure (i.e., entirely negative) risks of fire, wind, etc., the purchase of an office building at market price is subject to speculative (i.e., both positive and negative) risks, including an increasing demand for office space, as well as a decreasing supply of space (which, for example, could be caused by fire or wind damage to competing buildings). Likewise, stocks, bonds, and various financial indexes and derivatives generally trade at prices that recognize the potential for both increases and decreases in value.
In today’s business world, professional risk managers often construct extensive lists of pure and speculative risks, including every imaginable type of uncertainty to which individuals and firms are exposed. Among pure risks, one finds traditional “insurance” perils such as fire, wind, theft, disease, and professional negligence, along with more complex hazards such as substandard construction, inadequate security, technological obsolescence, and political instability.3 Speculative risks include real estate, common financial securities (stocks, bonds, commodities, etc.), and interest-and currency-derivative products, as well as market-specific changes in the prices of raw materials, human capital, and end-of-line goods and services. In Chapter 6, I will propose an alternative to the conventional pure/speculative risk dichotomy that distinguishes between the “aloof” and “quasi-aloof” risks of insurance and the “non-aloof” risks of other financial markets.
Fundamental Exposures
Fortunately, a remarkable simplicity underlies these myriad risks. Despite the great number of individual sources of risk, there are only a very few exposures subject to risk. These fundamental exposures are life, health, and possessions. Table 1.1 shows (in rough terms) how this short list of exposures can be applied at the levels of individuals, corporations, and society at large.
To simplify things further, one could collapse the two rightmost columns into one composite column representing quality of life. Probing this new category, one then might ask: Why should we be concerned about the quality of life? I would argue that the following two principles provide the answer:
• The Morbidity Principle. An individual/corporation/society whose quality of life is damaged will have a greater chance of imminent death.
• The Lost-Gratification Principle. An individual/corporation/society whose quality of life is damaged may not have the opportunity to enjoy recovery of health or restitution of possessions before death occurs (i.e., “a good quality of life today is worth more than a good quality of life tomorrow”).
Life, Health, and Possessions: The Fundamental Exposures

In short, the life exposure underlies all other types of exposures.
For individuals and societies, the morbidity principle would have been particularly evident in the Old Stone Age, when human beings had developed useful tools, but were still primarily hunter-gatherers. At that time, quality-of-life exposures, although they existed, could not be separated easily from the life exposure because the loss of health (through injury or illness) or possessions (clothing, shelter, or hunting implements) would increase significantly the chance of death in the near future. Hence, in many cases loss of quality of life would be tantamount to loss of life.
The morbidity principle continues to apply to individuals and societies today, but not as dramatically. Despite the various “safety nets” that modern governments provide for their more vulnerable citizens, it is still an empirical fact that the injured and ill, as well as the economically poor, die at faster rates than others. This is also true for societies at large, as can be seen in the declines of certain populations in Eastern Europe since the dissolution of the Soviet Union. With regard to corporations, reductions in revenue, market share, and/or profitability are in many cases harbingers of bankruptcy.
Although a cursory review of today’s financial products might give the impression that quality-of-life exposures actually overshadow the life exposure—after all, the only financial product that specifically addresses mortality is life insurance—the lost-gratification principle belies such a conclusion. If anything, the role of mortality is difficult to discern because it is so prevalent that we tend to overlook it.
The life exposure underlies all traditional insurance policies, whether held by individuals or commercial enterprises. This is because the policies are designed to provide reasonably quick medical attention or restitution of property, presumably before the policyholder’s life terminates. In addition, the life exposure is fundamental to all financial transaction risks. Lenders, whether they be individuals, corporations, or government bodies, must be compensated for the possibility that they will cease to exist before their loans are repaid; and the early death of a borrower can transform this possibility into a certainty. In other words, mortality is the essential reason, even in an economy with no expected change in either income or prices, “a dollar today is worth more than a dollar tomorrow,” and thus the reason the nominal risk-free rate of return (often taken to be the nominal return on a U.S. Treasury bill) must be strictly greater than 0.
Reading from the Book of the Dead
For corporations and societies, mortality risk is difficult to measure because times of “death” are often ambiguous.4 Moribund firms may merge with or be acquired by healthier firms, and analogous fates await societies in decline. For individuals, however, mortality is a well-defined and extensively studied phenomenon.
The first comprehensive mortality table was published in 1693 by British mathematician and astronomer Edmond Halley. Based upon historical age-at-death records from the Polish-German city of Breslau, Halley’s table permitted the British government to sell the world’s first actuarially based life annuity products.5 Given the age-old association of human mortality with concepts of fate and destiny, it seems rather felicitous that the man who made the first scientific prediction of a comet’s appearance—long considered a portent of good or bad fortune—should also offer the first scientific analysis of the human life span.
There are numerous ways to depict the risk of mortality graphically. One is to provide a theoretical histogram of the time of death for a newborn baby selected at random from a human population. This would look something like Figure 1.1, which is based upon the 2001 Commissioners Standard Ordinary (CSO) tables approved by the National Association of Insurance Commissioners.6 Since death can occur at any time of the year and at any time of the day, it is most realistic to treat the time of death as a continuous variable. In practice, however, insurance and annuity companies often make the simplifying (albeit disquieting) assumption that an individual’s death will occur on his or her birthday.
Figure 1.1 suggests that the great majority of people born today will die in the age-band from 50 to 100, with the most likely single time of death (mode) at about 83 for men and 88 for women. In addition, there is a much smaller, but noticeable, group of individuals that will die within the first couple years of life, primarily because of life-threatening congenital defects and disease vulnerabilities associated with infancy.
Although a simple histogram answers the question “What is the likelihood that a newborn will die at age x?” it fails to address another fundamental question of interest: What is the likelihood that an individual at age x will die within the next year? Using Figure 1.1 to compare the probability of death of a man at age 45 to that of a man at age 100, one might be tempted to conclude that they are approximately the same—after all, the height of the histogram is about the same at both ages. However, such an analysis fails to account for the fact that as x increases, there are progressively fewer people subject to the risk of death. In other words, although the histogram readings at 45 and 100 are approximately the same, one must adjust for the fact that there are many fewer individuals still alive at age 100 than at age 45.
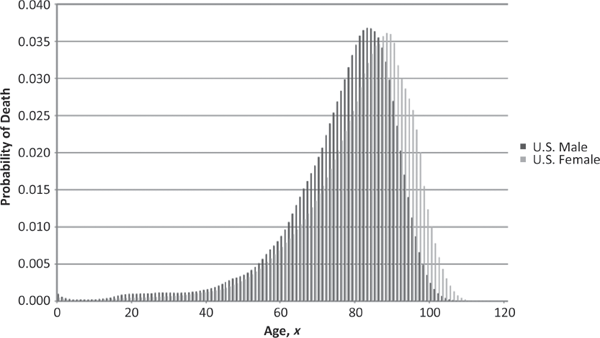
Histogram of Age at Death for One Individual (Selected Randomly at Birth) Source: Commissioners Standard Ordinary (CSO) Mortality Tables (2001).
Since the 100-year-olds who die are members of a smaller and more elite club (i.e., those who were lucky enough to survive to age 100), one naturally can conclude that the likelihood that a 100-year-old will die is greater than the corresponding likelihood for a 45-year-old. To show this result graphically, it is necessary to transform the histogram to adjust for the number of individuals alive at each age x. This is accomplished by dividing the value of the histogram at each point x by the proportion of individuals that survive to at least x, to obtain the one-year probability of death, or one-year mortality hazard rate, shown in Figure 1.2.7
From this figure, it can be seen quite clearly that the probability of death for a 100-year-old is vastly (approximately 135 times) greater than that for a 45-year-old. The mortality hazard rate makes such comparisons rather easy. Overall, the hazard rate decreases from age 0 to age 5 and then appears to increase (at least monotonically) after that, assuming an exponential-like growth beginning at about age 6. This general form tends to agree with intuition: the higher risk of infant mortality decreases as the child grows out of infancy, and then mortality risk increases thereafter as a result of the human aging process (i.e., senescence). However, there is no guarantee that such a straightforward hazard curve applies to every human population. For example, in Figure 1.2 the U.S. male population’s hazard rate actually decreases over the short range from 28 to 31 as the dramatic difference between male and female mortality risk—which begins in the early teenage years and is attributable to higher accident and homicide rates among males—begins to subside. (See Figure 1.3.)
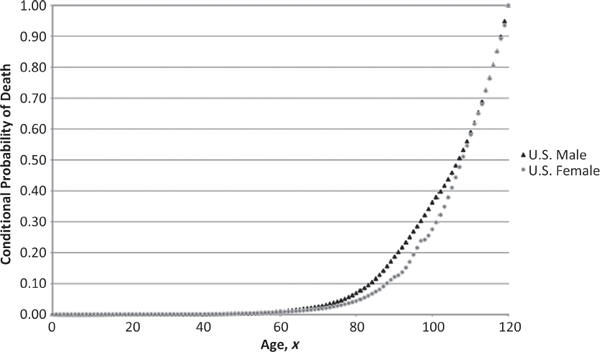
One-Year Mortality Hazard Rate Source: Commissioners Standard Ordinary (CSO) Mortality Tables (2001).
The smoothly increasing nature of the hazard curve from a certain age (32 for males, 6 for females) onward has led many demographers and actuaries to posit that human mortality follows a simple mathematical formula. Perhaps the most successful of these rules is the Gompertz-Makeham law, which states that the mortality hazard rate at age x can be written as the linear combination of a constant term and an exponentially increasing function of x.8 Although such a simplification of a complex process like human mortality is esthetically attractive, one must be careful not to imagine the presence of an underlying “scientific” principle where none exists. (I will say more about this in Chapter 12.)
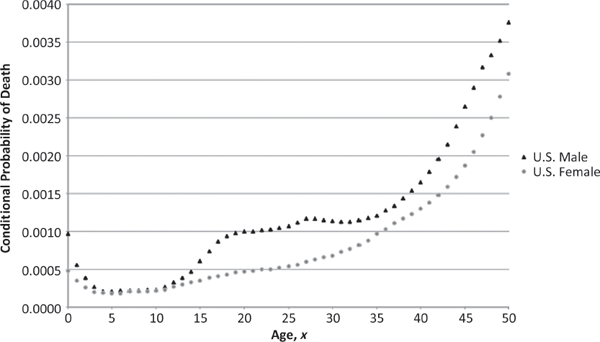
One-Year Mortality Hazard Rate (Ages ο to 50) Source: Commissioners Standard Ordinary (CSO) Mortality Tables (2001).
Of course, rarely does an individual of age x have precisely the mortality hazard rate shown by Figure 1.2 for age x. Just by virtue of ordinary genetic and lifestyle variations among individuals, some will tend to have a higher hazard rate than others. Furthermore, each time an individual is sick, his or her hazard rate rises a bit, and the more serious the illness, the higher it goes. A man diagnosed with testicular cancer at age 27, for example, might find his hazard rate higher than that of an ordinary 72-year-old. However, if he is fortunate enough to survive the disease (and treatments), then his hazard rate will drop back to about where it should have been in the first place. If the cured individual adopts a healthier lifestyle, with improved diet and exercise, then he even may achieve a hazard rate that is lower than the average for his age.
In short, there is considerable heterogeneity among the true mortality hazard rates associated with individuals of age x, and so actuaries recognize that the hazard rates presented in Figure 1.2 are simply averages across the insured U.S. population. In addition to dividing the population by gender, CSO data include separate tables for nonsmokers and smokers—two segments of the population with markedly different hazard curves. Although it is not feasible to assemble data for every possible subpopulation of interest (such as men diagnosed with testicular cancer) simply because the data would be too sparse for the smaller subpopulations, it is possible to account for the substantial heterogeneity that arises from one particularly salient (and controversial) factor: race.
The use of race as an insurance risk classification has been banned in the United States since the 1970s. Consequently, no separate CSO tables are published for this variable. However, the Centers for Disease Control and Prevention do collect an extensive amount of mortality-related information on the basis of race and ethnicity, which offers a number of sobering insights into contemporary American society. Figure 1.4 provides a simple summary of the relationship between the hazard curves of black and white Americans by plotting, for males and females separately, the ratios (black to white) of one-year mortality hazard rates for various ages. This figure shows that with the exception of ages 16 and 17 for young women, it is substantially more dangerous to be African American than European American for people of all ages from birth to the late 80s.
Although general health differences—resulting from a combination of economic, educational, cultural, and genetic factors—account for most of the discrepancy at age 35 and above, the most striking disparity involves the underlying causes of death for individuals aged 10 through 34. As can be seen in Table 1.2, black males are more than 3.5 times more likely to be murdered than white males by ages 10 through 14, and this increases to more than 9.0 times more likely by the ages of 25 through 34. Similarly, black females are more than 2.5 times more likely to be murdered than white females by ages 10 through 14, and this exceeds 4.0 times by ages 25 through 34.
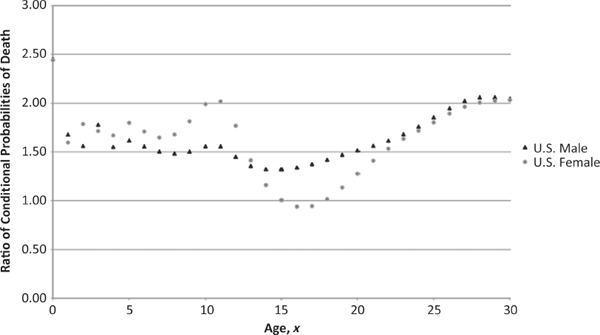
Mortality-Hazard-Rate Ratios (U.S. Blacks to U.S. Whites) Source: National Vital Statistics Reports, Centers for Disease Control and Prevention (2007).
One-Year Mortality Hazard Rates for Most Significant Causes of Death (by Age, Gender, and Race)
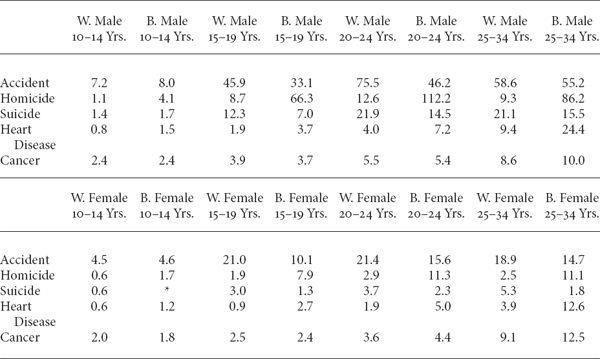
Notes: Mortality hazard rates are expressed in deaths per 100,000 individuals. Asterisk indicates category with insufficient data to provide a meaningful estimate.
Source: National Vital Statistics Reports, Centers for Disease Control and Prevention (2007).
Just as data from deceased black youths tell the story of one scandal, data from deceased white youths recount a second one. As is apparent from even a casual look at Figure 1.4, there are conspicuous “dips” in the ratios of black-to-white mortality hazard rates between ages 15 and 24. (The dip in the plot for females is especially dramatic.) What accounts for these dips, which appear—quite counterintuitively—just at the time black youths begin to be murdered in large numbers, is that white youths begin to die of accidents at a disproportionately high rate (as documented in Table 1.2). Of course, these “accidental” deaths are largely associated with automobile collisions, which—like homicides—could be reduced through improved social policies. It seems rather remarkable that U.S. policymakers find such high death rates among the nation’s youth a tolerable “cost of doing business.”
The Death of Mortality?
Will we ever be able to protect the life exposure from all mortality risks?
Looking to the distant future, it seems reasonable to believe that scientists and engineers will not only take control of the human aging process, but also develop techniques to preserve an individual’s consciousness and memory indefinitely in organic or inorganic media. As we approach that privileged time, the notion of risk inevitably will undergo dramatic change and perhaps even disappear from the human vocabulary.
Along these lines, one might ask: How will the mortality hazard curve change as modern health care technology continues to improve human longevity? Naturally, the value of the curve at each age x should diminish, but will this happen uniformly across all ages or will certain age groups benefit more than others?
In the last century, modern medical advances, while reducing the hazard curve for all ages, have achieved certain particularly marked effects at the extremes—both high and low—of the human life span. In other words, modern medicine has done more to help a newborn survive to age 1 and a 60-year-old survive to age 61 than a 30-year-old survive to age 31. Such a result is not surprising, since ages with lower mortality risk have less room to gain. Additionally, it might be observed that modern science tends to do more to treat the life-threatening illnesses associated with infant mortality and old age than to improve wellness generally.
Let us suppose that this general pattern continues into the future, and the net result is that the entire human mortality hazard curve—from age 0 onward—tends to flatten out toward its overall minimum value of about 0.0002, currently achieved around age 5. What would such a flat hazard curve imply?
Certainly, decreases in the mortality hazard rate anywhere (without corresponding increases elsewhere) imply an increase in life expectancy. However, a flattening of the curve would introduce an additional property. A flat hazard curve means that aging, or senescence, has little or no impact. People continue to die because of accidents and disease, but the rate of death is independent of age. No matter how long one already has lived, this fact becomes irrelevant in assessing how long he or she ultimately will live.
At first blush, the idea of a constant (or decreasing) mortality hazard rate seems counterintuitive—not just for human beings, but for any life form or other perishable entity. After all, how can the rate at which something expires not be affected by how long it already has existed? Does not existence, in and of itself, cause an entity to “wear out” by a natural aging process?
A Role Model, the Hydra
Interestingly, there is at least one life form that appears to possess a constant mortality hazard rate. The lowly hydra (Hydra vulgaris), favorite specimen for microscopic viewing in introductory biology courses, seems to have exactly this property; that is, regardless of how long a hydra has lived, its probability of dying in the next instant remains unchanged.
How can this work? What is the physiological or metabolic explanation of the hydra’s chance of dying being unaffected by age? Clearly, one cannot ignore the concept of wearing out (aging) over time. Hydras, like all other living organisms, are subject to wear from various types of body damage, including nonfatal accidents and illnesses. Therefore, if the hydra’s death rate is constant, then there must be some other factor—some other force—that counters the effect of wear; in fact, not only must this latent factor offset the effect of wear, but it must counter it exactly.
To understand just how special this type of phenomenon is, consider a metaphor from the physical sciences: the story of how Galileo challenged the accepted Aristotelian wisdom of his time that two stones of different weights would fall toward Earth at different speeds, with the heavier stone falling faster. In fact, Aristotle’s intuition was not that unreasonable. Even with the benefit of Newton’s Law of Gravity, it is known that the physical force between Earth and the heavier stone is actually greater than the corresponding force between Earth and the lighter stone. So why does the heavier stone not fall faster?
The answer to this question is comparable to the explanation of the hydra puzzle. Just as there must exist a latent factor or force that exactly counters the hydra’s wear over time, there must be a physical factor or force that exactly offsets the greater force between the heavier stone and Earth. In the case of gravity, the latent factor is the inertia of the heavier stone’s greater mass. In other words, just as Earth pulls harder on the heavier stone (i.e., the force of gravity is greater), the heavier stone offers greater resistance to Earth’s pull.
In the case of the hydra’s survival, the latent factor could be either (or a combination) of two things: (1) a physiological mechanism within the organism that rapidly repairs the damages of wear as they occur; or (2) the selection process that occurs as time passes and each particular organism lives or dies. The former possibility essentially means that the hydra suffers no natural senescence. The latter possibility is subtler and arises from the observation—made in conjunction with our discussion of the histogram in Figure 1.1—that a life form that survives longer becomes a member of a smaller, more selective club. Although a randomly selected hydra of age x2 has experienced more wear than a randomly selected hydra of age x2 (such that x1 is less than x2), the older organism also is a member of a more elite group: those whose track record demonstrates a greater ability to endure the natural wear of living.
Given that the hydra’s latent factor exactly offsets the effect of wear (aging), the first explanation seems more plausible (and appears to be supported by scientific research).9 This is because a physiological mechanism that repairs damage quickly and dependably easily explains the precise offsetting of wear; that is, the mechanism essentially erases the effect of wear as it appears, thereby making it irrelevant to the mortality hazard rate. This is comparable to the way in which the inertial force is proportional to the stone’s mass in the falling-body metaphor, thereby exactly offsetting the force of gravity, which also is proportional to the stone’s mass.
The second effect (selection), on the other hand, might easily overcompensate or undercompensate for the increased risk caused by greater wear. After all, the selection factor could be weaker than the wear factor, as it is for human beings above the age of 5, or stronger than the wear factor, as it is for human beings below the age of 5. (Essentially, human beings below the age of 5 manifest a decreasing mortality hazard rate because the selection effect—that is, the demonstration of greater hardiness that accompanies survival—more than offsets the small effect of aging in this group.)
The Hydra-ization of Humanity
Note that a constant mortality hazard rate provides no guarantee of long life. As the human hazard curve flattens from improved health care, the reason that the human life span increases is that the flattening occurs by reducing the curve’s higher portions, rather than raising its lower portions. Nevertheless, a constant hazard rate does provide one clearly positive effect: that an individual would never sense the approach of death as he or she grew older. Death would remain a significant and inevitable part of life, but people would never experience a feeling of “running out of time.”
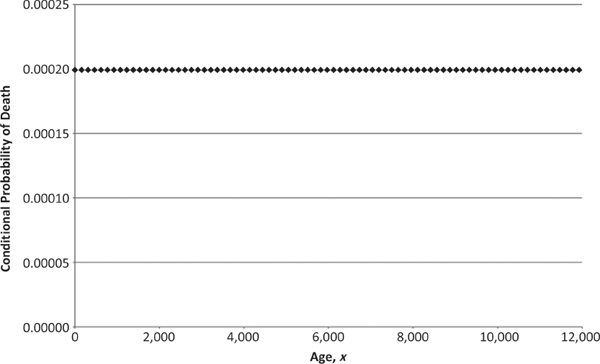
Constant One-Year Mortality Hazard Rate
Although a constant mortality hazard rate is not equivalent to immortality, it does allow for the possibility of arbitrarily long—but not infinite—life. In other words, if the hazard curve truly flattened to the constant 0.0002 mentioned earlier (as shown in Figure 1.5), then one would expect to see individuals surviving to ages beyond 200, 500, 1,000, 5,000, 10,000, etc., but with exponentially decreasing frequency (as shown in the age-at-death histogram of Figure 1.6). Note that the unboundedness of the age at death is a critical aspect of not knowing when death will occur. If human life were bounded—even at 100,000 years—then as people drew closer to the terminal age, they would know that their chance of dying was increasing.10
One wonders about perceptions of death in such a futuristic society. If life expectancy were 5,000 years—as would be the case with a one-year mortality hazard rate of 0.0002—then would death be seen as more terrible (because the amount of life lost is more significant) or as less terrible (because the increased supply of life makes it seem less valuable)? When the mortality hazard rate is constant over all ages and everyone, regardless of age, has the same expected remaining lifetime, will the death of an older person seem just as terrible as the death of a younger person (because the expected amount of life lost is the same)?
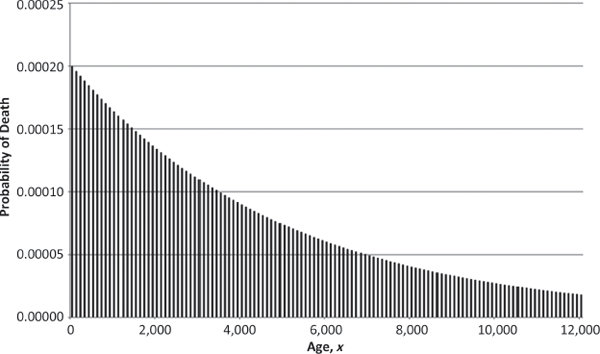
Histogram of Age at Death for One Individual (Subject to Constant Mortality Hazard Rate)
Ungrateful Mortals
While a young child (but old enough to be troubled by the knowledge that everyone eventually dies), I took a measure of comfort from a table of futuristic predictions made by British writer Arthur C. Clarke. Published as an appendix to his 1962 book, Profiles of the Future, Clarke’s table indicated that human immortality would be achieved sometime in the last decade of the twenty-first century.11
Doing the necessary arithmetic, I initially was discouraged by the fact that I would have to live beyond 130 years to survive until the desired time period. However, upon closer inspection, I noticed that Clarke also predicted a process of suspended animation by 2050—suggesting that I need survive only to about age 90, at which point I could be frozen promptly, and then thawed and immortalized in forty or so additional years.12
Apart from specific futuristic predictions, some would argue that human beings can take comfort in the anthropic principle—the idea that the universe must be conducive to our form of life for the simple reason that we exist to observe it. Stronger forms of the anthropic principle suggest that life can get only better and longer for intelligent beings because consciousness will continue to exist only in those realities that permit it to exist.
If hydras possessed the intelligence and consciousness necessary to ponder such things, they might conclude from their constant mortality hazard rate that their universe has been constructed according to a strong “hydra-opic” principle that not only ensures their ability to exist and observe the universe, but also ensures that mortality risk is constant from the moment of birth to that of death. Certainly, it would seem somewhat special to the intellectual hydra to be gifted with complete uncertainty as to when death is likely to occur, since growing older does not increase the rate of death.
In his novel Fiasco, Polish writer Stanislaw Lem offers a deep insight into the nature of human beings (as well as putative extraterrestrial intelligences) that directly challenges these anthropic ideas:13
Whatever had called them into existence gave them only one sure thing: their mortality. Indeed, they owed their very existence to mortality, for without it the billion-year alternations of emerging and dying species never would have taken place. They were spawned by the pit, by the deaths of the Archeozoic, the Paleozoic, the successive geological periods, and along with their Intelligence received the guarantee of their own demise.
Thus, according to Lem, mortality is the logically necessary price of intelligence—a scientific metaphor for the biblical idea that eating the fruit of the Tree of Knowledge led to banishment from paradise and the mortal nature of man. Extrapolating this reasoning into the future, one might conclude that, in a world in which human beings have developed the technological means of avoiding death, human intelligence and progress will stagnate as biological evolution reaches its terminus. So perhaps the much-feared mortality risk is actually a good thing.
ACT 1, SCENE 1
[A psychiatrist’s office. Doctor sits in chair; patient sits on couch.]
DOCTOR: Tell me, Mrs. Morton, what’s on your mind?
PATIENT: I hate to admit it, Doctor, but I think I’m suffering from hydraphobia.
DOCTOR: I see. That’s a fairly common problem, usually caused by a near-drowning or some other traumatic encounter with water in early childhood.
PATIENT: No, Doctor—that’s not what I mean.
DOCTOR: Of course, another common cause of hydrophobia is rabies; but the fear of water generally appears only in the later stages—and you don’t appear to be foaming at the mouth. You haven’t been bitten by any wild animals lately, have you? [Laughs.]
PATIENT: No, you’ve misunderstood. I said “hydraphobia,” not “hydrophobia.” I know it’s irrational, but I’m terrified of hydras.
DOCTOR: Hydras?
PATIENT: Yes. You know, those unpleasant little creatures with tentacles that one can see under the microscope.
DOCTOR: Oh, of course—hydras. And what’s the problem with hydras? They live in the water, don’t they? Are you sure it’s not the water you’re afraid of?
PATIENT: I’m quite sure it’s not the water. I’m simply afraid of being stung by hydras.
DOCTOR: I see—a fear of being stung by hydras. And what exactly is it that concerns you about being stung by hydras?
PATIENT: Well, first of all, I’m afraid it would hurt. But more importantly, I’m afraid of being poisoned.
DOCTOR: Ah—a fear of poisoning, eh? And what is it about being poisoned that bothers you?
PATIENT: Well, naturally, I’m afraid of dying.
DOCTOR: Dying, you say? I think we finally may be getting to the bottom of this. What is it about dying that frightens you?
PATIENT: I’d think that’s obvious, isn’t it? It would mean the end—the end of me, of my entire existence!
DOCTOR: Yes, of course, of course. But is that so bad? After all, it would mean the end of your hydrophobia as well, wouldn’t it?
PATIENT: That’s hydraphobia, Doctor.
DOCTOR: Yes, quite right—hydraphobia. Now, where were we?