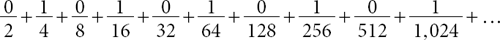
Knowable and Unknowable Complexity
Eenie-meenie-miney-moe, catch a tiger by the toe.
If he hollers, let him go. Eenie-meenie-miney-moe.
Few ideas in mathematics are as mysterious as the notion of randomness. As observed in Chapter 2, random variables are commonly used to model unknown quantities, including the full gamut of risks, in the physical world. However, this generally is done without either a formal definition of randomness or even a convincing demonstration that truly random processes actually exist. Another source of mystery—the conspicuous analogy between randomness as the uncertainty of the outside world and free will as the uncertainty of the mind—offers the alluring possibility that an understanding of randomness can offer an instructive glimpse, however metaphorical, into the fundamental principles of human behavior and ethics.
By addressing the subtleties and limitations associated with an understanding of randomness, the present chapter considers the first of several challenges to a science of risk. In subsequent chapters, I will explore the further challenges of modeling, analyzing, and drawing conclusions from various manifestations of uncertainty in our world—including those generated by the human mind itself.
God’s Dice
When one looks for instances of randomness among the ordinary experiences of life, numerous examples come to mind: stock prices, coin tosses, weather patterns, industrial accidents, etc.1 The most salient aspect of these and similar phenomena is their unpredictability; that is, they are unknown ahead of time and generally cannot be forecast with anything approaching perfect accuracy. There are, however, certain limited circumstances under which such phenomena can be predicted reasonably well: those in which the forecaster possesses what financial traders might call “insider” information.
Just as a stock trader who receives a confidential internal company report may be able to anticipate a significant upward or downward movement in the company’s stock price, so may a magician who is skilled at tossing coins be able to achieve Heads with a high degree of certainty, a meteorologist with the latest satellite imagery be able to forecast the emergence of a hurricane, and a worker who recognizes his employer’s poor safety practices foresee an accident “waiting to happen.” This type of information is obviously available in different degrees to different observers in different contexts. Thus, whereas a privileged stock trader may know with 90 percent certainty that a yet-to-be-disclosed profit report will cause a firm’s stock price to increase by at least 5 percent during the next trading day, an informed meteorologist may be only 80 percent certain that a category 5 hurricane will emerge within the next 48 hours. Moreover, whereas an experienced magician may be 99+ percent certain that his or her next coin toss will result in Heads, a novice magician may be only 75 percent certain of this outcome.
To be clear, therefore, about what is meant by “insider” information, I would say that it consists of any and all information potentially available to the most privileged, persistent, and conscientious observer, whether or not such an observer exists in practice. With regard to a given random variable, I will denote the amount of uncertainty that can be eliminated through such information as knowable complexity (KC). Any residual uncertainty, which cannot be dispelled by even the ideal observer, will be called unknowable complexity (UC).
To illustrate the difference between these two types of uncertainty—and indeed, to provide a concrete example of the latter form—consider what happens when a person tosses a coin onto a table. At the moment of releasing the coin, the individual imparts a certain velocity and rotation to it at a given distance above the table. As the coin travels through the air, it is slightly affected by friction from air molecules. When the coin strikes the surface of the table, the impact causes a succession of bounces and rolls that ultimately results in the coin’s coming to rest with one of its sides exposed.
Clearly, if one could measure the exact position and velocity of every molecule, every atom, and every subatomic particle in the coin tosser’s hand, the coin itself, the air, and the tabletop at the moment of the coin’s release, then the outcome of the toss could be determined with complete accuracy. Under this assumption, all sources of uncertainty would constitute KC. However, such an assumption would be wrong.
No magician, no matter how skillful, can force Heads to come up on every try. This is because the coin’s trajectory and final resting place are affected by events at the atomic level (for example, the minute change in momentum associated with the release of an alpha particle from a trace radioactive isotope in a sensitive nerve cell of the magician’s hand), and, according to Heisenberg’s uncertainty principle, an observer cannot know simultaneously both the exact position and the exact momentum of an elementary particle.2 Consequently, there will always be some residual uncertainty, or UC, associated with the behavior of the particles involved in the coin toss.
This UC affects not only coin tosses, but also stock prices, weather patterns, industrial accidents, and all other physical phenomena. In one sense, its existence is disturbing because it is difficult to believe that every coin and other object in the universe is composed of particles that move about in unpredictable ways—making decisions on their own, so to speak.3 Alternatively, however, one could view UC as an attractive “spice of life” and take comfort in the fact that, as technology provides ever-greater amounts of insider information, UC is the only thing preventing a bleakly deterministic future. Regardless of esthetic considerations, I would equate UC with true randomness.
Incompressibility
In the absence of overt insider information—in other words, when the relevant KC is actually unknown to the observer—probability theory can be used to model KC just as well as UC. This is apparent even without any knowledge of modern quantum physics and was noted by British philosopher David Hume in his famous treatise, An Enquiry Concerning Human Understanding (1748):4
It is true, when any cause fails of producing its usual effect, philosophers ascribe not this to any irregularity in nature [i.e., what I am calling UC—author’s note]; but suppose, that some secret causes, in the particular structure of parts [i.e., what I am calling KC—author’s note], have prevented the operation. Our reasonings, however, and conclusions concerning the event are the same as if this principle had no place…. Where different effects have been found to follow from causes, which are to appearance [emphasis in original] exactly similar, all these various effects must occur to the mind in transferring the past to the future, and enter into our consideration, when we determine the probability of the event.
Hume goes on to assert that “chance, when strictly examined, is a mere negative word, and means not any real power which has anywhere a being in nature.”5 In other words, the concept of chance denotes only the absence of information about underlying causes, and does not distinguish between UC and KC. So what, then, is the purpose of defining these two sources of uncertainty separately? And more pointedly, what is the purpose of seeking the meaning of true randomness?
The answer is that in real life, even in the absence of overt insider information, one often possesses more than one observation of a given random variable. Although one cannot be sure whether the uncertainty associated with a single outcome involves UC or KC, it may be possible to make this determination with a sequence of outcomes. Specifically, statistical methods can be developed to try to determine whether or not the observations evince the systematic behavior expected of KC.
In the 1960s, three mathematicians, Russian Andrey Kolmogorov and Americans Ray Solomonoff and Gregory Chaitin, independently proposed a formal definition of randomness that comports well with the present distinction between UC and KC.6 Working with (possibly infinite) sequences of integers, these researchers suggested that a sequence of integers of a given length is algorithmically random if and only if it cannot be encoded into another sequence of integers that is substantially shorter than the original sequence. Such a sequence is said to be incompressible.
For simplicity, and without loss of generality, one can work with sequences of only 0s and 1s, viewed as binary computer code. To illustrate their concept, consider the infinite sequence 0101010101 …, formed by endlessly alternating the digits 0 and 1, beginning with an initial 0. Clearly, such a sequence is not in any sense random; but to show that it is indeed compressible, one must find a means of mapping it to a shorter (finite) sequence. There are many ways to do this, and one of the most straightforward—but not necessarily most efficient—simply entails matching each letter of the English alphabet with its ordinal number expressed in base 2 (i.e., A = 00001, B = 00010, C = 00011,…, Z = 11010), and then assigning the remaining five-digit base-2 numbers to other useful typographical symbols (i.e., capital-letter indicator = 11011, space = 11100, apostrophe = 11101, comma = 11110, and period = 11111). Using these letters and symbols, one can write virtually any English-language phrase, and so it follows that the phrase “The infinite sequence formed by endlessly alternating the digits 0 and 1, beginning with an initial 0” can be transformed quite nicely into a finite sequence of 0s and 1s, thereby compressing the original sequence dramatically.
It is often convenient to treat (finite or infinite) sequences of 0s and 1s as base-2 decimal expansions between 0 and 1; for example, the sequence 0101010101 … may be interpreted as 0.0101010101 … in base 2, which equals
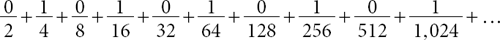
or 0.333 … in base 10. Viewing things this way, it can be shown that almost all of the real numbers between 0 and 1 (of which there are C) are incompressible. In other words, if one were to draw a real number from a continuous uniform probability distribution over the interval [0,1), then one would obtain an incompressible number with certainty. However, in the paradoxical world of the continuum, nothing is straightforward; so, although almost every real number in [0,1) is incompressible, Chaitin has shown that it is impossible to prove that any particular infinitely long decimal is incompressible!7
Simulated Whim
There are many scientific applications in which researchers and practitioners find it useful to simulate sequences of random variables.8 Examples range from computational methods for solving numerical problems by restating them in probabilistic terms to randomized controlled scientific studies to the testing of business and emergency management strategies under a variety of potential scenarios. Although the random variables employed in these applications could be generated by physical processes—like tossing coins and rolling dice—such processes generally are too cumbersome and time-consuming to be of practical use. Instead, researchers and practitioners typically use the chaotic behavior of certain deterministic mathematical processes to create sequences of pseudo-random variables (i.e., sequences that not only are characterized by KC, but also are known to the observer ahead of time).
One of the most common techniques for simulating random numbers is the linear congruential generator (LCG), a simple example of which is the following:
• Let the seed value of the pseudo-random sequence (that is, the 0th term, R0) be 1.
• To get the (i + 1)st term from the ith term, multiply Ri by 5, then add 3, and finally take the remainder after dividing by 16.
Applying this LCG yields the following values for R1 through R16:
8, 11, 10, 5, 12, 15, 14, 9, 0, 3, 2, 13, 4, 7, 6, l.
Unfortunately, the very next integer in the above sequence is 8, which means that the simple LCG begins to repeat itself after only 16 numbers. In fact, cycling occurs with all LCGs, although the length of the cycle may be made arbitrarily long (and is typically at least 2 X 2 X … X 2 [32 times] digits in practice). Other problems with LCGs—such as serial correlation—are not so easily remedied, so more sophisticated methods are often employed.
Now suppose that one would like to construct, very deliberately, an infinite sequence of numbers that is as “incompressible-looking” or “random-looking” as possible. (Keep in mind that it is known, from Chaitin’s impossibility result, that one cannot generate an infinite sequence that is actually incompressible.) To this end, simply using an LCR or other pseudo-random number generator will not suffice; after all, those methods are designed to simulate true randomness, not random-lookingness, so it is reasonably likely that any given sequence produced by such a method would contain noticeably patterned components from time to time, just as would any truly random sequence.
A Surprising Detour
To characterize formally what is meant by a random-looking sequence, it is helpful to introduce the surprise function, which is a highly intuitive mathematical transformation of probability. Basically, the surprise associated with the event x, denoted by s(x), is given by the negative of the base-2 logarithm of the probability p(x).9
Without delving into a formal derivation of surprise, I will make a few observations regarding its properties. First, it can be seen that as p(x) takes on values increasing from 0 to 1, s(x) takes on corresponding values decreasing from positive infinity to 0. Thus, when a specific event x is very unlikely to occur, with a probability approaching 0, its surprise becomes very large, approaching infinity. Likewise, when a specific event is very likely to occur, with a probability approaching 1, its surprise becomes very small, approaching 0. Finally, if x and y are two independent events with identical probability distributions, then the surprise associated with both x and y’s occurring is given by the sum of the surprise associated with x and the surprise associated with y. These properties correspond fairly well to intuitive notions of how the emotion of surprise should operate.
But the real intuitive advantage of working with surprise is that, in terms of metaphorical foundations, it is a more primitive concept than probability itself. As noted previously, the basic motivation for probability is the frequency interpretation—that is, the idea of a long-run rate with which a particular event occurs among a sequence of repeated independent observations. However, surprise is an innate human emotion that requires no underlying supposition of repeated trials. When something occurs, one simply finds it surprising or unsurprising in different degrees. In this way, the concept of surprise provides an elegant unification of the frequency and subjective interpretations of probability: probability as frequency is a transformation of surprise in a context in which repeated trials take place, whereas probability as cognitive metaphor (degree of belief) is just a generic transformation of surprise.
Figure 11.1 reveals how easily surprise can be substituted for probability in a real-world application. Essentially, this plot reproduces the mortality hazard rate data from Figure 1.2, using conditional surprises of death rather than conditional probabilities of death. One particularly striking aspect of this figure is the near linearity of the surprise hazard curve, meaning that as an individual ages by one year, the surprise associated with his or her death decreases by an almost constant amount. Although this approximate linearity may be explained mathematically by the fact that the logarithm of the surprise transformation roughly inverts the exponential component of the Gompertz-Makeham law,10 it also raises an intriguing possibility: Could the emotion of surprise be a biological mechanism calibrated specifically to recognize and assess the fragility of human life?
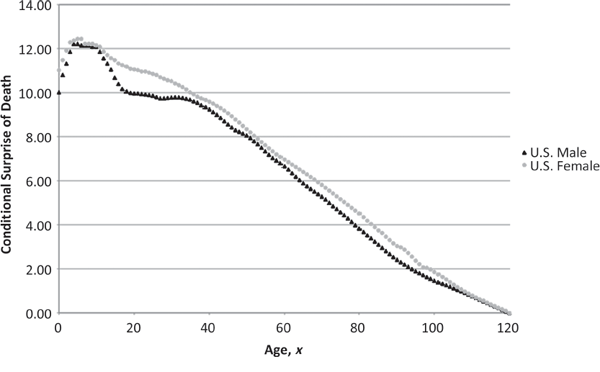
Surprise from One-Year Mortality Hazard Rate Source: Commissioners Standard Ordinary (CSO) Mortality Table (2001).
Least-Surprising Sequences
Consistent with the notation in our earlier discussion of incompressibility, let us consider sequences of independent coin tosses in which one side of the coin (Heads) is labeled with the number 1, the other side (Tails) is labeled with the number 0, and the probability of obtaining a 1 on a given toss is exactly 1/2. (For a real-world example, one might think of the numbers 1 and 0 as indicating whether or not individual insurance claims, as they are closed, are settled for amounts above the claim adjustor’s original forecast—in which case a 1 is recorded, or below the claim adjustor’s original forecast—in which case a 0 is recorded.) For any given sequence length, n, I now will seek the sequence that is least surprising among all sequences of that length and identify that as the most random-looking sequence.
In applying the notion of surprise, one has to identify carefully the probability function from which the least-surprising random sequence is drawn. For example, setting n equal to 5 yields a sample space of 32 possible sequences of 0s and 1s of length 5 (i.e., 00000, 00001, 00010, … 11111). Considering the unconditional probability that any one of these sequences occurs, one sees immediately that it must equal 1/32, so each of the 32 sequences occurs with exactly the same probability. Under this model, both the highly patterned sequence 00000 and the much less patterned sequence 10110 have the same surprise—given by the negative of the base-2 logarithm of 1/32, which equals 5—counter to the desired objective.
One way to construct a probability function that distinguishes between more highly patterned and less highly patterned sequences is to measure the statistical properties of a sequence of n independent coin tosses in terms of various sample parameters, and then to give greater weight to those sequences whose sample parameters are closer to their expected values. For example, one could consider the sample mean, which, for a sequence of 5 coin tosses may be written as
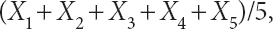
where each Xi is a 0 or 1 that denotes the outcome of the ith coin toss. Clearly, the expected value of this sample mean is 1/2 (which is also the expected value of any one of the Xi), so it would make sense for the probability function to give more weight to those sequences such as 10110 and 00011 whose sample means are close to 1/2 (i.e., 3/5 and 2/5, respectively), than to sequences such as 00000 and 11111 whose sample means are far from 1/2 (i.e., 0 and 1, respectively).
However, using the sample mean is not enough, because one also wants to give more weight to those sequences whose 0s and 1s are more convincingly “scrambled” (i.e., have fewer instances of either long strings of identical outcomes, such as 00011 or 11100, or long strings of strictly alternating outcomes, such as 01010 or 10101). Another way of saying this is that one wishes to favor sequences manifesting less structure from one term to the next—that is, less first-order structure. A useful sample parameter in this regard is given by
(Number of Times Two Successive Terms Are Different)/4,
whose expected value, like that of the sample mean, is 1/2. Extending this logic further, it is easy to develop analogous sample parameters to identify sequences possessing less second-order structure, third-order structure, and fourth-order structure, respectively.
For any given positive integer n, the sample mean and the other sample parameters may be combined in a statistically appropriate manner to form a comprehensive summary statistic, Sn.11 The least-surprising sequence of length n is then found recursively by choosing the value of Xn (i.e., 0 or 1) that minimizes Sn, given the least-surprising sequence of length n-1. This sequence begins as follows:
01110100100001000011111000111111111100101111101101 ….12
Converting the sequence to a base-2 decimal yields
0.01110100100001000011111000111111111100101111101101 …,
which is equivalent to the base-10 decimal 0.455142 ….
Heuristically, the above process admits of the following interpretation: Suppose one begins tossing a fair coin and reveals the successive coin tosses to an observer, one at a time. Assuming that there is some objective method of measuring the observer’s emotional reaction to each toss—and that the observer is able to keep track of second-, third-, and higher-order structures just as well as the first-order structure and overall mean—one would find that the sequence, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, … would seem less surprising (and therefore more random-looking) to the observer than would any other sequence. Also, one could think of the decimal 0.455142 … as representing the least-surprising (and so most random) selection of a continuous uniform random variable from the interval [0,1). This number presumably balances the expectation that such a random variable should be approximately 1/2 (the true mean) with the expectation that it cannot be too close to 1/2 without appearing somewhat artificial.
Cognition and Behavior
Where do the above discussions lead with regard to the understanding of uncertainty and the ability to identify and respond to manifestations of risk? If one associates incompressible sequences with UC and compressible sequences with KC, then the preceding analyses cast a shadow of doubt over statistical hypothesis testing and, indeed, over the entire approach to human understanding known as the scientific method.
Suppose one encounters an infinite sequence of observations and wishes to evaluate whether it evinces KC or UC. Given Chaitin’s impossibility result, it is illogical to state the null hypothesis as H0: “The sequence is characterized by KC” because that assertion could never be rejected (since its rejection would imply that the sequence is incompressible, which cannot be proved). On the other hand, if one were to state the null hypothesis as H0: “The sequence is characterized by UC,” but were confronted with observations from our least-surprising sequence, then one would fail to reject the null hypothesis (i.e., commit a type-2 error) with certainty, regardless of the sample size, because the data would provide no evidence of underlying structure. Although it might be argued, quite reasonably, that the total absence of such structure is itself a manifestation of structure, such “no-structure” structure could never be confirmed with a finite number of observations.
In short, no systematic approach to the study of randomness can ever: (1) confirm a source of uncertainty as UC; or (2) confirm some sources of uncertainty as KC without inevitably creating type-2 errors in other contexts. These are the cognitive constraints under which we operate.
With regard to constraints on human behavior, I would begin by noting the explicit parallel between randomness in the physical world and free will in the realm of the mind. In his analysis of human liberty (of action), Hume ultimately concludes that “liberty, when opposed to necessity, … is the same thing with chance; which is universally allowed to have no existence.”13 In other words, Hume views “liberty,” like “chance,” as a purely negative word; so the concept of liberty denotes only the absence of necessity in one’s actions.
To explore the characteristics of this absence of necessity, let us posit a simple model of human decision making. Assume that at any point in time, t, an individual must select a vast list of decision rules, D1(t),D2(t),...,Dn(t), which tell him or her what to do in any possible future situation. (For example, D1(t) might indicate which foods to eat, D2(t) might give directions on how hard to work, etc.) Assume further that these decision rules are chosen to maximize some overall evaluation function, V(t)(D1(t),D2(t),...,Dn(t)) The crucial question is: Where does V(t+1) come from?
One possibility is that people simply are born with the evaluation function V(0) and that V(t+1) equals V(0) for all t. However, this type of determinism hardly satisfies the absence of necessity that is sought. Another possibility is that a purely random (e.g., quantum-based) phenomenon causes the transition from V(t) to V(t+1). But although this explanation does permit an absence of necessity, it also envisions a detached and impersonal species of free will that is quite unsatisfying. This leaves one final possibility: that V(t) is used to select V(t+1), but in a way that does not converge too quickly to a limiting value. As more than one astute observer has noted, “The purpose of an open mind is to close it.”14 Clearly, however, a mind with free will should be expected to close with a certain degree of deliberation. One way to ensure this restraint is to introduce a certain amount of KC that is unknown to the individual.
Essentially, V(t) has to choose V(t+1), but in such a way that the choice is too complex to be foreseen or analyzed easily. In other words, the individual maximizes V(t)(D1(t),D2(t),...,Dn(t)) over D1(t),D2(t),...,Dn(t) and then sets V(t+1) = Di(t)for some i, where identifying the optimal Di(t) requires a procedure with sufficient KC that its outcome, ex ante, appears random. This may be accomplished simply by the optimization program’s requiring so many steps that it cannot be computed quickly. As any puzzle enthusiast knows, solving a difficult problem often requires a large number of separate attempts, many of which turn out to be false starts. Nevertheless, throughout the challenging process, the solver never feels anything less than the complete conviction that he or she is perfectly free to find the correct solution.
To illustrate (albeit somewhat crudely) how V(t) may be used to select V(t+1), one might imagine a newborn child’s entering the world with an innate philosophy of action, V(0), endowed by Darwinian evolution. Say, for example, that V(0) represents a primitive, clan-based tribalism. Then, as the child progresses through his or her first two decades, V(0) may be replaced by a form of religious monotheism to which the child’s parents subscribe and which the child adopts out of loyalty to its family. Let us call this new philosophy V(1) = Di(0). Assuming that the times are peaceful and resources plentiful, the young adult may find the love and social harmony espoused by V(1) to be a calling to some type of intellectual estheticism, denoted by V(2) = Di(1). Ultimately, after many years of contemplation, the individual may employ V(2) to conclude that the most elegant and intellectually satisfying philosophy of all is Bayesian utilitarianism—to be called V(3) = Di(2) —which is retained for the remainder of his or her life.
An interesting point to consider is whether or not improvements in artificial intelligence will have any impact on our perceptions of free will. Suppose that one could input all of the information relevant to V(t)(D1(t),D2(t),..., Dn(t)) into a computer and that the problem of solving for Di(t) = V(t+1) could be carried out in a relatively short period of time—say, a matter of minutes. In such an eventuality, one conceivably could run through the actual sequence V(t),V(t+1) = Di(t),V(t+2) = Di(t+1) etc. to a point at which it became clear that the sequence either converged or diverged. In the former case, one might adopt a jaded attitude, viewing oneself as nothing more than a mechanical construction of evolution. In the latter case, one might become depressed from knowing that all decisions are essentially ephemeral in nature. At that juncture, one might welcome a discovery that UC—perhaps in the form of minute quantum effects on the human brain—actually does inject some “spice” into one’s internal life.
ACT 3, SCENE 1
[Same psychiatrist’s office. Doctor sits in chair; patient sits on couch.]
DOCTOR: Good day, Mrs. Morton. How are things? Is your iatrogenic asterophobia under control?
PATIENT: My what? Oh, that! Yes, actually it’s fine, I mean, it was fine. It wasn’t a problem because I had avoided thinking about it … until you just mentioned it.
DOCTOR: I see. These iatrogenic—or perhaps in this case I should say iatroregenic—disorders can be very frustrating. Have you considered stopping your visits to the doctor?
PATIENT: Yes, as a matter of fact—
DOCTOR: Of course, if you stopped your doctor visits, then you wouldn’t be able to have your condition properly diagnosed as iatrogenic. So, there’s a bit of a paradox there, I suppose. [Laughs.]
PATIENT: Doctor, it’s funny that you should raise that issue … because I wanted to talk to you about switching psychiatrists.
DOCTOR: Switching? Do you mean you’d prefer to see a different doctor?
PATIENT: Yes. I’m sorry, but … I think it would be better for me.
DOCTOR: I see. And just what is it about my services that you find inadequate, if you don’t mind my asking? It’s not the business about the iatrogenic asterophobia, is it?
PATIENT: No, no. Please understand—it’s nothing personal. I just think that I’d feel more comfortable … communicating … with someone else.
DOCTOR: I’m not sure that I follow you. Are you saying that you’re having trouble expressing yourself to me?
PATIENT: Yes, I suppose that’s it.
DOCTOR: Or is it that you think I’m having trouble understanding what you’re saying?
PATIENT: Well, I’m not quite sure. But in any case, I’d like to ask you to recommend a new doctor.
DOCTOR: I’m sorry, Mrs. Morton, but I feel somewhat confused. If you’re dissatisfied with my services, then why would you want to rely on my recommendation?
PATIENT: Hmm, I see your point. But what alternative do I have? I found you by choosing a name at random from a medical directory, and I don’t want to repeat that procedure.
DOCTOR: No, naturally you don’t. Well, then, that leaves only one solution.
PATIENT: Really? What do you suggest?
DOCTOR: It’s quite obvious, isn’t it? You’ll just have to let me choose a name at random from the medical directory.
PATIENT: Doctor, you’re brilliant!
DOCTOR: Yes. So are you certain you still want to switch?