Trustworthy Transfer; Probable Pooling
People Who Do Things exceed my endurance;
God, for a man that solicits insurance!
I now wish to turn to the issue of what constitutes an insurance company. From the previous chapter, it is evident that such a firm somehow must engage in financial transactions involving aloof and quasi-aloof risks. However, the exact nature of these transactions is not absolutely clear. One fundamental ambiguity is whether a firm must engage in both risk transfer and risk pooling—that is, the two fundamental risk finance transactions that have been with us since the dawn of history—to be an insurance company. As will be seen, this question is fundamental to the legal definition of insurance as refined in U.S. case law.
I will begin by examining the basic or ganization al forms and operational functions of insurance companies as encountered in the most common institutional settings. Although these characteristics are fairly well defined in traditional insurance markets, they become less evident in the so-called alternative markets. Not surprisingly, it is in such less-traditional markets that a clear, guiding definition of an insurance company is most desirable.
Insurance Institutions
Organizational Forms
An insurance company may have one of a variety of ownership structures: stock, mutual, reciprocal exchange, syndicate, or nonprofit.2 Stock insurance companies, like other stock corporations, are owned by shareholders who have purchased common stock and have the right to vote for members of the firm’s board of directors. Mutuals and reciprocal exchanges are owned by their policyholders—the former existing as incorporated entities in which the policyholders elect the board of directors, and the latter as agreements among the policyholders formalized by a power-of-attorney transfer to the firm’s management. Syndicates, like those of Lloyd’s of London, are owned by groups of investors whose underwriters bid for insurance contracts against other syndicates. Nonprofit insurance companies operate much as other nonprofit organizations, but may be formed in accordance with laws and regulations designed specifically for nonprofit insurance entities.
Company Operations
With regard to business operations, there may be substantial diversity among insurance companies within a given market. However, general patterns of institutional practice reveal that certain operations are intrinsic to the insurance business. These include:
1. writing contracts of insurance, through which the responsibility for financial loss from an aloof or quasi-aloof risk is transferred to the insurance company in return for a premium payment made by the policyholder;
2. bearing risk, by taking ultimate responsibility for the payment of random loss amounts that may be substantially greater than premiums collected;
3. complying with insurance regulation, by securing company and agent licenses necessary to sell insurance, by satisfying required solvency standards, and by receiving the approval of policy forms and rates subject to regulatory authority;
4. pricing, by selecting premium levels to achieve a certain profit given an anticipated portfolio of policyholders;
5. underwriting, by selecting a portfolio of policyholders with various risk characteristics, where the losses generated by the selected policyholders are expected to allow a certain profit given current premium levels;
6. claim management, through which reported claims are evaluated to identify appropriate payments and loss reserves, unreported claims are forecast to establish additional loss reserves, paid losses may be offset by salvage and subrogation efforts, and potential fraud is investigated and challenged;
7. loss control, by designing products and setting prices to reduce moral hazard, morale hazard, and adverse selection and by working with policyholders to prevent and mitigate losses;
8. financial management, through which the insurance company’s invested assets are managed to achieve the desired balance between risk and return, as well as the matching of investment income with future loss payments, all subject to regulatory constraints on the types of investments permitted;
9. marketing, through which new primary and reinsurance business is generated and old business is retained, in concert with the marketing efforts of any brokers and independent agents involved in the production of business; and
10. administration, through which the various operations of the company are coordinated and accounting, auditing, and legal functions are carried out.
Although most traditional insurance companies perform the above operations in-house, it is not unusual for companies to outsource one or more of these functions to specialty firms. This is particularly true within the alternative insurance market, consisting of self-insurers (i.e., corporations that estimate and set aside financial reserves to cover their anticipated losses from aloof and quasi-aloof risks), risk-retention groups (i.e., groups of corporations that join together to form collective self-insurance funds), and captive insurance companies (i.e., subsidiary companies formed primarily to write insurance for their parent corporations). Interestingly, however, the risk bearing practices of these alternative entities do not deviate dramatically from those of traditional insurance companies. Although the alternative market does tend to place greater emphasis on the bearing of risk by policyholders, this is conceptually no different from what is commonly found in the mutuals and reciprocal exchanges of the traditional market.
Enterprise Risk Management
Whatever the particular corporate form and internal systems of an insurance company, its financial bottom line is given by its total rate of return (TROR), which may be expressed as follows for a fixed accounting period:
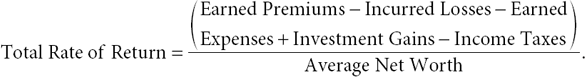
The TROR represents the insurance company’s earnings, net of taxes, as a proportion of the capital (net worth) invested in the insurance enterprise and is a random quantity that fluctuates with the company’s underwriting and investment results. The process of managing the company’s TROR—called enterprise risk management (ERM)—is a fundamental responsibility of the company’s officers and directors and often is accomplished by optimizing the trade-off between the TROR’s expected value and standard deviation (i.e., by mean-standard deviation optimization) supplemented by scenario-based stress testing using VaR and other tail-sensitive risk measures. If the tail of the TROR’s probability distribution is too heavy for the standard deviation to be finite, then mean-standard deviation optimization obviously cannot be used, and one must rely on alternative measures such as those discussed in Chapter 3.
To provide an overview of an insurance company’s ERM program, I will assume that the expected value of the TROR is well defined and that it possesses a fixed “target” expected value, thus leaving the company with the issue of minimizing the TROR’s variability. The ERM process then consists of four basic steps: (1) risk identification; (2) risk assessment; (3) risk control; and (4) risk finance.3
Risk Identification and Assessment
Quite naturally, the first step is the identification of all risks—aloof, quasi-aloof, and non-aloof—that the insurance company faces. Given the particular components of insurance operations summarized above, it is clear that these risks consist primarily of the losses paid to policyholders according to the terms of the various policy contracts sold, as well as the investment returns earned on both net worth and the premium-income stream prior to the payment of losses.
After all significant risks have been identified, an insurance company must assess the overall importance of each risk in terms of its potential impact on the firm. For the aloof and quasi-aloof risks associated with insurance underwriting, this is accomplished by estimating the expected value and variability of both the claim frequency and loss severity associated with each policyholder, along with statistical dependencies among policyholders (e.g., two buildings in the same coastal region may be vulnerable to damage from the same hurricane and therefore have positively correlated frequencies and severities). For non-aloof investment risks, the company similarly must estimate the expected values and variabilities of individual returns, as well as statistical dependencies among returns. In the case of investments, positive and negative correlations often play a much larger role, as would be expected from the fundamental character of non-aloof risks.
Risk Control and Finance
Figure 7.1 provides conceptual guidelines for controlling an insurance company’s aloof and quasi-aloof underwriting risks through the techniques of frequency mitigation, severity mitigation, and avoidance.
If a given exposure possesses a high expected frequency, but only a low or modest expected severity, then frequency mitigation is appropriate. For example, an insurance company offering property coverage for a low-value apartment building with numerous individual units—each of which could be the source of an accidental fire—is likely to address the high expected frequency by requiring the owner to install fire extinguishers and sprinkler systems. However, if an exposure possesses a high expected severity, but only a low or modest expected frequency, then severity mitigation is appropriate. For example, an insurance company writing medical malpractice liability coverage for a hospital with a small maternity ward—and therefore the potential of expensive “damaged baby” claims—is likely to address the high expected severity by taking an active role in claim settlement negotiations. Finally, if an exposure is characterized by both a high expected frequency and high expected severity, then total avoidance is likely the best approach. An example of this is the writing of asbestos liability coverage for a large asbestos-manufacturing plant with a poor safety record.

Risk Control for Aloof/Quasi-Aloof Risks (Conceptual)
For non-aloof investment risks, the paradigm of Figure 7.1 is less directly applicable because investment returns generally cannot be broken down so neatly into separate frequency and severity components. However, one certainly could equate severity mitigation and/or avoidance with deliberate efforts to eschew highly volatile investments, such as financial options, junk bonds, and certain categories of real estate.
Figure 7.2 summarizes “textbook” guidelines for reducing the variability of an insurance company’s aloof and quasi-aloof underwriting risks through the methods of diversification (via risk pooling) and hedging (via risk transfer).4 Having avoided (during the risk control step) those unacceptably costly exposures with both high expected frequencies and high expected severities, an insurance company can focus on the exposures exhibiting high expected frequencies or high expected severities alone. In the former case, the likely presence of a great number of similar and statistically independent claims permits the company to take advantage of the law of large numbers (LLN) by risk pooling/diversification.5 In the latter case—which includes regional catastrophes such as hurricanes, earthquakes, and even terrorist attacks—there presumably is an insufficient number of claims to diversify successfully, so the insurance company is more likely to employ risk transfer/hedging by purchasing reinsurance from another company. For exposures with both relatively low expected frequencies and relatively low expected severities, the insurance company will continue to pool (retain) these risks, but will do so informally (i.e., with less explicit contemplation of the LLN).
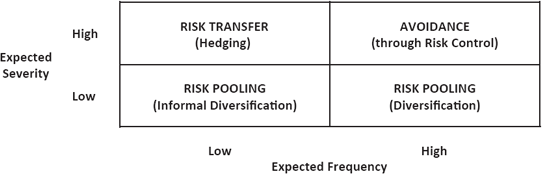
Risk Finance for Aloof/Quasi-Aloof Risks (Conceptual)
Although the scheme indicated by Figure 7.2 seems intuitively plausible, it presents two conceptual difficulties:
• By indicating risk transfer for exposures with low expected frequencies but arbitrarily high expected severities, the conventional paradigm suggests that there is always some reinsurance company willing to assume (and presumably pool) those catastrophe losses. However, this is inconsistent with actual market experience, in which certain types of catastrophe exposures—for example, damages from terrorist attacks—are not readily covered by private reinsurance.
• There is an apparent inconsistency between the effect of increasing expected frequencies on losses with low expected severities and those with high expected severities. In the former case, diversification appears to apply because risk pooling is effective for higher expected frequencies, whereas in the latter case, diversification does not appear to work because the firm must resort to avoidance. One possible explanation for this discrepancy is that losses with higher expected severities also possess heavier tails, thus inhibiting diversification. However, there is no obvious theoretical or empirical reason this should be true.
To reconcile Figure 7.2 with the above two objections requires the formal mathematical modeling of loss portfolios and a careful study of the boundaries separating the regions of risk pooling, risk transfer, and avoidance. Given the potentially significant role of heavy tails, it is particularly important to evaluate the decreasing benefits of risk pooling as the tails of the relevant loss distributions become heavier.
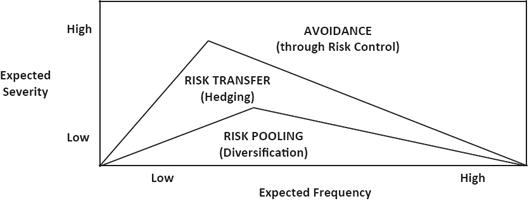
Risk Finance for Aloof/Quasi-Aloof Risks (More Realistic)
One such analysis, based upon a Lévy-stable approximation to a sum of Pareto losses, and employing the CBSD risk measure discussed in Chapter 3, yields Figure 7.3 as a more realistic and conservative alternative to Figure 7.2.6 Essentially, the new paradigm favors the safer alternative (i.e., avoidance over risk transfer, risk transfer over risk pooling) whenever there is ambiguity as to the optimal risk financing method. Therefore, beginning with the apex of either boundary (i.e., the upper one between avoidance and risk transfer, or the lower one between risk transfer and risk pooling), the indicated boundary must be increasing on the left as the relative efficacy of diversification grows over expected frequency for light-tailed losses and decreasing on the right as the relative efficacy of diversification diminishes over expected frequency for heavy-tailed losses.
For non-aloof investment risks, Figure 7.3 is less directly applicable because, as mentioned above, investment returns generally cannot be broken down into separate frequency and severity components. Consequently, the financing of investment risks is typically handled by selecting optimal diversification and hedging strategies in a risk-vs.-return analysis. This type of approach, like Figure 7.3, must account for the presence of heavy-tailed return distributions as necessary.
A Simple Model of Risk Finance
Given the complexities of modern insurance and other financial markets, it is rather remarkable that the financing of an insurance company’s aloof, quasi-aloof, and non-aloof risks is based largely upon only two fundamental tools: diversification and hedging.7 Interestingly, these two methods match precisely the two earliest forms of “insurance” attributed to the ancients: the division and swapping of cargoes among ships (diversification through risk pooling) and the use of bottomry contracts (hedging through risk transfer). To explore the properties of these two methods more deeply, and also to highlight the importance of a third tool of risk finance that is often overlooked, I will consider a simple analysis of the variability of a random loss or investment portfolio with finite standard deviation as the portfolio undergoes diversification and/or hedging.
Conceptually, diversification describes the marginal reduction in variability that occurs when the individual components of a portfolio become less positively correlated with each other, whereas hedging describes the marginal reduction in variability that arises when the individual components become more negatively correlated with each other. In both cases, it is assumed that these processes are implemented while keeping the overall expected value unchanged. Also, the qualification “marginal” is used to indicate that, although both processes should contribute toward some reduction in variability, there is no guarantee that either process, by itself, will reduce the portfolio’s total variability.
Mathematically, both processes can be captured using a simple “before-and-after” description of the portfolio. I will begin by modeling the initial portfolio as a random variable, X, which may be viewed as the sum of any number of distinct random components (e.g., insurance losses, stocks, cash, etc.) that can be mutually statistically independent or dependent. I then will assume that a portion of this portfolio, to be called XOut, is removed, and that another component, called XIn, is simultaneously added. In short, the “before” portfolio consists of X, and the “after” portfolio consists of X–XOut+XIn.
Now, if one wants the exchange of XIn for XOut to reduce the total variability (as measured by the standard deviation), then SD[X–XOut+XIn] must be less than SD[X]. Defining the subportfolio XKeep as the difference X–XOut, it can be shown that there are a number of ways this reduction in variability can be accomplished based upon the relationships among the three standard deviations—SD[XKeep], SD[XOut], and SD[XIn]—and the two pairwise correlations—Corr[XKeep, XOut] and Corr[XKeep, XIn].
Devilish Diversification
Formally, one can say that diversification occurs if Corr[XKeep, XOut] is positive and greater than Corr[XKeep, XIn]—in other words, if the portfolio is changed so that the resulting components are less positively correlated with each other. (Note that although Corr[XKeep, XIn] is often nonnegative in practice, there is no reason to make this a strict requirement of the definition of diversification.) As previously noted, one example of diversification is the retention of uncorrelated aloof/quasi-aloof risks by an insurance company (i.e., risk pooling). However, it is crucial to point out that such pooling must be accompanied by concomitant increases in the company’s invested capital so that the standard deviation of the total loss amount per ownership share decreases. This is analogous to increasing the number of boats as the total amount of cargo increases in the Chinese marine-trader story. If the amount of invested capital does not increase, and the insurance company simply pools a growing number of exposures, then this is comparable to stacking more and more cargo in a fixed number of boats, and a type of “false diversification,” in which the standard deviation actually increases, takes place.
For an insurance example in which it is unnecessary to assume increasing invested capital, consider an insurance company with a fixed amount of capital that elects to swap part of a group of insured Florida property exposures (subject to hurricane catastrophe risk) for part of another company’s insured California property exposures (subject to earthquake catastrophe risk). For non-aloof risks, an analogous example would arise from replacing some of the shares of one asset by those of another in an investment portfolio. Nevertheless, even with such simpler forms of diversification, there is still a devil lurking in the details. Specifically, SD[X–XOut+XIn] can easily be greater than SD[X] if SD[XIn] is too large compared to SD[XOut].
Heavenly Hedging
Next, one can say that hedging occurs if Corr[XKeep, XIn] is negative and less than Corr[XKeep, XOut]—that is, if the portfolio is altered so that the resulting components are more negatively correlated with each other. (In this case, note that Corr[XKeep, XOut] often is ο in practice because XOut is cash that is used to purchase the hedging instrument XIn; however, there is no reason to impose this condition on the definition of hedging.) As noted above, an insurance company’s purchase of a reinsurance policy to offset aloof/quasi-aloof risks constitutes one example of hedging (i.e., risk transfer). For non-aloof risks, purchasing one or more asset derivatives to offset part of an investment portfolio provides a comparable example of hedging.
With hedging, things generally are much more “blessed” than with diversification. This is because there is no obvious possibility of “false hedging,” and SD[X–XOut+XIn] is generally likely to be less than SD[X].
Purloined Pacification
Finally, one can say that pacification occurs if SD[XIn] is less than SD[XOut]—that is, if the portfolio is changed by replacing a portion with something less variable. This idea is quite simple and obvious, but—like Edgar Allen Poe’s purloined letter—appears to be overlooked by being “hidden in plain sight.”8 I have chosen the term “pacification” to suggest the calming or tranquilizing influence of the process on a portion of the original portfolio, and the process is essentially the opposite of gambling—that is, the taking of unnecessary risks for excitement.
The fundamental importance of pacification is seen very clearly by noting that: (1) neither the process of diversification nor that of hedging, by itself, can guarantee a reduction in a portfolio’s total variability, even with Corr[XKeep, XOut] as large as possible (i.e., 1) in the former case, and Corr[XKeep, XIn] as small as possible (i.e., -1) in the latter case; (2) diversification and hedging, taken together, are still insufficient to guarantee a reduction in a portfolio’s total variability, even with Corr[XKeep, XOut] as large as possible and Corr[XKeep, XIn] as small as possible;9 but (3) either diversification or hedging, taken together with pacification, is sufficient to guarantee a reduction in a portfolio’s total variability.
A Taxing Tale
In the United States, the legal definition of an insurance company has arisen repeatedly in the context of the government’s tax treatment of insurance premiums paid to captive insurance companies.10 This is not surprising, given that the notion of a captive insurance company seems, at first consideration, somewhat absurd. After all, how can a parent company buy insurance from (i.e., transfer risk to) a company that it owns? In this section, I will use certain observations regarding the captive insurance tax controversy to refine the definition of insurance.
Under U.S. federal law, the authorization to deduct certain types of business expenses derives from the Internal Revenue Code (IRC). An expense is commonly deductible in the computation of taxable income if either: (1) the expense is specifically identified by a section of the IRC; or (2) the expense is ordinary, necessary, reasonable in amount, and incurred in connection with a trade or business, and the expense is not a capital expenditure, personal expenditure, or an expenditure related to taxexempt income or contrary to public policy.
Insurance tax policy has consistently favored transfers of risk to traditional insurance companies over alternative risk management methods, most notably self-insurance. This bias goes back as far as the Tariff Act of 1909 and has persisted through subsequent laws to the present. The principal advantage given to traditional insurance over self-insurance is that commercial insurance premiums paid to traditional insurance companies are tax deductible as general business expenses, whereas self-insurance reserves are not.
In attempting to establish whether or not a transaction with a captive insurance company constitutes insurance, one encounters a fundamental conflict between two goals of federal tax policy: (1) respecting the legal separateness of corporate entities within an affiliated group of companies; and (2) challenging the economic substance of intercompany transactions that appear to be for no purpose other than minimizing taxes. These two goals collide in the case of captives because risk is being transferred to an affiliated corporation in a manner that may resemble self-insurance.
Economic-Family Theory
To avoid conflict with the doctrine of legal separateness while still denying the tax deductibility of premiums paid to captives, the IRS advanced its economic-family theory in 1977, which treated the parent and the captive as one unit for purposes of evaluating the economic impact of reductions in loss variability. Under this theory, no insurance transaction between a parent company and its captive insurance subsidiary results in any transfer of risk outside the corporate family, so such transactions do not justify tax deductions.
Clearly, the economic-family theory is intuitively appealing. It is hard to argue that buying insurance from a wholly owned captive provides any meaningful transfer of risk when every insurance loss paid by the captive results in an equivalent decrease in the value of the captive on the parent’s balance sheet. In effect, the economic-family theory seems reasonable because it questions the efficiency of risk transfers between a parent and its captive.
However, the credibility of the economic-family theory was severely strained in litigation with U.S. retailer Sears after the IRS denied tax deductions for premiums paid by Sears to its then wholly owned subsidiary Allstate Insurance Company.11 Although it was true that every insurance loss paid by Allstate simply decreased the value of Allstate on Sears’s balance sheet, it also was true that more than 99 percent of Allstate’s business came from unrelated risks, and it was difficult to see why Sears’s transaction with Allstate was really any different from a comparable transaction with any other major insurance company.
Variability-Reduction/Unrelated-Business Theory
Seeking to develop a coherent approach capable of respecting arrangements that intuitively look like insurance while still denying tax deductions in the case of wholly owned pure captives (i.e., wholly owned captives that write insurance for only their parents), the courts resorted to a definition of insurance advanced by the U.S. Supreme Court in the case of Helvering v. LeGierse.12 Although the facts of that particular case were far removed from the context of captives, the federal courts relied on the Supreme Court’s description of insurance as consisting of “risk shifting” (i.e., risk transfer) and “risk distribution” (i.e., risk pooling).13 This terminology is consistent with what is found in many conventional textbooks; however, there is not general agreement as to whether or not both of these characteristics are necessary in order for a transaction to qualify as insurance.
In a series of rulings in 1991 (including that of the Sears case), the U.S. tax courts looked for both risk transfer and risk pooling and rejected the IRS’s economic family theory in favor of the variability-reduction/unrelated-business theory.14 Specifically, the courts determined that the writing of unrelated exposures composing a significant portion of a captive’s business (as little as 29 percent of premiums in one case) caused substantial pooling of risk over the insurance premiums originating outside the corporate group and that this risk pooling in turn caused risk transfer to occur, thereby justifying tax deductions.
In these cases, the courts heard testimony from taxpayers’ experts to the effect that certain measures of “relative risk” or “average risk”—such as the ratio of the standard deviation of total insured losses to total insurance premiums—capture the statistical effects of risk pooling and decrease to ο as the number of exposure units from unrelated business increases to infinity. Accepting this type of argument, the courts concluded that if a captive writes a significant amount of unrelated business, then that will cause risk to be pooled over the premiums originating outside the corporate group and thereby transferred.
Apparently, the courts at that time were attracted by the intuitively reasonable approach of using unrelated business as a requirement for insurance. This approach is appealing because it appears to explain why the Sears/Allstate transaction should be treated as insurance, even though the risk transfer from Sears to Allstate is not efficient (i.e., losses are not removed from the parent’s balance sheet). However, by focusing on the statistical effects of unrelated exposure units, the courts overlooked the fact that “relative-risk” or “average-risk” ratios manifest the same statistical behavior with respect to the number of exposure units, regardless of whether those exposure units come from related or unrelated business. In contrast, an earlier (1989) federal appeals court decision in a case involving health service provider Humana, Inc., correctly observed that the statistical effects of risk pooling can be achieved through both related and unrelated business.15
Transfer-Efficiency/Market-Forces Theory
In the case of Humana, the government had sustained a setback on a different front. Initially, the IRS had denied the tax deductibility of premiums paid by both a parent and a number of brother/sister subsidiaries to a captive insurance company owned largely by the parent. Relying on a version of the economic-family theory commonly known as the net-worth approach, the government argued that risk and premium never leave the corporate group, so insurance purchased from the captive is tantamount to self-insurance. However, on appeal, the Sixth Circuit Court decided to allow tax deductions for premiums paid by brother/sister subsidiaries, but not for premiums paid by the parent.
The appellate court’s reasoning was based upon a balance-sheet analysis recognizing that from the perspective of a brother/sister subsidiary, risk is transferred because losses paid by the captive are not reflected in the subsidiary’s financial statement. In permitting tax deductions for brother/sister premiums, the court’s opinion effectively recognized that tax deductibility could be justified by the extent to which: (1) losses are removed from the policyholder’s balance sheet; and (2) the policyholder makes an independent decision to purchase insurance from the insurance marketplace.
This approach afforded the starting point for the transfer-efficiency/market-forces theory, which my colleague Moshe Porat and I developed together.16 According to this theory, tax deductions for transactions between a parent (or brother/sister) company and a captive can be justified by the degree to which the risk transfers are economically efficient in removing losses from the policyholder’s balance sheet. This efficiency in turn is ensured by the degree to which the captive is constrained by market forces to operate in the manner of a traditional insurance company.
Essentially, this theory provides a definition of an insurance company based upon the following refined notions of the roles played by risk transfer and risk pooling:
• Risk transfer involves the shifting of responsibility for the payment of losses from a ceding party (the policyholder) to an assuming party (the insurance company). In this process, risk is transferred efficiently if the assuming party provides a reasonable assurance that it will pay for losses.
• Risk pooling refers to increases in the stability of an insurance company or other financial entity primarily by increasing the number of uncorrelated exposure units and the operation of the LLN. In the case of a simple risk pool, in which each individual member cedes one exposure unit to the pool and assumes responsibility for paying a proportional share of the pool’s total losses, an increase in the number of members reduces the variability of each member’s loss payment. In the case of an insurance company, in which increased stability is associated with a smaller probability of insolvency, an increase in the number of exposure units must be accompanied by an appropriate adjustment in the level of invested capital.17 The manner in which the company does this will be dictated by market forces.
To summarize, I would offer the following definition: An insurance company is an enterprise engaged in the business of assuming financial responsibility for the transfer of aloof/quasi-aloof risks in an economically efficient manner by operating subject to the forces of the market place for transferring such risks.
ACT 2, SCENE 2
[Offices of Trial Insurance Company. Head clerk and supervisor both stand by clerk’s desk.]
BOSS: Mr. Sorter, it’s my pleasure to welcome you to your first day of employment at Trial Insurance. I suppose you’ve heard our motto: “If it’s not a Trial, it’s not a policy.” [Pauses.] And this, of course, is your desk. It’s rumored to have been used by Mr. Kafka, many years ago, naturally.
CLERK: Do you mean Franz Kafka, the writer?
BOSS: Yes. He’s one of many luminaries to have graced the insurance world—along with composer Charles Ives, poet Wallace Stevens, tenor Luciano Pavarotti, and course, psychic Edgar Cayce.
CLERK: Really? Edgar Cayce worked in insurance? Who would have predicted that? [Smiles.] What was he, an actuary?
BOSS: [Wags his finger facetiously.] Oh, Mr. Sorter, I can see that your dry sense of humor will be appreciated here.
CLERK: Thank you. Now I suppose I should get to work. But my desk appears empty, sir.
BOSS: Not for long. [Picks up tall stack of paper from side table and sets it definitively on Sorter’s desk.] This is today’s incoming mail. It consists of application forms, claim forms, complaint letters, advertisements for reinsurance, etc.
CLERK: And my job?
BOSS: Your job, as Trial’s head clerk, is to sort them into seven piles according to their area of relevance: Underwriting, Claim Adjustment, Accounting, Actuarial, Legal, Miscellaneous, and Other.
CLERK: I see. But what’s the difference between Miscellaneous and Other?
BOSS: [Looks around to make sure he is not overheard.] Miscellaneous actually means “Other,” and Other actually means “Suspicious.” That is, you should place any items that seem suspicious—suspicious applications for coverage, suspicious claim forms, etc.—into the Other pile.
CLERK: I see. But wouldn’t it be easier just to call Other “Other” and Suspicious “Suspicious”?
BOSS: Well, Mr. Sorter, you shall be forgiven because you are new to Trial Insurance. But the first thing you must understand is that the insurance business is like no other: We have no inventory; we have no physical product; all we sell is a promise that may or may not be acted upon, depending on circumstances. And those circumstances, Mr. Sorter—those circumstances are subject to manipulation!
CLERK: Manipulation?
BOSS: Yes, Mr. Sorter, manipulation. It’s like fighting a guerrilla insurgency: you never know which customer is your friend and which is your enemy. As I said, the insurance business is like no other: We actually prefer not to do business with those who are most eager to do business with us. Instead, our job is to be eternally suspicious: suspicious of adverse selection, suspicious of moral hazard, suspicious of excessive medical treatments, suspicious of malingerers, suspicious of suspicious claims, and so forth.
CLERK: Suspicious.
BOSS: Yes, Mr. Sorter, suspicious. But despite the fact that we are suspicious, we don’t want to be perceived as suspicious. It’s not good for our reputation, you understand. Legitimate customers wouldn’t want to do business with us if they felt that securing a policy or getting a claim paid were a trial, so to speak.
CLERK: I, I believe I understand, sir. But how do we form our suspicions? How do I know when to place something in the Other pile and when not to?
BOSS: A very good question, Mr. Sorter. And the answer can be summed up in one word: intuition—judgment—instinct—discernment—perceptivity—divination—precognition. Indeed, those are the characteristics of a truly great insurance executive. Now, Mr. Sorter, are you ready to do battle?
CLERK: I am, sir!
BOSS: Good. Then go to work!
[Sorter does not move toward papers on desk.]
BOSS: Mr. Sorter, I said it was time to work. What are you waiting for?
CLERK: Sir, I believe I’ll need to see your identification.