It has been often recognized that any probability statement, being a rigorous statement involving uncertainty, has less factual content than an assertion of certain fact would have, and at the same time has more factual content than a statement of complete ignorance.
In the first two chapters, we encountered a few simple probability distributions. Now, we will examine more complex distributions whose shapes make them appropriate for characterizing insurance and other financial risks. In particular, two important families of distributions will be introduced: the Pareto family and the symmetric Lévy-stable family, both of which are frequently used to model particularly “risky” random variables with heavy tails (i.e., with large amounts of weight spread over the more extreme values of the random variable).
To describe the measurement of risk, I will begin by defining the statistical moments of a distribution, and then show how these quantities are used to compute the expected value (mean), standard deviation, and other helpful parameters. Although many moments are quite informative, none of them—not even the mean—exist for all distributions. Interestingly, it is easy to show that “pathological” distributions without means, standard deviations, etc. can be generated by very simple and natural random processes and thus cannot be overlooked.
Probability Distributions and Risk
So far, we have seen graphical illustrations associated with four probability distributions: specifically, the PMFs of the discrete uniform and geometric distributions and the PDFs of the continuous uniform and exponential distributions. Although these distributions arise in a number of important contexts, they are not particularly useful for describing insurance loss amounts or the returns on investment portfolios. For the former case, I will focus on continuous random variables defined on the positive real numbers (since individual loss amounts generally are viewed as positive real numbers that are rounded to the nearest cent for convenience), and for the latter case, I will consider continuous random variables defined on the entire real number line (since investment returns generally are computed as natural logarithms of ratios of “after” to “before” prices, which can be either negative or positive).
Insurance Losses
Although the exponential distribution (whose PDF is shown in Figure 2.5) is defined on the positive real numbers, it is not commonly used to model insurance loss amounts because it cannot accommodate a very wide range of distributional shapes. This limitation arises from the fact that it is a one-parameter family; that is, the PDF contains only one mathematical quantity that can be varied to obtain the different members of the family. All members of the exponential family possess PDFs that look exactly like the one in Figure 2.5, except that their curves may be stretched or compressed horizontally. (Figure 2.5, the value of the parameter happens to equal 1/6.)
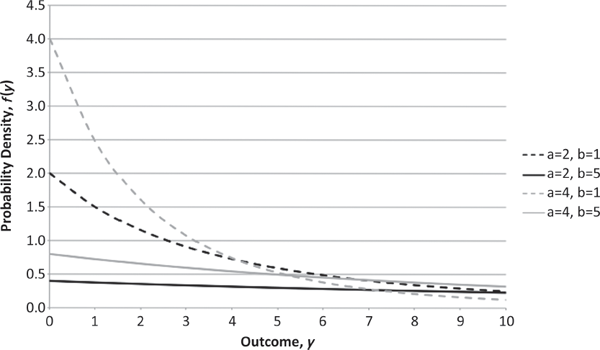
A richer, two-parameter family that is commonly used to model insurance losses is the Pareto family,2 for which several PDFs are plotted on the same pair of axes in Figure 3.1.3 From this figure, one can see that as the positive parameter a grows smaller, the tail of the PDF becomes heavier (thicker), so that more weight is spread over very large values in the sample space. Naturally, the heaviness of the PDF’s tails is crucial in determining how variable the associated random loss is.
PDFs of Pareto Random Variables with Various Parameters (Defined on Positive Real Numbers)
Asset Returns
In Chapter 6, I will offer an explanation of the fundamental qualitative differences between traditional insurance-loss risks and those, such as asset returns, arising in other financial contexts. For the moment, however, I simply observe that these two types of risks are quantitatively different in terms of the probability distributions commonly used to model them. As noted above, whereas insurance losses are generally taken to be positive real numbers, asset returns may take on any real values, negative or positive. Since asset prices tend to be set so that they have an approximately equal chance of going up or down, one also finds that asset-return distributions are fairly symmetrical.
The most commonly used family of probability distributions for modeling asset returns is the two-parameter Gaussian (or normal) family,4 for which several PDFs are plotted on the same pair of axes in Figure 3.2. In fact, much of financial portfolio theory is often derived by explicitly assuming that asset returns are Gaussian. However, since the seminal work of French mathematician Benoit Mandelbrot, it has become increasingly clear that the tails of the Gaussian PDF are too light (thin) to account for rare, but persistently observed large and small values of asset returns.5 Fortunately, it is quite straightforward to generalize the Gaussian distribution to the three-parameter symmetric Lévy-stable family6 by adding a parameter a that is analogous to the a parameter in the Pareto family (for values of a in the interval (0,2], where a equals 2 for the Gaussian case). As is shown in Figure 3.3, the tails of the symmetric Lévy-stable PDF become heavier as a becomes smaller. Here again, the heaviness of the PDF’s tails is crucial in determining how variable the associated random asset return is.
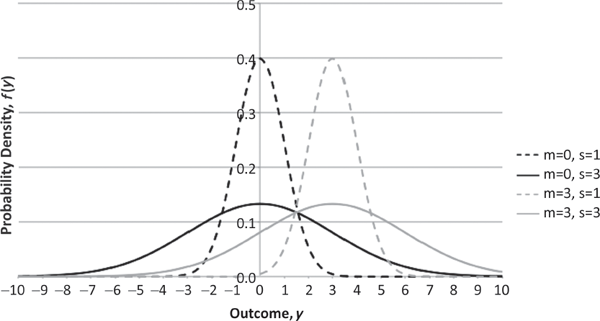
PDFs of Gaussian Random Variables with Various Parameters (Defined on All Real Numbers)
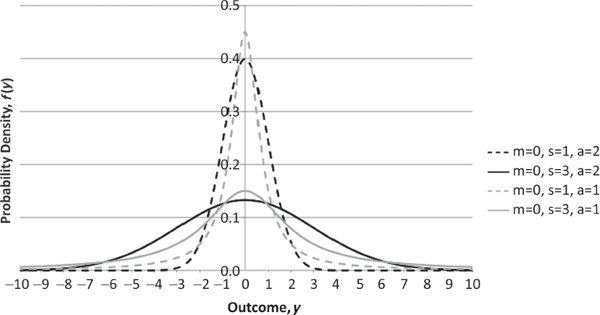
PDFs of Symmetric Lévy-Stable Random Variables with Various Parameters (Defined on All Real Numbers)
Moments to Remember
The above observations regarding the a parameter of the Pareto and symmetric Lévy-stable families introduce a very simple, yet remarkably powerful idea: that a single numerical quantity, by itself, can provide a useful measure of the total amount of variability embodied in a given random variable. Such a parameter is called a risk measure, and researchers have given much attention to the selection of quantities appropriate for this purpose.
Some, but not all, commonly used risk measures are based upon one or more of a random variable’s moments. To define a moment, one first needs to define the expected value or mean of a random variable. This quantity represents the weighted average of all values in the random variable’s sample space, which is found by multiplying each value by its corresponding probability, and then “adding up” the resulting products.
For the discrete uniform random variable X representing the outcome of a single die roll, it is known that the sample space consists of the integers {1, 2,…, 6} and that p(x) equals 1/6 for all possible values of x. Thus, in this case, the expected value—denoted by E[X]—is given by the simple sum
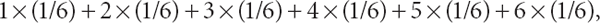
which equals 3.5. Analogously, for the continuous uniform random variable Y defined on the interval [0,1), we saw that the sample space may be partitioned into a large number (n) of small intervals, each of equal length, 1/n. Since p(yi) equals 1/n for each interval i, it follows that the expected value, E[Y], is given by the sum
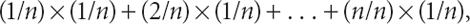
as n becomes infinitely large, which equals 0.5.
Once one knows how to compute the expected value of a given random variable, X, it is rather straightforward to define the expected value of any function of the original random variable, such as X2 (i.e., X squared, or XXX), in an analogous way. For example, if X represents the outcome of a single die roll, then the expected value of X2—denoted by E[X2]—is given by the sum
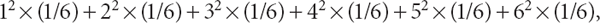
which equals approximately 15.2.
In general, the kth moment of a random variable X is simply the expected value of Xk (i.e., X to the power k, or XXXX … X X [k times]). Among other things, this means that the expected value of X, E[X], is the same thing as the first moment of X. This quantity is often used as an indicator of the central tendency (location) of the random variable, or more precisely, a forecast of what the random variable is likely to be (made before it is actually observed).
To capture the dispersion (spread) of the random variable X around its mean, one turns to the second moment, E[X2], and defines the difference E[X2]–(E[X])2 to be the variance of X, denoted by Var[X]. This is, in a sense, the most primitive measure of risk that is commonly calculated. However, it is often more useful to work with the square root of the variance, known as the standard deviation and denoted by SD[X], because the latter quantity possesses the same units as the original random variable.7 Hence, the standard deviation is actually the most broadly used risk measure.8 The next two higher moments, E[X3] and E[X4], are often employed in computing quantities to capture the random variable’s skewness (asymmetry) and kurtosis (peakedness), respectively.
In the insurance world, both standard deviations and variances are frequently used in the pricing of products. In particular, policyholder premiums are sometimes calculated explicitly as the expected value of losses plus a profit loading proportional to one of these two risk measures. Although this may be reasonable when an insurance company has a large loss portfolio (thereby justifying the Gaussian approximation, as will be discussed in Chapter 4), it is clearly inappropriate when dealing with large loss amounts from single events (such as large liability awards or catastrophe losses). Such loss distributions not only are highly asymmetric, but also can possess heavy tails that are inconsistent with the Gaussian approximation.
In financial portfolio theory, the standard deviation often is used to capture the risk dimension in a risk-versus-return analysis. Specifically, the expected value of a portfolio’s return is plotted against the standard deviation of the return, and the set of optimal portfolios is determined by the capital-market line (see Figure 3.4) formed by all possible weighted combinations of the risk-free asset (often taken to be a U.S. Treasury bill) and the average market portfolio.
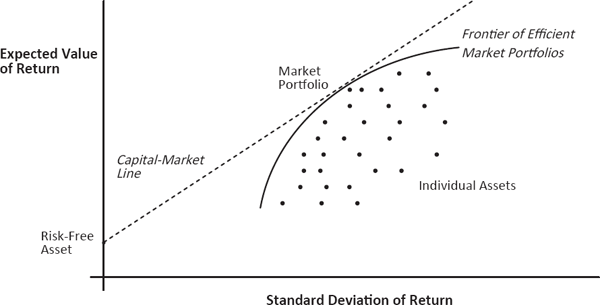
Risk vs. Return in Financial Portfolio Theory
The use of the standard deviation in financial portfolio theory is often justified mathematically by either (or both) of two assumptions: (1) that asset returns have a Gaussian distribution (so that the standard deviation captures all characteristics of the distribution not reflected in its expected value); or (2) that the investor’s utility function (a concept to be introduced in Chapter 5) is quadratic (so that the first and second moments of the investment-return distribution capture everything of importance in the investor’s decision making). Unfortunately, neither of these assumptions is particularly reasonable in practice.
Heavy Tails
Returning to Figures 3.1 and 3.2, one can see how the means and standard deviations are affected by distinct parameter values in the Pareto and Gaussian families. In the Pareto case, both the mean and standard deviation decrease as the a parameter increases (consistent with the tail’s becoming lighter), whereas both the mean and standard deviation increase as the b parameter increases. In the Gaussian case, the m and s parameters actually denote the mean and standard deviation, respectively, and so the relationships between the two parameters and these latter quantities are evident.
One intriguing aspect of the Pareto distribution is that the mean and standard deviation are not finite for all values of the a parameter. Whereas a can take any positive real value, the mean is finite if and only if a is greater than 1, and the standard deviation is finite if and only if a is greater than 2.9 This property is rather disturbing, for both theoretical and practical reasons. On the theoretical side, it seems rather counterintuitive that finite measures of location and spread do not exist in some cases. In particular, the fact that a well-defined random variable may not have a finite mean, or average, seems somewhat bizarre. On the practical side, the absence of these measures of location and spread makes it substantially more difficult to summarize the shape of the underlying distribution with one or two numerical quantities and certainly makes it impossible to compare the affected distributions with other distributions simply by comparing their respective means and standard deviations.
The underlying cause of the missing means and standard deviations is fairly easy to apprehend, even if the effect seems unnatural. As the a parameter becomes smaller, the tail of the Pareto distribution becomes heavier, and so there is increasingly more weight spread out over very large values in the sample space. Given that the sample space is unbounded above, one can imagine that at a certain value of a there is so much weight placed in the tail that when one multiplies each X in the sample space by its corresponding probability and then “adds up” the resulting products, one obtains an infinite value of E[X]. This occurs when a equals 1. Since X2 is much greater than X when X is large, it follows that this phenomenon should occur even sooner (i.e., at a larger value of a) for X2; and indeed, E[X2] (and therefore SD[X] as well) becomes infinite when a equals 2.
Although the Gaussian distribution does not possess sufficiently heavy tails to preclude the existence of any moments, the symmetric Lévy-stable generalization does have this property for values of its a parameter that are less than 2. As with the Pareto distribution, the second moment (and therefore the standard deviation) is infinite for all values of a less than 2, and the mean is not well defined for all values of a less than or equal to 1. What is even stranger in the symmetric Lévy-stable case, however, is that the mean is not infinite when a is less than or equal to 1, but rather indeterminate, revealing that it is not arbitrarily large (in either the positive or negative direction), but truly meaningless!
The Humble Origins of Heavy Tails
One reason that infinite or indeterminate means and infinite standard deviations defy intuition is that such phenomena are rarely encountered in practice and so tend to be viewed as somewhat “pathological.”10 Of course, this sentiment could be as much an effect as a cause; that is, the reason one fails to see these “pathologies” very often may be simply that one shies away from them because they are difficult to work with, sort of like the man who dropped his keys on the sidewalk at night but refused to look for them outside the area illuminated by a single streetlight. In the present section, I will argue that heavy-tailed insurance losses and asset returns are actually quite easy to generate from simple random processes and that the area outside the reach of the streetlight is therefore much too large to be ignored.
Heavy-Tailed Insurance Losses
Most commonly, insurance loss processes are modeled either as sums of random components or as waiting or first-passage times to a certain sum in an accumulation of random components. In particular, one can consider two basic models of accidental damage involving an abstract “box” containing a vulnerable “cargo item” and a large number of homogeneous “protective components” that are subject to destruction, one after the other, by the force of the accident.
In the first case, the accident lasts a fixed amount of real time, and a constant amount of damage is done to the cargo item for each protective component that is overcome (randomly) in sequence during that time period. If the components fail as independent random variables,11 each with the same small failure probability pFailure, then this model is appropriate for claim frequencies (i.e., numbers of individual loss events). In the second case, the accident lasts until a fixed number of the protective components are overcome (randomly), and a constant amount of damage is done to the cargo item for each unit of real time that passes before this event. If the components again fail as independent and identical random variables with small pFailure, then this model is appropriate for loss severities (i.e., sizes of individual losses).
It is the latter type of model—for loss severities—that creates the potential for heavy tails. Taking the simplest possible version of the model, in which the accident lasts until exactly one protective component is overcome (randomly), the resulting random variable will have the exponential distribution, which was discussed previously. Although this particular distribution is not heavy-tailed, it can easily become so through a simple transformation. Specifically, if the random variable L has an exponential distribution with parameter l, where l is itself an exponential random variable with parameter b, then the unconditional distribution of L is Pareto with parameters a = 1 and b, for which both SD[L] and E[L] are infinite.
Given the ease with which such infinite-mean losses can be generated from a simple model, it is not surprising that insurance companies have developed a rather peremptory technique for handling them: namely, the policy limit (cap), which cuts off the insurer’s coverage responsibility for a loss’s tail. Under a conventional policy limit, the raw loss amount, L, is capped at a fixed dollar amount, c, and the policyholder retains responsibility for that portion of the loss exceeding c. Naturally, such truncated losses have the lightest possible tails (i.e., no tails), and so all issues of infinite means and standard deviations should, in principle, vanish.
Unfortunately, there is one rather unsettling problem with the policy limit: like any contract provision, it is subject to litigation and so can be overturned by the whim of a civil court. Rather remarkably, this possibility, regardless of how slight, completely vitiates the policy limit as a protection against infinite means.
Suppose, for example, that a manufacturing company has accumulated a pool of toxic waste on its property and that the pool begins to leak into a nearby housing development, causing serious health problems as well as lowering property values. When the victims of the seepage seek financial recovery for their damages, the manufacturer’s insurance company will, under normal circumstances, set aside reserves and pay claims according to the provisions of the relevant pollution liability policy. However, if the total amount that the insurance company is required to pay under the contract is capped by a finite limit—say, $10 million—then the insurer will stop paying claims as soon as that amount is reached, leaving uncompensated claims as the sole responsibility of the manufacturer.
Now suppose further that: (1) when confronted with these unpaid claims, the manufacturer realizes that the only way to avoid bankruptcy is to challenge successfully the $10 million limit in civil court (based upon some novel reading of contract law proposed by a talented attorney); and (2) a court will overturn the policy limit with some small positive probability, pOverturn. Assuming that the raw total of pollution-related damage caused by the manufacturer is given by a Pareto random variable, L, with parameters a=1 and b (so that E[L] is infinite) and that the amount the insurance company originally agreed to pay under its contract, capped by the $10 million limit, is denoted by L* (where E[L*] must be finite), it then follows that the insurance company’s actual mean loss is given by
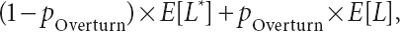
which is infinite. In other words, no matter how small the positive probability pOverturn, the insurer’s actual mean loss is truly infinite in a world Overturn with both infinite-mean raw losses and active civil courts.
Given the serious potential for overcoming policy limits in the highly litigious United States, it is rather strange that infinite-mean losses are not more frequently discussed. The subject is rarely identified as a significant solvency issue by insurance practitioners and regulators, although it is occasionally broached by academic researchers.12 Part of the reason for this omission is, of course, that the concept of an infinite mean is rather counterintuitive (as discussed above). However, I suspect that the principal explanation for the reluctance to discuss infinite-mean losses is something far more prosaic, as suggested by certain historical events.
Instructively, at the nadir of the U.S. asbestos/pollution liability “crisis” in the mid-1990s to late 1990s, it was not uncommon for insurance actuaries and executives to speak of “inestimable” incurred losses, characterized by infinite means.13 At the time, the concern was that such losses, upon entering the books of any member of an insurance group, could spread throughout the entire group and beyond. (This is because any proportional share of an infinite-mean liability, no matter how small the proportion, is yet another infinite-mean liability.) To defend against such statistical contagion, Lloyd’s of London formed the legally separate Equitas companies in 1996 to isolate its accrued asbestos/pollution liabilities and thereby protect the solvency of Lloyd’s as a whole. In the same year, Pennsylvania’s CIGNA Corporation worked out a similar scheme with state regulators to cast off its asbestos/pollution liabilities via the legally separate Brandywine Holdings—a controversial move that received final court approval only in 1999.
These dramatic developments suggest that the political fear of confronting the most pernicious aspect of infinite-mean losses—that is, their potential to spread like a dread disease from one corporate entity to another—may well offer the best explanation of their absence from common discourse. For if infinite-mean losses are observed and identified and cannot be effectively quarantined or amputated, then their ultimate financial course will be fatal. And in such circumstances, many patients simply prefer to remain undiagnosed.
Heavy-Tailed Asset Returns
When it comes to asset returns, I would offer a different, but equally simple model to show how heavy-tailed distributions can arise in the context of market prices for exchange-traded assets. In the spirit of Mandelbrot (1963), let Pt denote the market price of one pound of exchange-traded cotton at (discrete) time t, and consider the observed return given by the natural logarithm of the ratio Pt/Pt-1 (i.e., In(Pt/Pt-1)). I will begin by positing a simple descriptive model of cotton price formation—in other words, a characterization of how Pt (the “after” price) is formed from Pt-1 (the “before” price).
Assume that there are a fixed number of traders in the cotton market and that each trader can be in either of two states at any given time: (1) holding one pound; or (2) holding no pounds.14 Let us propose that Pt is given by the ratio
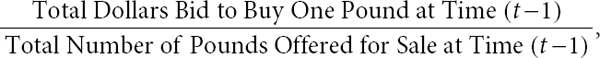
which in turn is equal to
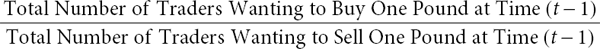
and therefore
If one assumes that an individual trader’s decision to buy or sell at time t–1 is governed by a random process reflecting his or her private information, then it is straightforward to show that the cotton-return random variable can be expressed as the natural logarithm of the ratio of two random proportions plus a constant; that is, In(Pt/Pt–1) may be written as In(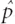
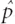Buy/Sell) + constant, where
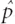Buy = Proportion of No-Pound Traders Wanting to Buy at Time (t–1)
and
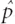Sell = Proportion of One-Pound Traders Wanting to Sell at Time (t–1).
A close analysis of the random variable In(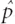Buy /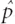Sell) shows further that under a variety of reasonable assumptions, this random variable has tails that are comparable with those of the exponential distribution, possibly with time-dependent parameters, lt–1.15
This finding is rather striking because exponential tails fall distinctly and conspicuously between the light-tailed Gaussian assumption so commonly (but unrealistically) employed in theoretical discussions of asset returns and the heavy-tailed symmetric Lévy-stable model (for values of a less than 2) borne out by many empirical studies.16 The observation yields two further implications of remarkable significance given the parsimony of the simple price-formation model employed:
• The Gaussian assumption provides a poor starting point for asset-pricing models (leaving one rather puzzled by its historical popularity).17
• Empirically observed heavy-tailed behavior is quite possibly the result of time-dependent components in the exponential tail parameters.18
Alternative Risk Measures
In the contexts of heavy-tailed insurance losses or asset returns, practitioners cannot use the standard deviation as a risk measure and therefore typically employ one or more “tail-sensitive” risk measures, with names such as: (1) value at risk (VaR); (2) tail value at risk; (3) excess tail value at risk; (4) expected deficit; and (5) default value.19 Unfortunately, none of risk measures (2) through (5) is well defined if the underlying loss or return random variable X has an infinite or indeterminate mean. Consequently, the only commonly used risk measure that works in the case of a badly behaved mean is the VaR, which, for a preselected small tail probability, αTail, is defined as the 100 X (1–αTail) percentile of X (i.e., the probability that X is less than or equal to the VaR is 1–αTail). Commonly chosen values of αTail would include 0.10, 0.05, 0.01, etc.
The insensitivity of the VaR to the existence of a finite mean undoubtedly explains some of this risk measure’s popularity in the finance and insurance literatures. However, knowing the VaR for only one (or even a few) fixed tail probabilities, αTail, leaves much to be desired in terms of characterizing the overall risk associated with a random variable. Percentiles can tell much about one tail of the distribution, but little or nothing about the center or other tail.
Certainly, if the VaR is known for all possible values of αTail, then one knows exactly how the random variable behaves; that is, this is equivalent to knowing the full PMF or PDF. However, the search for a single-quantity risk measure presupposes that working with entire PMFs or PDFs entails undesirable cognitive difficulties for human decision makers. Consequently, one must turn elsewhere for a comprehensive single-quantity measure of risk.
One robust risk measure that I like to promote is the cosine-based standard deviation (CBSD), developed in joint work with my son, Thomas Powers.20 Taking advantage of the fact that the cosine function is bounded both below and above (unlike the power function, which is used in computing moments), this risk measure is applicable to all probability distributions, regardless of how heavy their tails are. Although the CBSD requires the selection of a parameter to calibrate the trade-off between information about the tails and information about the rest of the probability distribution, this parameter may be chosen to maximize information about the distribution on the whole. Then, for the symmetric Lévy-stable family, the risk measure is proportional to 21/a X s, where s is a positive dispersion parameter of the symmetric Lévy-stable distribution that corresponds to the standard deviation in the Gaussian case (i.e., when a equals 2). This expression has the intuitively desirable properties of increasing both as a decreases (i.e., as the tails become heavier) and as s increases. It also is directly proportional to the ordinary standard deviation in the Gaussian case.
To illustrate the usefulness of this particular risk measure, consider the simple problem of adding two random asset returns. Suppose, for example, that X1 and X2 denote the returns from investments in cotton on two successive days and that these two random variables are independent observations from a Gaussian distribution with mean m and standard deviation s (for which a = 2). In that case, the CBSD is proportional to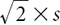 
for a single day and proportional to 2 X s for the sum of two days (i.e., for a two-day period), so that
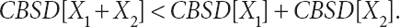
This property, known as subadditivity, indicates that risk-reduction benefits may be achieved through diversification (i.e., risk pooling), a fundamental technique of risk finance (to be discussed in Chapter 7).
Alternatively, if X1 and X2 are independent observations from a symmetric Lévy-stable distribution with parameters m, s, and a = 1,21 then the CBSD is proportional to 2 X s for a single day, and proportional to 4 X s for a two-day period, so that
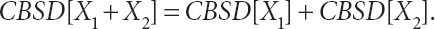
In this case, there is only simple additivity, and so diversification offers no risk-reduction benefits.
ACT 1, SCENE 3
[A basketball court. Young man practices shots from floor; Grim Reaper approaches quietly.]
REAPER: Good morning, Mr. Wiley. I’m the Grim Reaper.
MAN: I know who you are.
REAPER: Really? How so?
MAN: Your costume is rather … revealing.
REAPER: Yes, I suppose it is. Well then, you know why I’m here.
MAN: I suppose I do. But I’m a bit surprised that you don’t speak with a Swedish accent.
REAPER: Ah! I think you’ve been watching too many movies. Next I suppose you’ll want to challenge me to a contest to spare your life.
MAN: Well, is that permitted?
REAPER: Yes, it’s permitted, but generally discouraged. There’s no point in raising false hopes among the doomed.
MAN: But if it is allowed, what are the ground rules?
REAPER: Essentially, you can propose any challenge you like; and if I judge my probability of victory to be sufficiently great, I’ll accept. But I must warn you, I’ve lost only once in the past 5,000 years.
MAN: Well, then, I think I have just the game for you: a free-throw challenge.
REAPER: That hardly seems fair, given the wonderful physical shape you’re in.
MAN: Well, you didn’t seem to think my “wonderful physical shape” was any obstacle to dying.
REAPER: [Laughs.] A fair point, indeed!
MAN: But in any event, the challenge won’t be based upon our relative skill levels. Rather, you’ll simply make a series of free throws, and I’ll be permitted to live until you succeed in making one basket.
REAPER: [Confused.] But that’s not much of a challenge. From the free-throw line, I’d estimate my chance of making a basket to be about 1/2. That means there’s about a 1/2 chance it will take me one shot, about a 1/4 chance it will take two shots, about a 1/8 chance it will take three shots, and so on. Since those probabilities add up to 1, I’m destined to succeed.
MAN: Well, I’m thinking of something a little more challenging than that. My proposal is that you take your first shot from the free-throw line, with your regular chance of success: 1/2. However, if you don’t make the first shot, then you have to move a little farther from the basket; just enough so that your chance of making the second shot goes down to 1/3. If you don’t make the second shot, then you again have to move a little farther away, so that your chance of making the third shot becomes 1/4; and so on.
REAPER: That is a bit more challenging, I suppose. But you must realize, I’m fairly good at mathematics, so I can see that there’s about a 1/2 chance it will take me one shot, about a 1/6 chance it will take two shots, about a 1/12 chance it will take three shots, and so on. Since those probabilities again add up to 1, I’m still destined to succeed.
MAN: Well, we’ll see about that. Do you agree to my challenge?
REAPER: I certainly do.
[Young man passes basketball to Grim Reaper, who takes first shot from free-throw line, and misses. Reaper retrieves ball, takes second shot from slightly farther back, and again misses.]
MAN: It’s not so easy, is it?
REAPER: [Smiles confidently.] Not to worry, it’s just a matter of time until I win.
MAN: That’s exactly right. Eventually, you’ll win. But have you calculated how long it will take, on the average?
REAPER: [Stands silently as complacent expression turns to frustration.] Damn! On the average, it will take forever!
MAN: [Walks away.] Feel free to come for me when you’re finished.