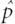Male(x) and 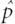Female(x). However, such complete information is not always available.Fool me once, shame on you; fool me twice, shame on me.
In Chapter 2, we considered two pairings of probability interpretations and estimation methods: (1) the frequency/classical approach, called frequentism; and (2) the subjective/judgmental approach, called Bayesianism. In the present chapter, we will explore a number of concepts and methods employed in the former approach. The latter will be addressed in Chapter 5.
To present the standard frequentist paradigm, I will begin by defining the concept of a random sample, and then summarize how such samples are used to construct both point and interval estimates. Next, three important asymptotic results—the law of large numbers, the central limit theorem, and the generalized central limit theorem—will be introduced, followed by a discussion of the practical validity of the independence assumption underlying random samples. Finally, I will consider in some detail the method of hypothesis testing, whose framework follows much the same logic as both the U.S. criminal justice system and the scientific method as it is generally understood.
Point Estimators and Interval Estimators
The starting point for all statistical methods, whether frequentist or Bayesian, is a random sample. This is a collection of some number, n, of independent observations, all from the same probability distribution, and is denoted by X1, X2,…, Xn. (As before, independent means that knowing something—or everything—about the values of one or more of the observations provides no new information about the other values in the sample.)
If the relevant probability distribution is known with certainty, then there is no need for statistical estimation. In our mortality example from Chapter 2, this would be equivalent to knowing the probabilities pMale(x) or pFemale(x) for all ages x in Figure 1.1, rather than having to estimate them with 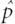Male(x) and 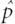Female(x). However, such complete information is not always available.
The simplest way to model unknown aspects of a probability distribution is to identify one or more parameters whose values are uncertain. For example, if a random sample comes from a Gaussian distribution (as shown in Figure 3.2), then there are two parameters—the mean, m, and the standard deviation, s—each of which may be known or unknown. For illustrative purposes, it will be assumed that only m is unknown and that the value of s is provided a priori.
There are two broad classes of estimators of an unknown parameter such as m: (1) point estimators, which are single real-valued numerical quantities that provide good guesses of the actual value of m; and (2) interval estimators, which provide (usually continuous) subsets of the real number line that are likely to contain the actual value of m. Each of these classes can yield a number of distinct estimators distinguishable from one another in terms of various optimality criteria. However, rather than delving into these differences, I simply will provide one example of each type of estimator.
In the case of a Gaussian random sample with unknown mean and known standard deviation, the most straightforward and commonly used point estimator of m is the sample mean, (X1 + X2 + … + Xn)/n. This estimator is not only intuitively reasonable, but also enjoys certain desirable properties, as discussed in the next section. The most straightforward and commonly employed interval estimator of m is the symmetric confidence interval constructed by using the sample mean as midpoint, and then subtracting an appropriate multiple of the standard deviation of the sample mean to obtain the lower bound and adding the same multiple of the same standard deviation to obtain the upper bound; that is:
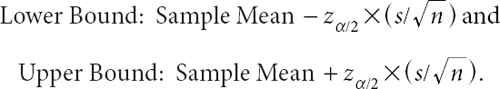
The length of the confidence interval,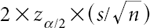 
, depends on the confidence level, 1–α, with which one wants to capture m. This is governed by the factor zα/2 (the 100 X (1–α/2)th percentile of the Gaussian distribution with mean 0 and standard deviation 1), which increases as the confidence level increases. Typical values of 1–α are 0.90, 0.95, and 0.99, and the corresponding values of zα/2 are 1.645, 1.96, and 2.575, respectively. (Since 0.95 is a particularly common choice of 1–α, it follows that the associated factor of 1.96—often rounded to 2—is correspondingly common, which is why people often speak of a confidence interval as consisting of “the sample mean plus or minus 2 standard deviations.”)
A few further words need to be said about the meaning of the confidence level. Although this number certainly has the “look and feel” of a probability, it is not quite the same thing. I say “not quite” because it is in fact a probability before the actual values of the random sample are observed, but falls in stature once those values are known. This rather odd state of affairs arises from the restricted nature of the frequentist paradigm. Prior to observing the random sample, one can say that the lower and upper bounds of the confidence interval, which depend on the sample mean, are truly random variables, and therefore have a probability (1–α) of capturing the unknown parameter m. However, once the random sample is observed, there is no remaining source of randomness because the elements of the random sample are known real numbers, and m is an unknown number. At that point, all one can say is that the confidence interval either does or does not capture m, without any reference to probability. In this context, confidence means the following: If one were to select a large number of random samples of size n and construct the same type of confidence interval from each sample, then one would tend to capture m about 100 X (1–α) percent of the time.
Once a frequentist statistician has settled on a particular point and/or interval estimator of m, he or she can use the estimator to provide forecasts of future observations of the underlying random variable. For example, having observed the random sample X1, X2,…, Xn, the statistician can use the sample mean as a good guess of the subsequent observation, Xn+1, and can construct confidence intervals for Xn+1 as well.
Asymptotic Results
Not surprisingly, the frequentist approach affords great deference to asymptotic results—that is, mathematical theorems describing properties of statistical estimators as the sample size, n, becomes arbitrarily large. Three particularly important results of this type are the law of large numbers (LLN), the central limit theorem (CLT), and the generalized central limit theorem (GCLT), stated briefly below.
Law of Large Numbers
If E[X] is well defined, then as the sample size, n, approaches infinity, the sample mean must converge to the actual mean.
This result, sometimes called the law of averages, provides a mathematical statement of the very intuitive notion that the sample mean should become closer and closer to the actual mean as the random sample grows larger. From the perspective of frequentist estimation, this is very important because it means that all estimators based upon sample means tend to become more and more accurate as more data are collected. Naturally, the LLN requires that E[X] be well defined; but it is very interesting to think about what happens to the sample mean in those cases in which E[X] is either infinite (such as for values of a less than or equal to 1 in the Pareto family) or indeterminate (such as for values of a less than or equal to 1 in the symmetric Lévy-stable family). In the former case, the sample mean naturally tends to grow larger and larger without bound as n increases. In the latter case, the sample mean simply “bounces” around the real number line, never settling down at any particular value.
Central Limit Theorem
If SD[X] is well defined, then as the sample size, n, approaches infinity, the distribution of the sample mean must converge to a Gaussian distribution with mean E[X] and standard deviation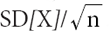 
.
For a random variable that possesses a finite standard deviation, the CLT expands on the LLN by describing the random behavior of the sample mean as it gets closer and closer to the actual mean for large sample sizes. Essentially, this result says that the sample mean approaches the actual mean in a smooth and systematic way, such that, for a large value of the sample size, the sample mean will have an approximately Gaussian distribution (that is consequently both approximately symmetric and light-tailed) about the actual mean with a standard deviation shrinking to 0.
Generalized Central Limit Theorem
As the sample size, n, approaches infinity, there exists a coefficient, cn, such that the distribution of cnX(Sample Mean) must converge to a (four- parameter) Lévy-stable distribution.
For clarification, the four-parameter Lévy-stable family is a generalization of the three-parameter symmetric Lévy-stable family, in which the additional parameter allows for asymmetry. The GCLT generalizes the CLT in the sense that the CLT represents a special case in which the coefficient cn equals 1 and the sample mean approaches the Gaussian distribution with mean E[X] and standard deviation 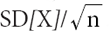.1 The GCLT goes well beyond the CLT by addressing all random variables that possess a limiting distribution, including those for which the standard deviation is infinite (e.g., those having a Pareto distribution with a less than or equal to 2).
The Meaning of Independence
In defining a random sample, I stated that the individual observations had to be independent of one another in the sense that knowing something (or everything) about the values of one or more of the observations provides no new information about the other values in the sample.2 Since this assumption is fundamental to frequentist (as well as Bayesian) analysis, it seems worthwhile to explore its meaning a bit further. To begin, I will clarify the relationship between statistical independence, on the one hand, and statistical uncorrelatedness, on the other.
Independence Versus Uncorrelatedness
Let us consider two random variables, Y1 and Y2, both from the same probability distribution. If they are independent of one another, then knowing something about Y1 (e.g., Y1 is less than 10) or even knowing everything about Y1 (e.g., Y1 equals 5), implies nothing about Y2, and vice versa. On the other hand, if the two random variables are uncorrelated (denoted by Corr[Y1, Y2] = 0), then knowing that Y1 is particularly high (or low) does not imply that Y2 will tend to be particularly high (or low), and vice versa. Since the definition of uncorrelatedness is weaker than the definition of independence, it follows that independence logically implies uncorrelatedness; that is, if Y1 and Y2 are independent, then they must be uncorrelated. However, it is important to note that uncorrelatedness does not imply independence.
As an example, suppose that a location is selected at random, and with uniform probability, from all points on the surface of the earth, and consider the statistical relationship between the following two random variables: Y1, the distance (measured along the surface of the earth) from the North Pole to the randomly chosen location; and Y2, the average annual temperature at the same location. Making the simplifying assumption that average annual temperatures decrease symmetrically as a point moves (either north or south) away from the equator, it follows that Yl and Y2 must be uncorrelated (because knowing that Y1 is particularly high and knowing that Y1 is particularly low both imply that Y2 will tend to be particularly low), but dependent (because knowing that Yl is particularly high does imply something about Y2, i.e., that it must be particularly low).
Of course, one also can look at things from the perspective of positive or negative correlation. Specifically: (1) Y1 and Y2 are positively correlated (denoted by Corr[Y1, Y2] > 0) if knowing that Y1 is particularly high implies that Y2 will tend to be particularly high and knowing that Y1 is particularly low implies that Y2 will tend to be particularly low; and (2) Y1 and Y2 are negatively correlated (denoted by Corr[Y1, Y2] < 0) if knowing that Y1: is particularly high implies that Y2 will tend to be particularly low and knowing that Y1 is particularly low implies that Y2 will tend to be particularly high. Here, positive or negative correlation logically implies statistical dependence, but dependence does not require either positive or negative correlation.
An Intriguing Intuition
Returning to the role of independence in a random sample, I would note that the relationship between independence and the LLN is not entirely intuitive. In fact, students of introductory statistics often sense a contradiction therein because the idea that the sample mean of the first n trials must converge to a fixed constant (i.e., the actual mean) seems to belie the fact that the outcome of the nth trial has nothing to do with the previous n–1 trials. Along these lines, one might ask: How can the simple average of a series of random variables be required to become arbitrarily close to the actual mean unless the individual random variables are forced to offset each other in some way? Or more precisely: How can the LLN be true unless the successive random variables are somewhat negatively correlated, with a relatively low value of one observation being offset by a relatively high value of a later one, and vice versa?
Usually, such naïve questioning is quickly nipped in the bud by the deft explanations of an experienced instructor. However, in some refractory cases (including my own) the intuition simply retreats underground, finding sanctuary in the brain’s subconscious. Then, while the individual’s conscious mind embraces the orthodox tenets of independence and the LLN, the subconscious surreptitiously nurtures the view that convergence results must imply negatively correlated outcomes in a random sample. After an indefinite period of time—several years or perhaps even decades—this secret conviction may cause one to engage in such superstitious behaviors as: buying talismans to ward off the “evil eye” (when things are going well) or to change one’s luck (when things are going badly); or more prosaically, betting heavily on red (after a long string of black) or on black (after a long string of red) in casino roulette.
In inquiring after the source of this strange intuition, I would note that certain negative-correlation structures—such as assuming that Corr[X1, X2], Corr[X2, X3], Corr[X3, X4], etc. equal some negative constant and that all other pairs of observations are uncorrelated—can cause the sample mean to converge to the actual mean faster than it would under the assumption of independence.3 In other words, such structures might be used to justify a “law of not-so-large numbers” (LNSLN). Therefore, it seems reasonable to believe that some people may confuse the LLN with some sort of LNSLN.
This sort of confusion is not difficult to imagine because the LLN is asymptotic in nature and thus can never truly be experienced in real life. Although most potential LNSLNs are also asymptotic, there is one particular LNSLN that applies to finite samples and not only can be experienced, but also is ubiquitous. I therefore would argue that this particular convergence result likely forms the basis for the intuition of negative correlations.
Remembrance of Fair Divisions Past
Consider a finite sequence of N random variables from the same probability distribution, whose sum is some constant (i.e., X1 + X2 + … + XN equals some fixed number k). Regardless of the value of the standard deviation of these random variables, it is easy to show that the correlation between any two of them is given by –1/(N–1), and that the following LNSLN applies: As the sample size, n, approaches N, the sample mean must converge to the actual mean. This constant-sum sampling model is intrinsic to the fair division of limited resources—a problem that would have been at least as familiar to our primitive human ancestors as it is to us today.
For example, consider what might have happened when N cooperative primitive hunters returned to their village after killing a single deer.4 Assuming that the carcass had to be divided equally among the hunters’ respective families, it is immediately obvious (to anyone with even the most cursory knowledge of cervine anatomy) that this division problem would have been rather difficult. Even if N is just 2, in which case the deer’s exterior bilateral symmetry would have provided a convenient guide for carving, the animal’s internal asymmetry would have rendered the division of flesh into truly equal parts—whether according to weight, nutritional value, or some other measure—somewhat random.
Without delving too deeply into the grisly details, let us assume that the weight of edible flesh was used as the measure for division and that a single deer yielded a total of 75 pounds. Assuming a total of five hunters, and letting X1 denote the weight allocated to hunter 1, X2 denote the weight allocated to hunter 2, and so on, it follows from the constant-sum model described above that the random variables X1, X2,…, X5 come from the same distribution, with mean 75/5 = 15 pounds and pairwise correlations –1/4. In short, each hunter would have been acutely aware that his actual share of the deer carcass was only approximately equal to his “fair share” (i.e., 15 pounds), and that his random gain (or loss) would have subtracted from (or added to) the shares of the other hunters.
Such fair-division problems would have been ubiquitous in primitive societies.5 Besides game meat, other resources that would have required careful partitioning include fruit and vegetable gatherings, favorable land for housing, and sometimes even human chattel (e.g., captives from raids on neighboring villages). In each case, the close connection between the negative correlations of the allocated shares and the convergence of the sample mean to a fixed constant would have been apparent.
Given the likely importance to social harmony of a good knowledge of fair division, a strong intuitive understanding of the statistical properties of constant-sum sampling should have provided a natural survival advantage. Thus, it seems reasonable to expect biological evolution to have imprinted human cognition with an intuitive awareness of the connection between negative correlations and the convergence of the sample mean.
Hypothesis Testing
One of the most important and widely used techniques of frequentist statistics is hypothesis testing. As will be seen in Chapter 14, this methodology also provides a conceptual framework for the scientific method as it is generally understood.
The formulation of any hypothesis test is based upon two statements: (1) a null hypothesis (denoted by H0) that describes the current state of belief regarding some quantifiable problem; and (2) an alternative hypothesis (denoted by H1) that provides the state of belief that naturally would follow if one were to reject the null hypothesis. In most statistical problems, each hypothesis is stated in the form of an equation. For example, in the Gaussian parameter-estimation problem discussed above, one might be interested in performing a formal hypothesis test in which the null hypothesis is given by H0: “m equals 10,” and the alternative hypothesis by H1: “m does not equal 10.”
To carry out a hypothesis test, two further items are needed: (1) a test statistic, whose value provides information about the relative credibilities of the null and alternative hypotheses; and (2) a level of significance, which enables one to identify those values of the test statistic for which the null hypothesis should be rejected (called the critical region). To test H0: “m equals 10” against H1: “m does not equal 10,” the most straightforward test statistic is the sample mean minus 10, for which smaller absolute values provide more support for the null hypothesis, and larger absolute values provide less support. The level of significance, denoted by α, is analogous to the complement of the confidence level (1–α) discussed above and represents the greatest probability with which the statistician is willing to reject the null hypothesis under the assumption that the null hypothesis is true. This probability is also called the probability of type 1 error. (In contrast, the probability that the statistician retains the null hypothesis under the assumption that the alternative hypothesis is true is called the probability of type 2 error. Interestingly, the latter probability is not fixed in advance because hypothesis testing embodies an institutional bias in favor of keeping the probability of type 1 error below a certain threshold, even at the expense of permitting a much greater probability of type 2 error.)
For a given level of significance, the complement of the critical region is constructed in a manner analogous to a confidence interval, but using the value of m under the null hypothesis (i.e., 10) as midpoint. Subtracting an appropriate multiple of the standard deviation of the sample mean to obtain the lower bound and adding the same multiple of the same standard deviation to obtain the upper bound, the complementary region is given by:
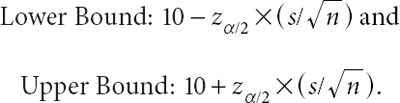
Consequently, the critical region itself consists of the portions of the real number line below the lower bound and above the upper bound. If the test statistic falls within this critical region, then it is said to be statistically significant, and the null hypothesis must be rejected.
Commonly chosen values of α are 0.10, 0.05, and 0.01, and the corresponding values of zα/2 are 1.645, 1.96, and 2.575, respectively. However, it is not unusual for statisticians to avoid the final step of declaring whether or not a particular null hypothesis is rejected at a given level of significance and instead to provide only the p-value (i.e., probability of type 1 error) associated with the observed test statistic. Given this quantity, one can determine whether or not to reject the null hypothesis at any proposed level of significance, α, simply by comparing the p-value to α. If the p-value is smaller, then the null hypothesis is rejected; if the p-value is larger, then the null hypothesis is retained.
The Criminal Justice Analogue
Rather remarkably, there exists a pronounced parallel between the methodology of hypothesis testing and the dialectical nature of criminal jurisprudence in the United States and many other nations. Beginning with the selection of the null hypothesis, H0: “The defendant is not guilty,” and the alternative hypothesis, H1: “The defendant is guilty,” the analogy proceeds to the choice of a level of significance (i.e., “beyond a reasonable doubt”), as well as the institutional bias in favor of keeping the probability of type 1 error small, even at the expense of permitting a much greater probability of type 2 error (i.e., “it is better to let ten guilty people go free than to convict one innocent person”).
Regrettably, I have not had the opportunity to serve on a criminal (or civil) jury. Although I possess no hard evidence in the matter, I speculate that my lack of experience in this area arises from the common desire of both prosecution and defense attorneys not to have individuals who identify themselves as statisticians sitting in the jury box. My impression is that attorneys on both sides prefer to have jurors with few preconceived notions regarding quantitative methods of decision making, presumably to ensure that the jury’s final verdict is more directly related to the quality of the lawyers’ courtroom presentations than to the intrinsic quality of the evidence. Although this may be fine for those with complete confidence in the adversarial system’s ability to arrive at the truth, I must admit that I am less than sanguine about the process. One simply need consider how frequently well-publicized jury trials result in outcomes that are surprising to both the prosecution and the defense to realize the high level of uncertainty inherent in a system that, inter alia, forbids the final decision makers (i.e., the jurors) to ask questions of witnesses or in some cases even to take notes.
Testing Hypothesis Testing
Despite my unfortunate lack of jury service, I have been fortunate enough to have had the opportunity to employ a critical “life or death” hypothesis test firsthand. Unfortunately, it was my life that was on the line at the time. More than two decades ago, I was informed that I would need to undergo several months of chemotherapy for a nasty tumor that had begun metastasizing through my body. Fortunately, the type of cancer involved (which, not coincidentally, was the same as that experienced by our 27-year-old man in Chapter 1) was highly curable, although there were always the usual potentially life-threatening complications of aggressive chemotherapy.
After consulting with various doctors, and reading a number of relevant medical journal articles, I was faced with a decision that required some formal statistical analysis. Although the particular cocktail of chemicals to be used in my treatment was fairly standard, there remained the basic question of whether I should undergo therapy in a geographically distant research hospital, where the health care providers would have had more experience with the treatment protocol, or in a nearby nonresearch hospital, where I might be the first patient to undergo the prescribed regimen.
Fortunately, before I had to make my decision, I came across a journal article that provided data on the very issue I was considering.6 As summarized in Table 4.1, the article presented a comparison of chemotherapy outcomes, using the specific protocol I would be having, in both research and nonresearch hospitals.
Chemotherapy Survival Analysis
Source: Williams et al. (1987).
What was particularly interesting (or perhaps I should say “challenging”) about using these data was that the observed proportion of treatment survivals at research hospitals (48/56, or approximately 0.86) was clearly larger, on an absolute basis, than the proportion of treatment survivals at nonresearch hospitals (54/67, or approximately 0.81). Therefore, at first blush, a research hospital would have seemed a substantially better choice. However, the true value of statistical analysis in this type of setting is to determine whether or not such absolute numerical differences—even if fairly large—are statistically meaningful. In the case at hand, this can be accomplished by a formal test of H0: “The treatment survival rates at research and nonresearch hospitals are equal,” against H1: “The treatment survival rates at research and nonresearch hospitals are not equal.”
Given the data in Table 4.1, one can apply a standard hypothesis test called a chi-squared test, which yields a test statistic of 0.5635 and an associated p-value of 0.4529. Therefore, for any reasonably small level of significance, the null hypothesis should be retained, suggesting that hospital type has no real impact on treatment survival rate.
Of course, the bottom line question is: When one’s life is at stake, is one willing to accept the dictates of an impersonal hypothesis test? In this case, my initial reaction was “Of course not! The research hospitals give a 5 percent better chance of survival, regardless of what the test says.” But then, after some agonizing, I decided that it would represent a profound betrayal of my formal statistical training to reject the entire methodology of hypothesis testing so early in my career. Consequently, I ended up selecting a local, nonresearch hospital that was logistically more convenient.
Although I survived the necessary treatment and am comfortable that my decision was the right one, I now must acknowledge, in retrospect, that it was poorly informed. As pleased as I was to have found the data in Table 4.1, I never noticed that they were from an observational study, rather than a randomized controlled study. In other words, the comparison of outcomes from research and nonresearch hospitals was based upon a set of patients who presumably had some choice as to which type of hospital they would use for treatment, rather than being assigned to one type or the other randomly. As will be discussed at some length in Chapter 12, this experimental design essentially vitiated any hypothesis test based upon the data, since there easily could have been other unobserved variables—such as a greater likelihood of healthier patients choosing nonresearch hospitals—that confounded the results.
ACT 1, SCENE 4
[The Garden of Eden. Adam and Eve stand before Tree of Life, as God (unseen) speaks from above.]
GOD; Adam and Eve, I’m very disappointed in both of you.
ADAM: Yes, Lord. We know that You commanded us not to eat from the Tree of Knowledge, and we’re very sorry.
GOD: Are you sorry for disobeying Me or simply for getting caught?
ADAM: Uh, I’m not sure what You mean, Lord. I—
EVE: [Interrupting.] He means we’re sorry for disobeying You, Lord.
GOD: Really? Well, no matter. It isn’t just that you disobeyed the letter of My command in this particular instance; it’s also the ways in which you’ve disobeyed the spirit of My commands on many occasions. For example, there are forty-five varieties of fruit on the Tree of Life, each representing a different virtue: Faith, Hope, Empathy, Courage, Patience, Kindness, … I could go on and on. And if you recall, I told you to maintain a balanced diet of all those different fruits—to eat a mixture, to diversify. But what did you do? Eve, you ate only the fruit called Deference; and Adam, you ate only the one called Acceptance.
ADAM: Yes, Lord. But once I tried Acceptance, I found I was quite happy with it.
EVE: And in my case, Lord, I would have explored beyond Deference, but the Serpent told me not to bother.
GOD: Ah, yes—the Serpent! Now, that brings Me to the other fruits: the forbidden ones. Unlike the Tree of Life, each fruit on the Tree of Knowledge is unique. And of all the thousands of different fruits growing there, Eve, which two did you pick?
EVE: I believe they were called How to Damage Things and How to Shift Responsibility, Lord.
GOD: Yes. What a sorry pair of choices those were! I notice that you passed up all sorts of more useful alternatives: How to Know Whom to Trust, How to Learn from One’s Mistakes, How to Predict the Future from the Past—even How to Make a Fruit Salad would have been better.
EVE: Well, Lord, it’s not entirely my fault. You see, the Serpent suggested that we try those two.
GOD: Ah, the Serpent again! Every time you mention the Serpent, it damages My heart to see you shifting responsibility.
ADAM: We’re sorry, Lord. We won’t mention the Serpent again.
GOD: Adam, will you ever stop making promises you can’t keep?
ADAM: Uh, I’m not sure how to answer that, Lord. I—
GOD: [Interrupting.] Then go! Just go! [Sighs.] Leave My sight! You are hereby banished from paradise!
[Adam and Eve turn and walk sadly away, out the gates of Eden.]
SERPENT: Banished from paradise? That’s quite a harsh punishment, isn’t it?
GOD: Yes. I’m afraid I had to make an example of those two so that others will benefit from their experience.
SERPENT: Hmm. How to Damage Things and How to Shift Responsibility. I can imagine starting an entire industry based upon those two concepts someday.
GOD: [His mood shifting.] What? Insurance?
SERPENT: No. I was thinking of civil litigation.