In the chemistry that we have worked with so far, the atoms of reactants rearrange to form product molecules different from those reactants. In such reactions, the outer electrons of the atoms may be transferred completely or in part from one atom to another. The nuclei of the atoms are unchanged.
There are other reactions in which the nuclei themselves are broken down and the products do not contain the same elements as the reactants. The chemistry of such nuclear reactions is called nuclear chemistry. Spontaneous disintegration of individual nuclei is usually accompanied by high-energy emissions and/or high-speed particles. These products and, sometimes, the reactions that produce them are referred to as radioactivity. Additionally, there are other nuclear changes resulting from the interactions of a neutron or high-energy photon with a nucleus, or from the impact of a high-velocity particle. The results of such nuclear bombardment are highly dependent on the energy involved.
Although there are particles not used here, the basic particles listed in Table 21-1 can be used to define and illustrate the concepts presented. Note that the proton and neutron are referred to as nucleons. The masses in Table 21-1 are presented in atomic mass units (u, Chapter 2) and their charges are expressed in multiples of the elementary charge (1.6022 × 10–19 C, Chapter 19). Note that the neutron has slightly more mass than the proton. Also, the mass of the electron is considered to be 1/1836 that of a proton or, if you prefer, the mass of 1 proton is 1836 times that of an electron.
The mass of an atom is generally not equal to the sum of the masses of its component protons, neutrons, and electrons. If we could imagine a reaction in which free protons, neutrons, and electrons combine to form an atom, we would find that the mass of the atom is slightly less than the total mass of the component particles (an exception is 1H as there is only 1 nuclear part, the proton). Further, a tremendous amount of energy is released during the reaction which produces the atom. The loss in mass is exactly equivalent to the released energy, according to Einstein’s famous equation,
The calculated gain of energy equivalent to the loss of mass is called the binding energy of the atom (or nucleus, if it is being considered independently of the electrons in the shells). When the binding energy calculations are
done with m in kilograms and c in meters per second, the value of E is in joules. A more convenient unit of energy for nuclear reactions is the MeV (Chapter 8). By the Einstein equation,
Nuclear equations, like chemical equations, are a method of keeping track of the involved particles and energy. The rules for balancing nuclear equations are different from those we have been using for balancing ordinary chemical equations. They are as follows:
1. Each particle is assigned a superscript equal to its mass number (number of nucleons), A, and a subscript equal to its atomic number or nuclear charge, Z.
2. A free proton is the nucleus of the hydrogen atoms, and is assigned the notation 
3. A free neutron is assigned zero atomic number because it has no charge. The mass number of a neutron is 1. The full notation for a neutron is 
4. An electron (e– or β–) is assigned the mass number zero and the atomic number –1. We will use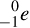 
for the full notation, if the electron is part of an atom. We will use 
or β– if the electron is emitted (a beta particle).
5. A positron (e+ or β+) is assigned the mass number zero and the atomic number +1. The full notation for a positron we will be using is 
or β+, since the positron is only to be covered as an emitted particle in this chapter (conforming to 4 above).
6. An alpha particle (α-particle) is a helium nucleus. The full notation for an α-particle is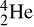 
7. A gamma ray (γ) is a very high-energy photon (Chapter 8). It has zero as the mass number and zero charge. The full notation for a gamma ray is 
.
8. In a balanced equation, the sum of the subscripts (atomic numbers), written or implied, must be the same on the two sides of the equation. The sum of the superscripts (mass numbers), written or implied, must also be the same on the two sides of the equation. For example, the equation for the first step in the radioactive decay of 226Ra is:
Notice that the charge associated with the helium nucleus without electrons (+2) can be ignored because electrons are eventually picked up from the environment to complete the atom.
Many nuclear processes may be indicated by a shorthand notation in which a light bombarding particle and a light product particle are represented by symbols in parentheses. These are located between the initial target nucleus and the final product nucleus. The symbols used are n, p, d, α, β–, β+, and γ, representing the neutron, proton, deuteron 
alpha, electron, positron, and gamma rays, respectively. The atomic numbers are commonly left out in this notation because the symbol for any element implies its atomic number. Examples of the longhand and shorthand notations are as follows:
Just as an ordinary chemical equation is a shortened version of the complete thermochemical equation which expresses both energy and mass balance, each nuclear equation has a term (written or implied) expressing energy balance. The symbol Q is usually used to designate the net energy released when all reactant and product particles of matter are at zero velocity. Q is the energy equivalent of the mass decrease (discussed above) accompanying the reaction. Q is usually expressed in MeV.
Special properties of radioactive nuclides (isotopes of an element, Chapter 2) make them useful tracers for following complex processes. Radiochemistry is the branch of chemistry which involves the applications of radioactivity to chemical problems, as well as the chemical processing of radioactive substances.
A radioactive nuclide (radioisotope) is spontaneously converted to another nuclide by one of the processes below; each definition is followed by an example. As discussed above, all are accompanied with a loss of mass and a release of energy.
1. Alpha decay. An α-particle 
is emitted and the daughter nucleus has an atomic number, Z, two units less. The mass number, A, is four units less than the parent nucleus.
2. Beta decay: A beta particle 
an electron, is emitted and the daughter has a Z-value one unit greater than the parent’s with no change in A.
3. Positron emission: A positron 
is emitted and the daughter has a Z-value one unit less than the parent’s with no change in A.
4. Electron capture: A proton captures an electron (beta particle). The result is a change into a neutron. The capture is in the first shell of the proton, the K orbit, and may be called K-electron capture. (Note: This is essentially the reverse of beta decay.)
A radioactive nucleus decays by a first-order process, so that (20-1), (20-2), and (20-3) apply. The stability of the nucleus with respect to spontaneous decay may be indicated by its first-order rate constant, k, or by the half-life, t1/2.
Radioactivity is measured by observing the high-energy particles produced directly or indirectly as a result of the disintegration process. A convenient unit of radioactivity is the curie, Ci, defined by
The activity of a sample, expressed in curies, depends both on the number of atoms of the radioisotope (determined from the mass of the sample) and on the half-life (disintegration rate constant). See Problem 21.14. The subunits are millicurie (mCi), microcurie (μCi), and others.
21.1. Provide the number of protons, neutrons, and electrons in each of the following atoms: (a) 3He; (b) 12C; (c) 206Pb.
(a) From the periodic table (chart), we see that the atomic number of helium is 2; there must be 2 protons. The mass number is 3, according to the question; there must be 1 neutron. The number of electrons is the same as protons in an atom, which is 2. (2p, 1n, and 2e–)
(b) Carbon’s atomic number is 6 and that is the number of protons. The mass number of 12 and the atomic number of 6 give us the number of neutrons, 12 – 6 = 6 neutrons. The number of electrons equals the number of protons. (6p, 6n, and 6e–)
(c) Lead has the atomic number 82, meaning there are 82 protons and 82 electrons in the atom. The mass number is 206, which tells us there are 124 neutrons. (82p, 124n, and 82e–)
21.2. Complete the following nuclear equations:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(a) The sum of the subscripts on the left is 7 + 2 = 9. The subscript of the first product on the right is 8. Then the second product on the right must have a subscript of 1 to achieve a balance.
The sum of the superscripts on the left is 14 + 4 = 18. The superscript of the first product on the right is 17. The second product must have a superscript of 1.
The particle missing on the right has nuclear charge of 1 and a mass number of 1. The particle must be 
(b) The nuclear charge of the second product particle is (4 + 2) – 6 = 0. The mass number of the particle is (9 + 4) – 12 = 1. The notation for the particle, which must be a neutron, is 
(c) The reactants have a combined nuclear charge of 5 and mass number of 10. In addition to the α-particle, a product will be formed with the charge of 5 – 2 = 3, and mass number 10 – 4 = 6. This is lithium, the element with atomic number 3. The notation is 
(d) The nuclear charge of the second particle is 15 – 14 = 1. The mass number is 30 – 30 = 0. The particle must be a positron, 
(e) The nuclear charge of the second particle is 1 – 2 = –1, while the mass number is 3 – 3 = 0. The electron, 
is the particle in question.
(f) The reactants 
Ca and 
He have a combined nuclear charge of 22 and a mass number of 47. The ejected product will have a charge of 22 – 21 = 1, and a mass number of 47 – 46 = 1. This is a proton and should be represented within the parentheses by p.
21.3. What is the total binding energy of 12C, and what is the average binding energy per nucleon?
Although “binding energy” is a term referring to the nucleus, it is more convenient to use the mass of the whole atom (nuclide) in calculations, since these are the masses that are given in tables. If M(X) is the atomic mass of nuclide X,
The nucleus of X consists of Z protons and A – Z neutrons. Then its binding energy, BE, is given by
Applying (1) both to the nucleus of X and to the proton, which is a 
nucleus, and substituting in (2),
Then, nuclear masses can be replaced by atomic (nuclidic) masses when calculating the binding energy. Whole atom masses can, in fact, be used for mass-difference calculations in all nuclear reaction types discussed in this chapter, except for β+ processes where there is a resulting annihilation of two electron masses (one β + and one β–).
The data needed for 12C are found in Tables 2-1 and 21-1. We cannot use average atomic masses from the periodic table for these calculations because our calculations call for the masses of single isotopes (1H, 12C, etc.).
Since there are 12 nucleons (6 protons and 6 neutrons), the average binding energy per nucleon is
21.4. Evaluate Q for the reaction 7Li(p, n)7Be.
The change in mass (u) for the reaction is calculated as follows:
A corresponding net amount of energy must be consumed. That energy is equal to
Note: The energy is supplied as kinetic energy from the bombarding proton and is part of the acceleration requirement for the proton supplied by the particle accelerator.
21.5. The Q-value for the 3He(n, p) reaction is 0.76MeV. What is the nuclidic mass of 3He?
The reaction is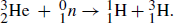 
The mass loss must be 0.76/931.5 = 0.00082 u. And the mass balance can be calculated on the basis of whole atoms and the particles involved.
The calculation now becomes: (x + 1.00866) – 4.02388 = 0.00082. Solving: x = 3.01604 u.
21.6. Calculate the maximum kinetic energy of the beta particle emitted in the radioactive decay of 6He.Assume that the beta particle has maximum energy when no other emission is involved.
The process referred to is 
The calculation of the mass change only requires the whole number atomic masses of the elements since, if we add two electrons to each side, we would have enough for a whole helium atom on the left and a whole lithium atom on the right.
The maximum kinetic energy of the β– + is 3.51MeV.
21.7. 13N decays by positron emission. The maximum kinetic energy of β+ is 1.20MeV. What is the nuclidic mass of 13N?
The reaction is 
This is a process, mentioned in Problem 21.3, in which a simple difference of whole atom masses is not the desired quantity because we are not adding the same particle to both sides and cannot do so. The calculation for the mass difference is
This expression must equal the mass equivalent of the maximum kinetic energy of the β+.
Then,
21.8. Consider the two nuclides of mass number 7, 7Li and 7Be. Which of the two is the more stable? How does the unstable nuclide decay into the more stable one?
Table 2-1 shows that 7Be has a larger mass than does 7Li. This tells us that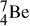 
can decay spontaneously into 
but the reaction does not go the other way. There are two types of decay processes in which Z is decreased by one unit without a change in the mass number, A: β– emission and electron capture. These two processes have different mass balance requirements.
Assume that the process is beta emission.
It was shown in Problem 21.7 (third line of mass difference equation) that a positron emission can occur (Q is + and the reaction is spontaneous) only if the nuclidic mass of the parent species exceeds the nuclidic mass of the daughter by at least twice the rest mass of the electron, 2(0.00055) = 0.00110 u. In the present case, the actual mass difference between parent and daughter nuclides is 7.01693 – 7.01600 = 0.00093 u. We can see that positron emission in this case is not possible. This means that7 Be must undergo electron capture.
Note that we have predicted only that 7Be should decay by electron capture into 7Li. We have said nothing about the rate of the process. Measurements show the half-life to be 53 days.
21.9. Lithium hydride, LiH, composed of two isotopes, 6Li and 2H, is proposed as a potential nuclear fuel. The reaction involved is
Calculate the expected power production, in megawatts, associated with the consumption of 1.00 g of 6Li2H per day assuming 100% efficiency.
The change in mass for the reaction is first calculated.
21.10. 18F is found to undergo 90% radioactive decay in 366 min. What is its calculated half-life?
The rate constant for the decay can be found from (20-2). Ninety percent decay corresponds to 10% or 0.10, survival. In dealing with radioactive decay, the total population of radioactive element is used in place of its concentration. (Remember that in first-order reactions, the rate constant and the half-life, as well, are independent of the concentration units.) So, in place of the concentration ratio [A]/[A]0, put the ratio of the numbers of atoms N/N0, or moles, or masses, of radioactive element. The mass of radioactive element encountered in the laboratory is exceedingly small; a typical sample can be measured only by its activity. Since its activity is proportional to its population, the observed ratio of activities, A/A0, can be used in place of the number ratio, N/N0.
Then, the half-life can be calculated from (20-3):
21.11. A piece of the linen wrapping an Egyptian mummy was analyzed and found to have a 14C activity of 8.1 counts (disintegrations) per minute for each gram of carbon. Estimate the age of the mummy.
The half-life of 14C is 5730 years. It is generally assumed that over at least the past 30,000 years the 14C content of the atmospheric carbon (as CO2) has been roughly constant. Living plants, which obtained their carbon from the air by photosynthesis, have had over this period a constant activity whose value has been found to be 15.3 counts per minute, per gram of carbon.
After the flax was harvested and made into linen, there was no longer any absorption of 14C from the atmosphere. From that point in time, the radioactivity dropped off at an assumed constant rate. Use (20-3) to find k, then (20-2) to find the time, t, for the activity to decay to its present level.
21.12. A sample of uraninite, a uranium-containing mineral, was found on analysis to contain 0.214 g of lead for every gram of uranium. Assume that the lead all resulted from the radioactive disintegration of the uranium since the geological formation of the uraninite. Also, assume that all isotopes of uranium other than 238U can be neglected. Estimate the date when the mineral was formed in the earth’s crust. The half-life of 238U is 4.5 × 109 years.
The radioactive decay of 238U leads, after 14 steps, to the stable lead isotope, 206Pb. The first of these steps is the α-decay of 238U (4.5 × 109 years half-life), which is more than 104 times as slow (in terms of half-life) as any of the subsequent steps. As a result, the time required for the first step accounts for essentially all the time required for the entire 10-step process.
In a sample containing 1 g U, there is
If each atom of lead in the mineral today is the daughter of a uranium atom that existed at the time of the formation of the mineral, then the original number of moles of uranium in the sample would have been
Then the remaining fraction is
Letting t be the elapsed time from the formation of the mineral to the present time, we have
21.13. A sample of 14CO2 was to be mixed with ordinary CO2 (containing 12C) for a biological tracer experiment. In order that 10 cm3 (S.T.P.) of the diluted gas should have 104 disintegrations per minute, how may microcuries of radioactive carbon are needed to prepare 60 L of the diluted gas?
21.14. The half-life of 40K is 1.25 × 109 years. What mass of this nuclide has an activity of 1 μCi?
Let us first calculate the rate constant and express it in s–1.
The disintegration rate is an instantaneous rate measured under conditions of essential constancy of the concentration (i.e., the population) of 40K atoms. The form of the rate equation is that used in Chapter 20, with the numerical value of the rate taken from the definition of the curie.
Dividing the desired rate by the rate constant provides us with the total number of atoms needed to produce the desired rate.
and the corresponding mass is
21.15. The radioisotope 237 Ac has a half-life of 21.8 years. The decay follows two parallel paths: one leading to 227Th, and one leading to 223Fr. The percentage yields of these two daughter nuclides are 1.4% and 98.6%, respectively. What is the rate constant, in y–1, for each of the separate paths?
The rate constant for the decay of Ac, kAc, can be calculated from the half-life.
The overall rate constant for a set of parallel first-order reactions must be equal to the sum of the separate rate constants.
The fractional yield of either process is equal to the ratio of the rate constant for that process to the overall rate constant.
21.16. Determine the number of protons, neutrons, and electrons in each of the following atoms: (a) 70Ge; (b) 72Ge; (c) 9Be; (d) 235U.
Ans. (a) 32 p, 38 n, 32 e–;
(b) 32 p, 40 n, 32 e–;
(c) 4 p, 5 n, 4 e–;
(d) 92 p, 143 n, 92 e–
21.17. Write the complete nuclear symbols for the most common isotope (by the mass number) of sodium, of phosphorus, and of iodine.
Ans. 
21.18. An alpha particle is emitted from 238U and the heavy residual nucleus is referred to as UX1. UX1 is also radioactive and emits a beta particle and its residual nucleus is referred to as UX2. Determine the atomic numbers and mass numbers of (a) UX1 and (b) UX2.
Ans. (a) 90, 234; (b) 91, 234
21.19. 
Np emits one β– and the residual heavy nucleus, also radioactive, gives rise to 235U by its radioactive process. What small particle is emitted simultaneously with the formation of 235U?
Ans. α-particle
21.20. Complete the following equations:
(a)
(b)
(c)
(d)
Ans. (a) 
(b)
(c)
(d)
21.21. Complete the following equations:
(a) 24Mg(d, a)?
(b) 26Mg(d, p)?
(c) 40Ar(a, p)?
(d) 12C(d, n)?
(e) 130 Te(d, 2n)?
(f) 55Mn(n, γ)? (g) 59Co(n, a)?
Ans. (a)22Na; (b) 27Mg; (c)43K; (d) 13N; (e) 130I; (f)56Mn; (g) 56Mn
21.22. If a nuclide of an element in Group IA (alkali metals) of the periodic table undergoes radioactive decay by emitting positrons, what is the chemical nature of the resulting element?
Ans. Group VIIIA element (also referred to as an inert gas or noble gas)
21.23. An alkaline earth element is radioactive. It and its daughter elements decay by emitting 3 alpha particles in succession. In what group should the resulting element be found?
Ans. Group IVA
21.24. A nuclear power reactor gets its energy from neutron-induced fission (atom split when hit by a neutron), usually 235U. The splitting is not symmetrical and different pairs of products result. Determine the missing fission product for the two examples given below.
(a) n + 235U – 4n + 139Cs + ?(b) n + 235U – 5n + 135I + ?
Ans. (a) 93 Rb; (b) 96Y
21.25. In the previous problem, notice how much higher the fission product’s mass number, A, is when compared to the stable element’s average atomic mass. All will decay by beta (e–) emission to achieve a more normal A to Z ratio. Write the decay reactions for the four fission products above.
Ans. 139Cs → β– + 139Ba 93Rb → β– + 93Sr 135I → β– + 135Xe 96Y → β– + 96Zr
21.26. Suppose an atom of 235U, after absorption of a slow neutron, undergoes fission to form an atom of 139Xe and an atom of 94Sr. What other particles are produced? How many of the particles are produced?
Ans. 2 neutrons
21.27. Which is the more unstable of each of the following pairs: (a) 16C or 16N, (b) 18For 18Ne? Also, indicate what type of process the unstable nucleus most likely undergoes to convert to the other nuclei?
Ans. (a) 16C, β–-decay; (b) 18Ne, both β+-decay and electron capture are possibilities on the basis of the given data.
21.28. One of the most stable nuclei is 55Mn. Its nuclidic mass is 54.938 u. Determine its total binding energy and average binding energy per nucleon.
Ans. 483 MeV, 8.78 MeV per nucleon
21.29. How much energy is released during each of the following fusion reactions?
(a) 
(b) 
Ans. (a) 17.4 MeV; (b) 17.6 MeV
21.30. If the energy released in reaction (a) in the previous problem is divided equally between the two alpha particles, what is the velocity?
Ans. 2.0 × 107m/s
21.31. 14C is believed to be made in the upper atmosphere by an (n, p) process on 14N. What is the Q for this reaction?
Ans. 0.62 MeV
21.32. In the reaction 32S(n, γ)33S with slow neutrons, the γ is produced with an energy of 8.65 MeV. What is the nuclidic mass of 33S?
Ans. 32.97146 u
21.33. If a β+ and a β annihilate each other and their rest masses are converted into two γ -rays of equal energy, what is the energy in MeV of each γ ?
Ans. 0.51 MeV
21.34. ΔE for the combustion of a mole of ethylene in oxygen is – 1.4 × 103 kJ. What would be the loss in mass (in u) accompanying the oxidation of one molecule of ethylene?
Ans. 1.6 × 10–8 u (This value is so small compared to the molecular mass that the change in mass, as in all chemical reactions, is ordinarily not taken into account.)
21.35. The sun’s energy is believed to come from a series of nuclear reactions, the overall result of which is the transformation of four hydrogen atoms into one helium atom. How much energy is released in the formation of one helium atom? (Hint: Include the annihilation energy of the two positrons formed in the nuclear reaction with two electrons.)
Ans. 26.8 MeV
21.36. The nuclear fusion reaction, 22H → 3H + 1H + energy, has been proposed as a way to produce the energy needed to generate electricity commercially. If the output is to be 50 MW and the energy of the above reaction is used with 30% efficiency, how many grams of deuterium fuel will be needed per day?
Ans. 149 g/d
21.37. A pure radiochemical preparation was observed to disintegrate at the rate of 4280 counts per minute at 1:35 p.m. At. 4:55 p.m. of the same day, the disintegration rate of the sample was only 1070 counts per minute. The disintegration rate is proportional to the number of radioactive atoms in the sample. What is the half-life of the substance?
Ans. 100 minutes
21.38. An atomic battery for pocket watches has been developed which uses the beta particles from 147Pm as the primary energy source. The half-life of147Pm is 2.62 years. How long would it take for the rate of beta emission in the battery to be reduced to 10% of its initial value?
Ans. 8.7 years
21.39. A set of piston rings weighing 120 g was irradiated with neutrons in a nuclear reactor. Some of the cobalt present in the steel was converted to 60Co, a radioisotope with a long enough half-life (5.3 y) so that there is essentially no mass loss during the investigation. Irradiation continued until the total 60Co activity was 360 mCi. The rings were inserted into an automobile engine which was operated for 24 hours under average conditions, following which, 0.27 μCi of 60Co activity was found in the oil filter. Calculate the rate of wear of the piston rings in mg/y based on the assumption that all the eroded metal was captured by the oil filter.
Ans. 33 mg/y
21.40. A charcoal sample taken from a fire pit in an archeological excavation of a rock shelter was believed to have been formed when early occupants of the shelter burned wood for cooking. A 100-mg sample of pure carbon from the charcoal was found in 1979 to have a disintegration rate of 0.25 counts per minute. How many millennia (1000 years) ago did the tree grow that was burned, producing the charcoal? (Use the data from Problem 21.11.)
Ans. 15 millennia ago
21.41. All naturally occurring rubidium cores contain 87Sr, resulting from the beta decay of 87Rb. In naturally occurring rubidium, 278 of every 1000 rubidium atoms are 87Rb. A mineral containing 0.85% rubidium was analyzed and found to contain 0.0089% strontium. Assuming that all of the strontium originated by radioactive decay of 87Rb, estimate the age of the mineral. Half-life for 87Rb is 4.9 × 1010 y.
Ans. 2.6 × 109 years
21.42. Transuranium elements (above atomic number 92) were believed not to occur in nature because of their relatively short half-lives. Then 244Pu was reported in natural ore. The half-life of 244Pu is 8.0 × 107 years. If this element is more stable than any of its radioactive predecessors and has not been produced in this ore in significant amounts since the ore was deposited, what fraction of the original 244Pu content would still be present? Assume the ore is 5 × 109 years old.
Ans. 10–19
21.43. Before the use of nuclear weapons, the specific activity of 14C in soluble ocean carbonates was found to be 16 disintegrations per minute per gram C. The amount of carbon in these carbonates has been estimated as 4.5 × 1016kg. How many megacuries of 14C did the ocean carbonates contain?
Ans. 320 MCi
21.44. Refer to Problems 21.13 and 21.11. Calculate the mass of pure 14C needed to provide 17 μCi of beta activity. (Note: Refer to the procedure followed in Problem 21.14.)
Ans. 3.1 × 10–6g
21.45. If the limit of a detection system is 0.002 disintegrations per second for a 1-g sample, what would be the maximum half-life that this system could detect for a 1-g sample of a nuclide whose mass number is around 200?
Ans. 3 × 1016 years
21.46. The activity of 30 μg of 247Cm is 1.8 nCi. Calculate the disintegration rate constant and the half-life of 247Cm.
Ans. 9.1 × 10–15 s–1, 2.4 × 107 years
21.47. How much heat would be developed per hour from a 1-Ci 14C source if we were able to capture all the energy of the β–-decay?
Ans. 3 J/h
21.48. 32P has a 14.3-day half-life and emits an energetic β– particle, making 21P useful for nutritional studies in plants and animals. A 0.01-μCi sample of 32P in the form of a soluble phosphate was added to a hydroponic bath containing a young tomato plant. Exactly three weeks later, the entire plant was rinsed, dried, and liquefied in a blender. A 
portion of the preparation was placed in a total activity counter. In a 1.00-min period an average of 625 counts was recorded. How efficient was the tomato plant in utilizing the phosphorus?
Ans. 78% efficient
21.49. Dr. Beaker had a solution which contained various sodium salts and wanted to determine the total sodium content. She added a quantity of HCl, which she judged to be in excess of the sodium ion equivalent. Then she added 0.4229 g of pure NaCl, which had a total 22Na activity of 22,110 counts per minute. (22Na is a positron emitter; its half-life is 2.6 years.) The solution was thoroughly mixed, then evaporated until crystals of NaCl were collected. The crystals were filtered off and repeatedly recrystallized until a small batch of pure NaCl was isolated. This NaCl sample had an activity of 483 counts/min per gram. What was the mass of sodium ion in Dr. Beaker’s original solution?
Ans. 17.8 g