
Fig. 3-0: The Crab Nebula, a supernova remnant in the constellation of Taurus, 6500 light years from Earth. The nebula is the expanding cloud that began with the supernova recorded by Chinese and Arab astronomers in 1054. The expansion rate is about 1500 km/sec, and the nebula is currently about 11 light years across. The size of our solar system out to the planet Neptune (~0.001 light years) would only be the size of a tiny spot on the image. The nebula was the first to be associated with a historical supernova explosion. (Courtesy of NASA, ESA, and Allison Loll/Jeff Hester (Arizona State University). Acknowledgment: Davide De Martin (ESA/Hubble))
During the explosive birth of our universe only two elements were formed in abundance: hydrogen and helium. Were this the end of the story, no planets and life could have appeared in the history of the universe. Our planet and the sun contain all the elements, so the other ninety elements in the periodic table must have been produced over the history of the universe. Stars are the universe’s element production factories. Stellar interiors are so hot that atomic nuclei can interact and fuse together, emitting massive energy and making heavier elements in the process. Nuclear fusion, however, can occur only up to nuclei with 56 atomic particles, which is the element iron (Fe). Stars that reach this point then explode, creating heavier elements in the process and casting forth into neighboring regions of the galaxy a mixture of all ninety missing elements. The frequency of these awesome explosions in galaxies like our own Milky Way is about one per thirty years.
Evidence that supports this origin is imprinted in the relative abundances of the elements that make up our solar system. For example, the high relative abundance of iron is consistent with the fact that it is the ultimate product of the nuclear fires at the centers of stars. Element production in stars is also demonstrated by the existence of the spectral lines imposed by elements with very short radioactive half-lives. The radioactive decay of 78-day half-life cobalt (Co) with 56 nuclear particles (56Co) dominates the light given off after a supernova explosion, demonstrating element production of heavy elements during such an event. The element technetium (Tc) is also found in stellar spectra. Since all the isotopes of Tc are radioactive with short half-lives, Tc can be present only in matter freshly produced by a nuclear furnace.
Because supernovae happen relatively frequently, the history of individual explosions can be monitored. Chinese astronomers observed a supernova in 1054. The debris cloud from this explosion continues to expand and is now known as the Crab Nebula (see frontispiece). Through the course of our galaxy’s history, the formation and demise of about 100 million red giants has converted about 2% of the galaxy’s hydrogen and helium into heavier elements. Contained in this 2% are the ingredients needed to build planets and form life. The processes of element creation are common to stars in all galaxies, and the raw material for planets and life is omnipresent in the universe.
By cosmic standards, our Earth and its fellow terrestrial planets are chemical mavericks. They consist primarily of four elements: iron (Fe), magnesium (Mg), silicon (Si), and oxygen (O). By contrast, we look out on stars that are made up almost entirely of two different elements, hydrogen and helium. For the universe as a whole, all elements other than hydrogen and helium are small potatoes; taken together they account for only about 2% of all of the 4% of matter that is not dark matter or dark energy.
Despite their rarity, the elements other than H and He are prerequisites for habitability. A habitable planet must have a solid or liquid exterior and an abundance of the element carbon (C). Objects made primarily of hydrogen and helium gas offer no solid base. Hence, high on our agenda must be an understanding of how elements heavier than hydrogen and helium were formed and how these elements were separated from the bulk gas and forged into rocky planets. In this chapter we tackle the first of these problems.
All stars form from the gravitational collapse of clouds of gas. Since the lion’s share of the matter in the collapsing clouds ends up in the star itself, the star’s chemical composition must be representative of the parent cloud. If we could somehow determine the chemical composition of the sun, we could constrain the composition of the galactic matter from which the sun formed.
As noted in Chapter 2, our information about the composition of stars comes from the dark lines in its spectrum that result from absorption by chemical elements in the atmosphere of the sun through which the light passes. The extent to which the light corresponding to each line is muted in the rainbow is a measure of the abundance of that particular element in the sun’s atmosphere. Fortunately for stars like our sun, except for hydrogen and helium, the atmosphere is thought to have a composition nearly identical to that of the star’s interior.
The strength of the lines can then be converted into the relative abundance of elements in the sun’s atmosphere. By “relative abundance” we mean the ratio of the number of atoms of a given element to the number of atoms of a reference element. By convention, astronomers use silicon as the reference element. The relative abundance of an element is stated as the number of atoms of that element for each 1 million atoms of silicon. These abundances are plotted versus element number on the graph in Figure 3-1. This graph has a logarithmic power of 10 scale. For example, helium atoms with a relative abundance lying between 109 and 1010 on this scale are 10 billion times more abundant than bismuth (Bi) atoms with a relative abundance lying between 10–1 and 100.
Other than the dominance of the abundances of hydrogen and helium over those of the other ninety elements, a prominent feature of the graph is the general decline in abundance with increasing element number. Superimposed on this decline are several obvious features. One is that the abundance of the element iron is 1,000 times higher than would be expected were the decline smooth. A second is that the elements lithium (Li), beryllium (Be), and boron (B) have abundances many orders of magnitude lower than would be expected were the decline smooth. A third is that the abundance curve has a saw-toothed appearance because elements with an odd number of protons are generally less abundant than their even-numbered neighbors. These characteristics of the abundance curve provide hot clues regarding the mode of origin of the elements heavier than hydrogen and helium.
Fig. 3-1: Relative abundances of the elements in our sun: as the abundances range over 13 orders of magnitude, they must be displayed on a power of 10 (logarithmic) scale. The abundance of each element is expressed as the number of atoms per million (i.e., 106) atoms of the element silicon. The gaps in the sequence of technetium and promethium represent elements that have only radioactive isotopes and are, therefore, absent in a relatively low temperature star such as the sun.
Physicists conjecture that at the instant of the Big Bang, all matter must have been contained in a very compact blob. The pressures and temperatures in this primordial blob were so high that stable combinations of neutrons and protons could not exist. Within seconds after the explosion, however, such combinations could and did form. At one time it was hypothesized that the blend of elements we see in our sun might have been generated entirely during the first hour of universe history. But subsequent work has shown that the only elements produced in significant amounts during this very early phase of universe evolution were hydrogen and helium. The others were produced billions of years later, inside giant stars.
The hydrogen and helium gas produced during the Big Bang eventually agglomerated into megaclouds. These megaclouds organized into the spiral and elliptical shapes we see in distant galaxies. Some of the gas in these newly formed galaxies in turn broke into far smaller subclouds that collapsed under their mutual gravitation into stars. So through their telescopes astronomers see a host of galaxies, each defined by billions of stars. Through careful observation, astronomers have been able to show that the process of star formation continues. They see new stars forming and old ones dying. By observing stars of all sizes and in all stages of their evolution, astronomers have been able to map out the history of these objects. Interwoven with this evolution is the conversion of hydrogen and helium to heavier elements. It is here, rather than in the Big Bang, that we must look for the production of the iron, magnesium, silicon, and oxygen of which Earth is largely comprised.
Again one might ask, How do scientists know that the elements heavier than helium were born in the centers of stars? As we shall see, a rather impressive case can be made. No jury could deny it. Like the Big Bang theory, the stellar synthesis theory of element origin gets a ranking of 9.9 out of a possible 10.
In order to comprehend the case to be put forth in support of the stellar synthesis hypothesis, we need to consider some of the simple facts about the architecture of atomic nuclei.
Each atom has a compact nucleus made of neutrally charged neutrons and positively charged protons (e.g., see Fig. 1-1). This nucleus carries nearly all of the atom’s mass and is incredibly small, only about 10–15 m in diameter. A fluff of negatively charged electrons fly in complicated orbits around the central nucleus and give the atom its size but add almost nothing to its mass. The diameter of this electron cloud is about 10–10 m (i.e., the atom is 100,000 times bigger than its nucleus). The electrons are held in captive orbits by the electrical attraction of the positively charged protons in the nucleus.
The power of the electrostatic force that keeps the protons and electrons together can be appreciated by comparing it to the power of gravity. A paper clip rests on a countertop because of the gravitational pull of the entire Earth. If a very small magnet is placed just above the paper clip, the paper clip jumps up to the magnet, because the electrostatic attraction of the little magnet is stronger than Earth’s gravity. By measuring such forces accurately, physicists find that the electrostatic force is 1036 times stronger than gravity! The only reason that large objects like Earth do not exert a powerful electromagnetic force is because the negative and positive charges of atoms exactly cancel each other out, making gravity the potent force for very massive objects. For tiny objects like an atom, gravity has no power, and the electrostatic force is essential.
Just as opposite charges attract, charges that are the same repel—two similar poles of a magnet repel each other if we try to put them together. This repulsive force doubles for every factor of two decreases in distance. This feature of the atom prevents two positively charged nuclei from approaching one another during normal chemical interactions. The electrons manage because they occupy such a large volume and can avoid one another. Normal chemistry depends on attraction as well as repulsion.
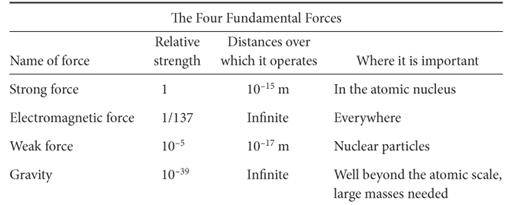
So far so good, but a little reflection leads to quite a paradox. Given the power of the electrostatic force and its large increase with decreasing distance, how can the multiple positively charged protons in the nucleus stay together in such a small volume? The repulsive force must be enormous! Given the huge repulsive forces that exist in the nucleus, some much stronger force must exist to hold the protons together. This “strong force” is 138 times more powerful even than electromagnetism, but it operates only over very short distances. It is analogous to glue, a force that can operate only when two objects “touch” one another. Because of this property of the strong force, physicists gave the particle that carries the force the name gluon. So imagine, for example, two powerful magnets that repel one another, with superglue on their surfaces. As they get closer and closer they are repelled ever more strongly, but if we get the surfaces to touch, the superglue holds them together despite the electrostatic repulsion. The relative power of these forces in the universe is shown in Table 3-1. Gravity that is so important to us is so puny in comparison to other forces!
At low temperatures, the repulsive power of the nucleus keeps atoms separate, and interactions between atoms occur by the sharing of electrons to form chemical compounds. During such chemical reactions, only the character of electron orbits changes; the nucleus remains intact. These reactions occur at temperatures of tens to thousands of degrees centigrade. To make nuclear reactions occur, the nuclei need to get so close together that they “touch,” allowing the strong force to exert its power. This can happen only if the nuclei have very high velocities. Velocity increases with temperature, so very high temperatures are necessary. To ignite the nuclear fires, temperatures of 50 million degrees or more must be achieved—no simple task for planetary beings. Only by accelerating charged particles in mighty cyclotrons or by setting off nuclear explosions can physicists create these high temperatures. This is why the alchemists dedicated to making gold from less valuable elements failed. They had no means by which to start a nuclear fire!
The places in the universe with natural furnaces with the temperatures required for nuclear fires are at the centers of stars. Every star must have such a fire at its core; otherwise, the star could not shine. Stars are the alchemists of the universe, where one element can be converted to another.
To understand which nuclides might be manufactured in stars, we must be aware that only certain combinations of neutrons and protons form stable units. The power of the repulsive force helps us to understand the important role of neutrons—they keep the protons separated from one another, reducing their electrostatic repulsion. Neutrons and protons also have a special relationship to one another, which is that they can be converted one to the other. Neutrons that are isolated are unstable, and they decay to a proton plus an electron (a hydrogen atom) with about half the neutrons decaying approximately every ten minutes. And given the right inducement, protons can convert to neutrons by capturing an electron—so the proton-neutron configuration of the nucleus is convertible in terms of the proportions of each. Neutrons are useful because they separate protons, but neutrons left to themselves decay. Protons are held together by gluons, but prefer to be separated. If the nucleus has too many neutrons, they decay to protons; if too many protons, they decay to neutrons. This balance causes stable nuclei to have roughly coequal amounts of both particles.
This balancing act in the nucleus leads to a band of stability, where there is no further preference for conversion of one nuclide to another. Figure 3-2 shows that out of all the possible neutron/proton combinations, relatively few are in this stable category. The rest are radioactive, and given enough time, will spontaneously transform into one of the stable combinations. The pathways for these transformations are shown in Figure 3-2.
There is one further aspect to stability of the nucleus. If the nucleus gets too large, there are so many protons that electrostatic repulsion becomes large enough for the nucleus to eject protons and neutrons. 209Bi is the stable nuclide with the most neutrons and protons. All nuclei with more than 209 particles are radioactive. At first nuclear parcels, like a helium nucleus containing two protons and two neutrons, are ejected. For still heavier nuclei, the entire nucleus falls apart, in a process called nuclear fission.
Those nuclides which, left to themselves, will forever remain unchanged end up making planets and life. They form a band of stability that traverses the chart of the nuclides running from 1H at one end to 209Bi at the other. The course of this band represents the most favorable ratio of neutrons to protons. This ratio is near unity for the low proton number elements. Larger nuclei become more neutron rich, with the ratio of neutrons to protons reaching 1.5 for bismuth (Bi).
All nuclei outside the band of stability are radioactive and decay to the band. Nuclei that are too neutron rich convert neutrons to protons +electrons, called beta decay. Nuclei that are too proton rich capture electrons to convert protons to neutrons in a process called electron capture. And nuclei that are too big eject a helium atom, called an alpha particle (because it was discovered first). Note that the first two processes do not change the number of nuclear particles in the nucleus, while alpha decay decreases the number of nuclear particles by four, two neutrons and two protons (Fig. 3-2).
Fig. 3-2: The chart of the nuclides. Stable nuclides (the band of stability) are indicated by the solid black boxes. Radioactive nuclides that decay back to the band of stability with variable half-lives are indicated by the gray field. Very heavy isotopes decay by fission, where they spontaneously break up into pieces. Heavy masses decay by alpha decay, ejecting a helium atom of two protons and two neutrons. Neutron-rich isotopes decay by beta decay, converting a neutron to a proton without changing the number of nuclides in the nucleus. Proton-rich isotopes decay by electron capture, converting a proton plus electron to a neutron. The N = Z line shows that at low masses the number of neutrons and protons is quite equal. Higher masses become neutron rich.
All stable nuclides are found on Earth, in meteorites, and on other planets, so all must somehow have been produced from hydrogen and helium at the centers of stars. As we shall see, this buildup from small to large occurs in many steps. To produce a carbon atom requires only two steps; to produce an iron atom requires a few more steps; to produce a bismuth atom requires many more steps. It is because of this stepwise buildup that the “light” elements are produced in greater abundance than the “heavy” elements.
Fig. 3-3: A blowup of a portion of the chart of the nuclides illustrating similar principles as Fig. 3-2. Electron capture and beta decay occur along isobars. The number of protons determines the element identity. Elements with even numbers of protons have many more stable isotopes than those with odd numbers of protons, which usually have only one isotope. Note the very small number of stable isotopes that are “odd-odd.”
Let’s examine what these steps are. In the fireball of the Big Bang, matter was largely in the form of neutrons. Once released from their dense confinement, neutrons underwent spontaneous radioactive decay to protons plus electrons, with half of the neutrons present decaying every 10.2 minutes—this time is referred to as the half-life of the decay. (For example, after three half-lives, one-eighth of the original atoms remain.) During those minutes of stability, many of the neutrons collided with a proton to make 2H, an isotope of hydrogen consisting of one proton and one neutron called deuterium. Other collisions could lead to masses 3 and helium atoms of mass 4. At this point there is a remarkable aspect of nuclear stability, which is that no stable nucleus of mass 5 or mass 8 exists (Fig. 3-4). A helium nucleus colliding with the abundant protons or neutrons would produce no reaction. Or two helium atoms colliding would also produce nothing. Instead, only rare reactions could jump over mass 5 to produce masses 6, 7, or 8. For example, a proton and a neutron would have to have collided at the same time with a 4He nucleus to produce 6Li. As is the case on a pool table, in the expanding gas cloud “three-ball” collisions were far less frequent than “two-ball” collisions, so infrequent, in fact, that the number of nuclei formed that were heavier than 4He was insignificant. Thus, at the end of Day One universe matter consisted almost entirely of the elements hydrogen and helium, with only very small amounts of the next three elements—lithium (Li), beryllium (Be), and boron (B). Further synthesis awaited the formation of galaxies and the formation of stars within these galaxies.
Physicists have made models of the collisions that would have occurred during the first day of universe history. They found that there would have been one helium atom for every ten hydrogen atoms.1 This is about the fraction of helium seen in young stars from throughout the universe, which was the third line of evidence for the Big Bang hypothesis discussed in Chapter 2.
Fig. 3-4: The lower left-hand corner of the chart of the nuclides. Stable nuclides with a particle number in the 1 to 11 range. Note that no stable nuclide exists with a neutron plus proton number totaling 5 or 8. It is these two gaps in the chain that prevented element formation during the Big Bang from continuing beyond helium to any significant extent.
Stars are hot inside for the same reason that brake shoes on a stopping car are hot. When a moving vehicle is brought to a stop, the energy associated with its motion is converted to heat in its brake linings. During the collapse of a cloud of gas, gravitational energy is likewise converted to heat. The amount of heat produced is so vast, and the insulation provided by the enshrouding envelope of gas so effective, that the core of the protostar becomes hot enough to ignite a nuclear fire.
For the nuclei in a star to react, they must touch. To touch, they must fly at one another at such high velocities that they overcome the electrical repulsion exerted by one proton on another. It is much like trying to throw a Ping-Pong ball into a fan. A very high velocity is required to prevent the ball from being blown back in your face.
The hotter atoms are, the faster they move. Temperature is a scale for molecular motion. Touching a hot stove causes the molecules in the skin of your finger to move so fast that the chemical bonds holding them in place are rent; we call this molecular damage a burn. For two protons to collide requires velocities equivalent to a temperature of about 60,000,000°C. Through a somewhat complicated series of collisions, four protons can combine to produce a helium nucleus (and two electrons). The helium nucleus contains two of the original protons and two neutrons. These neutrons come into being through the mergers of protons with electrons (for each proton in a star there must be one electron).
Table 3-2
Conversion of mass to energy
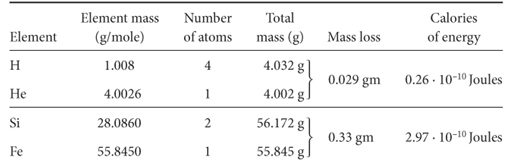
As first recognized by Einstein, for nuclear fusion to occur there must be a release of energy, and this energy release results in a reduction in mass. This lost mass reappears as heat. Indeed, the weight of a helium atom is just a little less than that of four hydrogen atoms (see Table 3-2), and this mass is converted to heat when the atom is manufactured in a star. As the proponents of fusion power are quick to point out, the amount of heat obtained in this way is phenomenal. So phenomenal, in fact, that once a protostar’s nuclear fire is ignited, its collapse is stemmed by the pressure created by the escape of the heat generated. The star stabilizes in size and burns smoothly for a very long time. For example, our sun has burned for 4.6 billion years and won’t run short of hydrogen fuel for several more billion years.
Most of the stars we see are emitting light created by the heat from a hydrogen-burning nuclear furnace. Thus, one might say that stars are continuing the job begun during the first day of universe history; they are slowly converting the remaining hydrogen in the universe to helium.
Our sun is small enough that hydrogen burning can take place for billions of years. Since helium nuclei have two protons, the force of electrical repulsion between them is four times the force of repulsion between two hydrogen nuclei. At the temperatures of hydrogen fusion, the velocities of the nuclei are insufficient to overcome this electrostatic repulsion. For this reason, fusion of helium atoms does not take place in small stars. Within the center of a large star, the gravitational attraction is larger, and to counter it the hydrogen fuel converts to helium relatively rapidly. So-called red giants run through their hydrogen supply in something like a million years. When the core of a red giant becomes depleted in hydrogen, the nuclear fire dims and the star loses its ability to resist the inward pull of gravity. It once again begins to collapse. The energy released by the renewed collapse causes the core temperature to rise and the pressure to increase. The higher temperatures reach the ignition temperature required for helium fusion. Then helium nuclei begin to combine to form carbon nuclei (three 4He nuclei merge to form one l2C nucleus). The mass of the carbon atom is less than that of the three helium atoms from which it was formed. This lost mass appears as heat. The heat from the rekindled nuclear fire stems the star’s collapse, and its size once again stabilizes.
In large stars this cycle of fuel depletion, renewed collapse, core temperature rise, and ignition of a less flammable nuclear fuel is repeated several times (Fig. 3-5). A carbon nucleus can fuse with a helium nucleus to form oxygen, or two carbons can merge to form magnesium nuclei, and so forth. Each merger leads to a small loss of mass and to the corresponding production of heat. This entire process can continue as long as fusion to produce heavier nuclei produces a loss of mass and production of heat. The extra heat is needed to prevent the star from collapsing and to keep it in a stable state where expansion from heat production balances contraction from gravitational attraction.
The maximum mass that can be created by this process is isotope 56 of Fe (56Fe). Above this mass, merger of nuclei does not lead to loss of mass, and instead heat must be added to nuclei if they are to merge. That is, since mass and energy are related by E = MC2, the mass of nuclei heavier than iron proves to be slightly larger than the mass of the nuclei that are merged to form them. These reactions are heat sinks rather than heat sources, and therefore cannot stem the gravitational collapse of the star. For this reason, the nuclear furnaces of stars can produce only elements ranging from helium through iron. It should be noted that included in this range are the elements carbon, nitrogen, oxygen, magnesium, and silicon.
Fig. 3-5: Three stars with progressively hotter nuclear fires. Like our sun, the star at the left burns hydrogen to form helium in its core; this core is surrounded by unburned fuel. The middle star is burning helium to form carbon and oxygen in its core. This core is surrounded by a layer of unburned helium. Outside of this is a layer in which hydrogen burns to produce helium. Finally, there is an outer layer of unburned hydrogen. The star on the right has a multilayered fire all the way up to Si-burning to create 56Fe. The approximate temperatures required to ignite the successive fuels are also given.
We are then left with two problems. First, there are many elements more massive than 56Fe. How can these be produced? And second, making elements in stellar interiors is not much use for planet building if the elements remain trapped inside. There must be some distribution mechanism that allows these elements to become broadly dispersed throughout the universe. We know this must be the case not only because of the compositions of the planets but also the composition of the sun itself. The materials from which the sun formed must have included all the elements, because the solar spectrum shows that all of these elements exist in the sun itself. It is not made up only of H and He.
Before discussing the solution to these two problems, let us briefly consider the fate of smaller stars like our sun. When the core of our sun runs out of hydrogen, several billion years from now, it will resume its collapse. However, our sun is just barely massive enough to generate the temperature necessary to start a helium fire. Then, after it has burned its core helium, it will collapse into a very dense object that will cool slowly until it gives off only a dull glow. A star to which this has happened is referred to as a white dwarf.
The solution to the two problems of heavy element creation and element distribution is solved thanks to the numbers of very massive stars that exist. These massive stars are ten to twenty-five times the mass of the sun and have such a large gravitational attraction that very high temperatures are required to prevent their collapse. They rapidly progress to the multilayered structure shown in Figure 3-5. Once Fe forms in their core, however, no further heat production is possible through fusion, and there is nothing to prevent their further collapse. The ensuing collapse is catastrophic, bringing the iron nuclei so close together that their nuclear shells begin to interpenetrate. The resistance for further compression generates a shock wave that pushes its exterior outwards. The result is like throwing gasoline onto a hot fire. An incredible explosion occurs, tearing the star asunder. Much of the interior material is blown free of the star’s gravity into the galactic surroundings (see Figure 3-0). Astronomers call these explosions type II supernovae. A second kind of supernova (called type I) evolves when a white dwarf accretes material from its companion stars. When its mass reaches a certain limit, 12C and 16O fuse to form 56Fe, leading to a gigantic nuclear explosion.
Nuclear reactions occurring during these explosions create elements heavier than iron. To understand these reactions we must consider the one nuclear reaction that can occur at “room temperature.” It is called neutron capture. Because the neutron has no charge, it is not repelled by any nucleus it happens to encounter; it can freely enter any nucleus, regardless of how slowly it is moving. This ability of the neutron to react with nuclides under “room temperature” conditions lies at the heart of the principle of nuclear power generation.
During the explosion that marks the death of a massive star, a host of nuclear reactions occur that release free neutrons. In the close-packed conditions inside the exploding star, the neutrons encounter a nucleus long before they get around to undergoing spontaneous decay to a proton plus an electron. Many of these encounters will be with Fe nuclei. The Fe nucleus absorbs the neutron and becomes heavier. In the supernova explosion, these neutron hits will be like bullets from a machine gun. No sooner is an Fe atom hit by one neutron than it is hit by another. The Fe nucleus gets heavier and heavier until finally it cannot absorb any more neutrons. This very brief pause in growth ends when one of the extra neutrons that have been plastered on undergoes beta decay by emitting an electron. Each neutron that decays becomes a proton and increases the atomic number by one, while maintaining the same total number of nuclear particles in the nucleus. The decay of one neutron converts the Fe nucleus to cobalt (Co). This is the first step along the chain of production of the heavy elements. The Co nucleus can in its turn absorb neutrons one after another, until it too becomes saturated. It then emits an electron and in so doing becomes a nickel (Ni) nucleus. These would be the first steps along the road from iron to uranium.
This sequence is repeated over and over again, driving matter along the neutron saturation route (Figs. 3-6 and 3-7). Because of the rapidity of the impacts, radioactivity proves to be no barrier to this buildup. The buildup zooms past bismuth and even past uranium (U) and thorium (Th), stopping only when the nuclei get so big that the neutron impacts cause them to fission. The fragments produced by a fission event are caught up in the bombardment and begin once again to move along the saturation route. The process of such rapid addition of neutrons that there is no time for decay has led to the name r-process (r for “rapid”) for this mode of heavy element creation that occurs during supernova explosions.
Since we are dealing with an explosion, this bombardment is as brief as it is intense. The flux of free neutrons stops suddenly, and no more neutrons are available to be added to nuclei. All the nuclei that have been generated, however, are very neutron rich and far from the band of stability. These neutron-rich isotopes convert one neutron after another to proton plus electron until they have achieved a stable neutron-to-proton ratio (Fig. 3-7). Those nuclides heavier than bismuth emit alpha particles (He nuclei) as well as electrons, moving toward stability as isotopes of the element lead (Pb). While for most nuclides this adjustment process is quickly completed, for a few nuclides with long radio decay half-lives, the adjustment process still goes on today. As we shall see, the radioactivity of these remaining long-lived isotopes plays a very important role in the evolution of planetary interiors and will provide us with timescales for planetary processes.
Fig. 3-6: The elements heavier than iron were built by neutron irradiation. Two quite different processes contributed to this production. One, the s-process, proceeds in a controlled way. Neutron hits are spaced out in such a way that the nuclides have time to achieve stability through beta decay. Thus, the buildup path follows the belt of stability shown in Fig. 3-2. For the same reason it terminates at 209Bi, the heaviest stable nuclide. The r-process (rapid process) occurs during the supernova explosion. No sooner has a nuclide absorbed one neutron than it is hit by another. No time exists between hits for radio decay. Instead, radio decay occurs only when the nuclide becomes so neutron rich that it cannot absorb any more, as indicated by the vertically hachured band in the figure.
It turns out that the rapid events during supernova explosions are not the only time that free neutrons that can be added to nuclei are produced. As part of the steady nuclear burn that characterizes most of a star’s history, side reactions occur that release neutrons. These neutrons also can build lighter elements into heavier elements, but they do it very slowly, one neutron after another, during the relatively long process of stellar evolution. Because the neutron addition is slow, it is called the s-process (s for “slow”). For the r-process, the frequency of neutron hits is extraordinarily high—so high, in fact, that even those nuclides with extremely short half-lives do not have a chance to undergo radio decay before being hit again with a neutron. In contrast, the neutron bombardment associated with the steady nuclear fires of stellar cores is far more leisurely. Adequate time exists between hits for all but the radio-isotopes with the longest half-lives to undergo radio decay (Fig. 3-8). The s-process produces most of the stable nuclides not produced by the r-process.
Fig. 3-7: A segment of the r-process pathway. Rapidfire neutron bombardment adds neutrons until a nuclide cannot hold any more. Only then does the nuclide undergo beta decay to become the next heavier element. This process—neutron capture to saturation followed by beta decay—is repeated over and over again, producing successively heavier elements. The r-process buildup occurs during the explosion that destroys the red giant. Hence it ends abruptly. The neutron flux stops and the highly radioactive isotopes on the r-process pathway emit beta particles one after another until stability is achieved. Note that in the case of those isobars for which two stable nuclides exist, only the neutron-rich nuclide of the pair is produced by the r-process.
The s- and r-processes combined create much of the complexity of the band of stability. As can be seen in Figures 3-2 and 3-7, there are generally two stable nuclides on each even-numbered isobar (as opposed to only one on each odd-numbered isobar). Of these two, the r-process produces only the stable nuclide with the most neutrons (Fig. 3-7). Some isotopes can be produced by both r- and s-process. Those which are neutron rich and separated from other isotopes are r-process only. Those isotopes which are shielded by a stable nucleus that is richer in neutrons along the same isobar are s-process only.
Careful inspection of the chart of the nuclides shows that there are a few nuclides that are produced by neither the r- nor the s-process. For example, in Figure 3-8, 58Ni, with 28 protons and 30 neutrons, is not intersected by either the r-process or s-process path. These isotopes are found in much lower abundance than their r- and s-process neighbors. They can be produced by the p-process of proton addition, or by disintegration of heavier nuclei made by the r- and s-processes.
To sum up, we have seen that a diversity of processes have combined to form all the elements. The governing diagram is the chart of the nuclides, with the band of stability revealing what nuclei can survive without decay. The Big Bang makes the raw material of H and He, with small amounts of Li, Be, and B. Fusion of nuclei in stellar interiors makes more He, and the elements from C to Fe. The larger the star, the shorter the lifetime and the heavier the elements that are formed, up to Fe. Within these stellar interiors, the s-process can create some heavier elements. For the most massive stars, collapse and explosion occur, leading to the r-process, formation of all the heavy elements from Fe to U, and distribution of the elements into space where they become available for stars of subsequent generations and the planets that surround them.
Fig. 3-8: Details of the s-process path. Each time neutron capture produces an unstable, radioactive isotope, decay occurs changing either a neutron into a proton or a proton into a neutron. Not all of the stable isotopes found in solar system matter can be produced in this way. Those stable isotopes lying below the path are produced by the r-process. Those stable isotopes lying above the path are produced by proton bombardment.
Shall we accept the progressively intensifying nuclear fires and catastrophic explosions proposed by astrophysicists to explain the synthesis of the ninety elements heavier than helium? Can this scenario be defended with hard evidence, or might it be merely a cosmic fairy tale? Clearly, no one has ever sent a probe into the core of a star, so we have no direct evidence regarding these phenomena. There are six indirect lines of evidence, however, that are compelling. First, the only conceivable source of energy that could keep stars burning and so hot is nuclear. The pressures and temperatures of the cores of very large stars are adequate to permit not only hydrogen to burn but also helium and even heavier elements. Second, explosions of large stars have been observed (Fig. 3-9).
A third line of evidence comes from the element technetium (Tc), which is not present in Earth because this element has no stable isotopes. Nor are its dark lines present in the spectra of the light reaching us from our sun or from distant stars. The reason is that all these objects are old enough that any technetium produced in stellar interiors has long decayed away. However, the dark lines characteristic of the element do appear in the spectra associated with supernovae explosions. Technetium has two isotopes with moderately long half-lives: 97Tc (2.6 × 106 years) and 98Tc (4.2 × 106 years). These isotopes persist for millions of years after their production. They would have completely disappeared, however, during the 4.5 × 109 years that have elapsed since our solar system formed. The presence of the dark lines of technetium in the atmospheres of a class of objects referred to as AGB stars provides powerful support for the hypothesis that elements are being formed in stars.
A fourth line of evidence comes from gamma rays emitted by 56Co formed from 56Fe during the r-process onslaught during a supernova. These gamma rays light up the nebula created by the explosion. We know this because the nebular glow decreases exponentially following the 78-day half-life of 56Co!
A fifth line of evidence comes from the relative abundances of the elements. Using experiments carried out in particle accelerators, astrophysicists have accumulated substantial data on the stability of nuclei and the forces that hold nuclear particles together. Elaborate calculations have been carried out to determine what the proportions of elements and isotopes should be if elements were produced in massive stars. These calculations reproduce very nicely the important features of the element-abundance curve.
Finally, nuclear physicists are able to produce many of the same reactions postulated for stellar interiors in particle accelerators, and of course in the hydrogen bombs, where the conversion of hydrogen to helium on even a small scale has very powerful effects. The detailed reactions proposed to occur during stellar nucleosynthesis are largely susceptible to experimental confirmation.
Fig. 3-9: Evidence for supernova explosions. Photographs taken before (top left) and after (bottom left) a supernova explosion. Panel on the right shows a closeup of a supernova in 1985 and 2007, revealing the rapid expansion of the cloud. (Photos on left courtesy of Hale Observatories. Right panel courtesy of NASA; http://science.nasa.gov/science-news/science-at-nasa/2008/14may_galactichunt)
All of these lines of evidence make nucleosynthesis in stars one of the established facts of nature, meriting a 10 on our theory scale.
The characteristics of the abundance curve are also central to the future habitability of planets, because planetary processes must be based on the elements that are abundant. For these reasons it is useful for us to examine the abundance curve in more detail.
In Figure 3-10 the nuclide abundances are plotted as a function of the number of nuclear particles. While there is great richness and complexity in the details of the element abundances, here we point out a few that are very important and easily grasped. One is the peak associated with iron (at particle number 56 in Fig. 3-10). If the stars that explode have cores of iron, then it is not surprising that the major nuclide of iron (56Fe) is more abundant than its neighbors in universe material. Since 56Fe is the end of the nuclear fusion assembly line, its abundance will stack up as more and more stellar material is processed. One might ask, in fact, why is the iron peak not even more prominent? If all the material at the star’s interior were converted to iron, then elements such as carbon, oxygen, magnesium, and silicon should be absent in the debris from supernovae. While this is the case for the star’s core, it is not for the layers of gas surrounding the core. When the cores collapse to form supernova, the outer layers are still in earlier states of nuclear fusion, forming lighter elements.
Fig. 3-10: Relative abundances of individual nuclides: In the mass range 10 to 100, nuclides with particle numbers divisible by 4 (i.e., 12, 16, 20, 24, 28, 32, …) have abundances far above those of their neighbors. They are referred to as the alpha particle nuclides. In the particle number range 50–100 the abundances of nuclides with an even particle number stand about a factor of 3 above those for their odd-numbered neighbors. Where more than one point is shown at a given mass number, two different nuclides with the same neutron plus proton number exist.
Another feature of the abundances is the prominence in the mass range 10 to 40 of those nuclides with mass numbers divisible by 4. These nuclei are aggregates of the very stable 4He nucleus, and are the primary products of nuclear fires. They are called alpha-particle nuclides, since they are made up of multiples of helium atoms.
Supporting evidence for nucleosynthesis by the processes we have described can be seen in the upper portion of Figure 3-11. Two humps appear in the element-abundance curve that punctuates the smooth decline with increasing proton number, one centered at about 55 protons and the other at about 80 protons. The same humps appear when plotted against the total number of nuclides in the nucleus (lower portion of Fig. 3-11) near masses 138 and 208. These peaks results from what physicists refer to as the magic neutron numbers 82 and 126. For example, the isotopes 138Ba (56 protons, 82 neutrons) and 208Pb (82 protons, 126 neutrons) are unusually abundant. It turns out that nuclear configurations involving either 82 or 126 neutrons are particularly stable. One expression of this stability is their lowered propensity to gobble passing neutrons. Thus, once formed during the s-process, nuclides with 82 or 126 neutrons are less likely to capture more neutrons and move further along the buildup chain. Because of this they were produced in higher abundance than their neighbors. In the r-process, radioactive nuclides with 82 and 126 neutrons also produce a bottleneck that causes them to be produced in greater abundance. Because the r-process nuclides are far from the band of stability, once the intense blast of neutrons is turned off, the extra neutrons are one by one converted to protons via beta decay. For example, one of these nuclides is the radioactive 124Mo (42p, 82n). As it decays back to the band of stability, 8 of its neutrons are converted to protons generating the stable nuclide 124Sn (50p, 74n). For this reason, the abundance peak for the r-process nuclides does not fall in the same place as that for the s-process nuclides. Rather, it is shifted toward lower particle number by 8 to 12 mass units. The existence of these twin peaks in the abundance curve provides strong support for the existence of both the r and the s neutron buildup process.
Finally, one last characteristic of the abundance curve merits comment. Both the element abundance and mass abundance plots in Figure 3-11 show a distinctive saw-toothed pattern. Odd elements and odd-particle-numbered nuclides have lower abundances than their even-numbered neighbors. This pattern reflects a preference in nuclear architecture for even numbers. Nuclides with both an even number of neutrons and an even number of protons are strongly favored. Except for 2H (1p, 1n), 6Li (3p, 3n), 10B (5p, 5n), and 14N (7p, 7n), no stable nuclide with both an odd number of neutrons and an odd number of protons exists in nature. Other odd-odd nuclides formed in stars subsequently undergo radio decay to form the preferred even-even nuclides (by converting a neutron to a proton).
Fig. 3-11: Top panel: Abundances of elements produced during nucleosynthesis in stars. The trough for Li, Be, and B exists because these elements were produced in small amounts during the Big Bang and then partially consumed in stellar interiors. The “sawtooth” is the result of nature’s preference for even-numbered elements. The highest peaks are the alpha particle nuclides that will become the raw materials for planets and life. Slight peaks at high mass number reflect the preference for nuclei with 82 or 126 neutrons. Bottom panel: The relative abundance of the isobars (i.e., some isobars have more than one element). Only two isobars of nuclear number less than 208 are not represented in nature, those of mass 5 and mass 8. The double peaks for magic neutron numbers are evidence for s-process and r-process operating during element formation.
After the Big Bang made hydrogen and helium, nucleosynthesis in stars produced the remaining elements. Particularities of nuclear stability had far-reaching consequences for the universe. The lack of stability of masses 5 and 8 prevented production of heavy elements during the Big Bang, creating the possibility for later development of stars and stellar evolution. The enhanced stability of alpha-particle nuclides during nuclear fusion led to the formation of certain elements in great abundance. These elements then became the raw material for planets and life later in the history of the Universe. The fact that 56Fe is the most stable nucleus and that nuclear fusion cannot occur beyond that point is what leads to instability of massive stars, the formation of heavier elements and the distribution of all the elements through the galaxies. All of these consequences that are central to the operation of the universe and its ultimate habitability are the result of the detailed laws of relative stabilities of atomic nuclei.
The size of stars is central to their role in the overall evolution of galaxies. Large stars have massive gravitational forces leading to intense nuclear fires and very bright, short lifetimes. These stars produce all the elements and distribute them through supernova explosions. Such stars provide the elements required for planets and life, but would not themselves form habitable solar systems because of their short lifetimes and expolosive deaths. Smaller stars like the sun, with their lesser gravitational contraction, are rendered stable with lower-temperature nuclear fires produced by fusion of hydrogen to form helium, and can have lifetimes of billions of years. This leads to long-lived solar systems where planets have a long and stable environment sufficient for complex planetary evolution. Both types of stars are necessary for a habitable universe.
Since the sun contains all the elements, it cannot have been among the first stars to form in the universe. Early stars contain only the hydrogen and helium produced by the Big Bang. Instead, the sun must be a latecomer. Its pallet of elements has been enhanced by the explosive deaths of large numbers of red giants that formed and died in our galaxy long before the sun advent. The multiple processes over galactic history have led to the abundances of stable elements as well as long-lived radioactive isotopes present on Earth (Fig. 3-12).
From what we have learned here, heavy element formation must have gone on in all the galaxies making up our universe, and spectra from these distant regions show evidence for the same elements that make up our sun. The ingredients for rocky planets and life surely are available everywhere in the universe. Hence, the generation of Earthlike planets has not been impeded by a lack of raw material!
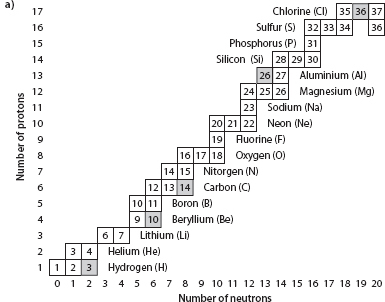
Fig. 3-12: Chart of the nuclides. Shown in this series of diagrams are all the nuclides present in nature. The shaded squares represent radioactive isotopes. Some of these are long-lived remnants of element production in stars. Others are being produced in very small quantities by cosmic rays bombarding our atmosphere. To avoid confusion, the decay chains of long-lived thorium and uranium isotopes are shown separately (see panel d).
C. A. Barnes, D. D. Clayton, and D. N. Schramm, eds. 1982. Essays in Nuclear Astrophysics. Cambridge: Cambridge University Press.
R. J. Tayler. 1972. The Origin of the Chemical Elements. London: Wykeham Publications, Ltd.
D. D. Clayton. 1983. Principles of Stellar Evolution and Nucleosynthesis. Chicago: University of Chicago Press.
1 While there are 100 4He atoms for every 1,000 1H atoms, because the helium atoms are four times as massive, they account for 4 × 100/1,400, or 29% of the universe mass.