
Fig. 6-0: Folds and “angular unconformities” in the geological record require great expanses of geological time. The older strata were first deposited horizontally, then buried and folded, then uplifted and eroded to create a land surface, after which the younger strata were deposited. Such evidence was used by James Hutton to enunciate his principle of “no vestige of a beginning, no prospect of an end.” This image is of the Carboniferous-Triassic unconformity on the southwestern coast of Portugal. (Reprinted by permission of Filipe Rosas)
Understanding any process requires knowledge of the time involved. Because our timescale as human beings is limited to centuries, early timescales for Earth and universe were thousands of years, time that seemed unimaginably long to human experience and imagination. Even Newton and Descartes, giants of modern physics, believed Earth formed in roughly 4000 BC. Early geologists, however, looking at the evidence apparent in the rocks around them, questioned these ideas. They noted that processes operating in the present could give rise to observed rocks and features of the landscape, but since these processes occurred very slowly, long times must be involved—perhaps many billions of years. Nineteenth-century physicists disputed these claims by calculating that Earth’s current heat flow was not consistent with such a long timescale. The discovery of radioactivity provided an additional heat source for Earth’s interior and revolutionized studies of Earth’s history by permitting quantitative dating. Radiogenic “parent” isotopes decay to stable “daughter” isotopes with a characteristic half-life—the time it takes for one-half of the parent atoms to decay. Measuring isotope ratios, then, constrains time. Long-lived radionuclides, such as uranium, thorium (Th), potassium, and rubidium (Rb), permitted the dating of ancient events and showed that the meteorites and Earth all formed as a group some 4.55 billion years ago. Some radiogenic parents are created in the atmosphere by cosmic rays today. The most famous of these is 14C, which with a 5,730-year half-life is used to date very recent events.
Radioactive isotopes constrain time in other ways as well:
(1) Theoretical calculations of the production rate of elements in stars, coupled with measurement of present-day abundances of the uranium and thorium isotopes, permit calculation of the age at which stars began to distribute elements in the galaxy. The timescale of roughly 10 billion years prior to solar system formation is consistent with the age of the universe inferred from the Big Bang.
(2) Extinct radionuclides, those with short half-lives so that the parent isotope no longer exists, constrain events in the early history of the solar system. 26Al, a radioactive isotope of Al created in supernovas with a half-life of less than one million years, produced isotope variations in its daughter Mg isotope that persist in chondritic meteorites today. The presence of 26Al in the solar nebula when meteorites formed indicates that supernovas exploded nearby at the initiation of the solar system. This suggests solar system formation within an interstellar cloud where many stars were forming and exploding. Extinct radio-nuclides would also have been an important heat source in the early solar system, and may have facilitated rapid planetary heating and differentiation.
Radioactive dating provides the essential timescale to understand Earth’s development as a habitable planet. It allows us to determine when Earth began, when life began, the rates at which life evolved and Earth’s tectonic plates move, and the duration of Homo sapiens on the planet. All the subsequent chapters in this book will make use of this timescale, deduced from sophisticated measurement of the decay products of minute atomic nuclei largely created in exploding stars. The quantification of geological time reveals that there is a long path from planetary accretion to advanced life.
Knowing what happened in the evolution toward a habitable planet requires a timeline. What is the appropriate timescale? Is it thousands, millions, or billions of years? When exactly did events happen? How long did they take? What is the sequence of events occurring at different places? All such questions, fundamental to the unraveling of Earth’s history and understanding our planet, depend on time.
All of us experience time personally, and we have a sense for how long things take and what “long” and “short” times are. Our personal experience is subjective—for most people time seemed to pass more slowly when they were children than as adults, and even as adults periods of intense activity, rich impressions, or great discomfort can make short periods of time feel longer. Objective time is also evident to us, as measured by the movements of the sun, moon, planets, and stars. A sense of time, of history, of ancestry, is intrinsic to us as human beings. Legends of our ancestors’ ancestors and various creation myths about the beginning of time have been an integral part of most cultures.
The modern recognition of the vast billion-year expanses of time depends on quantitative dating with radioactive isotopes, fully developed only in the second half of the twentieth century. The first precise age of Earth was not made until 1956. While this age has been abundantly confirmed, meriting a 10 on our theory scale, casual internet search of “age of the earth” reveals the intense activity by some groups, particularly in the United States, to convince others that geological time is limited to a few thousand years. The thousand-years timescale comes from a careful reading of the Bible’s “begat” paragraphs in Genesis (e.g., Adam begat Cain and Abel and so on). The most precise estimate was declared by Bishop James Ussher in 1640: the world began at 9 a.m., on a Monday, October 23, 4004 BC. Most scientists of the seventeenth century believed in this timescale. Descartes, for example, a great early physicist and one of the founders of modern science, supported the few-thousand-year timescale, and Newton did as well.
Then the geologists got involved. By the eighteenth century it was recognized that many rocks now on land formed under water. The new study of fossils also showed that many of fossils had no living representatives. Geologists observed processes creating rocks today similar to those observed in older strata, and the observed processes were very slow. Sediments were formed by slow deposition of erosion products carried by rivers. Vast thicknesses of volcanic lava were made up of thousands of flows, each one of which had the same appearance as recent flows known in human history. Relative times could be determined, since lavas or sediments at the bottom of a formation that is right side up are the oldest. Folded rocks underlying flat-lying strata must be still older (Figs. 6-0 and 6-1). This led James Hutton, in his classic work of 1788, to suggest a vast expanse of geological time, with “no vestige of a beginning, no prospect of an end.” Fifty years later, Charles Lyell enunciated the principle of uniformitarianism—that processes observable today, acting over long periods of time, created all the geological manifestations we see on Earth. Since the rates of these processes could be measured, it seemed likely that Earth was billions of years old. Quantitative timing of events, however, seemed an impossible task.
Fig. 6-1: A further, famous example of “angular unconformities” in the geological record, from the Grand Canyon of the western United States. Older strata with no fossils are overlain by younger, flat-lying, fossiliferous strata. See also color plate 1. (Geology pictures by Marli Bryant Miller, University of Oregon)
Responding to this challenge, physicists then took up the issue of Earth’s age. From the high level of Earth’s heat flow they calculated that a maximum timescale was tens of millions of years. How could the qualitative estimate of geologists be reconciled with the quantitative calculations of the physicists? Controversy reigned (see sidebar, next page).
The discovery of radioactivity provided a new internal heat source for Earth, and the understanding that solid rocks can move by convection (discussed at length in Chapter 11) provided a mechanism to actively transport heat close to the surface. Both of these contribute to the high heat flow the physicists were trying to explain, and vindicated the deductive reasoning of the geologists of the nineteenth century.
Radioactive isotopes still exist in Earth’s interior only because some of the radioactive isotopes produced during nucleosynthesis take a very long time to decay. These remnants of supernovae remaining in Earth are Earth’s long-lived battery power or internal heater and also provide us with Earth’s timescale. Since these isotopes are present only in trace amounts in rocks, their importance is rather remarkable.
It took a long period of technological development, reasoning, and discovery to read the memory of time that was contained in the radioactive isotopes and their daughter products. While it was known at the turn of the century that uranium decayed to lead, isotopes were not discovered for another twenty years, and without knowing that elements consist of various isotopes, reliable dating was not possible. Equipment to accurately measure the abundances of the isotopes (mass spectrometers) did not undergo major improvement until World War II. After 1950, these new machines opened up the world of isotope geochemistry, and radioactive dating became a growth industry. The radioactive elements and their daughter products contain the memory of what happened when—the task of the isotope geochemist is to learn how to read that memory.
Dating with radioactivity is possible because radioactive elements decay regularly. Any one atom has a fixed probability of decay. Because there are such huge numbers of atoms, this means that a fixed proportion of decays occurs in each time period, and the number of atoms decays exponentially. This behavior is conveniently described by the half-life of a radioisotope. The half-life is the time it takes for one half of any population of the parent isotope to decay to its daughter product. After one half-life, half the atoms have decayed, after two half-lives three quarters have decayed, and so on (Fig. 6-2). This is conveniently illustrated on a semilogarithmic diagram where a constant half-life leads to straight lines for the radioactive parent isotope (Fig. 6-2a).
Fig. 6-2: Illustration of how parent and daughter isotopes change during radioactive decay. The choice of initial numbers of atoms is arbitrary. The left diagram shows the log linear relationship from exponential decay, 99.9% of which occurs after ten half-lives. Right-hand diagram shows changes on a linear scale.
SIDEBAR
THE NINETEENTH-CENTURY DEBATE OVER THE AGE OF THE EARTH
The geological evidence for an ancient Earth ran into strong headwinds from nineteenth-century physicists, and particularly Lord Kelvin, the most famous and esteemed English scientist of his day. Physicists had developed precise equations to model the flow of heat, and Kelvin was able to make a sophisticated and accurate calculation of the cooling of Earth. If a body the size of Earth were at the highest temperature one could imagine, completely molten, how long would it take to cool enough to account for the present-day thermal gradient at Earth’s surface? His calculation came out to a maximum of 20 to 40 million years. He did another calculation for the sun and came up with 50 million years, in rather good agreement with his estimate for Earth. The certain and definite conclusion, based on rigorous theory, data from Earth’s heat flow, and quantitative calculation was that the geologists with their “qualitative deductions” were simply wrong.
Even in the face of the rigorous arguments of the physicists, the geologists would not back down, and this led to a lively and lengthy debate. Two developments led to the refutation of Kelvin’s conclusions. The discovery of radioactivity and nuclear fusion showed that there was another source of heat for the sun and for Earth’s interior. And the discovery that at high temperatures rocks could flow (convect) permitted much higher temperatures closer to the surface, accounting for Earth’s relatively high heat flow. These permitted an old age and also a much more constant flow of heat through time, permitting long-term stability of the temperatures of surface rocks.
If you were transported back to Lord Kelvin’s laboratory and told him that atoms were not immutable objects but that iron could be transformed to gold, that the heat source of the sun was something unknown and unimaginable to him, and that stars created the elements, what would have been his reaction? These statements would seem impossible and nonscientific based on knowledge at that time. It was not that Lord Kelvin was making faulty calculations or conclusions. There were simply other forces at play that were beyond his knowledge, and made the impossible possible. Will similar stories be told about the great scientists of today a hundred years from now?
The debate between Kelvin and the geologists did have the positive result that as the calculations were questioned and refined, geologists made more careful observations and tried to quantify their age assessments. The debate also led to significant improvements in the quantitative calculations of the cooling of solid objects, which had important practical applications in the late 1800s. Ultimately, physics and geology converged as the quantitative understanding of convection and radioactive dating led to a consistent understanding of Earth’s longevity.
Notice in Figure 6-2 that after ten half-lives only one atom per thousand remains of the parent isotope, and very few atoms are produced by further decay. This limits the utility of radioactive isotopes to about ten half-lives. If we want to study processes over billions of years, such as the age of Earth, we need isotopes with half-lives of at least hundreds of millions of years. Most radioactive isotopes produced in stars have very short half-lives and decay rapidly back to the band of stability. Fortunately, there are also a few long-lived radioactive isotopes, such as 238U, 235U, 87Rb, 40K, and 147Sm, that have long half lives (see Table 6-1), and substantial numbers of parent isotopes persist throughout the processes of formation of molecules, accretion of planets, and later planetary processes.
Table 6-1
Radionuclides of stellar origin found in meteorites
| Radionuclide | Half-life (yr) | Stable daughter product |
40K |
1.25 · 109 |
40Ca and 40Ar |
87Rb |
48.8 · 109 |
87Sr |
138La |
1.04 · 1011 |
138Ce and 138Ba |
147Sm |
1.06 · 1011 |
143Nd |
176Lu |
3.5 · 1010 |
176Hf |
187Re |
4.6 · 1010 |
187Os |
232Th |
1.401 · 1010 |
208Pb |
235U |
0.7038 · 109 |
207Pb |
238U |
4.4683 · 109 |
206Pb |
The long-lived radioisotopes are useful for long timescales, but they are problematic for short timescales (e.g., thousands of years) because not enough decay takes place to be measurable. For shorter timescales, elements with short half-lives are necessary. The choice of isotope tool depends on matching the half-life with the process of interest. It would seem we would be out of luck with short timescales because all the short-lived radioisotopes produced in stellar interiors would have decayed away long ago. As luck would have it, some elements that do not have long half-lives are produced continually by cosmic radiation in Earth’s atmosphere. These radioactive isotopes are called cosmogenic radionuclides, they are all around us and in us, and they are of great use to study relatively young events on Earth.
It is also apparent upon reflection that simply measuring the number of parent and daughter atoms does not provide age information. For example, if we measure a million atoms of the parent isotope, has no time passed because the rock started with a million atoms? Or have ten half-lives gone by because we started with a billion atoms? And if we measure the number of daughter atoms, how many were there to start with and how many have been produced by radioactive decay? For a precise date we need to know two things—the number of atoms at the beginning and the number now.
The most famous cosmogenic radionuclide is 14C, with a half-life of 5,730 years that decays to the stable isotope 14N. 14C generated by cosmic radiation today mixes with the much more abundant 12C and behaves chemically in the same way because it has the same electron shell structure. Plants and animals incorporate 14C and 12C into their tissues in the proportions they are present in the atmosphere, as long as they are alive and metabolizing carbon. Once the plant or animal is dead, the 14C decays away to 14N, which escapes as gas to the atmosphere, and the ratio of 14C/12C in the dead matter decreases progressively with time. To date using 14C we need to estimate the 14C/12C when the plant or animal died long ago. Since 14C is produced continually in the atmosphere, the assumption was made that the ratio observed in Earth’s atmosphere has stayed constant through time, which would provide a universal starting point. In that case, the 14C /12C ratio of the sample divided by that of the atmosphere gives the age (Fig. 6-3). 14C dating is the best tool we have to date organic materials, such as bones and charcoal. The rule of ten half-lives limits the 14C method to materials younger than about 60,000 years.
How solid is the assumption that the cosmogenic formation rate of 14C was constant? Edouard Bard and colleagues tested this proposition by measuring another short-lived isotope system that was not subject to such uncertainties. They found that the 14C ages could be off by as much as 10% for the oldest samples. Therefore, a distinction is now made between the “14C age” and the real age. Note that the discrepancies are small, consistent with small changes in cosmogenic nuclide production.
Fig. 6-3: Illustration of the principle of 14C dating. The line shows the 14C/12C ratio in the sample today, assuming that when it was formed the sample had the 14C/12C ratio of today’s atmosphere. After the organism stopped growing or breathing, it no longer incorporated carbon. If that happened long ago, very little remains and the sample today has a very low 14C/12C ratio. If death occurred today, the sample has the atmospheric ratio. Note the logarithmic scale of the vertical axis.
For almost all isotope systems other than 14C/12C, we do not have a starting reference point like 14C/12C in the atmosphere. We do, however, have the advantage that it is possible to measure both parent and daughter isotope ratios (The 14N produced by 14C decay is lost as a gas). Using both parent and daughter isotopes, isotope geochemists developed another clever technique to determine accurate time information—the isochron method.
Can we then just measure the amount of the parent and daughter and obtain an age? Unfortunately, it is not that simple. Consider, for example, the parent/daughter isotopic system 87Rb-87Sr. In common terrestrial rocks there are roughly twenty times more 87Sr atoms than 87Rb atoms. Could all of these 87Sr have been created by radioactive decay of 87Rb? For that to be true, some 95% of the original 87Rb would have had to decay away, since every decay of an atom of 87Rb gives rise to one atom of 87Sr. Decay of 95% of the atoms takes more than four half-lives. Since the half-life of 87Rb is 49 billion years, that would require some 200 billion years, far older than the estimate of the age of the universe in Chapter 2! There must have been a substantial amount of 87Sr already existing prior to the start of the decay—a fact that would in any case be predicted from nucleosynthesis in stars. To date accurately it is necessary somehow to determine the isotope ratios at the starting point.
The clever method developed by isotope geochemists can be illustrated with a simple numerical example. Consider two minerals, phlogopite and plagioclase, that both start with 700 atoms of 87Sr and 1,000 atoms of another isotope of Sr, 86Sr, that is not produced by radioactive decay on Earth. The 87Sr/86Sr ratio of the two minerals will be exactly the same (e.g., 0.700) when they form. Because of its crystal structure, phlogopite is able to take in much more Rb than can plagioclase. In this example we will assign 1,000 atoms of 87Rb to phlogopite and 100 atoms of 87Rb to plagioclase. At any subsequent point in time, a fixed percentage of the 87Rb in both minerals will have decayed away. When 5% of the 87Rb has decayed, for example, 50 atoms of 87Rb will have decayed to produce 50 atoms of 87Sr in the phlogopite, while only 5 atoms of 87Sr will have been produced in the plagioclase. Measurement of the minerals at this time would then yield 87Sr/86Sr of 0.750 in phlogopite and 0.705 in the plagioclase. When 10% of the 87Rb has decayed, much later in time, then phlogopite has 87Sr/86Sr of 0.800 and plagioclase 0.710. Therefore, the difference in Sr isotope ratio of the two minerals increases progressively with time. Then we can deduce the starting conditions by backtracking to determine the time when the 87Sr/86Sr ratios of both minerals would have been exactly the same. This is the age of formation, illustrated in Table 6-2 and Figure 6-4.
This behavior can be represented mathematically by considering the radioactive decay equation:

where e is the constant 2.718 and λ is the decay constant for the radioactive element. N(t) refers to the number of atoms at any time t, and N0 is the number of atoms at the beginning. If we define the amount of 87Sr and 87Rb at the start as 87Sr0 and 87Rb0 and the amount today as 87Sr(t) and 87Rb(t) then the amount of 87Sr added is related to the amount of 87Rb that has decayed, and hence:
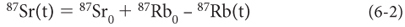
Table 6-2
Evolution of 87Sr/86Sr of three minerals from a uniform reservoir
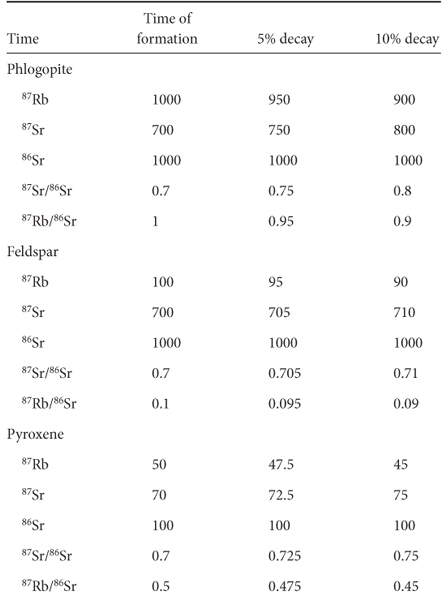
From the radioactive decay equation:

therefore

Substituting from one equation to the other, we obtain:
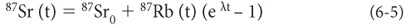
If we divide all terms by 86Sr we obtain:
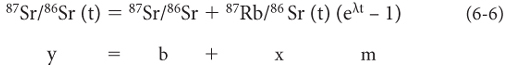
This equation is the equation of a straight line (y = b + mx) with a slope determined by the age and an intercept of the initial 87Sr/86Sr ratio. The line is called an isochron because samples that plot on it all formed at the same time. In each mineral, the 87Sr/86Sr (t) and 87Rb/86Sr (t) are values in rocks today and can be measured using mass spectrometry, defining a point on the isochron diagram. Slope and intercept are unknowns in this equation, so there are two unknowns. That means at least two measurements are required (i.e., two points define a line), so at least two different minerals must be measured to determine the isochron. Figure 6-4 illustrates the initial condition and evolution with time of an isochron.
Of course, there are things that can go wrong with this approach. For example, some of the Rb or Sr might be lost or added by a more recent event. To verify the validity of a date, it is important to measure as many minerals as possible to make sure they are all colinear and lie on the same isochron. The date from any one decay system can then be checked with isochrons from other parent/daughter systems. Since all elements behave differently, agreement among several methods leads to a high degree of confidence in the age.
What does the “age” really mean? The isochron technique dates the time when various materials formed from a uniform reservoir with no subsequent rehomogenization, loss, or gain of the parent and daughter isotopes. If the rock containing the minerals is remelted, for example, then all the Sr atoms mix together and re-homogenize the 87Sr/86Sr ratio, which would serve as a new initial value when new minerals crystallized. For this reason the rocks on Earth, which are continually being reprocessed, do not give an isochron age for Earth. An isochron for a granite that formed 100 million years ago gives an age of 100 Ma. To date the beginning of the solar system and Earth’s formation, we need materials that formed at that time and have been isolated ever since. Such materials are the chondritic meteorites, which escaped all planetary processing and have remained isolated in space until their recent arrival on Earth.
Fig. 6-4: Illustration of how isotopic composition changes with time in the Rb-Sr system. At the time of formation, three minerals form with uniform 87Sr/86Sr but variable ratios of 87Rb to 86Sr. As time passes, the 87Rb decays to 87Sr, increasing the 87Sr/86Sr ratio. The higher the 87Rb/86Sr ratio, the greater the change. At any time the three minerals plot on a straight line, called an isochron, whose intercept is the initial 87Sr/86Sr ratio. As the 87Rb decays, the slope of the line increases progressively with time. Therefore, slope gives time and intercept gives initial value. The intercept has the same value as a hypothetical mineral that formed with no Rb atoms.
Because of their unique importance for determining the age of the solar system, chondrites and other meteorites have been the subject of many dating investigations. Dates are summarized for nineteen different meteorites in Figures 6-5 and 6-6. As can be seen from the figures, the dates for these meteorites are in agreement and give an age of 4.56 billion years. Furthermore, many isotope systems have now been applied to the meteorites. These are summarized in Table 6-3. The agreement of the many separate meteorites for a single decay system, and the agreement among all the independent decay systems, makes the age of chondrite formation very well constrained. The agreement demonstrates that all chondritic meteorites formed at very nearly the same time from a well-mixed reservoir—the solar nebula—and fortifies our confidence in the ancient age of these objects.
Fig. 6-5: The light lines show the evolution with time (billions of years) of 87Sr and 87Rb in minerals from meteorites. At the time the solar system formed, all the minerals had compositions falling along the line marked zero, i.e., they had a range of 87Rb/86Sr ratios but all had a 87Sr/86Sr ratio near 0.7. With time each grain increased in 87Sr content and decreased in 87Rb content. All chondritic meteorites plot along a single isochron of 4.56 billion years.
Recall that the importance of the chondrites is that they contain chondrules that formed from a nebular cloud of dust and gas and hence reflect primitive objects in the solar system that escaped subsequent processes of planetary differentiation and have been preserved in the almost perfect vacuum of space. Therefore, the age of these objects reflects the time of nebular condensation.
To know if this age is also the age of Earth’s formation requires another step in reasoning. Because Earth underwent extensive differentiation at its formation, and is continuing to undergo melting, magmatism, erosion, etc., the isotopic systems are continually being reset. Since no rock on Earth has remained isolated like the chondrites since the early solar system, how can we determine whether Earth is made up of objects that formed at the same time as the meteorites?
Fig. 6-6: Summary of Rb-Sr ages obtained on nineteen different meteorites. As can be seen, all the results lie between 4.52 and 4.63 billion years. The mean of all measurements is 4.56 billion years (shown by a vertical black line). As the uncertainty in each measurement (shown by horizontal bars) in all but three cases spans this mean, there does not appear to be significant differences in age among these objects.
Table 6-3
Meteorite ages based on different isotope systems
| Isotope system | Age (Ga) | Uncertainty |
Rb-Sr |
4.56 |
0.05 |
Sm-Nd |
4.55 |
0.33 |
Pb-Pb |
4.56 |
0.02 |
Lu-Hf |
4.46 |
0.08 |
Th-Pb |
4.54 |
0.04 |
U-Pb |
4.54 |
0.04 |
If we consider Earth to be one very big meteorite, then the mean composition of Earth should plot on the same isochrons as the meteorites. Various lines of evidence show that this is indeed the case.
The evidence came from a clever realization that applied to the Pb isotopes. The isochron diagrams such as Figure 6-5 require knowledge of both element and isotopic concentrations. But for the U-Pb system, there are two possible isochrons, one for 235U-207Pb and one for 238U-206Pb. If these isochron equations are divided one by the other, the concentrations of uranium cancel out, and slopes on a diagram of 206Pb/204Pb vs. 207Pb/204Pb (204Pb is the nonradiogenic Pb isotope equivalent to 86Sr for the Rb-Sr system) can be used to determine an age. Rama Murthy and Claire Patterson determined these ratios for a large number of chondrites and also for oceanic sediments from Earth. The oceanic sediments were ideal because they reflect well-mixed erosion from all Earth’s continents, as well as some Pb contribution from the ocean crust, and are a pretty good Earth average. The initial value for the solar system could also be determined from the iron meteorites, which have lots of Pb and no U. What they found was that Earth’s sediments plotted exactly on the isochron coming from the meteorites, supporting a common origin and the same age (Fig. 6-7). Earth is one big collection of meteorites.
The relative abundances of the long-lived radioisotopes in meteorites also have something to tell us about when the heavy elements in the universe were produced. While this argument is somewhat complicated, the reasoning illustrates important principles that will be useful in our later discussion of Earth processes.
In general, when materials are created at a constant rate and decay at an exponential rate, they reach a steady state value—i.e., a value that persists through time relatively unchanged even though the system is dynamic and material and energy continue to flow through the system. Such a characteristic is very widespread throughout natural systems.
Let’s take a simple example to see how such a process develops. Imagine that you receive a paycheck that nets you $100 per week, and you decide to rigorously adopt the discipline that you will always spend exactly half of what you have in your bank account.
Fig. 6-7: Pb isotope results comparing sediments from Earth to meteorites. Each name refers to a different meteorite. Young galenas are lead sulfide minerals formed from fluids that may provide a good average for the continental crust. MORB are mid-ocean ridge basalts that represent the composition of the upper mantle. The fact that all the data plot along the same line shows that Earth and chondrites formed from the same reservoir at the same time.
At the end of the first week, you spent $50, then a new $100 brings you to $150, so the second week you spend $75. The next $100 brings you to $175 so you spend $87.50 and so on. Ultimately, when you reach $200 in your bank account, you will be at steady state, spending and receiving $100 per week. While funds are steadily flowing through your bank account, and you have a life working and spending, a person examining the balance at the end of the week would see a constant amount. During the approach to steady state, the person could also determine the number of weeks since you started working by looking at the amount of money in your bank account (Fig. 6-8).
The same kind of principle can be applied to the abundances of radioactive elements. They are produced at some rate in stellar interiors, and half of the total amount existing decays in a fixed period of time—linear production and exponential decay, which would lead eventually to steady state values in the universe. But the length of time it takes to arrive at steady state depends on the half-life (e.g., in the bank account example, if weeks are changed to decades, it would take six decades to reach steady state rather than six weeks). So if we examine elements with sufficiently long half-lives that the abundances have not yet arrived at steady state, we could date the time when elements first started to be created.
Fig. 6-8: Change in bank account balance following the rules given in the text. After six or so weeks, the account has reached steady state. Before that time, the balance in the bank account can be studied to give a good estimate of the amount of time that has passed since the bank account began.
But there remains one additional complication. We do not know the actual production rate for individual radioisotopes. We are able to estimate, however, the production ratios of production rates of different isotopes, because the ratios can be calculated from nuclear physics. Can we then obtain the same sort of time information?
Another example will, perhaps, illustrate this more complex case. Consider a special exhibit at the Louvre in Paris, such as the Leonardo da Vinci drawings. A constant flow of people arrives all day, a third of whom are artists and two-thirds of whom are tourists. This influx is steady throughout the day. We will then (arbitrarily) assign the rule that at the end of each hour one quarter of the artists who are present at the exhibition leave, but one-half of the tourists leave. These rules impose a steady, linear rate of new people and two different rates of exponential decrease, depending on whether the people are tourists (who have a short half-life in the museum) or artists (who have a longer half-life). This sets up the museum for an approach to steady state. Figure 6-9 illustrates how the number of people in the exhibition changes during the day. The number of tourists approaches steady state faster than the number of artists, owing to the shorter half-life of the tourists, and the ratio of artists to tourists increases progressively but never reaches its steady state value of 1 because the exhibit is not open long enough for this to occur. If you knew these rules and walked into the museum at any point, you could tell exactly how long the exhibit had been open by looking at the ratio of artists to tourists. For example, if the ratio of artists to tourists was 0.8, the exhibit had been open for four hours.
Fig. 6-9: How proportions of artists and tourists change with time of day for the example given in the text. Because the half-life of tourists is shorter than that of artists, they approach steady state more rapidly. Because steady state is never reached, the ratio of artists to tourists can provide the time since the exhibit has been open.
An analogous situation occurs for long-lived radioisotopes 235U, 238U, and 232Th. All these isotopes are produced continually in constant ratios to one another by supernova explosions. Once formed, they decay away according to their half-lives. We appear on the scene and can measure their ratios. By that measurement we can determine when they first started to appear—i.e., when element production began. We must use the proportions at the time of formation of the solar system rather than the values today because Earth has been isolated from new contributions by supernovas since the solar system formed (fortunately!). While element synthesis continues in the galaxy, there is no mechanism by which the elements produced over the last 4.55 billion years could have become incorporated into the sun or its planets. Therefore once the solar system formed, we became isolated from the great processes of element creation, supernovas and mixing that we observe taking place elsewhere in our galaxy in the great interstellar clouds.
Table 6-4
Different values of 235U, 238U, and 232Th in the early solar system
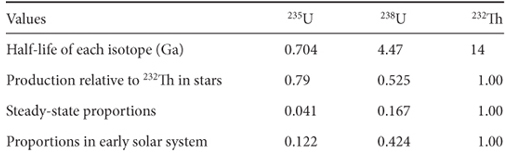
To calculate the values at the start of the solar system, we use the radioactive decay equation (6-1) given earlier in the chapter. We know the values of U and Th today, N(t), and we know the age of the solar system, t, so we can calculate the amounts present at the formation of the solar system, N0. The proportions in the early solar system as well as production ratios, half-lives and steady-state proportions are given in Table 6-4, with the proportions normalized to an arbitrary value for 232Th of 1.0. It is evident that the proportions in the early solar system are in between the production rates in stars and the steady-state values. This then permits a time to be estimated for the beginning of element production.
Figure 6-10 demonstrates how the isotope abundances will change with time during the evolution of the galaxy—note the similarity to the artists and tourists in Figure 6-9. In Figure 6-11 the solid curves show how the ratios change with time since element formation began. The dashed lines show the values for these ratios at the time of formation of the solar system. Where the curves intersect is the time elapsed between the formation of our galaxy and the formation of our solar system. For the 238U/235U ratio, the crossover is at about 12 billion years. For the 232Th/235U ratio, the crossover is at about 9 billion years. While both results have rather large uncertainties, they both suggest that element production began about 10 billion years before our solar system came into being. Since the age of the solar system is 4.55 billion years, that gives a total age of about 13.5–16 billion years since the creation of the first heavy elements.
Fig. 6-10: The evolution of the amounts of the three isotopes in our galaxy. The assumption is made that supernova events have occurred regularly over the entire history of the galaxy. The steady-state amounts occur when the isotope decays away at the same rate that is produced. Note the similarity in form to Figure 6-9.
The various isotope data then give an overall chronology that ties in well with the ages inferred from the red-shift distance relationship in Chapter 2, as summarized in Figure 6-12. The universe began about 13.7 billion years ago. Our galaxy formed sometime in the first billion years of universe history. Over our galaxy’s entire history, the largest stars have steadily synthesized and distributed elements that have been mixed together in interstellar clouds. After about 9 billion years of galactic history, our solar system formed and became isolated from the stellar processes 4.56 billion years ago. The radioisotopes incorporated into the planet then continued to decay to give us the values that we can measure in the laboratory today.
Fig. 6-11: The evolution of 238U, 235U, and 232Th if heavy element production occurred at a constant rate. Early in the galaxy’s history the ratios were equal to the production ratio in stars. With time the ratio changed favoring the longer-lived isotopes. The horizontal dashed lines correspond to the ratios at the time the solar system formed. The intersection of the dashed line with the solid evolution curves gives the time elapsed between the formation of our galaxy and the formation of the solar system. About 10 billion years elapsed between galaxy and solar system formation.
Fig. 6-12: Summary of the chronology of universe events recorded in the isotopes measured on Earth. The period of nucleosynthesis refers to the time interval over which the elements heavier than H and He that are found in our solar system were produced. For the galaxy as a whole, the period of nucleosynthesis extends right up to the present. The matter in the solar system was isolated from the galaxy 4.56 billion years ago.
Elements with short half-lives can give information for time spans only of about ten times their half-lives. This limits their utility as dating tools for long-lived processes, but there is still important information that can be obtained. The key is that the presence of the radioactive parent is preserved in variations in the isotope ratios of the daughter element even after all the radioactive parent has decayed away. For example, consider the Rb-Sr system that is now familiar to us. If we waited hundreds of billions of years until all the 87Rb had decayed away, there would still be large variations in the remaining 87Sr/86Sr of the minerals if they had not been subsequently homogenized. The 87Rb would be “extinct”—the daughter element isotope variations would remain, showing us that 87Rb once was present. In terms of the isochron diagram (Fig. 6-4), after a very long time the isochron points straight up along the y-axis. No further Sr isotope variations would grow in, because all the 87Rb would have decayed away.
A large number of short-lived radionuclides once existed and are now extinct. Because they decayed rapidly they created large isotopic variations in relatively short periods of time. Study of the daughter elements that record the presence of their highly radioactive parents has led to a surprising wealth of information concerning the early solar system and the processes that took place there.
26Al is one of the most important of the extinct radionuclides, in part because Al is a major constituent of stony meteorites and terrestrial planets. Unlike Rb, Sm, or U, which have concentrations of only a few parts per million or less in common rocks, Al has a concentration of 3 to 20% and is an essential constituent of many of the most common minerals. A small proportion of this Al would be 26Al if it were present.
26Al decays to 26Mg with a half-life of 0.73 million years (fig. 6-13). Therefore, it is a very sensitive indicator of processes happening within 10 million years after it was created. After that, only its daughter product 26Mg would remain to give evidence of its prior existence. 26Al is created by the r-process in supernova explosions. Evidence for 26Al would lead to the conclusion that a supernova explosion took place within 5–10 Ma of the time when the rocks containing evidence for 26Al were formed. The evidence would be in the isotope variations of the daughter element Mg.
Gerry Wasserburg and colleagues at the California Institute of Technology set out in 1974 to test whether any 26Al had existed in the nebular materials from which the meteorites formed. If the Mg isotopes showed that 26Al had been present, then three things would be clear about early solar system development:
(1) A supernova event occurred nearby just before the solar system formed.
(2) The meteorites must have formed very rapidly after the supernova.
(3) Extinct radionuclides would have been present in the early solar system, providing a powerful heat source for early planetary bodies.
Fig. 6-13: The isotopes of the elements Al and Mg and their relative proportions on Earth today. Aluminum has only one stable isotope and magnesium three. Early in solar system history, however, a second aluminum isotope was present—radioactive 26Al with a half-life of 0.73 million years. This isotope is now extinct, having long since decayed to 26Mg.
The critical materials to measure were those that were very high in Al and very low in Mg. Because 26Al is chemically identical to the stable 27Al, 26Al would have been incorporated along with the stable Al into aluminous minerals. (Aluminum foil from 26Al would look exactly the same as ordinary foil, but would be very deadly!). The lower the quantities of Mg, the more 26Mg would be created relative to the stable 24Mg. So, just as dating with the isochron diagram works best for large variations in parent/daughter ratios, finding evidence for the extinct Al would work best with a very large range of Al/Mg ratios. Those minerals that had the highest 26Al/24Mg (e.g., Ca-feldspar (CaAl2Si2O8) would after complete decay have the highest 26Mg/24Mg. Minerals with low Al/Mg would have the lowest 26Mg/24Mg. If there were no differences between these minerals, no 26Al was present when they formed.
The candidate material for this investigation was the largest carbonaceous chondrite ever found, named Allende, which fell in Mexico in 1969. By making very precise measurements of the 26Mg/24Mg ratio in the trace amounts of magnesium present in the feldspars and comparing them with similar measurements in high Mg mineral grains, Wasserburg and co-workers were able to show that the 26Mg/24Mg ratio was higher in the magnesium from the feldspar. The proof came from measuring several different minerals with very different Al/Mg ratios (Fig. 6-14), and a correlation was found between the Al/Mg ratios and the 26Mg/24Mg ratios. This clever diagram makes use of the fact that the present Al/Mg ratio of the minerals would correlate perfectly with the original 26Al /Mg ratio. Therefore, the higher the present-day Al/Mg, the more 26Mg relative to 24Mg should have been produced.
Fig, 6-14: Relationship between the ratio of 26Mg to 24Mg and the ratio of aluminum to magnesium in mineral grains from a chondritic meteorite. Feldspar grains with aluminum as a primary constituent and magnesium as a trace constituent have higher 26Mg/24Mg than minerals for which the Al/Mg ratio is lower. The 26Mg/24Mg ratio of average Earth material is 0.1394. This is not surprising, since the Al/Mg ratio in the Earth is about 0.1. (Based on Lee, Papanastassiou, and Wasserburg, Geophys. Res. Lett. 3 (1976):109–12)
The original amount of 26Al that would be needed to explain these results seemed too high, and there was substantial controversy over the interpretation of these results. Technical developments in instrumentation, however, have made it possible to measure isotope ratios that would be generated by many different extinct radionuclides in individual grains in meteorites, and these results conclusively show the importance of supernova products in the grains of the early solar system. In fact, the isotopic diversity of the tiny grains retained in the most primitive meteorites shows a contribution from many different types of stars and stellar explosions to the solar nebula material. All this evidence confirms the hypothesis of the solar system being generated in a huge cloud of interstellar gas and dust where star formation and element production were common occurrences. One or more supernovas occurred in close proximity in space and time to the region where the sun and its planets were originally formed.
Radioactive elements are ticking clocks that reside in the molecules that make up planetary materials. As these elements decay, they create daughter isotopes that change the isotopic makeup of their respective elements. Measurement of these isotope ratios permits the study of the timescales of a vast number of Earth processes. Cosmogenic radionuclides such as 14C can be used to date young organic materials. The long-lived radionuclides provide the tools needed to date ancient events that occurred in the early solar system and throughout Earth’s history. Because there are a number of independent systems, important measurements such as the age of the meteorites can be double and triple checked by independent means. All the data are consistent with an age for the early solar system of 4.56 billion years. The coherence of Earth with these measurements shows that Earth formed from the same types of materials that are observed in meteorites still impacting Earth’s surface from space. The long-lived radionuclides also permit an exploration of some of the fundamentals of a steady-state condition, and the timing of the beginning of element creation. This timing corresponds well with the estimates from the red shift/distance relationship from Chapter 2, and permits an overall chronology for Earth starting with the Big Bang and continuing with formation of elements in the galaxy through solar system formation to the present day. Short-lived radionuclides provide another set of tools that reveal processes that took place in the early solar system. Evidence for 26Al and other extinct radionuclides shows that the environment of solar system creation was a very active one, with contributions to the nebular dust from diverse stars and nearby supernovas. Earth appears to have formed in a stellar incubator similar to those observed by astronomers elsewhere in our galaxy, and our solar system appears to simply be one example of a common universal process. The extinct radionuclides confirm the very short timescale of early solar system history, with only a few million years between supernova explosions and formation of the sun, meteorites, and planets. The short-lived radionuclides decayed with such intensity that they would have provided a powerful and short-lived heat source that would have aided rapid heating and differentiation of early planetary objects.
Gunter Faure and Theresa Mensing. 2005. Isotopes, Principles and Applications, 3rd ed. New York: John Wiley & Sons.
Claude Allègre and Christopher Sutcliffe. 2008. Isotope Geology. Cambridge: Cambridge University Press.