1
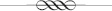
THE FIELD OF HARMONY
OUR INQUIRY BEGINS WITH THE CONSTRUCTION of a primal form: the circle-in-the-square. This simple shape is a source of innumerable forms, and its two elements can represent the polar opposites of mind and spirit or the finite and the infinite. The circle, symbolizing spirit, with its unknowable (because irrational) π circumference, is the first of the two forms to appear. We can imagine that it radiates from its center point of zero dimension, recalling the modern creation myth of the origin of the Universe from an infinitesimal singularity.
From the circle, symbol of primal unity, the enclosing square is generated. With its rational and thus measurable sides, each of which equals the circle diameter, the square is symbolic of reason and understanding. In enclosing the circle within the square we are symbolically attempting to understand, to bring within the realm of reason, that which can never be fully known. This attempt is amplified when we try to “square the circle”—that is, to construct, using only compass and straightedge, a circle and a square with equal perimeters or equal areas. The ancient practitioners who attempted circle squaring knew the resonant power of symbols, the true language of the unconscious. They believed that the symbol of the squared circle, which represents a congruence of mind and spirit, might, when perceived by the unconscious, help to manifest the symbolized unity in ordinary reality. The geometers were able to come very close to squaring the circle. But an exact circle squaring has, in modern times, been shown to be impossible—a meaningful discovery, which demonstrates our limits in our quest for unity with the divine: there will always be realms that are unreachable.
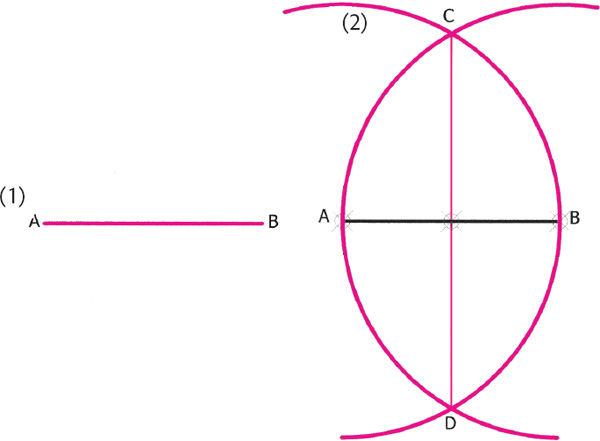
The present approach to geometric construction can begin with a straight line that is bisected using compass, straightedge, and scriber (drawing 1.1 [1] and [2]). The process also generates, as a kind of side effect, the vesica piscis mentioned in the introduction. Our purpose, however, is to construct the circle-in-the-square using these same classical tools of compass and straightedge and scriber. Those persons who would rather use a computer drawing program can maintain the purity of the classical method by proceeding one step at a time with circles and straight lines and letting each step be guided by the previous step—that is, by not simply measuring out figures but letting the inherent properties of one stage lead to the next stage such as we demonstrate in drawings 1 and 2.
Drawing 1.1. (1) The first steps in generating the primal form of the circle-in-the-square. Draw a line that will be the diameter of the circle. (2) Bisect the line with a vesica piscis, establishing a circle center and also the length of the radius.
Drawing 1.2. (1) After drawing the initial circle, draw (2) four circles with the same diameter as the circle in (1) with centers at the ends of the crossing diameters. The intersecting points of these four circles give us the corners of the enclosing square. Draw lines from these points to make the surrounding square.
THE RING FORM
The circle within a circle—the primal wave pattern symbolizing rhythmic temporal expansion or, in space, a vessel holding an essence—is the ring form, which exists throughout material and nonmaterial nature. It is the cell with its nucleus, the outer layers and core of celestial bodies, the orbits of planets around the Sun, the flesh and stone of a fruit. The ring symbol connects diverse phenomena—of all shapes. The classic temple, though generally a rectangle, is also a ring with its outer corridors protecting the inner sanctum in a manner similar to the way the outer bodies of animals protect their vital inner organs.

Figure 1A. “The voice is moved in an infinite number of undulating circles similar to those generated in standing water if a stone is cast into it, when we see innumerable rings spreading forth from the center and traveling out as far as they possibly can. . . .” wrote Vitruvius.1Here two stones cast into a pond generate with their ripples the form of the vesica, a two-dimensional symbol of the intersection of radiant energies in the three-dimensional world.
In nature it is common for the ring shape to be expanded to include several rings—a nesting of circles or other shapes. Thus, the inner Earth and the atmosphere consist of regions arranged in concentric layers. The human body consists of skin, muscle, fascia, and so forth, which protect and nourish the organs. Furthermore, it is believed that there are energetic rings surrounding the physical body—such as the subtle etheric and mental bodies—which correspond to the layers of atmosphere and magnetism surrounding the Earth. Figure 1B shows a few examples of the ring form in nature and art that, again, are a reminder of the universal occurrence of this form whose simplest expression are the rings spreading out from a raindrop falling into water. The geometer works with this idea of rings but in a context of harmony unaffected by the environmental factors of the physical world that tend to distort the purity of primal form. As we will see below, there are ring structures that we may generate with the vesica construction in which the relations among the rings are highly harmonious.
THE VESICA-TONE CONSTRUCTION
As an introduction to the vesica form, I present an example that shows how this form reveals the way we see the world. When a person stands on the edge of the sea, the horizon is about three miles away. Imagine a second person standing in a rowboat that is floating on the first person’s horizon. We can affirm that the circle of perception of both persons combined is about six miles in diameter. Furthermore their circles of perception intersect one another, forming a common vesica-shaped space (see drawing 1.3 below). The name for this particular vesica is the vesica piscis, formed when two circles intersect one another at their centers. Now let us imagine that the person in the rowboat begins rowing toward the person on the shore. The size of their circles of perception remain the same, but they begin to overlap one another more and more deeply. The vesica grows wider and wider as its shape traverses innumerable height-to-width ratios until the boat reaches the shore and the persons come together. Their two circles of perception have joined with the vesica, which has expanded into a circle; the three elements have become a single circle.
So, generally speaking, when we look at another person we are joined to them within a perceptual vesica whose size and shape depends on the distance we are from them. (This applies also to objects that we can imagine being sentient and having circles of perception.) But what is interesting for the present study is the tonal aspect of this phenomenon. If we imagine a straight line between our shore person and the rowboat person, this line can represent a stretched musical string. Now, as the rowboat person rows toward the shore person, tones are being sounded along the musical string. This is the basic idea behind the vesica constructions shown in drawings 1.4 and 1.5 on pages 13 and 14, respectively.
We begin with our circle-in-the-square. The horizontal diameter of the circle becomes our musical string. We now need to locate the points on the string that correspond to musical intervals. We note here the requirement for a number to be usable as a musical tone: it must be a fraction composed of whole numbers. An irrational number cannot be used as a tonal number for the simple reason that it cannot be exactly located on the musical string. To find a tone on the string we decide on a ratio, say 2/3, and measure out a one-third segment leaving a two-thirds segment. Then we place a stop (such as a finger) at the 2/3 point and pluck the 2/3 length. In this case we have sounded the interval of the musical fifth in relation to the open string, considered to be the fundamental (if we had plucked the 1/3 length, an octave fifth would have sounded). See drawing A2.2 for a description of the technique of diagonal crossings.

Figure 1B. Five rings both man-made and natural: (a) Aztec calendar stone; (b) rose window of Notre Dame de Paris; (c) Chinese pi disc; (d) cross section of a beet; (e) water ripples in a tide pool.
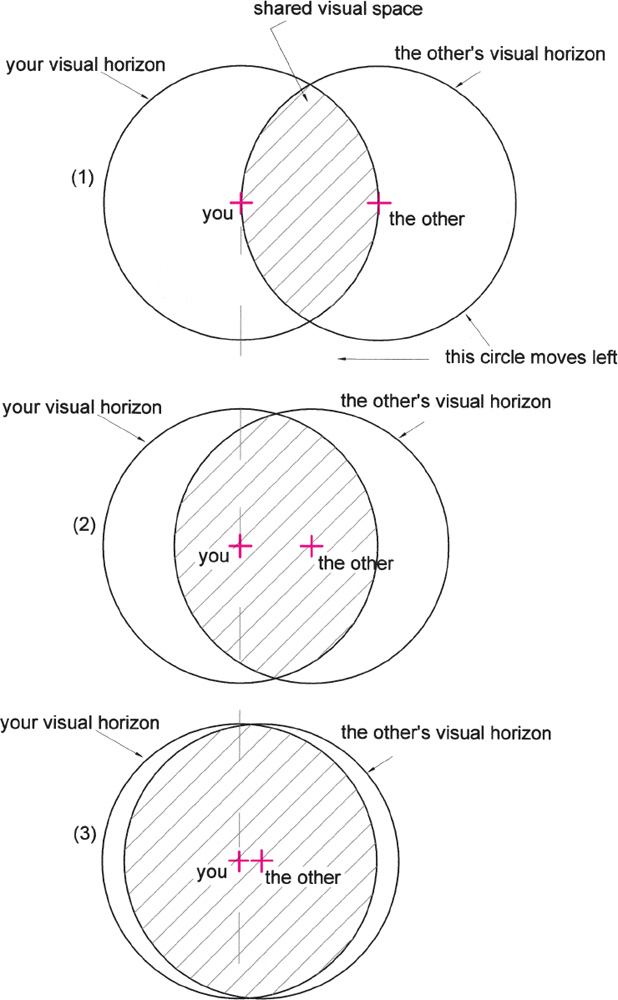
Drawing 1.3. As described in the text the vesical shape encloses the shared visually perceived space between a person standing on the shore and another person standing in a rowboat on the horizon (1). In (2) and (3) the other can be imagined to be rowing a boat toward the shore and in so doing altering the shape of the shared vesica. Thus we see a geometric connection between the psychic-numeric tools that determine the way we perceive and the vesica. In other words we live and move in circular space bordered by the horizon. Other beings move in and out of our circle, and our spatial relationship to them can be expressed in ideal terms—that is, as vesical geometry that reveals that the visual space we have in common has a vesica shape that widens or narrows as we approach or recede from one another.
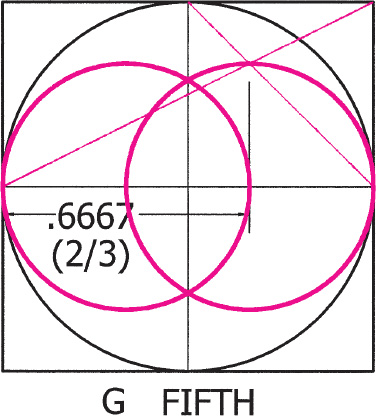
Drawing 1.4. The interval of the fifth on the string/diameter is generated from crossed diagonals.
Yet we would prefer, at least in our geometrical drawings, to locate tonal nodes without resorting to measurements or as few as possible. One important use of measurements that is employed in this book is to identify the ratio of the points on the string/diameter that are generated from the crossed diagonals. These points create rational divisions of the string/diameter, which, interestingly, are generated from irrational diagonals that are themselves generated from rational divisions of the sides of the square. We might say that the rational in the form of simple numbers applied to the sides of the square is transmuted in the cauldron of the irrational, in the form of crossed diagonals, into a new kind of rational number—namely, the numbers of the musical intervals. With the present method we can use the numerous crossings of the great variety of diagonals within the square as tools to locate our tonal nodes on the string/diameter of the circle in the square. The crossing of two diagonals locates a point, which, when a perpendicular from it is dropped to the string, locates a tonal node (see drawing 1.4). The diagrams in drawing 1.5 locate some of the tones of a common just-tuned scale using this method.
Let us now consider how the vesica itself is generated. It is instructive to consider this geometric construction as a symbolic enactment of cosmic process. This imaginative way of seeing is actually one of the principal virtues of sacred geometry. Thus, the original circle can be seen as the field of creation waiting for the initiating impulse. At the center of the circle is the primordial point from which the circular field was generated. Being at the halfway point of the string/diameter, it is tonally at the octave position of the whole string—that is, at the first octave. On either side, from center to diameter end, are innumerable tonal positions whose pitches become higher as they approach the ends.
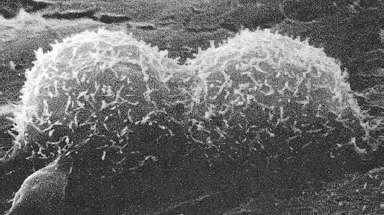
Figure 1C. Cells doubling during mitosis. The implied vesica between the daughter cells is symbolically moving through all the tones from the fundamental at the single cell position to the final separation when the octave will be sounded.
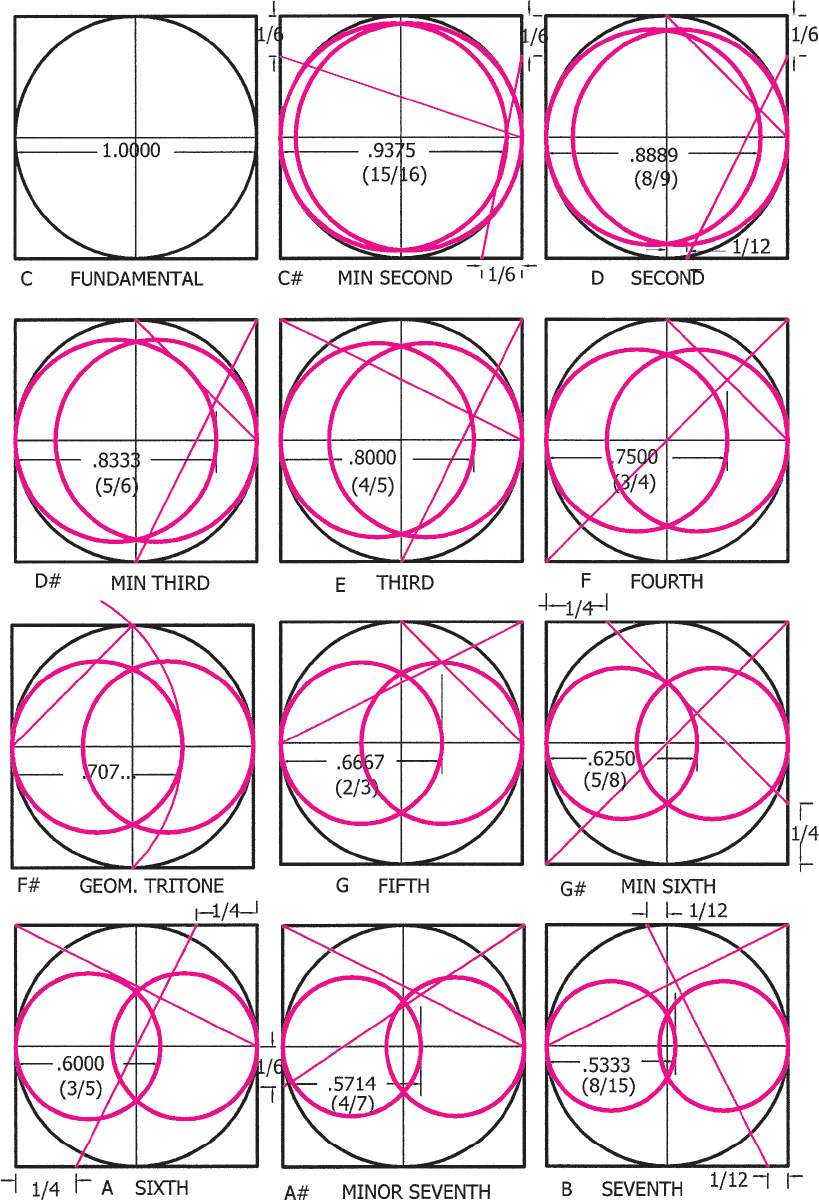
Drawing 1.5. The intersection of two diagonal lines that originate from integral division points of the containing square result in crossing nodes that, when a perpendicular is dropped to the main diameter or musical string, divide the string into rational or musical segments. When this diameter point is mirrored on the opposite side of the vertical axis and circles are drawn through these two points, a vesica is formed that can then be associated with the tone generated from the original intersection of diagonals. In this drawing twelve vesica-tone constructions created from various diagonals within the square result in a twelve-tone scale. The geometric tritone, the center of the scale, is an exception: being an irrational quantity, it is generated by a circle arc. This crossing of diagonals within the square is the beginning gesture that we will use to generate the vesica constructions throughout the book. (For the vesica ratios and other properties see drawing A2.1.)
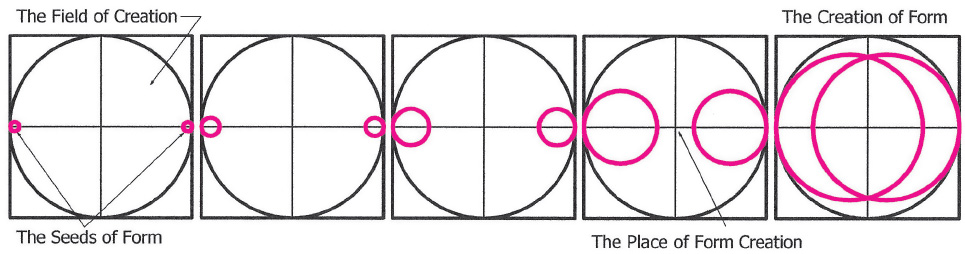
Drawing 1.6. The creation of form as symbolized by the intersection of waves and the resulting vesica, the symbol of form. This drawing might be considered as a preview of the separating cells in figure 1C: the male and female pronuclei join to form the first cell, then, as in 1C, they begin separating into two.
Now let us imagine a very high vibration beginning at each end that causes circular waves to begin rippling through the medium of the circular field. When the waves impinge on the string/diameter they cause a tone to issue from the string. So, as the wave front grows and moves along the string, a descending glissando of tones is sounded (or really a unison of the glissando, because there are two wave fronts, each moving from its pole toward the center). The waves have a destination represented by the central vertical diameter. This is the portal into the 2/1 ratio, the first octave, the place where the intersection of the two waves takes place and the series of vesicas begin. During this process we can accurately state that all tones are being produced. But now we decide that we only need a few of these tones for the scale we are building. Let us stop the process at, for example, 2/3 of the whole string length. We have noted above how geometrically we can find the 2/3 node on the string—with diagonals that connect integer nodes on the perimeter of the square. We now have an example of the symbolic purpose of the square that we have constructed around the circle. It is a workshop, a laboratory within which the transcendent circle may be studied and transmuted into a source of harmonious form. The tools that are employed are the diagonals and their generated points and numbers.
*
As we have noted, the crossings of these various diagonals of the square generate tonal nodes, places where the wave fronts, expanding from the equator ends, can be stopped and where the musical string can then be plucked to produce our geometrically derived tones. The node, in this case the 2/3 or musical interval of the fifth, is now sounded, and the vibrational wave of sound expands through the circular field until it is stopped at the limit of the field. This process takes place simultaneously on both sides of the vertical axis and generates a central vesica, a new form composed of circle arcs arising within an environment formerly dominated by circles and straight lines. Each vesica is unique with its own height-to-width ratio, its own ring structure, and its own tone, its song. A vesica can assume an innumerable variety of shapes, from the slenderest of grasslike forms to forms of near-circular fullness. The shape of the vesica depends on its tone, which corresponds to the point on the string/diameter where we have stopped the string.

Figure 1D. The ancient harmonicists used a device called a monochord that consisted of one or more strings stretched across a sounding board on which measurements could be made. On the monochord they could locate numerical ratios and hear them by stopping the string at the measured point and plucking it to sound the tone. Above, a three-string monochord.
*
The first octave, the place where the vesica takes form, could be called the realm of physical reality, of three-dimensional space, two dimensions of which, height and width, contain the geometry of the vesica. The third, depth, is suggested to the imagination but has no place in this symbolic geometry, because to include it would defeat this geometry’s purpose: the simplification of the overwhelming complexity of the world.
We recall that outside the central octave are higher octaves—that is, tonal positions on each side of the central octave. The circles of these higher octaves, in our present conception, have not yet “taken form” by entering the realm of the vesica by joining with their mirrors—that is, intersecting with their corresponding circles on the other side of the vertical axis representing the main octave. They exist as pure moving energy until they cross the threshold into form. They are represented by the growing circles that emanate from the diameter ends of the containing circle.
There is another interesting feature of the vesica construction. We note that there is an implied inner circle within the vesica and an implied circle that encloses the vesica (see drawing 1.7). The inner circle we will call C4, the outer circle C3, and the enclosing circle that is circumscribed by the containing square we will call C1. The two vesica-forming circles we will call C2. A striking property of vesica constructions is the geometric proportion that exists among the diameters of the nested circles:
C1 : C3 :: C3 : C4.
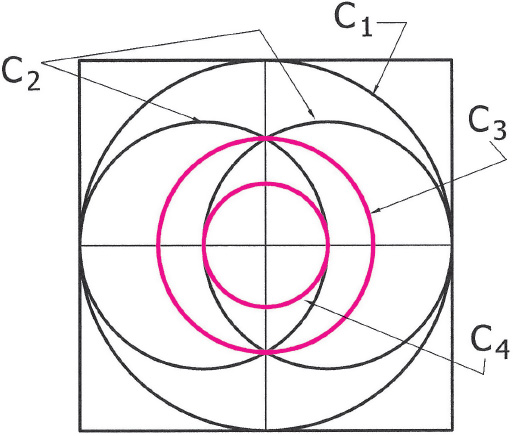
Drawing 1.7. The circles of the vesica construction: C1 , the enclosing circle; C2 , the two vesica-forming circles; C3 , the circle that encloses the vesica; C4 , the circle that is enclosed by the vesica.
In demonstration of this fact let us look more closely at the details of our vesica construction of the musical fifth (drawing 1.4). Given our circle in the square, whose construction is shown in drawings 1.1 and 1.2, we use the crossing of quarter-square and double-square diagonals to locate a tonal node on the circle diameter. We bisect the distance between this node and the farther diameter end to give us a center for our vesica-forming circle (C2). This circle is mirrored on the opposite side resulting in a vesica, in this case a vesica piscis, generated from two circles, each of which intersects the other’s center. With this vesica piscis generated by the vesica construction at the interval of the fifth the diameter proportion of the implied vesica rings is
C1 : C3 :: C3 : C4 = the irrational value of √3, or 1.732 . . ., which is the ratio of the inner diagonal between opposite corners of a cube to its side and also the distance between parallel sides of the hexagon.
It becomes apparent that the limitless variety of vesica constructions make available to us a wealth of proportional ring structures that are expressions of geometric and tonal realities. These ideal structures do not exist in a vacuum but instead correspond to the ubiquitous ring structures of organic and cosmic forms that underlie the natural world.
TONE
Tonal quantities are expressed as ratios composed of whole-number fractions of the string length, such as 2/3 for the fifth interval or 4/5 for the third. The inverse of these fractions—that is, 3/2 and 5/4—are the frequency ratios, the rate of vibrations of the string in relation to the vibration rate of the fundamental or open string, which is designated as 1/1. The octave, with frequency 2/1 at the center of the string, is the beginning point from which the series of vesicas unfold. The octave represents the principle of doubling that we encounter in most if not all life processes. The series 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and so forth, is an octave or doubling progression embedded in natural growth processes. The single egg or cell when activated divides into two; then the two become four, and so on. So the octave, the doubling of the fundamental tone, corresponds to this universal doubling gesture.
While it has been noted that the octave, fifth, and third have been present in musical scales throughout time and across cultures, there is an even firmer foundation for these and for the other intervals to be present in the harmonicists’ toolbox. This foundation is contained in the harmonic series in which all the intervals of the scale are present. Following is a simplified description.
An object when struck will vibrate in many different frequencies. The musical string is the model for this phenomenon because of its simplicity and minimum of distorting factors such as shape, size, and material composition. An open musical string will vibrate as a single whole but also simultaneously in two parts, three parts, four parts, five parts, and so on, in theory, to infinity. While this complex vibration is going on all the harmonics are being sounded with decreasing volume in higher and higher octaves. To draw on the tones within the harmonic series when constructing a scale or generating a vesica construction is thus a “lawful” way to proceed, since we are drawing on ratios which are embedded in the vibratory nature of existence.
In the following table we choose the first harmonic to be in the key of C—that is, the fundamental is the C tone that, because it is the tone sounded by our open musical string, has a ratio of 1/1. The second harmonic, with ratio 1/2, divides the string in two, sounding an octave of the fundamental. The third harmonic divides the string into thirds, sounding a fifth (1/3 is the octave of the 2/3 fifth interval and is multiplied by 2 to bring it into the main octave), and so on. The first nineteen harmonics generate the tones (less one) of the standard scale. Some are exact just-intonation tones, while others are close approximations. We have to jump to the twenty-seventh harmonic to find the final tone of the chromatic scale, the major sixth interval. This happens to be the Pythagorean sixth with ratio 16/27 (.5925), quite close to the just sixth of 3/5 (.60) ratio.
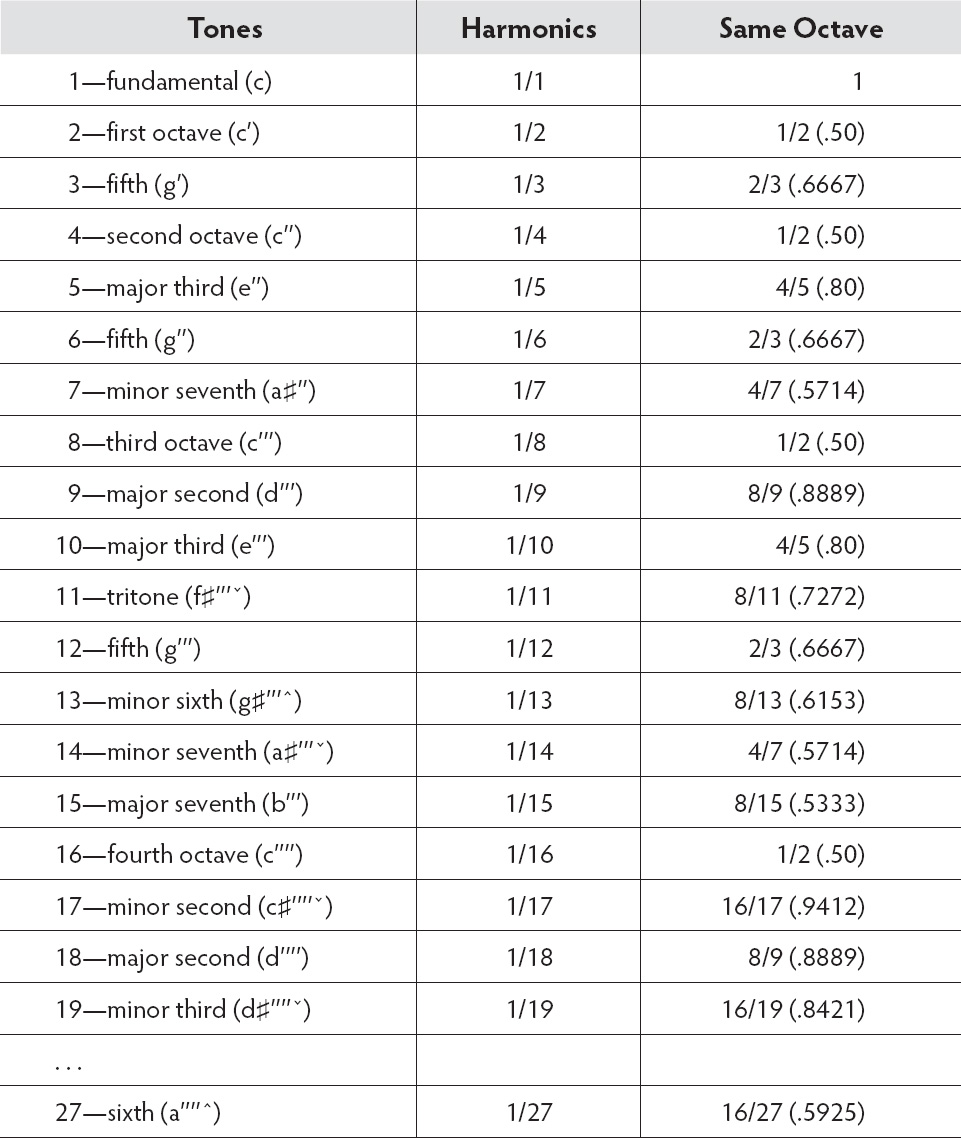
For clarity we have, through successive multiplications by 2, reduced the increasingly higher harmonics into the main octave—that is, between ½ and 1. For example, 1/14 × 2 = 1/7; 1/7 × 2 = 2/7; 2/7 × 2 = 4/7, the minor seventh in the main octave. Because the harmonics do not always exactly correspond to the ideal ratios the little arrows next to some of the octave tics indicate such discrepancies: up arrow means the tone is sharp of exact tuning; down arrow means the tone is flat.