Algebraic Logic

The analogy between physics and logic can be used to illuminate not only the role of this paper in the series, but, for that matter, the purpose of algebraic logic as a whole. It is fashionable nowadays to give a mathematical exposition of quantum mechanics in terms of certain algebraic systems. The concepts occurring in such an exposition, the terms used to describe them, and the problems selected for special emphasis are all suggested by the facts of physics. The algebra does not pretend to solve physical problems or to give new information about the state of the universe; its primary aim is to study a mathematical subject by mathematical methods. The mathematical machinery set up for this purpose is (unlike its extramathematical source) aesthetically attractive to and intellectually fathomable by the professional mathematician. It can happen that the mathematics will eventually come to be applicable to its own parent and capable of contributing to its growth, but the mathematics is of value even if that does not happen. It is of value not only in an intrinsic mathematical sense, but also because it can be used as a map with which the professional mathematician can venture into the territory of the professional physicist. If in the preceding description of the role of algebraic treatments of quantum mechanics words such as “physics” and “physicist” are replaced by “logic” and “logician”, the result is a fair description of the intended role of algebraic logic.

Not all the problems that interest a logician have their counterpart in algebraic logic. The reason for this is best seen in another analogy: roughly speaking, ordinary logic is to permutation groups as algebraic logic is to abstract (axiomatically defined) groups. Since the problems of transitivity and primitivity cannot even be expressed in the language of abstract group theory, the generality and elegance of that subject are obtained at the cost of some terminological and conceptual sacrifice. For some purposes a more illuminating ratio is this: ordinary logic is to free groups as algebraic logic is to abstract groups. This ratio is very suggestive. The logician’s customary exposition of the propositional calculus is, in fact, a description of the free Boolean algebra on a countable set of generators; similarly, the customary treatments of the functional calculi can be viewed as studies in the theory of free polyadic algebras. In group theory both the algebraic and the combinatorial methods have an important place; the reason for the existence of algebraic logic is the belief that the same is true in logic.

It is not claimed that the algebraic point of view simplifies all definitions and shortens all proofs; in many cases just the opposite is true. The pertinent analogy here is the relation between the classical theory of Hermitian matrices and the approach to the same subject via Hubert space. The definition of the conjugate transpose of a complex matrix can be given with perfect rigor on the first page of an elementary book. The corresponding definition in a book on Hubert space must wait its turn; many properties of inner products and linear functionals have to be established before the adjoint of an operator can make sense in an invariant, algebraic setting. An analogous situation in logic occurs, for instance, in connection with the concept of an individual constant. This simple concept is usually (and quite properly) dismissed with a few words in ordinary treatments of the subject; in the algebraic treatment (cf. § 12) it becomes a part of the most profound development of the theory.

The basic concepts of algebraic logic can be traced back to the work of Tarski and his collaborators; cf., for instance, [4], [6], and [7]. (Unfortunately the proofs of Tarski’s results on cylindric algebras have not yet been published, and it is, consequently, not easy to assess the exact extent of the overlap between the theories of cylindric algebras and polyadic algebras. It is probable that the basic difficulties are the same; the concepts and the techniques are likely to be different.) It will also be obvious to the reader familiar with some of the recent literature of logic that this paper was strongly influenced by Henkin’s thesis [3] and by some of the techniques introduced by Easiowa and Sikorski [5]. It is a pleasure, finally, to express my indebtedness to A. F. Bausch and to Alfred Tarski. I had many stimulating conversations about functional calculi with Bausch and about cylindric algebras with Tarski; I am grateful for their friendly advice and encouragement.

The principal results of the paper are the functional representation (Theorem 10.9), the adjunction of variables (Theorem 11.9), the adjunction of witnessing constants (Theorem 19.6), and the representation of simple algebras (Theorem 17.3). The reader who wants to get a quick snapshot of the subject, avoiding most of the technicalities, can proceed along the following course: glance at § 1 for the notation, read § 2, omit § 3 and § 4, read the definition of local finiteness in § 5, omit § 6 and § 7, read § 8 and § 9, read the remarks and the statements of the theorems (but not the proofs) in § 10, read the definition of dilations in § 11 and the definition of constants in § 12, omit § 13 and § 14, and read the definitions and the theorems in § 15, § 16, and § 17.

§ 1. Monadic algebras

For convenience of reference this section contains a summary of those definitions and theorems from the theory of monadic algebras that will be used in the sequel. The theorems in this summary all belong to the elementary part of the subject; their proofs are easy consequences of the definitions and of the standard theory of Boolean algebras. The details and the heuristic motivation are given in [2].

We begin by establishing the notation that will be used for Boolean algebras. The symbols and are used to indicate the supremum and the infimum, respectively, of sets in a Boolean algebra. Other Boolean symbols, which will be used without any further explanation below, are as follows: p∨q is the supremum of p and q, pq is the infimum of p and q, p′ is the complement of p, 0 is the zero element of the algebra, 1 is the unit element of the algebra, p – q( = pq′) is the difference between p and g, p + q( = (p − q)∨(q – p)) is the Boolean sum (or symmetric difference) of p and q. The symbols and will denote the natural order in a Boolean algebra, so that, for instance, means that pq = p. The identity mapping of a Boolean algebra onto itself will be denoted by e. It is understood that, by definition, a Boolean algebra contains at least two distinct elements. The symbol O will be used to denote the two-element Boolean algebra {0,1}, so that O is a Boolean subalgebra of every Boolean algebra.

A quantifier (or, properly speaking, an existential quantifier) is a normalized, increasing, and quasi-multiplicative mapping of a Boolean algebra into itself; in other words, it is a mapping such that if p and q are in the algebra, then

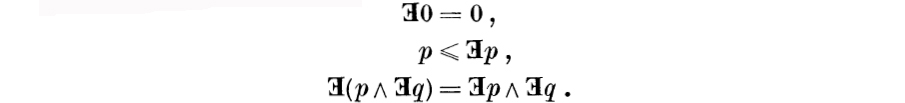
The discrete quantifier is the identity mapping e; the simple quantifier is the one for which whenever p ≠ 0. A hemimorphism is a normalized and additive mapping f from one Boolean algebra into another; in other words, it is a mapping f such that f0 = 0 and such that if p and q are in its domain, then f(p∨q) = fp∨fq. Clearly every Boolean homo-morphism (and, in particular, every Boolean endomorphism) is a hemimorphism.

The following simple facts are basic in the theory of quantifiers.

(1.1) A quantifier is idempotent i. e., ).

(1.2) A quantifier is monotone (i. e., if , then ).

(1.3) The range of a quantifier is a Boolean algebra.

(1.4) A quantifier is additive (i. e., ).

(1.5) If is a quantifier and if p and q are elements of its domain, then .

We observe that in view of (1.4) a quantifier is a hemimorphism; from this and from the elementary fact that a hemimorphism is monotone we can recapture (1.2). The reason for stating the facts in the order used above is that in the proof of (1.4) it is convenient to make use of (1.2).

A monadic algebra is a Boolean algebra A together with a quantifier on A. A subset B of a monadic algebra A is a monadic subalgebra of A (or a monadic ideal in A) if and only if B is a Boolean subalgebra of A (or a Boolean ideal in A) such that belongs to B whenever p belongs to B. A mapping f between monadic algebras is a monadic homomorphism if it is a Boolean homomorphism such that for every p in its domain. (The adjective “monadic” will be used with “subalgebra”, “ideal”, “homomorphism”, etc., whenever it is advisable to emphasize the distinction from other kinds of subalgebras, ideals, homomorphisms, etc. – e. g., from the plain Boolean kind. Usually, however, the adjective will be omitted and the context will unambigously indicate what is meant. A similar remark applies to the polyadic concepts that will be introduced later.) A monadic algebra is simple if {0} is the only proper ideal in it. A monadic ideal is maximal if it is not a proper subset of any proper ideal. A monadic algebra is semisimple if the intersection of all maximal ideals in it is {0}.

(1.6) A monadic algebra is simple if and only if its quantifier is simple.

(1.7) Every monadic algebra is semisimple.

If X is a non-empty set and if B is a Boolean algebra, the set of all functions from X into B is a Boolean algebra with respect to the pointwise operations. A B-valued functional monadic algebra with domain X is a Boolean subalgebra A of the algebra of all functions from X into B such that, for each p in A, the range of p has a supremum in B, and such that the (constant) function, whose value at every point of X is that supremum, belongs to A. If that constant function is denoted by , then is a quantifier on A, so that a functional monadic algebra is a monadic algebra.

(1.8) An O-valued functional monadic algebra is simple.

A constant of a monadic algebra A (with quantifier ) is a Boolean endomorphism c on A such that and .

(1.9) A constant is idempotent (i. e., cc = c).

(1.10) If c is a constant of a monadic algebra A with quantifier , then for every p in A.

§ 2. Functional polyadic algebras

If “proposition” is taken to mean an element of a Boolean algebra B, then it is natural to interpret “propositional function” as a function from some set into B. A propositional function of several variables becomes in this scheme a function from a Cartesian product of several sets into B. In order to keep the notation from becoming cumbersome, we shall restrict our attention to Cartesian powers, i. e., to sets of the form X^I, where I is an arbitrary index set. (Cf. also the discussion at the end of § 4.) An element of X^I is, by definition, a function from I into X; the value of such a function x at an index i will be denoted by a x_i.

The set of all functions from a non-empty set into a Boolean algebra is a Boolean algebra with respect to the pointwise operations. According to the usual conventions the set X^I is empty if and only if X is empty but I is not. In order to ensure the non-emptiness of X^I we shall always assume that the set X is not empty. Since the elements of the set X constitute the universe of discourse with which the propositions and propositional functions of the theory are concerned, this assumption is a reasonable one.

The main thing that distinguishes the abstractly given Boolean algebra B from the Boolean algebra of all B- valued functions on X^I is that the concrete representation of the latter automatically endows it with a lot of new structure. The additional structure comes from the presence of variables. Substituting some variables for others, or holding some variables fixed while forming a supremum over the others, we obtain new propositional functions out of old ones.

To make these indications more specific, we consider the set of all transformations on I, i. e., the set of all transformations whose domain is the set I and whose range is included in I. Since the transformations we consider are not necessarily one-to-one and not necessarily onto, the set of all such transformations does not form a group. Since, however, the product (i. e., composite) of two transformations on I is again a transformation on I, and since transformation multiplication is associative, the set of all transformations on I does form a semigroup. Since the identity mapping from I onto itself (which we shall always denote by δ) is a transformation on I, the semigroup contains a (necessarily unique) unit.

The idea of “substituting some variables for others” is to apply a transformation on I to the indices of the arguments of a function from X^I into B. The desideratum is to associate with each transformation τ on I, in a natural manner, a transformation S(τ) that sends propositional functions (i. e., functions from X^I into B) into propositional functions. The definition of S(τ) is most easily given in terms of an auxiliary transformation τ_* on X^I. The transformation τ_* is defined by

for all i in I and for all x in X^I. The functional transformation S(τ) associated with a transformation τ on I is defined by

for all x in X^I and for all functions p from X^I into B. (The symbol S(τ)p(x) is an abbreviation for (S(τ)p)(x). Such abbreviations will be used frequently without any further explanation.) The precise version of “substituting some variables for others” is the application of a transformation such as S(τ).

The formation of partial suprema is a slightly more delicate matter. If J is a subset of I (not necessarily proper), then there is associated with J in a natural manner a transformation that sends some (but not necessarily all) propositional functions into others. The definition of is most easily given in terms of an auxiliary binary relation J_* in X^I. The relation J_* is, by definition, such that

for all x and y in X^I. (The symbols and ∉ are used to indicate the relations of belonging and non-belonging, respectively.) The functional transformation is defined by

provided that the indicated supremum exists for every x in X^I. The idea is to form the supremum of the values of the function p over the points obtained from x by holding fixed the variables outside J and varying the variables in J arbitrarily.

Since need not exist for every function p from X^I into B, we cannot continue to insist on studying the Boolean algebra of all functions from X^I into B. We must and we shall be content with considering a Boolean subalgebra of that algebra, say A. By requiring that exist and belong to A for every subset J of I and for every element p of A we can circumvent the difficulty caused by the possible non-existence of suprema. Now, however, another difficulty arises. If τ is a transformation on I, then S(τ)p is a function from X^I into B whenever p is such, but if we assume that p A, that does not guarantee that S(τ)p A. This difficulty can be circumvented also, simply by requiring that A be closed under the operation S(τ) for every transformation τ on I.

We can summarize the preceding considerations as follows. Suppose that B is a Boolean algebra and that X and I are sets, with X non-empty. The elements of I will play for us the role of what are usually called variables (although they do not, in any sense of the word, vary), and the set X will play the role of the domain of the variables (although, in general, the variables do not belong to the domain). The elements of the Boolean algebra B will play the role of the propositions that can occur as the values of the propositional functions to be considered. A functional polyadic (Boolean) algebra is a Boolean subalgebra A of the algebra of all functions from X^I into B, such that S(τ)p A whenever p A and τ is a transformation on I, and such that exists and belongs to A whenever p A and J is a subset of I. Whenever it becomes desirable to indicate the constituents used in the definition, A will be called a B-valued functional polyadic algebra with domain X and variables I, or, more simply, a B-valued I-algebra over X. Functional polyadic algebras are the concrete objects in terms of which propositional functions can be studied; our main purpose is to investigate the abstract algebraic objects of which functional polyadic algebras are the typical representations.

§ 3. Substitutions

In order to find out what are the algebraic properties of the operators S(τ) and on a functional polyadic algebra, we shall make use of a concept in terms of which we can treat both kinds of operators at the same time. The concept (to be called substitution) is not an intuitive one; the only reason for introducing it here is that it is efficient for the purpose at hand. By a substitution in a set I we shall mean a function σ whose domain (doma) and range (rancr) are subsets of I. The fact that the domain of a substitution is not necessarily equal to I will be important for us. In what follows we shall reserve the use of the word transformation for a substitution τ such that domτ = I; this is in agreement with the use of that word in the preceding section.

If σ and τ are substitutions, their product στ is defined to be the substitution whose domain is the set of all those elements i of I for which i domτ and i domσ and whose value for each i in its domain is defined by (στ)i = σ(τi). It is easy to verify that substitution multiplication is associative, so that, with respect to multiplication as the law of composition, the set of all substitutions in I is a semigroup. This semigroup has a unit, namely the identity transformation δ.

There is another and more familiar semigroup associated with the set I, namely the set of all subsets of I, with respect to the formation of unions as the law of composition. This semigroup also has a unit, namely the empty set Ø. There is a close relation between (all) subsets of I and (some) substitutions in I. In order to study this relation we make correspond to each subset J the identity mapping, to be denoted by χ(J), on I–J. More explicitly, χ(J) is the substitution such that domχ(J) = I–J and χ(J)i = i for all i in I–J.

(3.1) LEMMA. The correspondence χ is a one-to-one correspondence from the set of subsets of I into the set of substitutions in I such that χ(Ø) = δ and χ(J∪K) = χ(J) χ (K).

Proof. Since domχ(J)χ(K) = (I–J)∩(I–K) = I–(J∪K), it follows that χ(J)χ(K) = χ(J∪K). The proof is completed by the observation that χ(J) = δ if and only if J = Ø.

We note that, in algebraic terms, the result of Lemma 3.1 is simply that the correspondence χ is a semigroup monomorphism.

There is a possible source of minor confusion in connection with the equation χ(Ø) = δ. The empty set Ø is also a substitution, namely the unique substitution with empty domain and empty range. It is notationally convenient to make a distinction between the empty set as a subset of I and the empty set as a substitution in I; we shall denote the latter by θ. It is clear that the substitution θ belongs to the range of the correspondence χ; in fact, θ = χ(I).

Transformations on I and subsets of I are more or less natural objects, whereas substitutions are apparently artificial constructs. In fact, however, substitutions arise quite naturally from transformations and subsets, via the correspondence χ.

(3.2) LEMMA. Every substitution a can be written in the form τχ(J), where τ is a transformation on I and J is a subset of I. The set J in this representation is uniquely determined as I – domσ; the transformation τ must agree with σ outside J and is arbitrary in J.

Proof. If σ = τχ(J), then domσ = domχ(J) = I–J, and, if i I–J, then τi = τχ(J)i = σi. This proves the uniqueness assertions. To prove the rest, let τ be an arbitrary transformation that agrees with σ in domσ; an immediate verification shows that if J = I — domσ, then σ = τχ(J).

What is the connection between the representation established in Lemma 3.2 and substitution multiplication? The next two results provide the answer to this question.

(3.3) LEMMA. If τ is a transformation and J⊂I, then χ(J)τ = τχ(τ⁻¹J).

Proof. An element i of I belongs to domχ(J)τ if and only if τi domχ(J) = I– J, i. e., if and only if i τ⁻¹(I–J) = I – τ⁻¹J. An element i of I belongs to domτχ(τ⁻¹J) if and only if i domχ(τ⁻¹J) = I–τ⁻¹J. In other words, χ(J)τ and τχ(τ⁻¹J) have the same domain; if i belongs to this common domain, then χ(J)τi = τi and τχ(τ⁻¹J)i = τi.

(3.4) LEMMA. If σ₁ = τ₁χ(J₁) and σ₂ = τ₁χ(J₁), where τ₁ and τ₁ are transformations, then .

Proof. Observe that σ₁σ₂ = τ₁χ(J₁)τ₂χ(J₂), and apply Lemma 3.3 to the product χ(J₁)τ₂.

We proceed now to introduce, without any immediately apparent motivation, a concept that will presently turn out to be useful. For substitutions σ and τ we shall say that σ follows τ, and we shall write σ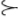τ, if τ never maps two distinct elements onto the same element of I – domσ. (The notation is not intended to suggest, and it is not in fact true, that the relation thereby defined is a partial order.) The definition can be rephrased as follows: σ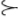τ if and only if the conditions i ≠ j and τi = τj = k imply that k domσ. 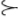Equivalently: στ if and only if τ is one-to-one on the set τ⁻¹(I – domσ). While none of these conditions has much intuitive appeal, the point in considering them is that in addition to being equivalent to each other they also turn out to be equivalent to an algebraically elegant and intuitively natural condition (cf. Theorem 3.8).

To prepare the ground for later work, and also as an aid in understanding this somewhat peculiar concept, we explicitly mention some useful special cases.

(3.5) LEMMA. If σ is a transformation, then σ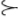τ for all τ. If τ is one-to-one, and, in particular, if τ = χ(J) for some J, then σ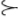τ for all σ.

Proof. The first assertion follows from the fact that if σ is a transformation, then I – domσ is empty. The second assertion is obvious.

(3.6) LEMMA. A necessary and sufficient condition that χ(J)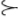τ is that τ be one-to-one on τ⁻¹J.

Proof. The condition means that the restriction of the function τ to the set τ⁻¹J is one-to-one, and this, in turn, means exactly that τ never maps two distinct elements onto the same element of J. Since J = I – dom χ(J), the proof is complete.

Now we consider again a Cartesian power X^I, where X is a non-empty set; we shall discuss the way in which the action of the substitutions discussed above is reflected in the set X^I. This is most easily done in terms of an auxiliary binary relation σ_* in X^I associated with each substitution σ in I. The relation σ_* (called the dual of σ) is, by definition, such that

(3.7) xσ_*y if and only if x_σi = y_i whenever i domσ

for all x and y in X^I.

The duals of transformations and the duals of substitutions of the form χ(J) are particularly simple. If τ is a transformation, then xτ_*y means that x_τi = y_i for all i. Hence, in this case, y is uniquely determined by x, so that the relation τ_* is a function; the value of the function τ_* at a point x of X is given by (τ_*x)_i = x_τi. (We have thus recaptured (2.1) as a special case of (3.7).) Note in particular that δ_* is the identity mapping on X^I. If σ = χ(J), then xσ_*y means that x_i = y_i,·whenever i ∉J. (We have thus recaptured (2.3) as a special case of (3.7).) In this case σ_* is obviously an equivalence relation; it is exactly the relation that we denoted by J_* in the preceding section. Since χ(Ø) = δ, the fact that δ_* is the relation of equality in X^I is the relation version of the characterization of δ_* stated just above in the language of mappings. We note that, at the opposite extreme, θ_* = I_* is the trivial equivalence relation that places all the points of X^I into the same equivalence class. Another worth while observation is that if J ⊂ K, then J_* ⊂ K_*. The inclusion sign here has its usual meaning if it is recalled that a relation is a set of ordered pairs; explicitly J_* ⊂ K_* means that xJ_*y implies that xK_*y whenever x and y are in X^I.

The terminology and the notation are designed to indicate that the mapping σ→σ_* behaves like duality mappings behave in many other parts of mathematics. Experience with such mappings makes it reasonable to conjecture that (στ)_* = τ_*σ_* (in the sense of relation product). Unfortunately, however, this equation does not always hold. It is at this point that our concept of one substitution “following” another becomes useful; that apparently ad hoc condition is, in all non-trivial cases, necessary and sufficient for the validity of the desired equation.

(3.8) THEOREM. If σ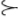τ, then (στ)_* = τ_*σ_*. If, conversely, X consists of more than one point, and (στ)_* = τ_*σ_*, then σ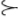τ.

Remark. The relation product τ_*σ_* is defined so that x(τ_*σ_*)z holds if and only if there exists a point y with yτ*z and xσ_*y. This order of events is in accordance with the standard functional notation. Indeed, if both τ_* and σ_* are single - valued, then τ_*σ_* is single - valued and x(τ_*σ_*) z means that z = τ_*σ_*. If, in this case, y = σ_*x, then z = τ_*y. These considerations have at least a mnemonic value even in the general case; the proper notational set-up for any relation product can be instantaneously rederived by pretending that the factors are functions.

If X consists of just one point, then the same is true of X^I. In this case σ_* is the identity mapping of X^I onto itself for every σ, and, consequently, (στ)_* = τ_*σ_* is universally valid.

Proof. Assume first that x(τ_*σ_*)z and let y be a witness to this connection; assume, in other words, that yτ_*z and xσ_*y. Suppose now that i domστ, so that idomτ and τi domσ. Since yτ_*z and i domτ, it follows that y_τi = z_i. Since xσ_*y and τi domσ, it follows that x_σ₍_τi₎ = y_τi Conclusion: x₍_στ₎_i = z_i whenever i domστ, and therefore x(στ)_*z. We have proved so far that τ_*σ_* ⊂ (στ)_*; note that the assumption σ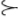τ was not used yet.

Assume next that x(στ)_*z; this means that x₍_στ₎_i = z_i whenever i domτ and τi domσ. To prove that x(τ_*σ_*)z, a witness y to this connection will be constructed in three stages, (i) If j domσ, put y_j = x x_σi. (ii) If j ranτ – domσ, then j I – domσ and therefore (here is where the assumption σ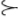τ comes in) there is at most one i such that j = τi; since also j ran τ, one such i (and therefore exactly one such i) does exist. In this case we may without ambiguity put y_j = z_i. (iii) If j I – – (ranτ∪domσ), define y_j arbitrarily; say, put y_j = x_j. This three-stage construction defines an element y_j of X^I. The fact that xσ_*y follows from (i) and from the definition of σ_*. To prove that yτ_*z, consider an element i in domτ. If τi domσ, then x_(στ)_i = z_i (because of the assumption x(στ)_*z), and y_τi = x_(στ)_i (by (i)). If, on the other hand, τi I –domσ, then τi ranτ – domσ and therefore y_τi = z_i (by (ii)). We have proved thus that x(τ_*σ_*)z, and hence that (στ)_* ⊂ τ_*σ_*; this completes the proof of the first assertion of the theorem.

To prove the second assertion, we assume that X consists of more than one point and that σ and τ are such that σ 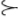τ is false. The latter assumption means that there exist two distinct elements j and k in domτ such that τj = τk I – domσ. Consider now an arbitrary point x in X^r and use it to define a point z as follows. If i domστ, put z_i = x_στi; define z_j and z_k arbitrarily, subject only to the proviso that z_j≠z_k; for all other indices i, define z_i completely arbitrarily. It follows from this definition that x(στ)_*z. On the other hand, it is false that x(τ_*σ_*)z; in fact, yτ_*z is false for all y. The reason is that τj = τk implies that y_τj = y_τk for all y; since z_j≠z_k, this makes it impossible that y_τi should be equal to z_i for all i in domτ. The proof of the theorem is complete.

§ 4. Polyadic algebras

Throughout this section (and, in fact, in most of the paper) we shall continue to use the notation established above; in particular the symbols B, X, and I will always retain their meanings.

If p is an arbitrary function from X^I into B, if x X^I, and if σ is a substitution in I, then {p(y): xσ_*y} is a subset of B, and, as such, it may or may not have a supremum in B. If p and σ are such that the supremum exists for all x, and if the value of the supremum for each x in X^I is denoted by q(x), then, of course, q is a function from X^I into B. In this situation we shall write q = S(σ)p, or, equivalently, we shall say that S(σ)p exists and has the value q. Explicitly

whenever the indicated supremum exists.

The point in considering substitutions at all is that they enable us to treat simultaneously the two kinds of operators that enter into the definition of a functional polyadic algebra. Indeed, if τ is a transformation on I, then the set {p(y): xτ_*y} consists of the single element p(τ_*x); this shows that the use of the symbol S in (4.1) is consistent with its earlier use in (2.2). If J is a subset of I, and if σ = χ(J), then, as we have already observed, the relation σ_* that occurs in (4.1) is identical with the relation J_* in (2.4), so that .

(4.2) LEMMA. If p is a function from X^I into B and if σ and τ are substitutions in I with σ 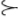τ, then S(στ)p = S(σ)S(τ)p, in the following sense: if both S(τ)p and S(σ)S(τ)p exist, then S(στ)p exists and the equality holds, and conversely, if τ is a transformation on I such that S(στ)p exists, then S(σ)S(τ)p exists and the equality holds again.

Proof. Assume first that both S(τ)p and S(σ)S(τ)p exist. If q = S(τ)p, then for all y in X^I. It follows that

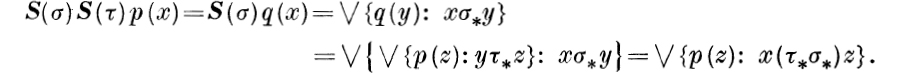
The proof in this case is completed by an application of Theorem 3.8 and of the definition of S(στ)p. Assume next that τ is a transformation such that S(στ)p exists. Since the definition of the product of two relations implies that {p(z): x(τ_*σ_*)z} = {p(τ_*y): xσ_*y}, it follows that

and the proof is completed by an application of the definition of S(σ)S(τ)p.

One consequence of the preceding result is that a functional polyadic algebra admits more operations than its definition demands.

(4.3) LEMMA. A necessary and sufficient condition that a Boolean algebra A of functions from X^I into B be a functional polyadic algebra is that S(σ)p exist and belong to A whenever p A and a is a substitution in I.

Proof. The sufficiency of the condition is obvious: if the condition is satisfied for every substitution, then it is satisfied, in particular, for every transformation and for every substitution of the form χ(J) where J is a subset of I. To prove necessity, we recall that, by Lemma 3.2, every substitution can be written in the form τχ(J), where τ is a transformation on I and J is a subset of I, and that, by Lemma 3.5, τ 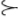χ(J). The desired result now follows from Lemma 4.2.

If A is a functional polyadic algebra (more explicitly, a B-valued I-algebra over X), then, for each substitution σ in I, S(σ) is an operator on A, i. e., a mapping of A into itself. In the remainder of this section we shall derive the basic properties of the operators S(σ).

(4.4) LEMMA. If τ is a transformation on I, then S(τ) is a Boolean endomorphism of the algebra of all functions from X^I into B (and hence of any functional I-algebra); the endomorphism S(δ) is the identity mapping e.

Proof. The assertion is an immediate consequence of (2.2) and of the fact that the Boolean operations in an algebra of functions are defined pointwise. (Recall also that δ_* is the identity mapping on X^I.)

(4.5) LEMMA. If J ⊂ I and if x and y are elements of X^I such that xJ_*y_, then for any function p from X^I into B, in the sense that if either term of the equation exists, then the other one exists and the two are equal.

Proof. Since J_* is an equivalence relation in X^I the assumption xJ_*y implies that either one of the conditions xJ_*z and yJ_*z is necessary and sufficient for the other. It follows that the sets {p(z): xJ_*z} and {p(z): yJ_*z} are the same and hence that if either one has a supremum, the other one has the same supremum.

(4.6) LEMMA. If J ⊂ I, then is a quantifier on A.

Proof. It is clear that is normalized, i.e., that . Since the equivalence relation J_* is reflexive, i. e., xJ_*x for all x, it follows that

so that is increasing. The fact that is quasi-multiplicative is a consequence, via Lemma 4.5, of the following computation:

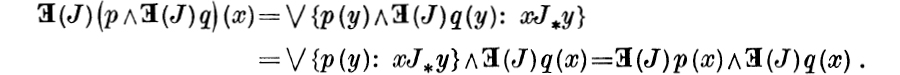
It follows from Lemmas 3.5 and 4.2 that if σ and τ are transformations on I, then S(στ) = S(σ)S(τ). Since χ(Ø) = δ, the fact that S(δ) = e can also be expressed by saying that is the discrete quantifier on A. From Lemma 3.1 we infer (using Lemmas 3.5 and 4.2 as before) that and hence, in particular, that whenever J and K are subsets of I. All these facts are rather near the surface; the next two results, though easy, are less obvious.

(4.7) LEMMA. If σ and τ are transformations on I, if J ⊂ I, and if σ = τ outside J, then S(σ) = S(τ) (J)p whenever p is a function from X^I into B such that exists.

Proof. The last assumption means that σi = τi whenever i I –J and hence that σχ(J) = τχ(J). The conclusion follows from Lemmas 3.5 and 4.2.

(4.8) LEMMA. If p is a function from X^I into B, if τ is a transformation on I and J is a subset of I such that τ is one-to-one on τ⁻¹J, and if exists, then exists and .

Proof. By Lemma 3.3, χ(J)τ = τχ(τ⁻¹J). By Lemma 3.6, the assumption on τ means that x(J) 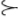τ. By Lemma 3.5, τ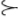χ(τ⁻¹J). By Lemma 4.2, S(τ) (τ⁻¹J)p = S(τχ(τ⁻¹J))p, so that S(χ(J)τ)p exists; the conclusion follows from another application of the same lemma.

The superficially complicated conclusions of Lemmas 4.7 and 4.8 are merely a condensed summary of the usual intuitively obvious relations between quantification and substitution. A couple of examples will make them clearer. Suppose that i and j are distinct elements of I and let τ be the transformation that maps i onto j and maps everything else (including j) onto itself. Since τ agrees with δ outside i, it follows from Lemma 4.7 that . (If J is a singleton, J = {i}, we write instead of .) This equation corresponds to the familiar fact that once a variable has been quantified, the replacement of that variable by another one has no further effect. To get another example, note, for the same τ, that τ⁻¹i is empty. It follows from Lemma 4.8 that . This equation corresponds to the familiar fact that once a variable has been replaced by another one, a quantification on the replaced variable has no further effect.

We are now ready to define the central concept of this paper. Abstracting from the functional case, we shall say that a polyadic (Boolean) algebra is a quadruple (A, I, S, ), where A is a Boolean algebra, I is a set, S is a mapping from transformations on I to Boolean endomorphisms of A, and is a mapping from subsets of I to quantifiers on A such that

(P₁) S(δ) is the identity mapping on A (i. e., S(δ) = e),

(P₂) S (στ) = S (σ) S (τ) whenever σ and τ are transformations on I,

(P₃) is the discrete quantifier on A (i. e., ),

(P₄) whenever J and K are subsets of I,

(P₅) if σ and τ are transformations on I, if J ⊂ I, and if σ = τ outside J, then ,

(P₆) if τ is a transformation on I, if J ⊂ I, and if τ is one-to-one on τ⁻¹J, then (J)S(τ) = S(τ) (τ^−lJ).

From this definition and from our preceding results it follows immediately that a functional polyadic algebra is a polyadic algebra.

Most of the time we shall use the same symbols (S and ) for the endomorphism and quantifier mappings of every polyadic algebra; only rarely will we find it necessary to use a more detailed notation in order to avoid confusion. We shall also commit the common simplifying solecism of identifying the Boolean algebra A with the polyadic algebra (A, I, S, ). We shall, accordingly, use expressions such as “the polyadic algebra A”, or “the polyadic algebra A with variables I”, or simply “the I-algebra A”. The cardinal number of I will be called the degree of the algebra and an algebra of degree n will be called an n-adic algebra.

If I is empty, then there is only one transformation, namely δ, and there is only one subset, namely Ø; in this extreme case θ = δ. Consequently, if A is an arbitrary Boolean algebra, if I is the empty set Ø, and if both S(δ) and are defined to be e, then A becomes a polyadic algebra of degree 0. We see thus that the classical theory Boolean algebras is subsumed under the 0-adic case of the theory of polyadic algebras.

If I consists of a single element, then there is only one transformation, namely δ, and there are two distinct subsets, namely Ø and I. Consequently if A is an arbitrary monadic algebra with quantifier , if I is a singleton, and if we write, by definition, and , then A becomes a polyadic algebra of degree 1. We see thus that the theory of monadic algebras is subsumed under the 1-adic case of the theory of polyadic algebras.

In a certain sense the definition of polyadic algebras above (and, correspondingly, the definition of functional polyadic algebras in § 2) is not sufficiently general. It often happens (e. g., in axiomatizations of Euclidean geometry) that the propositional functions to be considerep are functions of several different kinds of variables (e. g., points, lines, and planes). The appropriate way of allowing for this phenomenon from the point of view of functional polyadic algebras is to consider not one domain and its Cartesian powers but several possibly distinct sets and their Cartesian product. More explicitly, suppose that to each element i of I there corresponds a non-empty set X_i and let X₁ be the Cartesian product of this family of sets. The sets X_i may overlap or coincide among themselves quite arbitrarily. Functions from X_I to B form a Boolean algebra as before, and the theory of the operators carries over to the generalized situation with no significant change. If, however, τ is a transformation on I, then the definition of τ_*x is not always meaningful (since X_τi and X_i may have no points in common). The simplest way out of the difficulty is to restrict attention to such transformations τ (“special” transformations) for which Χ_τi = Χ_i for all i in I. The set of special transformations is a subsemigroup (containing the unit) of the set of all transformations on I. If we consider only the transformations in this subsemigroup (and, correspondingly, consider only those substitutions σ on I for which Χ_σi· = Χ_i for all i in domσ), then the results of § 2 and § 3 go through without any difficulties. The definition of a functional polyadic algebra will, naturally, become slightly different; in place of closure under S(τ) for all transformations τ, the modified definition requires only closure under S(τ) when τ is a special transformation.

The considerations of the preceding paragraph suggest a modification in the definition of abstract polyadic algebras also. The conditions referring to alone remain unmodified, but the conditions referring to S are required to hold only for a suitable subsemigroup of the semigroup of all transformations on I. The resulting concept is a generalization of the one defined above; the special case is obtained from the generalization by the consideration of the improper subsemigroup of all transformations. Polyadic algebras in the special sense will be called homogeneous algebras; they are the only ones with which we shall be concerned in this paper. The simplest and at the same time the most interesting polyadic algebras are homogeneous; most of the techniques that apply to homogeneous algebras apply with only minor modifications to the general case; and, finally, there are some known techniques (cf. [8]) for generalizing results about homogeneous polyadic algebras to arbitrary polyadic algebras. For these reasons, the details of the study of non-homogeneous polyadic algebras may safely be postponed to a later occasion.

§ 5. Locally finite algebras

In order to see the direction in which the theory of abstract polyadic algebras should develop, we take another look at propositional functions, i. e., at functions from a Cartesian power X^I into a Boolean algebra B. While, for logical purposes, it is frequently essential that the set of variables be infinite, each particular propositional function usually depends on a finite number of variables only. The precise definition of a function depending on a certain set of variables is best approached indirectly. A function p from X^I into B is independent of a subset J of I if p(x) = p(y) whenever xJ_*y. In other words, p is independent of J if and only if the replacement of an argument x of p by a point whose coordinates differ from those of x only when their index is in J leaves the value of p unchanged. Boughly speaking, p is independent of J when coordinates in J can be changed arbitrarily without changing p.

It turns out to be easy to express the concept of independence in algebraic terms.

(5.1) LEMMA. If p is an element of a functional I-algebra and if J ⊂ I, then a necessary and sufficient condition that p be independent of J is that = p.

Proof. If p is independent of J, then

If, conversely, = p, then, by Lemma 4.5, xJ_*y implies that

In view of Lemma 5.1 it is natural to define independence in an arbitrary polyadic algebra as follows: an element p of an I-algebra A is independent of a subset J of I if and only if . We note that the concept of independence is the algebraic substitute for familiar logical concepts usually described in terms of “free” and “bound” variables.

Dependence could now be defined in terms of independence in the obvious way. It is grammatically more convenient, however, to use a different term. We shall say that a subset J of I is a support of p (equivalent expression: J supports p) if and only if p is independent of I –J. The element p of A will be called finite - dimensional, or simply finite, if it has a finite support, or, equivalently, if there exists a cofinite subset J of I such that p is independent of J. (A cofinite subset of I is one whose complement is finite.) Roughly speaking, p is finite if and only if it is independent of almost all (i. e., all but a finite number) of the variables. The algebra A is locally finite - dimensional, or simply locally finite, if every one of its elements is finite. Throughout the rest of this paper we shall deal with locally finite polyadic algebras only. Unless in a special context we explicitly say the opposite, we shall automatically (and often tacitly) assume that every polyadic algebra we refer to is locally finite. The main reason for this procedure is that almost nothing is known as yet about polyadic algebras that are not locally finite. The “infinite logics” that give rise to such algebras might repay study; for the time being, however, we concentrate our attention on the algebraic systems whose logical counterparts are of already proven value.

The first thing we can do for locally finite algebras is to prove that, just as the functional algebras that suggested them, they admit more operations than their definition demands; the additional operations, moreover, have the same desirable multiplicative properties that they have in functional algebras.

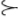(5.2) THEOREM. If A is a locally finite I-algebra, then there exists a unique mapping from substitutions in I to operators on A such that (i) whenever τ is a transformation on I, (ii) whenever J is a subset of I, and (iii) whenever σ and τ are substitutions in I such that σ τ.

Remark. A kind of converse of Theorem 5.5 is true and easy to prove (even in the absence of local finiteness.) Suppose in fact that A is a Boolean algebra and that is a mapping from substitutions in a certain set I to operators on A satisfying (iii) above and satisfying also the following three conditions, (a) is the identity mapping on A. (b) If τ is a transformation on I, then is a Boolean endomorphism of A. (c) If J ⊂ I, then is a quantifier on A. It follows that if S and are defined by (whenever τ is a transformation on I) and (whenever J is a subset of I), then A becomes an J-algebra. Indeed (P₁) and (P₃) follow from (a), and (P₂), (P₄), (P₅), and (P₆) follow from (b) and (c) via (iii) and Lemma 3.5. In other words, the conditions (a), (b), (c), and (iii) yield an alternative definition of polyadic algebras.

Once Theorem 5.5 is proved, there is no more necessity for maintaining a careful distinction between S and its extension ; in the future (after the proof of Theorem 5.5 is over) we shall use the same symbol S(τ) whether τ is a transformation on I or an arbitrary substitution in I.

Proof. If σ is a substitution in I, then, by Lemma 3.2, σ can be written in the form τχ(J), where τ is a transformation on I and J is a subset of I. Using (i), (ii), (iii), and Lemma 3.5, we conclude that . This proves the uniqueness assertion, and shows, incidentally, that is always a hemimorphism from A into itself.

To prove the existence assertion, we first note that if τ₁χ(J₁) = τ₁χ(J₁), where τ₁ and τ₂ are transformations, then Lemma 3.2 and (P₅) imply that . This proves that whenever σ = τχ(J) is a substitution, where τ is a transformation and J ⊂ I, then the equation unambigously defines a hemimorphism on A. The assertions (i) and (ii) are now obvious; it remains only to prove that satisfies (iii).

Suppose therefore that τ₁ and τ₂ are transformations and J₁ and J₂ are sets such that if σ₁ = τ₁χ(J₁) and σ₂ = τ₂χ(J₂), then σ₁ 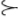σ₂. It is to be proved that if p A, then . Let J be a cofinite set such that = p and write . Since is finite, is cofinite and has a cardinal number greater than or equal to that of . It follows that there exists a transformation that agrees with τ₂ outside and that maps into in a one-to-one manner. Since maps and into disjoint sets, and since is one-to-one on , the only time that can send two distinct elements i and j onto the same element k is when i and j belong to and τ₂i = τ₂j = k. Since , it follows that both i and j belong to domσ₂ and σ₂i = σ₂j = k. The assumption σ₁ 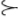σ₂ implies therefore that k domσ₁ = domχ(J₁). This proves that ; equivalently, by Lemma 3.6, is one-to-one on . The proof of Theorem 5.5 can now be completed by the following computation:

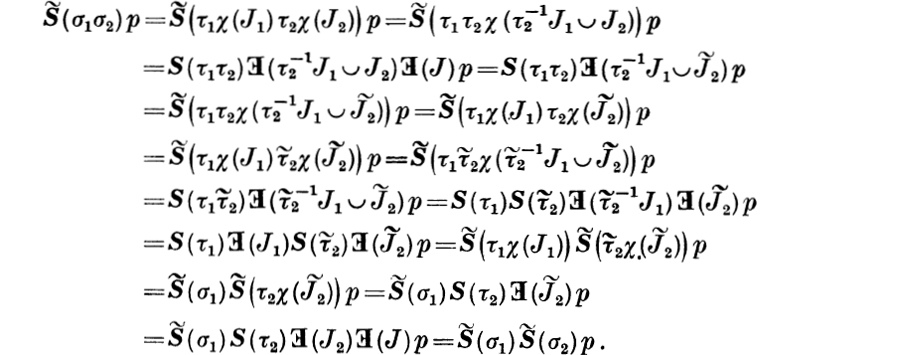
§ 6. Supports and independence

It is intuitively clear that if a propositional function depends on a finite number of variables only, then most of the action of a substitution on such a propositional function is wasted; all that matters is the behavior of the substitution on the finite set of variables in question. In order to make these considerations precise, we now make a digression into the appropriate part of the theory of substitutions.

We shall say that a subset J of a set I is a support of a substitution σ in I (equivalent expression: J supports σ) if σ agrees with the identity transformation outside the set J, or, more explicitly, if I – J ⊂ domσ and σi = i whenever i I –J.

(6.1) LEMMA. The set of all supports of a substitution σ in I is a Boolean filter (dual ideal) in the Boolean algebra of all subsets of I.

Proof. It follows immediately from the definition that J supports σ if and only if

This implies that I always supports σ, and hence that the set of supports of σ is never empty. It implies also that if J supports σ and J ⊂ K, then K supports σ, and that if both J and K support σ, then so does J∩K.

Remark. The proof shows more than the lemma asserts. The filter of supports of σ is, in fact, the principal filter generated by J₀, and, consequently, J₀ is the minimal support of σ. Despite this fact the language of supports is useful; it is often more convenient to use “a support” of σ than to insist on using “the support”.

The preceding result characterizes all supports of a fixed substitution; the following result goes in the other direction.

(6.2) LEMMA. The set of all substitutions with support J is a subsemigroup, containing the unit, in the semigroup of all substitutions.

Proof. Since δ agrees with δ outside J, it is trivial that J supports δ. If J supports both σ and τ, and if i I –J, then i domσ ∩ domτ and σi = τi = i; it follows that i domστ and (οτ)ι = σ(τi) = σi = i.

(6.3) LEMMA. If J supports σ and K supports τ, then J ∪ K supports στ.

Proof. By Lemma 6.1, J ∪ K supports both σ and τ; by Lemma 6.2, J ∪ K supports στ.

A substitution σ is finite if it leaves fixed almost all the elements of I. More precisely, σ is finite if domσ includes a cofinite subset of I on which σ agrees with the identity transformation δ. In the language of supports, σ is finite if and only if it has a finite support.

(6.4) LEMMA. The set of all f mite substitutions is a subsemigroup, containing the unit, in the semigroup of all substitutions.

Proof. Since there exists a finite set J (e. g., Ø) such that δ agrees with δ outside J, it is trivial that δ is finite. The fact that the set of all finite substitutions is closed under multiplication is an immediate consequence of Lemma 6.3.

(6.5) LEMMA. A necessary and sufficient condition that χ(J) be a finite substitution is that J be a finite set.

Proof. If J is finite, then, since χ(J) = δ outside J, it follows that χ(J) is finite. If, conversely, χ(J) = δ outside some finite set K, then it follows from the definition of χ(J) that J ⊂ K and hence that J is finite.

(6.6) LEMMA. Every finite substitution σ can be written in the form τχ(J), where τ is a finite transformation on I and J is a finite subset of I.

Proof. By Lemma 3.2, σ = τχ(J) with J = I –domσ and σ = τ outside J. The finiteness of σ implies that J is finite. The finiteness of σ and J, together with the fact that σ = τ outside J, implies that τ = σ outside a finite set, i. e., that τ is finite.

We proceed now to investigate the concepts of independence and support in an I-algebra A and the relation between these concepts and the algebraic structure of A. It is convenient to be able to phrase the results in the language of either independence or supports; because, however, of the intimate relation between these two concepts, it is generally sufficient to give the proof for only one of the two cases.

The first five of the results that follow are in a curious situation. They are valid for algebraic systems that are somewhat more general than polyadic algebras, and, in the next section, their generalized versions are needed. In order not to complicate the presentation, we shall state and prove them here for polyadic algebras only, and, in the next section, we shall point out the minor modifications that suffice to reach the generalization. Subsequently we shall refer to the generalized results by the same number as is borne by the special case; to avoid any possible confusion, systematic cross-references are provided at the appropriate places.

(6.7) LEMMA. If p A, then the set of all sets J such that p is independent of J is a Boolean ideal, and the set of all supports of p is a Boolean filter, in the Boolean algebra of all subsets of I.

Proof (cf. 7.1)). Since , it is trivial that p is independent of Ø. If = p and K ⊂ J, then

If , then

(6.8) LEMMA. If J ⊂ I, then the set of all elements p in A such that p is independent of J is a Boolean subalgebra of A, and the set of all elements p in A such that J supports p is a Boolean subalgebra of A.

Proof (cf. (7.2)). The set of all those elements p for which is simply the range of the quantifier . The desired result follows from the fact (1.3) that the range of a quantifier is always a Boolean algebra.

(6.9) LEMMA. If p is independent of J, then for every K; if J supports p, then for every K.

Proof (cf. (7.3)). For independence: (by Lemma 6.7). For supports: apply the result for independence to I –J.

(6.10) LEMMA. If p is independent of J (if J supports p), then is independent of J∪K (J – K supports ).

Proof (cf. (7.4)). .

(6.11) LEMMA. If p is independent of J and if σ and τ are transformations that agree outside J, then S(σ)p = S(τ)p.

Proof (cf. (7.5)). S(σ)p = S(σ) = S(τ) (by (P₅)) = S(τ)p.

For the proof of the main non-trivial relation between independence and transformations (Lemma 6.14) the following two technical lemmas are needed.

(6.12) LEMMA. If τ is a transformation, if J ⊂ I, and if K = I– τ(I –J), then τ⁻¹K ⊂ J.

Proof. This purely set - theoretic lemma is based on the fact that J ⊂ τ⁻¹τJ. Applying this inclusion to I –J in place of J and then forming the complement of both terms, we obtain

Since τ⁻¹Κ = τ⁻¹ (I – τ(I –J)) = I – τ⁻¹τ(I–J), the proof is complete.

(6.13) LEMMA. If τ is a transformation, if J ⊂ I, and if K = I – τ(I –J), then χ(K) 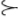τχ(J).

Proof. If τχ(J)i = j, then i I —J and therefore j τ(I –J), so that j I – K. In other words, the entire range of τχ(J) is included in I –K. Under these circumstances the substitution τχ(J) obviously never maps two distinct elements onto the same element of I – domχ(K) = K, because, in fact, it never maps anything at all into K.

(6.14) LEMMA. If τ is a transformation, if p is independent of J, and if K = I – τ(I –J), then S(τ)p is independent of K. If J supports p, then τJ supports S(τ)p.

Remark. The consideration of simple examples, and, in particular, of δ in the role of τ, shows that the result is in general best possible.

Proof. (by the assumed independence) = S(χ(K))S(τχ(J))p (by Theorem 5.5) = S(τχ(τ⁻¹K))χ(J))p (by Lemma 6.13 and Theorem 5.5) = S(τχ (J))p (by Lemma 3.3) = S(τχ(J))p (by Lemma 6.12) = (by Theorem 5.5) = S(τ)p (by the assumed independence).

It is to be noted that up to now the results of this section (together with their proofs) are valid even in the absence of local finiteness. In the following two results the assumption of local finiteness is essential.

(6.15) LEMMA. A necessary and sufficient condition that p be independent of J (that J support p) is that (Κ)p = p whenever K is a finite sub-set of J (of I –J).

Proof. The necessity of the condition is trivial from Lemma 6.7. To prove sufficiency, apply the definition of local finiteness to find a co-finite set J₀ such that p is independent of J₀ and note that (by Lemma 6.9) = p (by assumption, since J –J₀ is finite).

(6.16) LEMMA. If p A, then (i) to every subset K of I there corresponds a finite subset K₀ of I such that , (ii) to every transformation τ on I there corresponds a finite transformation r₀ on I such that S(τ)p = S(τ₀)p, and (iii) to every substitution σ in I there corresponds a finite substitution σ₀ in I such that S(σ)p = S(σ₀)p.

Proof. By the definition of local finiteness, p has a finite support J. The conclusion (i) folllows from Lemma 6.9. To prove (ii), write τ₀ί = τi when i J and τ₀i = i otherwise. Since J is finite, τ₀ is finite; (ii) follows from Lemma 6.11. The conclusion (iii) follows from (i) and (ii), together with Lemma 3.2, Theorem 5.5, and Lemma 6.4.

§ 7. Quasi-polyadic algebras

We began the preceding section with a vaguely formulated conjecture to the effect that in the study of (locally finite) poly adic algebras there is no loss of generality in restricting attention to finite substitutions only. Lemma 6.16 may be viewed as a precise formulation (and proof) of that vague conjecture. In this section we shall prove a much stronger result of the same type; for convenience in formulating that strengthened result we now introduce an auxiliary concept. The concept of a quasi-polyadic algebra is more general than that of a (locally finite) polyadic algebra; the difference between the two is that in the definition of quasi - polyadic algebras the mappings S and are assumed to be defined only for finite transformations on I and finite subsets of I. To avoid all possible misunderstanding, we formulate the pertinent definition explicitly as follows. A quasi - polyadic algebra is a quadruple (A, I, S, ), where A is a Boolean algebra, I is a set, S is a mapping from finite transformations on I into Boolean endomorphisms of A, and is a mapping from finite subsets of I to quantifiers on A, such that

(Q₁) S (δ) is the identity mapping on A,

(Q₂) S(στ) = S(σ)S(τ) whenever σ and τ are finite transformations on I,

(Q₃) is the discrete quantifier on A,

(Q₄) whenever J and K are finite subsets of I,

(Q₅) if σ and τ are finite transformations on I, if J is a finite subset of I, and if σ = τ outside J, then ,

(Q₆) if τ is a finite transformation on I, if J is a finite subset of I, and if τ is one-to-one on τ⁻¹J, then ,

(Q₇) if p A, then there exists a cofimite subset J of I such that whenever K is a finite subset of J.

A quasi-polyadic algebra is exactly what was called a polyadic algebra in [1]. The principal result of this section asserts essentially that the two definitions are equivalent, i. e., that every quasi - polyadic algebra is a (locally finite) polyadic algebra (or, rather, can be converted into one in a natural manner).

For a quasi - polyadic algebra the expression makes sense only if J is finite, and, consequently, the concept of independence cannot be defined in such an algebra the same way as in a polyadic algebra. On the basis of (Q₇) (cf. also Lemma 6.15) the remedy is clear; we shall say that p is independent of J if whenever K is a finite subset of J. The concept of support is defined in terms of independence, just as before.

It will follow from Theorem 7.7 that independence and support behave the same way in quasi - polyadic algebras as in ordinary polyadic algebras. In the course of the proof of Theorem 7.7 it is convenient to be able to make use of some of the elementary facts about independence and support. These facts (namely Lemmas 6.7-6.11) are almost as easy to prove for quasi - polyadic algebras as for polyadic algebras (and sometimes easier); in order to justify their use in the proof of Theorem 7.7 we proceed to indicate, very briefly, how the proofs go in the generalized situation.

(7.1) Proof of (6.7). If K ⊂ J, then finite subsets of K are finite subsets of J; this proves that if p is independent of J, then p is independent of K. The proof that independence is additive uses the additivity of not for the given sets but for their finite subsets.

(7.2) Proof of (6.8). For each finite set K, the set of all p with is a Boolean algebra; the desired result follows from the consideration of the intersection of all such Boolean algebras over all finite subsets K of J.

(7.3) Proof of (6.9). The assertion makes sense for finite sets K only; for them the proof is essentially the same as before.

(7.4) Proof of (6.10). Again K must be finite; in the proof replace J by an arbitrary finite subset of J.

(7.5) Proof of (6.11). This time σ and τ must be finite. If (cf. Lemma 6.1) K is a finite set that supports them both, then σ = τ outside J ∩ K; using this comment, we modify the proof by using J ∩ K in place of J.

We are now ready to fulfill our promise; we shall show that the concept of a polyadic algebra as defined in [1] is essentially equivalent to the concept of a locally finite polyadic algebra as defined in this paper.

(7.6) THEOEEM. If (A, I, S, ) is a quasi-polyadic algebra, then (i) there exists a mapping from transformations on I to Boolean endomorphisms of A such that whenever τ is a finite transformation, (ii) there exists a mapping from subsets of I to quantifiers on A such that whenever J is a finite set, (iii) the quadruple is a locally finite polyadic algebra, and (iv) the mappings and are uniquely determined by (i), (ii), and (iii).

Proof, (iv) Uniqueness is an immediate consequence of Lemma 6.16.

(i) If p A and if J₀ is a finite support of p, it is natural to try to define , for each transformation τ on I, by finding an appropriate finite transformation τ₀ on I and writing . The idea is easy: we write τ₀i = τi when i J₀ and τ₀i = i otherwise. The difficulty with this procedure is that appears to depend on the choice of the support J₀. To show that it does not in fact do so, we suppose that both J₁ and J₂ are finite supports of p and that x_x and r₂ are defined in terms of J₁ and J₂, respectively, just as τ₀ was defined in terms of J₀; we must prove that S(τ₁)p = S(τ₂)p. By Lemma 6.7, J₁ ∩ J₂ supports p, and, by definition, τ₁ and τ₂ agree in J₁ ∩ J₂; the desired equality follows from Lemma 6.11.

If τ itself happens to be finite, then the finite support J₀ of p can be chosen so as to be a support of τ at the same time. If that is done, then τ₀ = τ, and it follows that is indeed an extension of S.

If p₁ and p₂ are in A, then a finite set J₀ can be found that supports them both, and, consequently, supports their supremum as well. It follows that

The proof that preserves complementation is similar, but even easier. In other words, each is a Boolean endomorphism of A, and the proof of (i) is complete.

(ii) If p A and if J₀ is a finite support of p, it is natural to try to define , for each subset J of I, as . In order to justify this, however, we must show first that is the same no matter which support J₀ of p is used. In other words, we must prove that if both J₁ and J₂ are finite supports of p, then . Since, by Lemma 6.7, (J₁ ∩ J₂) supports p, the desired result follows, via Lemma 6.9, from the fact that both and are equal to .

In J happens to be finite, then the finite support J₀ of p can be chosen so that J ⊂ J₀. If that is done, then J ∩ J₀ = J, and it follows that is indeed an extension of .

Since Ø supports 0, it follows that , so that is normalized. To prove that is increasing, we merely note that . The proof of quasi - multiplicativity is, naturally, the hardest. Given p and q, we first find a finite set J₀ that supports them both. Next we note that J₀ supports (recall that and apply Lemma 6.10 and Lemma 6.7), and that J₀ supports (by Lemma 6.8). Quasi - multiplicativity now follows from the computation:

In other words, each is a quantifier on A, and the proof of (ii) is complete.

(iii) We must now prove that A together with and is a locally finite I-algebra. Local finiteness is immediate from (Q₇) and Lemma 6.15; it remains to prove that and satisfy (Ρ₁)-(Ρ₆).

(P₁) Immediate from (Q₁) and (i).

(P₂) Suppose that σ and τ are transformations on I, that p A, and that J₀ and K₀ are finite supports of p and of , respectively. (If we knew that Lemma 6.14 is valid for quasi - polyadic algebras, we could take K₀ = τJ₀.) If, as before, τ₀ί = τί when i J₀ and τ₀i = i otherwise, and if σ₀j = σj when j K₀ ∪ τJ₀ and σ₀j = j otherwise, then and . Since σ₀τ₀ is a finite transformation, and since σ₀τ₀ί = στί when i J₀, it follows easily that .

(P₃) Immediate from (Q₃) and (ii).

(P₄) If J and K are subsets of I, if p A, and if J₀ is a finite support of p, then J₀ supports (by Lemma 6.10 and Lemma 6.7, since . It follows that

(P₅) If σ and τ are transformations on I, if J ⊂ I, and if σ = τ outside J, it is to be proved that for each p in A. If J₀ is a finite support of p, and if σ₀ and τ₀ are defined as usual (σ₀ = σ and τ₀ = τ in J₀, and σ₀ = τ₀ = δ outside J₀), then σ₀ = τ₀ outside J∩J₀ and therefore

(P₆) This is the combinatorially most difficult part of the proof; it will be presented in three steps. We are given a transformation τ on I and a subset J of I, such that τ is one-to-one on τ⁻¹J. We are to prove that .

(a) Assume first that J is finite. If p A, write ; note that since τ is one-to-one on τ^–1J, it follows that τ^–1J is finite. Let J₀ be a finite support of p; then J₀ supports q. If σ is the transformation that agrees with τ on J₀ ∪ J ∪ τ⁻¹J and with δ outside that set, then σ is a finite transformation on I. The transformation σ is such that σ⁻¹J = τ⁻¹J. Indeed, if i τ⁻¹J then σi = τi J, so that i σ^–1J; this proves that τ^–1J ⊂ σ^–1J. If j σ^–1J, then (since σ always agrees with either τ or δ) either σj = j σ^–1J or σj = τj J. In the first case τj = j; (since σ and τ agree on J), so that, in either case, τj = σj, and therefore j σ⁻¹J; this proves that σ⁻¹J ⊂ τ⁻¹J

Since σ⁻¹J = τ⁻¹J and since σ = τ οn τ^–1J, it follows that σ is one-to-one on σ⁻¹J, Consequently

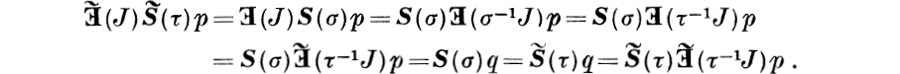
(b) Assume next that p A, , and ; let J₀ be a simultaneous finite support of both p and . It follows that J₀ – J is a simultaneous support of p and , and we may therefore assume, without any loss of generality, that J₀ is disjoint from J.

If K = τ⁻¹J ∩ J₀, then . If Η = τΚ, then, clearly, H ⊂ J and Κ = τ⁻¹Η (here is where the assumed one-to-one property of τ is used). Since, moreover, J₀ is finite, it follows that H and K are finite. Hence

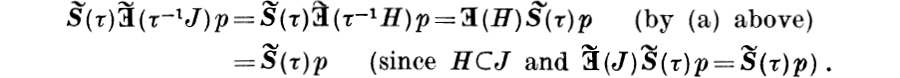
Since we have also assumed that , it follows that, in this case,

as desired.

(c) If p A, let J₀ be a simultaneous finite support of p and . If J₁ = J ∩ J₀ and J₂ = J –J₀, then J = J₁ ∪ J₂, the set J₁ is finite, and the set J₂ is such that and (since J₂ is disjoint from J₀). Moreover, since J₁ and J₂ are subsets of J, the transformation τ is one-to-one on τ⁻¹J₁ and on τ⁻¹J₂. It follows that

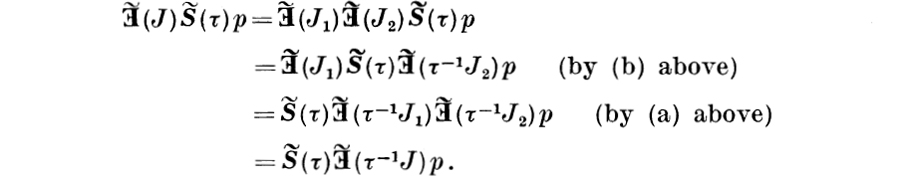
The proof of Theorem 7.7 is complete.

§ 8. Algebraic theory

The elementary algebraic theory of polyadic algebras is an easy part of universal algebra. The basic concepts are, as always, those of subalgebra, homomorphism, and ideal.

A subset B of a polyadic algebra A is a (polyadic) subalgebra of A if it is a Boolean subalgebra of A and if it is a polyadic algebra with respect to the operator mappings of A. More precisely, if A is an I-algebra and if B is a Boolean subalgebra of A such that, for all p in B, S(τ)p B whenever τ is a transformation on I, and B whenever J is a subset of I, then the I-algebra B is called a polyadic subalgebra of A. In the locally finite case this definition can be improved in two distinct directions. It follows from Theorem 5.5 that a Boolean subalgebra B of an I-algebra A is a polyadic subalgebra of A if and only if S(σ)p B whenever p B and σ is a substitution in I. It follows from Lemma 6.16 that a Boolean subalgebra B of an J-algebra A is a polyadic subalgebra of A if and only if, for all p in B, S(r)p e B whenever τ is a finite transformation on I and whenever J is a finite subset of I. We observe that every polyadic subalgebra of an I-algebra is itself an I - algebra. If A is an I - algebra and if I₀ is a subset of I, then, by appropriately restricting the operator mappings of A to I₀ we obtain an I₀-algebra, but that I₀-algebra is not a polyadic subalgebra of A. We observe also that every polyadic subalgebra of a locally finite algebra is locally finite.

If A and B are polyadic algebras (with the same set I of variables), a (polyadic) homomorphism is a mapping f from A into B such that f is a Boolean homomorphism and such that, for all p in A, fS(τ)p = S(τ)fp whenever τ is a transformation on I and whenever J is a subset of I. In the locally finite case this definition can be improved, just as for subalgebras, in two distinct directions. A Boolean homomorphism f from A into B is a polyadic homomorphism if and only if fS(σ)p = S(σ)fp whenever p A and σ is a substitution in I. Alternatively, a Boolean homomorphism f from A into B is a polyadic homomorphism if and only if, for all p in A, fS(τ)p = S(τ)fp whenever τ is a finite transformation on I and whenever J is a finite subset of I. We observe that the concept of a polyadic homomor-phism is defined only between algebras with the same set of variables. A polyadic algebra is, after all, a Boolean algebra with operators, and it is quite natural to insist that a homomorphism preserve the operator structure. The situation is analogous to the one encountered in the theory of groups with operators. We observe also that a homomorphism preserves supports and hence that every homomorphic image of a locally finite algebra is locally finite.

If A is an I-algebra, a (polyadic) ideal in A is a Boolean ideal M in A such that, for all p in M, S(τ)p M whenever τ is a transformation on I, and M whenever J is a subset of I. In the locally finite case a Boolean ideal M is a polyadic ideal if and only if S(σ)p M whenever p M and σ is a substitution in I. Alternatively, a Boolean ideal M is a polyadic ideal if and only if, for all p in M, S(τ)p M whenever τ is a finite transformation on I, and whenever J is a finite subset of I. For polyadic ideals (but not for subalgebras and homomorphisms) there is an even simpler characterization that is frequently very useful.

(8.1) LEMMA. A Boolean ideal M in A is a polyadic ideal if and only if whenever p M.

Proof. ïïalf of the assertion is trivial; if M is a polyadic ideal, then M is invariant under all the quantifiers of A, and, in particular, under . Suppose, to prove the converse, that M is a Boolean ideal invariant under . If p M and if τ is a transformation on I, then the inequality , together with the fact that S(τ) is a Boolean endomorphism of A, implies that . Since, trivially, τ = δ outside I, it follows from (P₅) and (P₁) that , and hence that . Since and since M is a Boolean ideal, we conclude that S(τ)p M. Similarly, if p M and J ⊂ I, then , and therefore the proof of the lemma is complete.

If p A and if J is a finite subset of I that supports p, then for all K. (If all the variables that p depends on are quantified out, the result is invariant under all further quantification.) The quantifier-invariant element thus associated with p will be called the logical closure of p according to an equivalent definition the logical closure of p is the element . In accordance with this definition, we shall speak also of the closed elements of A, meaning thereby the elements invariant under , or, equivalently, the range of the quantifier . The concept of logical closure as here defined is not quite the same as the concept usually covered by the same term. The usual closure is essentially the dual of the present one; it is obtained by prefixing an adequate supply of universal quantifiers (instead of existential ones). The present terminology seems preferable because of its harmony with the theory of closure algebras: an existential quantifier is, after all, a closure operation, whereas its dual, a universal quantifier, is not.

If A is an I-algebra and if J is a subset of I, then the Boolean algebra A, with the quantifier , is a monadic algebra that we shall denote by A(J). With this notation the result of Lemma 8.1 can be stated in the following form: a Boolean ideal M in A is a polyadic ideal in A if and only if it is a monadic ideal in A (I). In these terms we can also give a useful characterization of simple polyadic algebras. By definition, a polyadic algebra A is simple if {0} is the only proper polyadic ideal in A,

(8.2) LEMMA. An I-algebra A is simple if and only if the operation of forming logical closure is a simple quantifier (i. e., whenever p ≠ 0), or, equivalently, if and only if the monadic algebra A (I) is simple.

Proof. The equivalence of the simplicity of the polyadic algebra A with that of the monadic algebra A (I) follows immediately from Lemma 8.1; the characterization in terms of is a consequence of the corresponding monadic result (1.6).

If f is a polyadic homomorphism with domain A, then its kernel, i. e., the set M = {p: fp = 0}, is a polyadic ideal. Since f is in particular a Boolean homomorphism, so that f1 = 1, it follows that this polyadic ideal is proper (i. e., Μ ≠ Α). The homomorphism theorem for polyadic algebras asserts that, conversely, every proper ideal is a kernel. Suppose, indeed, that A is an I-algebra and that M is a proper polyadic ideal in A. Let B be the Boolean quotient algebra A/M and let f be the corresponding natural Boolean homomorphism from A onto B. We proceed to show that there is a unique, natural way of converting B into an I-algebra so that f becomes a polyadic homomorphism (with kernel M. for this purpose it is convenient to make use of the remark following Theorem 5.5. To define S(σ)q, where q B and σ is a substitution in I, find p in A so that fp = q and write S(σ)q = fS(σ)p. It is to be proved, of course, that this definition is unambiguous, i. e., that if fp₁ = fp₂, then fS(σ)p₁ = fS(σ)p₂. Equivalently, it is to be proved that if p₁ + p₂ M, then S(σ)p₁ + S(σ)p₂ M. To prove this, write σ = τχ(J), where τ is a transformation on I and J is a subset of I. It follows that

(since S(τ) is a Boolean endomorphism of A) and hence that

(by (1.5), together with the fact that a Boolean endomorphism preserves order). Since S(τ)(J)(p₁ + p₂) belongs to M along with p₁+ p₂, and since M contains all elements smaller than any of its elements, it follows, as desired, that M contains S(σ)p₁ + S(σ)p₂. A routine verification shows that the mapping S from substitutions in I into operators on B satisfies the conditions described in the remark following Theorem 5.5, so that B is an I-algebra, the quotient algebra of A modulo the ideal M.

Caution: the homomorphism theorem, together with Lemma 8.1, has the effect of making a false assertion seem plausible. If f is a polyadic homomorphism from A into B with kernel M, then, of course, f is in particular a monadic homomorphism from A (I) into B(I) with kernel M. If, conversely, f is a monadic homomorphism from A (I) into B(I) with kernel M, then, in view of Lemma 8.1, M is a polyadic ideal in A, and it might seem plausible to conjecture that f must be a polyadic homomorphism. The conjecture is false; finite, dyadic counter examples are easily constructed.

A polyadic ideal is maximal if it is a proper ideal that is not a proper subset of any other proper ideal. The connection between maximal ideals and simple algebras is an elementary part of universal algebra: the kernel of a homomorphism is a maximal ideal if and only if its range is a simple algebra. A polyadic algebra is semisimple if the intersection of all maximal ideals in it is {0}.

§ 9. Logics

The concepts of simplicity and semisimplicity play a central role in the theories of Boolean algebras and monadic algebras. Their relevance in the theory of polyadic algebras can be established by almost exactly the same argument as was used in sections 5, 6, and 7 of [2]; cf. also sections 4 and 5 of [1]. For the sake of completeness we proceed to review the most important points of that argument.

A polyadic logic is a pair (A, M), where A is a polyadic algebra and M is a polyadic ideal in A. If, heuristically, the elements of A are thought of as propositional functions, then the elements of M are to be thought of as the refutable ones among them. A moment’s thought shows that, from the point of view of logic, it is reasonable that the set of refutable elements form a polyadic ideal. Indeed, just as in the propositional calculus (i. e., the theory of Boolean logics) that set should form a Boolean ideal. That it should also form a polyadic ideal comes from the intuitively obvious requirement that if a propositional function p is refutable, then so also is every propositional function obtained from p by existential quantifications and substitutions of variables.

Within the theory of polyadic logics almost all logical terms are translatable into algebraic language. Thus, for example, a polyadic logic (A, M) is called simply consistent, or, simply, consistent, if M is a proper ideal in A (i. e., if not everything is refutable), and a polyadic logic (A, M) is called simply complete, or, simply, complete if either M = A or else M is a maximal ideal in A. We note that (A, M) is consistent if and only if for no element p of A do both p and p′ belong to M. (Indeed, if p and p′ are both in M, then so also is 1, since 1 = p ∨ p′, and therefore M = A; if, on the other hand, M = A, then 1 M and therefore there is at least one p, namely 0, such that both p and p′ are in M.) This formulation of the definition of consistency is probably the one that accords most closely with our intuitive ideas on the subject.

The algebraic properties of a consistent polyadic logic (A, M) are most conveniently studied in terms of the associated quotient algebra A/M. The concept of simple completeness, in particular, has an easy formulation in these terms.

(9.1) LEMMA. A consistent polyadic logic (A, M) is simply complete if and only if the polyadic algebra A/M is simple.

The proof of this lemma is an immediate consequence of the relation between simple algebras and maximal ideals. With the aid of this lemma the concept of simple completeness can be reformulated in still other ways that bring it closer to our intuitive notions. We note, first of all, that the set B of all closed elements in an I-algebra A is a Boolean subalgebra of A-, this follows from the fact that B is the range of the quantifier . If, moreover, M is a polyadic ideal in A, then N = B ∩ M is a Boolean ideal in B. We assert now that a consistent polyadic logic (A, M) is simply complete if and only if N is a maximal ideal in B. Indeed, let f be the natural homomorphism from A onto A/M. If A/M is simple, and if p B, then p = and therefore fp = f (I)p = fp. Since (cf. Lemma 8.2) is a simple quantifier on A/M, it follows that either fp = 0 or fp = 1. If fp = 0, then p M, and if fp = 1, then p′ M. In other words, if p is an arbitrary element of B, then either p N or p′ N; this proves that N is a maximal ideal in B. If, conversely, N is a maximal ideal in B, and if p A, then B and therefore either p N or ((I)p)′ N. Since f (I)p = fp_, it follows that either fp = 0 or (I)fp = l, i. e., that is a simple quantifier on A/M, and hence that A/M is simple.

It follows from the result (or, more directly, from the argument) of the preceding paragraph that a polyadic logic (A, M) is simply complete if and only if, for each closed p in A, either p M or p′ M. In logical terms, therefore, simple completeness means that, for every (closed) proposition p, either p or its negation is refutable (and therefore either p or its negation is provable). We see thus that the celebrated Gödel incompleteness theorem asserts that certain important polyadic logics are either (simply) incomplete or else (simply) inconsistent. In other words, if (A, M) is one of those logics, then either the ideal M is very large (M = A) or else it is rather small (non-maximal). In a later paper of this series we shall study the exact class of logics to which this assertion applies; most of the remainder of this paper is devoted to the problems centering around the concept of semisimplicity.

Just as simplicity turns out to be the algebraic counterpart of simple completeness, semisimplicity is the algebraic counterpart of another logical concept, called semantic completeness. The proof of this assertion is, however, quite deep; a significant part of the structure theory of polyadic algebras has to be developed first.

A model is an O-valued functional polyadic algebra. This definition is the same as the one given in [1]; it differs, in the monadic case, from the definition given in [2], where a model was defined not as an algebra but as a logic. Since the reduction of consistent logics to algebras is an easy step, the present, simpler definition seems to be more appropriate. If A is an O-valued functional algebra with domain X, then usually the set X itself is called a model. These differences in terminology are not significant; each author’s choice among them is dictated merely by which aspect of the concept he wishes to emphasize.

Once the concept of a model is defined, the other so-called “semantic” concepts of logic are easily translated into algebraic form. Thus, an interpretation of a polyadic algebra A is a homomorphism from A into a model; since the range of such a homomorphism is a subalgebra of the model and since a subalgebra of a model is itself a model, we could also have defined an interpretation as a homomorphism onto a model. An element p of A is false in an interpretation f if fp = 0, i. e., if p belongs to the kernel of f; an element p is universally invalid (or contravalid) if it is false in every interpretation. The algebra A is semantically complete if 0 is the only universally invalid element. The justification of this terminology is the same for polyadic algebras as for monadic algebras; cf. section 6 of [2].

If we knew that (a) every model is simple, and (b) every simple algebra is (isomorphic to) a model, then the class of all kernels of interpretations would coincide with the class of all maximal ideals, and we could conclude that a polyadic algebra is semantically complete if and only if it is semisimple. In fact, (a) is true, and (b) is true in all important cases, but the clarification and proof of the latter assertion will have to be postponed for a while. We shall conclude our discussion of these generalities by proving (a) and by proving a result that, in the presence of (b), is the algebraic version of Gödel’s completeness theorem.

(9.2) THEOREM. Every model is simple.

Proof. If A is an O-valued functional polyadic algebra, then

whenever p A and x X^I. Since xI_*y holds for every y, it follows that the value of at each x in X^I is the supremum of the range of p. In other words, the monadic algebra A (I) is an O-valued functional monadic algebra and therefore (1.8) A(I) is simple. The desired result follows from Lemma 8.2.

(9.3) THEOREM. Every polyadic algebra is semisimple.

Proof. Suppose that A is an I- algebra and that p is a non-zero element of A. By the semisimplicity of monadic algebras (1.7) there exists a maximal monadic ideal M in A (I) not containing p. By Lemma 8.1, M is a polyadic ideal in A, and, moreover, a maximal one, for any polyadic ideal including M would also be a monadic ideal (in A(I)) including the maximal monadic ideal M. This completes the proof.

§ 10. Functional representation

Since the only concrete examples of polyadic algebras at our disposal are the functional polyadic algebras, it is natural to conjecture that they are the only ones that exist. The conjecture says, in other words, that if A is an arbitrary I-algebra, then it is possible to construct a set X and a Boolean algebra B so that A is isomorphic to a functional polyadic algebra of functions from X^I into B. The main purpose of this section is to prove that the conjecture is true at least for the polyadic algebras of greatest interest in logic.

We begin by introducing some terminology and notation to be used in connection with transformations on I. If a transformation τ maps I one-to-one onto itself, we shall say that τ is a permutation; if, on the other hand, τ² = τ, we shall say that ris a retraction. If i and j are in I, the transformation τ for which τi = j, τj = i, and τk = k whenever k is distinct from both i and j, will be denoted by (i, j); any such transformation will be called a transposition. If τ = (i,j) is a transposition, the corresponding endomorphism S(τ) will be denoted by S(i,j). If i and j are in I, the transformation σ for which σi = j, σj = j, and σk = k whenever k is distinct from both i and j will be denoted by (i/j); any such transformation will be called a replacement. If τ = (i/j) is a replacement, the corresponding endomorphism S(τ) will be denoted by S(i/j). Clearly every transposition is a finite permutation and every replacement is a finite retraction.

With every subset J of I there is associated a binary relation J_* between transformations on I; the relation J_* is, by definition, such that

This concept is, as the notation indicates, a special case of the one defined by (2.3); the specialization is obtained by choosing the set X to be the same as I.

(10.1) THEOREM. If A is a locally finite I-algebra of infinite degree (i. e., if I is infinite), then

whenever p A, J ⊂ I, and τ is a transformation on I; the supremum indicated in (10.2) is extended over all those transformations σ on I for which σJ_*τ.

Remark, (a) It is, of course, not being assumed that A is a complete Boolean algebra, and, consequently, the supremum in (10.2) does not automatically exist. It is intended to be a part of the conclusion of the theorem that the supremum does exist.

(b) If τ = δ, (10.2) becomes

Warning: (10.2) cannot be recaptured from (10.3) simply by applying S(τ). The trouble is that even if the algebraic hurdle were conquered, i. e., even if we had already shown that , we would still have to prove that that is the right thing to show. There is no reason to assume that S(τ), which, being an endomorphism of A, preserves the finite Boolean operations, necessarily preserves the infinite Boolean operations also.

(We recall that stands for ; similarly i_* stands for {i}_*.) Now if σi_*δ, then σ must have the form (i/j) for some variable j; consequently (10.4) may be rewritten in the form

In this special form the result is due to Easiowa and Sikorski [5]. Equation (10.5) acquires intuitive significance if we (illegally) verbalize it by equating “p holds for some i” with “the result of replacing i by j in p holds for some j”.

(d) Finally we observe that the assumption that I be infinite cannot be omitted. Suppose, in fact, that I = {0,1}, and that the algebra A consists of the four elements {0,p,p′,1}. The actions of the transformations on A are uniquely determined by the equations S(0/l)p = S(l/0)p = 0 and S(0,1)p = p. If the quantifiers , , and are all required to coincide with the simple quantifier on A, then, with respect to this system of operators, A becomes an I- algebra. The relation (10.5), which in this case reduces to , does not hold; indeed and p∨S(0/1)p = p.

Proof. If σJ_*τ, then (by (P₅)). This observation proves half the theorem. What must now be proved is the assertion

(10.6) if whenever σJ_*τ, then .

Whenever the implication (10.6) holds for some triple (p,J,τ), then the equation (10.2) holds for that triple. Belying on this comment, we proceed to prove (10.6) in three successive stages of generality.

(I) τ and J are both finite. Let K be a set having the same number of elements as J, say J = {j₁,…,j_n}, K = {k₁,..._, k_n}, selected so that it is far from the scene of action as far as p, q, τ, and J are concerned. Precisely speaking, we require that , τ = δ on K and τ⁻¹Κ = Κ, and K is disjoint from J. Since I is infinite, a subset K of I can be found satisfying all these conditions.

We introduce the auxiliary transformations π, and σ defined by

We note that if j ∉ J, then σj = τj; in other words σJ_*τ. Since and π = outside K, it follows from Lemma 6.11 that

similarly, since and π = δ outside J ∪ K, we have

The proof of (I) is now completed as follows:

(II) τ is finite. Let K be a cofinite set such that ; it follows that . Since J – K is finite, it follows from (I) that

If σ(J – K)_*τ, then, a fortiori, σJ_*τ, and therefore . It follows that, in this case also, , as desired.

(III) The general case will be reduced to (II) pretty much the same way as (II) was reduced to (I). First we find a finite set K that supports p (and therefore also supports , cf. Lemma 6.10), and we define the (finite) transformation τ₀ to be τ in K and δ outside K. It follows (cf. Lemma 6.11) that S(τ)p = S(τ₀)p, and, more relevantly, . Hence, by (II), .

Now we maintain that whenever σ₀J_*τ₀. If this is admitted for a moment, then it follows from the preceding paragraph that , and, therefore, the proof is complete. To prove the assertion we define a transformation σ (not necessarily finite) as follows: σ = σ₀ in K and σ = τ outside K. It follows that S(σ)p = S(σ₀)p. If i I –J, then either i K, in which case σί = σ₀i (by the definition of σ) = τ₀i (by the assumption on σ₀) = τi (by the definition of τ₀), or I ∉ K, in which case σi = τi directly from the definition of σ. In other words σJ_*τ, and therefore (by the assumption on q) . The last two results imply that , and, therefore, complete the proof of the theorem.

We come now to the main theorem of this section. The result is powerful, and it looks even more powerful than it is. On first glance it looks as if it could single-handedly solve all the interesting problems about polyadic algebras. It cannot, but it is good to know anyway.

(10.9) THEOREM. Every locally finite polyadic algebra of infinite degree is isomorphic to a functional polyadic algebra whose domain has the same cardinal member as the set of variables.

Proof. Let A be an I-algebra with an infinite I; we are to manufacture a Boolean algebra B, a set X, and a one-to-one mapping f so that f maps A onto an appropriate class of functions from X^I into B in such a way that the polyadic operations are preserved. The proper choice of B and X looks deceptively simple; we write B = A and X = I. The choice is deceptively simple because the very fact that no complicated constructions were used to manufacture B and X will make for notational collisions. The major collision occurs in the consideration of X^I. An element of X^I is a function from I into X. Hence, in the present instance, an element of X^I is a function from I into itself, i. e., a transformation on I. The transformation point of view will be relevant in what follows; we shall call an object a point of X^I or a transformation on I, depending on which of its two roles needs to be emphasized at the moment.

If σ is a transformation on I and if τ X^I, what does σ_*τ mean? It means the element of X^I whose value at each i in I is τ(σί), and hence the element τσ; in other words σ_*τ = τσ.

We are now ready to define the mapping f (which will turn out to be the desired polyadic isomorphism) that associates a function from X^I into B (i. e., into A) with each element p of A. If τ X^I, we define to be S(τ)p; we proceed to investigate the properties of the mapping . The easiest thing to prove is that f is a Boolean isomorphism. If p A, , and τ X^I, then fp′(τ) = S(τ)p′ = (S(τ)p)′ (since S(τ) is a Boolean endomorphism) (by the definition of complementation in functional algebras), so that fp′ = (fp)′. If also q A and , then , so that f(p ∨ q) = fp ∨fq. If, finally, , then, in particular, ; it follows that p = S(δ)p = 0, so that f is indeed a Boolean isomorphism.

It must now be proved that (i) f (A) is a functional polyadic algebra and that (ii) f is a polyadic isomorphism between A and f (A). The first of these assertions means that (i)′ if and if σ is a transformation on I, then (cf. (2.2)), and (i)″ if and J is a subset of I, then exists and belongs to f(A) (cf. (2.4)). The second assertion means, of course, that, under the same assumptions on , σ, and J, (ii)′ fS(σ)p = S(σ)fp and (ii)″ . It turns out that the proofs of these two assertions (or, rather, two pairs of assertions) need not be considered separately. The fact that S(σ)fp f (A) is most easily proved by showing that S(σ)fp = fS(σ)p, and, similarly, both the existence and location of are settled by proving that the pertinent supremum is equal to .

Write q = S(σ)p, , and ; let τ be an arbitrary element of X^I and write π = τσ. It is to be proved that . The proof consists of the following computation:

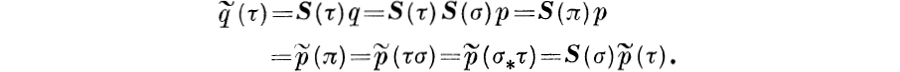
The result concerning quantification is obtained similarly. Write , , and . Then . Using Theorem 10.1 (here is where the assumption of infinite degree comes in), we conclude that

The proof of Theorem 10.1 is complete. Methods similar to the ones used in the proof can be found in the work of Henkin [3] and, more explicitly, in the work of Easiowa and Sikorski [5].

§ 11. Dilations

If I and I⁺ are sets such that I ⊂ I⁺, then there is a natural way of associating a transformation τ⁺ on I⁺ with every transformation τ on I; the transformation τ⁺ is defined by