It follows immediately from this definition that the mapping τ → τ⁺ is a homomorphism from the semigroup of all transformations on I into the semigroup of all transformations on I⁺, i. e., that

whenever σ and τ are transformations on I. We observe explicitly that the image δ⁺ of the identity transformation δ on I is the identity transformation on I⁺, and we note also that if a subset J of I supports τ, then J supports τ⁺ also. It follows in particular that if τ is finite, then the same is true of τ⁺.

        Suppose now that (A⁺, Z⁺, S⁺, ) is a polyadic algebra and write A for the range of the quantifier . (Equivalently, A consists of all the elements of A⁺ independent of I⁺ –I.) Clearly A is a Boolean subalgebra of A⁺. More than this is true: the Boolean algebra A can be converted into an I-algebra in a simple and canonical manner. If τ is a transformation on I, we write

and if J is a subset of I, we write

for every element p of A, Since (τ⁺)⁻¹(I⁺ –I) = I⁺ –I, and since τ⁺ is one-to-one on I⁺ –I, and since , it follows that

Since, even easier,

we may conclude that the algebra A is closed under the operations S(τ) and defined in (11.3) and (11.4). It is easy to verify that (A, I, S, ) is a polyadic algebra. Indeed, (P₁) follows from the fact that δ⁺ is the identity transformation on I⁺, and (P₂) follows from the multiplicativity relation (11.2). Since in the passage from to nothing changes, (P₃) and (P₄) are automatic. The condition (P₅) follows from the fact that if σ = τ outside J, then σ⁺ = τ⁺ outside J, and, similarly, (P₆) follows from the fact that if τ is one-to-one on τ^–1J, then τ⁺ is one-to-one on (τ⁺)^–1J and (τ⁺)^–1J = τ^–1J.

        We shall describe the relation between the I-algebra A and the I⁺- algebra A⁺ discussed in the preceding paragraph by saying that A is a compression of A⁺ and A⁺ is a dilation of A. More explicitly, if I and I⁺ are sets such that I ⊂ I⁺, then to say that an I⁺-algebra A⁺ is a dilation of an I-algebra A means that A consists of all the elements of A⁺ independent of I⁺ –I and that the operator mappings S and of A are related to the operator mappings S⁺ and of A⁺ by the equations (11.3) and (11.4). It follows from this definition that if A⁺ is locally finite, then the same is true of A. Indeed, if p A, then, since p A⁺ and A⁺ is locally finite, there exists a cofinite subset J⁺ of I⁺ such that . If we write J = J⁺ ∩ I, then J is a cofinite subset of I and (since ; this proves, as desired, that every element of A has finite support.

        The process of going from an algebra to one of its dilations might be thought of as the adjunction of new variables. It is not at all obvious that new variables can always be adjoined to an arbitrary polyadic algebra; this section is devoted to the discussion of the most important special cases of the problem. We shall discuss, in particular, certain functional algebras with value algebra B, say, and domain X. In this connection, and, in fact, in most discussions of the theory of dilations, it is useful to make a distinction between the operator mappings on I-algebras and those on I⁺-algebras; we shall always denote the former by S and , as before, and the latter by S⁺ and . For transformations and for subsets we shall continue to use familiar symbols (such as σ, τ, J, and K); a symbol such as τ⁺ will be used only in its special meaning defined by (11.1).

(11.5) LEMMA. If A is a B-valued I-algebra over X and if I ⊂ I⁺, then there exists a mapping f from A onto a Boolean algebra of functions from X^I+ into B such that (i) f is a Boolean isomorphism between A and f (A), (ii) fp is independent of I⁺ –I for all p in A, (iii) fS(τ)p = S⁺(τ⁺)fp whenever τ is a transformation on I and p A, and (iv) whenever J is a subset of I and p A.

        Remark. The concept of independence referred to in (ii) is to be interpreted in the sense of the functional independence defined at the beginning of § 5. The operators S⁺(τ⁺) in (iii) and in (iv) are to be interpreted in the functional sense defined in (2.2) and (2.4). The assertion of the equation in (iv) is intended to imply that its right term exists for every subset J of I and every element p of A.

        Proof. Let ϕ be the natural (projection) mapping from X^I+ onto X¹, i. e., if x⁺ X^I+, then for all i in I. We define the mapping f by writing (fp)(x⁺) = p(ϕx⁺) for all x⁺ in X^I+. The fact that f is a Boloean homomorphism follows immediately from the fact that the Boolean operations in algebras of functions are defined pointwise. Since, moreover, ϕ is onto, it follows that the kernel of f is trivial and hence that f is one-to-one. This proves (i). Suppose next that x⁺ and y⁺ are points of X^I+ such that x⁺(I⁺ –I)_*y⁺, i. e., such that whenever i I. It follows that ϕx⁺ = ϕy⁺ and hence that fp(x⁺) = fp(y⁺) for all p in A; this proves (ii). If τ is a transformation on I, then and whenever x⁺ X^I+ and i I. It follows that and hence that

for all p in A; this proves (iii). We observe finally that, because of (ii),

whenever x⁺ X^I+ and J ⊂ I. This implies that exists and is equal to . Thus (iv) is proved and the proof of the lemma is complete.

(11.6) LEMMA. If A is a locally finite, B-valued, functional I-algebra of infinite degree over X, and if I⁺ is a set including I and containing exactly one new element, I⁺ = I ∪{i⁺}, then there exists a locally finite B-valued, functional I⁺-algebra A⁺ over X such that A is isomorphic to a compression of A⁺.

        Remark. The lemma is true for every set I⁺ including I and the idea of the proof of the more general assertion is the same. Since, however, the notation and the details in the general case are monstrously complicated, it is preferable to state and prove the lemma in the special case, and then, if necessary in the applications, apply it many times. This process of repeated application leads in general to transfinite induction, whereas an application of the general form of the lemma does not. Thus the facts are that the transfinite inductions that will be occasionally mentioned below are avoidable, but the price for avoiding them is a significant loss in perspicuity.

        Proof. By Lemma 11.5, identifying A with its image under the mapping there described, we may and do assume that the elements of A are functions (independent of i⁺) from X^I+ into B. Lemma 11.5 guarantees that if S⁺ and denote the functional operations defined for functions from X^I+ into B by (2.2) and (2.4), and if S and are defined for A by (11.3) and (11.4), then (A, I, S, ) is a polyadic algebra isomorphic to the originally given functional algebra. (The elements of A are now not functions from X^I into B, but functions from X^I+ into B, and, consequently, we are not allowed to say that in its present form A is a functional I-algebra.)

        We are now ready to define the algebra A⁺ that will turn out to be the desired dilation of A. The elements of A⁺ are, by definition, all functions of the form S⁺(i/i⁺)p, where i I and p A. It is clear that A ⊂ A⁺ (choose i so that p is independent of it). What we must show is that (i) A⁺ is a Boolean algebra, (ii) if p⁺ A⁺ and if τ is a finite transformation on I⁺, then S⁺(τ)p⁺ A⁺, (iii) if p⁺ A⁺ and if J is a finite subset of I⁺, then exists and belongs to A⁺, (iv) if p⁺ A⁺, then there exists a cofinite subset J of I⁺ such that p⁺ is independent of J, and (v) if p⁺ A⁺ and p⁺ is independent of i⁺, then p⁺ A. Since every element of A is independent of i⁺, (v) implies that A consists exactly of all the elements of A⁺ independent of i⁺. Hence, as soon as we know that A⁺ is an I⁺- algebra, we can deduce from (v) that A is a compression of A⁺. The proof that A⁺ is a locally finite functional I⁺-algebra is an easy consequence of (i)-(iv) (cf. also Lemma 6.16 and Theorem 7.7). We take this easy argument for granted and proceed to complete the proof of the lemma by establishing (i)-(v).

        We begin with an auxiliary comment. The representation of an element of A⁺ in the form S⁺(i/i⁺)p (as described in the preceding paragraph) is far from unique. Indeed, if j I, if p is independent of j, and if q = S(i/j)p, then

(Warning: since we do not as yet know that A⁺ is a polyadic algebra, we are not allowed to apply to A⁺ our results about polyadic algebras. Thus the last step in (11.7), i. e., the conclusion that since p is independent of j therefore S⁺(j/i⁺)p = p, is a consequence not of our algebraic results but of the elementary geometric facts about Cartesian products that were the motivating background of our algebraic considerations all along. Similar warnings apply on a few other occasions in the course of this proof.)

        (i) If p⁺ A⁺, say p⁺ = S⁺(i/i⁺)p with i I and p A, then (p⁺)′ = S⁺(i/i⁺)p′; this proves that A⁺ is closed under complementation. Suppose next that p⁺ and q⁺ are in A⁺, so that p⁺ = S⁺(i/i⁺)p and q⁺ = S⁺(j/i⁺)q, with i and j in I, and p and q in A Let k be an element of I such that both p and q are independent of k. (The existence of k follows from the facts that A is locally finite and I is infinite.) By the preceding paragraph we may assume that both i and j are equal to &. Since now p⁺ = S⁺(k/i⁺)p and q⁺ = S⁺(k/i⁺)q (with not necessarily the same p and q as before), it follows that p⁺ ∨ q⁺ = S⁺(k/i⁺)(p ∨ q); this proves that A⁺ is closed under the formation of suprema.

        (ii) To prove that A⁺ is closed under the action of S⁺(τ) for all finite transformations τ on I⁺, we first show that if τ is a finite transformation on I⁺, then S⁺(τ)p A⁺ for every p in A. In the proof of this assertion we may assume that τi⁺ = i⁺, for (since p is independent of i⁺) we can always change τ so as to force it to have this property without changing S⁺(τ)p. Let i be an element of I such that p is independent of i and such that τ^–1{i} = {i}. If σ is the transformation on I (not I⁺) such that σj = i when τj = i⁺ and σj = τj otherwise, then τ = (i/i⁺)σ outside i; it follows that

The general case is easy now: if τ is a finite transformation on I⁺, then S⁺(τ)S⁺(i/i⁺)p A⁺ whenever i I and p A simply because τ(i/i⁺) is a finite transformation on I⁺.

        (iii) Suppose first that J is a finite subset of I and that p⁺ A⁺, so that p⁺ = S⁺(i/i⁺)p with i l and p A. Since (i/i⁺)⁻¹J = J – {i}, it follows that (i/i⁺) is one-to-one (in fact, equal to the identity) on (i/i⁺)⁻¹J. Since exists and belongs to A, it follows from Lemma 4.8 that exists, is equal to , and, consequently, belongs to A⁺. Suppose now that p⁺ A⁺, so that, as usual p⁺ = S⁺(i/i⁺)p with i I and p A. Since (i/i⁺) = (i,i⁺) outside i⁺ and since p is independent of i⁺, it follows that p⁺ = S⁺(i,i⁺)p Since, moreover, (i,i⁺)⁻¹{i⁺} = {i}, and since exists and belongs to A, it follows as before that exists and belongs to A⁺. If J is an arbitrary finite subset of I⁺, write J₀ = J ∩ I and J₁ = J – I. The fact that exists and belongs to A⁺ whenever p⁺ A⁺ follows from the preceding two special cases of this assertion together with Lemma 4.2.

        (iv) If p⁺ A⁺, say p⁺ = S⁺(i/i⁺)p with i I and p A, and if J is a finite support of p, then a direct geometric verification shows (cf. also Lemma 6.14) that (i/i⁺)J supports p⁺ and hence that p⁺ does indeed have a finite support.

        (v) Suppose now that p⁺ A⁺ and that p⁺ is independent of i⁺. We represent p⁺ in the form S⁺(i,i⁺)p, as in the proof of (iii) above. Since by now we know that A⁺ is an I⁺- algebra, in the remainder of this argument we can make free use of the technique of polyadic algebras. We have

Since S⁺(i,i⁺) is a Boolean automorphism (recall that (i,i⁺)² = δ⁺), it follows from (11.8) that and hence that

        This concludes the proof of Lemma 11.6.

        The main theorem of this section is a consequence of the preceding lemma and of Theorem 10.1.

(11.9) THEOEEM. If I is an infinite set and if I ⊂ I⁺, then every locally finite I-algebra is the compression of a locally finite I⁺-algebra] the dilation is uniquely determined to within an isomorphism that acts as the identity on the compression.

        Proof. The theorem as stated follows from the special case in which I⁺ = I ∪{i⁺} by repeated applications of that special case (i. e., by trans-finite induction). In the special case the only thing we still need to establish is uniqueness. Suppose that (A, I, S, ) is the given algebra and that (A⁺, I⁺, S⁺, ) is a dilation. If p⁺ A⁺ and if i is an element of I such that p⁺ is independent of i, then p⁺ = S⁺(i/i⁺)S⁺(i⁺/i)p⁺; this shows that every element of A⁺ has the form S⁺(i/i⁺)p where i I and p A. If both and are dilations of A, and if a mapping f from to is defined by , then f is a polyadic isomorphism from onto . To prove this it must be shown that if p⁺ A⁺, then fp⁺ is unambiguously defined (independently of the representation of p⁺ in the form , that f is a Boolean isomorphism, and that f transforms and into and respectively. The verifications of all these assertions are routine applications of frequently used techniques (cf., in particular, the proof of Lemma 11.6); we omit the details.

§ 12. Constants

        The main thing that makes Theorem 10.1 much less useful than it appears to be is that it does not even come close to answering the question of which simple algebras are models. If Theorem 10.1 is applied to a simple algebra, the representation it yields is not by a model; if, in fact, Theorem 10.1 is applied to a model, the representation it yields is not, as it ought to be, the identity representation. In the presence of a very strong cardinality restriction (namely, that A and I be count -ably infinite) Easiowa and Sikorski [5] were able to obtain the desired result, but their proof is inseparably tied to that cardinality restriction. To get a better grip on the problem we shall introduce below a new concept whose role in the theory of polyadic algebras is even more important than that of the well-known concepts of universal algebra (such as ideal and homomorphism).

        The main problem to be kept in mind is that of functional representation. Given an I-algebra A, we must try to construct a Boolean algebra B and a domain X so that A is isomorphic to an algebra of functions from X^I into B, and, moreover, the isomorphism must be a natural one in a very strong sense of the word. We might try to formulate the desideratum precisely as follows: if A is already a functional algebra, then the general method of constructing X and B should recapture the domain and the value - algebra in terms of which A is defined. A moment’s thought about the (analogous) representation theory of ordinary Boolean algebras shows that this desideratum is really more than is needed; by aiming in its general direction, however, we shall be able to get all the information we want about the problem of functional representation for polyadic algebras.

        We can hope to get a clue to the solution of our problem by assuming that A is a functional I-algebra, with domain X and value-algebra B, and trying to find a purely algebraic characterization of the elements of X. In order to avoid extraneous technical difficulties, we shall temporarily over-simplify the situation by assuming that B = O and that A is the set of all functions from X into O. The same intuitive considerations that motivate calling the elements of I variables suggest that the elements of X be thought of as the constants that constitute the subject matter of the values of the propositional functions in A. We shall adopt this terminology; accordingly we may say that we are now seeking an algebraic characterization of the constants of a polyadic algebra.

        If is a constant, i. e., , the only way we can connect with A is to consider an element p of A and to replace some or all of its arguments by . Suppose, to be more precise, that J is a subset of I, and associate with each point x in X^I the point x^J (this notation is only temporary) defined by when i J and ,·otherwise. If we write q(x) = p(x^J) for all x, then we may say that the function q was obtained by replacing some of the arguments of p (the ones with index in J) by . The passage from p to q is a transformation, depending on the set J, from A into itself. We shall denote this transformation by c(J), so that c(J)p = q. (We do not indicate the dependence of this transformation on .)

        It is not hard to see, directly from the definition, how c(J) depends on J and what are the relations between c(J) and the algebraic structure of A. Instead of listing the facts, we proceed forthwith to use them as the basis for a general definition. Abandoning functional polyadic algebras and our special assumptions, we define a constant of an arbitrary I-algebra A as a mapping c from subsets J of I into Boolean endomor-phisms c(J) of A, such that

whenever J and K are subsets of I and τ is a transformation on I. (It is easy to verify that in the special case of monadic algebras this definition reduces to the one given in § 1.) In case the set J happens to be a singleton, J = {i}, we shall write c(i) instead of c(J).

        In the theory of constants, as throughout the theory of (locally finite) polyadic algebras, it is sufficient to restrict attention to finite sets and finite transformations. The proofs that establish this fact are similar to but not immediately derivable from the corresponding proofs for quantifiers; cf. Theorem 7.7.

(12.1) LEMMA. If c is a constant of an I-algebra A and if p A, then to every subset K of I there corresponds a finite subset K₀ of I such that c(K)p = c(K₀)p.

        Proof. Let J be a finite support of p. If K₀ = K ∩ J, then

(12.2) LEMMA. If c is a constant of an I-algebra A, if p is an element of A with support J, and if K is a subset of I, then J supports c(K)p.

        Proof. Since J^K supports p, it follows that

        Remark. On one or two occasions below we shall refer to Lemma 12.2 even when c is not quite known to be a constant of A; as long as c satisfies the conditions used in the proof (i. e., (C₃) and (C₄)), such references are justified.

(12.3) THEOREM. If c is a mapping from all finite subsets of I into Boolean endomorphisms of A satisfying (C₁)-(C₅) whenever J and K are finite subsets of I and τ is a finite transformation on I, then there exists a unique constant of A such that for all finite subsets J of I.

        Proof. If J ⊂ I and p A, we find a finite support J₀ of p and we write . In order to justify this definition of , we must show first that c(J ∩ J₀)p is the same no matter which support J₀ of p is used. In other words, we must prove that if both J₁ and J₂ are finite supports of p, then c(J ∩ J₁)p = c(J ∩ J₂)p. Since, by Lemma 6.7, J₁ ∩ J₂ supports p, the desired result follows from the fact that both c (J ∩ J₁)p and c(J ∩ J₂)p are equal to c(J ∩ J₁ ∩ J₂)p. The proof of this fact, in turn, is reduced to the computation

together with the one obtained by interchanging the roles of J₁ and J₂.

        It J happens to be finite, then the finite support J₀ of p can be chosen so that J ⊂ J₀. If that is done, then J ∩J₀ = J, and it follows that is indeed an extension of c.

        It remains to prove that is a constant of A. Since , it follows that is the identity mapping on A. For the remainder of the proof we fix an element p of A with finite support J₀.

        We observe that J₀ supports c(K ∩ J₀)p (cf. Lemma 12.2) and hence that

        Since

and since

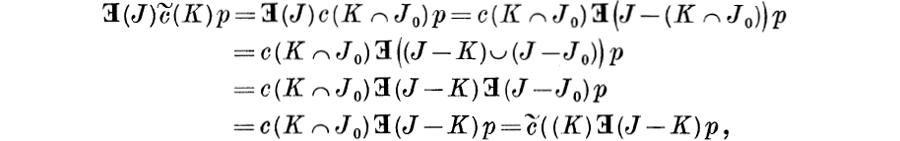
it follows that (C₃) and (C₄) hold for .

        To prove (C₅) we assume first that the transformation τ is finite. In this case

since J₀ ⊂ τ⁻¹τJ₀ and therefore τ⁻¹τJ₀ supports p. In the general case, i. e., if τ is not necessarily finite, let τ₀ be a finite transformation that agrees with τ in J₀. Since J₀ supports both p and (cf. Lemma 12.2), it follows from Lemma 6.11 that S(τ)p = S(τ₀)p and . Observe also that the agreement of τ and τ₀ in J₀ implies that ; from this it follows that

The existence part of the proof is now completed by the observation that

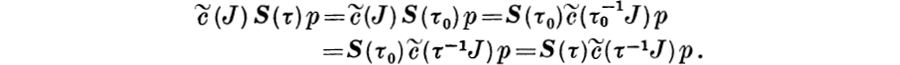
Since the uniqueness of is an immediate consequence of Lemma 12.1, the proof of Theorem 12.3 is complete.

§ 13. Factorization and commutativity

        We interrupt our discussion of constants in order to insert two auxiliary results, unrelated to each other and (except indirectly) to polyadic algebras. These results (Theorem 13.3 and Lemma 13.4) are of a certain amount of interest in themselves (especially Theorem 13.3); the main reason for presenting them, however, is their use in the proof of Theorem 14.1.

        Our first purpose is to generalize to arbitrary finite transformations (on a set I, say) the classical result on the expression of finite permutations by means of transpositions.

(13.1) LEMMA. A finite transformation τ is a retraction if and only if there exists a finite class {J₁, ... ,J_n} of finite subsets of I such that if i J_k and j J_k) then τi = τj J_k, and if i ∉ J₁ ∪ ... ∪J_n, then τi = i.

        Proof. If τ is a finite retraction, then there exists a cofinite set J such that τi = i whenever i J and such that τ(I – J) ⊂ I – J. If τ(I –J) = {j₁,…, j_n}, write Jk = r⁻¹{j_k}, k = 1,...,n. Clearly J₁ ∪ ... ∪ J_n = I –J, so that, indeed, τί = ί when i ∉ J₁ ∪...∪J_n. If i J_k, then τi = j_k, and, since τ is a retraction, τj_k = τi = j_k, so that j_k J_k and therefore τi J_k. This settles the “only if”. If, conversely, the condition is satisfied, and if i ∉ J₁ ∪...∪J_n, then τi = i and therefore τ²i = τi. If i J_k then, by assumption, τi J_k, and therefore, by another part of the assumption, τί = ττi = τ²i, so that τ is a retraction.

(13.2) LEMMA. Every finite transformation is the product of a finite permutation and a finite retraction.

        Proof. If τ is a finite transformation, then there exists a cofinite set J such that τi = i whenever I J and such that τ(I –J) ⊂ I –J. If τ(I –J) = {j₁,…,j_n}, write J_k = τ⁻¹{j_k}i and let i_k be an arbitrary element of J_k, k = l,...,n. Let π be a permutation such that πi = i whenever i J and such that πi_k = j_k, k = l,...,n; obviously π is finite. If σ = π⁻¹τ, then, clearly, σ is a finite transformation; it remains to prove that σ is a retraction. Clearly σi = i whenever i ∉ J₁ ∪…∪J_n. If i J_k, then σi = π⁻¹τi = π⁻¹j_k = i_k J_k; the desired result follows from Lemma 13.1.

(13.3) THEOREM. Every finite permutation is a finite product of trans-positions^ every finite retraction is a finite product of replacements-, every finite transformation is a finite product of transpositions and replacements.

        Proof. The first assertion is well-known, and the last assertion follows from the first two together with Lemma 13.2. To prove the second assertion, suppose that τ is a finite retraction, and let J₁,...,J_n be sets with the properties described in Lemma 13.1. If τi = j_k when i J_k, then, clearly,

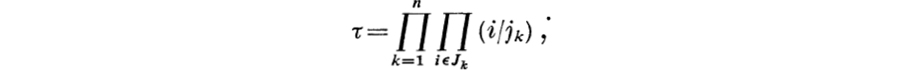
and the proof is complete. (The first proof of Theorem 13.3 was obtained in the course of a conversation with G. P. Hochschild.)

        Theorem 13.3 can be used to explain why general transformations (and, in particular, permutations) are almost never used in the traditional presentation of the functional calculi. Usually the only transformations that are visible are replacements. The reason is that in the usual discussion it is always assumed that the set I is infinite, and, under that assumption, it turns out that the action of any finite transformation on any element of a (locally finite) polyadic algebra can be achieved by replacements only. To prove this assertion it is sufficient, in view of Theorem 13.3, to prove it for transpositions only. It is to be proved, in other words, that if p is an element of an I-algebra (locally finite, of course) and if i and j are in I, then there exists a transformation τ that is a finite product of replacements and for which S(i,j)p = S(τ)p. To prove this, let J be a cofinite set such that and let k be an element of J such that k ≠ i and k ≠ j) (here is where we need an infinite I). If τ = (k/j)(j/i)(i/k), then (i,j) = τ outside J and therefore

It is easy to see that if the set I is finite, then the method just used breaks down, and, in fact, the result itself becomes false.

        Our second auxiliary result gives a sufficient condition for the commutativity of two Boolean endomorphisms under some rather special circumstances.

(13.4) LEMMA. If A is a monadic algebra with quantifier , if a is a constant of A, and if b is a Boolean endomorphism of A such that and such that either (i) ab = aba or (ii) abp = 0 whenever ap = 0, then ab = ba.

        Proof. Under the assumptions of the lemma the conditions (i) and (ii) are equivalent to each other. Indeed, (i) obviously implies (ii). If, on the other hand, (ii) is true, then ab(p ap′) = 0 for all p (since ab(p ap′) = 0)₇ so that . Applying this result to p′ in place of p and combining the two inequalities so obtained, we conclude that (i) is true. The proof that (ii), together with the preceding assumptions of the lemma, implies the desired commutativity, is a simple calculation, as follows :

§ 14. Constants from endomorphisms

        For the purpose of constructing constants an application of the definition itself is quite unwieldy. It is natural to guess, however, on the basis of intuitive considerations, that a constant c ought to be completely determined by the knowledge of c(i) for any one i in I. The idea is that if we know how to replace one particular variable by a constant, then, using the transformation laws at our disposal, we can deduce the effect of replacing any other variable by that constant. Our next purpose is to make these indications precise by showing that a constant is indeed uniquely determined by one suitably selected endomorphism.

(14.1) THEOREM. If A is a locally finite I-algebra, if f is a Boolean endomorphism of A, and if i is an element of I such that

then there exists a unique constant c of A such that c(i) = f.

        Remark. Note that the sufficient conditions of this theorem are also obviously necessary, in this sense: if c is a constant of A and if f = c(i), then f satisfies (i), (ii), and (iii).

        Proof. Uniqueness is easy. Suppose, indeed, that c is a constant of A. It follows from (C₂) that

for every finite subset J of I. (Since, conventionally, the empty product of endomorphisms is the identity endomorphism, the situation is in harmony with (C₁).) It follows (cf. Lemma 12.1 and Theorem 12.3) that a constant c is uniquely determined by the endomorphisms c(j), j I. Since (i,j)⁻¹{i} = {j}, it follows from (C₅) that

and hence that

for all j. This means that the endomorphisms c(j), in turn, are uniquely determined by any one of them, and the uniqueness assertion is proved.

        We shall need to make use of the fact that (i), (ii), and (iii) imply

Since f² = f (cf. (1.9)), (iv) is obviously true when j = i. It follows that for every p in A and for every j in I the two Boolean endomorphisms in (iv) agree on fp, and that f(p + fp) = 0. Since

it follows also that the endomorphisms in (iv) agree on p + fp. Since p = fp + (p + fp) for all p, the proof of (iv) is complete.

        The proof of uniqueness suggests an approach to the proof of existence; given f, we must write

for every finite subset J of I. In order to be sure, however, that this product unambiguously defines something (independently of the order of the factors) we must prove first of all that its factors commute. To do this, we begin by writing

whenever j is an element of I, and we go on to prove that a_j and a_k always commute. If j = k, then a_j = a_k and the result is obvious. If j ≠ k, we apply Lemma 13.4 with A = A(j), a = a_j, and b = a_k. We proceed to verify the hypotheses of Lemma 13.4; in the course of the verification we shall make use, without any further reference, of the following special cases of (P₆):

the latter in case k is distinct from both i and j.

        We have

and

this proves that a_j is a constant of A(j).

        We prove next that

The proof splits naturally into two parts. We have assumed that j ≠ k;, if also j ≠ i, then

If, on the other hand, j = i, then we must have i ≠ k (since j ≠ k), and therefore

This implies among other things that the hypothesis holds in the present case.

        If a_jp = 0, then (by (14.6)). Since our assumptions are symmetric in j and k, we know from (14.4) and (14.5) that a_k is a constant of A(k) and therefore that for all p in A. Putting these two facts together, we conclude that if a_jp = 0, then . This completes the verification of the hypotheses of Lemma 13.4; applying Lemma 13.4, we conclude that a_j and a_k commute. Since this holds for all j and k, we now know that all the factors of (14.2) commute and hence that the equation (14.2) unambigously defines a Boolean endomorphism c(J) of A for every finite subset J of I. In view of Theorem 12.3, what remains to be done is to prove that the mapping c from finite subsets of I to Boolean endomorphisms of A satisfies (C₁)-(C₅) whenever J and K are finite subsets of I and τ is a finite transformation on I.

        The validity of (C₁) (i. e., the fact that c(Ø) is the identity mapping on A) follows from the customary interpretation of the empty product. The validity of (C₂) (i. e., c(J ∪ K) = c(J)c(K)) follows from a straightforward application of the definition of c.

        To prove (C₃) we recall that in view of (P₄)

for every finite subset K of I. It follows from repeated applications of (14.5) and (14.6) that

and

Since (cf. (14.2) and (14.3))

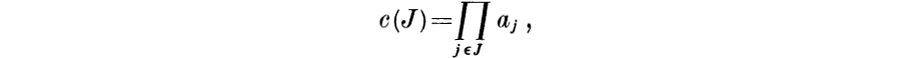
we obtain

        The derivation of (C₄) proceeds similarly; indeed, since

        and

        it follows that

        We begin the proof of (C₅) (i. e., c(J)S(τ) = S(τ)c(τ⁻¹J)) by assuming that J is a singleton, J = {j}, and that τ is a transposition or a replacement. If τ = (h,k) or if τ = (h/k), with h ≠ j and k ≠ j, then τ⁻¹{j} = {j}, and therefore the desired conclusion is that a_j and S(τ) commute. The result can be derived from Lemma 13.4 with A = A(j), a = a_j and b = S(τ). We already know that a_j is a constant of A(j) (cf. (14.4) and (14.5)). We know also that

(cf. (C₃)) and that

(cf. (P₅)). From (14.7) and the fact that for all p, it follows that . If p is such that a_jp = 0, then and therefore

The fact that follows from (P₆). Consequently Lemma 13.4 is indeed applicable and we have proved (C₅) in this case.

        In the next case τ = (j,k). Since τ⁻¹{j} = {k}, the desired conclusion is

If j = k, the conclusion is trivial; if j and k are distinct but one of them is equal to i, the conclusion is equivalent to the definition of the a’s (cf. (14.3)). If both j and k are distinct from i, then

and therefore

by the preceding paragraph. It follows that

        If τ = (j/k) with j ≠ k, then τ⁻¹{j} = Ø and the desired conclusion becomes

The proof is simple:

        The only other replacement τ can be is (k/j) with k ≠ j. Since τ⁻¹{j} = {j,k}, the desired conclusion is

If j = i, then

if k = i, then

If both j and k are different from i (and j ≠ k), then

and therefore

This completes the proof of (14.10) and hence of (C₅) in the special cases under consideration.

        If J and K are finite subsets of I and τ is a finite transformation on I such that

        and

        then

The fact that (C₅) holds whenever J is a singleton and τ is a transposition or a replacement, together with the result just obtained, implies that (C₅) holds whenever J is an arbitrary finite subset of I and τ is a transposition or a replacement.

        If τ and σ are finite transformations on I such that

and

for all finite subsets J of I, then

The fact that (C₅) for finite sets holds for transpositions and replacements, together with the result just obtained, implies that (C₅) for finite sets holds for all finite products of transpositions and replacements. In view of Theorem 13.3 this means that (C₅) holds in all finite cases, and, therefore, completes the proof of Theorem 14.1.

§ 15. Examples of constants

        It is instructive to see an example of a constant that is prima facie different from the ones that motivated the definition, i. e., from those constants of a functional polyadic algebra that are defined in terms of the replacement of variables by some element of the domain. The idea behind the example is that if, given an arbitrary polyadic algebra, we hold a certain variable fixed, i. e., if we steadfastly refuse to perform any transformations involving it, then that variable will act as a constant.

        Suppose, to be precise, that I and I⁺ are sets such that I is a proper subset of I⁺, and suppose that (A⁺, I⁺, S⁺, ) is a polyadic algebra. If we write A = A⁺ and if we define S and (for transformations on I and subsets of I) by (11.3) and (11.4), then it follows easily that (A, I, S, ) is a polyadic algebra. The proof is, in fact, the same as the one given for compressions in § 11; for this reason it is all the more important to note (in order to avoid confusion) that the I-algebra A is not a compression of the I⁺-algebra A⁺. (The part of the definition of compression that is not satisfied here is the requirement that A consist of all the elements of A⁺ independent of I⁺ –I.) We shall say that the algebra (A, I, S, ) is obtained from the algebra (A⁺, I⁺, S⁺, ) by fixing the variables in I⁺ –I. We note that if (A⁺, I⁺, S⁺, ) is locally finite, then the same is true of (A, I, S, ).

        If, in the notation of the preceding paragraph, i is an element of I⁺ –I, and if J is an arbitrary subset of I, we shall write (J/i) for the transformation τ such that τj = i when j J and τj = j otherwise; we shall denote the corresponding endomorphism S⁺(τ) by S⁺(J/i). We assert now that if c_i(J) = S⁺(J/i), then c_i·is a constant of the I-algebra A; it is in this sense that we may say that a fixed variable is (better: becomes or induces) a constant. The proof of our assertion is easy. Indeed (C₁) follows from (P₁) via the fact that (Ø/i) = δ, and (C₂) follows from (P₂) via the fact that (J/i)(K/i) = ((J ∪ K)/i). To prove (C₃) observe that ((J – K)/i)^–1K = K; then apply (P₆) to get and apply (P₅) to get . (Recall that throughout this proof the only relevant sets are subsets of I and that i I⁺ –I.) For (C₄), note that (k/i)⁻¹J = J – K and apply (P₆). The condition (C₅) follows immediately from (P₂) and the fact that (J/i)τ⁺ = τ⁺(τ⁻¹J/i) whenever τ is a transformation on I. The fact that each c_i(J) is a Boolean endomorphism of A follows from the fact that S⁺ maps transformations to Boolean endomorphisms of A⁺.

        Besides fixing variables, there are two other useful methods of constructing constants: lifting to dilations (Lemma 15.1) and transfer to quotients (Lemma 15.3).

(15.1) LEMMA. If (A, I, S, ) is a locally finite polyadic algebra of infinite degree, if (A⁺, I⁺, S⁺, ) is a dilation of it, and if e is a constant of A, then there exists a unique constant c⁺ of A⁺ such that c⁺(J)p = c(J)p whenever J ⊂ I and p A.

        Proof. We shall prove the result only in the special case in which I⁺ = I ∪ {i⁺}; the general case follows easily by transfinite induction. To construct c⁺ we apply Theorem 14.1 with i⁺ in the role of i. If p⁺ A⁺, so that p⁺ = S⁺(i/i⁺)p with i I and p A (cf. Theorem 11.9), we write fp⁺ = c(i)p. If

we select an element k in I such that both p and q are independent of k and we apply to (15.2) first S⁺(i⁺/k), obtaining S(i/k)p = S(j/k)q, and then c(k), obtaining (via (C₅))

Thus fp⁺ is unambiguously defined, independently of the representation of p⁺. A routine verification shows that f is a Boolean endomorphism of A⁺; cf. especially the techniques used in the proof of (i) under Lemma 11.6.

        We proceed now to verify the hypotheses of Theorem 14.1.

        (i) If p⁺ = S⁺(i/i⁺)p, then (since c(i)p A) = fp⁺.

        (ii) If p⁺ = S⁺(i/i⁺)p, then

        (iii) If j I and if p⁺ = S⁺(i/i⁺)p, we may assume that i ≠ j (cf. (11.7)). It follows that

        From the preceding paragraph we may conclude (via Theorem 14.1) that there exists a (unique) constant c⁺ of A⁺ such that c⁺(i⁺) = f. It follows that c⁺(i⁺)p = p whenever p A. If i I, then

whenever p A. This concludes the proof of the existence of c⁺. If c⁺ is a constant satisfying the conditions of the lemma, then

This establishes uniqueness and completes the proof.

(15.3) LEMMA. If f is a polyadic homomorphism from an I-algebra A onto an I-algebra B, and if a is a constant of A, then there exists a unique constant b of B such that fa(J) = b(J)f for every subset J of I.

        Proof. If p A, write b(J)fp = fa(J)p. If fp = fq, then f(p + q) = 0 and therefore . It follows that , and hence that fa(J)p = fa(J)q. This proves that b(J) is unambiguously defined. Straighforward computations serve to prove that b is indeed a constant of B. Uniqueness follows from the fact that f is onto.

        The main difficulty with constants is that they do not always exist. To see this, we examine first of all a situation in intuitive logic. Suppose that X is a set with at least two elements; to be specific, write X = {0,1}. Let us consider a microcosmic logical system designed to make statements about the concept of equality in X and about nothing else. The system, in other words, contains two propositions (corresponding to truth and falsity), a dyadic predicate (corresponding to equality), and the negation p′ of that predicate. If, in accordance with the intended interpretation, we write x₀ = x₁ in place of p(x₀,x₁) and x₀ ≠ x₁ in place of p′(x₀,x₁), the quantification and transformation rules of this system become obvious. Thus, for instance, the result of applying to p the existential quantifier corresponding to the variable in position 1 is the true proposition and the result of replacing in p′ the variable in position 1 by the variable in position 0 is the false proposition (x₀ ≠ x₀). The intuitively easily comprehended act of replacing the variable in position 1 by the “constant” 0 is not permissible; the system has no way of making a statement such as x₀ = 0.

        In precise terms, the system discussed in the preceding paragraph is a functional dyadic algebra, i. e., a functional polyadic algebra of degree 2. If, to be specific, we write 1 = {0,1}, then the pertinent algebra A can be described as an O-valued I-algebra over X. (The triple role of {0,1} as O, as X, and as I, is merely a notational simplification and is not likely to lead to confusion.) The algebra A consists therefore of functions from X^I into O. It does not, however, consist of all sixteen such functions; its elements are the characteristic functions of the empty set, the full set X^I, the diagonal {(x₀,x₁): x₀ = x₁}, and the opposite diagonal {(x₀,x₁): x₀ ≠ x₁}. The fact that the system is unable to say that x₀ = 0 is algebraically reflected by the fact that the algebra does not contain the characteristic function of the set {{( x₀,x₁): x₀ = 0}. (This example is essentially the same as the one described in the remark (d) following Theorem 10.1.)

        It is now easy to prove that the algebra A does not have any constants. The reason is that the quantifiers and on A are equal to each other; they are both the simple quantifier on A. If c were a constant of A, then we should have and , and therefore, since , it would follow that . This is impossible because c(0) must be a Boolean endomorphism of A, whereas is not.

        The fact that the algebra in the above example is of degree 2 is not essential. Using the same basic idea (systems that can talk about equality only), we can construct constantless algebras of any degree whatever, excepting only the degree 1. For the corresponding facts about monadic algebras see [2].

        If A had been the algebra of all functions from X^I into O, it could not have been used to illustrate the same phenomenon. An examination of the motivating considerations that preceded our definition of constants shows that a “full” functional algebra always has many of them. Roughly speaking, we may say that the absence of constants for a B-valued functional I-algebra over X indicates that the algebra is too small a subset of the set of all functions from X^I into B. In the next section we shall partially justify this rough description by showing that all useful polyadic algebras can be embedded into algebras with many constants.

§ 16. Rich algebras

        A finite set {c₁,...,c_n} of constants of a locally finite I-algebra A will be called a witness to an element p of A if there exists a corresponding finite set {j₁,...,j_n} of elements of I such that

we shall also say that {c₁,...,c_n} is a witness to p with respect to A, or more simply, in A. If A and A* are I-algebras such that A is a polyadic subalgebra of A* and such that every element of A has a witness in A*, we shall say that A* is a rich extension of A, or, more simply, that A* is rich for A. A rich algebra is one that is rich for itself.

        It is appropriate to remark at this point that the definition of rich algebras given above is not the same as the one that occurs in [1]. There it was required that for every p in A and for every j in I there exist a constant c of A such that . This requirement is much too strong. Most polyadic algebras fail to satisfy it, and, in fact, most polyadic algebras cannot even be embedded into an algebra satisfying it. (Theorem 1 of [1] is essentially true nevertheless, for algebras of infinite degree, if “rich” is interpreted in the sense of the preceding paragraph; cf. Theorem 16.9 below.) To see what is wrong with the strong definition of a rich algebra, suppose that a polyadic algebra A contains an element p such that for some particular pair of variables, say j and k, it is true that . (The constantless algebras given in § 15 satisfy these conditions.) Now we assert that there cannot be any constant c of A (or, for that matter, of any polyadic algebra including A as a polyadic subalgebra) such that . Indeed, if such a constant did exist, then, since c(j)p = 1, it “would follow that c(j)p′ = 0. Hence we should have

and this is a contradiction.

        There is a slight amount of unnaturality in connection with our present definition of a witness and the subsequent definitions of rich extensions and rich algebras, caused by the fact that the right term of (16.1) depends on the order in which the constants and the variables that enter into it are written down. Since, for several purposes, it is important to eliminate this unnaturality, we proceed to put on record a simple consequence of the commutativity lemma of § 13.

(16.2) LEMMA. If a and b are (not necessarily distinct) constants of an I-algebra A and if J and K are disjoint subsets of I, then the Boolean endomorphisms a(J) and b(K) of A commute with each other.

        Proof. We apply Lemma 13.4 to the monadic algebra A = A(J) with the quantifier (see § 8); the roles of a and b are to be played by a(J) and b(K) respectively. Clearly a(J) is a constant of A(J) and b(K) is a Boolean endomorphism of A(J). If a(J)p = 0, then

so that a(J) b (K)p = 0. Since

all the hypo theses of Lemma 13.4 are satisfied and the desired conclusion follows from the conclusion of that lemma.

(16.3) LEMMA. If A is a locally finite I-algebra of infinite degree, then there exists a locally finite I-algebra A* such that A* is a rich extension of A and such that every constant of A can be extended to A*.

        Remark. The statement about extending constants means that if c is a constant of A, then there exists a constant c* of A* such that c*(J)p = c(J)p whenever J ⊂ I and p A.

        For some purposes it is important to know the relation between the cardinal numbers of A and A*. The proof will show that A* can be constructed so that if A is finite, then A* is countable, and if A is infinite, then the cardinal number of A* is the same as that of A. We observe that it is perfectly feasible for a polyadic algebra of infinite degree to be finite. Thus, for example, if I is any set (finite or infinite), the Boolean algebra O can be converted into a polyadic I-algebra simply by setting both S(τ) and equal to e, for all transformation τ οn I and for all subsets J of I.

        Proof. Let I⁺ be a set including I such that if A is finite, then I⁺ –I is countably infinite, and if A is infinite, then the cardinal number of I⁺ –I is the same as that of A. By Theorem 11.9, there exists a locally finite polyadic algebra (A⁺, I⁺, S⁺, ) that is a dilation of the given algebra. We shall denote by (A⁺, I, S, ) the algebra obtained from (A⁺, I⁺, S⁺, ) by fixing the variables in I⁺ –I.

        It is easy to verify (cf. Lemma 11.6 and Theorem 11.9) that every element of A⁺ has the form S⁺(τ)p, where p A and τ is a transformation (on I⁺) that sends some of the elements of a finite support of p (in I) into I⁺ –I and is equal to the identity otherwise. It follows that if A is finite, then A⁺ is countable, and if A is infinite, then the cardinal number of A⁺ is the same as that of A. Since the algebra (A*, I, S, ) that we shall construct will be defined as a quotient algebra of (A⁺, I, S, ), the remark about cardinal numbers is already established.

        Since the algebra A is locally finite, it follows that to each element p of A there corresponds a finite subset J_p of I (a support of p) such that . In order to avoid a needless unambiguity argument below, we shall assume that J_p is the minimal support of p, i. e., that if , then j ∉ J_p From what we know about the cardinality of I⁺ –I we can conclude that there exists a disjoint family {K_p} of finite subsets of I⁺ –I such that K_p and J_p have the same number of elements for every p in A.

        We know that every element of I⁺ –I induces in a natural way a constant of the algebra (A⁺, I, S, ). We shall find it convenient to denote an element of I⁺ –I and the constant it induces by the same symbol. Thus if k I⁺ –I and J ⊂ I, then k(J)p = S⁺(J/k)p for every element p of A⁺.

        Suppose now that p is any element of A: we shall make correspond to p a Boolean endomorphism f_p on A⁺. If J_p is empty (i. e., if p is closed), let fp be e. If J_P = {j₁,...,j_n} and, correspondingly K_p = {k₁,…,k_n}, write fp = k₁(j₁)…k_n(j_n). (The indicated one-to-one correspondence between J_p and k_p is arbitrary, but fixed once and for all. The factors of f_p commute among each other by Lemma 16.2.) Eoughly speaking, the endomorphism f_p has the effect of replacing by a constant each of the variables that p really depends on. The replacements are such that two distinct variables of the same p, and any two variables (distinct or not) of two distinct p’s, are always replaced by distinct constants. The idea of the remainder of the proof is to force f_pp to be equal to , or, equivalently, to force to be 0. Precisely speaking, we shall consider the polyadic ideal M, in the algebra (A⁺, I, S, ), generated by all elements that have the form for some p in A, and we shall reduce A⁺ modulo M. Essentially the only thing to worry about is the preservation of A in the passage from A⁺ to A⁺/M. Technically speaking, we shall have to show that the natural (projection) mapping from A⁺ onto A⁺/M is one-to-one on A, or, equivalently, that Α∩Μ = {0}. A remark is in order concerning our use of . Since

it follows that is the same as the Boolean sum (or symmetric difference) . Since, furthermore, J_p supports p, we have ; it follows that identifying with 0 has exactly the same effect as identifying with f_pp, and, in view of the definition of witnesses, the latter is what we must do.

        Continuing with the notation of the preceding paragraph, we shall write g_P = S⁺(k₁/j₁)...S⁺(k_n/j_n). Clearly g_p is a Boolean endomorphism of A⁺ such that g_Pf_Pp = p· For later purposes we observe that if q A, then g_pq = q; this follows from the fact that the elements of A are independent of I⁺ –I.

        An element p of A⁺ belongs to the ideal M if and only if it is dominated by the supremum of a finite number of elements of the form with p A. Since , what we are trying to prove is that if q is an element of A such that

where m is a positive integer and P₁, ,P_m are distinct elements of A, then q = 0. If m > 1, we form the infimum of both sides of (16.4) with the complement of . The resulting inequality implies (after increasing its larger side by omitting from it the factor that

The smaller side of (16.5) belongs to the algebra obtained from (A⁺, I⁺, S⁺, ) by fixing the variables in I⁺ – (I ∪ K_pm), whereas the larger side of (16.5) is independent of I⁺ – (I ∪ K_pm) (Here is where the disjointness of the sets K_p comes in.) Thus it is only a matter of change of notation (replace I by I ∪K_Pm) to reduce the parameter m in the statement to be proved (i. e., the statement that if q A and (16.4) holds, then q = 0) to m – 1. It is therefore sufficient to prove that statement for m = 1, i. e., to prove that if p and q are in A and if

then q = 0. Since , the right term of (16.6) is invariant under ; consequently we may and do assume that q is closed. Since g_Pf_Pp = p, an application of g_p to (16.6) yields

Forming the infimum of both sides of (16.7) with p we obtain

Applying and using the fact that q is closed, we conclude that . Since, however, (by (16.7)), we can go on to conclude that q = 0, as desired.

        From what we have proved it follows that the I-algebra A* = A⁺/M includes i as a polyadic subalgebra. Since, by Lemma 15.3, the constants k in I⁺ –I induce constants on A*, the fact that A* is a rich extension of A follows from the fact that if p A, then the elements and f_pp of A⁺ are congruent modulo M. The assertion about the extendability of constants from A to A* follows in two steps. By Lemma 15.1 every constant of A can be lifted to a constant of A⁺, and, by Lemma 15.3, every constant of A⁺ can be transferred to A*. The proof of Lemma 16.3 is complete.

(16.9) THEOREM. Every locally finite polyadic algebra of infinite degree is a polyadic subalgebra of a locally finite rich algebra.

        Remark. As in the case of Lemma 16.3, the proof will show that the extension algebra A* of the given algebra A can be constructed so that if A if finite, then A* is countable, and if A is infinite, then the cardinal number of A* is the same as that of A.

        Proof. Given an algebra A, we write A₀ = A, and, given A_n, we let A_n+1 be a rich extension of A_n (n = 0,1,2,...) obtained by an application of Lemma 16.3. If A* is the set - theoretic union of the increasing sequence of polyadic algebras so obtained, then A* is in an obvious way a polyadic algebra that includes A as a polyadic subalgebra. Since an inductive application of Lemma 16.3 implies that every constant of each A_n can be extended to a constant of A*, it follows that A* has enough constants to bear witness to every element of A*, i. e., that A* is rich.

§ 17, Representation

        We have now reached the culmination of our work. In this section we shall prove the principal representation theorem of the theory of polyadic algebras and from it we shall deduce the representation theorem for simple algebras needed to guarantee that Theorem 9.3 is indeed the algebraic version of Gödel’s completeness theorem.

        We shall say that a locally finite functional I-algebra A, with domain X, say, is functionally rich if the elements of X constitute a sufficient supply of constants for A. In order to make this definition precise, we recall that to each finite subset J of I and to each element c of X there corresponds in a natural way a mapping, to be denoted by c(J), that sends every function from X^I into B onto another such function. If p is a function from X^I into B and if x X^I, the value of c(J)p at x is the value of p at the point that x becomes when x_i is replaced by c for each i in J (cf. § 12). To say that A is functionally rich means that A is closed under each of the operations c(J) so obtained (so that c is, from this point of view, a constant of A), and that each element of A has a witness {c_1,...,c_n} such that the constants c_1,...,c_n belong to X in the sense just described. (It is clear that a functionally rich algebra is rich in the sense of § 16.) It is a consequence of this definition that if A is functionally rich, then the suprema defining are always attained, or, more explicitly, that if p A, then there exists a point y in X^I such that for all x in X^I.

(17.1) THEOREM. Every rich, locally finite polyadic I-algebra A of infinite degree is isomorphic to a functionally rich functional algebra. The domain X of the functional algebra can be chosen so that if A is finite, then X is finite and if A is infinite, then the cardinal number of X is less than or equal to that of A.

        Proof. The value - algebra B of the functional algebra that we shall construct is defined as the Boolean algebra of all closed elements in A. For the domain X we select a sufficiently large set of constants of A; this means simply that each element of A is to have a witness {c_1,...,c_n} such that c_1,...,c_n belong to X. The assertion concerning the cardinal number of X follows immediately from this description of how X is to be chosen.

        We are now ready to define a mapping f that associates with each element p of A a function from X^I into B; the mapping f will turn out to be one of the isomorphisms whose existence the theorem asserts. If x X^I and if J is a finite subset of I, we shall write ; clearly x(J) is a Boolean endomorphism of A. Let J be a finite support of the given element p; the value of at x is, by definition, x(J)p. Since J supports p, it follows that x(J)p is closed, so that ; we must still prove, however, that is unambiguously defined, independently of the choice of the support J. To prove this, suppose that K is another finite support of p. We observe that x(J) = x(J ∩ K)x(J – K). Since K supports p, it follows that p is independent of J – K, and hence that x(J – K)p = p. We conclude that x(J)p = x(J ∩ K)p; since, similarly, x(K)p = x(J ∩ K)p, the proof of unambiguity is complete.

        To prove that f is a Boolean isomorphism, observe first that

this proves that f preserves complementation. To prove that f preserves suprema, given p and q in A, let J be a finite set that supports them both; then

Suppose finally that fp = 0. Let {c_1,...,c_n} be a witness to p, so that for a suitable finite subset J = {j₁,..,j_n} of I. If x is a point of X^I such that x_j1 = c₁,..._,x_jn = c_n, then

and therefore p = 0. This proves that f is indeed a Boolean isomorphism.

        We show next that f commutes with S(τ). By § 8, it is sufficient to treat the case in which τ is a finite transformation on I. Given an element p in A, let J = {j₁,...,j_n} be a finite subset of I such that J supports both p and τ and such that τ⁻¹J ⊂ J. Since, by Lemma 6.14, τJ supports S(τ)p, it follows that

If k τJ, then τ⁻¹{k} is a certain subset of J; say, for simplicity, τ⁻¹{k} = {j₁,...,j_m}. Then

Since, similarly, S(τ) can be pulled past each x_k(k) with k τJ, it follows that

Since fp(τ_*x) B, it is unaffected by the application of S(τ), so that

        In order to conclude that f is a polyadic isomorphism we must still show that f commutes with ; by § 8, it is sufficient to treat the case in which K = {k₁,...,k_m} is a finite subset of I. We are to prove, in other words, that if p A and x X^I, then the set {fp(y): xK_*y} has a supremum and that supremum is equal to . Let J be a finite support of p such that K ⊂ J and write q = x(J – K)p. Since K supports q (cf. Lemma 6.10), it follows from the definition of a rich algebra that there exist constants c₁,...,c_m in X such that

Let be the element of X^I for which , and when i ∉ K. It follows that and that

If y X^I and xK_*y, then, similarly,

Thus the set {fp(y): xK_*y) has a largest element, namely ; it follows that the supremum of that set certainly exists, and, of course, is equal to . What we must show therefore is that , or, since J – K supports , that . We already know that the fact that also follows from the fact that a multiple application of (C₃) allows us to pull past x(J – K).

        To prove that the image of A under f is functionally rich it suffices to observe that f carries an adequate supply of constants of A into (a necessarily adequate supply of) “functional” constants of the image algebra. The proof of the principal representation theorem for polyadic algebras is complete.

(17.2) LEMMA. If A is a functionally rich, locally finite, B-valued functional I-algebra over X, if f₀ is a Boolean homomorphism from B into a Boolean algebra B₀, and if (fp)(x) = f₀(p(x)) whenever p A and x X^I, then f is a polyadic homomorphism from A onto a B₀-valued functional I-algebra over X.

        Proof. The only non-trivial part of this assertion is that f commutes with for every finite subset K of I. The proof is similar in almost all details to the proof of the corresponding part of Theorem 17.1. (It is in fact possible, but not worth while, to formulate a highly technical lemma that could be cited in both places.) If a x X^I, J ⊂ I, and p A, we denote by x(J)p the function (in A) whose value at y is the value of p at the point that y becomes when y_j is replaced by x for each j in J. Suppose that p A and that K is a finite subset of I; we are to prove that, for each fixed x in X^I, the set {fp(y): xK_*y} has a supremum and that supremum is equal to . Let J be a finite support of p such that K ⊂ J and write q = x(J – K)p. It follows, as in the proof of Theorem 17.1, that there exists a point in X^I such that and such that . If y X^I and xK_*y, then

It follows that and hence that . Thus the set {fp(y): xK_*y} has as its largest element. Since

the proof of the lemma is complete.

(17.3) THEOREM. Every simple, locally finite polyadic I-algebra A of infinite degree is (isomorphic to) a model, i. e., an O-valued functional polyadic algebra. The domain X of the model can be chosen so that if A is finite, then X is countable, and if A is infinite, then the cardinal number of X is less than or equal to that of A.

        Proof. By Theorem 16.9, A is a polyadic subalgebra of a locally finite, rich I-algebra A*, such that if A is finite, then A* is countable and such that otherwise A and A* have the same cardinal number. By Theorem 17.1, we may assume that A* is a functionally rich functional algebra, with value - algebra B, say, and domain X; the information that Theorem 17.1 gives about the cardinality of X implies the second assertion of the present theorem. Let f₀ be an arbitrary Boolean homomor-phism from B into (and therefore onto) 0, and write (fp)(x) = f₀(p(x)) whenever p A* and x X^I. It follows from Lemma 17.2 (with A* and O playing the roles of A and B₀, respectively) that f is a polyadic homomorphism from A* onto a model with domain X. If g is the restriction of f to A, then g is a polyadic homomorphism from A onto such a model (in general a subalgebra of the model onto which f maps A*). Since the kernel of a polyadic homomorphism is a proper ideal, and since the only proper ideal of a simple algebra is trivial, it follows that q is an isomorphism, and the proof of the theorem is complete.

        The cardinality assertions of Theorem 17.1 constitute the algebraic version of the general Skolem - Löwenheim theorem.

Appendix

        The purpose of this appendix is to put on record some minor additions to the first paper in this series (i. e., [2]).

        The additions are as follows:

        (a) In order to apply Lemma 9 in the proof of Theorem 9, it is necessary to prove first that the product of two Boolean relations is again a Boolean relation. This result, in turn, follows from the fact that the direct image of a closed set under a Boolean relation is again closed. For the proof, suppose that ϕ is a Boolean relation from Y to X, and let ξ denote the projection from Y × X onto X. If F is a subset of Y, then ϕF = ξ((F ×X) ∩ ϕ);₁ it is, consequently, sufficient to prove that every Boolean relation is closed, i. e., that ϕ is a closed subset of Y × X. If (y₀,x₀) ∉ϕ, then it is false that for all p in the dual algebra A of X; let p₀ be an element of A such that p₀(x₀) = 1 and fp₀(y₀) = 0. The set

is a neighborhood of (y₀,x₀) disjoint from ϕ; this proves that the complement of ϕ is open. From this result it follows also that the inverse image of a closed set under a Boolean relation is again closed; all that is needed is to observe that if η is the projection from Y × X onto Y, and if E is a subset of X, then ϕ ⁻¹Ε = η((Υ × Χ) ∩ϕ). All the results in this paragraph are due to E. J. Blattner.

        (b) The first part of the proof of Lemma 18 must be completed by establishing that the mapping σ there constructed is indeed a cross section of π, i. e., that πσy = y for all y in Y. The argument runs as follows. Since , it follows that for all p and all x, and hence that πγx = πx for all x. If y Y_r then y = πx for some x in X, and σy = γx; the desideratum follows from the result of the preceding sentence by making the obvious substitutions.

        (c) In the laet paragraph of the proof of Lemma 19 it must be proved that if q A and if

where r I⁺, then q⁺ I⁺. There is no loss of generality in assuming that p₀ ≠ 0; let x₀ be a point of X such that p₀(x₀) = 1. Forming the infimum of both sides of the assumed inequality with , we see that it is sufficient to prove that if q A and if , then q I⁺. To say that means that

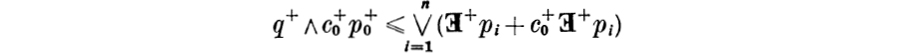
with p_i A⁺, i = 1,...,n. If we evaluate both terms of this inequality at (x₀, y), and if we recall that q⁺(x, y) = q+(x₀, y) = q(y) for all x and y, we obtain

If we write r_i(y) = p_i(x₀, y), then r_i A, and

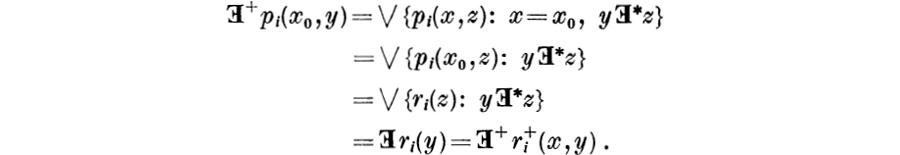
It follows that

and hence that q⁺ I⁺, as asserted.

References

        [1] P. R. Halmos, Polyadie Boolean algebras, Proc. Nat. Aead. Sci. U.S.A. 40 (1954), p. 296-301.

        [2] – Algebraic logic, I. Monadic Boolean algebras, Compositio Math., 12 (1955), p. 217-249.

        [3] L. Henkin, The completeness of the first-order functional calculus, J. Symbolic Logic 14 (1949), p. 159-166.

        [4] B. Jónsson and A. Tarski, Boolean algebras with operators, Amer. J. Math., 73 (1951), p. 891-939.

        [5] H. Rasiowa and R. Sikorski, A proof of the completeness theorem of Gödel, Fund. Math. 37 (1950), p. 193-200.

        [6] A. Tarski and F. B. Thompson, Some general properties of cylindric algebras, Bull. Amer. Math. Soc. 58 (1952), p. 65.

        [7] A. Tarski, A representation theorem for cylindric algebras, Bull. Amer. Math. Soc. 58 (1952), p. 65-66.

        [8] H. Wang, Logic of many-sorted theories, J. Symbolic Logic 17 (1952), p. 105-116.

UNIVERSITY OF CHICAGO

Reçu par la Rédaction le δ.4.19δδ