VII

EQUALITY

ALGEBRAIC LOGIC IV. EQUALITY IN POLYADIC ALGEBRAS(¹)

        Introduction. A standard way to begin the study of symbolic logic is to describe one after another the propositional calculus, the monadic functional calculus, the pure first-order functional calculus, and the functional calculus with equality. The algebraic aspects of these logical calculi belong to the theories of Boolean algebras, monadic algebras, polyadic algebras, and cylindric algebras respectively. The connection between the propositional calculus and Boolean algebras is well-known; for a recent exposition of it (and also of some aspects of the more advanced theories) see The basic concepts of algebraic logic, Amer. Math. Monthly vol. 63 (1956) pp. 363–387. Monadic algebras and polyadic algebras were studied in the first three papers of this sequence; [see Algebraic logic III, Trans. Amer. Math. Soc. vol. 83 (1956) pp. 430–470, and the references given there]. Cylindric algebras were introduced by Tarski and Thompson [Some general properties of cylindric algebras, Bull. Amer. Math. Soc. Abstract 58-1-85; see also Tarski, A representation theorem for cylindric algebras, Bull. Amer. Math. Soc. Abstract 58-1-86.]

        Most of what was done for polyadic algebras in [II] and [III] was restricted to locally finite polyadic algebras of infinite degree. (The Roman numerals refer to the other parts of this sequence.) Since it is known that every locally finite cylindric algebra of infinite degree possesses a natural polyadic structure, the results of those papers apply to cylindric algebras without any change. This paper, on the other hand, is mostly pre-cylindric; its main purpose is to discuss (in algebraic language) the introduction of equality.

        The paper is not self-contained. The notation introduced in §1 of [III] will be used without any further explicit reference, and some of the basic concepts studied in [III] (notably the concept of a predicate) will also be assumed known. (The most difficult part of [III], the theory of terms, is used in §9 only.) At one point (§6) the representation theorem for simple polyadic algebras is needed, and later (§7) we make use of the duality theory for monadic algebras. Most parts of the paper, however (and, in particular, all definitions and the statements of all the theorems) are accessible to anyone who has skimmed through [ill], provided that, in addition, he is acquainted with the elementary theory of functional polyadic algebras. For the convenience of the reader, the necessary facts from that theory are summarized in §1 below.

        §2 introduces the concept of equality and establishes the connection with cylindric algebras; §3 proves that equality is unique. §§4 and 6 study equality in functional algebras; the culmination of this work is the algebraic version of the completeness theorem for the functional calculus with equality. The most interesting negative results are in §5; it is shown there that an equality need not always exist (not even for the relatively well-behaved class of locally finite functional algebras). This fact makes it all the more pleasant to learn (§7) that an equality can always be adjoined. The last two sections are devoted to some results on the algebraic behavior of the description operator and touch on the algebraic meaning of the logical theorem that asserts the eliminability of that operator.

        1. Notation. In addition to the Boolean notation described in [III], we shall sometimes use p→q to denote p' ∨ q, and we shall use O to denote the simple Boolean algebra {0, 1}. The supremum and the infimum of a subset E of a Boolean algebra (if they exist) are denoted by and respectively.

        If I is a set and X is a nonempty set, we shall write X^I for the set of all functions from I into X; the value of a function x in X^I at an element i of I will always be denoted by x_i. If τ is a transformation on I, we denote by τ_* the mapping of X^I into itself such that (τ_*x)_i = x_τi for all i. If J is a subset of I, we denote by J_* the equivalence relation in X^I such that xJ_*y if and only if x_i = y_i for all i in I – J.

        If B is a Boolean algebra, then the set of all functions from X^I into B is a Boolean algebra with respect to the obvious pointwise operations. A function p from X^I into B is independent of a subset J of I if p(x) = p(y) whenever xJ_*y; the set J is a support of p (or J supports p) if p is independent of I – J. A function p is finite-dimensional if it has a finite support. If p is a function from X^I into B (not necessarily finite-dimensional), we write S(τ)p for the function defined by S(τ)p(x) =p(τ_*x). (A symbol such as S(τ)p(x), here and below, means (S(τ)p)(x).) If p is a function from X^I into B and if the set {p(y): xJ_*y} has a supremum in B for each x in X^I, we write for the function whose value at x is that supremum. A functional polyadic algebra is a Boolean subalgebra A of the algebra of all functions from X^I into B, such that S(τ)pA whenever pA and τ is a transformation on I, and such that exists and belongs to A whenever pA and J is a subset of I. The set X is called the domain of this functional algebra; when we wish to indicate the dependence of the algebra on I, X, and B, we call it a B-valued I-algebra over X. A functional polyadic algebra is a polyadic algebra with respect to the operator mappings S and defined above, and for elements of a functional algebra the set-theoretic and the algebraic definitions of support are equivalent.

        As in [III], we shall be working with a fixed (not necessarily functional) polyadic algebra (A, I, S, ); suitable warnings will indicate our few temporary deviations from this notation. The algebra (A, I, S, ) of [III] was assumed to be locally finite and of infinite degree. In this paper those conditions are needed only about half the time, and, consequently, they will not be assumed here; it will be clearer (and more elegant) to build them into the hypotheses of the theorems in which they are indispensable. When nothing is said to the contrary, the algebra A may have finite degree, or else, at the other extreme, it need not even be locally finite.

        2. Equality. A binary predicate E is reflexive if E(i, i) = 1 for every variable i. Except in the trivial case when the set of variables is empty (i.e., when the algebra A is simply a Boolean algebra with no additional polyadic structure), a predicate E is reflexive if and only if there exists at least one variable i₀ such that E(i₀, i₀) = 1. Indeed, if this is the case, and if i is any variable, then

        A binary predicate E of A is substitutive if p ∧ E(i, j)S(i/j)p whenever i and j are variables and pA. Except in the trivial case when the set of variables has fewer than two elements (i.e., when the algebra A is simply a Boolean algebra or else a monadic algebra), a predicate E is substitutive if and only if there exists at least one pair of distinct variables i₀ and j₀ such that p ∧ E(i₀, j₀) S(i₀/j₀)p whenever pA. Suppose, indeed, that this is the case and let i and j be any two variables. If i = j, the assertion is that p ∧ E(i, i) p for all p in A, and this is obvious. If i ≠ j, then there exists a permutation τ such that τi₀ = i and τj₀=j, and, consequently, such that τ(i₀/j₀)τ⁻¹ = (i/j). Since, by assumption,

whenever p∈A, the desideratum follows by applying S(τ) to both sides of this inequality.

        The condition used to define substitutivity implies a superficially stronger version of itself; if E is substitutive, then

whenever i and j are variables and pA. Substitutivity implies that the left side of (2.1) is dominated by the right side; it is, therefore, sufficient to prove that

The proof consists of the following straightforward computation:

From (2.1) we can derive still another version of substitutivity; the new version treats the variables i and j symmetrically. The assertion is that if E is substitutive, then

The proof of (2.2) is based on (2.1) and on the fact that (i/j)(i, j) = (i/j); it runs as follows:

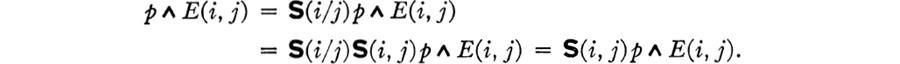
        A binary predicate E is symmetric if E(i, j) E(j, i) whenever i and j are variables; applying this condition with i and j interchanged, we conclude that E is symmetric if and only if

whenever i and j are variables. A binary predicate E is transitive if

whenever i, j, and k are variables. Techniques similar to the ones used above (for reflexivity and for substitutivity) show that, except in the cases when the number of variables is too small, E is symmetric if and only if there exists at least one pair of distinct variables i₀ and j₀ such that E(i₀, j₀) E(j₀, i₀), and similarly, E is transitive if and only if there exists at least one triple of distinct variables i₀,j₀, and k₀, such that E(i₀, j₀) ∧ E(j₀, k₀) E(j₀, k₀).

        An equality for A is a reflexive and substitute binary predicate of A. In the remainder of this section we derive some elementary consequences of this definition.

        (2.5) LEMMA. Every equality is symmetric and transitive.

        Proof. To prove that an equality E is symmetric, apply substitutivity to E'(i, j); to prove that it is transitive, apply substitutivity to E(j, k).

        (2.6) LEMMA. If E is an equality, then for all i and j. Proof. .

        (2.7) LEMMA. If E is an equality for A and if i and j are distinct variables, then for every p in A.

        Proof. Apply to (2.1) and use (2.6).

        (2.8) LEMMA. If E is an equality f or A and if p is an element of A independent of the variable i, then

        Proof. If i = j, the assertion is merely that , and this is true by assumption. If i ≠ j, replace p in (2.7) by S(j/i)p; the desired result follows from the fact that (i/j)(j/i) = (i/j), together with the fact that S(i/j)p=p (since p is independent of i).

        An alternative proof of (2.8) can be given directly (without reference to (2.7)) by another reference to (2.1).

        (2.9) LEMMA. If E is an equality for A and if i and j are distinct variables, then for every p in A.

        Proof. By (2.7), the two elements whose infimum is asserted to be 0 are equal to S(i/j)p and S(i/j)p'; the conclusion follows from the fact that S(i/j) is a Boolean homomorphism.

        (2.10) LEMMA. If E is an equality and if i, j, and k are variables such that i ' {j, k}, then

        Proof. Put p = E(j, k) in (2.8); the assumption i e' {j, k} guarantees that p is independent of i.

        A cylindric algebra is a Boolean algebra A, together with a set I, a mapping from I into quantifiers on A, and a mapping E from I² into A, such that (i) the values of commute with each other, (ii) E is reflexive, and (iii) Lemmas (2.9) and (2.10) hold for E. Thus the Lemmas (2.9) and (2.10), together with the more elementary properties of equalities, can be summed up by saying that a polyadic algebra with equality is a cylindric algebra.

        3. The uniqueness of equality. How many equalities is a polyadic algebra likely to possess? The answer is: not more than one. We shall presently see some examples of polyadic algebras for which, for one reason or another, there is no equality at all. First, however, we prove (in two different ways) that there can never be more than one.

        (3.1) LEMMA. If E and F are equalities f or the same polyadic algebra, then E = F (i.e., E(i, j) = F(i, j) for all i and j).

        Proof. Compute, as follows:

        Using a different method, we can recapture this result, and more.

        (3.2) THEOREM. If E is an equality for A, and if

        then the set D(i, j) has an infimum in A for each i and j, and

        REMARK. In intuitive language, the theorem says that to assert E(i, j) is the same as to assert, simultaneously, every proposition that becomes true when i is replaced by j.

        Proof. If S(i/j)p = 1, then, by (2.1), p ∧ E(i, j) = E(i, j), so that E(i, j) p; in other words, E(i, j) is a lower bound of D(i, j). Since S(i/j)E(i, j) =E(j, j) = 1, it follows that E(i, j) D(i, j). The preceding two sentences imply that the set D(i, j) contains a least element, namely E(i, j) ; this completes the proof of the theorem.

        Note that (3.2) does not assert that D(i, j) always has an infimum in A, nor that if D(i, j) does have an infimum in A, then A has an equality. There are polyadic algebras in which D(i, j) does not have an infimum for any pair of distinct variables i and j, and there are polyadic algebras in which D(i, j) has an infimum for every i and j, but if

then F is not an equality. The last point is worth a second glance. Suppose that A is such that D(i, j) has an infimum for every i and j and define F by (3.5). Since D(i, i) = {1}, it follows that

Since p' ∨ S(i/j)p D(i, j) for every p in A, it follows that

These two comments show that if F were a predicate, then F would be reflexive and substitutive. The only way F can fail to be an equality is that it fails to be a predicate, i.e., that it fails to be suitably related to the transformation structure of A. Our examples will show that this unpleasant phenomenon is realizable.

        4. Functional equality. Suppose that I is a set, X is a nonempty set, and B is a Boolean algebra. If i and j are any two (not necessarily distinct) elements of I, let E₀(i,j) be the function from X^I to B defined, for each x in X^I, by

The function-valued function E₀ (whose domain is I² and whose values are functions on X^I) will be called the functional equality associated with I, X_, and B. Note that since E₀(i,j)(x) O for all i,j, and x, the algebra B does not play an important role in this definition.

        If τ is a transformation on I, then

for all i and j. Indeed, for all x,

This result implies that whenever A is a B-valued functional I-algebra over X such that E₀(i_, j) A for all i and j, then E₀ is a predicate of A.

        Since, trivially,

for all i, it follows that whenever E₀ is a predicate of a functional algebra, it is automatically reflexive.

        If p is an arbitrary function from X^I into B, then

for all i and j. Indeed, if x is such that x_i ≠ y, then both sides of (4.4) vanish at x; if, on the other hand, x_i = x_j then both sides of (4.4) are equal, at x, to p(x). This result implies that whenever E₀ is a predicate of a functional algebra, it is automatically substitutive.

        From the preceding three paragraphs we conclude that whenever all the values of E₀ (i.e., all the functions E₀(i, j)) belong to a functional polyadic algebra A, then E₀ is an equality for A; this justifies the appellation “functional equality.”

        (4.5) LEMMA. If A is a functional I-algebra, then, for all i and j in I,

where E₀ is the associated functional equality.

        REMARK. It is not claimed that E₀(i, j) necessarily belongs to A; the assertion is merely that a necessary and sufficient condition that S(i/j)p = 1 is that E₀(i, j)(x) p(x) for all x.

        Proof. Suppose that S(i/j)p = 1, i.e., that p((i/j)_*x) = 1 for all x. If x is such that x_i = x_j, then (i/j)_*x = x, so that p(x) = 1, and therefore E₀(i, j)(x) p(x). If x_i ≠ x_j, the same inequality holds, because in that case, E₀(i, j)(x) = 0. Suppose now, conversely, that E₀(i, j) p. It follows (cf. (4.2)) that E₀(j, j) = S(i/j)E₀(i, j) S{i/j)p. Since (cf. (4.3)) E₀(j, j) = 1, this implies that S(i/j)p = 1.

        (4.6) COROLLARY. If E is an equality f or a functional I-algebra, then, for all i and j in I,

        

where E₀ is the associated functional equality.

        Proof. The result follows immediately from (4.5) and (3.2). It follows also, without the use of (3.2), by an application of (4.4) to E'(i, j) in the role of p.

        It is sometimes useful to know how a functional equality E₀(associated with I, X, and B, say) behaves with respect to quantification. Since the values of E₀(i, j) are always in O, the supremum that defines always exists; it is, in fact, given by

Indeed, E₀ is an equality for the functional polyadic algebra A of all functions from X^I into O; the desired conclusion follows from (2.6) together with the fact that (since E₀ is a predicate) {i, j} supports E₀(i, j).

        5. Examples. All the examples to be constructed in this section will be locally finite, O-valued functional algebras. Suppose that I is a set, X is a nonempty set, and C is a Boolean algebra of functions from X (not X^I) into O; the sets I and X and the Boolean algebra C will be held fixed throughout the construction.

        If J is a finite subset of I and if r_i is an element of C for each i in J, a function p from X^I into O is defined by

The function p may be called the tensor product of the functions r_i, for i in J. Let A be the Boolean algebra of functions from X^I into O generated by all such tensor products. It is easy to verify that every element of A is the supremum of a finite number of tensor products. It follows, in particular, that every function in A is finite-dimensional.

        We prove that A is a functional polyadic I-algebra over X. Suppose, for this purpose, that p A and that τ is a transformation on I; we must show that S(τ)p A. It is sufficient to treat the case in which p is given by (5.1). Since

it follows that if, for each j in τJ,

then

and hence that S(τ)p is the tensor product of the s_j, for j in τJ. This settles transformations.

        Suppose next that p A and that K is a subset of I; we must show that . Again it is sufficient to treat the case in which p is given by (5.1). Since, in that case,

it follows that is the tensor product of the r_i, for i in J – K, and hence that A is closed under the application of .

        The time has come to specialize: from now on we shall assume that X is the set of all integers. Let mbea fixed positive integer, and let C_m be the set of all those functions from X into O that are periodic of period m; in other words, r C_m if and only if r(x+m) = r(x) for all x in X. It is clear that C_{m is a Boolean algebra; we denote by Am the functional I-algebra obtained from Cm by the method of tensor products discussed above. We shall say that a function p from X^I into O is periodic of period m if it has that property in each coordinate separately, or, in other words, if, for each i in I, p(x) = p(y) whenever xi*y and xi = yi+m.}

        (5.2) LEMMA. A necessary and sufficient condition that a function p from X^I into O belong to A_m is that it be finite-dimensional and periodic of period m.

        Proof. The necessity of the condition is easy; we omit the proof. To prove sufficiency, suppose that p is a function from X^I into O with finite support J and period m. Let z be an element of X^I such that 0z_im – 1 when i J and z_i = 0 when i I – J. The set of all such z’s is finite, and, since p is independent of I – J and p is periodic of period m, the function p is uniquely determined by its restriction to that finite set. Suppose that p(z) = 1 at one such z. For each i in J, let r_i; be the function from X into O such that r_i is equal to 1 at every integer that is congruent to z_i modulo m and r_i·is equal to 0 otherwise; it follows that r_i C_m and that the tensor product of the r_i for i J, is dominated by p. Since the set of all z’s is finite, the set of all such tensor-products is also finite. The supremum of all such tensor products is exactly p, and therefore p A_m, as asserted.

        If i and j are in I, we define a function E_m(i, j) from X^I into O by

The definition implies that E_m(i, j) is finite-dimensional (in fact, {i, j} supports E_m(i, j)) and that E_m(i, j) is periodic of period m. It follows from (5.2) that E_m(i, j) A_m for all i and j. An obvious modification of the arguments used to show that a functional equality has the properties of an equality (cf. (4.2), (4.3), and (4.4)) serves to show that E_m is an equality for A_m.

        If A₀ is the set of all functions from X^I into O, then A₀ is a functional polyadic algebra and A_m is a polyadic subalgebra of A₀. Since E_m is not equal to the functional equality E₀, this example shows that a subalgebra of an algebra with equality may possess an equality different from the one that works for the large algebra. Since the functional algebras A_m and A₀ have the same domain, their elements, regarded as propositional functions, have the same subject matter. Accordingly we may say, in a very crude but nevertheless suggestive phrase, that the meaning of equality depends not so much on what we are talking about as on how much we are allowed to say about it. If we are allowed to say everything, then equality is the same as identity; if we are allowed to talk only in terms of a fixed modulus m, then equality is congruence modulo m.

        We now construct a new example by varying the auxiliary algebra C (but holding I and X fixed). We say that a function r from X into O is periodic (with unspecified period) if there exists a positive integer m such that r is periodic of period m. (Here it is essential that m be strictly positive.) Let C_* be the set of all periodic functions from X into O. It is clear that C_* is a Boolean algebra; we denote by A_* the functional I-algebra obtained from C_* by the method of tensor products.

        There is a useful relation connecting the “periodic” algebras defined so far (i.e., A_* and A_m, for m = 1, 2, · · ·). Since C_m is a Boolean subalgebra of C_*, it follows that A_m is a polyadic subalgebra of A_*; since, moreover, C_* , it follows that

All that needs proof is that if p A_*, then p A_m for some positive m. It is sufficient to treat the case in which p is given by (5.1), with r_i C_* for each i in J. If r_i is periodic of period m_i, let m be the least common multiple of all the m_i (i J); it follows that r_i is periodic of period w, and hence that p A_m, This result implies an analogue of (5.2) for A_*. We shall say that a function p from X^I into O is periodic (with unspecified period) if it has that property in each coordinate separately, or, in other words, if, for each i in I, there exists a (strictly) positive integer m such that p(x)=p(y) whenever xi_*y and x_i = y_i+m. It follows from (5.2) and from (5.4) that a necessary and sufficient condition that a function p from X^I into O belong to A_* is that it be finite-dimensional and periodic.

        (5.5) LEMMA. If D_*(i, j) = {p A_*: S(i/j)p = 1}, then the set D_*(i, j) has an infimum in A_* for each i and j, and

        Proof. Since D_*(i, i) = {1}, the case i =j is trivial. Suppose now that i ≠ j. By (4.5)

Since (cf. (5.4)) E_m(i_{, j}) A_* for every m, and since E₀(i, j) E_m(i, j) (by the definitions of E₀ and E_m), it follows that if q is a lower bound of D_*(i, j) in A_*, then q E_m(i, j) for every m. We shall show that this implies that q = 0. Indeed, if q(x) = 1, then E_m(i, j)(x) = 1 for every m, and therefore x_i = x_j (mod m) for every m. If, in other words, q(x) = 1, then x_i = x_j. By (5.4), q A_m for some positive m. It follows from (5.2) that q is periodic of period m, _{and hence that q(y) = 1 whenever each coordinate of y is congruent modulo m to the corresponding coordinate of x. This is a contradiction: even if xi = xj (as it must be if q(x) = 1), it does not follow that yi = yj (as it should be if q(y) = 1). The conclusion is that q(x) ≠ 1 for all x, and hence that q = 0.}

        Lemma (5.5) implies that the algebra A_* has no equality. Indeed, if E_* were an equality for A_*, then, by (3.3) and (5.5), we should have E_*(i, j) = 1 if i = j and E_*(i, j) =0 if i ≠ j. Since this particular function E_* from I² into A_* is not a predicate (S(i/j)E_*(i, j) ≠ E_*(j, j)), the algebra A_* can have no equality at all. Since A_m ⊂ A_*, it follows that an extension of an algebra with equality need not have an equality and, since A_* ⊂ A₀ it follows that a sub-algebra of an algebra with equality need not have one either.

        For our final example (still with the same I and X) we let C* be the Boolean algebra of all functions from X into O, and we denote by A* the functional I-algebra obtained from C* by the method of tensor products. There is a superficial reason for thinking that A* = A₀, but it is not so. In crude language the difference between A* and A₀ is that in A* we are allowed to say everything about the integers, but, so to speak, only a finite number of times, whereas in A₀ there are no restrictions.

        We already have an example (namely A_*) of a polyadic algebra that has no equality because the pertinent infima, although they exist, do not define a predicate. We shall prove that the algebra A_* does not have an equality either, but this time the reason is that the infima do not even exist. (This implies, in particular, that A* ≠ A₀.) We assert, in other words, that if

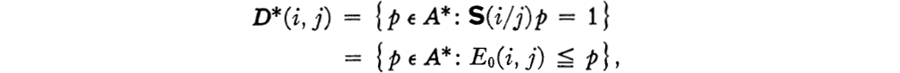
then the set D*(i, j) has no infimum in A* (unless i = j).

        We assert, to begin with, that if q is a lower bound of D*(i, j) in A* (i.e., if q p whenever E₀(i,j, p),then q E₀(i, j). Suppose, indeed, that E₀(i, j)(z) = 0; we are to show that q(z) =0. Let r be the characteristic function of the

singleton {z_i} in X and let s be the characteristic function of {z_j}. If, for every x in X^I,

then p A* and p(z) = 0. Since a direct verification shows that E₀(i, j) p, it follows that q p, and hence that q(z) = 0, as asserted.

        In view of the preceding paragraph, the assertion about D*(i, j) reduces to this: among the g’s in D* such that q E₀(i, j) (i.e., among the lower bounds of E₀(i, j) in A*) there is no greatest. For each c in X, let r^c be the characteristic function of {c} in X, and write

If q is the supremum of a finite number of functions such as q^c, then q E₀(i, j) but q can certainly not be the greatest lower bound of E₀(i, j) in A*, because the adjunction of an extra c makes it strictly greater. The proof will be completed by showing that if q is any lower bound of E₀(i, j) in A*, then q is dominated by the supremum of a finite number of functions such as q^c. In this argument we may and do assume that q ≠ 0.

        Since q A*, the function q is the supremum of a finite number of nonzero tensor products such as q₀, where

Here J is a finite subset of I and r_k C* for all k in J. We prove that i and j must belong to J. Indeed if, say, i ' J, let x be an element of X^I such that r_k(x_k) = 1 for all k in J (recall that q₀ ≠ 0) and such that x_i ≠ x_i. It follows that q₀(x) = 1, and therefore q(x) = l, whereas E₀(i, j)(x)=0; this contradiction implies that i J, as asserted. It remains only to prove now that both r_i and r_j have the form r^c for some c in X. We know that neither r_i nor r_j, vanishes identically. If either one took the value 1 at two distinct elements of X, then we could find an element x of X^I such that r_k(x_k) = 1 for all k in J and such that xi xj; since we just saw that this leads to a contradiction, the proof is complete.

        6. Equalities for functional algebras. We have seen that an equality for a locally finite functional algebra need not be a functional equality. Our next purpose is to show that, at least in the O-valued case, every example of such a situation is similar to the particular example (congruence with respect to a fixed modulus) that we constructed above, and that, by a suitable modification, every such example can be converted into a functional algebra with a functional equality. Throughout this section we shall assume that E is an equality (not necessarily the same as the functional equality E₀) for a locally finite, B-valued functional polyadic I-algebra A over a domain X; to exclude trivial cases we shall assume also that the cardinal number of I is greater than or equal to 3.

        Suppose that a and b are elements of X with the following property: there exists an element z of X^I and there exist distinct variables i and j such that z_i = a, z_j = b, and E(i, j)(z) = 1. If that is the case, we shall write a~b; we proceed to investigate the binary relation ~ in X.

        (6.1) LEMMA. If a~b, then E(i, j)(x) = 1 for all i and j and x such that x_i = a and x_j = b.

        Proof. By assumption, there exists an element z of X^I and there exist distinct variables i₀ and j₀ such that z_i0 = a, z_j0 = b, and E(i₀, j₀)(z) = 1. If τ = (i₀, j₀/i, j), then

for all i, j, and x. If, in particular, x_i = a and x_j = b, then (τ_*x)_i0 = a and (τ_*x)_j0 = b. It follows that τ_*x(I – { i₀, j₀ })_*z; since E(i₀, j₀) is independent of (I – { i₀, j₀ }), this implies that E(i, j)(x) = E(i₀, j₀)(z) = 1.

        (6.2) LEMMA. the relation ~ is an equivalence.

        Proof. Suppose that a X. If z_i = a for all i, then E₀(i, j)(z) = 1 for all i and j; it follows from (4.6) that E(i, j)(z) = 1, and hence that a~a.

        Suppose that a~b. If z X^I and if i and j are distinct variables such that z_i = a, z_j = b, and E(i, j)(z) = 1, then it follows from the symmetry of E that E(j, i)(z) = 1 and hence that b~a.

        Suppose, finally, that a~b and b~a. Let u and v; be elements of X^I and let i, j, and k be distinct variables such that u_i = a, u_j = v_j = b, v_k = c and E(i, j)(u) =E(j, k)(v) = 1. (The existence of these objects follows from (6.1).) Let z be an element of X^I such that z_i = a, z_j = b, and z_k = c. It follows that E(i, j)(z) = E (i, j)(u) = 1 and E(j, k)(z) = E(j, k)(v) = 1, so that, by the transitivity of E, E(i, k)(z) = 1, and hence a~c.

        REMARK. Lemma (6.2) is false for dyadic algebras. Suppose that I = {i, j} (with i ≠ j); write X = {0, 1, 2, 3} and B = O. If p is the characteristic function of {z X^I: |z_i – z_j| 1}, then A = {0, p, p', 1} is a functional I-algebra over X. If E(i, i) = E(j, j) = 1 and E(i, j) = E(j, i) =p_, then E is an equality for A. In this situation the assertions 0~1, 1~2, and 2~3 are true, but the assertions 0~2, 0~3, and 1~3 are false.

        (6.3) LEMMA. If p is an element of A with support J and if x and y are elements of X^I such that x_i~y_i whenever i J, then p(x) =p(y).

        Proof. Since p has a finite support, there is no loss of generality in assuming that J is finite. Let i be an element of J and let j be an element of I – J. If u is defined by

then xj_*u and, by (6.1), E(i, j)(u) = 1. Since p is independent of j, it follows

that p(x) =p(u), and, since E(i, j)(u) = 1, it follows that

If v = (i/j)_*u, then v_i = u_j = y_i, v_j = u_j = y_i, and v_k=u_k = x_k whenever k ' {i, j}. We know that p(x)=p(v). If

then vj_*w; it follows that p(y) = p(w) and hence that p(x)=p(w). We have proved thus that if we replace x_i by y_i for some i in J, then p(x) remains unchanged. An inductive repetition of this result implies that if z_i = y_i whenever i J and z_k = xk whenever k J, then p(x) =p(z). Since zJ_*y, it follows that p(z) =p(y) and hence that p(x) =p(y).

        Our next result has nothing directly to do with equality; it is a general statement (of some independent interest) about functional polyadic algebras. (The result, by the way, is true without any restrictions on the cardinal number of I.) Suppose that π is a mapping from the set X onto a set X^#. The mapping π induces a mapping π_* from X^I onto (X^#)^I; by definition,

for all i in I. The mapping π_*, in turn, induces a mapping ƒ that sends B-valued functions on (X^#)^I onto B-valued functions on X^I; by definition,

        (6.4) LEMMA. If π is a mapping from X onto a set X^#_, if f is the functional mapping induced by π, and if A^# is the set of all those B-valued functions q on (X^#)^I for which fq A, then A^# is a B-valued functional I-algebra over X^# and the mapping ƒ is a polyadic monomorphism from A^# into A.

        Proof. The verification that ƒ is a Boolean homomorphism (and that, therefore, A^# is a Boolean algebra) is routine. If q A^# and fq = 0, then q(π_*x) = 0 for all x in X^I; since π_* maps X^I onto (X^#)^I, it follows that q = 0, and hence that ƒ is a monomorphism.

        If τ is a transformation on I and if x X^I, then

        From this it follows that if q A^#, then

This, in turn, implies that A^# contains S(τ)q along with q, and that f preserves the transformation structure of A^#.

        Suppose, finally, that J is a subset of I and that x X^I. If x^# is an element of (X^#)^I such that

write y_i = x_i if i ' J, and, if i J, let y_i be an element of X such that . It follows that

If, conversely, x and y are elements of X^I and x^# is an element of (X^#)^I such that (6.6) holds, then x_i = y_i (and therefore πxi = πyi) whenever i J; it follows that whenever i ' J, and hence that (6.5) holds. From these considerations we deduce that if q A^#, then exists for all x^# in (X^#)^I, the function belongs to A^#, and ; the relevant computations run as follows:

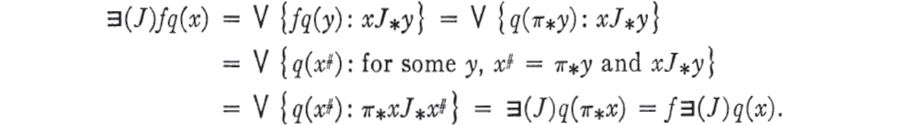
This completes the proof of Lemma (6.4).

        We shall say that an equality (such as E) on a functional algebra (such as A) is reduced if E(i, j)(x) = 1 implies that x_i = x_j whenever i and j are in I and x is in X^I.

        (6.7) THEOREM. If A is a locally finite, B-valued functional I-algebra of degree greater than or equal to 3, and if E is an equality f or A, then A is isomor-phic to a B-valued functional I-algebra A^# with a reduced equality E^#.

        Proof. Let X be the domain of A and let ~ be the equivalence relation induced by E in X. Let X^# be the set of all equivalence classes and let π be the canonical mapping from X onto X^#, so that πa = πb if and only if a~b. Let ƒ and A^# be the functional mapping and the functional algebra described in (6.4). We shall prove that ƒ is an isomorphism; all we need to do for this purpose is to prove that ƒ maps A^# onto A. Given an element p of A and an element x^# of (X^#)^I, find an x in X^I such that π_*x = x^# and write q(x^#) =p(x). This definition of q is unambiguous. Indeed, if π_*x = π_*y, then π_*x_i = π_*y_i for all i, so that x_i~y_i for all i; Lemma (6.3) implies that p(x) =p(y). The function q so defined belongs to A^# and is such that fq = p; indeed

        Let E^# be the equality for A^# corresponding to E, i.e., E^#=f⁻¹E, or, equivalently, ƒ E^# =E. If E^#(i, j)(x^#) = 1, find x so that π_*x = x^# Then E(i,j)(x) = E^#(i, i)(x^#) = l, so that (by the definition of ~) x_i~x_j·; this implies that π_*x_i = π_*x_j and hence that .

        (6.8) COROLLARY. If A is a locally finite, O-valued functional I-algebra of degree greater than or equal to 3, and if E is an equality for A, then A is iso-morphic to an O-valued functional I-algebra A₀ such that the functional equality E₀ is an equality for A₀.

        Proof. It follows from (4.6) and the definition of a reduced equality that a reduced equality for an O-valued functional algebra is the same as the associated functional equality.

        The results of this section furnish a proof of the algebraic version of the completeness theorem for first-order functional calculi with equality. Since all the details of this theory are similar to the corresponding details for pure functional calculi, we shall be satisfied with a highly condensed discussion.

        The relevant algebraic object is an equality algebra, i.e., a pair (A, E), where A is a polyadic algebra (an I-algebra, say), and E is an equality for A. If (A₁, E₁) and (A₂, E₂) are two such objects, then an equality homo-morphism is defined to be a polyadic homomorphism ƒ from A₁ into A₂ such that fE₁ = E₂. (This means, of course, that f E₁(i, j) = E₂(i, j) for all i and j in I.) Not every polyadic homomorphism is an equality homomorphism (witness the embedding of O into some nontrivial equality algebra), but if ƒ is a polyadic homomorphism from A₁ onto A_2, then it is necessarily an equality homomorphism. The reason is that, in that case, f E₁ is an equality for A_2, and hence, by the uniqueness of equality, f E₁ = E₂.

        It follows from the preceding discussion of equality homomorphisms that concepts such as ideal, maximal ideal, simplicity, semisimplicity, and quotient algebra are exactly the same for equality algebras as they are for just plain polyadic algebras. The only new concept is that of an equality model] this, by definition, is an algebra A with equality E such that A is a model in the polyadic sense (i.e., an O-valued functional algebra) and such that E is the associated functional equality. (The concept of an equality model is the algebraic version of what in logical terms is called a standard model for a first-order functional calculus with equality. The terminology is Henkin’s; see Completeness in the theory of types, J. Symbolic Logic vol. 15 (1950) pp. 81-91.) The only difficult part of the completeness theorem for equality algebras follows immediately from the corresponding theorem for polyadic algebras [II, (17.3)] together with (6.8); it is the following characterization of simple equality algebras.

        (6.9) THEOREM. Every locally finite simple equality algebra of infinite degree is isomorphic to an equality model.

        7. Adjunction of equality. We have seen that the existence of an equality for an I-algebra A (not necessarily functional, and with no restrictions on the size of I) depends on the existence and properties of certain infima. The sets whose infima are relevant are defined by

for each pair of variables i and j Even if ∧ D(i, j) always exists, the function (from I² into A) that it defines need not be a predicate. There are two difficulties encountered in trying to prove that it is one. If τ is a transformation on I, then we could try to prove that S(τ)(∧D(i, j)) = ∧D(τi, τj) by proving first that

and by proving next that

Neither of these equations is true in general. (A counter example to (7.2) is furnished by (5.5); take τ = (i/j).) It turns out, however, that (7.1) is nearly true and that (7.2) is often true. The purpose of this section is to make these assertions precise, and to infer from them that in a certain sense every poly-adic algebra has an equality after all.

        (7.3) LEMMA. If i and j are in I and τ is a transformation on I, then S(τ)D(i_,j)⊂D(τi_, τ_j).

        Proof. We are to prove that if S(i/j)p = l, then S(τi/τj)S(τ)p = 1. The result follows immediately from the observation that (τi/τj) τ = (τi/τj) τ (i/j).

        Lemma (7.3) asserts that (7.1) is half true. This can be improved, as follows. Let E(i, j) be the set of all those elements of D(i, j) that depend on i and j only; more precisely

The following lemma asserts that E(i, j) is not much smaller than D(i, j) ; combined with its successor it shows that (7.1) is nearly true, as asserted.

        (7.5) LEMMA. If p D(i, j) then there exists an element q of E(i, j) such that q p. If either ∧D(i, j) or ∧E(i, j) exists, then so does the other and the two are equal.

        Proof. To prove the first assertion, write q = ∀(I – {i, j})p . Then q p and {i, j} supports q; since (i, j) lives outside I – {i, j}, it follows that

and hence that q E(i, j). The second assertion is a consequence of the first assertion and of the fact that E(i, j) ⊂ D(i, j).

        (7.6) LEMMA. If i and j are in I and r is a transformation on I, then S(τ)E(i,j) = E(τi, τj).

        Proof. If p D(i, j), then S(τ)p D(τi, τj) (by (7.3)), and if {i, j} supports p, then { τi, τj} supports S(τ)p. This proves that S(τ)E(i, j) ⊂ E(τi, τj).

        We must show next that if q Ε(τi, τj), then q = S(τ)p for some p in E(i, j). If τi = τj, then q = 1, and we may write p = 1. If τ i τj, then there exists a permutation π on I such that πτi = i and πτj = j; we write p = S(π)q. Since {τi, τj} supports q and since π{τi, τj} = {i_, j}_} it follows that {i, j} supports p. Since (i/j)π = π(τi/τj) (both sides map τi onto j and every k distinct from τi onto τk), it follows that

and hence that p E(i, j). Since, finally, τ = π^–1 on {i, j), it follows that

and the proof of the lemma is complete.

        We go on now to show that (7.2) is often true, in the sense that every algebra can be embedded into one in which it is true. The idea is to use one of the standard methods of embedding a Boolean algebra into a complete Boolean algebra. The method that it is convenient to use is the one that goes via the representation theory; all we have to do is to pay attention to some polyadic details in the course of the embedding(²).

        If A is an arbitrary Boolean algebra, then there exists a Boolean space X such that A is isomorphic to the set of all continuous functions from X into O; there is, therefore, no loss of generality in assuming that A is the set of all such functions. If A⁺ is the Boolean algebra of all (not necessarily continuous) functions from X into O, then A is a Boolean subalgebra of A⁺. (For a detailed discussion of the concepts and results used in the remainder of this section see [I, Part 2].)

        In what follows we apply the duality theory of hemimorphisms and Boolean relations. If ƒ is a hemimorphism on A, we write ƒ* for its dual (so that f* is a Boolean relation in X). The hemimorphism ƒ can be extended to a hemimorphism f⁺ on A⁺; we write

whenever r A⁺ and x X. It is trivial that f⁺ is indeed a hemimorphism on A⁺; the fact that f⁺ is an extension of ƒ is expressed by

We proceed to show that all the essential properties of ƒ are reflected by f⁺.

        (7.9) LEMMA. If f is the identity mapping on A, then f⁺ is the identity mapping on A⁺; if f and g are hemimorphisms on A, then

        Proof. The first assertion follows from the fact that if ƒ is the identity mapping on A, then ƒ* is the identity mapping on X. The second assertion is proved by the computation:

(²) The method was used for essentially the same purpose by Jonsson and Tarski, Boolean algebras with operators, Amer. J. Math. vol. 73 (1951) pp. 891–939.

        (7.11) LEMMA. If f is a Boolean endomorphism (or a quantifier) on A, then f⁺ is a Boolean endomorphism (or a quantifier) on A⁺.

        Proof. If ƒ is an endomorphism, then f* is a function (from X to X),so that xf*y means y=f*x; the assertion about endomorphisms now follows easily from the definition (7.7). If ƒ is a quantifier, then f* is an equivalence relation (in X); in that case

and therefore f⁺ is a quantifier.

        The algebra A⁺ is, of course, a complete Boolean algebra; the supremum and the infimum of any family {r_α } of elements of A⁺ are given by

If ƒ is a hemimorphism on A, then

It follows that if ƒ is an endomorphism, then

        Suppose now that A has a polyadic structure, so that, say, (A, I, S, ) is a polyadic algebra. If τ is a transformation on I, we write S⁺(τ) = (S(τ))⁺, and, similarly, if J is a subset of I, we write . It follows from (7.9) and (7.11) that (A⁺, I, S⁺, ) is a polyadic algebra; (7.8) implies that this algebra has (A, I, S, ) as a polyadic subalgebra. Caution: the algebra A⁺ need not be locally finite, even if A is such.

        Let D⁺(i, j) and E⁺(i, j) be the sets defined for A⁺ as D(i. j) and E(i, j) were defined for A, and write

If r is a transformation on I, then, by (7.12),

and therefore, by (7.6),

We see thus that E⁺ is a predicate of A⁺. Since (7.5) implies that

it follows from (3.6) and (3.7) that E⁺ is an equality for A⁺.

        The set of all those elements of A⁺ that have a finite support is a polyadic subalgebra of A⁺; if A is locally finite, then that subalgebra includes A and contains every E⁺(i, j). It follows that E⁺ is an equality for the subalgebra; note that the subalgebra is locally finite if A is such.

        The important part of our results can be summed up as follows.

        (7.14) THEOREM. Every (locally finite) polyadic algebra is a polyadic subalgebra of a (locally finite) algebra with equality.

        It follows from (7.14) that every polyadic algebra can be embedded into a cylindric algebra. (Note that (7.14) does not say that if the given algebra already has an equality, then the embedding algebra must have the same equality.) The logical counterpart of the theorem asserts the consistency of equality. One way to put it is this: a consistent first-order functional calculus remains consistent when a (new) sign of equality is adjoined to its symbols and the usual requirements on an equality are adjoined to its axioms.

        8. Unique existence. We have studied the basic properties of equality and we have seen some situations in which equalities exist and others in which they do not. The question is: what can we do with an equality when there is one? Since equality is a fundamental logical concept of universal importance, and since algebraic logic is a faithful mirror of ordinary logic, the answer to the question is not a theorem but an extensive theory. The methods of developing that theory are algebraic adaptations of known logical methods. In what follows we shall illustrate the relevant techniques by studying the algebraic counterparts of propositions that assert the existence of a unique object satisfying certain conditions. From now on we shall always assume that the polyadic algebra we are given (denoted, as always, by (A, I, S, )) is locally finite and of infinite degree, and that it comes equipped with an equality (denoted, as before, by E).

        We begin with a theorem that asserts, essentially, that for constants equality is the same as identity.

        (8.1) THEOREM. If b and c are constants of A, then a necessary and sufficient condition that b = c is that E(b, c) = 1.

        REMARK. The theory of expressions such as E(b, c) is treated in [III, §10]. For present purposes it is sufficient to know that if P is a unary predicate, then P(c)=S(i/c)P(i) whenever i I, and if Q is a binary predicate, then Q(b, c) = S(i/b)S(j/c)Q(i, j) whenever i and j are distinct elements of I. Observe that if Q is a binary predicate, and if P(i) = Q(i, i) for every i in ƒ, then P is a unary predicate.

        Proof. The necessity of the condition is trivial; since E(i, f) = 1, it follows that

Suppose now that the condition is satisfied. We shall prove that b = c by provins that

whenever i I and p A; cf. the uniqueness assertion of the constant-construction theorem [II, (14.1)]. For this purpose, let j be a variable distinct from i and such that p is independent of j. Since (cf. (2.1))

it follows that

Since p is independent of j, it is clear that

On the other hand, since S(i/c)p is independent of both i and j, it follows that

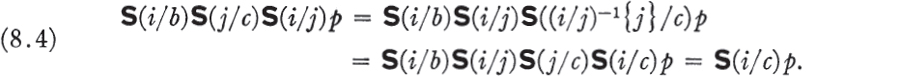
Putting these facts together with (8.2), and using the fact that E(b, c) = 1, we conclude that

as asserted.

        Our next result is an auxiliary statement (of some independent interest) about monadic algebras. If A is a monadic algebra with quantifier , and if c is a constant of A [I, §13], then A might contain an element q whose intuitive interpretation is the proposition “the (only) variable of A is equal to c.” The phrase “is equal to” is, to be sure, not expressible in a monadic algebra. The possibility just mentioned is realizable nevertheless. If, for instance, A is a functional monadic algebra over some domain X, if x₀ X_} and if the characteristic function q of the singleton {x₀} belongs to A, then, intuitively, q(x) can be thought of as the proposition “x = x₀” In this situation q is “true” (i.e., it is equal to 1), and, if p A, then is “false” (i.e., it is equal to 0). Conversely, and this is the main point, these two conditions guarantee the existence of a unique constant c such that “what q says is true about c and about nothing else.”

        (8.5) THEOREM. If A is a monadic algebra with quantifier , and if q is an element of A such that

and

then there exists a unique constant c of A such that cq = l. The constant c is defined by

for all p in A,

        Proof. If we define an operator c on A by (8.8), then, clearly, c1 = 1, and c(p₁ ∨ p₂) = cp₁ ∨ cp₂ whenever p₁ and p₂ are in A. Since, by (8.7), cp ∨ cp′ = 0 for all p, and since

it follows that cp' = (cp)', so that c is a Boolean endomorphism of A. Clearly

and

so that c is a constant of A; we note that

To prove uniqueness, suppose that b is a constant of A such that bq = 1. Since

and since both b and c are Boolean homomorphisms, it follows that b = c, and the proof of the theorem is complete.

        We return now to the polyadic algebra (A, I, S, ) with equality E. An existential assertion (“there is at least one i such that q”) corresponds, in algebraic terms, to an element of the form . What is the algebraic correspondent of an assertion of uniqueness (“there is at most one i such that q”)? The answer to this question will be denoted by !(i)q. To define !(i)q, select a variable j distinct from i and such that q is independent of j, and write

(Recall that if J is a subset of I, the universal quantifier ∀(J) is defined by for all p in A.) It is, of course, important to know that the definition (8.9) is unambiguous, i.e., that if k ≠ i and q is independent of k, then the right side of (8.9) remains unchanged when we replace j by k. The proof is a simple computation; since q is independent of {j, k}, we have

The algebraic correspondent of an assertion of unique existence (“there is exactly one i such that q^”) is denoted by ; it is defined by

The principal result concerning unique existence is that if is true, then there does indeed exist a unique constant for which q is true.

        (8.11) THEOREM. If {i} supports q and if , then there exists a unique constant c of A such that S(i/c)q = 1.

        Proof. The assumption , together with the definition (8.10), implies that

and

whenever j ≠ i. (Since {i} supports q, the element q is automatically independent of every j distinct from i.) To construct c, we shall apply (8.5) to A regarded as a monadic algebra with quantifier 3(f).

        From (8.12) we know that (8.6) is satisfied in the present situation. To prove (8.7), it is convenient to know that if p A and if j is a variable distinct from i such that p is independent of j, then

(To prove (8.14), replace by , observe that since p ∧ q is independent of j, it follows that S(i, j)(p ∧ q) = S(i/j)(p ∧ q), and use the fact that the right side of (8.14) is independent of {i, j}.) We are now ready to prove that

For this purpose, we select j distinct from i and such that p is independent of j; then

        It follows from (8.5) that if , then ƒ is a Boolean endo-morphism of A such that , , and fq = 1. If p A and if j ≠ i, then

It follows from the constant-construction theorem [II, (14.1)] that there exists a constant c of A such that S(i/c) = ƒ; this proves the existential assertion of the theorem.

        To prove uniqueness, suppose that b and c are constants of A such that

It follows from (8.13) that if j ≠ i then

Since (cf. (8.3) and (8.4)) this implies that

it follows from (8.16) that E(b, c) = 1. The proof of the theorem is completed by an application of (8.1).

        The constant c constructed in (8.11) (“the i such that q”) will be denoted by (i)q. (The traditional symbol is an inverted iota instead of an inverted T. The symbol here proposed is easier to read and more in harmony with the standard symbols ∀ and ; it might also serve as mnemonic for the initial letter of the article “the”. The standard discussion of the description operator is given by Hilbert and Bernays, Grundlagen der Mathernatik, Berlin, 1934; vol. I, §8.) The characteristic property of may be expressed as follows: if i supports q and if , then

        The construction of (i)q sheds light on the once controversial problem of contextual definitions. It might be said that the intuitively most satisfactory definition of some particular constant is an explicit definition, i.e., a definition that constructs the new constant from other constants, terms, and operations that are already available. It might also be said that a contextual definition of a constant c does not really define c, but, instead, describes in detail the effect of substituting c for a variable. According to the algebraic point of view, however, the latter kind of description is a constant, and no more primitive kind of definition can be hoped for. Assuming the existence of certain constants and manufacturing others from them is relatively easy and does not get at the root of the matter. Assuming merely a proposition of unique existence and constructing the unique constant whose existence is thereby implied is much harder, and, from the algebraic point of view much more explicit. We see thus that in algebraic logic the traditional terminology gets turned around; the so-called explicit definitions can be formulated only within a previously assumed context, whereas the so-called contextual definitions can be explicitly written down.

        9. Operations and predicates. We conclude our present study of equality by establishing its connection with the theory of terms, operations, and predicates. These concepts are studied in [ill], and, in this section, we shall make full use of the definitions and theorems of that paper.

        As for terms, the fact is that everything that can be said about constants can be generalized to terms. We illustrate this assertion by proving the generalization of (8.11).

        (9.1) THEOREM. If J is a finite set not containing i,if J ∪ {i} supports q, and if , then there exists a unique J-term t of A such that S(i/t)q = 1.

        Proof. Write I⁻ = I – J and let (A⁻, I⁻, S⁻, ) be the algebra obtained from A by fixing the variables of J. If j ≠ i and j ' J, then by assumption, and, therefore, ; this implies that {i} supports q in A⁻. The fact that in A^- implies that in A⁻. It follows from (8.11) that there exists a unique J-constant c of A such that S(i/c)q = 1. From this and from the theorem on extending J-constants to J-terms [III, (6.7)] we conclude that there exists a J-term t such that S(i/t)q = 1. The uniqueness of t is implied by the uniqueness assertions of (8.11) and of the extension theorem just referred to.

        The term t constructed in (9.1) will be denoted by.(i)q.

        The treatment of predicates in [III] is similar to the treatment of operations; the similarity is so great that it is natural to suspect the existence of a close connection between the two concepts. The connection is most clearly visible in the presence of an equality. There is a one-to-one correspondence between all operations and some predicates (namely, the ones that are single-valued) ; this is still another example of a well-known logical phenomenon that can be discussed within the framework of polyadic algebras with equality. The relevant definition is obvious: an (n + l)-place predicate P is single-valued (with respect to its first n arguments) if whenever (i₁ · · · , i_n) Iⁿ and j I – {i₁, · · · , i_n}. The connection between single-valued predicates and operations can be stated as follows.

        (9.2) THEOREM. If T is an n-place operation and if

whenever (i₁ · · · , i_n, j) Iⁿ⁺¹, then P is a predicate that is single-valued with respect to its first n arguments. If, conversely, P is an (n+1)-place predicate that is single-valued with respect to its first n arguments, then there exists a unique n-place operation T such that (9.3) holds] the operation T is such that

whenever (i₁, ···, i_n) Iⁿ and j I – {i₁, · · · , i_n}.

        Proof. For simplicity we shall discuss the case n = 1 ; the general case differs from this special case in notation only. The first assertion of the theorem (in the special case) starts with a unary operation T and the equation

If τ is a transformation on I then

so that P is a binary predicate. If i, j, and k are distinct variables, then

In order to complete the proof that P is single-valued, suppose now that h, i, j, and k are distinct variables, and recall that

Applying S(h/T(i)) to this inequality and using (9.5), we obtain

since this is equivalent to !(j)P(i, j) = 1, the proof of the first assertion of the theorem is complete.

        The second assertion (case n = 1 only) starts with a binary predicate P such that

whenever i ≠ j. It follows from (9.1) that for each i in t there exists a unique {i}-term, say T(i), such that

in fact T(i) is (j)P(i, j) whenever i ≠ j. Suppose now that i, j, and k are distinct variables, and observe that, by (9.6),

Applying S(k/T(i)) to this inequality and using (9.7) we obtain

On the other hand

applying S(k/T(i)) to this equation and using (9.7), we obtain

We have proved thus that P(i, j) = E(T(i), j) ; it remains only to prove that T is an operation.

        We must show that if τ is a transformation on I, then

Since P(i. T(i)) = 1 and since P is a predicate, we know that

On the other hand, replacing i by τi in (9.7), we obtain

The desired conclusion follows from (9.8) together with the fact that (9.9) characterizes Τ(τi), i.e., if t is a {τi}-term such that P(τi, t) = 1, then t = T(τi). This completes the proof of the theorem.

        10. Errata (Added in proof, June 4, 1957.) In the proofs of [III, (11.7)] and [III, (13.3)] it is asserted that S(i, j)p = p. This is false; what is true is that S(i, j)p is independent of (for (11.7)) and of K (for (13.3)). In view of this, the computations in the proofs have to be changed after the first step. The change is the same in both cases : replace S(i/t) by S(i,j)S(j/t)S(i_,j). The remaining steps in both computations are almost automatic; use the obvious commutation relations to pull the left S(i, j) to the extreme left, use the fact that the assumptions apply to S(i, j)p as well as to p, and, finally, replace S(i, j)S(j/v)S(i, j) by S(i/v). I am grateful to Mr. Leon Le-Blanc for calling these errors to my attention.

UNIVERSITY OF CHICAGO,

CHICAGO, ILL.