
STATISTICAL TESTS
STATISTICAL TESTS
GLOSSARY
σ The Greek letter sigma, which in statistics often represents the standard deviation of a population.
√ Mathematical symbol for the square root. The square root of a number, x, is another number, y, with the property that y × y = x.
ANOVA test ANalysis Of VAriance test used to examine statistical differences between two groups.
Chi-square distribution Also written as x2, a probability distribution with specific properties that can be used to test the ‘goodness of fit’ between an observed distribution and a theoretical one.
median The middle value in an ordered set of numbers.
mode The most common value in a set of numbers.
null hypothesis The default assumption of an experiment that there is no relationship between the variables under observation.
observation error A technical error introduced during measurements of quantities or values.
plausible values A range limit within which the real value is likely to be found.
point estimate A single or exact value for an unknown parameter.
reproducibility crisis A recent phenomenon in several scientific fields where attempts to reproduce many published studies have not been possible, leading to concerns of lack of rigour in publications and/or methodology.
scatter graph A plot of two continuous variables on x and y axes.
significance level The threshold defined where a statistical p-value is considered ‘significant’. Often set as 0.05.
t-test A pairwise test of two normally distributed datasets under the assumption that they are from the same distribution.
variance A measure of the variability in a sample or distribution. Also, the square of the standard deviation.
STATISTICAL TESTS
the 30-second calculation
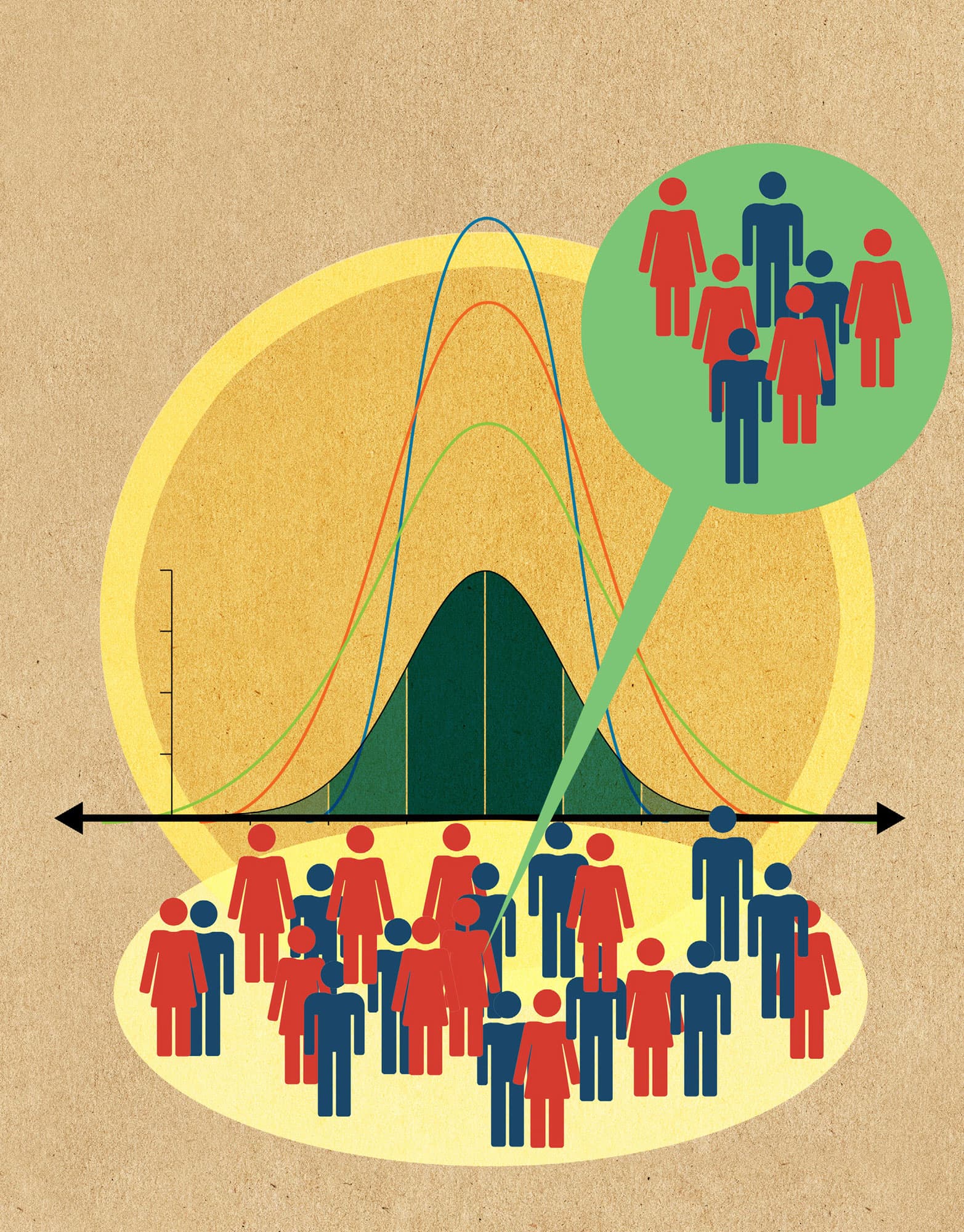
Statistical tests evaluate quantitatively the strength of evidence for a claim. The purpose of a statistical test is to ascertain whether there is enough evidence to reject or fail to reject a given claim. For example, a statistical test can be used to evaluate the claim that school A outperforms school B. The claim to be tested is called the hypothesis, which is subdivided into null and alternative hypotheses. A null hypothesis, denoted with H0, is a claim of equality (no difference) between variables being tested. By default, the null hypothesis is considered to be true unless there is enough evidence to prove otherwise. An alternative hypothesis, denoted with H1, is a statement of inequality (difference) between the variables being tested. For example, H0 claims that school A performs the same as school B; H1 claims that school A outperforms school B. A statistical test will test the claim H0 against H1 by computing a probability value called p-value. The null hypothesis is rejected if the p-value is below a particular threshold (see here) and it is accepted otherwise. Failing to reject H0 implies that there is enough evidence from data to support the claim of equality (no difference) between the variables being tested.
3-SECOND COUNT
A statistical test is a way to investigate if evidence from data is strong enough to support a given hypothesis.
3-MINUTE TOTAL
Depending on the specific questions of interest, there are different methods including T-test, ANOVA and Chi-square test for performing statistical tests. T-test is used to test the equality of two population means; for more than two populations, ANOVA test is used. Chi-square test compares categorical variables, testing for variable association or fitness of model.
RELATED TOPICS
See also
3-SECOND BIOGRAPHY
JOHN ARBUTHNOT
1667–1735
Scottish physician who was the first to use statistical tests to investigate human sex ratio at birth using 82 years of birth records in London
30-SECOND TEXT
Joyce Kafui Klu
Failing to reject a null hypothesis doesn’t mean that it is accepted as truth, only that there is enough evidence to support it.

MEAN
the 30-second calculation
Mean, also called average, is a central representation of data. Using mean is most convenient when reporting large datasets that need to be summarized with a single value. For example, at the end of a week, a doctor reporting on the total number of patients treated on a daily basis will need to report the mean, mainly because the number of patients treated each day will vary over the week. A teacher can summarize the performance of a class using the mean. Mean is computed by dividing the sum of all values by the number of values summed. Mean computed using this approach is termed arithmetic mean and is the most commonly used. For example, if the number of patients treated in a week are {3,5,7,2,4,3}, then on average four patients ([3 + 5 + 7 + 2 + 4 + 3]/6 = 4) are treated daily. In situations where taking arithmetic mean is not applicable, other types of mean, including geometric and harmonic, can be used. Geometric mean is used when comparing things with very different properties. Harmonic mean is used for finding the mean involving rates or ratios. Mean computed with all population data is termed population mean and mean from sample data is termed sample mean.
3-SECOND COUNT
Mean is a statistical term referring to a single value that describes a set of data by identifying the midpoint position of the data.
3-MINUTE TOTAL
Mean, median and mode are the three main but different statistical approaches for determining the central position of data. Median is a middle value that divides data into two equal halves – the median of {2,3,5,7,8} is 5. Mode is the most occurring value in data – the mode of {1,3,3,7,9} is 3. Where a few of the data values are extremely small or large (termed outliers), median is preferred over mean as mean is influenced by outliers.
RELATED TOPICS
See also
3-SECOND BIOGRAPHY
JAMES BRADLEY
1693–1762
English astronomer who used mean to describe his test of observations leading to the discovery of the aberration of light
30-SECOND TEXT
Joyce Kafui Klu
In most cases the population mean is estimated using sample mean because obtaining full population data can be impossible.

STANDARD DEVIATION
the 30-second calculation
Standard deviation measures how each value in a set of data deviates from the mean. Low standard deviation indicates that data values are close to the mean and high standard deviation indicates that data is widely spread. For example, a stock that pays an average of 5% with a standard deviation of 2% implies that one could earn around 3% (5 - 2) to 7% (5 + 2). Suppose the standard deviation is 12% instead, then one could make a loss of about 7% (5 - 12 = - 7) or a profit of about 17% (5 + 12). Standard deviation is calculated as the square root of the variance or average squared deviation from the mean. Suppose the test scores of a class are [63,70,55,82,59]. The standard deviation can be computed in the following three steps. First, find the mean using [63 + 70 + 55 + 82 + 59]/5 = 65.8. Second, find the variance using [(63 - 65.8)2 + (70 - 65.8)2 + (55 - 65.8)2 + (82 - 65.8)2 + (59 - 65.8)2]/(5 - 1) = 450.8/5 = 112.7. Finally, take the square root of variance as √(112.7) = 10.6. Assuming the only available information is a mean score of 65.8 and a standard deviation of 10.6, one can tell that the performance of the class ranges between 55.2 (65.8 - 10.6) and 76.4(65.8 + 10.6). Knowing the standard deviation associated with the mean of a data gives a better picture of how variable the data is and can be useful in decision making.
3-SECOND COUNT
Standard deviation is a statistical measure of how variable or spread a set of data is about the mean.
3-MINUTE TOTAL
To obtain the exact range of an unknown parameter, the standard deviation is used to compute a confidence interval; an interval with an associated probability of confidence. This is particularly useful for daily investment decision making. Given different investment options, standard deviation measures the associated risk or volatility of each option for deciding on the best available option.
RELATED TOPICS
See also
30-SECOND TEXT
Joyce Kafui Klu
Standard deviation tells how representative a reported mean is of a set of data.

MEASUREMENT ERROR
the 30-second calculation
Measurement error, also known as observation error, is the error associated with a measured value when compared with its true value. For example, a thermometer may give a temperature reading of 9°C when the true temperature is in fact 8°C. Measurement error can be random or systematic. Random errors occur naturally due to fluctuations in the readings of instruments. These errors cannot be controlled or avoided; as a result, a measurement repeated under the same conditions will produce different results. The effect of random errors can be reduced by taking repeated measurements and averaging the results. Systematic error, on the other hand, occurs due to the inaccuracies of instruments or incorrectly calibrated instruments and introduces a constant or predictable error to the true value, which affects all measurement. When systematic error is present, a measurement repeated under the same conditions will produce the same result. This makes systematic errors difficult to detect but, if the source of the error can be identified, easy to rectify. Systematic and random error account for the total error associated with a measurement. It may be impossible to avoid errors completely, especially random ones. However, taking careful steps to reduce errors in measurement is particularly important if results are to be trusted and relied upon.
3-SECOND COUNT
Measurement error is the difference between the value of a measured quantity and its true value.
3-MINUTE TOTAL
The estimation of measurement error (uncertainty) is an increasing requirement for testing laboratories to meet accreditation standards across the globe. The police and juries rely heavily on laboratories to estimate the amount of illegal substances in a person’s urine or blood. When the measured value of an illegal substance is obtained, an estimate of measurement uncertainty is subtracted from the measured quantity to account for possible error from instruments and method used.
RELATED TOPICS
See also
3-SECOND BIOGRAPHY
WILLIAM GEMMELL COCHRAN
1909–80
Scottish-American statistician and author of early text books on measurement or observation error and experimental designs
30-SECOND TEXT
Joyce Kafui Klu
In statistics, error is not considered a mistake but a deviation in measurements that could be inevitable even under correct experimental settings.

P-VALUES
the 30-second calculation
Many experiments revolve around case-control studies where two groups are tested: one is the ‘control’ and the other the ‘case’. The control group is subjected to ‘normal’ but controlled conditions, such as a constant temperature, whereas the case group is subjected to different temperatures. The response, such as plant growth, is measured. The average effect of the case group is compared to the control in what’s called the null hypothesis (H0) significance test (NHST). A statistical test (see here) allows us to determine whether the difference between conditions is significant or not. The statistical test calculates a p-value, which is the probability that the data is equal to or more extreme than its observed value. A p-value, like all probabilities, is between 0 and 1, with 1 meaning a near certainty and 0 a near impossibility. Thus, if the statistical test results in a value close to 0 then it is improbable that the observed effect is due to random chance and H0 can be rejected. In 1925 the statistician Ronald Fisher suggested that if p < 0.05, the result was statistically significant. Since then, this suggestion has become a rule, with the p-value being misinterpreted and over trusted. A purely statistically significant result does not reflect on the size of the effect, nor on its generalizability. Importantly, it does not guarantee the controlled variable is causal of the result.
3-SECOND COUNT
Calculate a p-value to check whether the results from an experiment are statistically significant.
3-MINUTE TOTAL
P-values are a useful aid for deciding whether a result is worthy of further investigation. Their overuse in the scientific literature, however, has controversially been implicated in a ‘reproducibility crisis’, with senior statisticians (such as the American Statistical Association) giving guidance on how to use statistical tests effectively.
RELATED TOPICS
See also
3-SECOND BIOGRAPHY
SIR RONALD AYLMER FISHER
1890–1962
Pioneering British statistician and geneticist whose work on randomness and variance had a huge impact on efficient farming practices
30-SECOND TEXT
Christian Cole
Scientific experiments control variables and measure outcomes multiple times in order to calculate statistical significance via p-values.

CONFIDENCE INTERVAL
the 30-second calculation
Confidence interval uses a sample data to compute a range of values that may contain the true value of an unknown population parameter of interest at a specified percentage probability. A probability of 90%, 95% or 99% is commonly used in practice. A 95% confidence interval means that if numerous samples are drawn from the same population and confidence interval is computed, then the resulting confidence interval will surface 95% of the cases to include the true population parameter. Confidence interval can be contrasted with point estimate, which computes a single or an exact value for the unknown parameter. The idea of confidence interval is to understand the variability associated with an estimated parameter and to enhance its reliability by computing a range of plausible values (rather than a single value) believed to contain the true value of the unknown parameter. The width of a confidence interval is influenced by the specified percentage probability, the size of the sample taken and the variability of data. A high percentage probability will broaden the estimated confidence interval. The higher the variability in data, the wider the estimated confidence interval. With a large sample size, a good estimate of the unknown population parameter with a narrow confidence interval can be achieved.
3-SECOND COUNT
Confidence interval is a statistical term referring to a range of values computed at a specified percentage probability that is believed to contain the true value of an unknown parameter.
3-MINUTE TOTAL
Confidence interval can be used to perform statistical hypothesis testing; a test to reject or accept a claim. For example, if it is claimed that drug A is ineffective, then this claim is supported if the computed confidence interval contains zero (e.g. —2 to 3), and it’s not supported if the confidence interval does not contain zero (e.g. 2 to 6). Hence, confidence interval significantly influences the decision-making process.
RELATED TOPICS
See also
3-SECOND BIOGRAPHY
JERZY NEYMAN
1894–1981
Polish mathematician and statistician who introduced the idea of confidence interval in 1937. His groundbreaking work in randomized experiments, sampling and hypothesis testing formed the basis for modern advanced techniques
30-SECOND TEXT
Joyce Kafui Klu
Retailers use confidence interval to help them make decisions about stock levels, such as how many items of different sizes to stock.

BOOTSTRAPPING
the 30-second calculation
Bootstrapping is a way of drawing samples over and over again from the same dataset. Bootstrapping generates multiple versions of dataset from which values of computed parameters can be compared to understand the variability of estimated parameters. For example, to estimate the average age of smokers in a community, it may be practically impossible to interview every single individual (the population), so a random sample of individuals are interviewed instead. Now, how confident can one be that the estimated average using the sample is close to that of the population? As it’s impractical to take samples again and again, bootstrapping provides a means of generating many different samples from the initially collected sample with replacement. Assuming the ages of five smokers are {18,21,25,28,31}, many (1000s of) bootstrap samples can be drawn from this data; {21,25,21,21,28}, {21,25,18,21,28}, {21,25,21,25,28}, {18,25,21,21,18}, {31,25,21,31,28}, and so on. The idea of bootstrapping is to generate many versions of a dataset to understand the stability of estimated results. Bootstrapping is particularly useful in situations where data is limited or difficult to acquire. The initial sample must be representative of the population so that the samples drawn are comparable to the population.
3-SECOND COUNT
Bootstrapping is a statistical technique of sampling from the same dataset multiple times to ascertain the variability (distribution) of an estimate.
3-MINUTE TOTAL
Due to the sensitive nature of most medical data, medical researchers rely on bootstrapping techniques. In most cases, the data obtained is too small for analysis and requires the use of bootstrap samples. The generated bootstrap samples are used to estimate standard deviations and confidence intervals, from which the distribution and variability associated with an unknown parameter of interest is analysed.
RELATED TOPICS
See also
3-SECOND BIOGRAPHY
BRADLEY EFRON
1938–
American statistician who first proposed the technique of bootstrap resampling. His work has impacted the field of statistics as a whole and its areas of application
30-SECOND TEXT
Joyce Kafui Klu
Advanced computing technology has improved the time and resources needed to generate many bootstrap samples for analysis.

STANDARD ERROR
the 30-second calculation
The standard error is closely related to, but not to be confused with, the idea of a standard deviation. Often in statistics we take a sample (i.e. we select some members from a larger population) and calculate statistics of that sample to infer something about the population as a whole. For example, we can take the mean of our sample. However, if we were to take a different sample (selecting different members of the overall population), then we would obtain a different mean, and so on. Note that each sample also has its own standard deviation. But none of the obtained sample means is equal to the population mean, which is what we really want to know. However, intuitively, as the sample size gets bigger (with respect to the population size) we would expect the sample mean to become closer to the population mean (after all, once the sample size and population size are equal the two are one and the same). This idea is captured in the definition of the standard error of the mean (SEM). The SEM is calculated as SEM = σ/√n. Here n is the size of the sample and σ can be either the population standard deviation (giving the exact SEM) or the sample standard deviation (giving an approximation to the SEM).
3-SECOND COUNT
The standard error measures the degree of variability of a statistic. The statistic in question is often the mean, in which case we have the ‘standard error of the mean’.
3-MINUTE TOTAL
The standard error of the mean is similar to – and often confused with – the standard deviation. The standard deviation describes the variability of a set of measurements. On the other hand, to describe the uncertainty associated with the estimate of the mean (of a population based on the mean of a sample), we use the standard error of the mean.
RELATED TOPICS
See also
30-SECOND TEXT
David Pontin
Calculating a statistic for a sample rather than a whole population leads to the idea of standard error.
LINEAR REGRESSION & CORRELATION
the 30-second calculation
Linear regression and correlation are related statistical approaches to determining how variables depend on one another. Linear regression seeks to express the expected value of a dependent variable in terms of one or more known independent variables. Correlation describes a relationship between variables that is symmetrical, with none necessarily dependent or independent. Simple linear regression refers to the case of a single independent variable. With two variables, the data can be represented by a 2-D scatter graph. The approach is to describe the relationship by finding the straight line which best fits the data, by some measure. The most common measure is that of ordinary least squares, which seeks to minimize the sum of the squares of deviations of observed data points from the line; but other measures are also used. Correlation between two variables is the amount one changes, on average, when the other changes by a certain amount. Linear regression is typically used when the independent variable is manipulated by the experimenter; for example, time, concentration, etc. Correlation, on the other hand, is more often used when the experimenter measures both variables. Correlation is not causation: the sales of ice cream and sun cream may be correlated but one does not cause the other.
3-SECOND COUNT
Linear regression examines the dependence of the expected value of a variable on one or more other variables. Correlation measures the interdependence between variables.
3-MINUTE TOTAL
Linear regression is employed in financial settings to analyse commodity pricing; in economics to relate important indicators such as (un)employment, inflation and GDP; in medical statistics to influence health spending policy; in the military and in numerous other settings. Correlation is similarly used, but is open to abuse.
RELATED TOPICS
See also
INDEPENDENT & DEPENDENT VARIABLES
3-SECOND BIOGRAPHY
KARL PEARSON
1857–1936
English mathematician for whom the widely used correlation coefficient is named. He founded the world’s first university statistics department at University College London
30-SECOND TEXT
John McDermott
There may be a near-straight line relationship between correlated variables.
