The Princeton Guide to Evolution

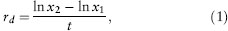
Macroevolutionary Rates

Luke J. Harmon

OUTLINE

1. How “fast” is evolution?

2. Rates of speciation and extinction

3. Rates of trait evolution

4. Are there relationships between rates of trait evolution and diversification?

Rates of evolution—both the rate of trait evolution and the rate at which new species form and go extinct—vary tremendously through time and across lineages. Variations in these rates relate to a number of core theories of evolutionary change over long timescales.

GLOSSARY

Adaptive Radiation. The rapid evolution of ecological differences among species in a diversifying lineage.

Birth-Death Model. A mathematical model describing speciation (birth) and extinction (death) of a branching lineage through time, in which the probabilities of speciation or extinction are constant, but the number of species fluctuates by chance.

Clade. A group of lineages that represent all the descendants of some common ancestor

Darwin (Evolutionary Rate). The rate of evolutionary change expressed as the difference in log-transformed trait values divided by the elapsed time in millions of years.

Diversification. The formation of many new species from a single common ancestor.

Diversification Rate. The rate at which new species form, typically in units of lineage⁻¹ my⁻¹.

Ecological Opportunity. The presence of unexploited niche space experienced by an evolving lineage.

Haldane (Evolutionary Rate). The rate of evolutionary change expressed in units of within-population standard deviations per generation.

Lineage. A group of organisms that form a line of descent from an ancestor.

Living Fossil. A lineage that experiences little or no trait change over a long period of evolutionary time.

Stasis. A lack of change in a species’ traits over evolutionary time.

Taphonomy. The study of the process of fossilization and its variation across lineages and through time.

Tree Balance. A measure of the relative sizes of sister clades in a phylogenetic tree; trees with sister clades of similar size are balanced, while trees with sister clades of dramatically different sizes are unbalanced.

1. HOW “FAST” IS EVOLUTION?

Darwin’s finches capture our attention because of their extremely rapid evolution. From one ancestor, these finches have radiated into a great diversity of species, each distinct from the others in size, feeding, song, and many other traits. All this has happened within just a few million years, which is—to evolutionary biologists—the blink of an eye. These species have diverged so rapidly that it is difficult to determine how the species are even related to one another. Reconstructions of their evolutionary history using genetic data show a nearly simultaneous explosion of species. Contrast the rapid radiation of Darwin’s finches to the coelacanth, a species of fish that was known only from fossils tens of millions of years old until it was discovered in the deep ocean in the early twentieth century. The coelacanth is often called a living fossil, a species that has undergone little or no evolutionary change over a very long period (stasis).

These examples seem exceptional, but how do we know whether Darwin’s finches and coelacanths are evolving extraordinarily rapidly (or slowly)? The answer is to calculate and compare their rates of evolution. Rates of evolution have been of primary importance since Darwin. Much of the current thinking on evolutionary rates traces to George Gaylord Simpson, who wrote about them in his book Tempo and Mode in Evolution. Rates of evolution still play a key role in several important controversies in evolutionary biology. For example, the debate over punctuated equilibrium is really a debate over whether the rate of evolutionary change at speciation is much faster than at other times in the history of lineages. Another example can be found in the debate about the importance (and existence) of adaptive radiations.

This chapter reviews the concept of evolutionary rates. The discussion includes rates of diversification (speciation and extinction) and rates of trait evolution, and how these might relate to one another. Both sections emphasize how measuring rates of evolution has enhanced our understanding of the history of life on earth.

2. RATES OF SPECIATION AND EXTINCTION

During the course of evolution, new species form while others go extinct. The rates of these events determine the number of species expected to form and go extinct in a given time interval. Most often, we are interested in the process of speciation and extinction within evolutionary clades—groups of lineages that represent all the descendants of some common ancestor. Thus, rates are typically calculated on a per lineage basis, that is, the average rates of speciation and extinction per lineage per million years. These rates vary tremendously across the tree of life.

The birth-death model is a useful mathematical model for describing the way lineages speciate or go extinct. In a homogeneous birth-death model, each lineage has a constant probability of either splitting to form a new species or going extinct per unit time. Over the long term, birth-death models predict that the total number of lineages in an evolving clade will increase exponentially (if speciation rate is greater than extinction rate) or decay to zero (if extinction rate is greater than speciation rate). Birth-death models are commonly used in two ways: (1) to estimate the rates of speciation and extinction in evolving clades over time and (2) as a reference point to compare to data. Any deviations from the expected pattern under a birth-death model might reflect biologically interesting phenomena, like higher rates of speciation in certain clades compared with others.

Fitting birth-death models to real data is more complex than one might expect, because direct and complete information about speciation and extinction rarely exists. The most common information about speciation and extinction rates comes from fossil occurrence data—that is, from the appearance and disappearance of lineages in the fossil record; however, in these data, many fossils cannot be identified to the level of individual species, and fossil preservation rates vary across both lineages and geologic time periods. (The study of variation in fossil preservation is called taphonomy; see chapter II.9). A variety of statistical approaches have been invented to estimate speciation and extinction rates from incomplete fossil records, and these rates have been estimated for a variety of clades and over a wide range of time intervals.

Studies of speciation and extinction rates have produced three general findings. First, speciation and extinction rates tend to be roughly equal to each other, at least over long periods and over large spatial scales, which suggests that the history of life is characterized by high turnover and that new species continually form and replace species that have gone extinct. Second, the total number of species in individual clades waxes and wanes through time. Thus, some clades, like mammals, that are now common were at one time much rarer; still other clades, like trilobites, were common in the past but have now gone entirely extinct. Finally, both speciation and extinction rates show tremendous variation, both through time and across clades. This variation is especially interesting because even homogeneous birth-death processes predict that clades will, by chance, have substantial variation in lineage diversity. However, real data sets show even more variation than expected from homogeneous birth-death models. For example, the earliest split in lepidosaurs (lizards and their relatives) separates two clades of extraordinarily different diversities: Sphenodontia (the tuatara, either one or two species depending on taxonomy) and Squamata (snakes and lizards, about 9000 species). This difference in diversity of two clades of the same age is even greater than what would be expected from the variability of the homogeneous birth-death process and likely reflects differences in the dynamics of diversification between the two clades. Patterns like this, in which a very diverse clade is closely related to a clade with low diversity, are very common in the tree of life.

Variation in diversification rates is perhaps most apparent at times of mass extinction, when multiple clades experience dramatically increased rates of extinction over a relatively short time interval. There have been several mass extinctions throughout the history of life on earth, the largest of which are known as the “big five” (see chapter VI.13). Interestingly, a number of studies have shown that some clades experience dramatically increased diversification rates following these mass extinctions. This result suggests that mass extinctions create widespread ecological opportunities that can be exploited by surviving lineages.

A second approach to estimating speciation and extinction rates relies on phylogenetic data. Phylogenetic trees show the evolutionary relationships among species, which occur at the tips of the branches of the tree. Typically, phylogenetic trees have branch lengths that reflect the time between splitting events (nodes) in the tree. The challenge of using phylogenetic data to study diversification is that only extant species are available, and the tree is missing data on the number and timing of extinction events. Even without direct information about extinct lineages, the shape and branching pattern of trees capture information about the relative propensity of clades to diversify.

For example, comparison of the number of descendant species (the diversity) among different clades within a tree reveals the relative propensities of these lineages to diversify. Such comparisons typically focus on sister clades, clades that are each other’s closest relative. Sister clades are by definition the same age, so that any differences in diversity might reflect differences in diversification rates. The earlier example of lepidosaurs reflects this approach. Information about differences in diversity across clades is captured in measures of tree balance, which summarize how evenly the tip species are distributed across every node in a phylogenetic tree. Trees can range from perfectly balanced—where every node or branching point on the tree has the same number of descendant species on each side—to perfectly imbalanced, where every node represents a contrast between a single species and a larger clade. Trees generated by a homogeneous birth-death process tend to have a balance intermediate between these two extremes. One strength of tree balance measurements is that the branch lengths of the tree have no effect. In cases where we don’t know anything about the timing of diversification, we can still use tree balance to learn about variation in diversification rates across clades.

One of the first generalities to emerge from the study of phylogenetic tree balance was that almost all phylogenies of taxa in nature are more imbalanced than would be expected from a homogeneous birth-death model. This observation is evidence that diversification rates—either speciation or extinction, or both—vary across lineages in phylogenetic trees. That is, lineages within some clades speciate faster than others, and other clades are more likely to go extinct. This result is concordant with results from the fossil record, which show great variation in speciation and extinction rates among lineages.

Often, phylogenetic trees include information about branch lengths, which represent the time intervals between recorded speciation events. Typically, these trees do not include any information about extinct species. Still, we can (at least in theory) use them to estimate rates of both speciation and extinction. Information about extinction is contained in the most recent branches, that is, those connecting the youngest species in the tree. If there is extinction, most young species haven’t yet had time to experience its effects, so we expect to see an overabundance of very short branches near the tips of the tree.

In practice, these methods can generate good estimates of net diversification rates (speciation minus extinction) but have difficulty estimating either speciation or extinction rates separately. The method of fitting birth-death models to real phylogenetic trees often yields unrealistic parameter estimates. Many studies using this approach have inferred very low (or even zero) rates of extinction in living clades, which seems to contradict results from the fossil record suggesting that almost all groups experience some extinction. More recent applications to very large trees have uncovered high turnover rates that are more consistent with fossil calculations. It is possible that some estimates are biased because the phylogenetic trees used are incorrect or because the mathematical assumption that constant rates of speciation and extinction apply across a whole tree is incorrect. Perhaps the rates vary through time or across clades, for example. Some authors have suggested that birth-death models are not an accurate description of the diversification of life on earth and that we need to consider models that take into account how species in communities might interact with one another. This is currently an active area of research.

Many phylogenetic studies have compared diversification rates across lineages and through time. Tests using branch lengths have confirmed that rates of speciation and extinction can vary dramatically among closely related groups, mirroring results from measurements of tree balance. For example, across vertebrates, some clades have very high rates of diversification: Boroeutheria (most placental mammals), Percomorpha (perches and perch-like fish), and Neoaves (most birds) all have net diversification rates close to 0.1 per lineage per million years. Such a rate will produce about 22,000 surviving species, on average, from a single ancestor in 100 million years. By contrast, other clades apparently diversify much more slowly. For example, old clades with low diversity like the bowfin, coelacanth, and tuatara might have net diversification rates 100 times slower than the high rates seen in other vertebrate clades.

Rates also appear to vary through time. For instance, phylogenetic trees often seem to show evidence that diversification rates slow as lineages approach the present day. This pattern has been cited as evidence for density dependence in diversification rates; that is, perhaps diversification rates slow as the number of lineages in a clade increases. The prevalence of this pattern across a wide range of organisms might even suggest that as clades diversify, they attain some environmentally determined “carrying capacity” for the number of species that can coexist. However, a number of biases could also explain this pattern. One possibility is that researchers are using biased estimates of phylogenetic trees. When phylogenetic trees are estimated from molecular data, a mathematical model must be applied describing how gene or protein sequences change through time; if the model is incorrect, the resulting tree will be biased. Another potential bias involves sampling—perhaps scientists are failing to include many young species from these trees. Typically, phylogenetic trees include only taxa that are considered “good species” (under various criteria) and leave out younger lineages not considered species but that might provide information about recent speciation events. Leaving out these young lineages might then falsely suggest a slowdown in speciation toward the present. Additionally, these temporal slowdowns seem to contradict ecological studies suggesting that hardly any natural species communities are “saturated” with species, preventing new species from forming and surviving. Instead, new species can almost always be added to natural communities without resulting in extinction. Still, the common observation of slowdowns in diversification through time is an intriguing general result that demands an explanation.

In summary, speciation and extinction rates vary among clades and through time. These patterns have been found in both fossil occurrences and phylogenetic trees, and patterns are more or less concordant across these two types of data. Other intriguing patterns, like density-dependent speciation rates, are still being investigated.

3. RATES OF TRAIT EVOLUTION

Lineages also have traits that evolve and change through time. Scientists estimate the rate of change of these species traits in two ways. First, they can carry out an allochronic study by measuring the difference in the mean trait of a lineage at the start and end of a given time interval. Dividing this difference by the amount of time yields the amount of change per unit time, which can be used to estimate the rate of evolution. Alternatively, they can carry out a synchronic study by measuring the difference of trait means of two present-day lineages that both diverged from a common ancestor at some known point in time. This difference divided by the time since the common ancestor yields the rate of divergence across these two lineages, which reflects the evolutionary rate. Both these methods yield average rates over time, which may underestimate the amount of change that occurs each generation. For example, if a trait oscillates rapidly over a timescale of a few generations, but measurements are available only every 100,000 generations, the average per generation rate of change of the character will be underestimated. Furthermore, synchronic data can miss important changes when species are all sampled from the same time slice—usually the present day. For example, if there has been a trend in the direction of trait change across multiple lineages, synchronic studies will not be able to distinguish it from present-day differences and, consequently, will underestimate evolutionary rates.

With either allochronic or synchronic rate estimates, the rate of evolution can be quantified in either of two ways. First, the rate in darwins can be calculated as

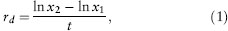
where x₁ and x₂ are the mean trait values for two populations or species, t is the elapsed time separating the populations, and ln stands for the natural logarithm. For synchronic studies, t is twice the time since divergence from a common ancestor, because both species have been evolving independently for that period.

Second, the evolutionary rate in haldanes can be calculated as

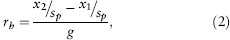
where x₁ and x₂ are the same as in equation (1), g is the elapsed time in generations, and s_p is the pooled standard deviation of traits within populations. Often, data are ln transformed before rates are calculated in haldanes, so that s_p is the pooled standard deviation of ln-transformed traits. This transformation is necessary when populations or species having higher trait means also have higher trait variances, which is usually the case for morphological characters.

Rates in darwins and haldanes are not directly comparable, and each has strengths and weaknesses. Darwins can easily be calculated and do not require extensive sampling within species. However, rates calculated in haldanes are in units of within-population trait variation. This means that haldanes relate more naturally to population genetics models of trait evolution than do darwins and are thus typically more informative about evolutionary processes (see later discussion). If one trait is more variable within species than another, then comparing their rates of evolution in haldanes is more appropriate than using darwins.

It is also possible to estimate rates of evolution from phylogenetic trees and trait data. The most common way to do this is to assume that trait evolution mimics a “random walk” and to model evolution of a quantitative trait (a trait that varies continuously among individuals) using a statistical process called Brownian motion. The rate of change under Brownian motion is described by a rate parameter σ² that describes how fast the traits “wander” through time. There are statistical techniques for estimating the rate (σ²) from data that include a phylogenetic tree and trait data for all available species at the tips of that tree. If the branch lengths in the tree are measured in millions of years, and the trait values are ln transformed, the square root of σ² is related to rate estimates measured in darwins.

Rates of trait evolution can be used directly to address many questions in evolutionary biology. For example, are traits in some lineages evolving more quickly than in others? Did a given lineage evolve more quickly at one time period than another? Both allochronic and synchronic studies have shown very convincing evidence that rates of evolution can vary tremendously across characters, lineages, and time periods. The highest rates, typically measured over very short timescales, can approach 1 haldane in rapidly changing lineages like Darwin’s finches. By contrast, rates measured over longer, paleontological timescales tend to be slower, ranging from 10⁻⁶ to 10⁻² haldanes.

If rates of evolution are measured in haldanes, it is possible to compare the rate of evolution in a lineage to what we would expect under specific evolutionary hypotheses. For example, one classic approach, pioneered by Russell Lande and Michael Lynch, is to compare observed rates with the expected rate of trait change through time under the hypothesis of genetic drift. If the observed trait is under directional selection, we expect to see much faster change than that expected under drift. By contrast, stabilizing selection around a fixed optimum predicts that the observed rate will be much slower than that predicted by genetic drift. By comparing the actual rate of evolution with the prediction under neutral (drift) and nonneutral models, we can infer whether processes like selection have long-term effects on patterns of trait evolution. Analyzing data in this way has revealed two main findings. First, when we look at trait change over very short timescales—say, from one generation to the next—rates of evolution are much faster than we would expect under genetic drift. The high rates mentioned earlier (~1 haldane for Darwin’s finches) are a good example of rates that are too high to explain using drift. This is perhaps not that surprising, because we know that many traits (especially the ones we prefer to study!) have strong effects on organismal fitness and are under selection. However, long-term data on evolutionary change have revealed a striking pattern in the opposite direction: differences across species are less than those expected under the hypothesis of genetic drift. For example, Lande pointed out that long-term rates of evolution across a variety of mammals show, on average, only about one-tenth the amount of change expected under genetic drift. That is, drift alone predicts that species should have traits that are much more different from one another compared with what we actually see in the tree of life. Another way to say this is that many species undergo stasis, long periods of time with little or no evolutionary change.

In fact, there is a general relationship between observed rates of evolution and the time interval over which that change is measured. We always measure the fastest rates over the shortest time intervals—from one generation to the next in Darwin’s finches, for example. This relationship seems at first to be a paradox (sometimes called the “paradox of stasis”). However, detailed analyses of microevolutionary studies suggest a resolution of this paradox. Although traits often show dramatic change from one generation to the next, this trend is rarely sustained over time. Instead, traits tend to change in dramatically different directions from one generation to the next. The result of these “balancing” changes is a slow net rate of evolutionary change. Selection is often strong, but populations tend to experience selection in different directions from one generation to the next. Only rarely do populations experience sustained directional change. This observation explains the difference in the rates of evolution measured over different time intervals.

Both haldanes and darwins measure evolution of quantitative characters, traits that vary continuously within species. However, we are also interested in the rate of evolution of discrete traits, those that can occupy one of a number of states (e.g., black, white) and tend not to vary within populations. Studies of discrete trait evolution have exhibited the same patterns as described for quantitative traits: rates of trait change vary dramatically among characters, among lineages, and through time.

One common pattern is that trait differences among species (trait disparity) in a clade are “bottom heavy”—that is, they evolve at peak rates early in a clade’s history. This pattern is often attributed to the effects of ecological opportunity in spurring evolutionary innovation. That is, early in a clade’s history, competition and an abundance of unused ecological niches (i.e., ecological opportunity) drive the rapid evolution of many species that are very different from one another.

A number of long-standing debates in evolutionary biology relate to rates of trait evolution. For example, the debate over punctuated equilibrium (see chapter VI.12) centers on the relationship between trait change and speciation but also reflects a debate about the constancy of evolutionary rates through time. Steven J. Gould contrasted “gradualism”—a caricatured view that rates of evolution are more or less constant through time—with his favored model of punctuated equilibrium, in which traits change only at speciation events and are in stasis the rest of the time. We now know of instances of trait change that are not strictly associated with speciation (see chapter VI.12). We also know that “stasis” isn’t really static. Species do not remain constant but instead typically undergo rapid changes over short intervals that may not be sustained over time. Nevertheless, traits of some species may undergo episodic bursts separated by relative stasis, although bursts of change may or may not be associated with speciation events.

In summary, it is clear that rates of trait evolution vary tremendously across different traits, lineages, and time periods. This pattern is concordant with what we have found for rates of speciation and extinction. For trait evolution, one general finding is that the apparent rate of evolution shows a negative relationship with the time interval over which that change is assessed. This pattern likely reflects the fact that evolution involves rapid change accompanied by frequent reversals.

4. ARE THERE RELATIONSHIPS BETWEEN RATES OF TRAIT EVOLUTION AND DIVERSIFICATION?

Elevated rates of both speciation and trait evolution are key components of the concept of adaptive radiations (see chapter VI.10). Although some clades have been shown to evolve faster than others, there has never been a systematic study showing that clades typically called adaptive radiations have faster rates of trait evolution or speciation than other clades. There is quite a bit of evidence that many clades follow a pattern whereby diversification rates start out high but slow through time; however, the corresponding pattern for trait evolution seems much less common.

One can also ask whether rates of trait evolution and rates of lineage diversification tend to change together—that is, are times of rapid lineage diversification also accompanied by rapid trait evolution? Such a relationship is postulated by several theories of macroevolution, most notably both punctuated equilibrium and the ecological theory of adaptive radiations; however, several studies have shown that rates of lineage diversification and trait evolution are “decoupled,” so that groups with many lineages may or may not harbor exceptional levels of trait disparity. More work is needed in this area.

Rates of evolution play a key role in a number of evolutionary ideas. Rates of speciation, extinction, and trait evolution can be estimated from both fossils and phylogenetic data. The two types of data are complementary in showing tremendous variation in rates, both through time and across lineages. A number of theories have been proposed to account for this variation in rates. The challenge for the future is to use our rich new knowledge of the tree of life to address long-standing questions in macroevolution.