Linear Functionals and the Dual Space

11.1 Introduction

In this chapter, we study linear mappings from a vector space V into its field K of scalars. (Unless otherwise stated or implied, we view K as a vector space over itself.) Naturally all the theorems and results for arbitrary mappings on V hold for this special case. However, we treat these mappings separately because of their fundamental importance and because the special relationship of V to K gives rise to new notions and results that do not apply in the general case.

11.2 Linear Functionals and the Dual Space

Let V be a vector space over a field K. A mapping ϕ: V → K is termed a linear functional (or linear form) if, for every u, v ∊ V and every a, b, ∊ K,

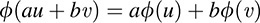
In other words, a linear functional on V is a linear mapping from V into K.

EXAMPLE 11.1

(a) Let π_i:Kⁿ ! K be the ith projection mapping; that is, π_i(a₁; a₂; … a_n … a_i. Then π_i is linear and so it is a linear functional on Kⁿ.

(b) Let V be the vector space of polynomials in t over R. Let J:V → R be the integral operator defined by 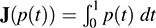. Recall that J is linear; and hence, it is a linear functional on V.

(c) Let V be the vector space of n-square matrices over K. Let T :V → K be the trace mapping

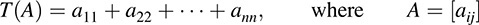
That is, T assigns to a matrix A the sum of its diagonal elements. This map is linear (Problem 11.24), and so it is A linear functional on V.

By Theorem 5.10, the set of linear functionals on A vector space V over A field K is also A vector space over K, with addition and scalar multiplication defined by

where ϕ and σ are linear functionals on V and k ∈ K. This space is called the dual space of V and is denoted by V*.

EXAMPLE 11.2 Let V ¼ Kⁿ, the vector space of n-tuples, which we write as column vectors. Then the dual space V*can be identified with the space of row vectors. In particular, any linear functional ϕ = (a₁; … ; a_nÞ in V* has the representation

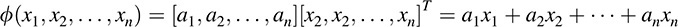
Historically, the formal expression on the right was termed a linear form.

11.3 Dual Basis

Suppose V is a vector space of dimension n over K. By Theorem 5.11, the dimension of the dual space V* is also n (because K is of dimension 1 over itself). In fact, each basis of V determines a basis of V* as follows (see Problem 11.3 for the proof).

THEOREM 11.1:   Suppose {ν₁; … ; ν_n} is a basis of V over K. Let ϕ₁; … ; ϕ_n ∈ V* be the linear functionals as defined by

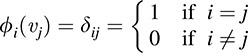
The above basis {ϕ} is termed the basis dual to {ν_i} or the dual basis. The above formula, which uses the Kronecker delta δ_ij, is a short way of writing

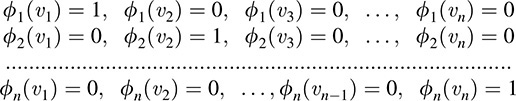
By Theorem 5.2, these linear mappings ϕ_i are unique and well defined

EXAMPLE 11.3 Consider the basis {ν₁ = (2, 1), v₂ = {3, 1} of R². Find the dual basis {ϕ₁, ϕ₂}. We seek linear functionals ϕ₁(x, y) = ax + by and ϕ(x, y) = cx + dy such that

These four conditions lead to the following two systems of linear equations:

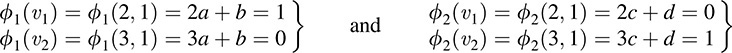
The solutions yield a = 1, b = 3 and c = 1, d = 2. Hence, ϕ₁(x; y) = x + 3y and ϕ₂(x; y) = x – 2y form the dual basis.

The next two theorems (proved in Problems 11.4 and 11.5, respectively) give relationships between bases and their duals.

THEOREM 11.2:   Let {v₁, … ; v_n} be a basis of V and let ff₁, … ; f_ng be the dual basis in V*. Then

(i) For any vector .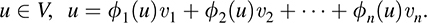

(ii) For any linear functional .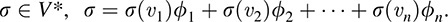

THEOREM 11.3:   Let {v₁, … ; v_n} and {w₁, … ; w_n} be bases of V and let {f₁, … ; f_n} and {s₁, … ; s_n} be the bases of V* dual to {v_i} and {w_i}, respectively. Suppose P is the change-of-basis matrix from {v_i} to {w_i}. Then (P^–1)T is the change-of-basis matrix from {f_i} to {s_i}.

11.4 Second Dual Space

We repeat: Every vector space V has a dual space V*, which consists of all the linear functionals on V. Thus, V* has a dual space V**, called the second dual of V, which consists of all the linear functionals on V*.

We now show that each v 2 V determines a specific element 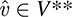. First, for any ϕ ∈ V*, we define

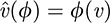
It remains to be shown that this map û :V* → K is linear. For any scalars a, b ∈ K and any linear functionals ϕ, ρ ∈ V*, we have

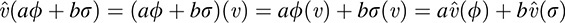
That is, û is linear and so û ∊ V**. The following theorem (proved in Problem 12.7) holds.

THEOREM 11.4:   If V has finite dimensions, then the mapping 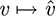is an isomorphism of V onto V**.

The above mapping 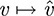is called the natural mapping of V into V**. We emphasize that this mapping is never onto V** if V is not finite-dimensional. However, it is always linear, and moreover, it is always one-to-one.

Now suppose V does have finite dimension. By Theorem 11.4, the natural mapping determines an isomorphism between V and V**. Unless otherwise stated, we will identify V with V** by this mapping. Accordingly, we will view V as the space of linear functionals on V* and write V = V**. We remark that if {ϕ_i} is the basis of V* dual to a basis {v_i} of V, then {v_i} is the basis of V** = V that is dual to {ϕ_i}.

11.5 Annihilators

Let W be a subset (not necessarily a subspace) of a vector space V. A linear functional ϕ ∈ V* is called an annihilator of W if ϕ(w) = 0 for every w ∈ W—that is, if f(W) = {0}. We show that the set of all such mappings, denoted by W⁰ and called the annihilator of W, is a subspace of V*. Clearly, 0 ∈ W⁰: Now suppose ϕ s ∈ W⁰. Then, for any scalars a, b, ∈ K and for any w ∈ W,

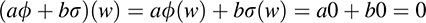
Thus, aϕ + bσ = W⁰, and so W⁰ is a subspace of V*.

In the case that W is a subspace of V, we have the following relationship between W and its annihilator W⁰ (see Problem 11.11 for the proof).

THEOREM 11.5:   Suppose V has finite dimension and W is a subspace of V. Then

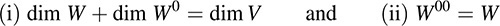
Here W⁰⁰ = {v ∈ V :ϕ(v)= 0 for every ϕ ∈ W⁰} or, equivalently, W⁰⁰ = (W⁰)⁰, where W⁰⁰ is viewed as a subspace of V under the identification of V and V**.

11.6 Transpose of a Linear Mapping

Let T :V → U be an arbitrary linear mapping from a vector space V into a vector space U. Now for any linear functional ϕ ∈ U*, the composition ϕ ° T is a linear mapping from V into K:

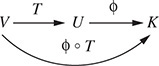
That is, ϕ ° T ∈ V*. Thus, the correspondence

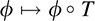
is a mapping from U* into V*; we denote it by T^t and call it the transpose of T. In other words, T^t :U* → V* is defined by

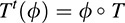
Thus, (T^t(ϕ))(v) = ϕ(T(v)) for every v ∈ V.

THEOREM 11.6:   The transpose mapping T^t defined above is linear.

Proof. For any scalars a; b ∈ K and any linear functionals ϕ; σ ∈ U*,

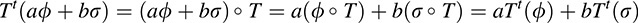
That is, T^t is linear, as claimed.

We emphasize that if T is a linear mapping from V into U, then T^t is a linear mapping from U* into V*. The same “transpose” for the mapping T^t no doubt derives from the following theorem (proved in Problem 11.16).

THEOREM 11.7:   Let T : V → U be linear, and let A be the matrix representation of T relative to bases {v_i} of V and {u_i} of U. Then the transpose matrix A^T is the matrix representation of T^t :U* → V* relative to the bases dual to {u_i} and {v_i}.

SOLVED PROBLEMS

Dual Spaces and Dual Bases

11.1.   Find the basis {ϕ₁, ϕ₂, ϕ₃} that is dual to the following basis of R³:

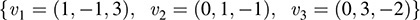
The linear functionals may be expressed in the form

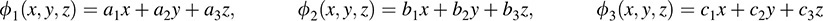
By definition of the dual basis, f_i(v_j) = 0 for i 6= j, but f_i(v_j) = 1 for i = j.

We find ϕ₁ by setting ϕ₁(ν₁) = 1; ϕ₁(ν₂) = 0; ϕ₁(ν₃) = 0: This yields

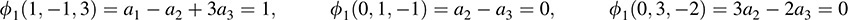
Solving the system of equations yields a₁ = 1, a₂ = 0, a₃ = 0. Thus, f₁(x; y; z) = x.

We find ϕ₂ by setting ϕ₂(ν₁) = 0, ϕ₂(ν₂) = 1, ϕ₂(ν₃) = 0. This yields

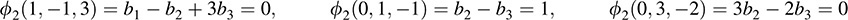
Solving the system of equations yields c₁ = 7, c₂ = 2, c₃ = 3. Thus, ϕ₂(x; y; z) = 7x – 2y – 3z.

We find ϕ₃ by setting ϕ₃(ν₁) = 0, ϕ₃(ν₂) = 0, ϕ₃(ν₃) = 1. This yields

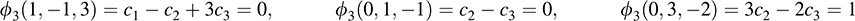
Solving the system of equations yields c₁ = 2, c₂ = 1, c₃ = 1. Thus, ϕ₃(x; y; z) = –2x + y + z.

11.2.   Let V = {a + bt : a; b ∈ R}, the vector space of real polynomials of degree ≥1. Find the basis {ν₁, ν₂} of V that is dual to the basis {ϕ₁, ϕ₂} of V* defined by

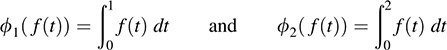
Let v₁ = a + bt and v₂ = c + dt. By definition of the dual basis,

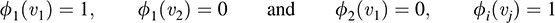
Thus,

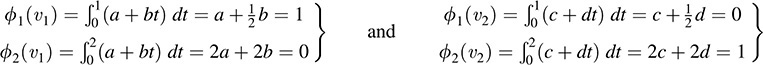
Solving each system yields a = 2, b = –2 and 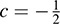, d = 1. Thus, 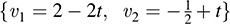is the basis of V that is dual to {ϕ₁, ϕ₂}.

11.3.   Prove Theorem 11.1: Suppose {ν₁, … ; ν_n} is a basis of V over K. Let ϕ₁, … ; ϕ_n ∈ V* be defined by ϕ_i(ν_j) = 0 for i ≠ j, but {_i(v_j) = 1 for i = j. Then {ϕ₁, … ; ϕ_n} is a basis of V*.

We first show that {ϕ₁, … ; ϕ_n} spans V*. Let ϕ be an arbitrary element of V*, and suppose

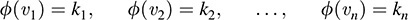
Set σ = k₁ϕ₁ +….+ k_nϕ_n. Then

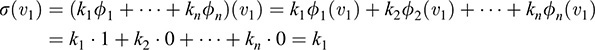
Similarly, for i = 2; … ; n,

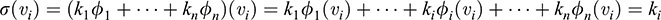
Thus, ϕ(ν_i) = σ(ν_i) for i = 1; … ; n. Because ϕ and σ agree on the basis vectors, ϕ = σ = k₁ϕ₁ + … + k_nϕ_n. Accordingly, {ϕ₁, … ; ϕ_n} spans V*.

It remains to be shown that {ϕ₁, … ; ϕ_n} is linearly independent. Suppose

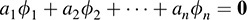
Applying both sides to ν₁, we obtain

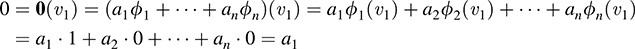
Similarly, for i = 2; … ; n,

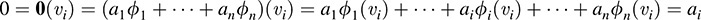
That is, a₁ = 0; … ; a_n = 0. Hence, {ϕ₁, … ; ϕ_n} is linearly independent, and so it is a basis of V*.

11.4.   Prove Theorem 11.2: Let {ν₁, … ; ν_n} be a basis of V and let {ϕ₁, … ; ϕ_n} be the dual basis in V*. For any u ∈ V and any s ∈ V*, (i) u = Σi ϕ_i(u)ν_i. (ii) σ = Σi ϕ(v_i)ϕ_i.

Suppose

Then

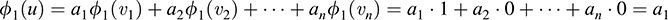
Similarly, for i = 2;... ; n,

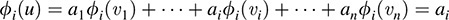
That is, ϕ₁(u) = a₁, ϕ₂(u) = a₂, … ; ϕ_n(u) = a_n. Substituting these results into (1), we obtain (i).

Next we prove (ii). Applying the linear functional s to both sides of (i),

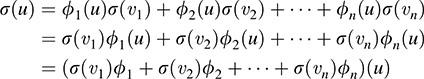
Because the above holds for every u ∈ V, σ = σ(ν₁)ϕ₂ + σ(ν₂)ϕ₂ + …. + σ(ν_n)ϕ_n, as claimed.

11.5.   Prove Theorem 11.3. Let {v_i} and {w_i} be bases of V and let {f_i} and {s_i} be the respective dual bases in V*. Let P be the change-of-basis matrix from {v_i} to {w_i}: Then (P^– is the change-of-basis matrix from {ϕ_i to σ_i}.

Suppose, for i = 1; … ; n,

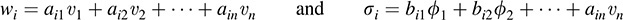
Then P = [a_ij] and Q = [b_ij]. We seek to prove that Q = (P^–1)^T.

Let R_i denote the ith row of Q and let C_j denote the jth column of P^T. Then

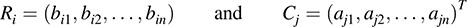
By definition of the dual basis,

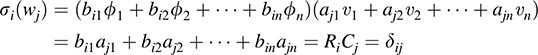
where ψ_ij is the Kronecker delta. Thus,

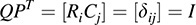
Therefore, Q = (P^T) = (P^–)^T, as claimed.

11.6.   Suppose ν ∈ V, ν ≠ 0, and dim V = n. Show that there exists ϕ ∈ V* such that ϕ(ν) ≠ 0.

We extend {ν} to a basis {ν; ν₂, … ; ν_n} of V. By Theorem 5.2, there exists a unique linear mapping ϕ:V → K such that ϕ(ν) = 1 and ϕ(ν_i) = 0, i = 2; … ; n. Hence, ϕ has the desired property.

11.7.   Prove Theorem 11.4: Suppose dim V = n. Then the natural mapping 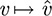is an isomorphism of V onto V**.

We first prove that the map 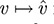is linear—that is, for any vectors v; w ∈ V and any scalars 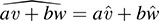. For any linear functional ϕ ∈ V*,

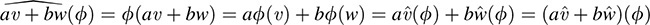
Because 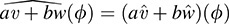for every ϕ ∈ V*, we have 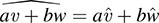. Thus, the map 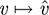is linear.

Now suppose ν ∈ V, ν ≠ 0. Then, by Problem 11.6, there exists ϕ ∈ V* for which ϕ(ν) ≠ 0. Hence, 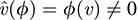, and thus 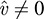. Because ν ≠ 0 implies û v ≠ 0, the map 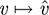is nonsingular and hence an isomorphism (Theorem 5.64).

Now dim V = dim V* = dim V**, because V has finite dimension. Accordingly, the mapping 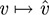is an isomorphism of V onto V**.

Annihilators

11.8.   Show that if ϕ ∈ V* annihilates a subset S of V, then ϕ annihilates the linear span L(S) of S. Hence, S⁰ = ½span(S) ⁰.

Suppose ν ∈ span(S). Then there exists w₁, … ; w_r ∈ S for which ν = a₁w₁ + a₂w₂ + … + a_rw_r.

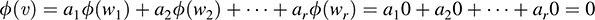
Because ν was an arbitrary element of span(S); ϕ annihilates span(S), as claimed.

11.9.   Find a basis of the annihilator W⁰ of the subspace W of R⁴ spanned by

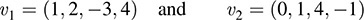
By Problem 11.8, it suffices to find a basis of the set of linear functionals ϕ such that ϕ(ν₁) = 0, where ϕ(x₁, x₂, x₃, x₄) = ax₁ + bx₂ + cx₃ + dx₄. Thus,

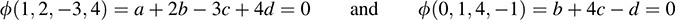
The system of two equations in the unknowns a, b, c, d is in echelon form with free variables c and d.

(1) Set c = 1, d = 0 to obtain the solution a = 11, b = 4, c = 1, d = 0.

(2) Set c = 0, d = 1 to obtain the solution a = 6, b = 1, c = 0, d = 1.

The linear functions ϕ₁(x_i) = 11x₁ 4x₂ + x₃ and ϕ₂(x_i) = 6x₁ x₂ + x₄ form a basis of W⁰.

11.10.   Show that (a) For any subset S of V; S ⊆ S⁰⁰. (b) If S₁ ⊆ S₂, then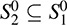

(a) Let ν ∈ S. Then for every linear functional ϕ ∈ S⁰, ûϕ = f(ν) = 0. Hence, 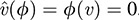. Therefore, under the identification of V and V**, v ∈ S⁰⁰. Accordingly, S ⊆ S⁰⁰.

(b) Let 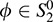. Then ϕ(ν) = 0 for every ν ∈ S₂. But S₁ ⊆ S₂, hence, ϕ annihilates every element of S₁ (i.e., 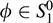). Therefore, .

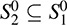11.11.   Prove Theorem 11.5: Suppose V has finite dimension and W is a subspace of V. Then

(i) dim W + dim W⁰ = dim V, (ii) W⁰⁰ = W.

(i) Suppose dim V = n and dim W = r ≤ n. We want to show that dim W⁰ = n – r. We choose a basis {w₁, … ; w_r} of W and extend it to a basis of V, say {w₁, … ; w_r, v₁, … ; v_n–r}. Consider the dual basis

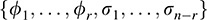
By definition of the dual basis, each of the above s’s annihilates each σ_i, hence, σ₁, … ; s_n–_r ∈ W⁰. We claim that {σs_i} is a basis of W⁰. Now {σ_j} is part of a basis of V*, and so it is linearly independent. We next show that {ϕ_j} spans W⁰. Let σ ∈ W⁰. By Theorem 11.2,

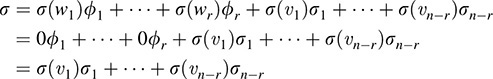
Consequently, {σ₁, … ; σ_n–r} spans W⁰ and so it is a basis of W⁰. Accordingly, as required

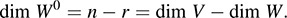
(ii) Suppose dim V = n and dim W = r. Then dim V* = n and, by (i), dim W⁰ = n r. Thus, by (i), dim W⁰⁰ = n – (n – r) = r; therefore, dim W = dim W⁰⁰. By Problem 11.10, W ⊆ W⁰⁰. Accordingly, W = W⁰⁰.

11.12.   Let U and W be subspaces of V. Prove that (U + W)⁰ = U⁰ ∩ W⁰.

Let ϕ ∈ (U + W)⁰. Then ϕ annihilates U + W; and so, in particular, f annihilates U and W: That is, ϕ ∈ U⁰ and ϕ ∈ W⁰; hence, ϕ ∈ U⁰ \ W⁰: Thus, (U + W)⁰ U⁰ \ W⁰:

On the other hand, suppose σ ∈ U⁰ \ W⁰: Then σ annihilates U and also W. If ν ∈ U + W, then ν = u + w , where u ∈ U and w ∈ W. Hence, s(v) = s(u)+ s(w) = 0 + 0 = 0. Thus, σ annihilates U + W; that is, s ∈ (U + W)⁰. Accordingly, U⁰ + W⁰ (U + W)⁰.

The two inclusion relations together give us the desired equality.

Remark: Observe that no dimension argument is employed in the proof; hence, the result holds for spaces of finite or infinite dimension.

Transpose of a Linear Mapping

11.13.   Let ϕ be the linear functional on R² defined by ϕ(x; y) = x – 2y. For each of the following linear operators T on R², find (T^t(f))(x; y):

(a) T(x, y) = (x, 0), (b) T(x, y) = (y, x + y), (c) T(x, y) = (2x – 3y, 5x + 2y)

By definition, T^t(f) = f T; that is, (T^t(f))(v) = f(T(v)) for every v. Hence,

(a) (T^t(ϕ))(x, y) = ϕ(T(x, y)) = ϕ(x, 0) = x

(b) (T^t(ϕ))(x, y) = ϕ(T(x, y)) = ϕ(y, x + y) = y 2(x + y) = 2x y

(c) (T^t(ϕ))(x, y) = ϕ(T(x, y)) = ϕ(2x 3y; 5x + 2y) = (2x 3y) 2(5x + 2y) = 8x 7y

11.14.   Let T : V → U be linear and let T^t :U* → V* be its transpose. Show that the kernel of T^t is the annihilator of the image of T—that is, Ker T^t = (Im T)⁰.

Suppose ϕ ∊ Ker T^t; that is, T^t (ϕ) = ϕ ° T then u = T(u) for some v ∊ V; hence,

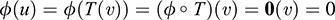
We have that ϕ(u) = 0 for every u ∈ Im T; hence, f ∈ (Im T)⁰. Thus, Ker T^t (Im ⊆ T)⁰.

On the other hand, suppose σ ∈ (Im ⊆ T)⁰; that is, σ(Im ⊆ T) = {0}. Then, for every v ∈ V,

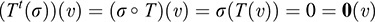
We have (T^t(σ))(ν) = 0(ν) for every ν ∈ V; hence, T^t(s) = 0. Thus, σ ∈ Ker T^t, and so (Im T)⁰ ⊆ Ker T^t.

The two inclusion relations together give us the required equality.

11.15.   Suppose V and U have finite dimension and T : V → U is linear. Prove rank(T) = rank(T^t).

Suppose dim V = n and dim U = m, and suppose rank(T) = r. By Theorem 11.5,

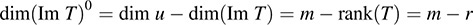
By Problem 11.14, Ker T^t = (Im T)⁰. Hence, nullity (T^t) = m – r. It then follows that, as claimed,

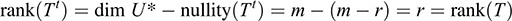
11.16.   Prove Theorem 11.7: Let T :V → U be linear and let A be the matrix representation of T in the bases {v_j} of V and {u_i} of U. Then the transpose matrix A^T is the matrix representation of T^t : U* → V* in the bases dual to {u_i} and {ν_j}.

Suppose, for j = 1; … ; m,

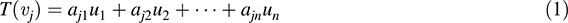
We want to prove that, for i = 1; … ; n,

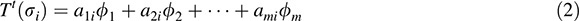
where {σ_i} and {ϕ_j} are the bases dual to {u_i} and {ν_j}, respectively.

Let v ∈ V and suppose v = k₁v₁ + k₂v₂ + … + k_mv_m . Then, by (1),

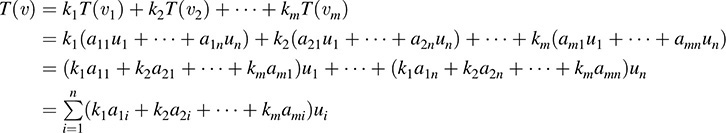
Hence, for j = 1; … ; n.

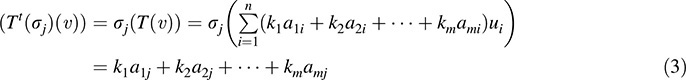
On the other hand, for j = 1; … ; n,

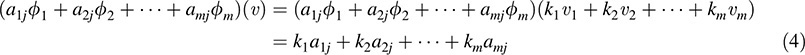
Because ν ∈ V was arbitrary, (3) and (4) imply that

which is (2). Thus, the theorem is proved.

SUPPLEMENTARY PROBLEMS

Dual Spaces and Dual Bases

11.17.   Find (a) ϕ + σ, (b) 3ϕ, (c) 2ϕ 5σ, where ϕ:R³ → R and σ:R³ → R are defined by

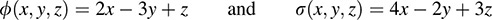
11.18.   Find the dual basis of each of the following bases of R³: (a) {(1; 0; 0); (0; 1; 0); (0; 0; 1)}, (b) {(1; 2; 3); (1; 1; 1); (2; 4; 7)}.

11.19.   Let V be the vector space of polynomials over R of degree ≥2. Let ϕ₁, ϕ₂, ϕ₃ be the linear functionals on V defined by

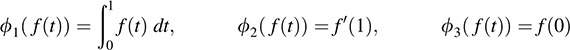
Here f(t) = a + bt + ct² ∈ V and f⁰(t) denotes the derivative of f(t). Find the basis { f₁(t); f₂(t); f₃(t)g of V that is dual to {ϕ₁, ϕ₂, ϕ₃}.

11.20.   Suppose u; v ∈ V and that ϕ(u) = 0 implies ϕ(v) = 0 for all ϕ ∈ V*. Show that v = ku for some scalar k.

11.21.   Suppose ϕ; σ ∈ V* and that ϕ(ν) = 0 implies σ(ν) = 0 for all ν ∈ V. Show that σ = kϕ for some scalar k.

11.22.   Let V be the vector space of polynomials over K. For a ∈ K, define f_a:V → K by ϕ_a(f(t)) = f(a). Show that (a) f_a is linear; (b) if a ≠ b, then ϕ_a ≠ ϕ_b.

11.23.   Let V be the vector space of polynomials of degree ≥2. Let a; b; c ∈ K be distinct scalars. Let ϕ_a, ϕ_b, ϕ_c be the linear functionals defined by ϕ_a(f(t)) = f(a), ϕ_b(f(t)) = f(b), f_c(f(t)) = f(c). Show that {ϕ_a, ϕ_b, ϕ_c} is linearly independent, and find the basis { ϕ₁(t); ϕ₂(t); ϕ₃(t)} of V that is its dual.

11.24.   Let V be the vector space of square matrices of order n. Let T : V → K be the trace mapping; that is, T(A) = a₁₁ + a₂₂ + … + a_nn, where A = (a_ij). Show that T is linear.

11.25.   Let W be a subspace of V. For any linear functional ϕ on W, show that there is a linear functional σ on V such that σ(w) = ϕ(w) for any w ∈ W; that is, ϕ is the restriction of σ to W.

11.26.   Let {e₁, … ; e_n} be the usual basis of Kⁿ. Show that the dual basis is {π₁, … ; π_n} where π_i is the ith projection mapping; that is, π_i(a₁, … ; a_n) = a_i.

11.27.   Let V be a vector space over R. Let ϕ₁, ϕ₂ ∈ V* and suppose σ:V → define by σ(ν) = ϕ₁(ν)ϕ₁(ν)ϕ₂(ν) also belongs to V*. Show that either ϕ₁ = 0 or ϕ₂ = 0.

Annihilators

11.28.   Let W be the subspace of R⁴ spanned by (1; 2; 3; 4), (1; 3; 2; 6), (1; 4; 1; 8). Find a basis of the annihilator of W.

11.29.   Let W be the subspace of R³ spanned by (1; 1; 0) and (0; 1; 1). Find a basis of the annihilator of W.

11.30.   Show that, for any subset S of V; span(S) = S⁰⁰, where span(S) is the linear span of S.

11.31.   Let U and W be subspaces of a vector space V of finite dimension. Prove that (U ∪ W)⁰ = U⁰ + W⁰.

11.32.   Suppose V = U ⊕ W. Prove that V^– = U⁰ ⊕ W⁰.

Transpose of a Linear Mapping

11.33.   Let ϕ be the linear functional on R² defined by ϕ(x; y) = 3x – 2y. For each of the following linear mappings T :R³ → R², find (T^t(ϕ))(x; y; z):

(a) T(x, y, z) = (x + y, y + z), (b) T(x, y, z) = (x + y + z, 2x – y)

11.34.   Suppose T₁:U → V and T₂:V → W are linear. Prove that .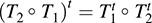

11.35.   Suppose T : V → U is linear and V has finite dimension. Prove that Im T^t = (Ker T)⁰.

11.36.   Suppose T : V → U is linear and u ∈ U. Prove that u ∈ Im T or there exists ϕ ∈ V* such that T^t(ϕ) = 0 and ϕ(u) = 1.

11.37.   Let V be of finite dimension. Show that the mapping T ↦ T^t is an isomorphism from Hom(V; V) onto Hom(V*; V*). (Here T is any linear operator on V.)

Miscellaneous Problems

11.38.   Let V be a vector space over R. The line segment 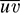joining points u; v ∈ V is defined by 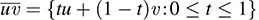. subset S of V is convex if u; v ∈ S implies 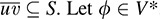. Let ϕ ∈ V*. Define

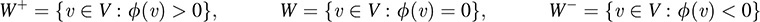
Prove that W⁺; W, and W^– are convex.

11.39.   Let V be a vector space of finite dimension. A hyperplane H of V may be defined as the kernel of a nonzero linear functional ϕ on V. Show that every subspace of V is the intersection of a finite number of hyperplanes.

ANSWERS TO SUPPLEMENTARY PROBLEMS

11.17.   (a) 6x 5y + 4z, (b) 6x – 9y + 3z, (c) –16x + 4y – 13z

11.18.   (a) ϕ₁ = x; ϕ₂ = y; ϕ₃ = z; (b) ϕ₁ = –3x –5y –2z; ϕ₂ = 2x + y; ϕ₃ = x + 2y + z

11.19.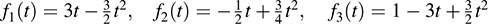   

11.22.   (b) Let f(t) = t. Then ϕ_a(f(t)) = a ≠ b = ϕ_b(f(t)); and therefore, ϕ_a ≠ ϕ_b

11.23.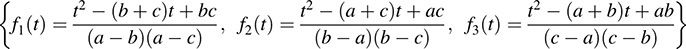   

11.28.   {ϕ₁(x; y; z; t) = 5x – y + z; ϕ₂(x, y, z, t) = 2y – t}

11.29.   {ϕ(x; y; z) = x – y + z}

11.33.   (a) (T^t(ϕ))(x; y; z) = 3x + y – 2z, (b) (T^t(ϕ))(x; y; z) = –x + 5y + 3z