CHAPTER 7
Energy and Chemical Reactions
Potential Energy Diagrams Revisited
By definition, chemistry is the study of matter. However, matter alone does not govern the processes that take place in a chemical reaction. Energy is a huge factor that governs what will occur for all processes that occur in the universe. Changes in heat energy were touched upon in Chapter 1 with the examination of potential energy diagrams. This chapter will review these diagrams to help you put all the pieces together regarding heat and changes in heat energy.
The potential energy diagram is a diagram that can tell
• Whether a reaction is endothermic or exothermic
• The change in heat (ΔH) of a reaction
• The potential energies of the reactants and products (PER and PEP)
• The amount of activation energy needed to start the reaction (Ea)
• The potential energy of the activated complex
These variables can be seen in the potential energy diagram in Figure 7.1:
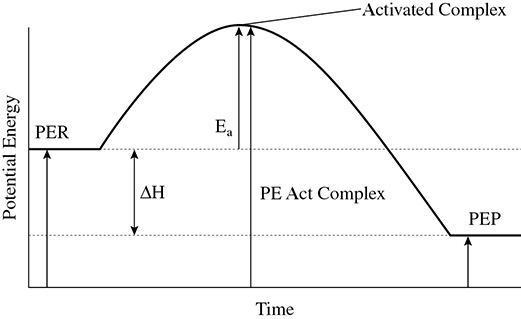
Figure 7.1 Potential Energy Diagram for an Exothermic Reaction
Problem:
In a chemical reaction the potential energy of the reactants is 40 kJ/mol, the potential energy of the products is 15 kJ/mol, and the activation energy is 25 kJ/mol. Find the potential energy of the activated complex and the heat of reaction.
Solution: The potential energy of the reactants is 40 kJ/mol. Add to this the activation energy, 25 kJ/mol, to find the potential energy of the activated complex, 65 kJ/mol. The heat of reaction is found using the equation ΔH = PEP − PER. This comes out to be ΔH = 15 kJ/mol − 40 kJ/mol = −25kJ/mol. The negative signals that the reaction is exothermic.
Heat and Changes in Phase
Adding heat energy to a substance can change the temperature and phase of that substance. Removing heat can have the same effect. Chapter 2 presented the heating curve for water. In that curve there were parts of the graph that showed a change in temperature and no phase change and other parts of the curve where there was no temperature change while a phase change took place. The heat needed to make water undergo changes in phase and changes in temperature can be calculated.
When heating water (a common process) you can calculate the amount of heat being absorbed by the water if you know the change in temperature. The equation q = mcΔT is used to find this amount of heat energy. The variable q in the equation stands for heat absorbed or released, m is the mass of the sample, ΔT is the change in temperature (final temperature minus the initial temperature), and c is the specific heat of a substance (a constant of 4.18 J/g °C for water).
When there is a phase change, there is no temperature change. Therefore, finding out how much heat is needed to melt a sample of ice or boil a sample of water is not going to be feasible using the equation q = mcΔT because ΔT will be zero. Instead, you use the equations q = Hfm and q = Hvm where Hf is the heat of fusion of water (333.6 J/g) and Hv is the heat of vaporization of water (2,259 J/g). Notice, from looking at the two constants, that it takes a larger amount of heat to vaporize one gram of water than to melt one gram of water from its solid state. This large value is due to the hydrogen bonds and dipole forces that exist between the molecules.
Problem:
A 20-gram sample of ice at 0°C completely melts and remains as a liquid at 0°C. How much heat was absorbed by the ice sample?
Solution: Because we are dealing with the melting of ice we will need to use the constant for the heat of fusion. The equation is q = Hfm.
Substituting we get: q = (333.6 J/g)(20 grams) = about 6660 joules of heat energy, 6672 joules actual.
Problem:
A 10-gram sample of water at 90°C is placed into a beaker. The beaker is heated and dangerously left unattended. A few minutes later the water is completely evaporated. How much energy was absorbed by this sample of water?
Solution: This problem requires two equations, one to calculate the amount of heat needed to heat the water to its boiling point and one to calculate the amount of heat absorbed during the change of phase from liquid to gas.
First we calculate the heat needed to raise the temperature of the water from 90°C to 100°C. We can set up and solve using q = mcΔT and get:
q = (10 grams)(4.18 J/g °C)(100°C – 90°C) = 418 joules of heat.
Next we calculate the amount of heat needed to completely boil the water at 100ºC. We use the equation q = Hvm. Substituting and solving gives:
q = (2259 J/g)(10 grams) = 22,590 joules of heat.
The total amount of heat needed to completely vaporize this sample of water is:
418J + 22,590J = 23,008J
Also take note of how much more energy is needed to boil water than raise the temperature.
Thermometry
Figure 7.2 shows two individual blocks of the same material of equal mass but at different temperatures. What will happen to the temperature of the blocks if they are brought together to touch? Let’s assume a closed system where heat cannot escape or enter.
Figure 7.2 Transfer of Heat
Thermometry says that heat flows from a higher temperature to a lower temperature. When this happens, the amount of energy lost by one system is the same as the amount of energy that is gained by the other system. In Figure 7.2, after the blocks make contact, they will eventually reach an equal temperature of 300 K.
THINK ABOUT THIS 
Hess’s Law
Many reactions require a number of other reactions to occur before the final products are formed. These reactions too have their own activation energies, heats of reaction, and so on. If you know the heats of reaction for the smaller, individual steps, you can calculate the final heat of the overall reaction using Hess’s law. The final heat of reaction will be the sum of the heats of reaction for the individual steps in the overall reaction. Consider the following overall reaction:
A + B → 2E. This overall reaction has the following intermediate reactions that occur:
To find the overall heat of reaction simply add up the three heats of reaction. Also, when adding up the individual reactions to find the overall reaction, you will see that substances C and 2D would cancel out because they appear on both sides of the equation (as indicated by the italics).
Consider another reaction where 2A + 2B → D + E. This reaction has the following individual steps:
To find the heat of reaction it is necessary to make some adjustments to the way the individual steps are written and to adjust the heats of reaction accordingly. This can be done by first doubling the first reaction:
This was done because the overall equation calls for 2A and 2B to be reactants. Next, switch the reactants and products for the second equation:
Here the sign for the heat of reaction has been changed. Now the two adjusted reaction steps can be added up to get the overall reaction:
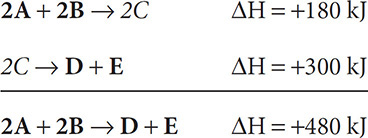
Problem:
Find the heat of reaction for 2C + 3H2 + ½O2 → C2H5OH if:
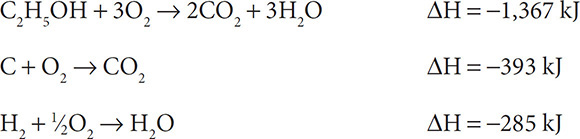
Solution: First reverse the first reaction to get C2H5OH on the right as a product.
The second reaction needs to be doubled so that 2C can enter the reaction:
The third reaction needs to be tripled so that 3H2 can enter the reaction:
Add up the three individual reactions:
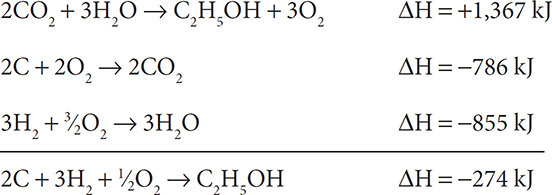
The amount of O2 may be confusing. Review it carefully: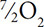 
on the left and 3O2 on the right gives ½O2 on the left.
Bond Dissociation Energy
The strength of a bond that has been formed depends upon how much energy was released when the bond was formed. Because a lower energy state is more stable and preferred, reactions that release greater amounts of energy will form more stable products that have stronger bonds. For example, consider the reaction of methane and oxygen gas. This reaction is an exothermic reaction that forms products that are more stable than the reactants. Proof of this lies in the fact that one of the products, carbon dioxide, has two double bonds in its molecule. The double bonds formed are stronger and more stable than the bonds found in the reactants. You can use the bond dissociation energies of the bonds found in the reactants and products to calculate the amount of heat absorbed and released in a reaction. The difference between the two will be the enthalpy of reaction.
In order to find the enthalpy of reaction, first look at a balanced equation of methane and oxygen gas reacting to form carbon dioxide and water: CH4 + 2O2 → CO2 + 2H2O. Using the bond dissociation energies found in Appendix 4, Reference Tables, you can perform the calculation. There are 4 C—H bonds, 2 O—O bonds, 2 C═O bonds and 4 H—O bonds. The heat of reaction will be the sum of the energies of the bonds broken minus the sum of the bond energies of the bonds formed. Setting up to solve:
Substituting gives:
Problem:
Find the heat of reaction for 2H2 + O2 → 2H2O.
Solution: In this problem there are 2 H—H bonds, 1 O—O bond, and 4 H—O bonds.
Set up to solve:
[2 (H—H) + 1(O—O)] − [4(H—O)]
[2 (435 kJ/mol) + 1(145 kJ/mol)] − [4(462 kJ/mol)]
[(870 kJ/mol) + (145 kJ/mol)] − [(1,848 kJ/mol)]
[1,015 kJ/mol] − [1,848 kJ/mol] = −833 kJ/mol
Entropy, Gibbs Free Energy, and Spontaneous Reactions
THINK ABOUT THIS
Why is it that when an object is dropped it continues to fall without any further intervention? Do objects need to be coached in how to fall? Of course not; gravity “takes over” once you let go of an object and no further intervention is needed to make the object hit the floor. Processes that occur without added external energy or without additional intervention are called spontaneous processes. Now imagine that the very same object that was dropped to the floor suddenly leaves the floor and comes back to your hand (assume no springs, rockets, or legs to jump with). That would be quite a surprise! An object that has fallen does not come back to your hand because that would be a nonspontaneous process. There are many spontaneous processes in our universe; for example, the spontaneous decay of the nucleus of an atom. It should be noted that if a reaction is spontaneous, the reverse reaction will not be spontaneous. If we are going to make a nonspontaneous reaction occur, then energy and outside intervention will be needed.
You already know that lower energy states are preferred by nature. This is why excited electrons release light energy and return back to their ground states. The desire to achieve a lower energy state can be seen when an egg is dropped. The egg will fall to the floor instead of “falling to the ceiling.” Something else happens to the egg once it hits the floor; the yolk and egg shells spread out all over making a big mess. Again, the egg shell and yolk do not come back together again, no matter what the nursery rhyme says. Nature prefers the egg’s yolk to spread out and make a mess. Chaos, randomness, and disorder are all states that are preferred by nature. The term entropy is used to describe chaos, randomness, and disorder. Changes in entropy are designated by the symbol and letter, ΔS.
By determining the changes in energy (or enthalpy) in a reaction and the changes in entropy, you can then determine if a reaction is spontaneous. Spontaneity can be determined by using the Gibbs Free Energy equation: ΔG = ΔH − TΔS. Let’s put the equation to work and see if we can determine the sign of ΔG for a spontaneous reaction.
Nature prefers a lower enthalpy state. To accomplish this, energy must be lost. This means that nature prefers a ΔH (−). Nature also prefers states of increased entropy and chaos. Therefore, nature prefers ΔS (+). Substituting into the Gibbs Free Energy equation (and remembering that the temperature is in Kelvin so that there can be no zeros or negative values):
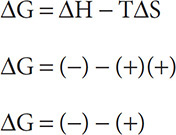
Remember, when subtracting change the minus sign to a positive sign and change the sign of the second number so ΔG = (−) + (−) = (−). ΔG = (−) is what is needed for a reaction or process to be spontaneous.
If ΔH is positive and ΔS is negative, then you can safely conclude that the sign of ΔG would be positive. The process would be classified as nonspontaneous and would not take place. What if ΔG had a value of zero? In this scenario the reaction is said to be in a state of equilibrium, where the forward and reverse reactions proceed equally.
Let’s look at one more possibility, ice melting at room temperature (about 293 K). This is a case where the entropy is increasing (ΔS is positive) because the molecules in the melting ice are spreading out, but at the same time the reaction is absorbing heat. This means that ΔH will be positive as well. If the signs for enthalpy and entropy are the same, then the temperature becomes the deciding factor in determining whether or not the reaction is spontaneous. At a very low temperature the ice will not melt, but at a higher temperature the ice will melt. These trends are summarized in the chart that follows:
THINK ABOUT THIS
Problems:
Give the signs for enthalpy and entropy for the following processes: The freezing of water, the big bang becoming the modern universe, and the submersion of potassium metal into water.
Solutions: The freezing of water requires that heat be released, so the enthalpy will be negative. The entropy will be negative as well because the molecules are more orderly in a solid. The universe has been expanding (entropy is positive) ever since the big bang (enthalpy is negative). Placing potassium metal in water will cause a violent reaction (enthalpy is negative) and the potassium atoms and water molecules will spread out as ions and a gas are formed (entropy is positive).
REVIEW QUESTIONS
1. Two systems at different temperatures come in contact. The heat will flow from the system at
(A) 30°C to a system at 317 K
(B) 40°C to a system at 323 K
(C) 50°C to a system at 303 K
(D) 60°C to a system at 358 K
(E) 70°C to a system at 370 K
2. How many joules of heat are released by a 100-gram sample of water that cools from 25°C to 15°C? (c for H2O is 4.18 J/gK)
(A) 78,375 joules
(B) 83.6 joules
(C) 720 joules
(D) 627 joules
(E) 4,180 joules
3. Calculate the number of joules required to completely vaporize 10 grams of water at 99°C. (Hv = 2259 J/g and c = 4.18 J/gK)
(A) 22,631.8 joules
(B) 40,512 joules
(C) 150 joules
(D) 40,662 joules
(E) 6.12 × 106 joules
4. Which process below has been described correctly for a temperature above 274K?
(A) H2O(l) → H2O(s) is exothermic and spontaneous.
(B) H2O(l) → H2O(s) is endothermic and spontaneous.
(C) H2O(g) → H2O(l) is endothermic and spontaneous.
(D) H2O(s) → H2O(l) is endothermic and spontaneous.
(E) H2O(s) → H2O(l) is exothermic and spontaneous.
5. Based on Gibbs Free Energy equation ΔG = ΔH − T ΔS, a process will occur spontaneously when
(A) ΔG is positive and ΔS is positive
(B) ΔH is positive and ΔT is negative
(C) ΔH is negative and ΔS is positive
(D) ΔH is negative and ΔS is negative
(E) ΔG is positive and ΔS is negative
6. The overall reaction: A + B + 1.5C →D has three individual reactions that take place,
Step 1: A + 2B → E
Step 2: F → B + C
Step 3: ?
What is the reaction that takes place in Step 3?
(A) D + F → C + E
(B)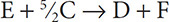 
(C)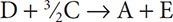 
(D) B + C → F + E
(E) A + B + 1.5C → D
7. Calculate the heat for the overall reaction: Mg(s) + ½O2 → MgO(s) given the heats of reaction below:
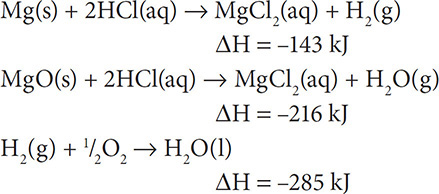
(A) –644 kJ
(B) –212 kJ
(C) +644 kJ
(D) –74 kJ
(E) +74 kJ
ANSWERS AND EXPLANATIONS
1. (C) Heat will flow from high to low—high temperatures to low temperatures, that is. Converting all of the Celsius temperatures to Kelvin with the use of the formula K = C + 273 we find that choice C has a heat flow from 323K to 303K.
2. (E) q = mcΔT is used here where the mass is 100 grams and the change in temperature is –10°C. Substitution gives –4,180 joules. Why the negative sign? This shows that the reaction is exothermic and that heat is released. The reason why this is not reflected in the answer is because the question clearly states that the energy was released.
3. (A) This is a two-step problem. First, we need to go from 99°C to 100°C by using the equation q = mcΔT. Then we need to evaporate the water at a constant temperature of 100°C using the equation q = Hvm. Substituting into the first equation, q = (10 grams)(4.18 J/gK)(1K) = 41.8 J. Substituting into the second equation, q = (2259 J/g)(10 grams) = 22,590 J. This is a total of 22631.8 J.
4. (D) Above 273K water will melt. To do so it must absorb heat (an endothermic process). Also, because this happens “by itself,” the process is spontaneous.
5. (C) Nature prefers a low energy state and a high entropy state. This is best described in choice C.
6. (B) In order to get to the overall reaction, we need to make sure that substances E and F are eliminated, as they do not appear in the overall reaction. This already leans us toward choice B as an answer because choice B has E as a reactant and F as a product. This will counter the reactions posted in Steps 1 and 2. Choice B also has 2.5 moles of C on the left, which will be countered by the one mole of C on the right in Step 2. These two reactions will produce the 1.5 moles of C in the overall reaction.
7. (B) In this reaction we need to keep the first reaction as is because we need Mg(s) to be on the left. This has a ΔH = −143 kJ. The second reaction needs to be switched so that the MgCl2, 2HCl, and H2O all cancel out. This has a ΔH = +216 kJ. The last reaction stays as is so that the H2 can cancel out and so that we have ½O2 on the left. This has a ΔH = −285 kJ. The sum of these three heats of reaction is –212 kJ.