If ρ₁ and ρ₂ are completely reducible representations, then we shall say that ρ₁ and ρ₂ are disjoint if they have no common irreducible constituents, that is, if there exists no irreducible representation that is isomorphic to a subrepresentation of both ρ₁ and ρ₂.

We have the following results, which are easy consequences of our definitions and of the F[G]-isomorphism of V₁*_F V₂ and hom_F(V_l, V₂).

PROPOSITION 5.8. (i) Let ρ_i, i = 1, 2, be a representation of a group G acting in Vi/F. Then the intertwining number ι(ρ₁, ρ₂) = [Inv ρ₁ * ρ₂ : F]. Moreover, if ρ₁ * ρ₂ is completely reducible, then ι(ρ₁, ρ₂) is the multiplicity of the unit representation in ρ₁ * ρ₂. (ii) If ρ₁, ρ₂, and ρ₁ * ρ₂ are completely reducible, then ρ₁ and ρ₂ are disjoint if and only if the unit representation is not a component of ρ₁ * ρ₂. (iii) Let F be algebraically closed and let ρ be a completely reducible representation of G acting in V/F such that ρ*ρ is also completely reducible. Then ρ is irreducible if and only if the unit representation has multiplicity one in ρ* ρ.

Proof.   (i) By definition, _l(ρ₁, ρ₂) = [hom_F[G](V₁, V₂) : F]. We have seen also that hom_F[G](V₁, V₂) = Inv ρ where ρ is the representation of G acting in hom_F(V_l, V₂) such that . Since ρ is equivalent to ρ₁ * ρ₂, [Inv ρ : F] = [Inv ρ₁ * ρ₂ : F]. Hence l(ρ₁, ρ₂) = [hom_F[G](V_l, V₂): F] = [Inv ρ: F] = [Inv ρ₁ * ρ₂ : F]. This proves the first statement in (i). The second statement is an immediate consequence of this and the fact that for ρ completely reducible, [Inv ρ: F] is the multiplicity of the unit representation in ρ. (ii) If ρ₁ and ρ₂ are completely reducible, then (94) and Schur’s lemma show that ρ₁ and ρ₂ are disjoint if and only if l(ρ₁, ρ₂) = 0. By (i), this holds if and only if Inv ρ₁ * ρ₂ = 0. If ρ₁ * ρ₂ is completely reducible, this holds if and only if the unit representation is not a component of ρ. (iii) By (94) and (95), if F is algebraically closed and ρ is completely reducible, then ρ is irreducible if and only if l(ρ, ρ) = 1. By (i), this holds if and only if [Inv ρ*ρ: F] = 1. If ρ*ρ is completely reducible, this is the case if and only if the unit representation has multiplicity one in ρ*ρ.    

The awkward hypotheses on complete reducibility in this proposition can be removed if G is finite and char . In this case we have the following criterion for irreducibility of induced representations.

THEOREM 5.20.   Let G be a finite group, H a subgroup, F an algebraically closed field of characteristic not a divisor of |G|, and let σ be a representation of H acting on U/F. Then σ^G is irreducible if and only if (1) σ is irreducible and (2) for every g H, the representations of H ∩ ^gH on U and on gU are disjoint.

Proof. Evidently (1) is a necessary condition for the irreducibility of σ^G. Now assume that σ is irreducible. By Proposition 5.8 (iii), σ^G is irreducible if and only if the unit representation has multiplicity 1 in (σ^G)*σ^G. Since (σ^G)* and (σ*)^G are equivalent (Theorem 5.18, p. 294), we can replace (σ^G)* by (σ*)^G. By Theorem 5.19, where g runs over a set of representatives of the set Δ of double cosets HgH. Now and mean the same thing: U* as module for F[H ∩ ^gH] determined by the contragredient action. Hence we have to consider the multiplicity in every of the trivial module (giving the unit representation). We now note that if K is any subgroup of G and τ is a representation of K on V/F, then the multiplicity of the unit representation τ₁ of K in τ is the same as the multiplicity of the unit representation ρ₁ of G in τ^G. Since we have complete reducibility, it suffices to show that if τ is irreducible, then ρ₁ has multiplicity 0 in τ^G unless τ = τ₁, in which case, the multiplicity is 1. This follows immediately from Frobenius reciprocity. We now apply this to K = H ∩ ^gH, g ∈ G, and . If g ∈ H, then these become H and U*U. Since σ is irreducible, the multiplicity of the unit representation in σ*σ is 1; hence, the component (U*U)^G contributes the multiplicity 1 for the unit representation of G on U*^GU^G. Hence σ^G is irreducible if and only if the multiplicity of the unit representation of H ∩ ^gH on is 0 for every g H. By Proposition 5.8, this is the case if and only if the representations of H ∩ ^gH on U and on gU are disjoint for every g H. This completes the proof.    

An interesting special case of Theorem 5.20 is obtained by taking σ to be a representation of degree 1 of H. Then the representation σ^G is called a monomial representation. It is clear from the form of the matrix representation of an induced representation given on page 288 that a monomial representation has a matrix representation in which all of the matrices have a single non-zero entry in every row and column and this occurs in the same position for all of the matrices. Theorem 5.20 reduces to the following criterion for irreducibility of monomial representations.

COROLLARY 1 (K. Shoda).   Let ρ be a monomial representation of a finite group G obtained by inducing on a degree one representation σ of a subgroup H of G. Assume that the base field is algebraically closed of characteristic not a divisor of |G|. Then ρ is irreducible if and only if for every g ∈ G – H there exists an h ∈ H ∩ ^gH such that σ(h) ≠ σ(ghg^{– 1}).

Another interesting special case of Theorem 5.20 is that in which . Then ^gH = H for every g ∈ G and the representation of H on gU is the conjugate representation ^gσ (p. 255). Evidently the irreducibility criterion of Theorem 5.20 gives the following

COROLLARY 2.   Let G, H, F, and σ be as in Theorem 5.20 and assume that . Then σ^G is irreducible if and only if σ is irreducible and for every g ∈ G – H, ^gσ and σ are inequivalent.

There is an important extension of this corollary, which we shall now derive. Again, let and let σ be an irreducible representation of H acting in U/F. Let

Then T(σ) is a subgroup of G containing H called the inertial group of σ. Then we have

COROLLARY 3.   Same hypothesis as Theorem 5.20, with . Let ψ be an irreducible representation of the inertial group T(σ) such that ψ_H has σ as an irreducible component. Then ψ^G is irreducible.

Proof. Let V be the F[T]-module on which ψ acts. By Clifford’s theorem applied to T = T(σ) and , σ is the only irreducible component of ψ_H. Now consider V^G, which we may assume contains V as a submodule, and consider the subspace gV of V^G as module for F[T ∩ ^gT]. Since , H ⊂ T ∩ ^gT and gV is a sum of irreducible F[H]-submodules isomorphic to gU. The representation ofH on gU is ^gσ and since g T, this is not equivalent to σ. It follows that the representations of H on V and on gV are disjoint. Hence this is the case for the representations of T ∩ ^gT on V and on gV. Then ψ^G is irreducible by Theorem 5.20.    

A consequence of Corollary 3 that will be useful in the sequel is

COROLLARY 4.   Let G be a finite group, , ρ an irreducible representation of G over an algebraically closed field F of characteristic not a divisor of |G|. Let σ be an irreducible component of ρ_H, T the inertial group of σ. Then ρ = ψ^G for some irreducible representation ψ of T.

Proof. Since σ is an irreducible component of ρ_H, there exists an irreducible component ψ of ρ_T such that σ is an irreducible component of ψ_H. Then ψ^G is irreducible by Corollary 3. Since ψ is an irreducible component of ρ_T, ρ is an irreducible component of ψ^G by Frobenius reciprocity. Hence ρ = ψ^G.    

The importance of this result is that if , then it gives a formula for ρ as an induced representation from a proper subgroup. This gives a way of establishing properties of irreducible representations of G by induction on |G|.

5.12   BRAUER′ S THEOREM ON INDUCED CHARACTERS

For the remainder of this chapter, G will be finite and the base field F will be a subfield of —usually itself. In this section, we shall prove a fundamental theorem of Brauer’s on induced characters. To state this, we need the following

DEFINITION 5.3.   A group G is called p-elementary if G = Z × P where Z is cyclic of order prime to p and P is a p-group (that is, a group of order pⁿ). G is called elementary if it is p-elementary for some prime p.

With this definition we can state

BRAUER’S THEOREM ON INDUCED CHARACTERS.   Any complex character of a group G is an integral linear combination of characters induced from linear characters of elementary subgroups of G.

The proof we shall give of this theorem is due to D. Goldschmidt and M. Isaacs. Brauer’s first proof was quite complicated. A considerably simpler one was given independently by Brauer and Tate and by K. Asano. These proofs as well as the Goldschmidt-Isaacs proof begin with the following simple observations.

Let ch(G) denote the set of -linear combinations of the complex irreducible characters χ_l, …, χ_s of the group G where χ₁ is the unit character. The elements of ch(G) are called generalized characters. Any complex character is a generalized character and since χ_iχ_j is the character of the tensor product of the irreducible representations affording χ_i and χ_j, χ_iχ_j ∈ ch(G). This implies that ch(G) is a ring, more precisely, a subring of the ring ^G of -valued functions on G with the usual component-wise addition and multiplication. χ₁ is the unit of ch(G). If H is a subgroup of G and ψ is a class function on H, then we define the induced class function ψ^G on G by

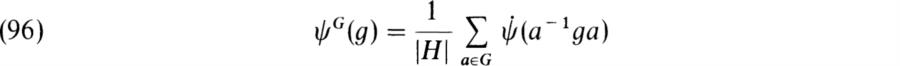
where ψ(h) = ψ(h) for h ∈ H and ψ(g) = 0 for g ∈ G – H. This is a class function on G and we have seen in (85) that if ψ is the character of a representation σ of H, then ψ^G is the character of σ^G. If χ is the character of a representation ρ of G, then we have

where χ_H is the restriction of χ to H, since (Theorem 5.17.3, p. 292). Also transitivity of induction of representations implies the following transitivity formula

if K is a subgroup of G containing H.

Now let be any family of subgroups of G and let ch (G) denote the set of -linear combinations of characters of the form ψ^G where ψ is a complex character of a subgroup H ∈ . It is clear from (97) that ch(G) is an ideal in ch(G). Hence ch(G) = ch(G) if and only if χ₁ ∈ ch(G).

The Goldschmidt-Isaacs proof of Brauer’s theorem is made in two stages: first, the proof that χ₁ ∈ ch(G) for a family of subgroups, the so-called quasi- elementary subgroups, which is larger than the family of elementary subgroups and second, the proof of Brauer’s theorem for quasi-elementary subgroups. For the proof of the second part we shall prove first an extension by Brauer of a theorem of H. Blichfeldt that any irreducible representation of a quasi- elementary group is monomial. Then we shall use this to prove Brauer’s theorem for quasi-elementary groups.

A group G is called p-quasi-elementary for the prime p if G contains a normal cyclic subgroup Z such that and G/Z is a p-group. Evidently, if G is p-elementary, it is p-quasi-elementary. A group G is called quasi-elementary if it is p-quasi-elementary for some prime p.

Let G be p-quasi-elementary, Z a normal cyclic subgroup such that and G/Z is a p-group. Any subgroup H of G is p-quasi-elementary. For, H ∩ Z is cyclic of order prime to p and H/(H ∩ Z) HZ/Z a subgroup of G/Z. Hence H/(H∩Z) is a p-group. The argument shows that if , then |H/(H ∩ Z)| = 1 so H ⊂ Z. It follows that the subgroup Z specified in the definition of p-quasi-elementary is unique and hence this is a characteristic subgroup of G (p. 109). One can give a useful alternative definition of p-quasi-elementary, namely, G = AP where A is cyclic and normal in G and P is a p-group. For, if this is the case, then we write A = Z × W where and |W| = p^k. Then Z and W are unique, hence characteristic in A and hence these are normal subgroups of G. Evidently G/Z WP, which is a p-group. Conversely, suppose G is p-quasi-elementary and Z is as in the definition. Let P be a Sylow p-subgroup of G. Then P ∩ Z = 1 and PZ = ZP is a subgroup such that |PZ| = |G|. Hence G = ZP where Z is cyclic and normal in G and P is a p-group. It is readily seen that a p-quasi-elementary group G is elementary if and only if the subgroup Z is contained in the center and if and only if a Sylow p-subgroup is normal. It follows that a subgroup of a p-elementary group is p-elementary.

The first part of the proof of Brauer’s theorem is based on

LEMMA 1 (B. Banaschewski).   Let S be a non-vacuous finite set, R a subrng (rng = ring without unit, BAI, p. 155) of ^s. Then either R contains l_s (and hence is a subring) or there exists an x ∈ S and a prime p such that f(x) is divisible by p for every f ∈ R.

Proof.   For any x ∈ S let I_x = {f(x)|f ∈ R}. This is a subgroup of the additive group of and hence either I_x = or there exists a prime p such that p|f(x) for every f ∈ R. If we have this for some x, then we have the second alternative. Now assume I_x = for every x ∈ S. Then for each x, we can choose an f_x ∈ R such that f_x(x)= 1 and hence (f_x – l_s) (x) = 0. Then . Expanding this gives an expression for l_s as a polynomial in the f_x with integer coefficients. Thus l_s ∈ R.    

We shall also require

LEMMA 2.   For any g ∈ G and any prime p there exists a p-quasi-elementary subgroup H of G such that is not divisible by p (σ₁ the unit representation of H).

Proof. We can write = Z × W where and |W| = p^k. Let N be the normalizer of Z in G and let be a Sylow p-subgroup of containing the p-group /Z (BAI, p. 81). Then = H/Z where H is a subgroup of N containing . Since and and |H/Z| is a power of p, H is p-quasi-elementary. We wish to show that is not divisible by p. By (86), this is equivalent to showing that the number of cosets aH such that g(aH) = aH is not divisible by p. If aH satisfies this condition, then a^{– l}ga ∈ H and hence a^{– l}Za ⊂ H. Since H is p-quasi-elementary, Z is the only subgroup of H of order |Z|. Hence we have a^{– 1}Za = Z and a ∈ N. Hence we have to count the number of cosets aH of H in N such that g(aH) = aH. Now consider the action of on N/H. Since and Z ⊂ H, z(aH) = aH if z ∈ Z and a ∈ N. Hence Z is contained in the kernel of the action of on N/H. Hence we have the action of /Z on N/H in which (gZ)(aH) = gaH. Since |/Z| = p^k, every orbit of the action of /Z and hence of on N/H has cardinality a power of p (BAI, p. 76). It follows that the number of non-fixed cosets aH under the action of g is divisible by p. Hence the number of fixed ones, (mod p). Since H contains a Sylow p-subgroup of N, [N: H] is not divisible by p. Hence is not divisible by p.    

We can now complete the first part of the proof of Brauer’s theorem by proving

THEOREM 5.21.   Any complex character of G is an integral linear combination of characters induced from quasi-elementary subgroups.

Proof.   In the notation we introduced, this means that if Q denotes the family of quasi-elementary subgroups of G, then ch_Q(G) = ch(G). Since ch_Q(G) is an ideal in ch(G), it suffices to show that χ₁ ∈ ch_Q(G). Now let R be the subrng of ch_Q(G) generated by the induced characters σ₁^G of unit characters σ₁ of quasi-elementary subgroups of G. It is clear that σ₁^G ∈ ^G; hence, R ⊂ ^G. Hence, by Banaschewski’s lemma, if , then χ₁ R and so for some g ∈ G there exists a prime p such that χ(g) ≡ 0 (mod p) for every χ ∈ R. This contradicts Lemma 2, which provides for any g ∈ G and any prime p, a χ ∈ R such that χ(g) is not divisible by p. Hence ch_Q(G) = ch(G).    

We prove next that any irreducible complex representation of a p-quasi-elementary group is monomial and has degree a power of p. In terms of characters this has the following form

THEOREM 5.22 (Blichfeldt-Brauer). Let χ be an irreducible character of a p-quasi-elementary group G. Then

            (1) the degree χ(1) is a power of p, and

            (2) χ = λ^G for some linear character λ of a subgroup of G.

Proof.   We have G = ZP where , Z is cyclic with , and P is a p-group. Let ρ be a representation of G affording χ.

(1) Let σ be an irreducible component of ρ_z, and T the inertial group of σ. Then and the index of T in G is a power of p. By Corollary 4 to Theorem 5.20, ρ = ψ^G for an irreducible representation ψ of T. Hence if T ≠ G, the result follows by induction on |G|. Thus we may assume T = G. Since Z is abelian, σ is of degree 1, and since = T and ρ is irreducible, it follows from Clifford’s theorem that every a ∈ Z acts as a scalar in the space V on which ρ acts. Evidently this implies that ρ_P is irreducible. Since P is a p-group, the degree of ρ, which is a factor of |P|, is a power of p.

(2) Let the degree χ(1) = pⁿ. We shall use induction on n. The result is clear if n = 0 since in this case χ is linear. Hence we assume n > 0. If λ is a linear character of G, then χλ is a character whose degree χλ(1) = χ(l). Hence either χ = χλ or χ is not a component of χλ. The condition χ = χλ is equivalent to (χ|χλ) = 1 and since

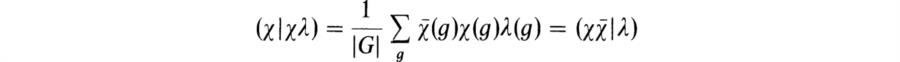
it is equivalent also to . Now is the character of ρρ* and is equivalent to the fact that the multiplicity of λ in is 1. Let Λ be the set of linear characters λ of G such that χλ = χ. It is clear that Λ is a group under multiplication. We have

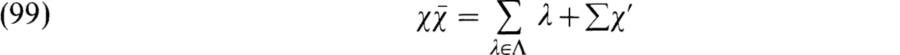
where the χ' are non-linear characters. Since χ(1) and the χ'(l) are divisible by p and λ(1) = 1, it follows from (99) that |Λ| ≡ 0 (mod p). It follows that there exists a λ₁ ∈ Λ such that λ₁ ≠ χ₁ (the unit character) and λ₁^p = χ₁. Since λ₁ is linear, it is a homomorphism of G into the multiplicative group of complex numbers, and since λ₁^p = χ₁ and λ₁ ≠ χ₁ the image is the group of pth roots of unity. Hence, if K = ker λ₁ then and [G :K] = p. By (99), we have

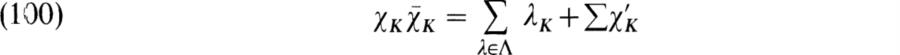
and λ_1K = χ_1K. This shows that the multiplicity of the unit representation in ρ_Kρ_K* is at least two and hence if (|)_K denotes the scalar product on K, then . Then , which implies that ρ_K is reducible. Let σ be an irreducible component of ρ_K, ψ the character of σ. Since χ(1) and ψ(l) are powers of p and ψ(l) < χ(1), we have χ(1) ≥ pψ(1). Since σ is an irreducible component of ρ_K, ρ is an irreducible component of σ^G by Frobenius reciprocity. Since ψ^G(l) = pψ(1) and χ(l) ≥ pψ(1), it follows that χ = ψ^G. The result now follows by induction.    

We shall now make the passage from quasi-elementary groups to elementary ones. As before, let G = ZP where Z is a cyclic normal subgroup of G of order prime to p and P is a p-group. Let W = C_Z(P) ≡ Z ∩ C_G(P), H = WP. Then H is a p-elementary subgroup of G with P as normal Sylow p-subgroup. We shall need the following

LEMMA.   Let λ be a linear character of G such that H ⊂ ker λ. Then λ = χ₁, the unit character of G.

Proof.   It suffices to show that Z ⊂ ker λ. Let K = Z ∩ ker λ. Let b ∈ Z, d ∈ P. Then λ(b^{– 1}dbd^{– 1}) = 1 since λ is a homomorphism. Hence d(bK)d^{– 1} = bK and so every coset bK of K in Z is stabilized under the conjugations by the elements of P. Thus we have an action of P by conjugations on the coset bK. Since |P| is a power of p and |bK| = |K| is prime to p, we have a fixed point under this action. Thus bK ∩ C_Z(P) ≠ Ø, which implies that λ(b) = 1. Since b was arbitrary in Z, we have Z ⊂ ker λ.    

We can now prove

THEOREM 5.23.   Any irreducible character of a quasi-elementary group is an integral linear combination of characters induced from linear characters of elementary subgroups.

Proof. Let χ be a complex irreducible character of a p-quasi-elementary group G. If χ(1) > 1, the result follows from Theorem 5.22 by induction on |G|. Hence assume χ(l) = 1, that is, χ is linear. Let H be the p-elementary subgroup WP defined above and let η = χ_H. By the Frobenius reciprocity theorem the multiplicity of χ in η^G is 1. Now let χ' be a linear component of η^G. Again, by Frobenius reciprocity, η is a constituent of χ'_H. Hence χ'_H = η = χ_H. Then χ'' = χ'χ^{– 1} is a linear character on G such that H ⊂ ker χ''. Hence by the lemma, χ'' is the unit character on G. Then χ' = χ. Thus η^G = χ + θ where θ is a sum of characters of degree > 1. Since the induction on |G| implies that θ is an integral linear combination of characters induced from linear characters of elementary subgroups and since η is linear on the elementary subgroup H, the required result follows for χ = η^G – θ.    

Evidently Brauer’s theorem is an immediate consequence of Theorems 5.22 and 5.23 and transitivity of induction.

We shall now derive an important consequence of the theorem: a characterization of generalized characters among the class functions. Let cf(G) denote the set of complex class functions on G. Evidently cf(G) is a subring of ^G containing ch(G). We know also that cf(G) is the -vector space spanned by the irreducible characters χ₁, …, χ_s and we have defined ψ^G for a class function on a subgroup H by (96). Since the maps χ χ_H and ψ ψ^G are linear, it is clear that formula (97), χ^Gχ = (ψχ_H)^G, is valid also for class functions. We can use this to establish

BRAUER’S CHARACTERIZATION OF GENERALIZED CHARACTERS.   A class function φ on G is a generalized character if and only if φ_H is a generalized character for every elementary subgroup H of G.

Proof.   Let ch(G)' be the set of class functions φ of G satisfying the stated condition. It is clear that ch(G)' is a subring of cf(G) containing ch(G). Now let ψ be a character on some elementary subgroup H of G and let χ ∈ ch(G)'. Then χ_H ∈ ch(H), so ψχ_H ∈ ch(H) and (ψχ_H)^G ∈ ch(G). Then . Since any element of ch(G) is an integral linear combination of characters of the form ψ^G, ψ a character on some elementary subgroup, this implies that ch(G) is an ideal in ch(G)'. Since χ₁ ∈ ch(G), we have ch(G)' = ch(G), which is equivalent to the statement of the criterion.    

We remark that Brauer’s characterization also gives a characterization of Ihe irreducible characters, since χ ∈ ch(G) is an irreducible character if and only if (χ|χ) = 1 and χ(1) > 0. This is clear since χ ∈ ch(G) if and only if , n_i ∈ , and implies that all n_i = 0 except one that has the value ± 1. The condition χ(1) > 0 then gives χ = χ_j for some j.

EXERCISES

        1. A group G is called an M-group if every irreducible complex representation is monomial. Note that Theorem 5.22.2 states that every quasi-elementary group is an M-group. Show that the direct product of M-groups is an M-group. Show that any nilpotent group is an M-group (see BAI, pp. 250–251, exercises 4–11).

        2. (Taketa.) Show that every M-group is solvable. (Sketch of proof: If the result is false, then there is a minimal counterexample: a non-solvable M-group G with |G| minimal. Since any homomorphic image of an M-group is an M-group, if and A ≠ G, then G/A is solvable. Let A and B be minimal normal subgroups of G. If A ≠ B, then A ∩ B = 1 and G is isomorphic to a subgroup of G/A × G/B and so is solvable by the minimality of G. Hence A = B and there exists a unique minimal normal subgroup A of G. There exist irreducible representations ρ of G such that ker . Let ρ be one of minimal degree and let ρ = σ^G where σ is a representation of degree 1 of a subgroup H. Put ρ' = σ₁^G where σ₁ is the unit representation of H. Show that ker ρ' is an abelian normal subgroup ≠ 1 of G. Then G is solvable contrary to hypothesis.)

The following exercises sketch a proof of an important theorem on induced characters due to Artin:

THEOREM 5.24.   Let χ be a complex character of G that is rational valued. (χ(g) ∈ for all g ∈ G.) Then

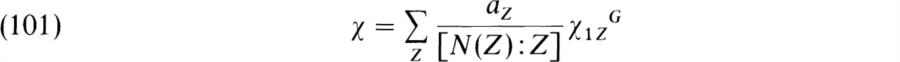
where χ₁ is the unit character, the a_z ∈ , and the summation is taken over the cyclic subgroups Z of G.

        3. Let χ be a rational valued character on G and let g, h ∈ G satisfy = . Show that χ(g) = χ(h). (Hint: If || = m, then h = g^k where (k, m) = 1. Let Λ^(m) be the cyclotomic field of mth roots of unity over , so Λ^(m) = (ε) where ε is a primitive mth root of unity. Show that there exists an automorphism σ of Λ^(m)/ such that σε = ε^k and that if g diag {ε_l, ε₂, …, ε_n}, ε_i ∈ Λ^(m)is a matrix representation, then h = g^k diag {σε_l, σε₂, …, σε_n}. Hence conclude that χ(g) = χ(h).)

        4. Let χ be as in exercise 3. Define an equivalence relation ≡ in G by g ≡ h if and are conjugate in G ( = aa^{– 1} for some a ∈ G). Let D₁, D₂, …, D_t be the distinct equivalence classes determined by ≡. Note that these are unions of conjugacy classes and we may assume D₁ = {1}. Let g_i ∈ D_i and let || = n_i, N(), the normalizer of . Show that

(φ the Euler φ-function). Let Φ_i be the characteristic function of D_i, so Φ_i(g) = 1 if g ∈ D_i and Φ_i(g) = 0 otherwise. Prove by induction on n_i that

for a_j ∈ where a_j = 0 unless is conjugate to a subgroup of .

        5. Note that χ is an integral linear combination of the functions Φ_i. Use this and (103) to prove Artin’s theorem.

5.13   BRAUER’S THEOREM ON SPLITTING FIELDS

In this section, we shall prove that if m is the exponent of a finite group G, that is, the least common multiple of the orders of its elements, then the cyclotomic field Λ^(m) of mth roots of unity over is a splitting field for G. This result was conjectured by Maschke around 1900, but was not proved in complete generality until 1945 when a proof was given by Brauer, based on his theory of modular representations. Subsequently, Brauer discovered his theorem on induced characters and observed that the splitting field theorem is an easy consequence. We shall follow this approach here.

We recall that a representation ρ of G acting on V/F is called absolutely irreducible if the extension representation ρ_k is irreducible for any field K/F (p. 263). The field F is a splitting field for G if every irreducible representation of G over F is absolutely irreducible. We have proved (Theorem 5.8, p. 264) that F is a splitting field for G if and only if F[G] is a direct sum of matrix algebras M_n(F).

We now suppose that F is a subfield of . Then we can give an alternative, more intuitive definition of splitting fields. For, as we shall show, F is a splitting field for G if and only if for any representation ρ acting on a vector space V/, there exists a base for V such that for the corresponding matrix representation, the matrices have all of their entries in F. Since we have complete reducibility of the representations, this holds if and only if it holds for the irreducible representations. It is clear also that the condition can be formulated completely in matrix terms: Any complex matrix representation is similar to a matrix representation over F. Now suppose F is a splitting field. Then F[G] = M_n1(F) … M_ns(F) and [G] = F[G] = M_n1() … M_ns(). If I_j is a minimal left ideal in M_nj(F), then this is an irreducible module for F[G] and {I_j|l ≤ j ≤ s} is a set of representatives for the irreducible F[G]-modules. The degree of the representation afforded by I_j is n_j and |G| = Σn_j². Now I_j is a left ideal contained in the simple component M_nj(). Since [I_j : ] = n_j, I_j is a minimal left ideal in M_nj() and hence the I_j, 1 ≤ j ≤ s, constitute a set of representatives of the irreducible modules for [G]. Since any base for I_j/F is a base for I_j/, it is clear that the irreducible complex matrix representations are similar to matrix representations over F. Conversely, suppose this condition holds for a field F. Then every irreducible complex representation has the form σ where σ is a representation of G over F. Let ρ_l, …, ρ_s be a set of representatives of the irreducible representations of G, n_j the degree of ρ_j, and choose a representation σ_j of G over F such that σ_j = ρ_j. Then the σ_j are inequivalent and irreducible, and the relation implies that F[G] = M_n1(F) … M_ns(F) (see p. 259). Hence F is a splitting field for G.

Let χ and χ' he characters of inequivalent irreducible representations ρ and ρ' of G over F. If where the Δ_i are division algebras, then we may suppose that ρ acts on a minimal left ideal I ⊂ M_m1(Δ₁) and ρ' acts on a minimal left ideal I' of M_m2(Δ₂). When we pass to , M_m1(Δ₁) and M_m2(Δ₂) split as direct sums of simple components of [G] and these ideals in [G] have no common simple components. It follows that if χ₁, χ₂, …, χ_s are the complex irreducible characters, then and where the m_i and m'_i are nonnegative integers and for every i, either m_i = 0 or m'_i = 0. Thus and (χ|χ') = 0. Moreover, χ is an irreducible complex character if and only if (χ|χ) = 1, in which case, the complex irreducible representation whose character is χ is the extension ρ. It is also clear that F is a splitting field for G if and only if for every irreducible complex character χ_i there exists a representation ρ_i of G over F such that .

We can now prove

THEOREM 5.25.   If m is the exponent of G, then the cyclotomic field Λ^(m)/ of the mth roots of unity is a splitting field for G.

Proof.   Let χ be an irreducible complex character of G. By Brauer’s theorem on induced characters, χ is an integral linear combination of characters of the form λ^G where λ is a linear character of a subgroup H of G. Now λ is a homomorphism of H into the multiplicative group * of complex numbers and if h ∈ H, then h^m = 1 so λ(h)^m = 1. Hence λ(h) ∈ Λ^(m). It is clear from the definition of induced representations that the representation affording λ^G has a representation by matrices with entries in Λ^(m). Thus λ^G is the character of a representation of G over Λ^(m). It follows that where the k_j ∈ and φ_l, …, φ_r are the characters of the inequivalent irreducible representations of G over Λ^(m). Then and since every (φ_j|φ_j) is a positive integer, all of the k_j but one are zero and the non-zero one is 1. Hence χ is a character of an irreducible representation of G over Λ^(m). This implies that Λ^(m) is a splitting field.    

5.14   THE SCHUR INDEX

In this section, we shall study relations between irreducible representations of a finite group G over and over a subfield F of . We use the notations of the previous section: where the Δ_i are division algebras. We write also A_i = M_m1 (Δ_i).

Let χ be an irreducible complex character of G, ρ a representation of G over affording χ. We may assume that ρ is the restriction of the regular representation of G to a minimal left ideal V of one of the simple components M_nj(). Then V is contained in exactly one of the A_i. If V ⊂ A_i then A_iV ≠ 0, but A_i' V = 0 for every i' ≠ i. This property is independent of the choice of the representation ρ affording χ.We shall say that A_i is the simple component of F[G] belonging to χ. We can associate also a subfield of /F with χ, namely, the subfield over F generated by the complex numbers χ(g), g ∈ G. We denote this as F(χ). We have the following

PROPOSITION 5.9.   Let χ be an irreducible complex character of the finite group G, F a subfield of , and let A = A_i be the simple component of F[G] belonging to χ. Then F(χ) is isomorphic over F to the center of A.

Proof.   As indicated, we may take the representation ρ affording χ to be the restriction of the regular representation to a minimal left ideal V ⊂ A. We can regard ρ as a representation of [G] and identify F[G] with an F-subalgebra of [G]. Since ρ is irreducible, it follows from Schur’s lemma that ρ(cent[G]) = 1. We recall that the centers of F[G] and [G] are spanned by the elements where C₁, …, C_S are the conjugacy classes of G. If g ∈ C_i then is a non-zero multiple of . Hence the centers are spanned by the elements . We have ρ(c_g) = γ1, γ ∈ , and hence tr ρ(c_g) = nγ, where n = χ(1), the degree of ρ. On the other hand, . Hence

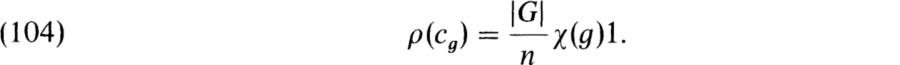
We now restrict the -algebra homomorphism ρ of [G] to F[G]. This gives an F-algebra homomorphism of F[G], which maps cent F[G] onto the set of F-linear combinations of the elements χ(g) 1. Since ρ maps every simple component A_i ≠ A into 0, we have a homomorphism of cent A onto F(χ) 1. Since cent A is a field, we have an isomorphism of cent A onto F(χ).    

We shall now say that a complex character χ of G is realizable over the subfield F of if χ is the character of a representation σ of G over F. Since a representation is determined up to equivalence by its character, it is clear that χ is realizable over F if and only if ρ is equivalent to σ for any representation ρ affording χ. Also, as we noted before, this is the case if and only if there exists a base for the space V on which ρ acts such that the entries of the matrices of the ρ(g), g ∈ G, are all in F. Evidently, if χ is realizable over F, then F contains every χ(g), g ∈ G.

We shall now show that if χ is an irreducible complex character of G and F is a subfield of containing all the χ(g), then there exists a positive integer d such that the character dχ (of the direct sum of d copies of the representation ρ affording χ) is realizable over F. The minimum such d is called the Schur index of χ over F. We prove the existence of the Schur index and give a structural description of this integer in the following

THEOREM 5.26.   Let χ be an irreducible complex character of G, F a subfield of containing all of the χ(g), g ∈ G, and let A = M_m(Δ), where Δ is a division algebra, be the simple component of F[G] belonging to χ. Then [Δ : F] = d² and the character dχ is realizable over F. Moreover, if d' is any positive integer such that d'χ is realizable over F, then d|d' and hence d is the Schur index of χ over F.

Proof.   Since F = F(χ), A is central simple by Proposition 5.9. Hence Δ is central, [Δ : F] = d² (p. 222), and [A : F] = m²d². Any two minimal left ideals of A are isomorphic as A-modules, hence as vector spaces over F, and A = I_l…I_m where I_j, 1 ≤ j ≤ m, is a minimal left ideal. Hence [I : F] = md² and [I : ] = md². Since A is central simple, A is simple and hence this is one of the simple components of [G]. Since [A : ] = m²d², we have A = M_md() and the calculation we gave for F shows that if V is a minimal left ideal of A, then [V : ] = md. We have seen that the representation ρ affording χ can be taken to be the restriction of the regular representation to a minimal left ideal contained in A. We may take this to be V. Now I is a left ideal in A, and [I : ] = md² while [V : ] = md. Hence I is a direct sum of d left ideals isomorphic to V. This implies that the direct sum of d complex irreducible representations equivalent to ρ is equivalent to τ where τ is the representation of G acting on I/F. Hence dχ is realizable over F. Now suppose d' is a positive integer such that d'χ is realizable over F. Then the [G]-module V^(d'), a direct sum of d' copies of V, is isomorphic to a module I' where I' is a module for F[G]. Now V^(d') is annihilated by every simple component of F[G] except A and hence I' is annihilated by every simple component of F[G] except A. It follows that where I is a minimal left ideal of A. Then . Hence d' = dh. Evidently this implies that d is the Schur index.    

The foregoing result shows that the Schur index of χ is 1 if and only if Δ = F and A = M_m(F). Hence χ is realizable over F = F(χ) if and only if A = M_m(F).

Now let E be a subfield of containing F = F(χ) and consider E[G]. Since the simple component A of F[G] belonging to χ is central simple, A_E is a simple component of E[G]. Evidently this is the simple component of E[G] belonging to χ. Hence χ is realizable over E if and only if A_E M_n(E), that is, E is a splitting field over F of A (p. 220). This is the case if and only if E is a splitting field for the division algebra Δ such that A = M_m(Δ). The basic criterion for this was given in Theorem 4.7 (p. 218). According to this result, a finite dimensional extension field E/F is a splitting field for a finite dimensional central division algebra Δ/F if and only if E is isomorphic to a subalgebra E' of a matrix algebra M_r(Δ) such that the centralizer of E′ in M_r(Δ) is E′, and if this is the case then [E : F] = rd where [Δ : F] = d². This result and Theorem 5.26 give the following

THEOREM 5.27.   Let the notations be as in Theorem 5.26 and let E be a finite dimensional extension field of F contained in . Then χ is realizable over E if and only if E is isomorphic to a subalgebra E' of the matrix algebra M_r(Δ) such that C_Mr(Δ)(E') = E'. Moreover, in this case [E : F] = rd where d is the Schur index of χ over F.

5.15   FROBENIUS GROUPS

We shall conclude this chapter by applying the theory of characters to derive an important theorem of Frobenius on finite groups. Frobenius’ theorem can be viewed in two different ways: first as a theorem on transitive permutation groups and second as a theorem on abstract groups. Also, as we shall show, the result is related to the study of fixed-point-free automorphisms of finite groups. Finally, we shall consider an example of a Frobenius group whose character analysis leads to a variant of a classical proof of the quadratic reciprocity law of number theory.

First, let G be a permutation group of the set N = {1, 2, …, n}, n > 1, such that (1) G is transitive; (2) For any i, the stabilizer Stab i = {g ∈ G|gi = i} ≠ 1; and (3) No element of G except 1 fixes more than one element of {1, …, n}. Let H_i = Stab i. Then condition (3) is equivalent to H_i ∩ H_j = 1 if i ≠ j. Also any two of the subgroups of H_i, H_j are conjugate: H_j = ^gH_i = gH_ig^{– 1}. For, there exists a g ∈ G such that gi = j. Then Stab j = Stab gi = g(Stab i)g^{– 1}. It is clear also that if g H_i then gi = j ≠ i and ^gH_i = H_j ≠ H_i. We remark also that since n ≥ 2, H_i ≠ G.

We now introduce the following

DEFINITION 5.4.   A finite group G is called a Frobenius group if G contains a subgroup H such that (i) , and (ii) for any g ∈ G – H, H ∩ ^gH = 1. The subgroup H is called a Frobenius complement in G.

It is clear from the foregoing remarks that if G is a permutation group satisfying conditions (1), (2), and (3) above and n ≥ 2, then any one of the subgroups H = H_i satisfies the conditions of Definition 5.4. Hence G is a Frobenius group with H a Frobenius complement in G. Conversely, suppose G is Frobenius with Frobenius complement H, and consider the action of G on the set G/H of left cosets of H. We know that this action is transitive. Moreover, a(gH) = gH if and only if a ∈ ^gH, so Stab(gH) = ^gH. Then the kernel of the action is . Hence we can identify G with the corresponding group of permutations of G/H. It is clear that condition (2) holds and condition (3) is equivalent to . This follows from (ii) in the definition of a Frobenius group.

Thus we see that the concept of a Frobenius group is the abstract version of the permutation group situation we considered first. We can now state

FROBENIUS’ THEOREM.   Let G be a Frobenius group with Frobenius complement H. Put

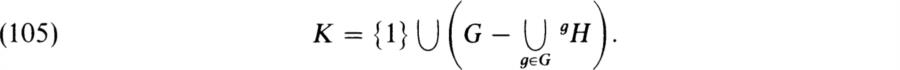
Then K is a normal subgroup of G, G = KH, and K ∩ H = 1.

If we adopt the permutation group point of view, we see that K can be described as the union of {1} and the set of transformations that fix no i ∈ N.

For the proof we require the following

LEMMA.   Let G be a Frobenius group with Frobenius complement H and let φ be a class function on H such that φ(1) = 0. Then (φ^G)_H = φ.

Proof.   By definition

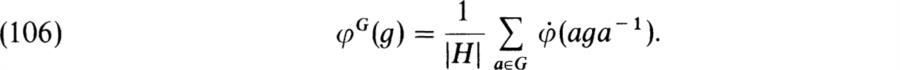
Then φ^G(1) = 0 since φ(1) = 0. Now let h ∈ H, h ≠ 1, and let a ∈ G – H. Then aha^{– l} H and . Hence

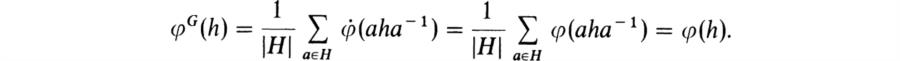
Thus (φ^G)_H = φ.    

We can now give the

Proof of Frobenius’ theorem. We note first that the definition of Frobenius complement H implies that distinct conjugates ^g₁H and ^g₂H have only the unit element in common and the normalizer N_G(H) = {g|^gH = H} = H. Hence |{^gH}| = [G : N_G(H)] = [G : H]. Then and so, by (105),

Now let ψ be a complex irreducible character of H different from the unit character ψ₁ and put φ = ψ – ψ(1)ψ₁. Then φ is a generalized character of H satisfying φ(1) = 0. Hence, by the lemma, φ^G is a generalized character of G such that (φ^G)_H = φ. Then, by Frobenius reciprocity,

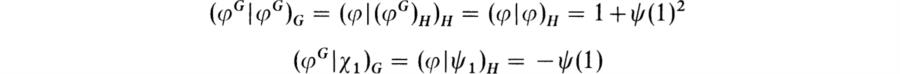
for χ₁, the unit character of G. Now put ψ* = φ^G + ψ(1)χ₁. Then ψ* is a generalized character of G and

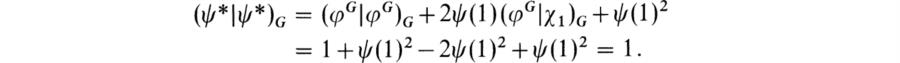
Also

Since ψ* is a generalized character of G satisfying (ψ*|ψ*)_G = 1 and ψ*(1) = ψ(1) > 0, ψ* is a complex irreducible character of G. Thus for each irreducible complex character ψ ≠ ψ_l of H, we have defined an irreducible complex character ψ* of G that is an extension of ψ. If ρ* is a representation of G affording ψ*, then ker ψ* = {g ∈ G | ψ*(g) = ψ*(1)} = ker ρ* (p. 271). Now put

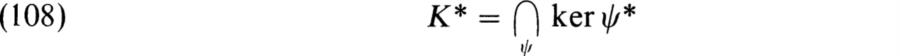
where the intersection is taken over the irreducible characters ψ of H, ψ ≠ ψ₁. Evidently K* is a normal subgroup of G. Let k ≠ 1 be in K. Then k ^gH for any g ∈ G and φ^G(k) = 0, by definition (106). Hence ψ*(k) = ψ*(1). Thus K ⊂ K*. Next let h ∈ H ∩ K*. Then ψ(h) = ψ*(h) = ψ*(1) = ψ(1). Thus h is in the kernel of every irreducible character of H. Then ρ(h) = 1 for the regular representation ρ of H and hence h = 1. Hence H ∩ K* = 1. Thus we have , and |G| = |H|[G: H] = |H||K|. Hence HK* is a subgroup of G and , so is a factor of |G| = |H| |K|. Hence |K*||K| and since K* ⊃ K, K = K*. We now have and |K| = [G : H]. Then |KH| = |K||H| = |G| and hence G = KH. This completes the proof.    

The subgroup K is called the Frobenius kernel of the Frobenius group G with complement H. We note that no proof of Frobenius’ theorem without characters is known.

Now let A be a group of automorphisms of a finite group G. We shall say that A is fixed-point-free if no α ≠ 1 in A fixes any g ≠ 1 of G. We shall now relate the study of pairs (G, A) where G is a finite group and A is a fixed-point-free group of automorphisms ≠1 of G to the study of Frobenius groups. We recall the definition of the holomorph Hol G of a group G as the group of transformations G_L Aut G where G_L is the set of left multiplications g_L : x gx (BAI, p. 63). If α ∈ Aut G, then αg_L = (αg)_Lα. Hence if g_i ∈ G, α_i ∈ Aut G, then . Aut G and G_L are subgroups of Hol G, G_L is normal, G_L ∩ Aut G = 1, and Hol G = G_L Aut G. It is clear that if A is a subgroup of Aut G, then G_LA is a subgroup of the holomorph. Now suppose A ≠ 1 and A is fixed-point-free. If g ≠ 1 is in G, then . Hence and for any u ∈ G_LA – A. Thus G_LA is a Frobenius group with Frobenius complement A. It is clear also that G_L is the Frobenius kernel.

Conversely, suppose that G is a Frobenius group with Frobenius complement H and let K be the Frobenius kernel. The group H acts on K by conjugation and these maps are automorphisms of K. Suppose h ∈ H and k ∈ K satisfies ^hk = k. Then kh = hk and ^kh = h ∈ H. It follows that either h = 1 or k = 1. This implies that the homomorphism of H into Aut K sending h into the map x hxh^{– l} is a monomorphism, so H can be identified with a subgroup of Aut K. Moreover, this group of automorphisms is fixed-point-free.

A result that had been conjectured for a long time and was proved by Thompson is that the Frobenius kernel of a Frobenius group is nilpotent. The foregoing considerations show that this is equivalent to the following fact: A finite group having a group of automorphisms ≠ 1 that is fixed-point-free is nilpotent. For a proof of this theorem, see page 138 of Characters of Finite Groups by W. Feit (see References).

EXAMPLE

Let B be the subgroup of GSL₂(F), F = /(p), p an odd prime, consisting of the matrices of the form

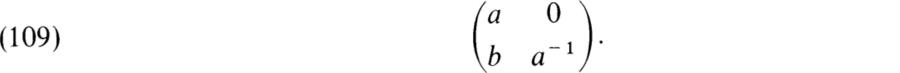
Evidently, |B| = p(p – 1). B contains subgroups K and D where K is the set of matrices (109) with a = 1 and D is the set of diagonal matrices. We have , B = DK, D ∩ K = 1. Moreover,

and

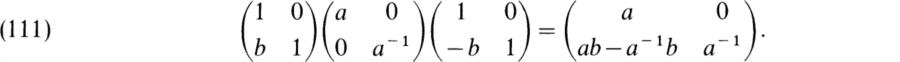
Put G = B/{1, – 1} and let denote the image in G of a subset A of B under the canonical homomorphism of B onto G. We may identify K with . Since the matrix (111) is contained in D if and only if a = ±1, it follows that G is a Frobenius group with as a complement and K as the kernel.

We wish to obtain a character table for G. Let v be a generator of the cyclic multiplicative group F* of the field F. Then the elements of are , 1 ≤ i ≤ (p – l)/2. Since elements in a complement in a Frobenius group are conjugate in the group if and only if they are conjugate in the complement, the (p – l)/2 elements of determine (p – 1 )/2 distinct conjugacy classes. The class has a single element and the classes of the elements , 1 ≤ i ≤ (p – 3)/2, have cardinality p. Formulas (110) and (111) imply that we have two more conjugacy classes with representatives

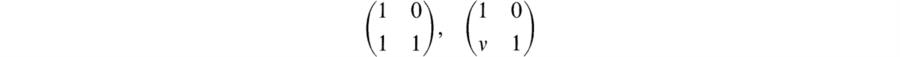
(since v is not a square in F*). The number of elements in these classes is (p – l)/2. Altogether we have (p – l)/2 + 2 = (p + 3)/2 conjugacy classes and hence we have this many irreducible complex characters.

Since is cyclic of order (p – 1)/2, it has (p– 1)/2 linear characters. Using the homomorphism of G onto G/K , we obtain (p – l)/2 linear characters for G, which give the following table:

Since the conjugacy class of has cardinality p, the orthogonality relation (60) implies that the remaining entries in the columns headed by this class are 0’s.

The subgroup K of G is cyclic with generator . Hence we have a homomorphism σ of K into mapping the generator into the primitive pth root of unity ζ = e^2πi/p. This defines the representation ρ = σ^G of G. By (110),

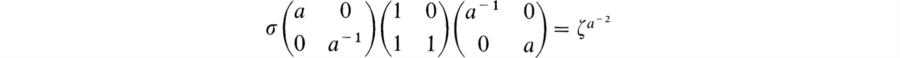
where the exponent is an integer. If a ≠ ±1, then ζ^{a– 2} ≠ ζ. Hence the representation of K such that

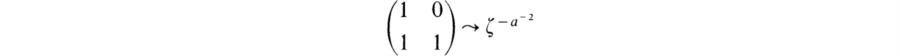
is inequivalent to σ. It follows from Corollary 2 to Theorem 5.20 (p. 304) that ρ = σ^G is an irreducible representation of G. If χ is its character, then the degree of ρ is χ(1) = (p – l)/2. Let χ' be the remaining irreducible character. The relation

gives χ'(l) = (p – l)/2. Hence the last two rows of the character table have the form

The orthogonality relations (60) for columns 1 and 2 give (p – 1 )/2 + c(p – l)/2 + c'(p – l)/2 = 0, so c + c' = –1. Similarly, d + d' = –1. The orthogonality of χ with χ₁ gives (p – l)/2 + c(p – l)/2 + d(p – l)/2 = 0, so c + d = –1. These relations imply that c' = d, d' = c. Hence the last two rows have the form

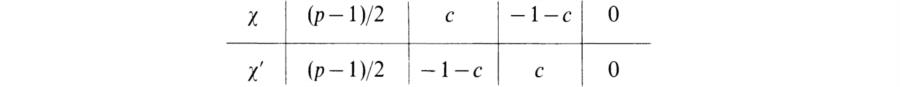
and it remains to determine c. We need to distinguish two cases:

Case 1. (– 1/p) = 1, that is, – 1 is a quadratic residue mod p, or equivalently, p ≡ 1 (mod4) (BAI, p. 133). In this case is conjugate to . Then c is real. Then the orthogonality relation (60) applied to the second and third columns gives (p – 1 )/2 – 2c(l + c) = 0, which implies that .

Case 2. (–1/p) = –1, –1 is a non-square mod p, so p = 3 (mod4). In this case, is not conjugate to its inverse and hence c . Then χ' = χ*, so . Then the orthogonality relation (60) for the second and third columns gives (p – 1 )/2 + c² + (1 + c)² = 0, which implies that .

These two cases complete the character tables, although we do not know which determination of the signs gives the character χ of ρ = σ^G. We can amalgamate the two cases by writing ρ* = (– 1 /p)p. Then in both cases we have

We now apply the induced character formula (85) to the character χ of ρ. Since is a cross section of G relative to K, we obtain

where S is the set of positive integers less than p that are squares modulo p.

We proceed to apply formula (113) to give a proof of the law of quadratic reciprocity of elementary number theory. We introduce the Gauss sum

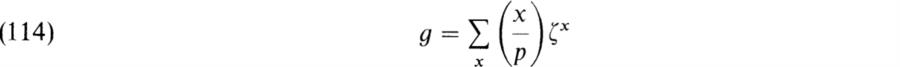
where 1 ≤ x ≤ p – 1. Since (by the factorization , we obtain from (113) the formula

Now let q be an odd prime ≠p. We note that (p*/q) ≡ p*^{(q – 1)/2} (modq) (BAI, p. 129, exercise 13). We now work in the ring R of integers of the cyclotomic field (ζ) and use congruences modulo qR (BAI, pp. 278–281). We have

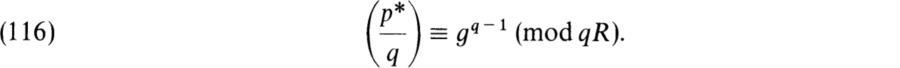
Since for (mod qR), we have

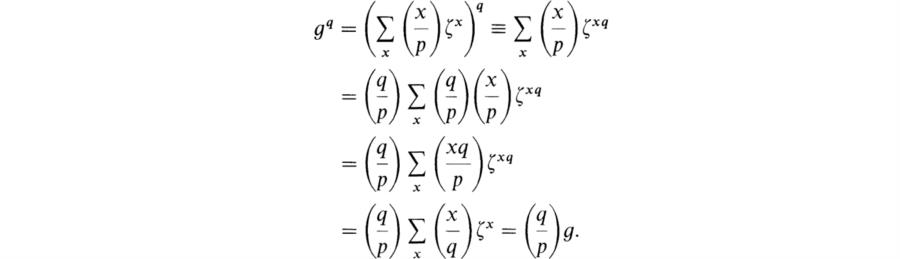
Hence

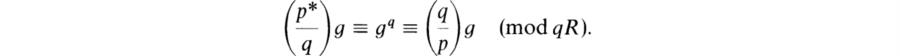
Then (p*/q)g² ≡ (q/p)g² and (p*/q)p* ≡ (q/p)p*. Since the coset of p* = (– 1/p)p is a unit in R/qR, this implies that (p*/q) ≡ (q/p). Since the coset of 2 is a unit, it follows that (p*/q) = (q/p). Hence

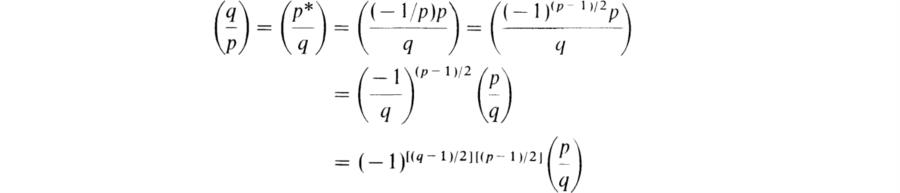
which is the law of quadratic reciprocity whose first proof was published by Gauss in 1801.

Iam indebted to D. R. Corro for pointing out this example of a Frobenius group with its application to the reciprocity law. The derivation following the formula g² = p* is classical (apparently first given by Jacobi in 1827). See Sechs Beweise des Fundamentaltheorems uber quadratische Reste von Carl Friederich Gauss in W. Ostwald’s “Klassiker der exacten Wissenschaften,” pp. 107–109.

EXERCISES

        1. Show that if G is a Frobenius group with complement H, then the Frobenius kernel is the only normal subgroup of G satisfying G = KH, K ∩ H = 1.

        2. Show that if G is a dihedral group of order 2m, m odd, generated by a and b such that a^m = 1, b² = 1, bab^{– 1} = a^{– 1}, then G is a Frobenius group.

        3. A subset S of a group G is called a T.I. set (trivial intersection set) if S ≠ Ø and for any g ∈ G, either ^gS = S or ^gS ∩ S ⊂ {1}. Show that if S is T.I., then N_G(S) = {g ∈ G|S^g = S} is a subgroup containing S. Show that if G is a Frobenius group with Frobenius complement H, then H is a T.I. set.

        4. (Brauer-Suzuki.) Let S be a T.I. set in G and let N = N_G(S). Suppose that φ and ψ are complex class functions on N such that φ and ψ are 0 outside of S and φ(1) = 0. Show that (i) φ^G(g) = φ(g) for any g ≠ 1 in S, and (ii) (φ|ψ)_N = (φ^G|ψ^G)_G.

        5. (Brauer-Suzuki.) Let S, G, and N be as in exercise 4 and let ψ₁, …, ψ_m be complex irreducible characters of N such that ψ₁(l) = … = ψ_m(1). Show that there exists ε = ±1 and complex irreducible characters χ₁, …, χ_m of G such that .

        6. Let G be a Frobenius group with Frobenius complement H and Frobenius kernel K Assume K is abelian. Use exercise 8, p. 63 of BAI to show that if ρ is an irreducible representation of G. then either (i) K ⊂ ker ρ or (ii) ρ is induced from a degree one representation of K. Conclude that G is an M-group if and only if H is an M-group. (This result holds without the hypothesis that K is abelian.)

   Sketch of proof: Suppose that (i) fails. Then, by Clifford’s theorem, there exists an irreducible constituent λ of ρ_K such that λ is not the unit representation λ₁ of K. We claim that T_G(λ) = K. Otherwise, by Corollary 2, p. 304, there exists an such that ^xλ = λ. But H acts fixed-point-freely on K; so does ^gH for any g (since ). Thus x induces a fixed-point-free automorphism of K, so by the exercise cited

Then

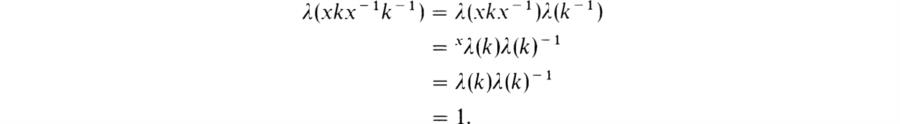
Hence K ⊂ ker λ, contrary to λ ≠ λ₁. Thus T_G(λ) = K and so (ii) follows from Corollary 4 on p. 305.

        7. Let F be a finite field with q = p^m elements, p a prime. Define the following subgroups of GL₂(F):

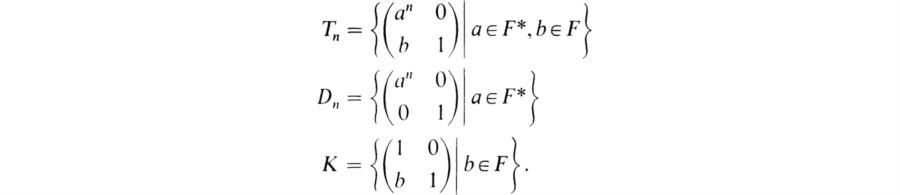
Show that if D_n ≠ 1, then T_n is a Frobenius group with Frobenius complement D_n and Frobenius kernel K.

   (Note: These groups have been used by W. Feit to obtain an estimate for the number of solutions in F⁽ⁿ⁾ of an equation of the form . See Feit, p. 140, in the references below.)

REFERENCES

C. W. Curtis and I. Reiner, Representation Theory of Finite Groups and Associative Algebras, Wiley-Interscience, New York, 1962.

W. Feit, Characters of Finite Groups, Benjamin, New York, 1967.

I. M. Isaacs, Character Theory of Finite Groups, Academic, New York, 1976.