Classical Representation Theory of Finite Groups
One of the most powerful tools for the study of finite groups is the theory of representations and particularly the theory of characters. These subjects as generalized to locally compact groups constitute a major area of modern analysis that generalizes classical Fourier analysis. The subject of representation theory of finite groups is almost wholly the creation of Frobenius. Notable improvements and simplifications of the theory are due to Schur. During the past fifty years, very deep results have been added to the -theory by Brauer, and representation theory has played an important role in the explosive growth of the structure theory of finite groups, which began with the Feit-Thompson proof of a hundred-year-old conjecture by Burnside that every finite group of odd order is solvable.
In this chapter, we are concerned with the classical theory of representations of finite groups acting on finite dimensional vector spaces over the field ![]() of complex numbers or more generally over fields of characteristics not dividing the group order. This restriction on the characteristic implies complete reducibility of the representation or, equivalently, semi-simplicity of the group algebras. This permits the application of the structure and representation theory of finite dimensional semi-simple algebras to the representation theory of finite groups. However, there is considerably more to the story than this, namely, the theory of characters, much of which can be developed without recourse to the theory of algebras.
of complex numbers or more generally over fields of characteristics not dividing the group order. This restriction on the characteristic implies complete reducibility of the representation or, equivalently, semi-simplicity of the group algebras. This permits the application of the structure and representation theory of finite dimensional semi-simple algebras to the representation theory of finite groups. However, there is considerably more to the story than this, namely, the theory of characters, much of which can be developed without recourse to the theory of algebras.
We shall derive the classical results of Frobenius, Schur, and Burnside as well as Brauer’s results on induced characters and splitting fields. One of the most important contributions of Brauer is his modular theory, which deals with representations over fields whose characteristics do divide the group order and the relation between the representations over such fields and representations over ![]() . We shall not consider this theory in our account. A number of applications of character theory to structural results on finite groups will be given.
. We shall not consider this theory in our account. A number of applications of character theory to structural results on finite groups will be given.
5.1 REPRESENTATIONS AND MATRIX REPRESENTATIONS OF GROUPS
DEFINITION 5.1. By a representation ρ of a group G we shall mean a homomorphism of G into the group GL(V) of bijective linear transformations of a finite dimensional vector space V over afield F.
We shall say that ρ is a representation of G over F and that it acts on V/F. The dimensionality of V is called the degree of the representation. The defining conditions for a representation are that ρ is a map of G into GL(V) such that
![]()
for gi ∈ G. These have the immediate consequences that ρ(l) = lv, ρ(g–1) = ρ(g)–1 and in general, ρ(gm) = ρ(g)m for m ∈ ![]() . We remark also that the conditions that ρ(g)∈ GL(V) and (1) holds can be replaced by the following: ρ(g) ∈ EndFV, (1) holds, and ρ(l) = 1. These immediately imply that ρ(g)∈ GL(V), so p is a representation.
. We remark also that the conditions that ρ(g)∈ GL(V) and (1) holds can be replaced by the following: ρ(g) ∈ EndFV, (1) holds, and ρ(l) = 1. These immediately imply that ρ(g)∈ GL(V), so p is a representation.
Let B = (u1, u2,…, un) be a base for V/F. If a ∈ EndF V, we write
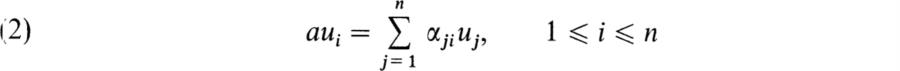
and obtain the matrix (α) whose (i, j)-entry is αij. The map a ![]() (α) is an isomorphism of EndF V onto Mn(F). Hence if ρ is a representation of G acting on V, then the map
(α) is an isomorphism of EndF V onto Mn(F). Hence if ρ is a representation of G acting on V, then the map
![]()
where ρB(g) denotes the matrix of ρ(g) relative to the base B, is a homomorphism of G into the group GLn(F) of invertible n × n matrices with entries in F. Such a homomorphism is called a matrix representation of G of degree n. A change of the base B to C = (v1, …, vn) where vi = Σμji uj and (μ) ∈ GLn(F) replaces ρB by ρc where
![]()
This matrix representation is said to be similar to ρB. It is clear that any matrix representation can be obtained from a representation in the manner indicated above.
A homomorphism of G into the symmetric group Sn or, equivalently, an action of G on the finite set {1, 2, …, n} (BAI, p. 71), gives rise to a representation. Let the action be described by
![]()
where π is the homomorphism of G into Sn. Let V be the vector space with base (u1, u2, …, un) and let ρ(g) be the linear transformation of V such that
![]()
Then ρ(g1g2) = ρ(g1)ρ(g2) and ρ(l) = 1, so ρ is a representation of G. Representations of this type are called permutation representations. They are characterized by the property that they are representations that stabilize some base B of V/F. Of particular interest is the permutation representation obtained from the action of G on itself by left translations (BAI, p. 72). The corresponding representation of G is called the regular representation.
EXAMPLES
1. Let G = ![]() , the cyclic group generated by an element g of order n. We have the homomorphism of G into Sn mapping g into the cycle (12…n). This action is equivalent to the action of G on itself by left translations. The associated permutation representation maps g into the linear transformation ρ(g) such that
, the cyclic group generated by an element g of order n. We have the homomorphism of G into Sn mapping g into the cycle (12…n). This action is equivalent to the action of G on itself by left translations. The associated permutation representation maps g into the linear transformation ρ(g) such that
![]()
This gives a matrix representation in which g is represented by the matrix

This is obtained by specializing (2) to (6)
2. Let G = S3 whose elements are
![]()
The identity map is an isomorphism of G onto itself. This gives rise to a permutation representation and an associated matrix representation in which

For a given group G and given field F we now consider the class Σ(G, F) of representations of G acting on vector spaces over F as base field. There is a rich algebraic structure that can be defined on Σ(G, F). First, let ρ1 and ρ2 be representations of G acting on the vector spaces V1/F and V2/F respectively. Form the vector space Vl ![]() F V2 and define ρ1
F V2 and define ρ1 ![]() ρ2 by
ρ2 by
![]()
where, as usual, a1 ![]() a2 for the linear transformations ai of Vi is the linear transformation of V1
a2 for the linear transformations ai of Vi is the linear transformation of V1 ![]() V2 such that
V2 such that
![]()
If bi, i = l, 2, is a second linear transformation of Vi, then we have (a1 ![]() a2)(b1
a2)(b1 ![]() b2) = a1b1
b2) = a1b1 ![]() a2b2. It follows that if g1, g2 ∈ G, then
a2b2. It follows that if g1, g2 ∈ G, then
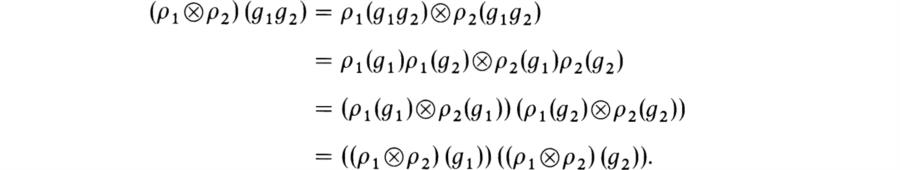
Hence ρ1 ![]() ρ2 is a representation. We call this the tensor product of the given representations ρ1 and ρ2.
ρ2 is a representation. We call this the tensor product of the given representations ρ1 and ρ2.
If (u1, u2,…, un) is a base for V1/F and (v1, v2,…, vm) is a base for V2/F, then the mn vectors ui ![]() vj constitute a base for (V1
vj constitute a base for (V1 ![]() V2)/F. We order these lexicographically:
V2)/F. We order these lexicographically:
![]()
Then if al ∈ EndF Vl has the matrix (α(1)) relative to the base (ul, …, un), and a2 ∈ EndF V2 has the matrix (α(2)) relative to (v1, …, vm), we have
![]()
and
![]()
Hence the matrix of a1 ![]() a2 relative to the base (11) is
a2 relative to the base (11) is

We denote this matrix as ((α(1)) ![]() (α(2))). In particular, we see that if ρ1B1(g) is the matrix of ρ1(g) relative to B1 = (ul, …, un) and ρ2B2(g) is the matrix of ρ2(g) relative to B2 = (vl, …, vm), then the matrix of (ρ1
(α(2))). In particular, we see that if ρ1B1(g) is the matrix of ρ1(g) relative to B1 = (ul, …, un) and ρ2B2(g) is the matrix of ρ2(g) relative to B2 = (vl, …, vm), then the matrix of (ρ1 ![]() ρ2) (g) relative to the base (11) is ρ1B1(g)
ρ2) (g) relative to the base (11) is ρ1B1(g) ![]() ρ2B2(g).
ρ2B2(g).
As usual, we denote the dual space of linear functions on V/F by V*. If (ul, u2, …, un) is a base for V/F, we have the dual (or complementary) base (ul*, u2*, …, un*) of V*/F where ui* is the linear function on V such that ui*(uj) = δij, 1 ≤ j ≤ n. If a is a linear transformation in V/F, we have the transposed transformation a* in V* such that
![]()
for y ∈ V and x* ∈ V*. If aui = Σjαjiuj and a*u*k = Σβlku*l, then ![]() . Hence βik = αki and so the matrix of a* relative to the dual base (u1*, …, un*) of (ul, …, un) is the transpose of the matrix of a relative to (ul, …, un). The map a
. Hence βik = αki and so the matrix of a* relative to the dual base (u1*, …, un*) of (ul, …, un) is the transpose of the matrix of a relative to (ul, …, un). The map a ![]() a* is an anti-isomorphism of the algebra EndF V onto EndF V* and hence a
a* is an anti-isomorphism of the algebra EndF V onto EndF V* and hence a ![]() (a*) –1 is an isomorphism of the group GL(V) of bijective linear transformations in V into GL(V*).
(a*) –1 is an isomorphism of the group GL(V) of bijective linear transformations in V into GL(V*).
Now let ρ be a representation of G acting on V. We compose this with the isomorphism a ![]() (a*)–1 of GL(V) onto GL(V*). This gives a representation g
(a*)–1 of GL(V) onto GL(V*). This gives a representation g ![]() (ρ(g)*)–1 of G acting on V*. We call this the contragredient representation of ρ and denote it as ρ*. Evidently it has the same degree as ρ. Moreover, if B = (ul, …, un) and B* is the dual base for V*, then we have the following relation for the matrix representations g
(ρ(g)*)–1 of G acting on V*. We call this the contragredient representation of ρ and denote it as ρ*. Evidently it has the same degree as ρ. Moreover, if B = (ul, …, un) and B* is the dual base for V*, then we have the following relation for the matrix representations g ![]() ρB(g) and g
ρB(g) and g ![]() ρ*B*(g): ρ*B*(g) = (tρB(g))–1
ρ*B*(g): ρ*B*(g) = (tρB(g))–1
The map ρ ![]() ρ* may be regarded as a unary composition in Σ(G, F). We also have an important nullary composition. This is the unit representation 1 or 1G for which V is one-dimensional and 1(g) = 1v for all g. The corresponding matrix representation (determined by any base) is g
ρ* may be regarded as a unary composition in Σ(G, F). We also have an important nullary composition. This is the unit representation 1 or 1G for which V is one-dimensional and 1(g) = 1v for all g. The corresponding matrix representation (determined by any base) is g ![]() (1) where (1) is the l × l matrix with entry 1.
(1) where (1) is the l × l matrix with entry 1.
Let ρi, i = 1, 2, be a representation of G acting on Vi/F. Then we say that ρ1 and ρ2 are equivalent if there exists a bijective linear map η of V1 onto V2 such that
![]()
EXERCISES
1. Let ρ be the representation of the cyclic group ![]() given in example 1. Let
given in example 1. Let ![]() be the base field. Show that ρ is equivalent to the representation ρ' such that ρ'(g)ui = ζiui where ζ = e2πi/n.
be the base field. Show that ρ is equivalent to the representation ρ' such that ρ'(g)ui = ζiui where ζ = e2πi/n.
2. Let pi, i = 1, 2, be a representation of G acting on Vi/F and put V = homF(Vl, V2). If l ∈ V, define ρ(g)l = ρ2(g)lρ1(g)–1. Verify that ρ is a representation and show that ρ is equivalent to ρ1* ![]() ρ2.
ρ2.
3. Let l denote the identity map of GL(V). This is a representation of GL(V) acting on V. Consider the representation l* ![]() l acting on V*
l acting on V*![]() V. Show that the set of vectors c ∈ V*
V. Show that the set of vectors c ∈ V* ![]() V such that (l*
V such that (l* ![]() l)(a)c = c for all a ∈ GL(V) is a one-dimensional subspace of V*
l)(a)c = c for all a ∈ GL(V) is a one-dimensional subspace of V* ![]() V. Find a non-zero vector in this space.
V. Find a non-zero vector in this space.
4. Show that if pi, i = 1, 2, is a representation acting on Vi, then ρ1 ![]() ρ2 and ρ2
ρ2 and ρ2 ![]() ρ1 are equivalent.
ρ1 are equivalent.
5.2 COMPLETE REDUCIBILITY
The study of the representations of a group G can be reduced to the study of the representations of the group algebra of G. Let G be a group, F a field, then the group algebra F[G] is the algebra over F having the set G as base and multiplication defined by
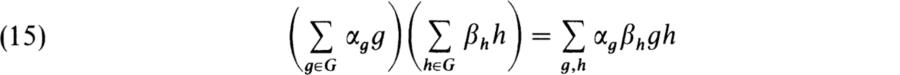
for αg, βh ∈ F. Let ρ be a representation of G acting on the vector space V/F. Then the group homomorphism ρ has a unique extension to the algebra homomorphism
![]()
of F[G] into EndFV. Conversely, given a homomorphism ρ of F[G] into EndF V, where V is a finite dimensional vector space over F, the restriction of ρ to G is a representation since ρ(l) = 1, which implies that every ρ(g) ∈ GL(V). Now we recall that a representation of F[G] ( = homomorphism of F[G] into EndFV) can be used to make V into an F[G]-module. One simply defines the action of F[G] on V by
![]()
for x ∈ V. Again, this can be turned around: Given a module V for F[G], this is a module for F, hence, a vector space over F and, assuming finite dimensionality of V/F, we obtain a representation ρ of G where ρ(g) is the map x ![]() gx, which is a linear transformation of V/F. Thus representations of G acting on (finite dimensional) vector spaces over a field F are equivalent to F[G]-modules, which as F-modules are finite dimensional.
gx, which is a linear transformation of V/F. Thus representations of G acting on (finite dimensional) vector spaces over a field F are equivalent to F[G]-modules, which as F-modules are finite dimensional.
The standard concepts of module theory can be carried over to representations of groups via the group algebra. If ρ is a representation of G acting on V, a submodule U of V as F[G] -module is the same thing as a subspace of V that is ρ(G)-invariant in the sense that it is stabilized by every ρ(g), g ∈ G. Then we obtain a representation ρ|U of G acting on U in which (ρ|U) (g) is the restriction of ρ(g) to U. We shall call this a subrepresentation of ρ. We also have the module V/U. The associated representation of G is ρ|V/U where (ρ|V/U) (g) is the linear transformation x + U ![]() ρ(g)x + U. This will be called a factor representation of ρ.
ρ(g)x + U. This will be called a factor representation of ρ.
Let B = (ul, …, un) be a base for V such that (ul, …, ur) is a base for the ρ(G)-invariant subspace U. Consider the matrix representation ρB determined by B. Since U is stabilized by every ρ(g), ρ(g)ui for 1 ≤ i ≤ r is a linear combination of the vectors (ul, …, ur). Hence every matrix ρB(g), g ∈ G, has the “reduced” form
The matrices in the upper left-hand corner are those of the matrix representation of G acting on U associated with the base (u1, …, ur) and those in the lower right-hand corner are the matrices of the representation of G on V/U relative to the base (ur + 1 + U, …, un + U). It is clear that conversely if there exists a base (u1, …, un) such that the matrices of the ρ(g) relative to this base all have the form (18), then U = Σ1rFuj is a ρ(G)-invariant subspace, hence, an F[G]-submodule of V.
If v = U ![]() U' where U and U' are submodules, then we can choose a base B = (ul, …, un) for V such that (u1, …, ur) is a base for U and (ur + 1,…, un) is a base for U'. Then the corresponding matrices ρB(g) have the form (18) in which the r × (n – r) blocks in the upper right-hand corner are all 0. If ρ1 = ρ|U and ρ2 = ρ|U' then we say that the representation ρ is a direct sum of the subrepresentations ρ1 and ρ2 and we write ρ = ρ1
U' where U and U' are submodules, then we can choose a base B = (ul, …, un) for V such that (u1, …, ur) is a base for U and (ur + 1,…, un) is a base for U'. Then the corresponding matrices ρB(g) have the form (18) in which the r × (n – r) blocks in the upper right-hand corner are all 0. If ρ1 = ρ|U and ρ2 = ρ|U' then we say that the representation ρ is a direct sum of the subrepresentations ρ1 and ρ2 and we write ρ = ρ1 ![]() ρ2. Let p be the projection on U determined by the decomposition V = U
ρ2. Let p be the projection on U determined by the decomposition V = U ![]() U'. Then if we write any x ∈ V as x = y + y', y ∈ U, y' ∈ U', we have ρ(g)x = ρ(g)y + ρ(g)y' with ρ(g)y ∈ U, ρ(g)y' ∈ U' for all g ∈ G. Since p is the map x
U'. Then if we write any x ∈ V as x = y + y', y ∈ U, y' ∈ U', we have ρ(g)x = ρ(g)y + ρ(g)y' with ρ(g)y ∈ U, ρ(g)y' ∈ U' for all g ∈ G. Since p is the map x ![]() y, we have pρ(g)x = ρ(g)y = ρ(g)px. Thus p commutes with every ρ(g). Conversely, suppose U is any ρ(G)-invariant subspace and there exists a projection p of V on U that commutes with every ρ(g). We can write V = pV
y, we have pρ(g)x = ρ(g)y = ρ(g)px. Thus p commutes with every ρ(g). Conversely, suppose U is any ρ(G)-invariant subspace and there exists a projection p of V on U that commutes with every ρ(g). We can write V = pV ![]() (l – p)V and pV = U. Also, ρ(g) (1 – p)V = (1 – p)ρ(g)V = (1 – p)V. Hence U' = (1 – p)V is ρ(G)-invariant and we have the decomposition V = U
(l – p)V and pV = U. Also, ρ(g) (1 – p)V = (1 – p)ρ(g)V = (1 – p)V. Hence U' = (1 – p)V is ρ(G)-invariant and we have the decomposition V = U ![]() U'.
U'.
We shall call a representation ρ of G irreducible (completely reducible) if the corresponding F[G]-module is irreducible (completely reducible). We recall that a module V is completely reducible if and only if it satisfies either one of the following conditions: (1) V = ΣVi where the Vi are irreducible submodules, (2) V ≠ 0 and for every submodule U there exists a submodule U' such that V = U ![]() U' (Theorem 3.10, p. 121). We shall use these conditions to prove two theorems giving sufficient conditions for complete reducibility. The first of these is a fundamental theorem in the representation theory of finite groups. This is
U' (Theorem 3.10, p. 121). We shall use these conditions to prove two theorems giving sufficient conditions for complete reducibility. The first of these is a fundamental theorem in the representation theory of finite groups. This is
MASCHKE’S THEOREM. Every representation ρ of a finite group G acting on a vector space V/F such that the characteristic char ![]() is completely reducible.
is completely reducible.
Proof. Let U be a ρ(G)-invariant subspace of V and write V = U ![]() U0 where U0 is a second subspace (not necessarily invariant). Let p0 be the projection on U determined by this decomposition. We shall now construct by an averaging process a projection on U that commutes with every ρ(g), g ∈ G. We put
U0 where U0 is a second subspace (not necessarily invariant). Let p0 be the projection on U determined by this decomposition. We shall now construct by an averaging process a projection on U that commutes with every ρ(g), g ∈ G. We put

Since char ![]() , |G|–1 exists in F and p is well defined. If g' ∈ G, then
, |G|–1 exists in F and p is well defined. If g' ∈ G, then
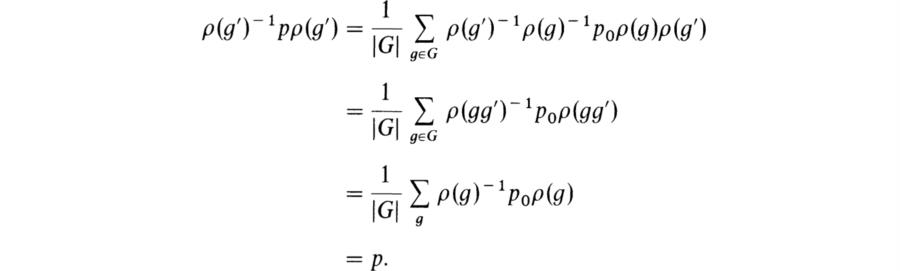
Hence ρ(g')p = pρ(g') for g' ∈ G. Evidently, p ∈ EndFV. If y ∈ U, then p0y = y and since ρ(g)y ∈ U, p0ρ(g)y = ρ(g)y. Hence ρ(g)–1 p0ρ(g)y = y and
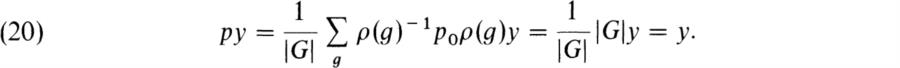
If x ∈ V, then p0x ∈ U and ρ(g)–1 p0ρ(g)x ∈ U. Hence px ∈ U. The two conditions on p ∈ EndF V, py = y for y ∈ U and px ∈ U for x ∈ V, imply that p is a projection on U. Then V = U ![]() U' where U' = (l – p)V and since p commutes with every ρ(g), U' is ρ(G)-invariant.
U' where U' = (l – p)V and since p commutes with every ρ(g), U' is ρ(G)-invariant.![]()
This result has a formulation in terms of matrix representations that should be obvious from the discussion above. The result in its matrix form was proved by H. Maschke for the case in which F = ![]() . The validity of the result for any F with char
. The validity of the result for any F with char ![]() was first noted by L. E. Dickson.
was first noted by L. E. Dickson.
If ρ is a completely reducible representation of G acting on V, then the F[G]-module V decomposes as ![]() where the Vik are irreducible and
where the Vik are irreducible and ![]() for any k, l but
for any k, l but ![]() . By Theorem 3.12 (p. 123), the submodules
. By Theorem 3.12 (p. 123), the submodules ![]() are the homogeneous components of V. If ρi is any irreducible representation of G equivalent to the subrepresentation determined by the Vi(k), then we write
are the homogeneous components of V. If ρi is any irreducible representation of G equivalent to the subrepresentation determined by the Vi(k), then we write
![]()
We call ρi an irreducible constituent of ρ and mi its multiplicity. By Theorem 3.14, the equivalence classes of the irreducible constituents and their multiplicities are uniquely determined. We remark also that the multiplicity mi = qi/ni where qi = dim Wi, ni = dim Vi(k), which shows also that mi is independent of the particular decomposition of V as a direct sum of irreducible submodules.
If H is a subgroup of G and ρ is a representation of G acting on V, then the restriction of ρ to H is a representation of H that we shall denote as ρH. We shall now show that if ![]() and ρ is completely reducible, then ρH is completely reducible. It suffices to prove this for ρ irreducible. Moreover, in this case we can say considerably more on the relation between the irreducible constituents and their multiplicities. First, we need to give a definition of conjugacy of representations of a normal subgroup of a group.
and ρ is completely reducible, then ρH is completely reducible. It suffices to prove this for ρ irreducible. Moreover, in this case we can say considerably more on the relation between the irreducible constituents and their multiplicities. First, we need to give a definition of conjugacy of representations of a normal subgroup of a group.
Let ![]() and let σ be a representation of H acting on U. For any g ∈ G we can define the map
and let σ be a representation of H acting on U. For any g ∈ G we can define the map
![]()
This is the composite of the automorphism h ![]() ghg–1 of H with the homomorphism σ. Hence (22) is a representation of H acting on U, which we shall denote as gσ. Any representation equivalent to gσ will be called a conjugate of σ or, more precisely, a g-conjugate of σ. Evidently, any σ(H)- invariant subspace is gσ(H)-invariant and since σ = g–1 (gσ), it is clear that σ and gσ have the same lattices of F[H]-submodules. In particular, if σ is irreducible, then any conjugate of σ is irreducible. Now suppose σ1 and σ2 are equivalent representations of H acting on U1 and U2 respectively. Then we have a bijective linear map η of U1 onto U2 such that σ2(h) = ησl(h)η–1, h ∈ H. Then also,
ghg–1 of H with the homomorphism σ. Hence (22) is a representation of H acting on U, which we shall denote as gσ. Any representation equivalent to gσ will be called a conjugate of σ or, more precisely, a g-conjugate of σ. Evidently, any σ(H)- invariant subspace is gσ(H)-invariant and since σ = g–1 (gσ), it is clear that σ and gσ have the same lattices of F[H]-submodules. In particular, if σ is irreducible, then any conjugate of σ is irreducible. Now suppose σ1 and σ2 are equivalent representations of H acting on U1 and U2 respectively. Then we have a bijective linear map η of U1 onto U2 such that σ2(h) = ησl(h)η–1, h ∈ H. Then also, ![]() are equivalent.
are equivalent.
We can now prove
(A. H.) CLIFFORD’S THEOREM. Let ![]() and let ρ be an irreducible representation of G. Then ρH is completely reducible and all of its irreducible constituents are conjugate and have the same multiplicity.
and let ρ be an irreducible representation of G. Then ρH is completely reducible and all of its irreducible constituents are conjugate and have the same multiplicity.
Proof. Let ρ act on V and let U be an irreducible F[H]-submodule of V. Evidently, Σg ∈ Gρ(g)U is a ρ(G)-invariant subspace of V containing U. Hence V = Σρ(g)U. Let h ∈ H, y ∈ U. Then
![]()
Thus ρ(g)U is ρ(H)-invariant. Let σ denote the representation of H acting on U and σ' the representation of H acting on ρ(g)U. Now by (23), ![]() . Since y
. Since y ![]() ρ(g)y is a bijective linear map of U onto ρ(g)U, we see that σ' is a conjugate of σ. Hence ρ(g)U is an irreducible F[H]- module and V = Σρ(g)U is a decomposition of V as sum of irreducible F[H]- modules such that the corresponding representations are conjugates. Then V is a direct sum of certain ones of the ρ(g)U. Hence ρH is completely reducible and its irreducible constituents are conjugate. If U1 and U2 are isomorphic irreducible F[H]-submodules, then ρ(g)U1 and ρ(g)U2 are isomorphic F[H] submodules. It follows that every ρ(g) permutes the homogeneous components of V as F[H]-module. Thus we have an action of G through ρ(G) on the set S of homogeneous components of V as F[H]-module. Moreover, this action is transitive since if U is any irreducible F[H]-submodule, then any other irreducible F[H]-submodule is isomorphic to a ρ(g)U for some g ∈ G. This implies that all of the irreducible constituents have the same multiplicity.
ρ(g)y is a bijective linear map of U onto ρ(g)U, we see that σ' is a conjugate of σ. Hence ρ(g)U is an irreducible F[H]- module and V = Σρ(g)U is a decomposition of V as sum of irreducible F[H]- modules such that the corresponding representations are conjugates. Then V is a direct sum of certain ones of the ρ(g)U. Hence ρH is completely reducible and its irreducible constituents are conjugate. If U1 and U2 are isomorphic irreducible F[H]-submodules, then ρ(g)U1 and ρ(g)U2 are isomorphic F[H] submodules. It follows that every ρ(g) permutes the homogeneous components of V as F[H]-module. Thus we have an action of G through ρ(G) on the set S of homogeneous components of V as F[H]-module. Moreover, this action is transitive since if U is any irreducible F[H]-submodule, then any other irreducible F[H]-submodule is isomorphic to a ρ(g)U for some g ∈ G. This implies that all of the irreducible constituents have the same multiplicity.![]()
EXERCISES
1. Prove the following extension of Maschke’s theorem. Let ρ be a representation of a group G that is not necessarily finite. Suppose G contains a normal subgroup H of finite index [G : H] not divisible by char F. Show that if ρ|H is completely reducible, then ρ is completely reducible.
2. Let F = ![]() and let H(x, y) be a hermitian form on V/
and let H(x, y) be a hermitian form on V/![]() that is positive definite in the sense that H(x, x) > 0 for all x ≠ 0 (BAI, pp. 381–384). Let ρ be a representation of a group G acting on V such that every ρ(g) is unitary with respect to H, (H(ρ(g)x, ρ(g)y) = H(x, y), x, y ∈ V). Such a representation is called unitary. Show that if U is a ρ(G)-invariant subspace, then
that is positive definite in the sense that H(x, x) > 0 for all x ≠ 0 (BAI, pp. 381–384). Let ρ be a representation of a group G acting on V such that every ρ(g) is unitary with respect to H, (H(ρ(g)x, ρ(g)y) = H(x, y), x, y ∈ V). Such a representation is called unitary. Show that if U is a ρ(G)-invariant subspace, then ![]() is ρ(G)-invariant. Use this to prove that ρ is completely reducible.
is ρ(G)-invariant. Use this to prove that ρ is completely reducible.
3. Same notations as in exercise 2. Let G be finite, ρ a representation of G acting on V. Let H0(x, y) be any positive definite hermitian form on V/![]() . Put
. Put ![]() . Show that H(x, y) is positive definite hermitian and that every ρ(g) is unitary relative to H. Use this and exercise 2 to prove Maschke’s theorem for F =
. Show that H(x, y) is positive definite hermitian and that every ρ(g) is unitary relative to H. Use this and exercise 2 to prove Maschke’s theorem for F = ![]() .
.
4. Define the projective linear group PGL(V) of a finite dimensional vector space V/F as GL(V)/F*1 where F* is the multiplicative group of non-zero elements of F. A homomorphism ρ of a group G into PGL(V) is called a projective representation of G. For each g ∈ G let μ(g) denote a representative in GL(V) of the coset of ρ(g) ∈ PGL(V). Then μ(g1g2) = γg1,g2μ(g1)(g2) where γg1,g2 ∈ F*. Define ρ(G)-invariant subspaces and complete reducibility as for ordinary representations. Prove the analogue of Maschke’s theorem for projective representations.
5. Show that ρ is irreducible (completely reducible) if and only if ρ* is irreducible (completely reducible).
6. Let ψ be a representation of G acting on W, V a ψ(G)-invariant subspace. Put ρ = ψ|V. Show that ρ* ![]() ψ has a subrepresentation equivalent to the unit representation.
ψ has a subrepresentation equivalent to the unit representation.
7. Let ψ and ρ be representations of G acting on W and V respectively. Assume ρ is irreducible and ρ* ![]() ψ has a subrepresentation equivalent to the unit representation. Show that ψ has a subrepresentation equivalent to ρ.
ψ has a subrepresentation equivalent to the unit representation. Show that ψ has a subrepresentation equivalent to ρ.
8. Show that the following are irreducible groups of linear transformations of the finite dimensional vector space V/F: (1) GL(V), (2) O(V, Q) the group of orthogonal linear transformations relative to a non-degenerate quadratic form Q, (3) O+ (V, Q) the rotation subgroup of O(V, Q). (See Chapter 6 of BAI.)
5.3 APPLICATION OF THE REPRESENTATION THEORY OF ALGEBRAS
There are two main methods for developing the representation theory of finite groups: the structure and representation theory of finite dimensional algebras applied to group algebras and the theory of characters. Many results can be obtained by both methods, and the choice of the method is often a matter of taste. The first method is introduced in this section and the theory of characters appears in section 5. Our primary concern will be with representations of finite groups over fields whose characteristics do not divide the order of the group. However, the first two theorems that are given do not require these restrictions.
We begin by defining certain algebras of linear transformations associated with a representation ρ of a group G acting on a vector space V/F. First, we have the enveloping algebra Env ρ(G), which is the set of linear transformations of the form ![]() . If we extend ρ to a homomorphism ρ of A = F[G] as in (16), then Env ρ(G) = ρ(A). Next we have the algebra A' = EndA V. Evidently, this is the set of linear transformations of V that commute with every a ∈ ρ(A), so EndAV is the centralizer in EndFV of ρ(A). If ρ is irreducible, then by Schur’s lemma, A' is a division algebra. Next we have A′ = EndA, V, which is the algebra of linear transformations that commute with every a' ∈ A'. Evidently, A" ⊃ Env ρ(G) = ρ(A). We remark that if we define A"' = EndA"V, then it is trivial to see that A"' = A'. Hence the process of creating algebras by taking endomorphism algebras breaks off with A". We call this the double centralizer of ρ(A) and we say that ρ has the double centralizer property if A" = ρ(A). We have the following general result on completely reducible representations.
. If we extend ρ to a homomorphism ρ of A = F[G] as in (16), then Env ρ(G) = ρ(A). Next we have the algebra A' = EndA V. Evidently, this is the set of linear transformations of V that commute with every a ∈ ρ(A), so EndAV is the centralizer in EndFV of ρ(A). If ρ is irreducible, then by Schur’s lemma, A' is a division algebra. Next we have A′ = EndA, V, which is the algebra of linear transformations that commute with every a' ∈ A'. Evidently, A" ⊃ Env ρ(G) = ρ(A). We remark that if we define A"' = EndA"V, then it is trivial to see that A"' = A'. Hence the process of creating algebras by taking endomorphism algebras breaks off with A". We call this the double centralizer of ρ(A) and we say that ρ has the double centralizer property if A" = ρ(A). We have the following general result on completely reducible representations.
THEOREM 5.1. Any completely reducible representation ρ of a group G has the double centralizer property.
Proof. It is easily seen that this is a special case of Theorem 4.10 (p. 222). However, it is somewhat simpler to base the proof directly on the density theorem: Let (u1, u2, … ,un) be a base for V/F and let l be an element of the double centralizer of ρ(A). By the density theorem, there exists an a ∈ ρ(A) such that aui = lui, 1 ≤ i ≤ n. Hence l = a ∈ ρ(A) and A" = ρ(A).![]()
We state next
THEOREM 5.2. A finite group has only a finite number of inequivalent irreducible representations.
This follows by applying Theorem 4.5 (p. 208) to the artinian ring A = F[G]. We omit the details, since this result will not play any role in the sequel. We shall now prove
THEOREM 5.3. The group algebra A = F[G] of a finite group G over a field F is semi-simple if and only if char ![]() .
.
Proof. Suppose first that char ![]() . Then every representation of G is completely reducible. Hence A regarded as (left) A-module is completely reducible. Then A is semi-simple by the structure theorem for semi-primitive artinian rings (p. 203). Now suppose char F| |G|. Consider the element
. Then every representation of G is completely reducible. Hence A regarded as (left) A-module is completely reducible. Then A is semi-simple by the structure theorem for semi-primitive artinian rings (p. 203). Now suppose char F| |G|. Consider the element
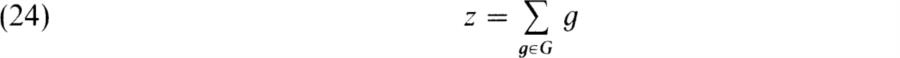
of A. This is non-zero and we evidently have
![]()
for all g' ∈ G. Hence FZ is an ideal in A. From (25) we obtain ![]() , since char F| |G|. Hence FZ is a non-zero nilpotent ideal in A and A is not semi-simple.
, since char F| |G|. Hence FZ is a non-zero nilpotent ideal in A and A is not semi-simple.![]()
For the remainder of this section, we assume that G is finite and that char ![]() . We have
. We have
![]()
where the Ai are the simple components. By the matrix form of Wedderburn’s theorem,
![]()
where Δi is a division algebra over F. If Ii is a minimal left ideal of Ai, it is a minimal left ideal of A and hence gives an irreducible representation of G. Moreover, Ii ![]() Ij if i ≠ j and every irreducible representation of G is equivalent to one obtained from one of the Ii (Theorem 4.4, p. 208). Hence there are s equivalence classes of irreducible representations of G. We determine next the degree of the irreducible representations provided by Ii. Let {eij|1 ≤ i, j ≤ n} be the usual set of matrix units in Mn(Δ), Δ a division algebra. Then
Ij if i ≠ j and every irreducible representation of G is equivalent to one obtained from one of the Ii (Theorem 4.4, p. 208). Hence there are s equivalence classes of irreducible representations of G. We determine next the degree of the irreducible representations provided by Ii. Let {eij|1 ≤ i, j ≤ n} be the usual set of matrix units in Mn(Δ), Δ a division algebra. Then
![]()
and Mn(Δ)eii is a minimal left ideal and every minimal left ideal of Mn(Δ) is isomorphic as Mn(Δ)-left module to Mn(Δ)eii. We have the subalgebra Δ1 of matrices d1 = diag{d, d, …, d} and we can regard Mn(Δ) as (left) vector space over Δ by defining d(a) for the matrix (a) to be (d1)(a). Then Mn(Δ) has the base {eij} over Δ, so its dimensionality over Δ is n2. Similarly, Mn(Δ)eii = Δe1i ![]() …
…![]() Δeni, so the dimensionality of Mn(Δ)eii over Δ is n. Then the dimensionality of Mn(Δ)eii over F is
Δeni, so the dimensionality of Mn(Δ)eii over Δ is n. Then the dimensionality of Mn(Δ)eii over F is
![]()
where d = [Δ : F]. It now follows that [Ii : F] = nidi where di = [Δi : F] and this is the degree of the irreducible representation provided by Ii. We can summarize these results as
THEOREM 5.4. Let A = F[G] be the group algebra of a finite group G over a field F such that char ![]() and let A = A1
and let A = A1 ![]() …
…![]() As where the Ai are the simple components of the semi-simple algebra A. Assume that Ai
As where the Ai are the simple components of the semi-simple algebra A. Assume that Ai ![]() Mni(Δi) where Δi is a division algebra and let [Δi : F] = di. If Ii is a minimal left ideal of Ai, then Ii provides an irreducible representation of G and the irreducible representations obtained from the Ii for 1 ≤ i ≤ s form a set of representatives of the equivalence classes of irreducible representations of G. Moreover, the degree of the irreducible representation provided by Ii is nidi.
Mni(Δi) where Δi is a division algebra and let [Δi : F] = di. If Ii is a minimal left ideal of Ai, then Ii provides an irreducible representation of G and the irreducible representations obtained from the Ii for 1 ≤ i ≤ s form a set of representatives of the equivalence classes of irreducible representations of G. Moreover, the degree of the irreducible representation provided by Ii is nidi.
Let {ρi|l ≤ i ≤ s} be a set of representatives of the equivalence classes of irreducible representations of G. As above, we may take ρi to be the irreducible representation provided by a minimal left ideal Ii of Ai At any rate we may assume that ρi is equivalent to the irreducible representation determined by Ii. If ρ is any representation of G acting on V, then V = V1 ![]() …
…![]() Vr where the Vj are ρ(G)-invariant and ρ|Vj is irreducible. Then ρ|Vj
Vr where the Vj are ρ(G)-invariant and ρ|Vj is irreducible. Then ρ|Vj ![]() ρi for some i and the number mi of j such that ρ|Vj
ρi for some i and the number mi of j such that ρ|Vj ![]() ρi for a fixed i is independent of the decomposition of V as V1
ρi for a fixed i is independent of the decomposition of V as V1 ![]() …
…![]() Vr. As on p. 254, we can write ρ ~ mlρl
Vr. As on p. 254, we can write ρ ~ mlρl ![]() m2ρ2
m2ρ2![]() …
… ![]() msρs and call mi the multiplicity of ρi in the representation ρ.
msρs and call mi the multiplicity of ρi in the representation ρ.
Now consider A as (left) A-module. Let ρ denote the representation of G determined by this module. The base G of A is stabilized by every ρ(g): x ![]() gx. It is clear that ρ is the regular representation of G (p. 248). The decompositions (26) and (28) show that the multiplicity of the irreducible representation ρi determined by Ii in the regular representation is ni. We therefore have the following result on the regular representation of G.
gx. It is clear that ρ is the regular representation of G (p. 248). The decompositions (26) and (28) show that the multiplicity of the irreducible representation ρi determined by Ii in the regular representation is ni. We therefore have the following result on the regular representation of G.
THEOREM 5.5. Let the notation be as in Theorem 5.4. Then the multiplicity of ρi in the regular representation is ni.
The number of equivalence classes of irreducible representations of G is the number s of simple components Ai of A = F[G]. Let cent A denote the center of A. Then
![]()
where the center, cent Ai, is isomorphic to the center of Mni(Δi) and hence to the center of Δi. Hence cent Ai is a field and is a simple component of the semisimple commutative algebra cent A. Then s is the number of simple components of cent A. We now determine a base for this algebra.
PROPOSITION 5.1. Let G = C1( = {1}) ∪ C2 ∪ … ∪ Cr be the decomposition of G into conjugacy classes (BAI, P. 74). Put

Proof. If g ∈ G, then ![]() since the map x
since the map x ![]() g–1xg permutes the elements of the conjugacy class Ci. Hence ci commutes with every g ∈ G and with every
g–1xg permutes the elements of the conjugacy class Ci. Hence ci commutes with every g ∈ G and with every ![]() . Thus ci ∈ centF[G]. Now let
. Thus ci ∈ centF[G]. Now let ![]() ∈ cent F[G]. If h ∈ G,
∈ cent F[G]. If h ∈ G,
![]()
so the condition h–1ch = c gives γhgh–1 = γg, h ∈ G. Thus any two elements g and g' in the same conjugacy class have the same coefficient in the expression ![]() and hence c is a linear combination of the ci. It is clear that the ci are linearly independent and so (c1, c2, … , cr) is a base for cent F[G].
and hence c is a linear combination of the ci. It is clear that the ci are linearly independent and so (c1, c2, … , cr) is a base for cent F[G].![]()
Both the foregoing result and the fact that the number s of equivalence classes of irreducible representations of G is the number of simple components show that s ≤ r, the number of conjugacy classes. More precisely, we have r = Σ1s [cent Ai : F]. This shows that s = r if and only if cent Ai = F for all i, that is, the Ai are central simple. Since cent Ai is a finite dimensional field extension of F, we have cent Ai = F for all i if F is algebraically closed. Hence in this important case the number of equivalence classes of irreducible representations is the number of conjugacy classes. In the algebraically closed case we have the following important result.
THEOREM 5.6. Let G be a finite group, F an algebraically closed field such that char ![]() . Let s be the number of conjugacy classes of G. Then the number of equivalence classes of irreducible representations over F (acting on vector spaces V/F) is s and if ρ1, …, ρs are representatives of these classes and ni is the degree of ρi, then
. Let s be the number of conjugacy classes of G. Then the number of equivalence classes of irreducible representations over F (acting on vector spaces V/F) is s and if ρ1, …, ρs are representatives of these classes and ni is the degree of ρi, then

Proof. The first statement has been proved. To see the second, we use (26) and (27) and the fact that since F is algebraically closed, the only finite dimensional division algebra over F is F itself. Then A = F[G] = A1 ![]() …
… ![]() and Ai
and Ai ![]() Mn(F). Then
Mn(F). Then ![]() and Theorem 5.4 shows that ni is the degree of the irreducible representation ρi associated with Ai.
and Theorem 5.4 shows that ni is the degree of the irreducible representation ρi associated with Ai. ![]()
EXAMPLES
1. Let G = ![]() , the cyclic group of order n generated by z and let F =
, the cyclic group of order n generated by z and let F = ![]() . Then A =
. Then A = ![]() [G] is a direct sum of n copies of
[G] is a direct sum of n copies of ![]() . Hence we have n inequivalent irreducible representations, all of degree 1. It is clear that in the corresponding matrix representations we have z
. Hence we have n inequivalent irreducible representations, all of degree 1. It is clear that in the corresponding matrix representations we have z ![]() (e2πir/n) where ( ) is a 1 × 1 matrix and r = 1, 2, …, n.
(e2πir/n) where ( ) is a 1 × 1 matrix and r = 1, 2, …, n.
2. Let G = Dn, the dihedral group of order 2n generated by two elements r, s such that rn = 1, s2 = 1, srs–1 = r–1 (BAI, pp. 34, 70). The elements of Dn are rk, rks, 0 ≤ k ≤ n – 1, and we have the relation srk = r–ks. Hence (rks)2 = 1, so the n elements rks are of period two. Using the multiplication table: ![]() , it is readily seen that if n is odd = 2v + l, v ≥ 1, then there are v + 2 conjugacy classes with representatives: 1, rk, 1 ≤ k ≤ v, s, and if n = 2v, v ≥ 1, then there are v + 3 conjugacy classes with representatives 1, rk, 1 ≤ k ≤ v, s, rs. On the other hand, we can list these numbers of inequivalent irreducible matrix representations over C as follows:
, it is readily seen that if n is odd = 2v + l, v ≥ 1, then there are v + 2 conjugacy classes with representatives: 1, rk, 1 ≤ k ≤ v, s, and if n = 2v, v ≥ 1, then there are v + 3 conjugacy classes with representatives 1, rk, 1 ≤ k ≤ v, s, rs. On the other hand, we can list these numbers of inequivalent irreducible matrix representations over C as follows:
n = 2v +1, v ≥ 1.
ρ1, the unit representation.
ρ2, the matrix representation of degree 1 such that r ![]() (1), s
(1), s ![]() (–1).
(–1).
σl, 1 ≤ l ≤ v, the matrix representation of degree 2 such that

where ω = e2πi/n.
n = 2v, v ≥ 1.
ρl, the unit representation.
ρ2, the matrix representation of degree 1 such that r ![]() (1), s
(1), s ![]() (– 1).
(– 1).
ρ3, the matrix representation of degree 1 such that r ![]() (–1), s
(–1), s ![]() (1).
(1).
ρ4, the matrix representation of degree 1 such that r ![]() (–1), s
(–1), s ![]() (– 1).
(– 1).
The representations σl, 1 ≤ l ≤ v – 1, as above.
It is easy to verify that the representations listed are irreducible and inequivalent. Hence they constitute a set of representatives of the equivalence classes of irreducible representations of Dn. As a check, we can verify the degree relation (32) in the two cases:
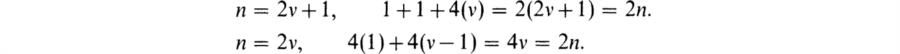
We shall consider next a process of extension of the base field of a representation. We need to recall some simple facts about extension of the base field of a vector space. For our purpose, it suffices to restrict our attention to finite dimensional vector spaces. Thus let V/F be an n-dimensional vector space over the field F and let K be an extension field of F. We can form the tensor product VK = K ![]() F V, which can be regarded as a vector space over K. The injective map v
F V, which can be regarded as a vector space over K. The injective map v ![]() l
l ![]() v permits us to regard V as contained in VK as an F-subspace such that KV = VK. Moreover, F-independent elements of V are K-independent and any base for V/F is a base for Vk/K (see p. 220). A linear transformation l of V/F has a unique extension to a linear transformation of VK/K. We denote the extension by / also. These extensions span EndK VK as vector space over K, that is, EndK VK = K EndF V. Moreover, EndK VK
v permits us to regard V as contained in VK as an F-subspace such that KV = VK. Moreover, F-independent elements of V are K-independent and any base for V/F is a base for Vk/K (see p. 220). A linear transformation l of V/F has a unique extension to a linear transformation of VK/K. We denote the extension by / also. These extensions span EndK VK as vector space over K, that is, EndK VK = K EndF V. Moreover, EndK VK ![]() K
K ![]() F EndFV.
F EndFV.
Now suppose we have a representation ρ of G acting on V/F. Then the defining relations ρ(g1g2) = ρ(g1)ρ(g2), ρ(l) = 1V give the relations ρ(g1g2) = ρ(g1)ρ(g2), ρ(l) = 1VK for the extensions. Hence ρK : g ![]() ρ(g) (in VK) is a representation of G acting on VK. We call this the representation obtained from ρ by extending the base field to K. It is clear that if A = F[G], then K[G]
ρ(g) (in VK) is a representation of G acting on VK. We call this the representation obtained from ρ by extending the base field to K. It is clear that if A = F[G], then K[G] ![]() AK and
AK and ![]() . We also have the following useful result.
. We also have the following useful result.
Proof. The elements of EndF[G]V (EndK[G]VK) are the linear transformations of V (VK) that commute with every ρ(g), g ∈ G. Hence it is clear that K EndF[G] V ⊂ EndK[G] VK. To prove the reverse containment, we choose a base (λi) for K/F. Then any element of EndK VK can be written in one and only one way in the form Σλili where li ∈ EndFV. The conditions that this commutes with every ρ(g) imply that the li commute with every ρ(g), hence, that li ∈ EndF[G] V. Thus Σλili ∈ EndK[G] VK and EndK[G] VK = K EndF[G]V. We have noted that ![]() . This implies that if E is any subspace of EndFV/F, then
. This implies that if E is any subspace of EndFV/F, then ![]() . In particular, we have
. In particular, we have ![]() .
. ![]()
It is clear that if U is a ρ(G)-invariant subspace of V, then KU ![]() UK is a ρ(G)-invariant subspace of VK. Hence if ρK is irreducible, then ρ is irreducible. The converse need not hold, as the following examples show.
UK is a ρ(G)-invariant subspace of VK. Hence if ρK is irreducible, then ρ is irreducible. The converse need not hold, as the following examples show.
EXAMPLES
1. Let G = ![]() , the cyclic group of order 4 and let F =
, the cyclic group of order 4 and let F = ![]() . We have the representation of degree two over
. We have the representation of degree two over ![]() in which ρ(g) is the linear transformation with matrix
in which ρ(g) is the linear transformation with matrix
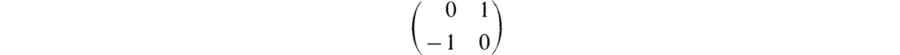
relative to the base (u, v) of V/![]() . Since the characteristic polynomial of this matrix is λ2 + 1, ρ(g) acts irreducibly on V. Now consider ρ
. Since the characteristic polynomial of this matrix is λ2 + 1, ρ(g) acts irreducibly on V. Now consider ρ![]() . We have the base (z = u + iv, w = u – iv) for V
. We have the base (z = u + iv, w = u – iv) for V![]() /
/![]() and
and
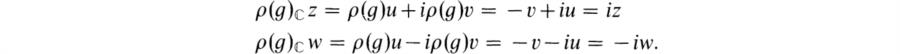
Hence ![]() Z and
Z and ![]() w are ρ
w are ρ![]() (G)-invariant subspaces. The irreducible representations ρ
(G)-invariant subspaces. The irreducible representations ρ![]() |
|![]() Z and ρ
Z and ρ![]() |
| ![]() w are inequivalent.
w are inequivalent.
2. Let G be the quaternion group {± 1, ±i, ±j, ±k}, which is a subgroup of the multiplicative group of Hamilton’s quaternion algebra ![]() over
over ![]() . Let ρ be the representation of G such that ρ(g) is the left multiplication x
. Let ρ be the representation of G such that ρ(g) is the left multiplication x ![]() gx, x ∈
gx, x ∈ ![]() , g ∈ G. ρ is irreducible since
, g ∈ G. ρ is irreducible since ![]() is a division algebra. On the other hand,
is a division algebra. On the other hand, ![]()
![]()
![]() M2(
M2(![]() ) since
) since ![]() is a splitting field for
is a splitting field for ![]() (p. 228). Since M2(
(p. 228). Since M2(![]() ) is a direct sum of two minimal left ideals, it follows that
) is a direct sum of two minimal left ideals, it follows that ![]()
![]() is a direct sum of two ρ
is a direct sum of two ρ![]() (G)-invariant subspaces I1 and I2. The representations ρ
(G)-invariant subspaces I1 and I2. The representations ρ![]() |I1 and ρ
|I1 and ρ![]() |I2 are irreducible and equivalent.
|I2 are irreducible and equivalent.
A representation ρ is called absolutely irreducible if ρk is irreducible for every extension field K of the base field F. We have the following criterion for irreducibility and absolute irreducibility.
THEOREM 5.7. Let G be a finite group, ρ a representation of G acting on V/F where char ![]() , A = F[G]. Then ρ is irreducible if and only if A' = End A V is a division algebra and ρ is absolutely irreducible if and only if A' = F1.
, A = F[G]. Then ρ is irreducible if and only if A' = End A V is a division algebra and ρ is absolutely irreducible if and only if A' = F1.
Proof. If ρ is irreducible, then A′ is a division algebra by Schur’s lemma and if ρ is absolutely irreducible, then ![]() is a division algebra for every extension field K of F. This implies that A' = F1. For, suppose that A' ≠ F1 and let c ∈ A',
is a division algebra for every extension field K of F. This implies that A' = F1. For, suppose that A' ≠ F1 and let c ∈ A', ![]() F1. Then the minimum polynomial f(λ) of c over F has degree > 1 and this is irreducible since A' is a division algebra. Put K = F[λ]/(f(λ)) and consider A'K. The minimum polynomial of c ∈ A'K is f(λ) and this is reducible in K[λ]. Hence A'K is not a division algebra, contrary to what we had proved. Hence A' = F1.
F1. Then the minimum polynomial f(λ) of c over F has degree > 1 and this is irreducible since A' is a division algebra. Put K = F[λ]/(f(λ)) and consider A'K. The minimum polynomial of c ∈ A'K is f(λ) and this is reducible in K[λ]. Hence A'K is not a division algebra, contrary to what we had proved. Hence A' = F1.
Next assume ρ is reducible, so we have a ρ(G)-invariant subspace U ≠ V, 0. By Maschke’s theorem, there exists a projection p on U that commutes with every ρ(g). Then p is an idempotent ≠ 0, 1 in A' and A′ is not a division algebra. Thus if A' is a division algebra, then ρ is irreducible. Since A′ = F1 implies A'K = K1, it follows that if A' = F1, then ρ is absolutely irreducible. ![]()
A field F is called a splitting field for the group G if every irreducible representation of G over F is absolutely irreducible. We have the following
THEOREM 5.8. Let G be a finite group, F a field with char ![]() . Then F is a splitting field for G if and only if F[G] is a direct sum of matrix algebras Mn(F).
. Then F is a splitting field for G if and only if F[G] is a direct sum of matrix algebras Mn(F).
Proof. Let A = F[G] = A1![]() …
…![]() AS where the Ai are the simple components of A and let Ii be a minimal left ideal of Ai The representation ρi of G acting on Ii is irreducible and every irreducible representation of G over F is equivalent to one of the ρi. Hence F is a splitting field for G if and only if every ρi is absolutely irreducible. By Theorem 5.7, this is the case if and only if EndAIi = F1 for 1 ≤ i ≤ s. Now EndAIi = Δ'i is a division algebra and by Theorem 5.1,
AS where the Ai are the simple components of A and let Ii be a minimal left ideal of Ai The representation ρi of G acting on Ii is irreducible and every irreducible representation of G over F is equivalent to one of the ρi. Hence F is a splitting field for G if and only if every ρi is absolutely irreducible. By Theorem 5.7, this is the case if and only if EndAIi = F1 for 1 ≤ i ≤ s. Now EndAIi = Δ'i is a division algebra and by Theorem 5.1, ![]() where
where ![]() and ni is the dimensionality of Ii as vector space over Δ'i. On the other hand, since the Aj, j ≠ i, annihilate Ii and Ai is simple,
and ni is the dimensionality of Ii as vector space over Δ'i. On the other hand, since the Aj, j ≠ i, annihilate Ii and Ai is simple, ![]() . Thus
. Thus ![]() . Now suppose F is a splitting field. Then Δ'i = F and
. Now suppose F is a splitting field. Then Δ'i = F and ![]() . Conversely, suppose
. Conversely, suppose ![]() for some n'i. Then
for some n'i. Then ![]() . By the isomorphism theorem for simple artinian algebras, this implies that n'i = ni and
. By the isomorphism theorem for simple artinian algebras, this implies that n'i = ni and ![]() . Then Δi = F1, EndA Ii = Δ'i = F1, and F is a splitting field.
. Then Δi = F1, EndA Ii = Δ'i = F1, and F is a splitting field. ![]()
1. Let G be finite, ρ an irreducible representation of G over F where char ![]() . Show that
. Show that ![]() if ρ is the unit representation and
if ρ is the unit representation and ![]() otherwise.
otherwise.
2. Let G be a finite group, F = ![]() or
or ![]() /(ρ) where
/(ρ) where ![]() . Show that there exists a finite dimensional extension field of F that is a splitting field for G.
. Show that there exists a finite dimensional extension field of F that is a splitting field for G.
3. Let ρ1 and ρ2 be representations of G over an infinite field F and let K be an extension field. Show that if ρ1K and ρ2K are equivalent, then ρ1 and ρ2 are equivalent. Does this hold for F finite?
5.4 IRREDUCIBLE REPRESENTATIONS OF Sn
It is generally a difficult problem to determine the structure of the group algebra F[G] for a given finite group G. As we saw in the previous section, if char ![]() , this amounts to determining a set of representatives for the equivalence classes of irreducible representations of G over F, or, as we shall now say more briefly, determining the irreducible representations of G over F. In this section, we give one important example for which this can be done: G = Sn. We shall determine a set of idempotents generating minimal left ideals of F[Sn] (char
, this amounts to determining a set of representatives for the equivalence classes of irreducible representations of G over F, or, as we shall now say more briefly, determining the irreducible representations of G over F. In this section, we give one important example for which this can be done: G = Sn. We shall determine a set of idempotents generating minimal left ideals of F[Sn] (char ![]() ) that give the irreducible representations of Sn over F. These results are due to Frobenius and to A. Young; our exposition follows one due to J. von Neumann as presented in van der Waerden’s Algebra vol. 2, p. 246.
) that give the irreducible representations of Sn over F. These results are due to Frobenius and to A. Young; our exposition follows one due to J. von Neumann as presented in van der Waerden’s Algebra vol. 2, p. 246.
We recall that the number of conjugacy classes of Sn is p(n) the number of (unordered) partitions of n (BAI, p. 75). If {r1, r2, …, rh} is such a partition (that is, ri ≥ 1 and ![]() , then the permutations that are products of disjoint cycles of lengths r1, r2, …, rh form a conjugacy class and every conjugacy class is obtained in this way. For the partition α = {r1, r2, …, rh} we assume
, then the permutations that are products of disjoint cycles of lengths r1, r2, …, rh form a conjugacy class and every conjugacy class is obtained in this way. For the partition α = {r1, r2, …, rh} we assume ![]() and we use this order to order the set of partitions lexicographically. Thus if β = {s1, s2, …, sk} with
and we use this order to order the set of partitions lexicographically. Thus if β = {s1, s2, …, sk} with ![]() then α > β if ri > si at the first place where ri ≠ si. Each partition α = {r1, r2, …, rh} defines a (Young) tableau
then α > β if ri > si at the first place where ri ≠ si. Each partition α = {r1, r2, …, rh} defines a (Young) tableau

and each tableau defines a set of diagrams D, E,… obtained by distributing the numbers 1, 2, …, n in the boxes so that no two numbers appear in the same box. For example, if α = {3, 2, 2}, then one of the D is

If D ( = D ) is a diagram, we define the group R(D) of row permutations of D to be the subgroup of Sn of permutations stabilizing the subsets filled in the rows of D. Thus, for D as in (34), R(D) is the set of products of cycles all of whose numbers appear in one of the rows {1, 3,7}, {2, 6), or {4, 5} (so R(D) = {1, (13), (17), (37), (137), (173), (26), (45), (13), (26), etc.}). Similarly, we define the subgroup C(D) of column permutations of D to be the subgroup of Sn of permutations stabilizing the columns of D.
If Dα is a diagram and σ ∈ Sn, then σDα is the diagram obtained from Dα by applying σ to its entries. Evidently this is an Eα and every Eα is a σDα for some σ ∈ Sn. It is clear that ![]() .
.
With each diagram D ( = Dα) we shall associate elements of the group algebra F[Sn] as follows: Put
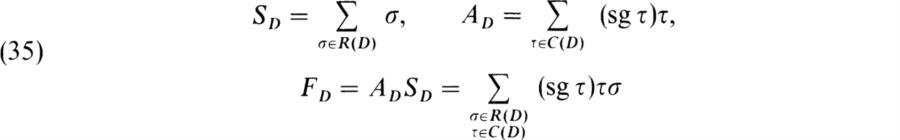
where sg τ denotes the sign of the permutation τ. Evidently, SD ≠ 0 and AD ≠ 0 in F[Sn]. But also FD ≠ 0. To see this, we observe that R(D) ∩ C(D) = 1, since an element common to these subgroups stabilizes every row and every column and hence fixes every element in {1, 2, …,n}. It now follows that if σ1, σ2 ∈ R(D) and τ1, τ2 ∈ C(D), then τ1σ1 = τ2σ2 implies ![]() and σ1 = σ2 and τ1 = τ2. Thus the products τσ appearing in FD are distinct and hence FD ≠ 0.
and σ1 = σ2 and τ1 = τ2. Thus the products τσ appearing in FD are distinct and hence FD ≠ 0.
Since ![]() and
and ![]() for ρ ∈ Sn and
for ρ ∈ Sn and ![]() , it follows that
, it follows that ![]() , and
, and ![]() . Also if σ ∈ R(D) and τ ∈ C(D), then the definition (35) gives
. Also if σ ∈ R(D) and τ ∈ C(D), then the definition (35) gives
![]()
The main properties of the elements SD, AD, FD will be derived from the following combinatorial result.
LEMMA 1. Let α and β partitions such that α ≥ β and let Dα and Eβ be associated diagrams. Suppose no two numbers appearing in the same row in Dα are in the same column of Eβ. Then α = β and Eα = στDβ for some σ ∈ R(Dα) and τ ∈ C(Dα).
Proof. The number of entries in the first row of Dα is the same as or exceeds that in the first row of Eβ. If greater, then since the number of columns of Eβ is the number of entries in the first row of Eβ, two entries of the first row of Dα occur in the same column in Eβ, contrary to hypothesis. Hence both diagrams have the same number of entries in the first row. Also we have a column permutation τ'1 of Eβ so that the first row of τ'1 Eβ has the same entries as the first row of Dα. Next we note that the entries in the second row of Dα occur in distinct columns of τ'1 Eβ and in rows after the first. It follows that Dα and τ'1Eβ and hence Dα and Eβ have the same number of entries in the second row and a column permutation τ'2 of τ'1 Eβ (and of Eβ) brings these into the second row. Continuing in this way, we see that β = α and there exists τ' ∈ C(Eα) such that the entries of each row of τ'Eα and of Dα are the same. Hence there is a σ ∈ R(Dα) such that ![]() . Now
. Now ![]() . Hence
. Hence ![]() and
and ![]() . Then
. Then ![]() .
.
Now assume α > β. Then Lemma 1 implies that there exist i, j, i ≠ j, in a row of Dα and in a column of Eβ. If π = (ij) then π ∈ R(Dα). Then, by (36), ![]() . Hence
. Hence
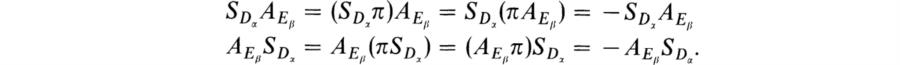
Hence ![]() . If ρ is any element of Sn, then
. If ρ is any element of Sn, then ![]() and since
and since ![]() we have
we have ![]() . Thus
. Thus
![]()
LEMMA 2. An element a ∈ F[Sn] satisfies the equations τaσ = (sgτ) a for all σ ∈ R(D) and τ ∈ C(D) if and only if a = γFD, γ ∈ F, FD = AD SD.
Proof. We have ![]() . Hence any γFD, γ ∈ F, satisfies the conditions. Next let
. Hence any γFD, γ ∈ F, satisfies the conditions. Next let ![]() satisfy the given conditions. Then
satisfy the given conditions. Then
![]()
for σ ∈ R(D) and τ ∈ C(D). In particular, γτσ = γ1 sg τ, so if we can show that γρ = 0 if ρ is not of the form τσ, τ ∈ C(D), σ ∈ R(D), then we shall have a = γ1 FD by (35). Hence suppose ![]() . Then
. Then ![]() . Then ρ–1D ≠ στD and Lemma 1 implies that there exists a transposition
. Then ρ–1D ≠ στD and Lemma 1 implies that there exists a transposition ![]() . Then π = ρ–1π'ρ where π' is a transposition contained in C(D). Then ρ = π'ρπ and
. Then π = ρ–1π'ρ where π' is a transposition contained in C(D). Then ρ = π'ρπ and ![]() by (38). Hence γρ = 0 and the proof is complete.
by (38). Hence γρ = 0 and the proof is complete.![]()
Now let x ∈ F[Sn] and consider the element FD x FD = AD SD x AD SD. By (36) we have ![]() for σ ∈ RD, τ ∈ CD. Hence, by Lemma 2, FD x FD = γ FD for γ ∈ F. In particular, FD2 = γFD. We proceed to show that γ ≠ 0. For this purpose, we consider the map x
for σ ∈ RD, τ ∈ CD. Hence, by Lemma 2, FD x FD = γ FD for γ ∈ F. In particular, FD2 = γFD. We proceed to show that γ ≠ 0. For this purpose, we consider the map x ![]() FDx of F[Sn] into itself. If γ = 0, FD2 = 0 and the map x
FDx of F[Sn] into itself. If γ = 0, FD2 = 0 and the map x ![]() FDx is nilpotent and hence has trace 0. On the other hand, if ρ ∈ Sn, then if we look at the matrix of x
FDx is nilpotent and hence has trace 0. On the other hand, if ρ ∈ Sn, then if we look at the matrix of x ![]() ρx relative to a base, we see that the trace of this map is 0 if ρ ≠ 1 and is n! if ρ = 1. Since the formula (35) for FD shows that the coefficient of 1 in the expression for FD is 1, the trace of x
ρx relative to a base, we see that the trace of this map is 0 if ρ ≠ 1 and is n! if ρ = 1. Since the formula (35) for FD shows that the coefficient of 1 in the expression for FD is 1, the trace of x ![]() FDx is n! ≠ 0 (since char
FDx is n! ≠ 0 (since char ![]() ).
).
We now put eD = γ–1 FD. Then eD2 = eD ≠ 0 and eDF[Sn]eD = FeD. Also, if α and β are distinct partitions, then ![]() follows from (37) if Dα is a diagram associated with α and Eβ is one associated with β.
follows from (37) if Dα is a diagram associated with α and Eβ is one associated with β.
We recall that if e and f are idempotents of a ring A, then the additive groups homA(Ae, Af) and eAf are isomorphic and the rings EndAAe and eAe are anti-isomorphic (p. 180). If we apply this and Theorem 5.7 to the representations of G acting on F[Sn]eD , we see that this representation is absolutely irreducible and that if α ≠ β, then the representations provided by F[Sn]eDx and F[Sn]eEβ are inequivalent. Since the number of conjugacy classes of Sn is p(n), we obtain in this way a full set of representatives of the equivalence classes of irreducible representations. In terms of the group algebra F[Sn] the result we have proved is
THEOREM 5.9. If F is a field of characteristic 0 or of prime characteristic exceeding n, then
![]()
The method of proof is constructive and in theory it can be used to carry out the decomposition of F[Sn] into simple components. The determination of the ni, which are the degrees of the irreducible representations, can be made by calculating the characters of Sn as defined in the next section for an arbitrary group. There is an extensive literature on the characters of Sn. We shall not consider any of this here. Evidently, Theorem 5.9 has the following consequence.
COROLLARY. The field ![]() and any field
and any field ![]() /(p) with p > n is a splitting field for Sn.
/(p) with p > n is a splitting field for Sn.
5.5 CHARACTERS. ORTHOGONALITY RELATIONS
DEFINITION 5.2. If ρ is a representation of a group G acting on a vector space V/F, then the F-valued function on G defined by
![]()
where tr ρ(g) is the trace of the linear transformation ρ(g), is called the character of G afforded by ρ. If p is irreducible, then χρ is called irreducible and if F = ![]() , then χρ is called a complex character. The degree of ρ is called the degree of χρ.
, then χρ is called a complex character. The degree of ρ is called the degree of χρ.
As we shall see in a moment, two representations of G over ![]() are equivalent if and only if they have the same character. Moreover, a great deal of experience has shown that the characters encapsulate precisely the information on the representations that is useable for the applications. For these reasons, it is fair to say that the central problem of representation theory is that of determining the complex irreducible characters of a given group, or, more precisely, of developing methods for this purpose.
are equivalent if and only if they have the same character. Moreover, a great deal of experience has shown that the characters encapsulate precisely the information on the representations that is useable for the applications. For these reasons, it is fair to say that the central problem of representation theory is that of determining the complex irreducible characters of a given group, or, more precisely, of developing methods for this purpose.
We begin by listing some simple facts about characters.
1. Equivalent representations have the same character. If ρ1 on V1 is equivalent to ρ2 on V2, then there exists a bijective linear map η of V1 onto V2 such that ρ2(g) = ηρ1(g)η–1. This implies that trρ2(g) = trρ1(g) and χρ2 = χρ1.
2. Any character is a class function, that is, it is constant on every conjugacy class and hence it defines a map of the set of conjugacy classes into the base field. Let g, h ∈ G. Then ![]() . Hence
. Hence ![]() .
.
3. If char F = 0, then the degree of ρ is χρ(1). This is clear since ρ(l) = lv, so χρ(1) = trρ(l) = dim V.
4. Let U be a ρ(G)-invariant subspace of the space V on which ρ acts and let ρ|U and ρ|V/U be the corresponding subrepresentation and factor representation. Then .
![]()
This follows by choosing a base (u1, … , un) for V such that (u1, … , ur) is a base for U (and hence (ur + l + U, … un + U) is a base for V/U). Then the matrices of the ρ(g) all have the reduced form (18). The result follows from this.
5. If ρ1 and ρ2 are representations of G, then
![]()
that is, for every g ∈ G, ![]() . To see this, we refer to the matrix (12) for the linear transformation a1
. To see this, we refer to the matrix (12) for the linear transformation a1![]() a2 in Vl
a2 in Vl ![]() V2 where ai is a linear transformation in Vi. It is clear from this that tr (a1
V2 where ai is a linear transformation in Vi. It is clear from this that tr (a1 ![]() a2) = (tr a1) (tr a2). Hence
a2) = (tr a1) (tr a2). Hence ![]() .
.
For the applications we are interested primarily in complex characters. We shall now note some of their properties.
6. If G is finite, then any complex character of G is a sum of mth roots of unity where m is the exponent of G, defined to be the least common multiple of the orders of the elements of G. If g ∈ G, then gm = 1 and hence ρ(g)m= 1. Hence the minimum polynomial of ρ(g) is a factor of λm – 1, and so it has distinct roots that are mth roots of unity. It follows that ρ(g) has a matrix of the form
![]()
where the ωi are mth roots of unity. Then ![]() .
.
There are several useful consequences of this result. First we have the following
PROPOSITION 5.3. Let ρ be a complex representation of degree n of a finite group G. Then for any g ∈ G
![]()
and
![]()
if and only if ρ(g) = ω1 where ω is an mth root of unity, m the exponent of G. In particular, if
![]()
then ρ(g) = 1.
Proof. We have ![]() an mth root of unity. Then
an mth root of unity. Then ![]() . Moreover, equality holds if and only if all the ωi are on the same ray through the origin. Since they are on the unit circle, this holds if and only if they are equal. Hence
. Moreover, equality holds if and only if all the ωi are on the same ray through the origin. Since they are on the unit circle, this holds if and only if they are equal. Hence ![]() if and only if ρ(g) = ω1. The last statement is an immediate consequence of this.
if and only if ρ(g) = ω1. The last statement is an immediate consequence of this. ![]()
The fact that ![]() implies ρ(g) = 1, and the obvious converse of this leads us to define the kernel of the character χρ as the set of g such that
implies ρ(g) = 1, and the obvious converse of this leads us to define the kernel of the character χρ as the set of g such that ![]() (the degree of ρ). Then ker χρ = ker ρ is a normal subgroup of G. Also we define
(the degree of ρ). Then ker χρ = ker ρ is a normal subgroup of G. Also we define
![]()
Then we have shown that Z(χρ) is the set of g such that ρ(g) = ω1. It is clear that these form a normal subgroup of G containing ker χρ and Z(χρ)/ker ρ is isomorphic to a subgroup of the multiplicative group of rath roots of unity. Hence Z(χρ)/ker ρ is cyclic.
Another important consequence of the proof of property 6 is
7. Let ρ be a complex representation of a finite group G, ρ* the contragredient representation. Then
![]()
(that is, ![]() . To see this, we suppose g ∈ G and we choose a base B in V such that the matrix of ρ(g) relative to this base is (39). Then the matrix of ρ*(g) relative to the dual base B* (p. 250) is
. To see this, we suppose g ∈ G and we choose a base B in V such that the matrix of ρ(g) relative to this base is (39). Then the matrix of ρ*(g) relative to the dual base B* (p. 250) is ![]() . Hence
. Hence ![]() .
.
EXAMPLES
1. Let 1 be the unit representation: V is one-dimensional and 1(g) = 1V, g ∈ G. The character afforded by this is the unit character χ1:g ![]() 1 ∈ F.
1 ∈ F.
2. Let G be finite, ρ the regular representation of G. To determine χρ we use the base G = {g1 = l, g2, …, gn} for F[G]. We have χρ(1) = n. On the other hand, if i > 1, then all of the diagonal elements of the matrix of ρ(gi) relative to the base G are 0 since gigj ≠ gj. Hence, χρ(gi) = 0. Thus the character of the regular representation is given by
![]()
3. Let G = Dn, the dihedral group of order 2n generated by r, s such that rn = 1, s2 = 1, srs–1 = r–1. If we refer to the results given in example 2, p. 261, we obtain the following character tables:
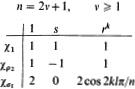
In these tables, the representatives of the conjugacy classes are listed in the top row and the rows correspond to the irreducible representations given before. In both cases, 1 ≤ k ≤ v, and 1 ≤ l ≤ v if n = 2v + l, l ≤ l ≤ v – 1 if n = 2v.
We shall derive next some fundamental orthogonality relations connecting the irreducible complex characters of a finite group. We consider first a more general result in the situation in which G is a finite group, F a splitting field for G with char ![]() . Let {ρ1, …, ρs} be a set of representatives of the (absolutely) irreducible representations of G over F and suppose ρi acts on Vi, 1 ≤ i ≤ s. We assume also that ρ1 is the unit representation. Let 1 ≤ i, j ≤ s and consider homF(Vi, Vj). We have a representation ρij of G acting on homF(Vi, Vj) obtained by defining
. Let {ρ1, …, ρs} be a set of representatives of the (absolutely) irreducible representations of G over F and suppose ρi acts on Vi, 1 ≤ i ≤ s. We assume also that ρ1 is the unit representation. Let 1 ≤ i, j ≤ s and consider homF(Vi, Vj). We have a representation ρij of G acting on homF(Vi, Vj) obtained by defining
![]()
for l ∈ homF(Vi, Vj). It is clear that this gives a representation of G (exercise 2, p. 251). Now let l be any element of homF(Vi, Vj) and form the element

We have
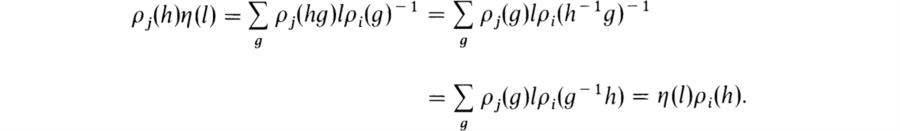
This implies that η(l) is a homomorphism of Vi regarded as F[G]-module into Vj regarded as F[G]-module, that is, η(l) ∈ homF[G](Vi, Vj). Now if i ≠ j, then Vi and Vj are irreducible and non-isomorphic F[G]-modules. Hence by Schur’s lemma,
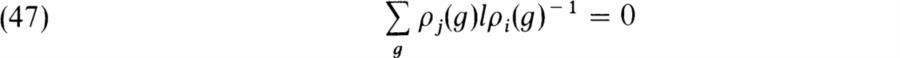
if i ≠ j and l is any element of homF(Vi Vj). Next suppose i = j. Then η(l) ∈ EndF[G] Vi = F1, so we have
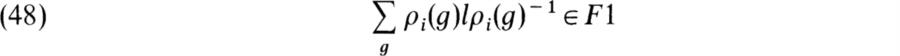
for any l ∈ EndFVi. We can use (47) and (48) to derive the following result, which is due to Schur.
THEOREM 5.10. Let G be a finite group, F a splitting field for G with char ![]() . Let {ρ1, …, ρs} be a set of representatives of the equivalence classes of irreducible representations of G over F and for each i let ρ(i) be a matrix representation given by ρi Then char
. Let {ρ1, …, ρs} be a set of representatives of the equivalence classes of irreducible representations of G over F and for each i let ρ(i) be a matrix representation given by ρi Then char ![]() and we have the following relations:
and we have the following relations:

These relations are called the Schur relations.
Proof. Let ![]() be a base for the space Vi on which ρi acts so that
be a base for the space Vi on which ρi acts so that ![]() and let flr be the element of homF(Vi, Vj) such that
and let flr be the element of homF(Vi, Vj) such that ![]() . Then
. Then ![]() . Then (47) implies the first set of relations (49). Also for j = i, the foregoing relations and (48) give
. Then (47) implies the first set of relations (49). Also for j = i, the foregoing relations and (48) give
![]()
Hence
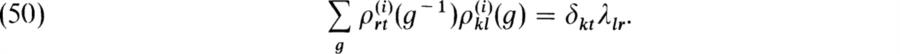
Put t = k in these equations and sum on k. This gives
![]()
which shows that char ![]() and
and ![]() . Substituting this in (50) gives the second set of Schur’s relations.
. Substituting this in (50) gives the second set of Schur’s relations. ![]()
We have ![]() . Hence if we put l = k and t = r in (49) and sum on k and r, we obtain
. Hence if we put l = k and t = r in (49) and sum on k and r, we obtain

Now suppose F = ![]() . Then it is clear from the fact that ρi(g) has a matrix of the form diag {ω1, …, ωn} where the ω’s are roots of unity (see property 6 above) that
. Then it is clear from the fact that ρi(g) has a matrix of the form diag {ω1, …, ωn} where the ω’s are roots of unity (see property 6 above) that ![]() . Hence we obtain from (51) the basic orthogonality relations for irreducible complex characters:
. Hence we obtain from (51) the basic orthogonality relations for irreducible complex characters:
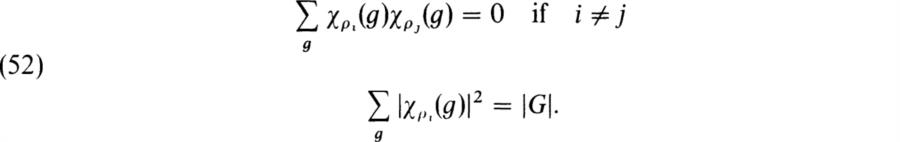
We now consider the complex vector space ![]() G of complex valued functions on G. We have the usual definitions of addition and multiplication by complex numbers: If
G of complex valued functions on G. We have the usual definitions of addition and multiplication by complex numbers: If ![]() for a ∈
for a ∈ ![]() . We define a hermitian form on
. We define a hermitian form on ![]() G by
G by
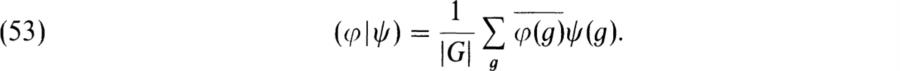
Then
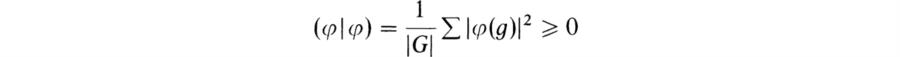
and equality holds if and only if φ = 0. Hence (φ|ψ) is positive definite. We shall now write χi for χρi. Then the relations (52) are equivalent to
![]()
These state that {χ1, …, χs} is an orthonormal set of vectors in ![]() G, that is, they are mutually orthogonal and all have length one. It is clear from this that the irreducible complex characters are linearly independent over
G, that is, they are mutually orthogonal and all have length one. It is clear from this that the irreducible complex characters are linearly independent over ![]() . We have observed that characters are class functions. The set of class functions forms a subspace cf (G) of
. We have observed that characters are class functions. The set of class functions forms a subspace cf (G) of ![]() G whose dimensionality is the number of conjugacy classes. We have seen that this number is the same as the number s of irreducible representations over
G whose dimensionality is the number of conjugacy classes. We have seen that this number is the same as the number s of irreducible representations over ![]() . Hence, it is clear that the irreducible characters constitute a base for cf (G).
. Hence, it is clear that the irreducible characters constitute a base for cf (G).
Now let ρ be an arbitrary complex representation of G, χ its character. We have defined the multiplicity mi of ρi in ρ on p. 255. It is clear from the definition and from the fact that the representations are completely reducible that two representations are equivalent if and only if for every i = 1, 2, …, s, the multiplicity of ρi in the two representations is the same. It is clear also that we have the formula
![]()
where mi is the multiplicity of ρi in ρ. Now, by (54),
![]()
Hence the mi, are determined by χ and consequently complex representations are equivalent if and only if they have the same character. Also, by (55), we have
![]()
and this has the value 1 if and only if one of the mi is 1 and the rest are 0. This shows that a character is irreducible if and only if it has length 1 in the hermitian metric for ![]() G.
G.
Let C1 = {1}, C2, …, CS be the conjugacy classes of G and let hk = |Ck|. We now write χik for χi(g), g ∈ Ck. Then the orthogonality relations give
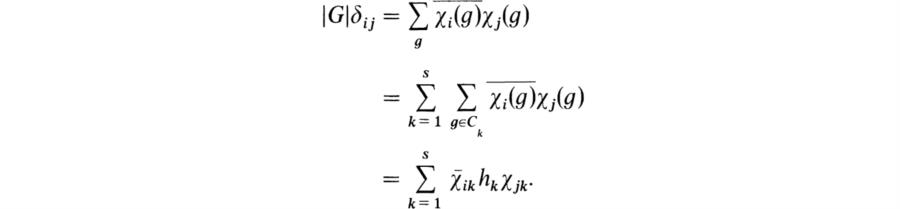
Thus we have

Let X = (χij) ∈ Ms(![]() ) and let H = diag {hl, …, hs}. Then the foregoing relations amount to the matrix equation
) and let H = diag {hl, …, hs}. Then the foregoing relations amount to the matrix equation
![]()
From this, one deduces ![]() , which is equivalent to
, which is equivalent to

We shall call (58) and (60) the row and the column orthogonality relations respectively for the characters. We remark that if we take j = k = 1 in (60) we obtain ![]() . This is the relation (32) that we had obtained in a more general situation by using the theory of algebras.
. This is the relation (32) that we had obtained in a more general situation by using the theory of algebras.
If ρ is a representation of a group G acting on V/F, then ρ has a unique extension to a homomorphism of F[G] into EndFV. This maps the element ![]() of the group algebra into
of the group algebra into ![]() . We shall denote this extension by ρ also. Similarly, the character χρ defined on G can be extended uniquely to a linear map χρ of F[G] into F by putting
. We shall denote this extension by ρ also. Similarly, the character χρ defined on G can be extended uniquely to a linear map χρ of F[G] into F by putting ![]() . If c ∈ cent F[G], the center of the group algebra, then ρ(c) is in the centralizer of ρ, so if ρ is absolutely irreducible, then ρ(c) = ω(c)1 where ω(c) ∈ F. If the degree of ρ is n, then χρ(c) = nω(c) so
. If c ∈ cent F[G], the center of the group algebra, then ρ(c) is in the centralizer of ρ, so if ρ is absolutely irreducible, then ρ(c) = ω(c)1 where ω(c) ∈ F. If the degree of ρ is n, then χρ(c) = nω(c) so

Since the map c ![]() ρ(c) is an algebra homomorphism of cent F[G] into F1, it is clear that c
ρ(c) is an algebra homomorphism of cent F[G] into F1, it is clear that c ![]() (1/n)χρ(c) is an algebra homomorphism.
(1/n)χρ(c) is an algebra homomorphism.
We have seen that if we put ![]() , then (c1, …, cs) is a base for cent F[G]. Evidently,
, then (c1, …, cs) is a base for cent F[G]. Evidently, ![]() where the njkg ∈
where the njkg ∈ ![]() , the set of nonnegative integers. Since cjck ∈ cent F[G], we have h–1cjckh = cjck, h ∈ G. This gives
, the set of nonnegative integers. Since cjck ∈ cent F[G], we have h–1cjckh = cjck, h ∈ G. This gives ![]() . It follows that we have a multiplication table of the form
. It follows that we have a multiplication table of the form

where mjkl ∈ ![]() for the base (cl, …, cs) of centF[G] over F. It is readily seen that mjkl is the number of pairs (x, y), x ∈ Cj, y ∈ Ck, such that xy is a given z in Cl.
for the base (cl, …, cs) of centF[G] over F. It is readily seen that mjkl is the number of pairs (x, y), x ∈ Cj, y ∈ Ck, such that xy is a given z in Cl.
Now suppose F = ![]() and let the notation be as before. We apply the representation ρi to (62) to obtain
and let the notation be as before. We apply the representation ρi to (62) to obtain ![]() . If ni = deg ρi = χi(1), then we have
. If ni = deg ρi = χi(1), then we have ![]() . Hence we have the character relation
. Hence we have the character relation
![]()
If we use the definition of ![]() and the fact that characters are class functions, we obtain
and the fact that characters are class functions, we obtain ![]() for any gj ∈ Cj, so χi(cj) = hjχij. Hence we have the character relation
for any gj ∈ Cj, so χi(cj) = hjχij. Hence we have the character relation


By a character table for a group G, we mean a table giving the values χij for the irreducible complex characters. A fundamental problem for the study of a given group G is the computation of its character table. As an illustration of this, we consider the following
EXAMPLE
We wish to determine a character table for S4. The following is a list of representatives for the conjugacy classes: (1, (12), (123), (1234), (12) (34)). We denote the corresponding conjugacy classes as (Cl, C2, C3, C4, C5). Their cardinalities are respectively (h1, h2, h3, h4, h5) = (1, 6,8, 6,3). The alternating group A4 is a normal subgroup of index 2 in S4, and V = {1, (12) (34), (13) (24), (14) (23)} is a normal subgroup of index 6 in S4 (BAI, p. 261, exercise 4). If we let S3 denote the subgroup of S4 fixing 4, then S4 is a semi-direct product of V and S3: Any element of S4 can be written in one and only one way as a product sv where s ∈ S3, v ∈ V. If si ∈ S3 and vi ∈ V, then (s1v1)(s2v2) = (s1s2)(s2–1v1s2v2) and s2–1v1s2 ∈ V. Hence sv ![]() s is a homomorphism η of S4 onto S3 with kernel V. If ρ is a representation of S3, then ρη is a representation of S4 whose character is χρη.
s is a homomorphism η of S4 onto S3 with kernel V. If ρ is a representation of S3, then ρη is a representation of S4 whose character is χρη.
Now S3 ![]() D3 under a map such that (12)
D3 under a map such that (12) ![]() s, (123)
s, (123) ![]() r. Hence the character table for D3 gives the following character table for S3:
r. Hence the character table for D3 gives the following character table for S3:

We denote the characters obtained by composing this with η again by χl, χ2, χ3 Since. (12) (13) (24) = (1324), the part of the character table obtained from these characters is

If ni is the degree of χi 1 ≤ i ≤ 5, then Σni2 = 24 gives n42 + n52 = 18. Hence n4 = n5 = 3, so the missing two irreducible characters are of degree three. Hence the last two rows of the character table have the form (3, α, β, γ, δ) and (3, α', β', γ', δ'). If we use the relation (60) with j = 1 and k = 2, 3,4, 5, we obtain
![]()
Hence the last row is (3, –α, –β, –γ, – 2 – δ). If we use (58) with i = 4 and j = 1, 2, 3, we obtain the relations

These equations give β = 0, δ = – 1, γ = –α. The orthogonality relation (60) for j = 2, k = 4 gives ![]() = – 1. On the other hand, α = χ4(12) is a sum of square roots of 1, hence real. Thus
= – 1. On the other hand, α = χ4(12) is a sum of square roots of 1, hence real. Thus ![]() = α( –
= α( – ![]() ) = – α2 = – 1 and α2 = 1, so α = ± 1, γ =
) = – α2 = – 1 and α2 = 1, so α = ± 1, γ = ![]() 1. Thus the last two rows are either (3, 1,0, – 1, – 1) and (3, – 1, 0,1, – 1) or (3, – 1, 0,1, – 1) and (3, 1,0, – 1, – 1). Both determinations give the same table except for the order of the last two rows.
1. Thus the last two rows are either (3, 1,0, – 1, – 1) and (3, – 1, 0,1, – 1) or (3, – 1, 0,1, – 1) and (3, 1,0, – 1, – 1). Both determinations give the same table except for the order of the last two rows.
The foregoing example illustrates how the orthogonality relations plus other information that one can get a hold of can be used to calculate a character table. Further results that we shall derive presently will supply additional information useful for calculating character tables. We should note also that there is a substantial literature on the characters of Sn, beginning with a classical paper published by Frobenius in 1900 that gives formulas for the characters of any Sn. See, for example, Weyl’s Classical Groups, p. 213.
EXERCISES
1. Determine a character table for A4.
2. Determine a character table for the quaternion group.
3. Let G be a subgroup of Sn, ρ the corresponding permutation representation of G over ![]() , χ its character. Show that
, χ its character. Show that ![]() where r is the multiplicity of the unit representation ρ1 in ρ. Show that
where r is the multiplicity of the unit representation ρ1 in ρ. Show that ![]() is also the total number of fixed points in {1, 2, …, n} for all g ∈ G.
is also the total number of fixed points in {1, 2, …, n} for all g ∈ G.
4. Let the notations be as in exercise 3. Show that the number of orbits of G in {1, 2, …, n} is the multiplicity r of ρ1 in ρ.
5. A permutation group G is called k-fold transitive for k = 1, 2, … if given any two k-tuples (i1, i2, …, ik) and (j1, j2, …, jk) of distinct i’s and j’s, there exists a g ∈ G such that gi1 = ji, l ≤ l ≤ k. Let G be doubly ( = 2-fold) transitive, ρ the corresponding permutation representation. Show that ρ ~ ρ1 ![]() ρi where ρi is an irreducible representation ≠ ρ1.
ρi where ρi is an irreducible representation ≠ ρ1.
6. Let χ1, …, χs be the irreducible complex characters of G and C1 = {1}, C2, …, Cs be conjugacy classes of G, hi = |Ci|. Put ![]() and
and ![]() where χij = χi(g) for some g ∈ Cj. Show that the ei are orthogonal idempotents in the center of
where χij = χi(g) for some g ∈ Cj. Show that the ei are orthogonal idempotents in the center of ![]() [G] and Σei = 1.
[G] and Σei = 1.
7. Show that an element g in a finite group G is conjugate to its inverse g–1 if and only if χ(g) ∈ ![]() for every irreducible complex character χ.
for every irreducible complex character χ.
5.6 DIRECT PRODUCTS OF GROUPS. CHARACTERS OF ABELIAN GROUPS
It is easy to see that if G1 and G2 are finite groups, then F[G1 × G2] ![]() F[G1]
F[G1] ![]() F F[G2]. If char
F F[G2]. If char ![]() and F is a splitting field for G1 and G2, this can be used to reduce the study of the representations over F of G1 × G2 to that of the components Gi. In the most important case, in which F =
and F is a splitting field for G1 and G2, this can be used to reduce the study of the representations over F of G1 × G2 to that of the components Gi. In the most important case, in which F = ![]() , we can obtain the results also by using characters. We shall follow this approach.
, we can obtain the results also by using characters. We shall follow this approach.
Let ρi, i = 1, 2, be a representation of Gi acting on Vi over any F. If we compose the projection (g1, g2) ![]() g1 with ρ1, we obtain a representation ρ'1 of G1 × G2. Evidently G2 ⊂ kerρ'1. Similarly, we obtain a representation ρ'2 of G1 × G2 by composing the projection (g1, g2)
g1 with ρ1, we obtain a representation ρ'1 of G1 × G2. Evidently G2 ⊂ kerρ'1. Similarly, we obtain a representation ρ'2 of G1 × G2 by composing the projection (g1, g2) ![]() g2 with the representation ρ2 of G2. We now form ρ'1
g2 with the representation ρ2 of G2. We now form ρ'1 ![]() ρ'2, which we denote as ρ1 ≠ ρ2. Then
ρ'2, which we denote as ρ1 ≠ ρ2. Then
![]()
and hence
![]()
We have the canonical imbeddings g1 ![]() (gl, 12) and g2
(gl, 12) and g2 ![]() (11, g2) of G1 and G2 in G1 × G2. Then
(11, g2) of G1 and G2 in G1 × G2. Then
![]()
Similarly,
![]()
All of this has an immediate extension to direct products of more than two factors.
Now suppose the Gi are finite, F = ![]() , and ρi is an irreducible representation of Gi. Then we have
, and ρi is an irreducible representation of Gi. Then we have
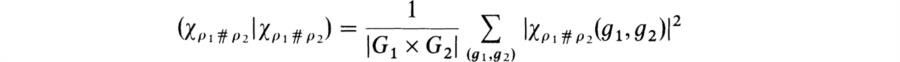
Hence ρ1 # ρ2 is an irreducible representation of G1 × G2. Next suppose the irreducible characters of Gi are χ1 (i), … , χs (i) and let ρk(i) be a representation affording χk(i). The representations ρk(1) # ρl(2) of G1 × G2 are irreducible and (67) and (68) imply that ρk(1) # ρl(2) and ρk'(1) # ρl'(2) have distinct characters and hence are inequivalent if (k', l') ≠ (k, l). Hence we obtain in this way s1, s2 inequivalent irreducible representations. Since the degree of ρk(1) # ρl(2) is the product of the degree of ρk(1) and the degree of ρl(2), the sum of the squares of the degrees of the ρk(1) # ρl(2) is the product of the sum of the squares of the degrees of the irreducible representations of G1 and the sum of the squares of the degrees of the irreducible representations of G2. This is |G1||G2| = |G1 × G2|. It follows that the set of representations {ρk(1) # ρl(2)} is a set of representatives of the equivalence classes of the irreducible representations of G1 × G2. This proves
THEOREM 5.11. Let G1 and G2 be finite groups, {ρ1(i), …, ρs(i)} a set of representatives of the equivalence classes of irreducible representations over ![]() of Gi. Then every ρk(1) # ρl(2) is an irreducible representation of G1 × G2 and {ρk(1) # ρl(2)} is a set of representatives of the equivalence classes of irreducible representations of G1 × G2.
of Gi. Then every ρk(1) # ρl(2) is an irreducible representation of G1 × G2 and {ρk(1) # ρl(2)} is a set of representatives of the equivalence classes of irreducible representations of G1 × G2.
A character χ of degree one is called linear. Evidently, such a character is irreducible and may be identified with the representation affording it. Thus χ is a homomorphism of the given group into the multiplicative group of a field. Conversely, any homomorphism of a group G into the multiplicative group F* of a field F is a linear character of G. We recall that these characters have played an important role in the Galois theory of fields (BAI, p. 291). If χ and χ' are linear characters of G, then χ1χ2 defined by (χχ')(g) = χ(g)χ'(g) is a linear character. In this way the set of linear characters of G form a group with the unit character: g ![]() 1 as unit and the inverse of χ as g
1 as unit and the inverse of χ as g ![]() χ(g)–1.
χ(g)–1.
If G is an abelian group, every irreducible complex character of G is linear. For, if ρ is an irreducible representation of G acting on V over ![]() , then End
, then End![]() [G]V =
[G]V = ![]() l and since G is abelian, Env ρ ⊂ End
l and since G is abelian, Env ρ ⊂ End![]() [G]V so Env ρ =
[G]V so Env ρ = ![]() l. Then any subspace is ρ(G)-invariant and since ρ is irreducible, V is onedimensional. Hence χρ is linear. Since G is abelian, every conjugacy class consists of a single element; hence the number of these is |G|. Then G has |G| irreducible complex characters.
l. Then any subspace is ρ(G)-invariant and since ρ is irreducible, V is onedimensional. Hence χρ is linear. Since G is abelian, every conjugacy class consists of a single element; hence the number of these is |G|. Then G has |G| irreducible complex characters.
The last result can also be seen without using representation theory. In fact, we can easily determine the structure of the group of irreducible (= linear) complex characters of any finite abelian group. If G is any abelian group, the group of irreducible complex characters is called the character group of G. Now let G be finite abelian. Then G is a direct product of cyclic groups (BAI, p. 195): G = G1 × G2 × … × Gr where ![]() and gi has order ei. We may assume the Gi are subgroups and every element of G can be written in one and only one way as
and gi has order ei. We may assume the Gi are subgroups and every element of G can be written in one and only one way as ![]() where 0 ≤ ki < ei. Let
where 0 ≤ ki < ei. Let ![]() , the character group of G. Then
, the character group of G. Then ![]() so χ(gi) is an eith root of unity. The set of these is a cyclic subgroup Zei of the multiplicative group
so χ(gi) is an eith root of unity. The set of these is a cyclic subgroup Zei of the multiplicative group ![]() *. We now define a map of
*. We now define a map of ![]() into Ze1 × Ze2 × … × Zer by
into Ze1 × Ze2 × … × Zer by
![]()
It is clear that this is a homomorphism. The kernel is the set of χ such that χ(gi) = l, 1 ≤ i ≤ r. Then ![]() and χ = 1. Hence (69) is a monomorphism. Moreover, the map is surjective. For, if (u1, …, ur) ∈ Ze1 × … × Zer, then uiei = 1 and hence we have a homomorphism of
and χ = 1. Hence (69) is a monomorphism. Moreover, the map is surjective. For, if (u1, …, ur) ∈ Ze1 × … × Zer, then uiei = 1 and hence we have a homomorphism of ![]() into Zei sending gi
into Zei sending gi ![]() ui. Then we have a homomorphism χ of G = G1 × … × Gr into
ui. Then we have a homomorphism χ of G = G1 × … × Gr into ![]() * sending gi
* sending gi ![]() ui 1 ≤ i ≤ r. Evidently, χ is a character that is mapped into (ul, …, ur) by (69). Hence we have an isomorphism of G with its character group
ui 1 ≤ i ≤ r. Evidently, χ is a character that is mapped into (ul, …, ur) by (69). Hence we have an isomorphism of G with its character group ![]() .
.
EXERCISES
1. Show that the number of complex linear characters of a finite group is the index [G: G'], G' the commutator group of G.
2. Let G be a finite group, ρ the regular representation of G over the field F. Form the field F(xg1, …, xgm) in m-indeterminates where m = |G| and gi ![]() xgi is 1–1. The determinant
xgi is 1–1. The determinant
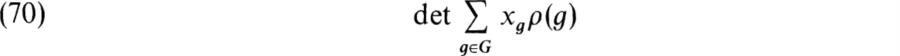
is called the group determinant of G over F. (The study of such determinants was one of the chief motivations for Frobenius’ introduction of the theory of characters.) Show that if F = ![]() and G is abelian, then
and G is abelian, then
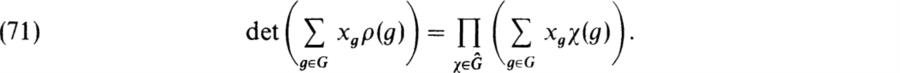
This result is due to R. Dedekind.
3. Let Fab denote the category of finite abelian groups with homomorphisms as morphisms. We have a contravariant functor D from Fab to itself such that ![]() and if f: A → B, then
and if f: A → B, then ![]() is defined by ψ
is defined by ψ ![]() χ where χ(x) = ψ(f(x)), x ∈ A. Show that
χ where χ(x) = ψ(f(x)), x ∈ A. Show that ![]() is naturally equivalent to the identity functor (cf. p. 22).
is naturally equivalent to the identity functor (cf. p. 22).
4. Show that if H is a subgroup of a finite abelian group G, then the subgroup of ![]() of χ such that χH = 1H can he identified with
of χ such that χH = 1H can he identified with ![]() and hence its order is |G/H|. Use this to show that the map χ
and hence its order is |G/H|. Use this to show that the map χ ![]() χH of
χH of ![]() into
into ![]() is surjective. Note that this implies that any linear character of H can be extended to a linear character of G.
is surjective. Note that this implies that any linear character of H can be extended to a linear character of G.
5.7 SOME ARITHMETICAL CONSIDERATIONS
In this section, G will be finite and all representations and characters are complex. We shall apply some elementary results on integral complex numbers that were given in BAI, pp. 279–281, to obtain important results on the degrees of the irreducible representations and on the characters of Sn.
We recall that a ∈ ![]() is called algebraic if a is algebraic over the subfield
is called algebraic if a is algebraic over the subfield ![]() , that is, a is a root of a non-zero polynomial with coefficients in
, that is, a is a root of a non-zero polynomial with coefficients in ![]() . The complex number a is called integral (or an integer) if a is a root of a monic polynomial with integer coefficients. A useful criterion to prove integrality is that a is integral if and only if there exists a finitely generated
. The complex number a is called integral (or an integer) if a is a root of a monic polynomial with integer coefficients. A useful criterion to prove integrality is that a is integral if and only if there exists a finitely generated ![]() -submodule M of
-submodule M of ![]() such that 1 ∈ M and aM ⊂ M. The subset A of
such that 1 ∈ M and aM ⊂ M. The subset A of ![]() of algebraic numbers is a subfield and the subset I of integral complex numbers is a subring. Moreover, if a ∈
of algebraic numbers is a subfield and the subset I of integral complex numbers is a subring. Moreover, if a ∈ ![]() is a root of a monic polynomial in A[λ] (in I[λ]), then a ∈ A (I). We showed also that a is integral if and only if a is algebraic and its minimum polynomial over
is a root of a monic polynomial in A[λ] (in I[λ]), then a ∈ A (I). We showed also that a is integral if and only if a is algebraic and its minimum polynomial over ![]() has integer coefficients, and that the only rational numbers that are integral in
has integer coefficients, and that the only rational numbers that are integral in ![]() are the elements of
are the elements of ![]() .
.
We have seen that the characters of G are sums of roots of unity (property 6 on p. 270). Since roots of unity are integral, it follows that χ(g) is integral for any character χ and any g ∈ G. We recall the following notations that were introduced in section 5.5.
1. χ1, …, χs are the irreducible characters. χ1 is the unit character, that is, the character of the unit representation ρ1.
2. C1 = {1}, C2, …, Cs are the conjugacy classes.
3. χij = χi(gj) where gj ∈ Cj.
4. ni = χi1. This is the degree of the representation ρi such that χρi, = χi.
5. hj = |Cj|.
We recall also the following character relations (p. 276):
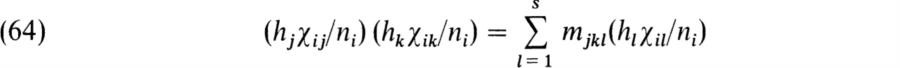
where the mjkl ∈ ![]() . We shall deduce from these equations
. We shall deduce from these equations
PROPOSITION 5.4. The complex numbers hjχij/ni are integral.
Proof. Fix i and put uk = hkχij/ni, 1 ≤ k ≤ s, u0 = 1. Let ![]() . Then (64) shows that ukM ⊂ M. Hence uk is integral by the criterion we noted above.
. Then (64) shows that ukM ⊂ M. Hence uk is integral by the criterion we noted above.
We can now prove
THEOREM 5.12. ni||G|.
Proof. We use the formula (58) for i = j to obtain ![]() . Since the
. Since the ![]() and
and ![]() are integral, so is |G|/ni. Since this is rational, it is contained in
are integral, so is |G|/ni. Since this is rational, it is contained in ![]() . Hence ni||G|.
. Hence ni||G|.![]()
The foregoing result is due to Frobenius. We also have the theorem that every ni = 1 if G is abelian. Both of these results are special cases of the following more general theorem, which is due to Schur.
THEOREM 5.13. ni|[G: Z], Z the center of G.
Proof. (Tate). Let m be a positive integer and let Gm = G × G × … × G, m times. Let ρi be an irreducible representation of G over ![]() affording the character χi, V the vector space on which ρi acts. We have the representation ρ of Gm acting in Vm = V
affording the character χi, V the vector space on which ρi acts. We have the representation ρ of Gm acting in Vm = V ![]() …
… ![]() V, m times, such that ρ(g1, …, gm) = ρi(g1)
V, m times, such that ρ(g1, …, gm) = ρi(g1) ![]() …
… ![]() ρi(gm) (see section 5.6). By iterating the result of Theorem 5.11, we see that ρ is irreducible. If c ∈ Z, the irreducibility of ρi implies that
ρi(gm) (see section 5.6). By iterating the result of Theorem 5.11, we see that ρ is irreducible. If c ∈ Z, the irreducibility of ρi implies that ![]() . Evidently γi is a homomorphism of Z into
. Evidently γi is a homomorphism of Z into ![]() *. By the definition of ρ we have
*. By the definition of ρ we have
![]()
and hence for cj ∈ Z,
![]()
It follows that the subset D of elements of Gm of the form (c1, c2, … ,cm), ci ∈ Z, ![]() is in the kernel of ρ. Evidently D is a normal subgroup of Gm and ρ defines a representation
is in the kernel of ρ. Evidently D is a normal subgroup of Gm and ρ defines a representation ![]() of Gm/D that is irreducible. We now apply Theorem 5.12 to
of Gm/D that is irreducible. We now apply Theorem 5.12 to ![]() to obtain
to obtain ![]() . This implies that
. This implies that ![]() and this holds for all m. Put u = |G|/ni|Z|. Then the relation shows that the
and this holds for all m. Put u = |G|/ni|Z|. Then the relation shows that the ![]() -submodule
-submodule ![]() Of
Of ![]() is contained in
is contained in ![]() |Z|–1. Since
|Z|–1. Since ![]() is noetherian, so is
is noetherian, so is ![]() |Z|–1 and hence so is M. Thus M is finitely generated as
|Z|–1 and hence so is M. Thus M is finitely generated as ![]() -module. Since 1 ∈ M and uM ⊂ M, it follows that u ∈
-module. Since 1 ∈ M and uM ⊂ M, it follows that u ∈ ![]() . This proves that (ni|Z|)||G|. Then ni[G : Z] as required.
. This proves that (ni|Z|)||G|. Then ni[G : Z] as required. ![]()
Let F be a subfield of ![]() . Then I ∩ F is a subring of F called the ring of algebraic integers of F. The study of the arithmetic of such rings constitutes the theory of algebraic numbers. We shall give an introduction to this theory in Chapter 10. Now suppose F is a splitting field for the finite group G. Then F[G] = Mn1(F)
. Then I ∩ F is a subring of F called the ring of algebraic integers of F. The study of the arithmetic of such rings constitutes the theory of algebraic numbers. We shall give an introduction to this theory in Chapter 10. Now suppose F is a splitting field for the finite group G. Then F[G] = Mn1(F)![]() …
… ![]() Mns(F) and s is the number of conjugacy classes of G (see p. 280). We have s inequivalent irreducible representations ρi over F and these remain irreducible on extension of F to
Mns(F) and s is the number of conjugacy classes of G (see p. 280). We have s inequivalent irreducible representations ρi over F and these remain irreducible on extension of F to ![]() . Thus {ρ1
. Thus {ρ1![]() , …, ρs
, …, ρs![]() } a set of representatives of the classes of the irreducible complex representations. If ρi acts on Vi/F, then to compute χρ1(g), g ∈ G, we choose a base for Vi/F and take the trace of the matrix of χρ1(g) relative to this base. Nothing is changed if we pass to
} a set of representatives of the classes of the irreducible complex representations. If ρi acts on Vi/F, then to compute χρ1(g), g ∈ G, we choose a base for Vi/F and take the trace of the matrix of χρ1(g) relative to this base. Nothing is changed if we pass to ![]() . Thus we see that χρι
. Thus we see that χρι![]() (g) = χρι(g). This shows that the irreducible complex characters have values in F. We know also that these values are contained in I. Since any character is an integral combination of irreducible characters, this gives the following
(g) = χρι(g). This shows that the irreducible complex characters have values in F. We know also that these values are contained in I. Since any character is an integral combination of irreducible characters, this gives the following
THEOREM 5.14. Let F be a subfield of ![]() that is a splitting field for the finite group G. Then any complex character of G has values that are integral algebraic numbers of F.
that is a splitting field for the finite group G. Then any complex character of G has values that are integral algebraic numbers of F.
In section 4, we showed that ![]() is a splitting field for Sn. Hence we have the
is a splitting field for Sn. Hence we have the
COROLLARY. The complex characters of Sn have values in ![]() .
.
5.8 BURNSIDE’S paqb THEOREM
One of the earliest applications of the theory of characters was to the proof of the following beautiful theorem due to Burnside.
THEOREM 5.15. If p and q are primes, then any group of order paqb is solvable.
Quite recently, John Thompson succeeded in giving a proof of this theorem that does not use representation theory. However, this is considerably more complicated than the original proof with characters, so the original proof—which we shall give here—remains a good illustration of the use of representation theory to obtain results on the structure of finite groups.
We prove first the following
LEMMA. Let χ be an irreducible complex character of a finite group G, ρ a representation affording χ. Suppose C is a conjugacy class of G such that (|C|, χ(l)) = 1. Then for any g ∈ C, either χ(g) = 0 or ρ(g) ∈ ![]() 1.
1.
Proof. Since (|C|, χ(1)) = 1, there exist integers l and m such that l|C| + mχ(l) = 1. Then
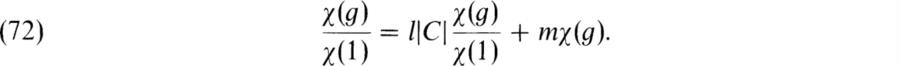
Now χ(g) is an algebraic integer, and by Proposition 5.4 (p. 283), ![]() , where n = deg ρ = χ(l), is an algebraic integer. Hence χ(g)/n is an algebraic integer. We recall also that χ(g) ≤ n and this was proved by showing that χ(g) is a sum of n roots of unity (p. 270). Thus χ(g) = ωl + … + ωn where the ωi ∈ W, a cyclotomic field of complex roots of unity (BAI, p. 252). Let H = Gal W/
, where n = deg ρ = χ(l), is an algebraic integer. Hence χ(g)/n is an algebraic integer. We recall also that χ(g) ≤ n and this was proved by showing that χ(g) is a sum of n roots of unity (p. 270). Thus χ(g) = ωl + … + ωn where the ωi ∈ W, a cyclotomic field of complex roots of unity (BAI, p. 252). Let H = Gal W/![]() . and let s ∈ H. Then s maps roots of unity into roots of unity. Hence sχ(g) is a sum of n roots of unity. Hence
. and let s ∈ H. Then s maps roots of unity into roots of unity. Hence sχ(g) is a sum of n roots of unity. Hence ![]() . It is clear that since a = χ(g)/χ(1) is an algebraic integer, so is sa = sχ(g)/χ(1) and |sa| ≤ 1. Then the norm
. It is clear that since a = χ(g)/χ(1) is an algebraic integer, so is sa = sχ(g)/χ(1) and |sa| ≤ 1. Then the norm ![]() satisfies |NW/
satisfies |NW/![]() (a)| ≤ 1. Since this is an algebraic integer and a rational number, it follows that |NW/
(a)| ≤ 1. Since this is an algebraic integer and a rational number, it follows that |NW/![]() (a)| ∈
(a)| ∈ ![]() +. Hence either NW/
+. Hence either NW/![]() (a) = 0, in which case a = 0 and χ(g) = 0, or |NW/
(a) = 0, in which case a = 0 and χ(g) = 0, or |NW/![]() (a)| = 1. In the latter case, |a| = 1, |χ(g)| = n, and Proposition 5.3 shows that ρ(g) = ωl, ω a root of unity.
(a)| = 1. In the latter case, |a| = 1, |χ(g)| = n, and Proposition 5.3 shows that ρ(g) = ωl, ω a root of unity. ![]()
We recall that the only abelian simple groups are the cyclic groups of prime order. Since this class of simple groups is rather trivial, one generally excludes it from the study of simple groups. We follow this convention in the following
THEOREM 5.16. Let G be a finite (non-abelian) simple group. Then no conjugacy class of G has cardinality of the form pa, p a prime, a > 0.
Proof. Suppose C is a conjugacy class of G such that |C| = pa, p prime, a > 0. Let ρ1, …, ρs be the irreducible representations of G, χ1, …, χs the corresponding characters. We assume ρ1 is the unit representation, so χ1(g) = 1 for all g. Let ni = χi(1), the degree of ρi. If ![]() then the foregoing lemma shows that either χi(g) = 0 or ρi(g) ∈
then the foregoing lemma shows that either χi(g) = 0 or ρi(g) ∈ ![]() l for every g ∈
l for every g ∈ ![]() . Now the elements g ∈ G such that ρi(g) ∈
. Now the elements g ∈ G such that ρi(g) ∈ ![]() l form a normal subgroup Gi of G. Hence if χi(g) ≠ 0 for some g ∈ C, then Gi ≠ 1. Then Gi = G since G is simple. Also since G is simple and ρi is not the unit representation for i > 1, it follows that G
l form a normal subgroup Gi of G. Hence if χi(g) ≠ 0 for some g ∈ C, then Gi ≠ 1. Then Gi = G since G is simple. Also since G is simple and ρi is not the unit representation for i > 1, it follows that G ![]() ρi(G) if i > 1. Since ρi(G) is abelian, this is excluded. Hence if
ρi(G) if i > 1. Since ρi(G) is abelian, this is excluded. Hence if ![]() and i > 1, then χi(g) = 0 for all g ∈ C. We now use the orthogonality relation (60), which gives
and i > 1, then χi(g) = 0 for all g ∈ C. We now use the orthogonality relation (60), which gives
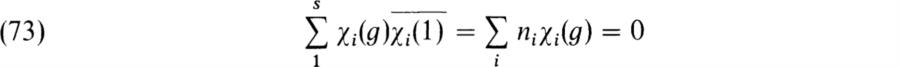
for g ∈ C. Since nl = 1 and χ1(g) = 1, we have some ni, i > 1, divisible by p. Let n2, …, nt be the ni, i > 1, divisible by p. Then (73) gives the relation

Since the nj are divisible by p and the χj(g) are algebraic integers, this implies that 1/p is an algebraic integer, contrary to the fact that the only rational numbers that are algebraic integers are the elements of ![]() .
. ![]()
We can now give the
Proof of Theorem 5.15. Let |G| = paqb where p and q are primes. Let P be a Sylow p-subgroup of G. Since P is of prime power order, its center Z ≠ 1. If z ≠ 1 is in Z, then the centralizer C(z) of z contains P, so [G : C(z)] is a power of q. Now [G:C(z)] is the cardinality of the conjugacy class C containing z (BAI, p. 75). Hence if [G:C(z)] > 1, then G is not simple non-abelian by Theorem 5.16. On the other hand, if [G: C(z)] = 1, then z is in the center of G. Then the center of G is not trivial, so again G is not simple non-abelian. It is now clear that unless G is cyclic of prime order, it contains a normal subgroup H ≠ 1, ≠G. Using induction on |G| we can conclude that H and G/H are solvable. Then G is solvable (BAI, p. 247). ![]()
5.9 INDUCED MODULES
Let G be a group, H a subgroup of finite index in G, σ a representation of H acting on the vector space U/F. There is an important process, introduced by Frobenius, for “extending” σ to a representation σG of G. We recall that we have an action of G on the set G/H of left cosets of H in G. If G/H = {H1 = H, H2, …, Hr} and g ∈ G, then gHi = Hπ(g)i and π(g) is a permutation of {l, …, r}. The map π : g ![]() π(g) is a homomorphism of G into the symmetric group Sr (BAI, p. 72). Now put UG ≡ U(r), the direct sum of r copies of U. Let {s1, s2, …, sr} be a set of representatives of the left cosets of H, say, Hi = siH, 1 ≤ i ≤ r. From now on we shall call such a set a (left) cross section of G relative to H. If g ∈ G, then
π(g) is a homomorphism of G into the symmetric group Sr (BAI, p. 72). Now put UG ≡ U(r), the direct sum of r copies of U. Let {s1, s2, …, sr} be a set of representatives of the left cosets of H, say, Hi = siH, 1 ≤ i ≤ r. From now on we shall call such a set a (left) cross section of G relative to H. If g ∈ G, then
![]()
where μi(g) ∈ H. We can define an action of G on UG = U(r) by
![]()
where the uj ∈ U. Using the fact that π is a homomorphism,and that H acts on U, we can verify that (75) does indeed define an action of G on UG. Since this action is by linear transformations in a finite dimensional vector space, we have a representation σG of G acting on UG. We can verify also that another choice of cross section of G relative to H defines an equivalent representation. All of this will become apparent without calculations by giving an alternative, conceptual definition of σG, as we shall now do.
Let B = F[H] the group algebra of H, and A = F[G], the group algebra of G. To be given a representation σ of H amounts to being given a module U for B that is finite dimensional as vector space over F. Now B is a subalgebra of A and hence A is a B-B-bimodule in which the actions of B on A are left and right multiplications by elements of B. We can form A ![]() B U, which is a left ,A-module in which for a1, a2 ∈ A and u ∈ U we have
B U, which is a left ,A-module in which for a1, a2 ∈ A and u ∈ U we have
![]()
We shall now show that [A ![]() B U : F] < ∞, so the A = F[G]-module A
B U : F] < ∞, so the A = F[G]-module A ![]() B U defines a representation of G. Moreover, we shall see that this representation is equivalent to σG as defined above.
B U defines a representation of G. Moreover, we shall see that this representation is equivalent to σG as defined above.
As before, let {sl, s2, …, sr} be a cross section of G with respect to H. Then any element of G can be written in one and only one way in the form sih, h ∈ H. Since the elements of G form a base for A, it follows that A regarded as right B-module is free with (sl, …, sr) as base. It follows that every element of A ![]() B U can be written in one and only one way in the form
B U can be written in one and only one way in the form
![]()
ui ∈ U. Hence if (u(1), …, u(n)) is a base for U/F, then
![]()
is a base for A ![]() B U, so [A
B U, so [A ![]() B U : F] = rn < ∞. Thus the module A
B U : F] = rn < ∞. Thus the module A ![]() B U defines a representation of G.
B U defines a representation of G.
Now let g ∈ G. Then, by (76) and (74), we have
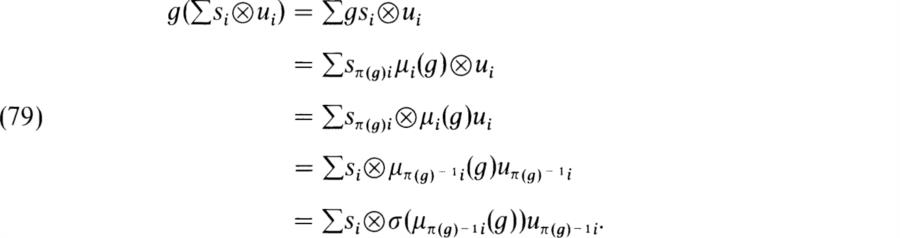
Comparison of this with (75) shows that the map ![]() is an equivalence of the induced representation of G as defined first with the representative of G provided by A
is an equivalence of the induced representation of G as defined first with the representative of G provided by A ![]() BU.
BU.
The module UG (or A ![]() BU) is called the induced G-module U and the associated representation σG is called the induced representation of G. As we have seen, if (u(1), …, u(n)) is a base for U/F, then (78) is a base for the induced module. Now suppose
BU) is called the induced G-module U and the associated representation σG is called the induced representation of G. As we have seen, if (u(1), …, u(n)) is a base for U/F, then (78) is a base for the induced module. Now suppose
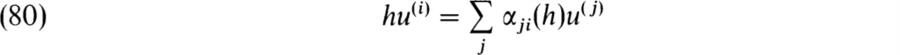
for h ∈ H, so h ![]() α(h) = (αij(h)) is a matrix representation of H determined by σ and
α(h) = (αij(h)) is a matrix representation of H determined by σ and
![]()
is the character of σ. By (79), the matrix of σG(g) relative to the base (78) is obtained by applying the permutation π(g) to the r rows of n × n blocks in the matrix
![]()
Only the non-zero diagonal blocks of the matrix thus obtained contribute to the trace. These blocks occur in the ith row (of blocks) if and only if π(g)i = i, which is equivalent to gsiH = siH and to si–1 gsi ∈ H.It follows that the character
![]()
where the summation Σ' is taken over all i such that si–1 gsi ∈ H. This can be put in a better form by extending the definition of the function χσ from H to F to a function ![]() on G defined by
on G defined by ![]() = 0 if g ∈ G – H. Using this, we obtain the formula
= 0 if g ∈ G – H. Using this, we obtain the formula
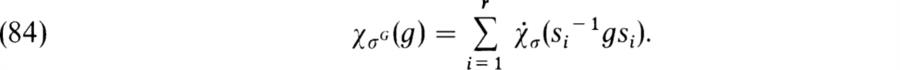
This can be written in another form if G is a finite group, by noting that ![]() . This is clear if g ∈ H since χσ is a class function and if
. This is clear if g ∈ H since χσ is a class function and if ![]() , then
, then ![]() . Hence
. Hence
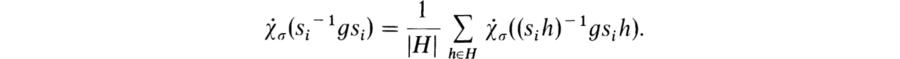
Then (84) gives the formula

EXAMPLES
1. Let G be the dihedral group Dn of order 2n generated by r, s, such that rn = 1, s2 = 1, srs–1 = r–1. Let H = ![]() , σ a representation of degree 1 of H such that r
, σ a representation of degree 1 of H such that r ![]() ω1 where ωn = 1. We may take S1 = 1, s2 = s as representatives of the cosets of H. Then π(r) = 1, π(s) = (12), and
ω1 where ωn = 1. We may take S1 = 1, s2 = s as representatives of the cosets of H. Then π(r) = 1, π(s) = (12), and
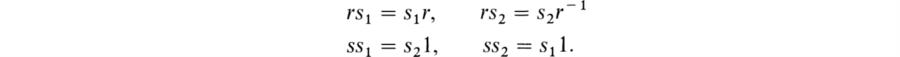
It follows that a matrix representation determined by σG maps
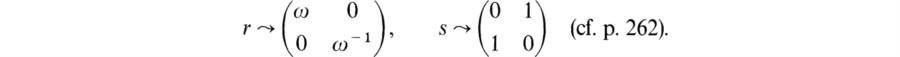
2. Let G be as in example 1, but now let H = ![]() . Let σ be the representation of degree 1 such that s
. Let σ be the representation of degree 1 such that s ![]() –1. We have
–1. We have ![]() , so we may take {si} where si = ri – 1, 1 ≤ i ≤ n, as a set of coset representatives. We have
, so we may take {si} where si = ri – 1, 1 ≤ i ≤ n, as a set of coset representatives. We have

It follows that we have a matrix representation determined by σG such that
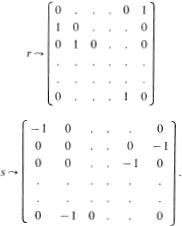
3. An interesting special case of induction is obtained by beginning with the unit representation 1 = 1H of the subgroup H acting on a one-dimensional space U1 = Fu. Let {s1, …, sr} be a cross section of G relative to H and suppose ![]() where μi(g) ∈ H. The set of elements si
where μi(g) ∈ H. The set of elements si ![]() u, 1 ≤ i ≤ r, is a base for U1G and, by definition of the induced representation, the action of g on U1G is given by
u, 1 ≤ i ≤ r, is a base for U1G and, by definition of the induced representation, the action of g on U1G is given by ![]() . On the other hand, we have the action of G on the set G/H of left cosets {siH|l ≤ i ≤ r} given by
. On the other hand, we have the action of G on the set G/H of left cosets {siH|l ≤ i ≤ r} given by ![]() . It is clear from this that 1G is the permutation representation obtained from the action of G on G/H.
. It is clear from this that 1G is the permutation representation obtained from the action of G on G/H.
We can determine the character χ1G for the representation 1G. It is clear from the formula ![]() that the trace of the matrix of 1G(g) relative to the base (S1
that the trace of the matrix of 1G(g) relative to the base (S1![]() u, …, sn
u, …, sn![]() u) is the number of fixed points of π(g). This is the number of cosets aH such that g(aH) = aH. Hence we have the formula
u) is the number of fixed points of π(g). This is the number of cosets aH such that g(aH) = aH. Hence we have the formula
![]()
We note also that the condition gaH = aH is equivalent to a–lg = a–1ga ∈ H.
We recall that the action of G in G/H is transitive and any transitive action of G on a finite set N = {1, 2, …} is equivalent to the action of G on a set of left cosets relative to a subgroup H of index n in G (BAI, p. 75). In fact, if G acts transitively on N, then we can take H to be the stabilizer of any element of N. It is clear from this that the study of induced representations of the form 1HG, where 1H is the unit representation of a subgroup H of finite index in G, is essentially the same thing as the study of transitive actions of G on finite sets.
We shall now give two useful characterizations of induced modules in the general case in which H is a subgroup of G of finite index in G, U a module for H. Let A = F[G], B = F[H], {s1, …, sr} a cross section of G relative to H, and consider the induced module UG of G. We have UG = A ![]() BU =
BU = ![]() (si
(si![]() U) and [si
U) and [si ![]() U: F] = [U: F] = n. Hence the map x
U: F] = [U: F] = n. Hence the map x ![]() si
si ![]() x of U into si
x of U into si ![]() U is a linear isomorphism. Since we may take one of the si = 1, we see that the map x
U is a linear isomorphism. Since we may take one of the si = 1, we see that the map x ![]() 1
1 ![]() x is a linear isomorphism of U onto the subspace 1
x is a linear isomorphism of U onto the subspace 1 ![]() U = {1
U = {1 ![]() ) x|x ∈ U] of UG. If b ∈ B, then b( 1
) x|x ∈ U] of UG. If b ∈ B, then b( 1 ![]() x) = b
x) = b ![]() x = bl
x = bl ![]() x = 1
x = 1 ![]() bx. Hence x
bx. Hence x ![]() 1
1 ![]() x is a B-isomorphism of U onto 1
x is a B-isomorphism of U onto 1 ![]() U, which is a B-submodule of UG. We shall now identify U with its image 1
U, which is a B-submodule of UG. We shall now identify U with its image 1 ![]() U and so regard U as a B-submodule of UG. It is clear also that we have UG = s1U
U and so regard U as a B-submodule of UG. It is clear also that we have UG = s1U ![]() …
… ![]() srU, a direct sum of the subspaces siU. The properties we have noted give a useful internal characterization of UG that we state as
srU, a direct sum of the subspaces siU. The properties we have noted give a useful internal characterization of UG that we state as
PROPOSITION 5.5. Let V be an A-module. Then V is isomorphic to UG for some B-module U if and only if V contains U (strictly speaking a B-submodule isomorphic to U) such that V = s1U ![]() …
… ![]() srU for some cross section {s1, …, sr} of G relative to H.
srU for some cross section {s1, …, sr} of G relative to H.
Proof. We have shown that UG has the stated properties for the B-submodule U ( = 1 ![]() U) and any cross section of G relative to H. Conversely, let V be an A-module having the stated properties. Then V = AU. Since si ∈ G, si is invertible in A and hence the map x
U) and any cross section of G relative to H. Conversely, let V be an A-module having the stated properties. Then V = AU. Since si ∈ G, si is invertible in A and hence the map x ![]() six is a bijection. It follows that [siU : F] = [U : F] and since
six is a bijection. It follows that [siU : F] = [U : F] and since ![]() . We have the map (a, x)
. We have the map (a, x) ![]() ax of A × U into V, which is F-bilinear. Since (ab)x = a(bx) for b ∈ B, it follows that we have an F-linear map η of A
ax of A × U into V, which is F-bilinear. Since (ab)x = a(bx) for b ∈ B, it follows that we have an F-linear map η of A ![]() BU into V such that η(a
BU into V such that η(a ![]() x) = ax. Evidently, η is an A-homomorphism. Since V = AU, η is surjective and since [V : F] = [A
x) = ax. Evidently, η is an A-homomorphism. Since V = AU, η is surjective and since [V : F] = [A ![]() BU : F] < ∞, η is injective. Hence V and UG are isomorphic, A-modules.
BU : F] < ∞, η is injective. Hence V and UG are isomorphic, A-modules. ![]()
The second characterization of UG that we shall give is a categorical one that applies to any ring A and subring B. We consider the categories of modules A-mod and B-mod. If M is an A-module, we can regard M as B-module. Evidently, homomorphisms of A-modules are homomorphisms of B-modules. In this way we obtain a functor R from the category A-mod to B-mod sending an A-module M into M regarded as B-module and A-homo-morphisms into the same maps regarded as B-homomorphisms. We call R the restriction of scalars functor from A-mod to B-mod. Now let N be a given B-module. Then we can form A ![]() BN and regard this as an A-module in the usual way. We have a B-homomorphism u of N into A
BN and regard this as an A-module in the usual way. We have a B-homomorphism u of N into A ![]() BN sending y ∈ N into 1
BN sending y ∈ N into 1 ![]() y. We claim that the pair (A
y. We claim that the pair (A ![]() N, u) constitutes a universal from N to the functor R (p. 42). This means that if M is a (left) A-module and η is a B-homomorphism of N into RM = M, then there exists a unique homomorphism
N, u) constitutes a universal from N to the functor R (p. 42). This means that if M is a (left) A-module and η is a B-homomorphism of N into RM = M, then there exists a unique homomorphism ![]() of A
of A ![]() BN into M (as A-module) such that
BN into M (as A-module) such that

is commutative. To see this, we consider the map (a, y) ![]() a(ηy) of the product set A × N into M. Evidently this is additive in a and y and if b ∈ B, then (ab)(ηy) = a(b(ηy)) = a(η(by)). Hence (a, y)
a(ηy) of the product set A × N into M. Evidently this is additive in a and y and if b ∈ B, then (ab)(ηy) = a(b(ηy)) = a(η(by)). Hence (a, y) ![]() a(ηy) defines a balanced product from A × N into M (p. 126). Hence we have a group homomorphism
a(ηy) defines a balanced product from A × N into M (p. 126). Hence we have a group homomorphism ![]() of A
of A ![]() N into M such that
N into M such that ![]() . It is clear that
. It is clear that ![]() is a homomorphism of A-modules and if y ∈ N, then
is a homomorphism of A-modules and if y ∈ N, then ![]() . Hence (87) is commutative. Now let η' be any A-homomorphism of A
. Hence (87) is commutative. Now let η' be any A-homomorphism of A ![]() BN into M such that ηy = η'uy = η'(l
BN into M such that ηy = η'uy = η'(l ![]() y). Then η′(a
y). Then η′(a ![]() y) = η′(a(l
y) = η′(a(l ![]() y)) = aη'(l
y)) = aη'(l ![]() y) = a(ηy). Hence
y) = a(ηy). Hence ![]() , so
, so ![]() is unique.
is unique.
The fact that for any B-module N, (A ![]() BN, u) is a universal from N to the functor R implies that we have a functor from B-mod to A-mod sending any B-module N into the A-module A
BN, u) is a universal from N to the functor R implies that we have a functor from B-mod to A-mod sending any B-module N into the A-module A ![]() BN and mapping any homomorphism η of B-modules into 1
BN and mapping any homomorphism η of B-modules into 1 ![]() η, which is a homomorphism of A-modules. This functor is a left adjoint of the functor R (p. 49).
η, which is a homomorphism of A-modules. This functor is a left adjoint of the functor R (p. 49).
This is applicable in particular to A = F[G] and B = F[H] where H is a subgroup of finite index in G. In this case for a given B-module U such that [U : F] < ∞, we obtain the universal object UG = A ![]() BU, which is finite dimensional over F and hence provides a representation of G.
BU, which is finite dimensional over F and hence provides a representation of G.
EXERCISE
1. Let G be a finite group, H a subgroup, and let σ be the regular representation of H. Show that σG is the regular representation of G.
5.10 PROPERTIES OF INDUCTION. FROBENIUS RECIPROCITY THEOREM
We shall now derive the basic properties of induced representations. We prove first
THEOREM 5.17. Let K be a subgroup of finite index in G, H a subgroup of finite index in K, σ a representation of H acting on U, ρ a representation of G acting on V, ρH the restriction of ρ to H. Then
(1) H is of finite index in G and σG and (σK)G are equivalent.
(2) If W is a σ(H)-invariant subspace of U, then WG is a σG(G)-invariant subspace of UG. Moreover, if U = Wl ![]() W2 where Wi is σ-invariant, then UG = W1G
W2 where Wi is σ-invariant, then UG = W1G ![]() W2G.
W2G.
(3) σG ![]() ρ and (σ
ρ and (σ ![]() ρH)G are equivalent.
ρH)G are equivalent.
Proof. (1) Write A = F[G], B = F[H], C = F[K]. It is clear that H is of finite index in G. (In fact, [G : H] = [G : K] [K : H].) Now σK acts on ![]() acts on
acts on ![]() , and σG acts on A
, and σG acts on A ![]() BU. The A-modules
BU. The A-modules ![]() and
and ![]() are isomorphic (Proposition 3.7, p. 135) and A
are isomorphic (Proposition 3.7, p. 135) and A ![]() CC and A are isomorphic as left A-modules (Proposition 3.2, p. 130). Hence
CC and A are isomorphic as left A-modules (Proposition 3.2, p. 130). Hence ![]() and A
and A ![]() BU are isomorphic as A-modules, which means that (σK)G and σG are equivalent.
BU are isomorphic as A-modules, which means that (σK)G and σG are equivalent.
(2) If W is σ(H)-invariant subspace of U, then this is a B-submodule of U. Since A is free as right module over B, WG = A ![]() BW can be identified with its image in UG = A
BW can be identified with its image in UG = A ![]() BU. Then (σ|W)G is a subrepresentation of σG. The second statement follows in the same way.
BU. Then (σ|W)G is a subrepresentation of σG. The second statement follows in the same way.
(3) The two A-modules we have to consider are ![]() and
and ![]() . In the first case the action of g ∈ G is
. In the first case the action of g ∈ G is ![]() and in the second case we have
and in the second case we have ![]() . Hence the F-isomorphism of
. Hence the F-isomorphism of ![]() onto
onto ![]() sending
sending ![]() is not an A-isomorphism. We shall define an A-isomorphism of
is not an A-isomorphism. We shall define an A-isomorphism of ![]() onto
onto ![]() such that
such that ![]() and hence
and hence ![]() . For a fixed g ∈ G we consider the map
. For a fixed g ∈ G we consider the map ![]() into
into ![]() . Since this is F-bilinear, we have an F-homomorphism τg of U
. Since this is F-bilinear, we have an F-homomorphism τg of U ![]() F V into
F V into ![]() such that
such that ![]() . Since G is a base for A/F, for any
. Since G is a base for A/F, for any ![]() we can define an F-homomorphism τa of U
we can define an F-homomorphism τa of U ![]() FV into
FV into ![]() by
by ![]() . Then
. Then ![]() . We now have a map
. We now have a map
![]()
of A × (U ![]() FV) into
FV) into ![]() , which is F-bilinear. Moreover, if h ∈ H, then
, which is F-bilinear. Moreover, if h ∈ H, then
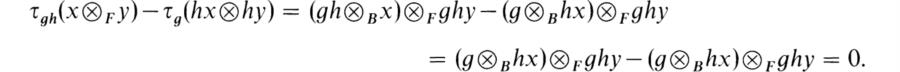
It follows that we have a balanced product of A as right B-module and U ![]() FV as left B-module. Hence we have a homomorphism of
FV as left B-module. Hence we have a homomorphism of ![]() into
into ![]() sending
sending ![]() . This is an F-homomorphism and if g' ∈ G, then
. This is an F-homomorphism and if g' ∈ G, then ![]() and
and ![]() . Hence our map is an A-homomorphism. It is clear also that the map is surjective and since the two modules have the same dimensionality over F, the map is an isomorphism.
. Hence our map is an A-homomorphism. It is clear also that the map is surjective and since the two modules have the same dimensionality over F, the map is an isomorphism. ![]()
For our next result on contragredience and induction we shall make use of an involution in the group algebra (BAI, p. 112). We note first that if g, h ∈ G, then (gh)– 1 = h– 1 g– 1 and (g– 1)– 1 = g. Hence if ![]() is the linear transformation of A = F[G] into itself such that
is the linear transformation of A = F[G] into itself such that ![]() , then
, then ![]() and
and ![]() . Thus
. Thus ![]() is an involution in A. We shall call this the main involution of A and denote it as j. If H is a subgroup of G, then the main involution in B = F[H] is the restriction to B of the main involution in A. Now let H have finite index and let {sl, …, sr} be a cross section. Any element of A can be written in one and only one way as
is an involution in A. We shall call this the main involution of A and denote it as j. If H is a subgroup of G, then the main involution in B = F[H] is the restriction to B of the main involution in A. Now let H have finite index and let {sl, …, sr} be a cross section. Any element of A can be written in one and only one way as ![]() , we define
, we define
![]()
and we have the map (a, c) ![]() (a|c) of A × A into B. We list its important properties:
(a|c) of A × A into B. We list its important properties:
(i) (a|c) is independent of the choice of the representatives si, since any other choice has the form Sihi, hi ∈ H. Using these replaces bi by hi– 1bi, ci, by hi– lci. Then ![]() and (88) is unchanged.
and (88) is unchanged.
(ii) (a|c) is F-bilinear. Clear.
(iii) If b ∈ B, then
![]()
This is clear from the definition.
(iv) If e ∈ A, then
![]()
It suffices to prove this for e = g ∈ G. Then ![]() where π(g) ∈ Sr and μi(g) ∈ H. Then
where π(g) ∈ Sr and μi(g) ∈ H. Then ![]() and
and ![]() , so
, so ![]() . Hence
. Hence
Thus (ga|c) = (a|g– 1c) holds for all g ∈ G.
(v) (si|sj) = δijl.
This is clear from the definition.
We shall now establish commutativity of induction and contragredience. This is given in
THEOREM 5.18 If H is a subgroup of finite index and o is a representation of H, then (σG)* and (σ*)G are equivalent.
Proof. Let U be the vector space on which σ acts and let U* be the dual space of linear functions on U. lf x ∈ U and y* ∈ U*, we write ![]() . Then
. Then ![]() is F-bilinear. The space U* is a left B-module defined by the contragredient representation σ* of H and we can make this a right B-module by defining
is F-bilinear. The space U* is a left B-module defined by the contragredient representation σ* of H and we can make this a right B-module by defining ![]() , b ∈ B. Since
, b ∈ B. Since ![]() for h ∈ H, by definition of σ*, we have
for h ∈ H, by definition of σ*, we have ![]() , which implies that
, which implies that
![]()
for x ∈ U, y* ∈ U*, b ∈ B. We now introduce
![]()
This is defined for x ∈ U, a, c ∈ A, y* ∈ U*, and is F-bilinear in c and x for fixed a and y*. Moreover, if b ∈ B, then by property (iii) above,
![]()
By definition of the tensor product, this implies that we have an F-linear map of A ![]() BU into F sending
BU into F sending ![]() . Thus we have an element φa, y* of the dual space (A
. Thus we have an element φa, y* of the dual space (A ![]() BU)* such that
BU)* such that
![]()
Now the map (a, y*) ![]() φa, y* is F-bilinear and since
φa, y* is F-bilinear and since
![]()
φab, y* = φa, by*. Hence we have a linear map η of A![]() BU* into (A
BU* into (A![]() BU)* sending a
BU)* sending a![]() y* into φa, y*. If g ∈ G,
y* into φa, y*. If g ∈ G, ![]() . On the other hand,
. On the other hand, ![]() . Hence by (iv),
. Hence by (iv), ![]() , which implies that η is an A-homomorphism. To conclude the proof, we shall show that η is injective. Since A
, which implies that η is an A-homomorphism. To conclude the proof, we shall show that η is injective. Since A![]() BU* and (A
BU* and (A![]() BU)* have the same finite dimensionality over F, this will imply that η is an isomorphism. Now suppose
BU)* have the same finite dimensionality over F, this will imply that η is an isomorphism. Now suppose ![]() . We can write
. We can write ![]() and the condition
and the condition ![]() implies that
implies that ![]() for all c ∈ A, x ∈ U and hence
for all c ∈ A, x ∈ U and hence ![]() for all c. If we take c = Sj and use (v), we obtain zj* = 0 and hence
for all c. If we take c = Sj and use (v), we obtain zj* = 0 and hence ![]() . This concludes the proof.
. This concludes the proof. ![]()
Our next main objective is to derive an important reciprocity theorem due to Frobenius, which in its original form states that if ρ is an irreducible complex representation of a finite group and σ is an irreducible complex representation of a subgroup H, then the multiplicity of ρ in σG is the same as the multiplicity of σ in the representation ρH of H. As we shall show below, this can be proved by a simple calculation with characters. We shall first give a conceptual proof of an extension of Frobenius’ theorem. Our proof will be based on the important concept of intertwining numbers for representations and on the following proposition.
PROPOSITION 5.6. If H is a subgroup of finite index in G, U a module for B = F[H], and V a module for A = F[G], then homA(UG, V) and homB(U, VH) are isomorphic as vector spaces over F.
Proof. We remark that this result can be deduced from a general result on adjoint functors applied to the restriction functor from F[G]-mod to F[H]-mod and its left adjoint. However, we shall give an independent proof. As before, let u be the map of U into UG sending x ![]() l
l ![]() x. This is a B-homomorphism. Hence if ζ ∈ homA(UG, V), then ζu ∈ homB(U, VH). The map ζ
x. This is a B-homomorphism. Hence if ζ ∈ homA(UG, V), then ζu ∈ homB(U, VH). The map ζ ![]() ζu is an F-linear map of hom A(UG, V) into homB(U, VH). The result we proved in diagram (87) is that the map ζ
ζu is an F-linear map of hom A(UG, V) into homB(U, VH). The result we proved in diagram (87) is that the map ζ ![]() ζu is surjective. It is also injective. For, if ζu = 0, then ζ (l
ζu is surjective. It is also injective. For, if ζu = 0, then ζ (l![]() x) = 0 for all x ∈ U. Since ζ is an A-homomorphism, ζ(a
x) = 0 for all x ∈ U. Since ζ is an A-homomorphism, ζ(a![]() x) = ζ(a(l
x) = ζ(a(l![]() x)) = aζ(l
x)) = aζ(l![]() x) = 0 for all a ∈ A, x ∈ U. Hence ζ = 0. Thus ζ
x) = 0 for all a ∈ A, x ∈ U. Hence ζ = 0. Thus ζ ![]() ζu is an isomorphism of homA(UG, V) and homB(U, VH) as vector spaces over F.
ζu is an isomorphism of homA(UG, V) and homB(U, VH) as vector spaces over F. ![]()
If ρ and τ are representations of G acting on F and W respectively, then the dimensionality
![]()
is called the intertwining number l(ρ, τ) of ρ and τ(or of V and W as F[G]-modules). If V = V1![]() …
… ![]() Vm where the Vi are ρ(G)-invariant subspaces, then we write ρ = ρ1
Vm where the Vi are ρ(G)-invariant subspaces, then we write ρ = ρ1 ![]() …
… ![]() ρm where ρi = ρ|Vi. Similarly, let τ = τ1
ρm where ρi = ρ|Vi. Similarly, let τ = τ1 ![]() …
… ![]() τl where τj = τ|Wj and Wj is τ-invariant. We have the vector space decomposition
τl where τj = τ|Wj and Wj is τ-invariant. We have the vector space decomposition
![]()
This implies that
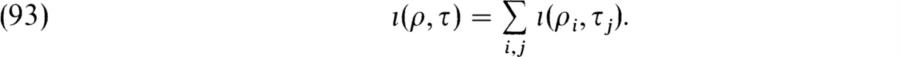
If ρ and τ are completely reducible and the ρl and τj are irreducible, then this formula reduces the calculation of l(ρ, τ) to that of the l(ρi, τj) where ρi and τi are irreducible. If ρ and τ are irreducible and inequivalent, then l(ρ, τ) = 0 by Schur’s lemma. It is clear also that l(ρ, τ) is unchanged if we replace ρ or τ by an equivalent representation. Hence if ρ and τ are equivalent, then l(ρ, τ) = l(ρ, ρ) = [EndA(V, V):F]. Hence if ρ and τ are irreducible and F is algebraically closed, then
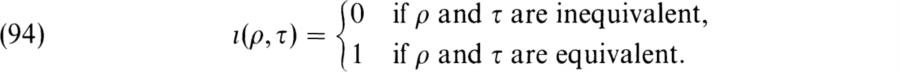
An immediate consequence of (93) and (94) is
PROPOSITION 5.7. If F is algebraically closed, ρ is irreducible, and τ is completely reducible, then l(ρ, τ) = l(τ, ρ) = multiplicity of ρ in τ (that is, the number of irreducible components of τ isomorphic to ρ).
We can now prove the fundamental
FROBENIUS RECIPROCITY THEOREM. Let F be an algebraically closed field, ρ an irreducible representation of G over F, σ an irreducible representation of a subgroup H of finite index in G. Assume that σG and ρH are completely reducible. Then the multiplicity of ρ in σG is the same as the multiplicity of a in ρH.
Proof. By Proposition 5.6, l(σG, ρ) = l(σ, ρH). By Proposition 5.7, l(σG, ρ) is the multiplicity of ρ in σG and i(σ, ρH) is the multiplicity of σ in ρH. Hence these multiplicities coincide. ![]()
The Frobenius reciprocity theorem is usually stated for finite groups and algebraically closed fields whose characteristics do not divide the group order. In this situation the hypothesis that H is of finite index and that σG and ρH are completely reducible is automatically satisfied. The proof of this result and some of the others we gave on induced representations of finite groups can be made by calculations with characters. As an illustration of this method, we shall now prove the Frobenius reciprocity theorem for G finite and F = ![]() by using characters. Let the notation be as above and let χρ, χσ,etc. denote the characters of ρ, σ, etc. We recall that if ρ is irreducible and τ is arbitrary, then (χρ|χτ) = (χτ|χρ) is the multiplicity of ρ in τ. The Frobenius reciprocity theorem is equivalent to
by using characters. Let the notation be as above and let χρ, χσ,etc. denote the characters of ρ, σ, etc. We recall that if ρ is irreducible and τ is arbitrary, then (χρ|χτ) = (χτ|χρ) is the multiplicity of ρ in τ. The Frobenius reciprocity theorem is equivalent to
![]()
We use the formula (85) for χσG Then we obtain
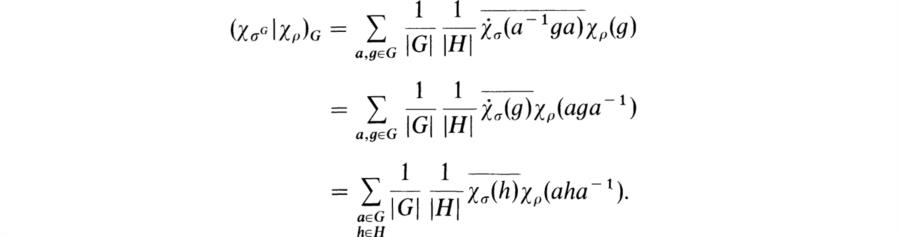
On the other hand,
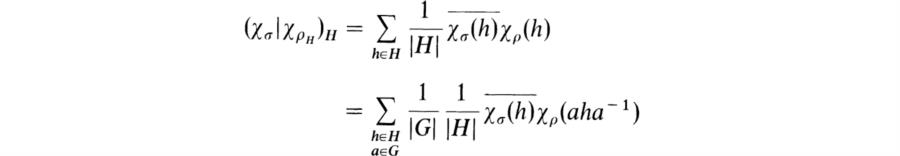
since χρ is a class function on G. Comparison of the two formulas gives (95).
1. Construct a character table for G = A5. Sketch: There are five conjugacy classes in G with representatives 1, (12) (34), (123), (12345), (13524) = (12345)2 with respective cardinalities 1, 15, 20, 12, 12. Let χ1 be the character of the unit representation, v the permutation representation obtained from the natural action of G on {1, 2, 3, 4,5}. We have the following table

Calculation of (χv|χv) and (χv|χ1) gives χv = χ1 + χ2 where χ2 is irreducible. This and the above table give χ2. To obtain the three missing irreducible characters, we look at the induced characters obtained from linear (degree 1) characters of the subgroup
We find that ![]() has index two in H, so we have the linear characters λ1 and λ2 on H where λ1 ≡ 1 and
has index two in H, so we have the linear characters λ1 and λ2 on H where λ1 ≡ 1 and ![]() . The set
. The set
![]()
is a cross section of G relative to H. Using this we can compute λ1G and λ2G as

Using (λiG|λiG), i = 1, 2, and (λ1G|χ1), we obtain λ1 = χ1 + χ3 where χ3 is irreducible. Also we have ![]() , which implies that λ2G = χ4 + χ5 where χ4 and χ5 are irreducible. The values of χi(l), 1 ≤ i ≤ 3, and
, which implies that λ2G = χ4 + χ5 where χ4 and χ5 are irreducible. The values of χi(l), 1 ≤ i ≤ 3, and ![]() give χ4 = 3 = χ5(1). It follows that we have the table
give χ4 = 3 = χ5(1). It follows that we have the table

Since (54321) = (12345)– 1 is conjugate to (12345), χ4 and χ5 are real (exercise 7, p. 279). Using χ4 + χ5 = λ2G, we obtain a + a' = – 2, b + b' = 0, c + c' = 1 = d + d'. Using (χ4|χi) = δi4 for i = 1, 2, 3, 4, we obtain a system of equations for a, b, c, d whose solutions are a = – 1, b = 0, c = (1 ± ![]() )/2, d = 1 – c. Either determination can be used to complete the table.
)/2, d = 1 – c. Either determination can be used to complete the table.
2. Prove Theorems 5.17 and 5.18 for complex representations of finite groups by character calculations.
3. Let B be a subring of a ring A, M a (left) B-module. Then homB(A, M) becomes a left A-module if we define (af)x = f(xa) for f ∈ homB(A, M), a, x ∈ A (Proposition 3.4, p. 134). This is called the produced module of A determined by M. Note that the map v: f ![]() f1 of homB(A, M) into M is a B-homomorphism. Show that the pair (homB(A, M), v) constitutes a universal from the restriction of scalars functor R to M (p. 137).
f1 of homB(A, M) into M is a B-homomorphism. Show that the pair (homB(A, M), v) constitutes a universal from the restriction of scalars functor R to M (p. 137).
4. Let G be a group, H a subgroup of finite index, A = F[G], B = F[H], and let U be the B-module determined by a representation σ of H. Then homB(A, U) is finite dimensional over F and defines the produced representation Gσ of G. Show that G(σ*) is equivalent to (σG)*. (This shows that in the theory of finite dimensional representations, produced modules are superfluous.)
5. Let G be finite, and let F be an algebraically closed field whose characteristic does not divide |G|. Let ρ be the permutation representation of G determined by the action of G on G/H where H is a subgroup. Use Frobenius reciprocity to show that the dimensionality of the space Inv ρ = {x|gx = x, g ∈ G} is one.
6. (Addendum to Clifford’s theorem.) Let ρ be an irreducible representation of G acting on V/F and let ![]() . Let W be a homogeneous component of V as F[H]-module. (Recall that ρH is completely reducible by Clifford’s theorem.) Let T be the subgroup of G stabilizing W. Show that (i) H ⊂ T ⊂ G and [G: T] = m, the number of homogeneous components of V as F[H]-module, and (ii) if ψ is the representation of T acting on W, then ρ = ψG and ψ is irreducible.
. Let W be a homogeneous component of V as F[H]-module. (Recall that ρH is completely reducible by Clifford’s theorem.) Let T be the subgroup of G stabilizing W. Show that (i) H ⊂ T ⊂ G and [G: T] = m, the number of homogeneous components of V as F[H]-module, and (ii) if ψ is the representation of T acting on W, then ρ = ψG and ψ is irreducible.
7. (Mackey.) Let H be a subgroup of finite index in G and let U be an F[H]-module. Let V be the set of maps f:G → U such that f(hg) = hf(g). Using the usual vector space structure on V and an action of G defined by (gf) (x) = f(xg), f ∈ V, g, x ∈ G. Show that V becomes an F[G]-module isomorphic to UG.
5.11 FURTHER RESULTS ON INDUCED MODULES
One of the main problems that we shall consider in this section is that of obtaining useable criteria for an induced representation (or character) to be irreducible. To this end we shall need to study the following problem: Suppose that H and K are subgroups of a group G, H of finite index in G, and σ is a representation of H acting on the vector space U/F. What can be said about the structure of σGK = (σG)K, the restriction to K of the induced representation of σG of G? If V is an F[G]-module, we denote V regarded as an F[K]-module by VK. Thus we are interested in the structure of UGK ≡ (UG)K. We identify U with the F[H]-submodule 1![]() U of UG. If g ∈ G, then gU is stabilized by the action of the subgroup gH = {ghg– 1|h ∈ H} since if x ∈ U, then [ghg– l)gx = ghx ∈ gU. Hence we have the submodules (gU)gH and (gU)K ∩ gH of UGgH and UGK ∩ gH respectively. We remark that since gH is of finite index in G, K ∩ gH is of finite index in K. Hence we can form the induced F[K]-module
U of UG. If g ∈ G, then gU is stabilized by the action of the subgroup gH = {ghg– 1|h ∈ H} since if x ∈ U, then [ghg– l)gx = ghx ∈ gU. Hence we have the submodules (gU)gH and (gU)K ∩ gH of UGgH and UGK ∩ gH respectively. We remark that since gH is of finite index in G, K ∩ gH is of finite index in K. Hence we can form the induced F[K]-module ![]() . We shall obtain a decomposition of UGK into submodules of the form
. We shall obtain a decomposition of UGK into submodules of the form ![]() . To describe this, we require some simple remarks on double cosets.
. To describe this, we require some simple remarks on double cosets.
We recall that G is a disjoint union of the double cosets KgH (BAI,p. 53). Moreover, KgH is a union of left cosets kgH, k ∈ K, and since H is of finite index in G, the number of left cosets of H contained in KgH is finite. We now note that if k1, k2 ∈ K, then k1gH = k2gH if and only if k1(K ∩ gH) = k2(K ∩ gH). For, k1gH = k2gH if and only if k2g = k1gh, h ∈ H, and this holds if and only if kl– 1 k2 = ghg– l, h ∈ H. This last condition is equivalent to k1(K ∩ gH) = k2(K ∩ gH). It now follows that {ki} is a cross section of K with respect to K ∩ gH if and only if {kig} is a set of representatives of the left cosets of H contained in KgH.
We can use this result to prove the following important theorem:
MACKEY’S DECOMPOSITION THEOREM. Let H be a subgroup of finite index in G, K an arbitrary subgroup of G, and let U be an F[H]-module. Identify U with the F[H]-submodule 1 ![]() U of UG and let Δ be the set of double cosets D = KgH. Then
U of UG and let Δ be the set of double cosets D = KgH. Then
![]()
where ![]() is an F[K]-submodule of UGK and
is an F[K]-submodule of UGK and ![]() for any g ∈ D.
for any g ∈ D.
Proof. Let {s1, …, sr} be a cross section of G with respect to H. Then UG = s1U ![]() …
… ![]() srU (Proposition 5.5, p. 290). If g ∈ G, then D = KgH = si1H ∪ … ∪ sikH where the sij are distinct. Then DU = KgHU = si1U
srU (Proposition 5.5, p. 290). If g ∈ G, then D = KgH = si1H ∪ … ∪ sikH where the sij are distinct. Then DU = KgHU = si1U ![]() ….
…. ![]() sikU. It follows that
sikU. It follows that ![]() . Now DU = KgU is an F[K]-submodule of UGK and DU contains gU, which is an F[K ∩ gH]-submodule. We have seen that if {ki|l ≤ i ≤ q] is a cross section of K with respect to K ∩ gH, then {kig} is a set of representatives of the left cosets of H contained in D = KgH. Thus we may assume that {kig} = {si1, …, sik}, so q = k and
. Now DU = KgU is an F[K]-submodule of UGK and DU contains gU, which is an F[K ∩ gH]-submodule. We have seen that if {ki|l ≤ i ≤ q] is a cross section of K with respect to K ∩ gH, then {kig} is a set of representatives of the left cosets of H contained in D = KgH. Thus we may assume that {kig} = {si1, …, sik}, so q = k and
![]()
By Proposition 5.5, this implies that DU as F[K]-module is isomorphic to ![]() .
. ![]()
We shall derive next a theorem on the structure of the tensor product of two induced representations. This is
THEOREM 5.19 (Mackey). Let Hi, i = 1, 2, be a subgroup of finite index in G, σi a representation of Hi acting on Ui/F, and let R be a set of representatives of the double cosets H1gH2. Put H(1, g) = H1 ∩ gH2. Then the F[G] module
![]()
Proof. By Theorem 5.17.3, σlG![]() σ2G is equivalent to (σ1
σ2G is equivalent to (σ1![]() (σ2G)H1)G, and by Mackey’s decomposition, (U2G)H1 is a direct sum of the F[H1]-submodules isomorphic to the modules ((gU2)H(1, g))H1, g ∈ R. Hence U1G
(σ2G)H1)G, and by Mackey’s decomposition, (U2G)H1 is a direct sum of the F[H1]-submodules isomorphic to the modules ((gU2)H(1, g))H1, g ∈ R. Hence U1G![]() U1G is F[G] isomorphic to
U1G is F[G] isomorphic to
![]()
By Theorem 5.17.3,
![]()
Hence, by the transitivity of induction (Theorem 5.17.1),
![]()
Substituting this in the formula for U1G![]() U2G proves the theorem.
U2G proves the theorem. ![]()
The foregoing result can be used to obtain a criterion for an induced module to be irreducible. We shall require also some general results on modules, some of which have been indicated previously in exercises (p. 251). We note first that if Vi, i = 1, 2, is a finite dimensional vector space over a field F, then we have a canonical isomorphism between V1*![]() FV2, V1* the dual space of linear functions on Vl, and homF(V1, V2). This maps u*
FV2, V1* the dual space of linear functions on Vl, and homF(V1, V2). This maps u*![]() v for u* ∈ V1*, v ∈ V2, into the linear map [u*, v] such that [u*, v](x) = u*(x)v for x ∈ V1 (p. 165). The fact that we have such an isomorphism can be seen by noting that u*
v for u* ∈ V1*, v ∈ V2, into the linear map [u*, v] such that [u*, v](x) = u*(x)v for x ∈ V1 (p. 165). The fact that we have such an isomorphism can be seen by noting that u*![]() v is bilinear. Hence we have a linear map η of V1*
v is bilinear. Hence we have a linear map η of V1*![]() FV2 into homF(Vl, V2) such that η(u*
FV2 into homF(Vl, V2) such that η(u*![]() v) = [u*, v]. It is readily seen that η is surjective and since the two spaces V1*
v) = [u*, v]. It is readily seen that η is surjective and since the two spaces V1*![]() F V2 and homF(Vl, V2) have the same dimensionality [V1 : F] [V2 : F], it follows that η is a linear isomorphism.
F V2 and homF(Vl, V2) have the same dimensionality [V1 : F] [V2 : F], it follows that η is a linear isomorphism.
Now suppose ρi, i = 1, 2, is a representation of a group G acting on Vi/F. As on p. 272, we obtain a representation ρ of G acting on homF(Vl, V2) if we define ρ(g)l = ρ2(g)lρ1(g)– l, g ∈ G, l ∈ homF(Vl, V2). The isomorphism η of V1*![]() F V2 with homF(Vl, V2) is an equivalence of the representations ρ1 *
F V2 with homF(Vl, V2) is an equivalence of the representations ρ1 * ![]() ρ2 and ρ. To see this, let u* ∈ V1*, v ∈ V2. Then η(ρl *(g)u*
ρ2 and ρ. To see this, let u* ∈ V1*, v ∈ V2. Then η(ρl *(g)u*![]() ρ2(g)v) is the map
ρ2(g)v) is the map
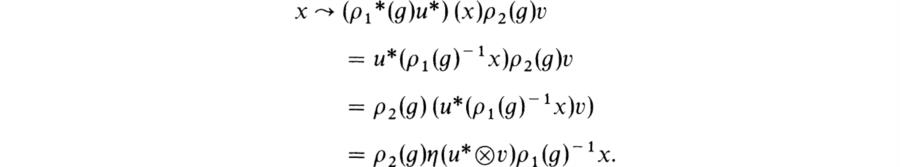
Hence η(ρl *(g)u*![]() ρ2(g)v) = ρ(g)η(u*
ρ2(g)v) = ρ(g)η(u*![]() v), which implies that η is an F[G]-isomorphism of V1*
v), which implies that η is an F[G]-isomorphism of V1*![]() V2 onto homF(Vl, V2).
V2 onto homF(Vl, V2).
We now consider the vector space homF[G](Vl, V2). Evidently, this is a subspace of homF(Vl, V2) and we can identify this subspace with the set of l ∈ homF(Vl, V2) such that ρ(g)l = l, g ∈ G. For this condition is equivalent to ρ2(g)lρ1(g)– 1 = l and to ρ2(g)l = lρ1(g), which is the condition that l ∈ homF[G](Vl, V2). In general, if ρ is a representation of G acting on V, then the set of x ∈ V such that ρ(g)x = x for all g ∈ G is denoted as Inv ρ. Evidently this is a subspace. It is clear also that x ≠ 0 is in Inv ρ if and only if Fx is a onedimensional ρ(G)-invariant subspace and the restriction of ρ to Fx is the unit representation. Hence if ρ is a completely reducible representation of G, then [Inv ρ : F] is the multiplicity of the unit representation in ρ.