The CAPM provides consensus expected returns. A multiple-factor model can help to control risk. Consensus forecasts and risk control are available to all active managers. We need one more crucial ingredient in order to be effective: accurate forecasts of expected return. This chapter will discuss those forecasts of expected return and outline a procedure to transform those forecasts into portfolios.
The chapter is a gradual migration from theory to practice. In theory, we consider an all-embracing market consisting of all assets; in practice, there is a great degree of specialization, so we consider a benchmark with a limited number of assets. In theory, the investor is an individual concerned for his or her own needs; in practice, investment decisions are made by professionals who are one or more levels removed from the eventual beneficiary of those decisions. In theory, active management is a dubious undertaking; in practice, we must provide guidelines for the attempt. This chapter shows how theory is adapted to these institutional realities and the needs of the active manager.
The results of this chapter are as follows:
■ The components of expected return are defined. Exceptional expected return is the difference between our forecasts and the consensus.
■ Benchmark portfolios are a standard for the active manager.
■ Active management value-added is expected exceptional return less a penalty for active variance.
■ Management of total risk and return is distinct from management of active risk and return.
■ Benchmark timing decisions are distinct from stock selection decisions.
This chapter sets out the ground rules used throughout the book. Those who don’t like benchmarks should find some comfort in the notion that choosing the risk-free portfolio F as a benchmark puts one back in the traditional position of balancing expected return against total risk.
There are two things that this chapter does not do:
■ Set up criteria for the proper choice of a benchmark for a specialist manager.
■ Set a target for strategic asset allocation.
Strategic asset allocation establishes a benchmark for an entire pension fund. Strategic asset allocation is a vital question for the fund, for consultants, and for balanced mangers. We don’t address that important question in this book.
In many practical situations, an active manager will be asked to outperform a benchmark portfolio that cannot, in good conscience, be called “the market.” Some would argue that this is always the case. Even that old standby, the S&P 500, represents only a fraction of the world’s traded equities. If we toss in debt and real property, the S&P 500 will not look like a representative slice of the universe available to the institutional investor. For that reason, we are going to phase out the word market and shift to the word benchmark. The benchmark portfolio is also known by the aliases bogey and normal portfolio.
A benchmark portfolio is a consequence of institutional investment management. A trustee or sponsor generally hires several managers to invest the funds. These managers will typically specialize. So included among the managers will be a bond manager, an equity manager, an international manager, etc. The specialization can become finer.1 The managers may specialize in passive equity strategies, growth stocks, value stocks, small-capitalization stocks, etc.
The sponsor should give all managers clear instructions regarding their responsibilities and any limitations on their actions. One of the best ways for an owner of funds to communicate those responsibilities is to specify a benchmark portfolio. For example, the benchmark for a U.S. international equity manager may be the Morgan Stanley Capital International EAFE index or the Financial Times EUROPAC index. The benchmark for a smaller-capitalization manager in the United States may be the Frank Russell 2000 index. The benchmark for an Australian manager of resource stocks may be a special index containing only the stocks in the Australian resource sector.
The manager’s performance is judged relative to the performance of the benchmark. The manager’s active return is the difference between the return on the manager’s portfolio and the return on the benchmark portfolio.
The reader may feel that this practice has theoretical limitations. It undoubtedly does. However, it also has undeniable practical benefits. First, it allows investment managers to specialize and concentrate their expertise on a smaller collection of assets. The sponsors take charge of asset allocation. Second, it focuses the manager’s attention on performance relative to the benchmark.
What guidelines can we provide for an institutional manager whose performance is judged relative to a benchmark? The manager’s attention is directed toward the difference between the managed portfolio’s returns and the benchmark portfolio’s returns. The market portfolio is not specified and plays no direct role.
We have thrown out the market portfolio and are willing to work with a more ad hoc benchmark portfolio. At the same time, we don’t want to abandon all the useful scaffolding that we had built up around the market.
The most important item to salvage is beta. As discussed in previous chapters, we can define beta outside of the CAPM context. If rB is the excess return on the benchmark portfolio and rn is the excess return on stock n, then we can define βn as
We have robbed beta of its universal definition. Beta is no longer an absolute term. It is not beta with respect to the market, but beta with respect to a benchmark. Our notion of residual risk will also become relative. It is no longer residual to the market but residual to a benchmark.
The active position is the difference between the portfolio holdings and the benchmark holdings. The active holding in the risky assets is given by hPA,
and the active cash holding is
The active variance is the variance of the active position. If we let Ψp be the active risk, we have
If we use our notion of beta relative to the benchmark and residual return θP relative to the benchmark, then we can write the active variance as
where βp is the active beta (i.e., βp − 1) and ωP is the residual risk:
Our definition of a benchmark will assist us in separating expected return into its component parts.
We can decompose expected return forecasts into four parts: a riskfree component (the time premium), a benchmark component (the risk premium), a benchmark timing component (exceptional benchmark return), and an alpha (expected residual return). If Rn is the total return on asset n, then we write
We will now discuss each component and various combinations.
This is the return an investor receives for parting with the investment stake for a year. It is referred to as the time premium, i.e., the compensation for time. Since we know the return on a riskfree asset in advance, we can assign the time premium in advance.
We are borrowing from the CAPM here. The expected excess return on the benchmark, μB, is usually estimated by analysts as a very long run (70 + years) average (although other estimation methods are common). A number between 3 and 7 percent per annum is reasonable for most equity markets. Notice that low-beta assets will have lower risk premiums and high-beta assets will have greater risk premiums.
The expected excess return on the benchmark μB cited above is based on very long run considerations. If you believe that the next year (or quarter, or month) will be quite different, then ΔfB is your measure of that difference between the expected excess return on the benchmark in the near future and the long-run expected excess return.
Alpha is the expected residual return, αn = E{θn}.
Consider this breakdown of the −0.60% total return for the MMI portfolio over the month of December 1992, using the S&P 500 as a benchmark. Over this month, the forecast beta of the portfolio versus the S&P 500 was 0.96. Over this same month, the risk-free return was 26 basis points and the S&P 500 return was 131 basis points; we will assume an expected long-run excess S&P 500 return of 50 basis points, so there was a benchmark surprise of 55 basis points. Given this information, we can break down the realized portfolio return as in Table 4.1.
We can combine these components of expected returns in various ways.
Consensus expected excess return βn · μB. The consensus expected excess return is the expected excess return obtained if one accepts the benchmark as an ex ante efficient portfolio with expected excess return μB. This set of expected excess returns will cause us to choose our portfolio to exactly match the benchmark portfolio.
Feeding these expected returns into an optimizer will lead to combinations of the benchmark portfolio and cash, with the cash fraction dependent on μB.
Expected excess return 
. The expected excess return, denoted fn, is made up of the risk premium, the response to an exceptional benchmark forecast, and the alpha.
Exceptional expected return 
. The exceptional expected return is the key to active management. The first component, 
, measures benchmark timing,2 and the second component, αn, measures stock selection.
Table 4.1
MMI Return Breakdown: 12/92
Starting with a list of expected returns E{Rn}, asset betas βn, the weight of each asset in the benchmark hB(n), a risk-free rate iF, and a long-run expected excess return on the benchmark μB, we can separate the expected returns into their component parts. The recipe is a simple and interesting spreadsheet exercise.
Step 1. Calculate the expected excess return on the benchmark.
Step 2. The exceptional benchmark return is
Table 4.2 presents expected returns for MMI stocks in the United States, assuming a risk-free rate of 3.16 percent, an S&P 500 benchmark with an expected excess return of 6 percent, and historical alphas and betas over the 60-month period ending December 1992. The expected returns vary widely from stock to stock, much more than the betas vary. This happens because we are using historical alphas (which vary widely) to calculate expected returns.
Note that we have included cash and a benchmark composite in the list. Cash is the one asset that we are sure we can get right. The benchmark composite will have zero alpha, since there is by definition no residual return for the benchmark.
The traditional (Markowitz-Sharpe) approach to modern portfolio theory is to consider the risk/expected return trade-offs available to the manager. In this section, we will follow that path. In the following sections, we will expand the risk/expected return framework to distinguish between benchmark and active risk.
The return/risk choices available with the consensus forecast are presented in Fig. 4.1. The horizontal axis measures portfolio risk and the vertical axis expected excess returns using the consensus forecast μ, which is β · μB. The hyperbola describes the combinations of expected excess return and risk that we can obtain with fully invested portfolios. The fully invested portfolio with the highest ratio of expected excess return to risk is the benchmark, B. There is no surprise here; consensus in implies consensus out.
Table 4.2
Expected Returns for MMI Stocks
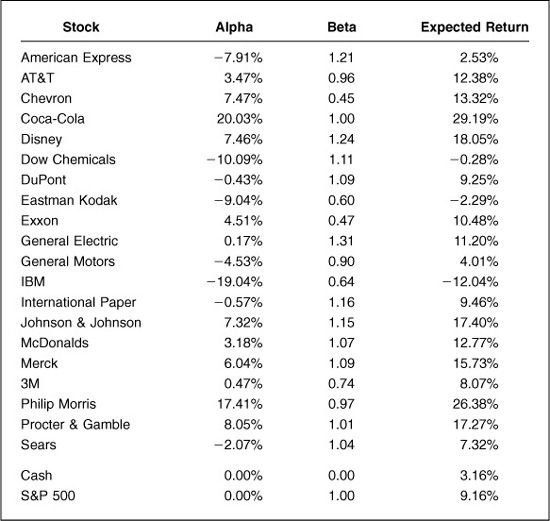
Active management starts when the manager’s forecasts differ from the consensus. If the manager has forecasts f of expected excess returns, then we have the risk/return choices shown in Fig. 4.2.
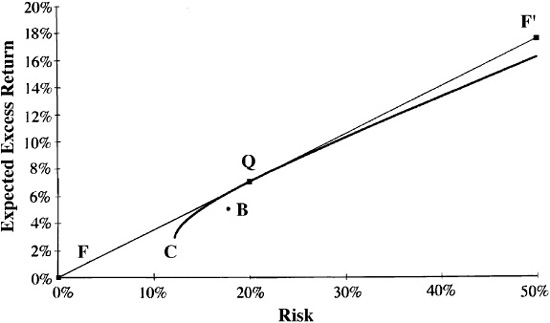
In Fig. 4.2, the benchmark is not on the efficient frontier. A fully invested portfolio Q that differs from B has the maximum ratio of fP to σp. There are possibilities for doing better than B!
We can express the forecast of expected excess return for stock n as
where fB is the forecast of expected excess return for the benchmark, βn is stock n’s beta, and αn is stock n’s forecast alpha. These forecasts will differ from consensus forecasts to the extent that fB differs from the consensus estimate μB and αn differs from zero.
The portfolio we select will depend on our objective. The traditional approach uses a mean/variance criterion for portfolio choice.3 We will call that criterion our expected utility, denote it as U[P], and define it as
where fP is the expected excess return and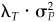 
is a penalty for risk. The parameter λT measures aversion to total risk, where total risk includes systematic risk (driven by the benchmark) and residual risk (from asset selection). Note that some authors have equivalently defined utility in terms of a risk acceptance parameter τ instead of a risk aversion parameter λ, where τ = 1/λ. Still other authors have, for later mathematical convenience, used λ/2 instead of λ in Eq. (4.11).
Figure 4.3 shows the lines of constant expected utility U[P]. The trick is to find an eligible portfolio with the highest possible expected utility.
We can get a reasonable feel for the total risk aversion λT by trying some typical numbers. Consider a portfolio with a risk of 20 percent. If we think that the penalty for risk is on the order of one-half the expected excess return on the portfolio, then we anticipate a penalty of 3 or 4 percent. To get 3 percent, we would use λT = 0.0075, since 3 = 0.0075 · 400. To get 4 percent, we would use λT = 0.01, since 4 = 0.01 · 400. As discussed in Chap. 3, λT is not dimensionless. In particular, it depends on whether we represent risk and return in percent or decimal, and whether we annualize.
Figure 4.3 Constant expected utility lines.
There is a more scientific way to get a reasonable value for λT. Consider the case where we have no information, i.e., f = μ, our forecasts are equal to the consensus. The expected benchmark excess return is μB, and the benchmark risk is σB. The level of total risk aversion that would lead4 us to choose the benchmark portfolio is
If μB = 6 percent and σB = 20 percent, then we find λT = 0.0075.
If μB = 8 percent and σB = 16 percent, we find λT = 0.0156.
If we are willing to have cash in our portfolio, then we have the situation shown in Fig. 4.4. The efficient frontier consists of all the portfolios on the line from F through Q. The optimal portfolio, call it P, is the portfolio on the frontier with the highest risk-adjusted return.5 Portfolio P will be a mixture of Q and F. The beta of P is
Using Eq. (4.12), and defining ΔfB ≡ fB — μB to be the forecast of exceptional benchmark return, the beta of portfolio P becomes
The active beta βPA, the difference between βP and 1, is the ratio of our forecast for benchmark exceptional return ΔfB to the consensus expected excess return on the benchmark μB.
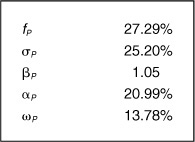
We will argue that this expected utility criterion will typically lead to portfolios that are too aggressive for institutional investment managers.6
Consider, for example, our expected return forecasts for the MMI stocks. Table 4.3 shows the attributes of the portfolio that we obtain using these stocks with a typical level of risk aversion (λ = 0.0075).
These portfolios are far too risky for the institutional manager. This is not due to the extravagant nature of the expected returns. The problem is not the total portfolio risk σp, it is the residual risk ωP.
In total risk/return analysis, small levels of information lead to very high levels of residual risk.
In order to develop an objective that gives results that are more in line with institutional practice, we need to focus on the active component of return, and look at active risk/return tradeoffs.
In the previous section, we discovered that portfolio selection using an expected utility objective leads to levels of residual risk that are much higher than those observed among institutional portfolio managers. The root cause is our even-handed treatment of benchmark and active risk. There is actually a double standard— investment managers and pension plan sponsors are much more averse to the risk of deviation from the benchmark than they are averse to the risk of the benchmark.
Why are institutional money managers willing to accept the benchmark portfolio with 20 percent risk and loath to take on a portfolio with 21.00 percent risk if it contains 20 percent benchmark risk and 6.40 percent residual risk? The variance in the first case will be 400, and that in the second case will be 441 = (21%)2. The difference in risk between 20 percent and 21 percent seems small.
The explanation lies in the allocation of that risk. The owner of the funds, a pension fund or an endowment, bears the benchmark component of the risk. The owner of the funds assumed that risk when invested in that particular benchmark. The active manager, on the other hand, bears the responsibility for the residual risk.7
Let’s say the benchmark is the S&P 500. Hundreds of managers are compared to the S&P 500. All of these managers will experience the same benchmark return. The S&P 500 is the tide that raises or lowers all boats. The managers cannot influence the tide. They will be separated by the residual returns. A high level of residual risk means that there is a large chance of being among the worst managers and a resulting possibility of termination. This is not a happy prospect, and so managers reduce their residual risk in order to avoid the business risk inherent in placing low in the table.
Fortunately, our view of risk and return allows us to accommodate this double standard for benchmark and residual risk.
In the technical appendix to this chapter, we will more rigorously derive the objective for the active manager, which splits risk and return into three parts, as described below.
Intrinsic, fB —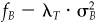 
. This component arises from the risk and return of the benchmark. It is not under the manager’s control. Note that we have used λT as aversion to total risk. Timing, βPA · ΔfB — 
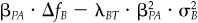. This is the contribution from timing the benchmark. It is governed by the manager’s active beta. Note the risk aversion λBT to the risk caused by benchmark timing.
Residual, 
This is due to the manager’s residual position. Here we have an aversion λR to the residual risk.
The last two parts of the objective measure the manager’s ability to add value. The amount of value added is
The two components of the value-added objective are similar to the mean/variance utility objective that we considered in Eq. (4.11). In each component, there is an expected return term and a variance term. The risk aversion—λBT for benchmark timing and λR for residual risk—transforms the variance into a penalty deducted from the amount of expected returns. The value added is a risk-adjusted expected return that ignores any contribution of the benchmark to the risk and expected return.
The objective [Eq. (4.15)] splits the value added into value added by benchmark timing and value added by stock selection. We consider benchmark timing briefly in the section below, and in more detail in Chap. 19. We will consider stock selection in the next chapter.
Benchmark timing is the choice of an appropriate active beta, period by period. The bulk of this book will concentrate on the management of residual return. The exceptions are Chap. 18, “Asset Allocation,” and Chap. 19, “Benchmark Timing.”
We take this approach for four reasons:
■ A majority of U.S. institutional managers and a growing minority of non-U.S. institutional managers do not use benchmark timing.
■ It greatly simplifies the discussion. This will help the reader who accepts this premise or is at least willing to temporarily suspend disbelief.
■ We may succeed. Recall the Russian proverb, “The man who chases two rabbits will catch neither.”
■ A more subtle reason, suggested in Chap. 6, “The Fundamental Law of Active Management,” is that there is less chance of deriving substantial8 value added through benchmark timing.
This separation of benchmark timing and stock selection is evident in Eq. (4.15). We can choose beta to maximize the first term in that equation. The optimal level of active beta will be
Very high levels of aversion to benchmark timing risk λBT will keep βPA (and hence benchmark timing) close to zero. No benchmark forecast, i.e., ΔfB = 0, will also keep active beta equal to zero.
Our active management framework is quickly moving toward a focus on residual return and residual risk. How does this connect with the manager’s goal of significant active return?
The residual return and risk are
while the active return and risk are
As long as the manager avoids benchmark timing and sets βP = 1, active and residual returns (and risks) are identical. This is the case for most institutional equity managers, and for good reasons, which we will cover in Chap. 6. If the manager does engage in benchmark timing, then, as we can see in Eq. (4.19), the active return is the sum of the residual return and the benchmark timing return.
Previous chapters have discussed consensus expected returns and risk. This chapter turns to the heart of active management: exceptional returns. In particular, it has focused on the components of exceptional returns and introduced the notion of a benchmark portfolio. The benchmark is determined by institutional considerations and can differ considerably from what is commonly considered the market portfolio.
We have looked at possible criteria for the active manager. The traditional criterion of maximizing expected utility does not appear to give results that are consistent with investment practice. The main reason for this is that the expected utility function approach fails to distinguish between sources of risk. But the client bears the benchmark risk, and the active manager bears the active risk of deviating from the benchmark.
In the appendix, we derive an objective that separates active risk into two components: active risk that is correlated with the benchmark, resulting from a choice of active beta (benchmark timing), and active residual risk that is uncorrelated with the benchmark and based on forecasts of residual return (alpha). A reader who has difficulty with this approach should realize that it is a generalization of the usual risk/expected return approach. If we take the risk-free asset, portfolio F, as the benchmark, then all return is residual return. If we equate the risk aversions for total risk, benchmark timing, and residual risk, i.e., λT = λBT = λR, then we are back in the traditional risk/expected return framework.
We turn to the management of residual return in the next chapter.
1. Assume a risk-free rate of 6 percent, a benchmark expected excess return of 6.5 percent, and a long-run benchmark expected excess return of 6 percent. Given that McDonald’s has a beta of 1.07 and an expected total return of 15 percent, separate its expected return into
Time premium
Risk premium
Exceptional benchmark return
Alpha
Consensus expected return
Expected excess return
Exceptional expected return
What is the sum of the consensus expected return and the exceptional expected return?
2. Suppose the benchmark is not the market, and the CAPM holds. How will the CAPM expected returns split into the categories suggested in this chapter?
3. Given a benchmark risk of 20 percent and a portfolio risk of 21 percent, and assuming a portfolio beta of 1, what is the portfolio’s residual risk? What is its active risk? How does this compare to the difference between the portfolio risk and the benchmark risk?
4. Investor A manages total return and risk 
, with risk aversion λT = 0.0075. Investor B manages residual risk and return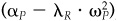 
, with risk aversion λR = 0.075 (moderate to aggressive). They each can choose between two portfolios:
f1 = 10%
σ1 = 20.22%
f1 = 16%
σ2 = 25%
Both portfolios have β = 1. Furthermore,
fB = 6%
σB = 20%
Which portfolio will A prefer? Which portfolio will B prefer? (Hint: First calculate expected residual return and residual risk for the two portfolios.)
5. Assume that you are a mean/variance investor with total risk aversion of 0.0075. If a portfolio has an expected excess return of 6 percent and risk of 20 percent, what is your certainty equivalent return, the certain expected excess return that you would fairly trade for this portfolio?
Jacobs, Bruce I., and Kenneth N. Levy. “Residual Risk: How Much Is Too Much?” Journal of Portfolio Management, vol. 22, no. 3, Spring 1996, pp. 10-16.
Markowitz, H. M. Portfolio Selection: Efficient Diversification of Investment. Cowles Foundation Monograph 16 (New Haven, Conn.: Yale University Press, 1959).
Merton, Robert C. “An Analytical Derivation of the Efficient Portfolio.” Journal of Financial and Quantitative Analysis, vol. 7, September 1972, pp. 1851-1872.
Messmore, Tom. “Variance Drain.” Journal of Portfolio Management, vol. 21, no. 4, Summer 1995, pp. 104-110.
Roll, Richard. “A Mean/Variance Analysis of Tracking Error.” Journal of Portfolio Management, vol. 18, no. 4, Summer 1992, pp. 13-22.
Rosenberg, Barr. “How Active Should a Portfolio Be? The Risk-Reward Tradeoff.” Financial Analysts Journal, vol. 35, no. 1, January/February 1979, pp. 49-62.
——. “Security Appraisal and Unsystematic Risk in Institutional Investment.” Proceedings of the Seminar on the Analysis of Security Prices, (Chicago: University of Chicago Press), November 1976, pp. 171-237.
Rudd, Andrew. “Business Risk and Investment Risk.” Investment Management Review, November/December 1987, pp. 19-27.
Rudd, Andrew, and Henry K. Clasing, Jr. Modern Portfolio Theory, 2d (Orinda, Calif.: Andrew Rudd, 1988).
Sharpe, William F. “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk.” Journal o/Finance, vol. 19, no. 3, September 1964, pp. 425-442.
In this appendix, we derive the objective for value-added management that we use throughout the book. The value-added objective looks at two sources of exceptional return and active risk. The sources are residual risk and benchmark timing.
We begin by separating three items—a forecast of excess returns f, the portfolio holdings hP and the portfolio variance 
a benchmark and a residual (to the benchmark) component. Let hPR represent portfolio P’s residual holdings in the risky stocks. We have
and
where the beta, βp is Cov{rP rB}/Var{rB}, i.e., beta with respect to the benchmark.
We can decompose the expected excess return on portfolio P, fP into the sum of several items. If we recall that ΔfB = fB — μB is the difference between our forecast of the benchmark’s excess return and the long-run consensus, and that the portfolio beta βP = 1 + βPA, where βPA is the active beta, Eq. (4A.2) leads to
and
These expected excess return items are
1. fB, expected benchmark excess return
2. 
, return due to active beta and consensus forecast
3. 
, return due to active beta and exceptional forecast
4. αP, return due to stock alphas and stock selection
We can’t do anything about item 1. Items 3 and 4 link our exceptional forecasts, ΔfB and α, with our active positions βPA and hPR. Item 2 is curious. This is the effect on expected return of varying beta. Notice that item 2 contains no forecast information.
Starting with Eq. (4A.3), we can also split the portfolio’s variance into several parts:
and
These variance items are, in turn,
6. 
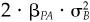covariance due to active beta
7. 
, variance due to active beta
8. 
, variance due to stock selection
Now consider a utility function which trades off exceptional return against risk. We start with a general utility function of the form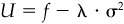 
and apply the breakdowns of expected return and risk shown in items 1 through 8. Grouping together related return and risk items (1 and 5, 2 and 6, 3 and 7, 4 and 8), we generalize the usual approach by allowing three types of risk aversion, λT, λBT and λR for total, benchmark timing, and residual risk aversion. Items 5 and 6 contribute to total risk, item 7 to benchmark timing, and 8 to residual risk. The idea is to distinguish the inherent risk from owning the benchmark portfolio and the active risks the manager takes in trying to outperform by either benchmark timing or taking on residual risk.
We need to keep in mind why we are defining a utility function. It will lead us to choose a portfolio that maximizes that utility. So we will analyze terms based on their influence over our optimal portfolio.
The result of these manipulations is an overall utility function comprising the following elements:
9. 
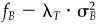, the benchmark component; it combines items 1 and 5. It is all forecast and no action (i.e., it has no influence on the optimal portfolio).
10. 
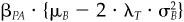, cross effects; it combines items 2 and 6. It includes action, but no forecast.
11. 
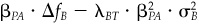, benchmark timing; it combines items 3 and 7. It includes both forecast and action.
12. 
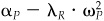, stock selection; it combines items 4 and 8. It includes both forecast and action.
The first term, 9, is a constant and does not influence the active decision. It has no influence on our choice of optimal portfolio.
We will argue that the second term, 10, is zero regardless of the choice of βPA. Item 10 does not depend on any forecast information; it is a permanent part of the objective that is not influenced by our investment insights. In addition, Eq. (4.12) implies that the expression in the curly brackets in 10 should be zero. Finally, imagine what would happen if our forecasts agreed with the consensus; i.e., if f = μ. In that case, we would have ΔfB = 0 and α = 0. The portfolio construction procedure should lead us to hold the benchmark; i.e., βPA = 0, and ωp = 0. That will happen only if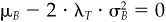 
.
After ignoring the constant term 9 and the zero term 10, we are left with the value-added objective:
The objective of active management is to maximize this value added.
1. Derive the benchmark timing result:
1. Using a performance analysis software package, analyze the return on the MMI portfolio relative to an S&P 500 benchmark. Assume an expected excess return to the benchmark of 6 percent. What was the
Time premium
Realized risk premium
Exceptional benchmark return
Realized alpha
2. Examine the risk of the MMI portfolio relative to the S&P 500. Determine σMMI, σs&p500, βMMI, and ωMMI.
, benchmark variance