In the previous chapter we presented the CAPM as a model of consensus expected return. Expected return is the protagonist in the drama of active management. Risk is the antagonist.
This section will present the definition of risk that is used throughout the book. The important lessons are:
■ Risk is the standard deviation of return.
■ Risks don’t add.
■ Many institutional investors care more about active and residual risk than about total risk.
■ Active risk depends primarily on the size of the active position, not the size of the benchmark position.
■ The cost of risk is proportional to variance.
■ Risk models identify the important sources of risk and separate risk into components.
We start with our definition of risk.
Risk is an abstract concept. An economist considers risk to be expressed in a person’s preferences. What one individual perceives as risky may not be perceived as risky by another.1
We need an operational and therefore universal and impersonal definition of risk. Institutional money managers are agents of pension fund trustees, who are themselves agents of the corporation and the beneficiaries of the fund. In that setting, we cannot hope to have a personal view of risk. For this reason, the risk measure we seek is what an economist might call a measure of uncertainty rather than of risk.
We need a symmetric view of risk. Institutional money managers are judged relative to a benchmark or relative to their peers. The money manager who does not hold a stock that goes up suffers as much as one who holds a larger than average amount of a stock that goes down.
We need a flexible definition of risk. Our definition of risk should apply both to individual stocks and to portfolios. We should be able to talk about realized risk in the past and to forecast risk over any future horizon.
We want to limit ourselves to a measure of risk that we can accurately forecast. Partly for this reason, we want a measure of risk that we can build up from assets to portfolios. We need not only the risk for each asset, but also the risk for every possible combination of assets into portfolios.
So our definition of risk must meet several criteria. At the same time, we have a choice of several potential risk measures. Let’s review them.
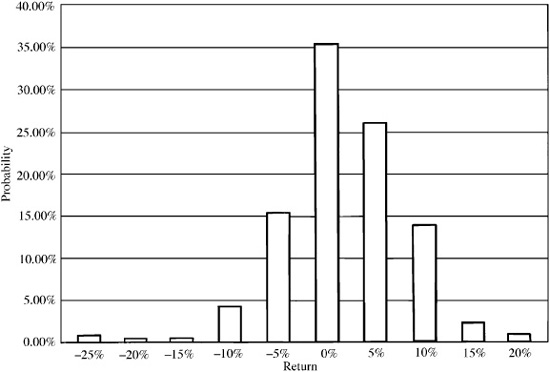
To begin with, all definitions of risk arise fundamentally from the probability distributions of possible returns. This distribution describes the probability that the return will be between 1 and 1.01 percent, the probability of a return between 1.01 and 1.02 percent, etc. For example, Fig. 3.1 displays the empirical distribution of monthly returns for the Fidelity Magellan Fund, based on its performance from January 1973 to September 1994. According to this distribution, 26 percent of the Magellan Fund monthly returns fell between 2.5 and 7.5 percent.
The distribution of returns describes the probabilities of all possible outcomes. As a result, it is complicated and full of detail. It can answer all questions about returns and probabilities. It can be a forecast or a summary of realized returns. Conceptually, it applies to every fund type: equity, bond, or other. Unfortunately, the distribution of returns is too complicated and detailed in its entirety. Hence all our risk measure choices will attempt to capture in a single number the essentials of risk that are more fully described in the complete distribution. Because of this simplification, each definition of risk will have at least some shortcomings. Different measures may also have shortcomings based on difficulties of accurate estimation. As we will discuss later, by assuming a normal distribution, we can calculate all these risk measures as mathematical translations of the mean and standard deviation. But first we will discuss these alternatives without that assumption.
Figure 3.1 Magellan Fund. January 1973-September 1994.
The standard deviation measures the spread of the distribution about its mean. Investors commonly refer to the standard deviation as the volatility. The variance is the square of the standard deviation. For our Magellan Fund example, the standard deviation of the monthly returns was 6.3 percent and the mean was 1.6 percent. If these returns were normally distributed, then two-thirds of the returns would lie within 6.3 percentage points of the mean, i.e., in the band between -4.7 and 7.9 percent. In fact, 73 percent of the Magellan Fund returns were in that band, reasonably close to the normal distribution result. The Magellan Fund’s annual mean and standard deviation were 19.2 percent and 21.8 percent, respectively. Roughly two-thirds of the fund’s annual returns were in a band from −2.6% to 41 percent.
As the standard deviation decreases, the band within which most returns will fall narrows. The standard deviation measures the uncertainty of the returns.
Standard deviation was Harry Markowitz’s definition of risk, and it has been the standard in the institutional investment community ever since. We will adopt it for this book. It is a very well understood and unambiguous statistic. It is particularly applicable to existing tools for building portfolios. Knowing just asset standard deviations and correlations, we can calculate portfolio standard deviations. Standard deviations tend to be relatively stable over time (especially compared to mean returns and other moments of the distribution), and financial economists have developed very powerful tools for accurately forecasting standard deviations.
But before we discuss the standard deviation in more detail, we will discuss some alternative definitions. Critics of the standard deviation point out that it measures the possibility of returns both above and below the mean. Most investors would define risk as involving small or negative returns (although short sellers have the opposite view). This has generated an alternative risk measure: semivariance, or downside risk.
Semivariance is defined in analogy to variance, but using only returns below the mean. If the returns are symmetric—i.e., the return is equally likely to be x percent above or x percent below the mean—then the semivariance is exactly one-half the variance. Authors differ in defining downside risk. One approach defines downside risk as the square root of the semivariance, in analogy to the relation between standard deviation and variance.
From January 1973 to September 1994, the Magellan Fund had a realized semivariance of 21.6, which was 55 percent of its variance of 39.5. According to Fig. 3.1, the distribution extended slightly farther to the left (negative returns) than to the right (positive returns), and so the semivariance was slightly more than half the variance.
A variant of this definition is target semivariance, a generalization of semivariance that focuses on returns below a target, instead of just below the mean.
Downside risk clearly answers the critics of standard deviation by focusing entirely on the undesirable returns. However, there are several problems with downside risk. First, its definition is not as unambiguous as that of standard deviation or variance, nor are its statistical properties as well known. Second, it is computationally challenging for large portfolio construction problems. Aggregating semivariance from assets to portfolios is extremely difficult to do well.2
Third, to the extent that investment returns are reasonably symmetric, most definitions of downside risk are simply proportional to standard deviation or variance and so contain no additional information. Active returns (relative to a benchmark) should be symmetric by construction.
To the extent that investment returns may not be symmetric, there are problems in forecasting downside risk. Return asymmetries are not stable over time, and so are very difficult to forecast.3 Realized downside risk may not be a good forecast of future downside risk.
Moreover, we estimate downside risk with only half of the data, and so we lose statistical accuracy. This problem is accentuated for target semivariance, which often focuses even more on events in the “tail” of the distribution.
Shortfall probability is another risk definition, and one that is perhaps closely related to an intuitive conception of what risk is. The shortfall probability is the probability that the return will lie below some target amount. For example, the probability of a Magellan Fund monthly loss in excess of 10 percent was 3.4 percent.
Shortfall probability has the advantage of closely corresponding to an intuitive definition of risk. However, it faces the same problems as downside risk: ambiguity, poor statistical understanding, difficulty of forecasting, and dependence on individual investor preferences.
Forecasting is a particularly thorny problem, and it is accentuated as the shortfall target becomes lower. At the extreme, probability forecasts for very large shortfalls are influenced by perhaps only one or two observations.
Value at risk is similar to shortfall probability. Where shortfall probability takes a target return and calculates the probability of returns falling below that, value at risk takes a target probability, e.g., the 1 percent or 5 percent lowest returns, and converts that probability to an associated return. For the Magellan Fund, the worst 1 percent of all returns exceeded a 20.8 percent loss. For a $1000 investment in the Magellan Fund, the value at risk was $208.
Value at risk is closely related to shortfall probability, and shares the same advantages and disadvantages.
Where does the normal distribution fit into this discussion of risk statistics? The normal distribution is a standard assumption in academic investment research and is a standard distribution throughout statistics. It is completely defined by its mean and standard deviation. Much research has shown that investment returns do not exactly follow normal distributions, but instead have wider distributions; i.e., the probability of extreme events is larger for real investments than a normal distribution would imply.
The above definitions of risk all attempt to capture the risk inherent in the “true” return distribution. An alternative approach would be to assume that returns are normally distributed. Then the mean and standard deviation immediately fix the other statistics: downside risk, semivariance, shortfall probability, and value at risk. Such an approach might robustly estimate the quantities that are of most interest to individual investors, using the most accurate estimates and a few reasonable assumptions.
More generally, this points out that the choice of how to define risk is separate from the choice of how to report risk. But any approach relying on the normal distribution would strongly motivate us to focus on standard deviation at the asset level, which we can aggregate to the portfolio level. Reporting a final number then as standard deviation or as some mathematical transformation of standard deviation is a matter of personal taste, rather than an influence on our choice of portfolio.
The definition of risk that meets our criteria of being universal, symmetric, flexible, and accurately forecastable is the standard deviation of return.4 If RP is a portfolio’s total return (i.e., a number like 1.10 if the portfolio returned 10 percent), then the portfolio’s standard deviation of return is denoted by σP≡Std{RP}. A portfolio’s excess return rp differs from the total return Rp by RF (a number like 1.04 if Treasury bills return 4 percent), which we know at the beginning of the period. Hence the risk of the excess return is equal to the risk of the total return. We will typically quote this risk, or standard deviation of return, on a percent per year basis.
The standard deviation has some interesting characteristics. In particular, it does not have the portfolio property. The standard deviation of a portfolio is not the weighted average of the standard deviations of the constituents. Suppose the correlation between the returns of stocks 1 and 2 is ρ12. If we have a portfolio of 50 percent stock 1 and 50 percent stock 2, then
and
with the equality in Eq. (3.2) holding only if the two stocks are perfectly correlated (ρ12 = 1). For risk, the whole is less than the sum of its parts. This is the key to portfolio diversification. Figure 3.2 shows a simple example.
The risk of a portfolio made up of IBM and General Electric is plotted against the fraction of GE stock in the portfolio. The curved line represents the risk of the portfolio; the straight line represents the risk that we would obtain if the returns on IBM and GE were perfectly correlated. As of December 1992, the risk of GE was 27.4 percent/year, the risk of IBM was 29.7 percent/year, and the two returns were 62.9 percent correlated. The difference between the two lines is an indication of the benefit of diversification in reducing risk.
Figure 3.2 Fully invested GE/IBM portfolio.
We can see the power of diversification in another example. Given a portfolio of N stocks, each with risk σ and uncorrelated returns, the risk of an equal-weighted portfolio of these stocks will be
Note that the average risk is o, while the portfolio risk is o/VN.
For a more useful insight into diversification, now let us assume that the correlation between the returns of all pairs of stocks is equal to p. Then the risk of an equally weighted portfolio is
In the limit that the portfolio contains a very large number of correlated stocks, this becomes
To get a feel for this, consider the example of an equal-weighted portfolio of the 20 Major Market Index constituent stocks. In December 1992, these stocks had an average risk of 27.8 percent, while the equal-weighted portfolio has a risk of 20.4 percent. Equation (3.4) then implies an average correlation between these stocks of 0.52.
Risks don’t add across stocks, and risks don’t add across time. However, variance will add across time if the returns in one interval of time are uncorrelated with the returns in other intervals of time. The assumption is that returns are uncorrelated from period to period. The correlation of returns across time (called autocorrelation) is close to zero for most asset classes. This means that variances will grow with the length of the forecast horizon and the risk will grow with the square root of the forecast horizon. Thusa5percentannual active risk is equivalent to a 2.5 percent active risk over the first quarter or a 10 percent active risk over four years. Notice that the variance over the quarter, year, and four-year horizon (6.25, 25, and 100) remains proportional to the length of the horizon.
We use this relationship every time we “annualize” risk (i.e., standardize our risk numbers to an annual period). If we examine monthly returns to a stock and observe a monthly return standard deviation of σmonthly, we convert this to annual risk through
Relative risk is important. If an investment manager is being compared to a performance benchmark, then the difference between the manager’s portfolio’s return rP and the benchmark’s return rB is of crucial importance. We call this difference the active return rPA. Correspondingly, we define the active risk Ψp as the standard deviation of active return:
We sometimes call this active risk the tracking error of the portfolio, since it describes how well the portfolio can track the benchmark.
In Fig. 3.3, we consider a simple example. Suppose our benchmark is 40 percent IBM and 60 percent GE. The figure shows the active risk as a function of the holding of GE when the remainder of the portfolio is invested in IBM. The active position moves from +60 percent IBM and -60 percent GE at the left to -40 percent IBM and +40 percent GE at the right. Notice that the active holdings always add to zero.
Figure 3.3 Fully invested GE/IBM portfolio.
There is a notion among investors that active risk is proportional to the capitalization of the asset. Thus, if the market weight for IBM is 4 percent, investors may set position limits of 2 percent on the low side and 6 percent on the high side, with the idea that this is a 50 percent over-weighting and a 50 percent underweighting. For another stock that is 0.6 percent of the benchmark, they may set position limits of 0.3 percent and 0.9 percent. So they limit the active exposure of IBM to ±2.0 percent, and that of the other stock to ±0.3 percent. But active risk depends on active exposure and stock risk. It does not depend on the benchmark holding of the stock. So while there may be cost and liquidity reasons for emphasizing larger stocks, it is not necessarily true that an active position of 1 percent in a large stock is less risky than an active position of 1 percent in a small stock.
Besides active risk, another relative measure of risk, residual risk, is also important. Residual risk is the risk of the return orthogonal to the systematic return. The residual risk of portfolio P relative to portfolio B is denoted by wP and defined by
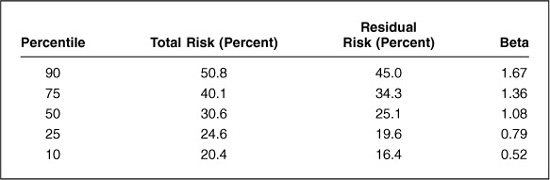
To provide a more intuitive understanding of total risk, residual risk, and beta at the asset level, we have calculated these numbers for large U.S. equities (the BARRA HICAP universe of roughly the largest 1200 stocks) using 60-month windows as of three widely varying dates: June 1980, June 1990, and December 1998. Table 3.1 presents a distribution of these numbers, where we have averaged over the distributions at the three dates.
So we can see that asset typical total risk numbers are 25 to 40 percent, typical residual risk numbers are 20 to 35 percent, and typical betas range from 0.80 to 1.35. For the risk numbers, the distributions varied very little from 1980 through 1998, with the exception of the 90th percentile (which increased for 1998). The betas varied a bit more over time, decreasing from 1980 through 1998. Note that the median beta need not equal 1. Only the capitalization-weighted beta will equal 1.
TABLE 3.1
Empirical Distribution of Risk Measures
Variance is the square of standard deviation. In this book we will consistently use variance to measure the cost of risk. The cost of risk equates risk to an equivalent loss in expected return. In the context of active management, we will generally associate this cost with either active or residual risk. Figure 3.4 shows the cost of active risk based upon an active risk aversion of 0.1. With that level of active risk aversion, a 4 percent active risk translates into a 0.1 · (4 percent)2 = 1.6 percent loss in expected return.
Now we turn our attention to models of stock risk.
The last section hinted at a significant problem in determining portfolio risk. With two stocks in a portfolio, we need the volatility of each, plus their correlation [see Eq. (3.1)]. For a 100-stock portfolio, we need 100 volatility estimates, plus the correlation of each stock with every other stock (4950 correlations). More generally, as the number of stocks N increases, the required number of correlations increases as N(N — 1)/2.
We can summarize all the required estimates by examining the covariance matrix V:
where we denote the covariance of ri and rj by σij, and = σij. The covariance matrix contains all the asset-level risk information required to calculate portfolio-level risk. The goal of a risk model is to accurately and efficiently forecast the covariance matrix. The challenge arises because the covariance matrix contains so many independent quantities.
In this section, we consider three elementary stock risk models. The first is the single-factor diagonal model, which assigns each stock two components of risk: market risk and residual risk. The second is a model that assumes that all pairs of stocks have the same correlation. The third is a full covariance model based on historical returns.
The single-factor model of risk was an intellectual precursor to the CAPM, although the two models are distinct.5 This model starts by analyzing returns as
where βn is stock n’s beta and θn is stock n’s residual return. The single-factor risk model assumes that the residual returns θn are uncorrelated, and hence
and
Of course, residual returns are correlated. In fact, the market-weighted average of the residual returns is exactly zero:
Therefore, the residual correlation between stocks must be in general negative,6 although we might expect a positive residual correlation among stocks in the same industry, e.g., large oil companies. Nevertheless this simple model of risk is attractive, since it isolates market and residual risk and gives a conservative estimate, namely 0, of the residual covariance between stocks.
The second elementary risk model requires an estimate of each stock’s risk σn and an average correlation ρ between stocks. That means that each covariance between any two stocks is
This second model has the virtue of simplicity and can be helpful in some “quick and dirty” applications. It ignores the subtle linkage between stocks in similar industries and firms with common attributes.
The third elementary model relies on historical variances and covariances. This procedure is neither robust nor reasonable. Historical models rely on data from T periods to estimate the N by N covariance matrix. If T is less than or equal to N, we can find active positions7 that will appear riskless! So the historical approach requires T > N. For a monthly historical covariance matrix of S&P 500 stocks, this would require more than 40 years of data. And, even when T exceeds N, this historical procedure still has several problems:
■ Circumventing the T > N restriction requires short time periods, one day or one week, while the forecast horizon of the manager is generally one quarter or one year.
■ Historical risk cannot deal with the changing nature of a company. Mergers and spinoffs cause problems.
■ There is selection bias, as takeovers, LBOs, and failed companies are omitted.
■ Sample bias will lead to some gross misestimates of covariance. A 500-asset covariance matrix contains 125,250 independent numbers. If 5 percent of these are poor estimates, we have 6262 poor estimates.
The reader will note limited enthusiasm for historical models of risk. We now turn to more structured models of stock risk.
In the previous section, we considered elementary risk models and found them either wanting or oversimplified. In this section, we look at structural multifactor risk models and trumpet their virtues.
The multiple-factor risk model is based on the notion that the return of a stock can be explained by a collection of common factors plus an idiosyncratic element that pertains to that particular stock. We can think of the common factors as forces that affect a group of stocks. These might be all the stocks in the banking industry, all stocks that are highly leveraged, all the smaller-capitalization stocks, etc. Below, we discuss possible types of factors in detail.
By identifying important factors, we can reduce the size of the problem. Instead of dealing with 6000 stocks (and 18,003,000 independent variances and covariances), we deal with 68 factors. The stocks change, the factors do not. The situation is much simpler when we focus on the smaller number of factors and allow the stocks to change their exposures to those factors.
A structural risk model begins by analyzing returns according to a simple linear structure with four components: the stock’s excess returns, the stock’s exposure to the factors, the attributed factor returns, and the specific returns. The structure is
where rn(t) = excess return (return above the risk-free return) on stock n during the period from time t to time t+ 1
Xn,k(t) = exposure of asset n to factor k, estimated at time t. Exposures are frequently called factor loadings. For industry factors, the exposures are either 0 or 1, indicating whether the stock belongs to that industry or not.9 For the other common factors, the exposures are standardized so that the average exposure over all stocks is 0, and the standard deviation across stocks is 1.
bk(t) = factor return to factor k during the period from time t to time t + 1.
un(t) = stock n’s specific return during the period from time t to time t + 1. This is the return that cannot be explained by the factors. It is sometimes called the idiosyncratic return to the stock: the return not explained by the model. However, the risk model will account for specific risk. Thus our risk predictions will explicitly consider the risk of un.
We have been very careful to define the time structure in this model. The exposures are known at time t, the beginning of the period. The asset returns, factor returns, and specific returns span the period from time t to time t + 1. In the rest of this chapter, we will suppress the explicit time variables.
We do not mean to convey any sense of causality in this model structure. The factors may or may not be the basic driving forces for security returns. In our view, they are merely dimensions along which to analyze risk.
We will now assume that the specific returns are not correlated with the factor returns and are not correlated with each other. With these assumptions and the return structure of Eq. (3.16), the risk structure is
where Vn,m = covariance of asset n with asset m. Ifn =m, this gives the variance of asset n
Xn,k1 = exposure of asset n to factor k1, as defined above.
Fk1,k2 = covariance of factor k1 with factor k2. If k1 = k2, this gives the variance of factor k1.
Δn,m — specific covariance of asset n with asset m. We assume that all specific return correlations are zero, and so this term is zero unless n = m. In that case, this gives the specific variance of asset n.
The art of building multiple-factor risk models involves choosing appropriate factors. This search for factors is limited by only one key constraint: All factors must be a priori factors. That is, even though the factor returns are uncertain, the factor exposures must be known a priori, i.e. at the beginning of the period.
Within the constraint that the factors be a priori factors, a wide variety of factors are possible. We will attempt a rough classification scheme. To start, we can divide factors into three categories: responses to external influences, cross-sectional comparisons of asset attributes, and purely internal or statistical factors.10 We will consider these in turn.
One of the prevalent themes in the academic literature of financial economics is that there should be a demonstrable link between outside economic forces and the equity markets. The response factors are an attempt to capture that link. These factors include responses to return in the bond market (sometimes called bond beta), unexpected changes in inflation (inflation surprise), changes in oil prices, changes in exchange rates, changes in industrial production, and so on. These factors are sometimes called macrofactors. These measures can be powerful, but they suffer from three serious defects. The first is that we must estimate the response coefficient through regression analysis or some similar technique. A model with nine macrofactors covering 1000 stocks would require 1000 time series regressions each month, with each regression estimating nine response coefficients from perhaps 60 months of data. This leads to errors in the estimates, commonly called an error in variables problem.
The second drawback is that we base the estimate on behavior over a past period of generally 5 years. Even if this estimate is accurate in the statistical sense of capturing the true situation in the past, it may not be an accurate description of the current situation. In short, these response coefficients can be nonstationary. For example, the company may have changed its business practice by trying to control foreign exchange exposure.
Third, several of the macroeconomic data items are of poor quality, gathered by the government rather than observed in the market. This leads to inaccurate, delayed, and relatively infrequent observations.
These factors compare attributes of the stocks, with no link to the remainder of the economy. Cross-sectional attributes generally fall into two groups: fundamental and market. Fundamental attributes include ratios such as dividend yield and earnings yield, plus analysts’ forecasts of future earnings per share. Market attributes include volatility over a past period, return over a past period, option implied volatility, share turnover, etc. To some extent, market attributes such as volatility and momentum may have the same difficulties (errors in variables, nonstationarity) that we described in the section above on the external response factors. Here, however, the factor interpretation is somewhat different. Take, for example, a momentum factor. Let’s say this measures the price performance of the stock over the past 12 months. This factor is not intended as a forecast of continued success or of some mean reversion. It is merely a recognition that stocks that have been relatively successful (unsuccessful) over the past year will quite frequently behave in a common fashion. Sometimes the momentum will be reinforced, at other times it will be reversed, and at yet other times it will be irrelevant. We are accounting for the fact that in 5 or 6 months of the year, controlling for other attributes, previously successful stocks behave in a manner that is very different from that of previously unsuccessful stocks. We could say the same for stocks with high historical volatility, or other such factors. In our experience, these cross-sectional comparisons are quite powerful factors.
It is possible to amass returns data on a large number of stocks, turn the crank of a statistical meat grinder, and admire the factors produced by the machine: factor ex machina. This can be accomplished in an amazingly large number of ways: principal component analysis, maximum likelihood analysis, expectations maximization analysis. One can use a two-step approach by getting first the factors and then the exposures, simultaneously estimate both factors and exposures, or turn the problem on its head in the imaginative approach taken by Connor and Korajczyk (1988). We usually avoid statistical factors, because they are very difficult to interpret, and because the statistical estimation procedure is prone to discovering spurious correlations. These models also cannot capture factors whose exposures change over time. The statistical estimation machinery assumes and relies on each asset’s constant exposure to each factor over the estimation period. For example, statistical models cannot capture momentum factors.
Given the many possible factors, we choose those which satisfy three criteria: They are incisive, intuitive, and interesting. Incisive factors distinguish returns. For example, if we look along the volatility axis, we will find that low-volatility stocks perform differently from high-volatility stocks at least three times per year. If we don’t monitor our overall volatility exposure, then our returns can be upset with disturbing frequency.
Intuitive factors relate to interpretable and recognizable dimensions of the market. Credible stories define these factors. For example, size distinguishes the big companies at one end from the small companies at the other. Momentum separates the firms that have performed well from the firms that have done relatively poorly. Intuitive factors arise from recognizable investment themes. Factors in the U.S. equity market include industries, plus size, yield, value, success, volatility, growth, leverage, liquidity, and foreign currency sensitivity.
Interesting factors explain some part of performance. We can attribute a certain amount of return to each factor in each period. That factor might help explain exceptional return or beta or volatility. For example, stocks of large companies did well over a particular period. Or, high-volatility stocks are high-beta stocks.
Research leading to the appropriate factors, then, depends on both statistical techniques and investment intuition. Statistical techniques can identify the most incisive and interesting factors. Investment intuition can help identify intuitive factors. Factors can have statistical significance or investment significance or both. Model research must take both forms of significance into account.
Given the above general discussion on choosing appropriate factors for a multiple-factor risk model, what typical factors do we choose? They fall into two broad categories: industry factors and risk indices. Industry factors measure the differing behavior of stocks in different industries. Risk indices measure the differing behavior of stocks across other, nonindustry dimensions.
Industry groupings partition stocks into nonoverlapping classes. Industry groupings should satisfy several criteria:
■ There should be a reasonable number of companies in each industry.
■ There should be a reasonable fraction of capitalization in each industry.
■ They should be in reasonable accord with the conventions and mindset of investors in that market.
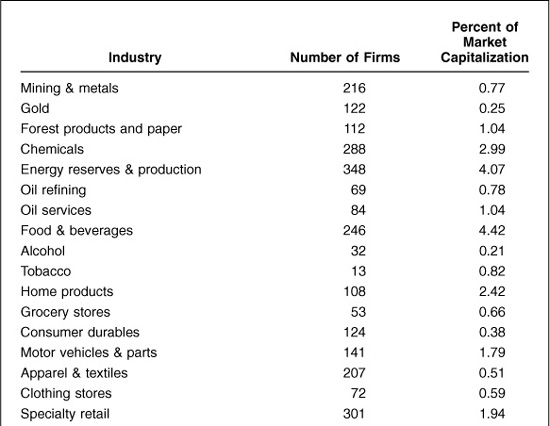
For example, Table 3.2 shows the breakdown of a broad universe of over 11,000 U.S. stocks by BARRA industry group as of the end of August 1998.
Industry exposures are usually 0/1 variables: Stocks either are or are not in an industry. The market itself has unit exposure in total to the industries. Since large corporations can do business in several industries, we can extend the industry factors to account for membership in multiple industries. For example, for September 1998, BARRA’s U.S. Equity risk model classified GE as 58 percent financial services, 20 percent heavy electrical equipment, 8 percent media, 7 percent medical products, and 7 percent property & casualty insurance.
Industries are not the only sources of stock risk. Risk indices measure the movements of stocks exposed to common investment themes. Risk indices we have identified in the United States and other equity markets fall into these broad categories:
TABLE 3.2
U.S. Equity Market Industry Breakdown: August 1998
Volatility. Distinguishes stocks by their volatility. Assets that rank high in this dimension have been and are expected to be more volatile than average.
Momentum. Distinguishes stocks by recent performance. Size. Distinguishes large stocks from small stocks.
Liquidity. Distinguishes stocks by how much their shares trade.
Growth. Distinguishes stocks by past and anticipated earnings growth.
Value. Distinguishes stocks by their fundamentals, in particular, ratios of earnings, dividends, cash flows, book value, sales, etc., to price: cheap versus expensive, relative to fundamentals.
Earnings volatility. Distinguishes stocks by their earnings volatility.
Financial leverage. Distinguishes firms by debt-to-equity ratio and exposure to interest-rate risk.
Any particular equity market can contain fewer or more riskindices, depending on its own idiosyncrasies.
Each broad category can typically contain several specific measurements of the category. We call these specific measurements descriptors. For instance, volatility measures might include recent daily return volatility, option-implied volatility, recent price range, and beta. Though descriptors in a category are typically correlated, each descriptor captures one aspect of the risk index. We construct risk index exposures by weighting the exposures of the descriptors within the risk index. We choose weights that maximize the explanatory and predictive power of the model. Relying on several different descriptors can also improve model robustness.
How do we quantify exposures to descriptors and risk indices? After all, the various categories involve different sets of natural units and ranges. To handle this, we rescale all raw exposure data:
where (xraw) is the raw exposure value mean and Std[xraw] is the raw exposure value standard deviation, across the universe of assets. The result is that each risk index exposure has mean 0 and standard deviation 1. This standardization also facilitates the handling of outliers.
As an example of how this works, BARRA’s U.S. Equity model assigns General Electric a size exposure of 1.90 for September 1998. This implies that, not surprisingly, General Electric lies significantly above average on the size dimension. For the same date, the model assigns Netscape a size exposure of —1.57. Netscape lies significantly below average on this dimension.
The technical appendix discusses in detail how Eq. (3.16); the structural return equation, together with observed asset returns, leads to estimates of factor returns and specific returns. It also describes how those returns, estimated historically, lead to forecasts of the factor covariance matrix and the specific covariance matrix of Eq. (3.17). Here, we will assume that we have these covariance matrices and focus on the uses of a risk model.
A model of risk has three broad uses. They involve the present, the future, and the past. We will describe them in turn, mainly focusing here on uses concerning the present. We will treat future and past risk in more detail in later chapters.
The multiple-factor risk model analyzes current portfolio risk. It measures overall risk. More significantly, it decomposes that risk in several ways. This decomposition of risk identifies the important sources of risk in the portfolio and links those sources with aspirations for active return.
One way to divide the risk is to identify the market and residual components. An alternative is to look at risk relative to a benchmark and identify the active risk. A third way to divide the risk is between the model risk and the specific risk. The risk model can also perform marginal analysis: What assets are most and least diversifying in the portfolio, at the margin?
Risk analysis is important for both passive management and active management. Passive managers attempt to match the returns to a particular benchmark. Passive managers run index funds. However, depending on the benchmark, the manager’s portfolio may not include all the stocks in the benchmark. For example, for a passive small-stock manager, transactions costs of holding the thousands of assets in a broad small-stock benchmark might be prohibitive. Current portfolio risk analysis can tell a passive manager the risk of his or her portfolio relative to the benchmark. This is the active risk, or tracking error. It is the volatility of the difference in return between the portfolio and the benchmark. Passive managers want minimum tracking error.
Of course, the focus of this book is active management. The goal of active managers is not to track their benchmarks as closely as possible, but rather to outperform those benchmarks. Still, risk analysis is important in active management, to focus active strategies. Active managers want to take on risk only along those dimensions where they believe they can outperform.
By suitably decomposing current portfolio risk, active managers can better understand the positioning of their portfolios. Risk analysis can tell active managers not only what their active risk is, but why and how to change it. Risk analysis can classify active bets into inherent bets, intentional bets, and incidental bets:
Inherent. An active manager who is trying to outperform a benchmark (or market) must bear the benchmark risk, i.e., the volatility of the benchmark itself. This risk is a constant part of the task, not under the portfolio manager’s control.
Intentional. An active portfolio manager has identified stocks that she or he believes will do well and stocks that she or he believes will do poorly. In fact, the stocks with the highest expected returns should provide the highest marginal contributions to risk. This is welcome news; it tells the portfolio manager that the portfolio is consistent with his or her beliefs.
Incidental. These are unintentional side effects of the manager’s active position. The manager has inadvertently created an active position on some factor that contributes significantly to marginal active risk. For example, a manager who builds a portfolio by screening on yield will have a large incidental bet on industries that have higher than average yields. Are these industry bets intentional or incidental? Incidental bets often arise through incremental portfolio management, where a sequence of stock-by-stock decisions, each plausible in isolation, leads to an accumulated incidental risk.
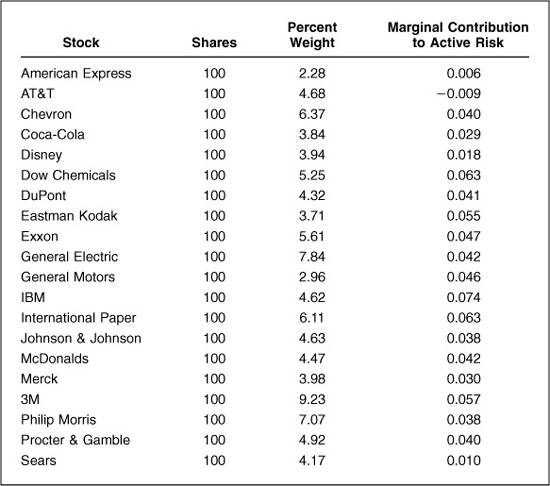
To understand portfolio risk characterization more concretely, consider the following example. Using the Major Market Index (MMI) as an investment portfolio, analyze its risk relative to the S&P 500 as of the end of December 1992. The portfolio is shown in Table 3.3.
Comparing risk factor exposures versus the benchmark, this portfolio contains larger, less volatile stocks, with higher leverage and foreign income, and lower earnings variability: what you might expect from a portfolio of large stocks relative to a broader index. The portfolio also contains several industry bets.
The multiple-factor risk model forecasts 20.5 percent volatility for the portfolio and 20.1 percent volatility for the index. The portfolio tracking error is 4.2 percent. Assuming that active returns are normally distributed, the portfolio annual return will lie within 4.2 percentage points of the index annual return roughly two-thirds of the time. The model can forecast the portfolio’s beta. Beta measures the portfolio’s inherent risk: its exposure to movements of the index. The MMI portfolio beta is 0.96. This implies that if the S&P 500 excess return were 100 basis points, we would expect the portfolio return to be 96 basis points.
As all economists know, life is led at the margin. The risk model will let us know the marginal impact on total, residual, or active risk of changes in portfolio exposures to factors or changes in stock holdings. The technical appendix provides mathematical details.
As an example, Table 3.3 also displays each asset’s marginal contribution to active risk, the change in active risk given a 1 percent increase in the holdings of each stock. According to Table 3.3, increasing the holdings of American Express from 2.28 to 3.28 percent should increase the active risk by 0.6 basis point. Table 3.3 also shows AT&T—with the smallest (and in fact negative) marginal contribution to active risk—to be the most diversifying asset in the portfolio, and IBM—with the largest marginal contribution to active risk—to be the most concentrating asset in the portfolio.
A risk model helps in the design of future portfolios. Risk is one of the important design parameters in portfolio construction, which trades off expected return and risk. Chapter 14, “Portfolio Construction,” will discuss this use of the risk model in some detail.
A risk model helps in evaluating the past performance of the portfolio. The risk model offers a decomposition of active return and allows for an attribution of risk to each category of return. Thus, the risks undertaken by the manager and the outcomes from taking those active positions will be clear. This allows the manager to determine which active bets have been rewarded and which have been penalized. There will be more on this topic in Chap. 17, “Performance Analysis.”
We have chosen standard deviation as the definition of risk in part to facilitate aggregating risk from assets into portfolios. We have chosen the structural risk model methodology in order to accurately and efficiently forecast the required covariance matrix. Here we will describe some evidence that this methodology does perform as desired.
We will consider evidence from two studies. First, we will discuss a comparison of alternative forecasts of standard deviations: portfolio-based versus historical. The portfolio-based approach, aggregating from assets into portfolios, utilized structural risk models. Second, we will describe a comparison of historical forecasts of different risk measures: standard deviation versus alternatives. These alternative measures—e.g., downside risk—must forecast entirely on the basis of historical risk. These two levels of tests imply that we can forecast only standard deviations from historical data, and that portfolio-based forecasts of standard deviation surpass those historical estimates. We will not discuss comparisons of alternative structural risk models, but for more information, see Connor (1995) or Sheikh (1996).
The first study [Kahn (1997)] looked at 29 equity and bond mutual funds. For each fund, at a historical analysis date, the study generated two alternative forecasts of standard deviation: portfolio-based, using structural risk models, and historical, using the prior three-year standard deviation (from monthly returns). The study then analyzed each fund’s performance over the subsequent year. The analysis period was 1993/1994. The study obviously was not exhaustive, as it analyzed only 29 funds, chosen based on the criteria of size, investor interest, and return patterns. The difficulty of obtaining fund holdings makes a comprehensive study of this type quite difficult.
The study analyzed how many funds experienced returns more than two standard deviations from the mean. With accurate risk forecasts, such returns should occur only about 5 percent of the time.
Using structural risk models and portfolio holdings to predict standard deviations, the study found zero three-sigma events and one two-sigma outcome (3 percent of observations); 76 percent of the observations were less than one sigma in magnitude. The historical risk results were not nearly as encouraging: there were one three-sigma outcome (3 percent of observations) and five two-sigma outcomes (17 percent of observations), and then 72 percent of the outcomes were less than one sigma in magnitude.
Of course, the portfolio-based forecasts could have outperformed the historical forecasts in this test by consistently overpredicting risk. Accurate risk forecasts should lead to few surprises, not zero surprises. However, subsequent analysis found no statistically significant evidence that either method over- or underpredicted risk on average.
A final test compared the two alternative forecasts to the standard deviation of the excess returns over the following year: the realized risk. The result: There was a much stronger relationship between portfolio-based forecasts and subsequent risk than between historical risk and subsequent risk.
The second study [Kahn and Stefek (1996)] compared the persistence of alternative risk measures (standard deviation, semivariance, target semivariance, shortfall probability) for 290 domestic equity mutual funds, 185 domestic bond mutual funds, and 1160 individual U.S. equities. In each case, the study looked at two consecutive five-year periods: January 1986 through December 1990 and January 1991 through December 1995 for the mutual funds; and September 1986 through August 1991 and September 1991 through August 1996 for the individual equity returns.
Because the alternative risk measures are in large part a function of the variance—for example, the semivariance is to first order just half the variance—the study explicitly examined the persistence of the information beyond that implied by the variance. So, for instance, it investigated the persistence of abnormal semivariance: semivariance minus half the variance. After all, the only reason to choose an alternative risk measure is for the information beyond variance that it contains.
The tests for persistence within each group of funds or assets simply regressed the risk measure in period 2 against the risk measure in period 1. Evidence of persistence includes high R2 statistics for the regression and significant positive t statistics. The study tests whether higher- (lower-) risk portfolios in period 1 are also higher- (lower-) risk portfolios in period 2. We can use historical risk to forecast a future risk measure only if that risk measure persists.
To summarize the study results, standard deviation and variance exhibit very high persistence. The alternative risk measures exhibited no persistence beyond that implied by just the persistence of variance. It appears that we cannot forecast risk information beyond variance. Many other studies have shown that asset returns exhibit wide distributions, implying that we should be able to forecast something beyond variance (e.g., kurtosis). But this study investigates a different question; whether a portfolio with a wider distribution than average persists in exhibiting a wider distribution than average. This is the important question for portfolio selection, and the answer appears to be no.
Overall, these two studies confirm the important roles played by standard deviation and structural risk models in active management.
Active management centers on the trade-off between expected returns and risk. This chapter has focused on risk. We have quantified risk as the standard deviation of annual returns, and the cost of risk as the variance of annual returns. Active managers care mainly about active and residual risk. Risk models, and structural risk models in particular, can provide insightful analysis by decomposing risk into total and active risk, market (or benchmark) and residual risk, model and specific risk; and by identifying inherent, intentional, and incidental bets. Risk models can analyze the present risks and bets in a portfolio, forecast future risk as part of the portfolio construction process, and analyze past risks to facilitate performance analysis. The evidence shows that structural risk models perform as desired.
1. If GE has an annual risk of 27.4 percent, what is the volatility of monthly GE returns?
2. Stock A has 25 percent risk, stock B has 50 percent risk, and their returns are 50 percent correlated. What fully invested portfolio of A and B has minimum total risk? (Hint: Try solving this graphically (e.g. in Excel), if you cannot determine the answer mathematically.)
3. What is the risk of an equal-weighted portfolio consisting of five stocks, each with 35 percent volatility and a 50 percent correlation with all other stocks? How does that decrease as the portfolio increases to 20 stocks or 100 stocks?
4. How do structural risk models help in estimating asset betas? How do these betas differ from those estimated from a 60-month beta regression?
Arrow, Kenneth J. Essays in the Theory of Risk-Bearing. (Chicago: Markham Publishing Company, 1971).
Bernstein, Peter L. Against the Gods: The Remarkable Story of Risk. (New York: John Wiley & Sons, 1996).
Bollerslev, Tim, Ray Y. Chou, and Kenneth F. Kroner. “ARCH Modeling in Finance.” Journal of Econometrics, vol. 52, 1992, pp. 5-59.
Borch, Karl H. The Economics of Uncertainty. (Princeton, N.J.: Princeton University Press, 1972).
Connor, Gregory. “The Three Types of Factor Models: A Comparison of Their Explanatory Power.” Financial Analysts Journal, vol. 51, no. 3, May/June 1995, pp. 42-46.
Connor, Gregory, and Robert A. Korajczyk. “Risk and Return in an Equilibrium APT: Application of a New Test Methodology.” Journal of Financial Economics vol 21, no. 2, September 1988, pp. 255-289.
Engle, Robert F. “Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation.” Econometrica vol. 50, 1982, pp. 987-1008.
Fama, Eugene, and James MacBeth. “Risk, Return, and Equilibrium: Empirical Tests.” Journal of Political Economy vol. 81, May-June 1973, pp. 607-636.
Grinold, Richard C., and Ronald N. Kahn. “Multiple Factor Models for Portfolio Risk.” In A Practitioner’s Guide to Factor Models, edited by John W. Peavy III. (Charlottesville, Va.: AIMR, 1994).
Jeffery, R. H. “A New Paradigm for Portfolio Risk.” Journal of Portfolio Management vol. 10, no. 1, Fall 1984, pp. 33–40.
Kahn, Ronald N. “Mutual Fund Risk.” BARRA Research Insights (Berkeley, Calif.: BARRA, 1997).
Kahn, Ronald N., and Daniel Stefek. “Heat, Light, and Downside Risk.” BARRA manuscript, 1996.
Kosmicke, R. “The Limited Relevance of Volatility to Risk.” Journal of Portfolio Management vol. 12, no. 1, Fall 1986, pp. 18-21.
Litterman, Robert. “Hot Spots and Hedges.” Journal of Portfolio Management December 1996, pp. 52-75.
Markowitz, H. M. Portfolio Selection: Efficient Diversification of Investment. Cowles Foundation Monograph 16 (New Haven, Conn.: Yale University Press, 1959).
Raiffa, H. Decision Analysis: Introductory Lectures on Choices under Uncertainty (Reading, Mass.: Addison-Wesley, 1968).
Rosenberg, B. “Extra-Market Components of Covariance in Security Markets.” Journal of Financial and Quantitative Analysis, March 1974, pp. 263-274.
Rosenberg, B., and V. Marathe. “The Prediction of Investment Risk: Systematic and Residual Risk.” Proceedings of the Seminar on the Analysis of Security Prices (Chicago: University of Chicago Press), November 1975, pp. 85-224.
Rudd, Andrew, and Henry K. Clasing, Jr. Modern Portfolio Theory (Orinda, Calif.: Andrew Rudd, 1988), Chaps. 2 and 3.
Sharpe, William F. “A Simplified Model for Portfolio Analysis.” Management Science vol. 9, no. 1, January 1963, pp. 277-293.
Sheikh, Aamir. “BARRA’s Risk Models.” BARRA Research Insights (Berkeley, Calif.: BARRA, 1996).
We define the risk model in two parts. First, we model returns as
where r is an N vector of excess returns, X is an N by K matrix of factor exposures, b is a K vector of factor returns, and u is an N vector of specific returns.
We assume that
A1. The specific returns u are uncorrelated with the factor returns b; i.e., Cov{un,bk} = 0 for all n and k.
A2. The covariance of stock n’s specific return un with stock m’s specific return um is zero if m ≠ n; i.e. Cov{un,um} = 0 if m ≠ n.
With these assumptions, we can complete the definition of the risk model by expressing the N by N covariance matrix V of stock returns as
where F is the K by K covariance matrix of the factor returns and Δ is the N by N diagonal matrix of specific variance.
Given exposures to the industry and risk index factors, we estimate factor returns via multiple regressions, using the Fama-MacBeth procedure (1973). The model is linear, and Eq. (3A.1) has the form of a multiple regression. We regress stock excess returns against factor exposures, choosing factor returns which minimize the (possibly weighted) sum of squared specific returns. In the United States, for example, BARRA uses a universe of 1500 of the largest companies, calculates their exposures from fundamental data, and runs one regression per month to estimate 65 factor returns from about 1500 observations. The R2 statistic, which measures the explanatory power of the model, tends to average between 30 and 40 percent for models of monthly equity returns with roughly 1000 assets and 50 factors. Larger R2 statistics tend to occur in months with larger market moves.
In this cross-sectional regression, which BARRA performs every period, the industry factors play the role of an intercept. The market as a whole has an exposure of 1 to the industries, and industry factor returns tend to pick up the market return. They are the more volatile factors in the model. The market has close to zero exposure to the risk indices, and risk index factor returns pick up extra-market returns. They are the less volatile factors in the market.
To efficiently estimate factor returns, we run generalized least squares (GLS) regressions, weighting each observed return by the inverse of its specific variance. In some models, we instead weight each observation by the square root of its market capitalization, which acts as a proxy for the inverse of its specific variance.11
While these cross-sectional regressions can involve more than 50 factors, the models do not suffer from multicollinearity. Most of the factors are industries (52 out of 65 in BARRA s U.S. Equity risk model in 1998), which are orthogonal. In addition, tests of variance inflation factors, which measure the inflation in estimate errors caused by multicollinearity, lie far below serious danger levels.
This regression approach to estimating factor returns leads to an insightful interpretation of the factors. Weighted regression gymnastics lead to the following matrix expression for the estimated factor returns:
where X is the exposure matrix, Δ-1 is the diagonal matrix of GLS regression weights, and r is the vector of excess returns. For each particular factor return, this is simply a weighted sum of excess returns:
In this form, we can interpret each factor return bk as the return to a portfolio, with portfolio weights ck,n. So factor returns are the returns to factor portfolios. The factor portfolio holdings are known a priori. The factor portfolio holdings ensure that the portfolio has unit exposure to the particular factor, zero exposure to every other factor, and minimum risk given those constraints.12
Factor portfolios resemble the characteristic portfolios introduced in the technical appendix to Chap. 2, except that they are multiple-factor in nature. That is, characteristic portfolios have unit exposure to their characteristic, but not necessarily zero exposure to a set of other factors.
There are two different interpretations of these portfolios. They are sometimes interpreted as factor-mimicking portfolios, because they mimic the behavior of some underlying basic factor. We interpret them more simply as portfolios that capture the specific effect we have defined through our exposures.
Factor portfolios typically contain both long and short positions. For example, the factor portfolio for the earnings-to-price factor in the U.S. market will have an earnings-to-price ratio one standard deviation above the market, while having zero exposure to all other factors. Zero exposure to an industry implies that the portfolio will hold some industry stocks long and others short, with longs and shorts balancing. Factor portfolios are not investible portfolios, since, among other properties, these portfolios contain every single asset with some weight.
Once we have estimates of factor returns each period, we can estimate a factor covariance matrix: an estimate of all the factor variances and covariances. To effectively operate as a risk model, this factor covariance matrix should comprise our best forecast of future factor variances and covariances, over the investor s time horizon.
Forecasting covariance from a past history of factor returns is a subject worthy of a book in itself, and the details are beyond the scope of this effort. Basic techniques rely on weights over the past history and bayesian priors on covariance. More advanced techniques include forecasting variance conditional on recent events, as first suggested by Engle (1982). Such techniques assume that variance is constant only conditional on other variables. For a review of these ideas, see Bollerslev et al. (1992).
To generate an asset-by-asset covariance matrix, we need not only the factor covariance matrix F, but also the specific risk matrix A. Now, by definition, the model cannot explain a stock s specific return un. So the multiple-factor model can provide no insight into stock specific returns. However, for specific risk, we need to model specific return variance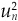 
(assuming that mean specific return is zero).
In general, we model specific risk as13
and
So S(t) measures the average specific variance across the universe of stocks, and vn captures the cross-sectional variation in specific variance.
To forecast specific risk, we use a time series model for S(t) and a linear multiple-factor model for vn(t). Models for vn(t) typically include some risk index factors, plus factors measuring recent squared specific returns. The time dependence in the model of vn(t) is captured by time variation in the exposures. We estimate model coefficients via one pooled regression over assets and time periods, with outliers trimmed.
A portfolio P is described by an N-element vector hP that gives the portfolio’s holdings of the N risky assets. The factor exposures of portfolio P are given by
The variance of portfolio P is given by
A similar formula lets us calculate Ψp, the active risk or tracking error. If hB is the benchmark holdings vector, then we can define
Notice that we have separated both total and active risk into common-factor and specific components. This works because factor risks and specific risks are uncorrelated.
The decomposition of risk is more difficult if we want to separate market risk from residual risk. We must define beta first.
The N vector of stock betas relative to the benchmark hB is defined by the equation
If we define b and d as
then we can write beta as
So each asset’s beta contains a factor contribution and a specific contribution. The specific contribution is zero for any asset not in the benchmark. In most cases, the industry factor contribution dominates beta.
The portfolio beta is
A similar calculation yields the active beta.
The systematic and residual risk are then given respectively by the two terms
where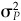 
is given by Eq. (3A.9) and βP by Eq. (3A.17). It is possible to construct a residual covariance matrix
In some cases, it is possible to attribute a portion of risk to a single cause. We can separate market risk from residual risk, and we can separate common-factor risk from specific risk. In both cases, the two risk components are uncorrelated. When two sources of risk are correlated, then the covariance between them makes it difficult to allocate the risk. We will describe one approach, which first requires the introduction of marginal contributions to risk.
Although total allocation of risk is difficult, we can examine the marginal effects of a change in the portfolio. This type of sensitivity analysis allows us to see what factors and assets have the largest impact on risk. The marginal impact on risk is measured by the partial derivative of the risk with respect to the asset holding. We will see in the technical appendix to Chap. 5 that marginal contributions to residual risk are directly proportional to alphas, with the constant of proportionality dependent on the information ratio.
We can compute marginal contributions for total risk, residual risk, and active risk. The N vector of marginal contributions to total risk is
The MCTR(n) is the partial derivative of aP with respect to hP(n). We can think of it as the approximate change in portfolio risk given a 1 percent increase in the holding of asset n, financed by decreasing the cash account by 1 percent. Recall that the cash holding hP(0) is given by hP(0) = 1 — eP To first order,
In a similar way, we can define the marginal contribution to residual risk as
where hPR = hP — βP · hB is the residual holdings vector for portfolio P.
Finally, the marginal contribution to active risk is given by
We can further decompose this marginal contribution to active risk into a market and a residual component.
where
and
We see that 0 ≤ k2 ≤ 1, and k2 = 1 when βPA = 0 and k1 = 0.
Sometimes we wish to calculate sensitivities with respect to factor exposures instead of asset holdings. Let’s think about what this means.
At the asset level, the marginal contributions capture the change in risk if we change the holding of just one asset, leaving all other assets unchanged.
At the factor level, the marginal contributions should capture the change in risk if we change the exposure to only one factor, leaving other factor exposures unchanged. To increase the portfolio’s exposure to only factor k, we want to add a portfolio with exposure to factor k, and zero exposure to the other factors. A reasonable and well-defined choice is a factor portfolio. The factor portfolio has the proper exposures, and minimum risk given those exposures, so it is as close as we can come:
where [(XT Δ-1 · X)-1 · XT · Δ-1] is the K by N vector of factor portfolios, and δk is a K by 1 vector containing zeros except in the kth row, where it contains δk.
To find the effect on risk of adding this portfolio, we need only multiply the changes in each asset holding times the marginal contributions at the asset level. We present here only the calculation for marginal contribution to active risk:
We can simplify this result by using the factor decomposition of the covariance matrix. The result is
The first term above captures the change in factor risk due to changing the factor exposure. It resembles the form of the marginal contribution to active risk at the asset level [Eq. (3A.23)]. It would be the complete answer if we could change factor exposures while leaving asset holdings unchanged. The second term captures the change in specific risk due to changing the factor exposures using the actual factor portfolio. Remember that the factor portfolios have minimum specific risk among all portfolios with unit exposure to one factor and zero exposure to all other factors. Empirically, we find that the second term is much smaller than the first term.14 Hence we typically make the reasonable approximation
Having broached the subject of factor marginal contributions, we should also briefly mention sector marginal contributions The idea is that we typically group industry factors into sectors The sectors play no role in risk model estimation or risk calculation, but they are convenient and intuitive constructs. So once we have determined how increases in industry exposures might affect risk, we may also want to know how an increase in sector exposure might affect risk.
This is a reasonable question. Unfortunately, its answer is ambiguous. When we calculated factor marginal contributions, we used a linear contribution of asset-level marginal contributions and relied on the relative unambiguousness of the factor portfolios. At the sector level, we want to calculate a linear combination of the industry factor marginal contributions, but the weights are less ambiguous now. We could increase the exposure to a sector by increasing only one particular industry in the section, increasing each industry the same amount, increasing each industry based on the portfolio industry weights, or increasing each industry based on the benchmark industry weights. One reasonable choice is to use the total (as opposed to active) industry weights from the portfolio. For example, consider a computer sector comprising two industries: software and hardware. If the portfolio contains only computer hardware manufacturers, then calculate computer sector marginal contributions based only on the hardware industry. If the portfolio’s exposure to computers is 70 percent software and 30 percent hardware, use the 70/30 weights to calculate sector marginal contributions. In other words, assume that the investor would increase (or decrease) the exposure to computers in exactly the current proportions.
Clearly, the most important point about sector marginal contributions is to understand what calculation you need and what calculation you are receiving.
We can use the marginal contributions to define a decomposition of risk. For concreteness, we will focus on a decomposition of active risk, but the ideas apply equally well to total or residual risk. First note the mathematical relationship
But Eq. (3A.31) implies an attribution of active risk. The amount of active risk Ψp which we can attribute to asset n is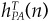 
= MCAR(n). We can furthermore divide Equation (3A.31) by Ψp, to give a percentage breakdown of active risk:
We can use Eq. (3A.32) to attribute to asset n a fraction 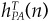= MCAR(n)/Ψp of the overall active risk.
How can we interpret this attribution scheme? In fact, the attributed returns are relative marginal contributions to active risk. Here is what we mean. As before, if we increase the holding in asset n,
But we can rewrite this as
So the change in active risk depends on the relative change in the active holding of asset n, ΔhPA(n)/hPA(n), times the amount of active risk attributed to asset n. Hence we can interpret this amount of risk attributed to asset n as a relative marginal contribution, RMCAR(n):
and
If we changed asset n’s active holding from 1 percent to 1.01 percent, we could estimate the change in active risk as 0.01 times the RMCAR for asset n.15
This is a straightforward extension of the previous ideas. Using the factor risk model, we have
We can therefore define the factor marginal contributions, FMCAR, as
But note that
Hence, we can attribute active risk Ψ to the factors and specific sources. We attribute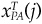 
· FMCAR(j) to factor j, and 
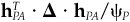· Δ hPA/Ψp overall to specific sources. Once again, we can interpret these attributions as relative marginal contributions.
As a final topic, we can illustrate one use of the simple one-factor model to understand the observed relationship between asset correlations and market volatility: Typically asset correlations increase as market volatility increases.
According to this simple model, the correlation between assets n and m is
The only contribution of the model is the simple form of the covariance in the numerator of Eq. (3A.40). But now let’s assume that both assets have betas of 1, and identical residual risk. Then Eq. (3A.40) becomes
We can now see that if residual risk is independent of market volatility, as market volatility increases, asset correlations increase. In periods of low market volatility, asset correlations will be relatively low.
1. Show that:
2. Verify Eq. (3A.24).
3. Show that
4. Using the single-factor model, assuming that every stock has equal residual risk ω0, and considering equal-weighted portfolios to track the equal-weighted S&P 500, show that the residual risk of the N-stock portfolio will be
What estimate does this provide of how well a 50-stock portfolio could track the S&P 500? Assume ω0 = 25 percent.
5. This is for prime-time players. Show that the inverse of V is given by
V-1 = Δ-1 – Δ-1 · X · {XT · Δ-1 · X + F-1}-1 · XT · Δ-1
As we will see in later chapters, portfolio construction problems typically involve inverting the covariance matrix. This useful relationship facilitates that computation by replacing the inversionofan N by N matrix with the inversion of K by K matrices, where K << N. Note that the inversion of N by N diagonal matrices is trivial.
1. Calculate the average correlation between MMI assets. First, calculate the average volatility of each asset. Second, calculate the volatility of the equal-weighted portfolio of the assets. Use Eq. (3.4) to estimate the average correlation.
2. What are the average total risk, residual risk, and beta of the MMI assets (relative to the CAPMMI)?
3. Using MMI assets, construct a 20-stock portfolio to track the S&P 500. Compare the resulting tracking error to the answer to Exercise 4, where ω0 is the average residual risk for MMI assets.
