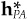, active risk 
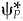and an ex ante information ratio IR with a direct unconstrained mean/variance optimization using a modified set of alphas and the appropriate level of risk aversion.1 The modified alphas areImplementation is the efficient translation of research into portfolios. Implementation is not glamorous, but it is important. Good implementation can’t help poor research, but poor implementation can foil good research. A manager with excellent information and faulty implementation can snatch defeat from the jaws of victory.
Implementation includes both portfolio construction, the subject of this chapter (and to some extent the next chapter), and trading, a subject of Chap. 16. This chapter will take a manager’s investment constraints (e.g., no short sales) as given and build the best possible portfolio subject to those limitations. It will assume the standard objective: maximizing active returns minus an active risk penalty. The next chapter will focus specifically on the very standard no short sales constraint and its surprisingly significant impact. This chapter will also take transactions costs as just an input to the portfolio construction problem. Chapter 16 will focus more on how to estimate transactions costs and methods for reducing them.
Portfolio construction requires several inputs: the current portfolio, alphas, covariance estimates, transactions cost estimates, and an active risk aversion. Of these inputs, we can measure only the current portfolio with near certainty. The alphas, covariances, and transactions cost estimates are all subject to error. The alphas are often unreasonable and subject to hidden biases. The covariances and transactions costs are noisy estimates; we hope that they are unbiased, but we know that they are not measured with certainty. Even risk aversion is not certain. Most active managers will have a target level of active risk that we must make consistent with an active risk aversion.
Implementation schemes must address two questions. First, what portfolio would we choose given inputs (alpha, covariance, active risk aversion, and transactions costs) known without error? Second, what procedures can we use to make the portfolio construction process robust in the presence of unreasonable and noisy inputs? How do you handle perfect data, and how do you handle less than perfect data?
How to handle perfect data is the easier dilemna. With no transactions costs, the goal is to maximize value added within any limitations on the manager’s behavior imposed by the client. Transactions costs make the problem more difficult. We must be careful to compare transactions costs incurred at a point in time with returns and risk realized over a period of time.
This chapter will mainly focus on the second question, how to handle less than perfect data. Many of the procedures used in portfolio construction are, in fact, indirect methods of coping with noisy data. With that point of view, we hope to make portfolio construction more efficient by directly attacking the problem of imperfect or “noisy” inputs.
Several points emerge in this chapter:
■ Implementation schemes are, in part, safeguards against poor research.
■ With alpha analysis, the alphas can be adjusted so that they are in line with the manager’s desires for risk control and anticipated sources of value added.
■ Portfolio construction techniques include screening, stratified sampling, linear programming, and quadratic programming. Given sufficiently accurate risk estimates, the quadratic programming technique most consistently achieves high value added.
■ For most active institutional portfolio managers, building portfolios using alternative risk measures greatly increases the effort (and the chance of error) without greatly affecting the result.
■ Managers running separate accounts for multiple clients can control dispersion, but cannot eliminate it.
Let’s start with the relationship between the most important input, alpha, and the output, the revised portfolio.
Active management should be easy with the right alphas. Sometimes it isn’t. Most active managers construct portfolios subject to certain constraints, agreed upon with the client. For example, most institutional portfolio managers do not take short positions and limit the amount of cash in the portfolio. Others may restrict asset coverage because of requirements concerning liquidity, self-dealing, and so on. These limits can make the portfolio less efficient, but they are hard to avoid.
Managers often add their own restrictions to the process. A manager may require that the portfolio be neutral across economic sectors or industries. The manager may limit individual stock positions to ensure diversification of the active bets. The manager may want to avoid any position based on a forecast of the benchmark portfolio’s performance. Managers often use such restrictions to make portfolio construction more robust.
There is another way to reach the same final portfolio: simply adjust the inputs. We can always replace a very sophisticated (i.e., complicated) portfolio construction procedure that leads to active holdings 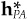, active risk 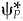and an ex ante information ratio IR with a direct unconstrained mean/variance optimization using a modified set of alphas and the appropriate level of risk aversion.1 The modified alphas are
and the appropriate active risk aversion is
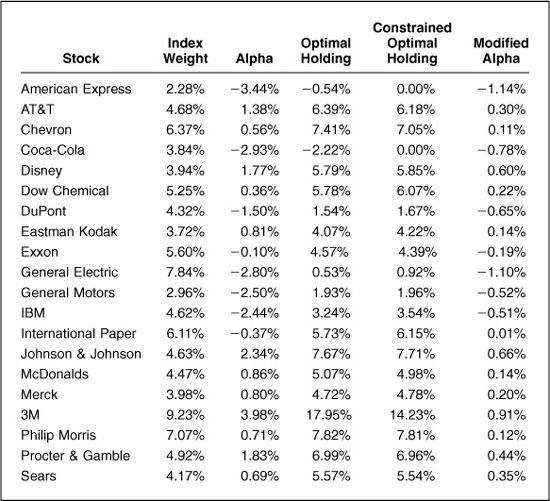
Table 14.1 illustrates this for Major Market Index stocks as of December 1992. We assign each stock an alpha (chosen randomly in this example), and first run an unconstrained optimization of risk-adjusted active return (relative to the Major Market Index) using an active risk aversion of 0.0833. Table 14.1 shows the result. The unconstrained optimization sells American Express and CocaCola short, and invests almost 18 percent of the portfolio in 3M. We then add constraints; we disallow short sales and require that portfolio holdings cannot exceed benchmark holdings by more than 5 percent. This result is also displayed in Table 14.1. The optimal portfolio no longer holds American Express or Coca-Cola at all, and the holding of 3M moves to exactly 5 percent above the benchmark holding. The other positions also adjust.
This constrained optimization corresponds to an unconstrained optimization using the same active risk aversion of 0.0833 and the modified alphas displayed in the last column of Table 14.1. We derive these using Eqs. (14.1) and (14.2). These modified alphas are pulled in toward zero relative to the original alphas, as we would expect, since the constraints moved the optimal portfolio closer to the benchmark. The original alphas have a standard deviation of 2.00 percent, while the modified alphas have a standard deviation of 0.57 percent.
We can replace any portfolio construction process, regardless of its sophistication, by a process that first refines the alphas and then uses a simple unconstrained mean/variance optimization to determine the active positions.
This is not an argument against complicated implementation schemes. It simply focuses our attention on a reason for the complexity. If the implementation scheme is, in part, a safeguard against unrealistic or unreasonable inputs, perhaps we can, more fruitfully, address this problem directly. A direct attack calls for either refining the alphas (preprocessing) or designing implementation procedures that explicitly recognize the procedure’s role as an “input moderator.” The next section discusses preprocessing of alphas.
We can greatly simplify the implementation procedure if we ensure that our alphas are consistent with our beliefs and goals. Here we will outline some procedures for refining alphas that can simplify the implementation procedure, and explicitly link our refinement in the alphas to the desired properties of the resulting portfolios. We begin with the standard data screening procedures of scaling and trimming.2
Alphas have a natural structure, as we discussed in the forecasting rule of thumb in Chap. 10: α = volatility · IC · score. This structure includes a natural scale for the alphas. We expect the information coefficient (IC) and residual risk (volatility) for a set of alphas to be approximately constant, with the score having mean 0 and standard deviation 1 across the set. Hence the alphas should have mean 0 and standard deviation, or scale, of Std{α} ~ volatility · IC.3 An information coefficient of 0.05 and a typical residual risk of 30 percent would lead to an alpha scale of 1.5 percent. In this case, the mean alpha would be 0, with roughly two-thirds of the stocks having alphas between −1.5 percent and +1.5 percent and roughly 5 percent of the stocks having alphas larger than +3.0 percent or less than −3.0 percent. In Table 14.1. the original alphas have a standard deviation of 2.00 percent and the modified alphas have a standard deviation of 0.57 percent. This implies that the constraints in that example effectively shrank the IC by 62 percent, a significant reduction. There is value in noting this explicitly, rather than hiding it under a rug of optimizer constraints.
The scale of the alphas will depend on the information coefficient of the manager. If the alphas input to portfolio construction do not have the proper scale, then rescale them.
The second refinement of the alphas is to trim extreme values. Very large positive or negative alphas can have undue influence. Closely examine all stocks with alphas greater in magnitude than, say, three times the scale of the alphas. A detailed analysis may show that some of these alphas depend upon questionable data and should be ignored (set to zero), while others may appear genuine. Pull in these remaining genuine alphas to three times scale in magnitude.
A second and more extreme approach to trimming alphas is to force4 them into a normal distribution with benchmark alpha equal to 0 and the required scale factor. Such an approach is extreme because it typically utilizes only the ranking information in the alphas and ignores the size of the alphas. After such a transformation, you must recheck benchmark neutrality and scaling.
Beyond scaling and trimming, we can remove biases or undesirable bets from our alphas. We call this process neutralization. It has implications, not surprisingly, in terms of both alphas and portfolios.
Benchmark neutralization means that the benchmark has 0 alpha. If our initial alphas imply an alpha for the benchmark, the neutralization process recenters the alphas to remove the benchmark alpha. From the portfolio perspective, benchmark neutralization means that the optimal portfolio will have a beta of 1, i.e., the portfolio will not make any bet on the benchmark.
Neutralization is a sophisticated procedure, but it isn’t uniquely defined. As the technical appendix will demonstrate, we can achieve even benchmark neutrality in more than one way. This is easy to see from the portfolio perspective: We can choose many different portfolios to hedge out any active beta.
As a general principle, we should consider a priori how to neutralize our alphas. The choices will include benchmark, cash, industry, and factor neutralization. Do our alphas contain any information distinguishing one industry from another? If not, then industry-neutralize. The a priori approach works better than simply trying all possibilities and choosing the best performer.
The first and simplest neutralization is to make the alphas benchmark-neutral. By definition, the benchmark portfolio has 0 alpha, although the benchmark may experience exceptional return. Setting the benchmark alpha to 0 ensures that the alphas are benchmark-neutral and avoids benchmark timing.
In the same spirit, we may also want to make the alphas cash-neutral; i.e., the alphas will not lead to any active cash position. It is possible (see Exercise 11 in the technical appendix) to make the alphas both cash- and benchmark-neutral.
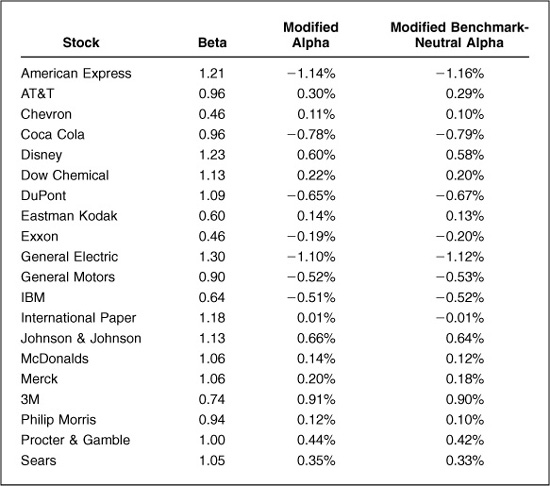
Table 14.2 displays the modified alphas from Table 14.1 and shows how they change when we make them benchmark-neutral. In this example, the benchmark alpha is only 1.6 basis points, so subtracting βn · αB from each modified alpha does not change the alpha very much. We have shifted the alpha of the benchmark Major Market Index from 1.6 basis points to 0. This small change in alpha is consistent with the observation that the optimal portfolio before benchmark neutralizing had a beta very close to 1.
The multiple-factor approach to portfolio analysis separates return along several dimensions. A manager can identify each of those dimensions as either a source of risk or a source of value added. By this definition, the manager does not have any ability to forecast the risk factors. Therefore, he or she should neutralize the alphas against the risk factors. The neutralized alphas will include only information on the factors the manager can forecast, along with specific asset information. Once neutralized, the alphas of the risk factors will be 0.
For example, a manager can ensure that her portfolios contain no active bets on industries or on a size factor. Here is one simple approach to making alphas industry-neutral: Calculate the (capitalization-weighted) alpha for each industry, then subtract the industry average alpha from each alpha in that industry.
The technical appendix presents a more detailed account of alpha analysis in the context of a multiple-factor model. We can modify the alphas to achieve desired active common-factor positions and to isolate the part of the alpha that does not influence the common-factor positions.
Up to this point, the struggle has been between alpha and active risk. Any klutz can juggle two rubber chickens. The juggling becomes complicated when the third chicken enters the performance. In portfolio construction, that third rubber chicken is transactions costs the cost of moving from one portfolio to another. It has been said that accurate estimation of transactions costs is just as important as accurate forecasts of exceptional return. That is an over-statement,5 but it does point out the crucial role transactions costs play.
In addition to complicating the portfolio construction problem, transactions costs have their own inherent difficulties. We will see that transactions costs force greater precision on our estimates of alpha. We will also confront the complication of comparing transactions costs at a point in time with returns and risk which occur over an investment horizon. The more difficult issues of what determines transactions costs, how to measure them, and how to avoid them, we postpone until Chap. 16.
When we consider only alphas and active risk in the portfolio construction process, we can offset any problem in setting the scale of the alphas by increasing or decreasing the active risk aversion. Finding the correct trade-off between alpha and active risk is a one-dimensional problem. By turning a single knob, we can find the right balance. Transactions costs make this a two-dimensional problem. The trade-off between alpha and active risk remains, but now there is a new trade-off between the alpha and the transactions costs. We therefore must be precise in our choice of scale, to correctly trade off between the hypothetical alphas and the inevitable transactions costs.
The objective in portfolio construction is to maximize risk-adjusted annual active return. Rebalancing incurs transactions costs at that point in time. To contrast transactions costs incurred at that time with alphas and active risk expected over the next year requires a rule to allocate the transactions costs over the one-year period. We must amortize the transactions costs to compare them to the annual rate of gain from the alpha and the annual rate of loss from the active risk. The rate of amortization will depend on the anticipated holding period.
An example will illustrate this point. We will assume perfect certainty and a risk free rate of zero; and we will start and end invested in cash. Stock 1’s current price is $100. The price of stock 1 will increase to $102 in the next 6 months and then remain at $102. Stock 2’s current price is also $100. The price of stock 2 will increase to $108 over the next 24 months and then remain at $108. The cost of buying and selling each stock is $0.75. The annual alpha for both stock 1 and stock 2 is 4 percent. To contrast the two situations more clearly, let’s assume that in 6 months, and again in 12 months and in 18 months, we can find another stock like stock 1.
The sequence of 6-month purchases of stock 1 and its successors will each net a $2.00 profit before transactions costs. There will be transactions costs (recall that we start and end with cash) of $0.75, $1.50, $1.50, $1.50, and $0.75 at 0, 6, 12, 18, and 24 months, respectively. The total trading cost is $6, the gain on the shares is $8, the profit over 2 years is $2, and the annual percentage return is 1 percent.
With stock 2, over the 2-year period we will incur costs of $0.75 at 0 and 24 months. The total cost is $1.50, the gain is $8, the profit is $6.50, and the annual percentage return is 3.25 percent.
With the series of stock 1 trades, we realize an annual alpha of 4 percent and an annualized transactions cost of 3 percent. With the single deal in stock 2, we realize an annual alpha of 4 percent and an annualized transactions cost of 0.75 percent. For a 6-month holding period, we double the round-trip transactions cost to get the annual transactions cost, and for a 24-month holding period, we halve the round-trip transactions cost to get the annual transactions cost. There’s a general rule here:
The annualized transactions cost is the round-trip cost divided by the holding period in years.
Chapter 16, “Transactions Costs, Turnover, and Trading,” will deal with the issues concerning the estimation and control of transactions costs. For the remainder of this chapter, we will assume that we know the cost for each anticipated trade.
Before proceeding further in our analysis of portfolio construction, we should review some practical details concerning this process. First, how do we choose a risk aversion parameter?
We briefly discussed this problem in Chap. 5. There we found an optimality relationship between the information ratio, the risk aversion, and the optimal active risk. Repeating that result here, translated from residual to active return and risk,
The point is that we have more intuition about our information ratio and our desired amount of active risk. Hence, we can use Eq. (14.3) to back out an appropriate risk aversion. If our information ratio is 0.5, and we desire 5 percent active risk, we should choose an active risk aversion of 0.05. Note that we must be careful to verify that our optimizer is using percents and not decimals.
A second practical matter concerns aversion to specific as opposed to common-factor risk. Several commercial optimizers utilize this decomposition of risk to allow differing aversions to these different sources of risk:
An obvious reaction here is, “Risk is risk, why would I want to avoid one source of risk more than another?” This is a useful sentiment to keep in mind, but there are at least two reasons to consider implementing a higher aversion to specific risk. First, since specific risk arises from bets on specific assets, a high aversion to specific risk reduces bets on any one stock. In particular, this will reduce the size of your bets on the (to be determined) biggest losers. Second, for managers of multiple portfolios, aversion to specific risk can help reduce dispersion. This will push all those portfolios toward holding the same names.
The final practical details we will cover here concern alpha coverage. First, what happens if we forecast returns on stocks that are not in the benchmark? We can always handle that by expanding the benchmark to include those stocks, albeit with zero weight. This keeps stock n in the benchmark, but with no weight in determining the benchmark return or risk. Any position in stock n will be an active position, with active risk correctly handled.
What about the related problem, a lack of forecast returns for stocks in the benchmark? Chapter 11 provided a sophisticated approach to inferring alphas for some factors, based on the alphas for other factors. We could apply the same approach in this case. For stock-specific alphas, we can use the following approach.
Let N1 represent the collection of stocks with forecasts, and N0 the stocks without forecasts. The value-weighted fraction of stocks with forecasts is
The average alpha for group N1 is
To round out the set of forecasts, set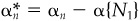 
for stocks in N1 and 
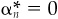for stocks in N0. These alphas are benchmark-neutral. Moreover, the stocks we did not cover will have a zero, and therefore neutral, forecast.
How often should you revise your portfolio? Whenever you receive new information. That’s the short answer. If a manager knows how to make the correct trade-off between expected active return, active risk, and transactions costs, frequent revision will not present a problem. If the manager has human failings, and is not sure of his or her ability to correctly specify the alphas, the active risk, and the transactions costs, then the manager may resort to less frequent revision as a safeguard.
Consider the unfortunate manager who underestimates transactions costs, makes large changes in alpha estimates very frequently, and revises his portfolio daily. This manager will churn the portfolio and suffer higher than expected transactions costs and lower than expected alpha. A crude but effective cure is to revise the portfolio less frequently.
More generally, even with accurate transactions costs estimates, as the horizon of the forecast alphas decreases, we expect them to contain larger amounts of noise. The returns themselves become noisier with shorter horizons. Rebalancing for very short horizons would involve frequent reactions to noise, not signal. But the transactions costs stay the same, whether we are reacting to signal or noise.
This trade-off between alpha, risk, and costs is difficult to analyze because of the inherent importance of the horizon. We expect to realize the alpha over some horizon. We must therefore amortize the transactions costs over that horizon.
We can capture the impact of new information, and decide whether to trade, by comparing the marginal contribution to value added for stock n, MCVAn, to the transactions costs. The marginal contribution to value added shows how value added, as measured by risk-adjusted alpha, changes as the holding of the stock is increases, with an off setting decrease in the cash position. As our holding in stock n increases, αn measures the effect on portfolio alpha. The change in value added also depends upon the impact (at the margin) on active risk of adding more of stock n. The stock’s marginal contribution to active risk, MCARn, measures the rate at which active risk changes as we add more of stock n. The loss in value added due to changes in the level of active risk will be proportional to MCARn. Stock n’s marginal contribution to value added depends on its alpha and marginal contribution to active risk, in particular:
Let PCn be the purchase cost and SCn the sales cost for stock n. For purposes of illustration, we take PCn = 0.50 percent and SCn = 0.75 percent. If the current portfolio is optimal,6 then the marginal contribution to value added for stock n should be less than the purchase cost. If it exceeded the purchase cost, say at 0.80 percent, then a purchase of stock n would yield a net benefit of 0.80 percent − 0.50 percent = 0.30 percent. Similarly the marginal contribution to value added must be greater than the negative of the sales cost. If it were −1.30 percent, then we could decrease our holding of stock n and save 1.30 percent at the margin. The cost would be the 0.75 percent transactions cost, for a net benefit of 1.30 percent − 0.75 percent = 0.55 percent.
This observation allows us to put a band around the alpha for each stock. As long as the alpha stays within that band, the portfolio will remain optimal, and we should not react to new information. The bandwidth is the total of the sale plus purchase costs, 0.50 percent + 0.75 percent = 1.25 percent in our example. If we just purchased a stock, its marginal contribution to value added will equal its purchase cost. We are at the upper end of the band. Any increase in alpha would lead to further purchases. The alpha would have to decrease by 1.25 percent before we would consider selling the stock. The situation before new information arrives is
or, using Eq. (14.7),
This analysis has simplified the problem by subsuming the amortization horizon into the costs SC and PC. To fully treat the issue of when to rebalance requires analyzing the dynamic problem involving alphas, risks, and costs over time. There are some useful results from this general treatment, in the very simple case of one or two assets.
Leland (1996) solves the asset allocation problem of rebalancing around an optimal stock/bond allocation. Let’s assume that the optimal allocation is 60/40. Assuming linear transactions costs and a utility function penalizing active variance (relative to the optimal allocation) and transactions costs over time, Leland shows that the optimal strategy involves a no-trade region around the 60/40 allocation. If the portfolio moves outside that region, the optimal strategy is to trade back to the boundary. Trading only to the boundary, not to the target allocation, cuts the turnover and transactions costs roughly in half, with effectively no change in risk over time. The size of the no-trade region depends on the transactions costs, the risk aversion, and the expected return and risk of stocks and bonds. Obviously, changing the size of the no-trade region will change the turnover for the strategy.
This result concerns a problem that is much simpler than our general active portfolio management problem: The solved problem is one-dimensional and does not involve the flow of information (the target allocation is static). Still, it is useful in motivating rebalancing rules driven not purely by the passage of time (e.g., monthly or quarterly rebalancing), but rather by the portfolio’s falling outside certain boundaries.
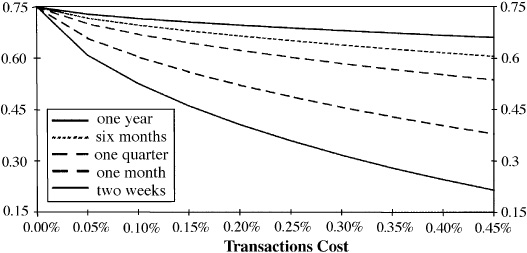
Figure 14.1 After-cost information ratio for various half-lives.
Another approach to the dynamic problem utilizes information horizon analysis, introduced in Chap. 13. Here we apply trading rules like Eq. (14.9) in the dynamic case of trading one position only, over an indefinite future,7 with information characterized by an information horizon. Figure 14.1 shows how the after-cost information ratio declines as a function of both the (one-way) cost and the half-life of the signals. Two effects are at work. First, when we trade, we pay the costs. Second, and more subtle, the transactions costs makes us less eager; we lose by intimidation.
There are as many techniques for portfolio construction as there are managers. Each manager adds a special twist. Despite this personalized nature of portfolio construction techniques, there are four generic classes of procedures that cover the vast majority of institutional portfolio management applications:8
■ Screens
■ Stratification
■ Linear programming
■ Quadratic programming
Before we examine these procedures in depth, we should recall our criteria. We are interested in high alpha, low active risk, and low transactions costs. Our figure of merit is value added less transactions costs:
We will see how each of these procedures deals with these three aspects of portfolio construction.
Screens are simple. Here is a screen recipe for building a portfolio from scratch:
1. Rank the stocks by alpha.
2. Choose the first 50 stocks (for example).
3. Equal-weight (or capitalization-weight) the stocks.
We can also use screens for rebalancing. Suppose we have alphas on 200 stocks (the followed list). Divide the stocks into three categories: the top 40, the next 60, and the remaining 100. Put any stock in the top 40 on the buy list, any stock in the bottom 100 on the sell list, and any stock in the middle 60 on the hold list. Starting with the current 50-stock portfolio, buy any stocks that are on the buy list but not in the portfolio. Then sell any assets that are in the portfolio and on the sell list. We can adjust the numbers 40, 60, and 100 to regulate turnover.
Screens have several attractive features. There is beauty in simplicity. The screen is easy to understand, with a clear link between cause (membership on a buy, sell, or hold list) and effect (membership in the portfolio). The screen is easy to computerize; it might be that mythical computer project that can be completed in two days! The screen is robust. Notice that it depends solely on ranking. Wild estimates of positive or negative alphas will not alter the result.
The screen enhances alphas by concentrating the portfolio in the high-alpha stocks. It strives for risk control by including a sufficient number of stocks (50 in the example) and by weighting them to avoid concentration in any single stock. Transactions costs are limited by controlling turnover through judicious choice of the size of the buy, sell, and hold lists.
Screens also have several shortcomings. They ignore all information in the alphas apart from the rankings. They do not protect against biases in the alphas. If all the utility stocks happen to be low in the alpha rankings, the portfolio will not include any utility stocks. Risk control is fragmentary at best. In our consulting experience, we have come across portfolios produced by screens that were considerably more risky than their managers had imagined. In spite of these significant shortcomings, screens are a very popular portfolio construction technique.
Stratification is glorified screening. The term stratification comes from statistics. In statistics, stratification guards against sample bias by making sure that the sample population is representative of the total population as it is broken down into distinct subpopulations. The term is used very loosely in portfolio construction. When a portfolio manager says he uses stratified sampling, he wants the listener to (1) be impressed and (2) ask no further questions.
The key to stratification is splitting the list of followed stocks into categories. These categories are generally exclusive. The idea is to obtain risk control by making sure that the portfolio has a representative holding in each category. As a typical example, let’s suppose that we classify stocks into 10 economic sectors and also classify the stocks in each sector by size: big, medium, and small. Thus, we classify all stocks into 30 categories based on economic sector and size. We also know the benchmark weight in each of the 30 categories.
To construct a portfolio, we mimic the screening exercise within each category. We rank the stocks by alpha and place them into buy, hold, and sell groups within each category in a way that will keep the turnover reasonable. We then weight the stocks so that the portfolio’s weight in each category matches the benchmark’s weight in that category. Stratification ensures that the portfolio matches the benchmark along these important dimensions.
The stratification scheme has the same benefits as screening, plus some. It is robust. Improving upon screening, it ignores any biases in the alphas across categories. It is somewhat transparent and easy to code. It has the same mechanism as screening for controlling turnover.
Stratification retains some of the shortcomings of a screen. It ignores some information, and does not consider slightly over-weighting one category and underweighting another. Often, little substantive research underlies the selection of the categories, and so risk control is rudimentary. Chosen well, the categories can lead to reasonable risk control. If some important risk dimensions are excluded, risk control will fail.
A linear program (LP) is space-age stratification. The linear programming approach9 characterizes stocks along dimensions of risk, e.g., industry, size, volatility, and beta. The linear program does not require that these dimensions distinctly and exclusively partition the stocks. We can characterize stocks along all of these dimensions. The linear program will then attempt to build portfolios that are reasonably close to the benchmark portfolio in all of the dimensions used for risk control.
It is also possible to set up a linear program with explicit transactions costs, a limit on turnover, and upper and lower position limits on each stock. The objective of the linear program is to maximize the portfolio’s alpha less transactions costs, while remaining close to the benchmark portfolio in the risk control dimensions.
The linear program takes all the information about alpha into account and controls risk by keeping the characteristics of the portfolio close to the characteristics of the benchmark. However, the linear program has difficulty producing portfolios with a prespecified number of stocks. Also, the risk-control characteristics should not work at cross purposes with the alphas. For example, if the alphas tell you to shade the portfolio toward smaller stocks at some times and toward larger stocks at other times, you should not control risk on the size dimension.
Quadratic programming (QP) is the ultimate10 in portfolio construction. The quadratic program explicitly considers each of the three elements in our figure of merit: alpha, risk, and transactions costs. In addition, since a quadratic program includes a linear program as a special case, it can include all the constraints and limitations one finds in a linear program. This should be the best of all worlds. Alas, nothing is perfect.
One of the main themes of this chapter is dealing with less than perfect data. The quadratic program requires a great many more inputs than the other portfolio construction techniques. More inputs mean more noise. Does the benefit of explicitly considering risk outweigh the cost of introducing additional noise? A universe of 500 stocks will require 500 volatility estimates and 124,750 correlation estimates.11 There are ample opportunities to make mistakes. It is a fear of garbage in, garbage out that deters managers from using a quadratic program.
This fear is warranted. A lack of precision in the estimate of correlations is an inconvenience in the ordinary estimation of portfolio risk. For the most part, the estimation errors will cancel out. It is an obstacle in optimization. In optimization, the portfolio is selected to, among other things, have a low level of active risk. Because the optimizer tries to lower active risk, it will take advantage of opportunities that appear in the noisy estimates of covariance but are not present in reality.
An example can illustrate the point. Suppose we consider a simple cash versus market trade-off. Let ζ be the actual volatility of the market and σ our perceived volatility. If VA* is the optimal value added that we can obtain with the correct risk estimate ζ, then the loss12 we obtain with the estimate σ is
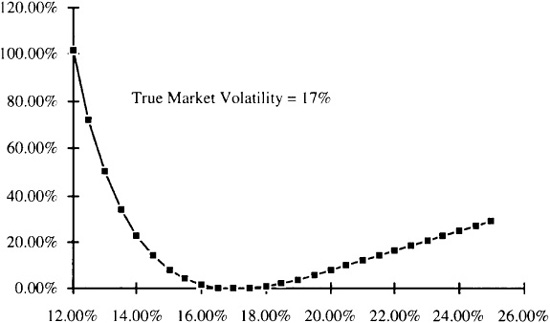
Figure 14.2 Estimated market volatility.
Figure 14.2 shows the percentage loss, Loss/VA*, as a function of the estimated market risk, assuming that the true market risk is 17 percent. In this example market volatility estimates within 1 percent of the true market volatility will not hurt value added very much but as estimation error begin to exceed 3 percent the effect on value added becomes significant especially if the error is an underestimate of volatility. In fact an underestimate of 12 percent market volatility (5 percent below the “true” volatility) leads to a negative value added.
There are two lessons here. The first is that errors in the estimates of covariance lead to inefficient implementation. The second which is more positive and indeed more important is that it is vital to have good estimates of covariance. Rather than abandon the attempt try to do a good job.
We can test the effectiveness of these portfolio construction procedures by putting them on an equal footing and judging the performance of their outputs. In this case we will input identical alphas to four procedures described below and ignore transactions costs.13
The alphas are great. They include the actual returns to the 500 stocks in the S&P 500 over the next year plus noise combined so that the correlation of the alphas with the returns (the information coefficient) is 0.1. The fundamentallaw of active management therefore predicts14 an information ratio of 2.24. So not only will we feed the same alphas into each portfolio construction method but we know what the final result should be.
The four portfolio construction techniques are
Screen I. Take the N stocks with the highest alphas and equal-weight them. Use N = 50, 100, and 150 for low, medium, and high risk aversion, respectively.
Screen II. Take the N stocks with the highest alphas and capitalization-weight them. Use N = 50, 100, and 150 for low, medium, and high risk aversion, respectively.
Strat. Take the J stocks with the highest alphas in each of the BARRA 55 industry categories. Use J = 1, 2, and 3 for low, medium, and high risk aversion portfolios, which will have 55, 110, and 165 stocks, respectively.
QP. Choose portfolios which maximize value added, assuming low, medium, and high risk aversion parameters. Use full investment and no short sales constraints, and constrain each position to constitute no more than 10 percent of the entire portfolio.
Portfolios were constructed in January 1984 and rebalanced in January 1985, January 1986, and May 1987, with portfolio performance tracked over the subsequent year. Table 14.3 contains the results.
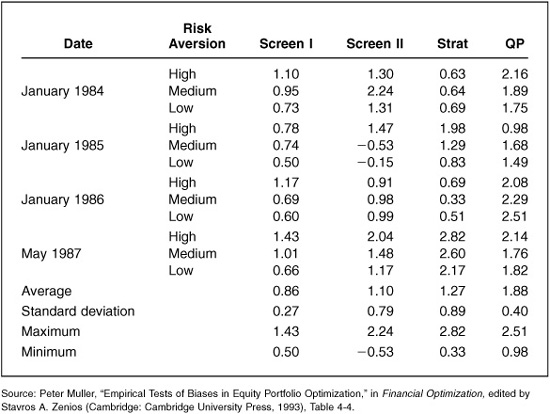
Table 14.3 displays each portfolio’s ex post information ratio. In this test, the quadratic programming approach clearly led to consistently the highest ex post information ratios. On average,it surpassed all the other techniques, and it exhibited consistent performance around that average. A stratified portfolio had the single highest ex post information ratio, but no consistency over time. The screening methods in general do not methodically control for risk, and Table 14.3 shows that one of the screened portfolios even experienced negative returns during one period.
Recall that the ex ante target for the information ratio was 2.24. None of the methods achieved that target, although the quadratic program came closest on average. Part of the reason for the shortfall is the constraints imposed on the optimizer. We calculated the target information ratio ignoring constraints. As we have seen, constraints can effectively reduce the information coefficient and hence the information ratio.
In Chap. 3, we discussed alternatives to standard deviation as risk measurements. These included semivariance, downside risk, and shortfall probability. We reviewed the alternatives and chose standard deviation as the best overall risk measure. We return to the issue again here, since our portfolio construction objective expresses our utility, which may in fact depend on alternative measures of risk. But as two research efforts show, even if your personal preferences depend on alternative risk measures, mean/variance analysis will produce equivalent or better portfolios. We present the research conclusions here, and cite the works in the bibliography.
Kahn and Stefek (1996) focus on the forward-looking nature of portfolio construction. The utility function includes forecasts of future risk. Mean/variance analysis, as typically applied in asset selection, relies on sophisticated modeling techniques to accurately forecast risk. Chapter 3 discusses in detail both the advantages of structural risk models and their superior performance.
Forecasting of alternative risk measures must rely on historical returns-based analysis. Kahn and Stefek show that higher moments of asset and asset class return distributions exhibit very little predictability, especially where it is important for portfolio construction. Return kurtosis is predictable, in the sense that most return distributions exhibit positive kurtosis (“fat tails”) most of the time.
The ranking of assets or asset classes by kurtosis exhibits very little predictability. The only exception is options, where return asymmetries are engineered into the payoff pattern.
The empirical result is that most alternative risk forecasts reduce to a standard deviation forecast plus noise, with even the standard deviation forecast based only on history. According to this research, even investors with preferences defined by alternative risk measures are better served by mean/variance analysis.15
Grinold (1999) takes a different approach to the same problem, in the specific case of asset allocation. First, he adjusts returns-based analysis to the institutional context: benchmark-aware investing with typical portfolios close to the benchmark. This is the same approach we have applied to mean/variance analysis in this book. Then he compares mean/variance and returns-based analysis, assuming that the benchmark holds no options and that all options are fairly priced.
The result is that portfolios constructed using returns-based analysis are very close to mean/variance portfolios, although they require much more effort to construct. Furthermore, managers using this approach very seldom buy options. If options are fairly priced relative to the underlying asset class, then optimization will pursue the alphas directly through the asset class, not indirectly through the options.
So Kahn and Stefek argue the asset selection case for mean/variance, and Grinold argues the asset allocation case for mean/variance. Furthermore, Grinold shows why institutional investors, with their aversion to benchmark risk, will seldom purchase options—the only type of asset requiring analysis beyond mean/variance.
As a final observation, though, some active institutional investors do buy options. We argue that they do so typically to evade restrictions on leverage or short selling, or because of liquidity concerns. Only in the case of currency options do we see much evidence of investors choosing options explicitly for their distributions. Many managers have a great aversion to currency losses, and options can provide downside protection. We still advocate using mean/variance analysis generally and, if necessary, treating currency options as a special case.
Dispersion plagues every manager running separate accounts for multiple clients. Each account sees the same alphas, benchmark, and investment process. The cash flows and history differ, however, and the portfolios are not identical. Hence, portfolio returns are not identical.
We will define dispersion as the difference between the maximum return and minimum return for these separate account portfolios. If the holdings in each account are identical, dispersion will disappear. If transactions costs were zero, dispersion would disappear. Dispersion is a measure of how an individual client’s portfolio may differ from the manager’s reported composite returns. Dispersion is, at the least, a client support problem for investment managers.
In practice, dispersion can be enormous. We once observed five investors in a particular manager’s strategy, in separate accounts, incur dispersion of 23 percent over a year. The manager’s overall dispersion may have been even larger. This was just the dispersion involving these five clients. In another case, with another manager, one client outperformed the S&P 500 by 15 percent while another underperformed by 9 percent, in the same year. At that level, dispersion is much more than a client support problem.
We can classify dispersion by its various sources. The first type of dispersion is client-driven. Portfolios differ because individual clients impose different constraints. One pension fund may restrict investment in its company stock. Another may not allow the use of futures contracts. These client-initiated constraints lead to dispersion, but they are completely beyond the manager’s control.
But managers can control other forms of dispersion. Often, dispersion arises through a lack of attention. Separate accounts exhibit different betas and different factor exposures through lack of attention. Managers should control this form of dispersion.
On the other hand, separate accounts with the same factor exposures and betas can still exhibit dispersion because of owning different assets. Often the cost of holding exactly the same assets in each account will exceed any benefit from reducing dispersion.
In fact, because of transactions costs, some dispersion is optimal. If transactions costs were zero, rebalancing all the separate accounts so that they hold exactly the same assets in the same proportions would have no cost. Dispersion would disappear, at no cost to investors. With transactions costs, however, managers can achieve zero dispersion only with increased transactions costs. Managers should reduce dispersion only until further reduction would substantially lower returns on average because much higher transactions costs would be incurred.
To understand dispersion better, let’s look at a concrete example. In this example, the manager runs an existing portfolio and receives cash to form a new portfolio investing in the same strategy. So at one point in time, the manager is both rebalancing the existing portfolio and constructing the new portfolio. The rebalanced portfolio holdings will reflect both new and old information. With zero transactions costs, the manager would rebalance to the new optimum. Given an existing portfolio, though, he rebalances only where the new information more than overcomes the transactions costs, as in Eq. (14.9).
This trade-off does not affect the new portfolio in the same way. The manager starts from cash, and while he would still like to minimize transactions costs, he assumes a fairly high transactions cost for the initial portfolio construction. For this example, we’ll assume that the new portfolio he builds is optimal and reflects entirely the manager’s new information.
Clearly there will be dispersion between the existing portfolio and the new portfolio. There are two methods by which the manager could reduce dispersion to zero. He could invest the new portfolio in the rebalanced existing portfolio. This sacrifices returns, since the new portfolio will reflect both new and old information instead of just new information. The other choice is to invest the composite in the new optimum. But this would require paying excess transactions costs. By treating the existing portfolio and the new portfolio separately, the manager accepts some level of dispersion in order to achieve higher average returns. Furthermore, he can hope that this dispersion will decrease over time.
We will now perform some static analysis to understand the causes of dispersion. First, consider dispersion caused by different betas or factor exposures. If the separate account betas range from 0.9 to 1.1 and the market return is 35 percent one year, then the dispersion would be 7 percent based just on the differing betas. This range of betas is quite large for an efficient, quantitatively run optimal process, and yet it doesn’t come close to explaining some of the extreme war stories.
Now let’s consider static analysis of managed dispersion— where the manager has matched factor exposures but not assets across all accounts—to try to understand the magnitude of the effect. In this simple model, we will consider N portfolios, all equally weighted with identical factor exposures. Each portfolio contains 100 stocks, and out of that 100 stocks, M stocks appear in all the portfolios and 100 – M stocks are unique to the particular portfolio. Furthermore, every stock has identical specific risk of 20 percent. Figure 14.3 displays the results, assuming normal distributions.
We can use the model to show that dispersion will depend on the number of stocks the portfolios have in common, the overall levels of specific risk, and the overall number of portfolios under management.
We have seen how some level of dispersion is optimal and have discussed why dispersion arises. The next question is whether dispersion decreases over time: Do dispersed portfolios converge, and how fast? In general, convergence will depend on the type of alphas in the strategy, the transactions costs, and possibly the portfolio construction methodology.
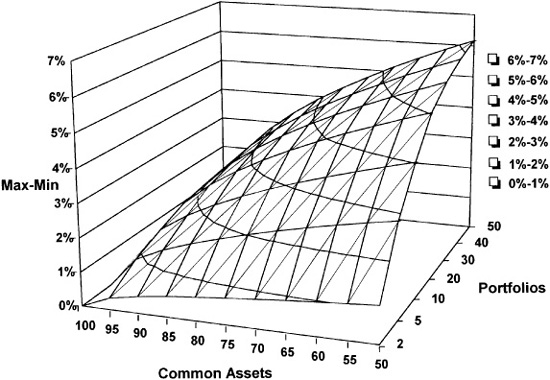
Figure 14.3 Dispersion: 100 stock portfolios.
If alphas and risk stay absolutely constant over time, then dispersion will never disappear. There will always be a transactions cost barrier. An exact matching of portfolios will never pay. Furthermore, we can show (see the technical appendix) that the remaining tracking error is bounded based on the transactions costs and the manager’s risk aversion:
where TC measures the cost of trading from the initial portfolio to the zero transactions cost optimal portfolio (which we will refer to as portfolio Q), and we are measuring tracking error and risk aversion relative to portfolio Q. With very high risk aversion, all portfolios must be close to one another. But the higher the transactions costs, the more tracking error there is. Given intermediate risk aversion of λA = 0.10 and round-trip transactions costs of 2 percent, and assuming that moving from the initial portfolio to portfolio Q in volves 10 percent turnover, Eq. (14.12) implies tracking error of 1 percent.
Since tracking error is bounded, dispersion is also bounded. Dispersion is proportional to tracking error, with the constant of proportionality dependent on the number of portfolios being managed:
where this constant of proportionality involves the inverse of the cumulative normal distribution function φ, and ψ is the tracking error of each portfolio relative to the composite (see the technical appendix for details). Figure 14.3 displays this function. For a given tracking error, more portfolios lead to more dispersion because more portfolios will further probe the extremes of the return distribution.
If the alphas and risk vary over time—the usual case—then convergence will occur. We can show that with changing alphas and risk each period, the portfolios will either maintain or, more typically, decrease the amount of dispersion. Over time, the process inexorably leads to convergence, because each separate account portfolio is chasing the same moving target. These general arguments do not, however, imply any particular time scale.
As an empirical example, we looked at five U.S. equity portfolios in a strategy with alphas based on book-to-price ratios and stock-specific alphas. Roughly two-thirds of the strategy’s value came from the book-to-price factor tilt, with one-third arising from the stock-specific alphas. We started these five portfolios in January 1992 with 100 names in each portfolio, but not the same 100 names in each portfolio. Each portfolio had roughly 3 percent tracking error relative to the S&P 500. We analyzed the initial level of dispersion and then looked at how that changed over time. We used a consistent alpha generation process and standard mean/variance optimization with uniform transactions costs. To understand convergence and transactions costs, we looked at behavior as we changed the overall level of transactions costs.
What we found was a steady decrease in average tracking error (relative to the composite) and dispersion, with the smallest dispersion exhibited when we assumed the lowest transactions costs. Figure 14.4 displays the results. So even though our starting portfolios
Figure 14.4 Convergence. (Courtesy of BARRA.)
differed, they steadily converged over a roughly 5-year period. In real-life situations, client-initiated constraints and client-specific cash flows will act to keep separate accounts from converging.
One final question is whether we can increase convergence by changing our portfolio construction technology. In particular, what if we used dual-benchmark optimization? Instead of penalizing only active risk relative to the benchmark, we would also penalize active risk relative to either the composite portfolio or the optimum calculated ignoring transactions costs.
Dual-benchmark optimization can clearly reduce dispersion, but only at an undesirable price. Dual-benchmark optimization simply introduces the trade-off we analyzed earlier: dispersion versus return. Unless you are willing to give up return in order to lower dispersion, do not implement the dual-benchmark optimization approach to managing dispersion.
The theme of this chapter has been portfolio construction in a less than perfect world. We have taken the goals of the portfolio manager as given. The manager wants the highest possible after-cost value added. The before-cost value added is the portfolio’s alpha less a penalty for active variance. The costs are for the transactions needed to maintain the portfolio’s alpha.
Understanding and achieving this goal requires data on alphas, covariances between stock returns, and estimates of transactions costs. Alpha inputs are often unrealistic and biased. Covariances and transactions costs are measured imperfectly.
In this less than perfect environment, the standard reaction is to compensate for flawed inputs by regulating the outputs of the portfolio construction process: placing limits on active stock positions, limiting turnover, and constraining holdings in certain categories of stocks to match the benchmark holdings.
These are valid approaches, as long as we recognize that their purpose is to compensate for faulty inputs. We prefer a direct attack on the causes. Treat flaws in the alpha inputs with alpha analysis: Remove biases, trim outlandish values, and scale alphas in line with expectations for value added. This strengthens the link between research and portfolio construction. Then seek out the best possible estimates of risk and transactions costs. As appropriate, use a powerful portfolio construction tool with as few added constraints as possible.
Near the end of the chapter, we returned to the topic of alternative risk measures and alternatives to mean/variance optimization. For most active institutional managers (especially those who do not invest in options and optionlike dynamic strategies such as portfolio insurance), alternatives to mean/variance analysis greatly complicate portfolio construction without improving results. At the stock selection level, results may be much worse.
Finally, we analyzed the very practical issue of dispersion among separately managed accounts. We saw that managers can control dispersion—especially that driven by differing factor exposures—but should not reduce it to zero.
1. Table 14.1 shows both alphas used in a constrained optimization and the modified alphas which, in an unconstrained optimization, lead to the same holdings. Comparing these two sets of alphas can help in estimating the loss in value added caused by the constraints. How? What is that loss in this example? The next chapter will discuss this in more detail.
2. Discuss how restrictions on short sales are both a barrier to a manager’s effective use of information and a safeguard against poor information.
3. Lisa is a value manager who chooses stocks based on their price/earnings ratios. What biases would you expect to see in her alphas? How should she construct portfolios based on these alphas, in order to bet only on specific asset returns?
4. You are a benchmark timer who in backtests can add 50 basis points of risk-adjusted value added. You forecast 14 percent benchmark volatility, the recent average, but unfortunately benchmark volatility turns out to be 17 percent. How much value can you add, given this misestimation of benchmark volatility?
5. You manage 20 separate accounts using the same investment process. Each portfolio holds about 100 names, with 90 names appearing in all the accounts and 10 names unique to the particular account. Roughly how much dispersion should you expect to see?
Chopra, Vijay K., and William T. Ziemba. “The Effects of Errors in Means, Variances, and Covariances on Optimal Portfolio Choice.” Journal of Portfolio Management, vol. 19, no. 2, 1993, pp. 6-11.
Connor, Gregory, and Hayne Leland. “Cash Management for Index Tracking.” Financial Analysts Journal, vol. 51, no. 6, 1995, pp. 75-80.
Grinold, Richard C. “The Information Horizon.” Journal of Portfolio Management, vol. 24, no. 1, 1997, pp. 57-67.
________. “Mean-Variance and Scenario-Based Approaches to Portfolio Selection.” Journal of Portfolio Management, vol. 25, no. 2, Winter 1999, pp. 10-22.
Jorion, Philippe. “Portfolio Optimization in Practice.” Financial Analysts Journal, vol. 48, no. 1, 1992, pp. 68-74.
Kahn, Ronald N. “Managing Dispersion.” BARRA Equity Research Seminar, Pebble Beach, Calif., June 1997.
Kahn, Ronald N., and Daniel Stefek. “Heat, Light, and Downside Risk.” BARRA Preprint, December 1996.
Leland, Hayne. Optimal Asset Rebalancing in the Presence of Transactions Costs. University of California Research Program in Finance, Publication 261, October 1996.
Michaud, Richard. “The Markowitz Optimization Enigma: Is ‘Optimized’ Optimal?” Financial Analysts Journal, vol. 45, no. 1, 1989, pp. 31-42.
Muller, Peter. “Empirical Tests of Biases in Equity Portfolio Optimization.” In Financial Optimization, edited by Stavros A. Zenios (Cambridge: Cambridge University Press, 1993), pp. 80-98.
Rohweder, Herold C. “Implementing Stock Selection Ideas: Does Tracking Error Optimization Do Any Good?” Journal of Portfolio Management, vol. 24, no. 3, 1998, pp. 49-59.
Rudd, Andrew. “Optimal Selection of Passive Portfolios.” Financial Management, vol. 9, no. 1, 1980, pp. 57-66.
Rudd, Andrew, and Barr Rosenberg. “Realistic Portfolio Optimization.” TIMS Study in the Management Sciences, vol. 11, 1979, pp. 21-46.
Stevens, Guy V. G. “On the Inverse of the Covariance Matrix in Portfolio Analysis.” Journal of Finance, vol. 53, no. 5, 1998, pp. 1821-1827.
This appendix covers three topics: alpha analysis, in particular how to neutralize alphas against various factor biases; the loss of value added due to errors in the estimated covariance matrix; and dispersion.
Our goal in this section is to separate alphas into common-factor components and specific components, and correspondingly to define active portfolio positions arising from these distinct components. This will involve considerable algebra, but the result will allow us to carefully control our alphas: to neutralize particular factor alphas and even to input factor alphas designed to achieve target active factor exposures.
We will analyze stock alphas in the context of a multiple-factor model with N stocks and K factors:
We make the usual assumptions that b and u are uncorrelated, and that the components of u are uncorrelated. The model has the covariance structure
The unconstrained portfolio construction procedure leads to an active position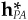 
determined by the first-order conditions:
where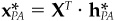 
is the active factor position.
We now want to separate α into a common-factor component αCF and a specific component αSP, and similarly separate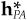 
into common-factor holdings hCF and specific holdings hSP. We will eventually see that each component will separately satisfy Eq. (14A.3), with the common-factor alpha component leading to the common-factor active positions and the specific alpha component leading to the specific active positions and containing zero active factor positions.
Equation (14A.3) uniquely determines the optimal active holdings 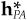and optimal active factor exposures 
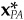. However, it does not uniquely determine a separation of 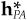into hCF and hSP: There are an infinite number of portfolios with active factor exposures 
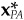. We can uniquely define the separation if we stipulate that hCF is the minimum-risk portfolio with factor exposures .
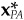Let H be the K by N matrix with factor portfolios as rows. The matrix H is
Note that H · X = I; each factor portfolio has unit exposure to its factor and zero exposure to all the other factors. Also remember that each factor portfolio has minimum risk, given its factor exposures.
Then, starting with the uniquely defined 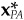and our definition of hCF as the minimum-risk portfolio with these factor exposures, we find
Knowing that hCF and hSP add up to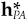 
and applying additional algebra, we find that
Exercise 1 at the end of this appendix asks the reader to demonstrate Eq. (14A.5), i.e., that, as defined, hCF does lead to the minimum-risk portfolio with factor exposures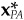 
. Exercise 2 asks the reader to demonstrate that hSP does not contain any common-factor exposures, i.e., that XT · hSP = 0.
The separation of the optimal holdings into common-factor and specific holdings has been the hard part of our task. With this behind us, the easier part is to separate α into a common-factor component αCF and a specific component αSP. These are
and
Notice that 
is the alpha of each of the K factor portfolios. Call 
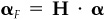the factor alphas. Then 
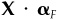maps those factor alphas back onto the assets.
So we have separated both the optimal active holdings and the alphas into common-factor and specific pieces. We can also check the correspondence between common-factor alphas and common-factor holdings, and between specific alphas and specific holdings. According to Eq. (14A.3), the optimal active common-factor exposures are
Exercises 4, 5, and 6 help to show that just using αCF will lead to active holdings hCF and common-factor exposures 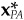and that αSP will lead to active holdings hSP and common-factor exposures of zero.
How can we use this glut of algebra? Suppose we believe that our alphas contain valuable information only for specific stock selection. Instead of relying on any factor forecasts inadvertently contained in our alphas, we have defined a target active position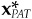 
for the common factors. To achieve this target, we can replace the original alpha α with α′, where
The first term on the right-hand side of Eq. (14A.10) replaces αCF and will result in an active common-factor exposure of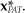 
The second term on the right-hand side of Eq. (14A.10) does not affect the common-factor positions and preserves the pure stock selection information from the original set of alphas.
The columns of the N by K matrix V · HT are of particular interest. Column k of V · HT leads to an active factor position that is positive for factor k and zero for all other factors. This insight can provide us with pinpoint control over the factors. Let’s say we partition the factors so that x = {y,z}, where we are willing to take an active position on the y factors and no active position on the z factors. Then we could set
where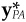 
is the y component of 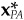. This would result in no active position on the z factors. If we wanted no active positions on any of the factors, we could set 
.
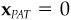We now turn to the second topic of this technical appendix: the erosion in value added due to inaccuracies in our estimated covariance matrix.
Consider a situation where the true covariance matrix is V, but the manager uses a covariance matrix U ≠ V. To simplify matters, assume that the manager imposes no constraints. Using Eq. (14A.3), the manager then will choose optimal active positions
Using V and 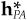, the value added (risk-adjusted return) for the manager will be 
:
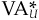If the manager had known the true covariance matrix, the active position would have been
with value added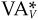 
:
The loss in value added is just the difference between 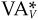and 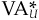. Using Eqs. (14A.12) and (14A.14), this becomes
where we have defined the loss as a positive quantity (i.e., the amount lost). You can see that if U = V, this term becomes zero.
Here we derive two results stated in the main text. First, we derive a bound on tracking error in the presence of transactions costs. Start with initial portfolio I and zero transactions cost optimal portfolio Q, which we will treat as a benchmark. To find an optimal solution, portfolio P, we will trade off tracking error relative to portfolio Q against the transactions costs of moving from portfolio I to portfolio P:
where PC is a vector of purchase costs, SC is a vector of sell costs, the inner maximum functions look element by element to determine whether we are purchasing or selling, and we have defined the active portfolio relative to portfolio Q. This optimization includes alphas implicitly, in portfolio Q.
At optimality,
where the elements of PC′ match those of PC only if at optimality hPA(n) > hIA(n) and are zero otherwise. We similarly define the elements of SC′ based on whether we are selling the asset.
If we multiply Eq. (14A.18) by 
, we find
Now focus on an asset n that we purchased, hP(n) > hI(n). For this asset, we expect hQ(n) ≥ hP(n), i.e., if it were not for transactions costs, we would have purchased even more and moved all the way from h1(n)to hQ(n). Therefore,
and, once again for purchased assets,
Similar arguments hold for sold assets. If we define
then Eqs. (14A.20), (14A.21), and (14A.19) imply
This is the result in the main text.
The other dispersion result we want to derive here concerns the expected dispersion for N portfolios, each with tracking error of ψ relative to a composite portfolio. Assuming that active returns rPA relative to the composite are independent and normally distributed with mean 0 and standard deviation ψ, the probability of observing an active return less than some rPA,max is
The probability of observing N independent active returns, each less than rPA,max, is
We can therefore solve for the expected (median) rPA,max as
or
Assuming symmetry, we will find a similar result for the expected minimum Hence
as reported in the main text.
1. Show that the minimum-risk portfolio with factor exposures XP is given by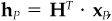 
where H is defined in Eq. (14A.4). Recall that a portfolio is diversified with respect to the factor model (X,F,Δ), diversified for short, if it has minimum risk among all portfolios with the same factor exposures. This result says that all diversified portfolios are made up of a weighted combination of the factor portfolios.
2. Show that the optimal specific asset holdings hSP, defined in Eq. (14A.6), have zero exposure to all the factors, i.e.,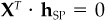 
.
3. Establish the following: If the benchmark portfolio is diversified and the alphas are benchmark-neutral, then both αCF and αSP are benchmark-neutral.
4. Establish the identities
Hint: Recall Exercise 5 in the technical appendix of Chap. 3.
5. Establish the identity
6. Show that the common-factor component of alpha leads to the common-factor holdings, i.e.,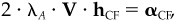 
and that the specific component of alpha leads to the specific holdings, i.e., 
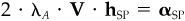This implies the identities
and
7. This exercise invokes regression to separate the components of alpha. Show that we can calculate the factor alphas αF using a weighted regression, α = X · αF + ε, with weights inversely proportional to specific variance. The residual of this regression, i.e., ε, will equal αSP.
8. Suppose we wish to constrain the common-factor exposures to satisfy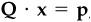 
where Q is a J by K matrix of rank J. This could constrain some factor exposures and leave others unconstrained. Let p* be the result using the original alpha and an unconstrained optimization, i.e., 
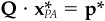. Show that the revised alpha
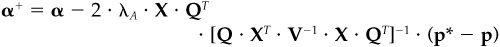
will result in a portfolio that satisfies the constraints.
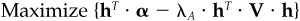
subject to the inequality constraints
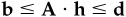
Show that any modified α+, where α+ satisfies
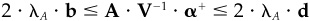
will produce a portfolio that satisfies the inequality constraints. How would you choose α+?
10. Input alphas are cash-neutral if they lead to an active cash position of zero. Show that alphas are cash-neutral if and only if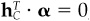 
, where hC is the fully invested portfolio with minimum risk.
11. To make the alphas both benchmark- and cash-neutral, modify them as follows:
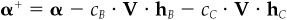
Choose the constants cB and cC to ensure benchmark neutrality,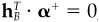
, and cash neutrality, 
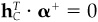. Why?
For these exercises, you will need alphas from a dividend discount model for all MMI stocks. (Alternatively, you could use alphas from some other valuation model, but it would be useful to have some intuition for these sources of alphas.)
1. Generate the unconstrained optimal portfolio using moderate active risk aversion of λA = 0.10 and the CAPMMI as benchmark. What is the optimal portfolio beta? What are the factor exposures of the optimal portfolio? Discuss any concerns over these factor exposures.
2. Now industry-neutralize the alphas and reoptimize. What are the new factor exposures? Compare the benefits of this portfolio to the previous optimal portfolio. How would you justify an argument that the first portfolio should outperform the second?
