In Chap. 5, the information ratio played the role of the “assumed can opener” for our investigation of active strategies. In this chapter, we will give that can opener more substance by finding the attributes of an investment strategy that will determine the information ratio.
The insights that we gain will be useful in guiding a research program and in enhancing the quality of an investment strategy. Major points in this chapter are:
■ A strategy’s breadth is the number of independent, active decisions available per year.
■ The manager’s skill, measured by the information coefficient, is the correlation between forecasts and results.
■ The fundamental law of active management explains the information ratio in terms of breadth and skill.
■ The additivity of the fundamental law allows for an attribution of value added to different components of a strategy.
The information ratio is a measure of a manager’s opportunities. If we assume that the manager exploits those opportunities in a way that is mean/variance-efficient, then the value added by the manager will be proportional to the information ratio squared. As we saw in Chap. 5, all investors seek the strategies and managers with the highest information ratios. In this chapter, we investigate how to achieve high information ratios.
A simple and surprisingly general formula called the fundamental law of active management gives an approximation to the information ratio. We derive the result in the technical appendix. The law is based on two attributes of a strategy, breadth and skill. The breadth of a strategy is the number of independent investment decisions that are made each year, and the skill, represented by the information coefficient, measures the quality of those investment decisions. The formal definitions are as follows:
BR is the strategy’s breadth. Breadth is defined as the number of independent forecasts of exceptional return we make per year.
IC is the manager’s information coefficient. This measure of skill is the correlation of each forecast with the actual outcomes. We have assumed for convenience that IC is the same for all forecasts.
The law connects breadth and skill to the information ratio through the (approximately true) formula:
The approximation underlying Eq. (6.1) ignores the benefits of reducing risk that our forecasts provide. For relatively low values of IC (below 0.1), this reduction in risk is extremely small. We consider the assumptions behind the law in detail in a later section.
To increase the information ratio from 0.5 to 1.0, we need to either double our skill, increase our breadth by a factor of 4, or do some combination of the above.
In Chap. 5, we established a relationship [Eq. (5.10)] between the level of residual risk and the information ratio. With the aid of the fundamental law, we can express that relationship in terms of skill and breadth:
We see that the desired level of aggressiveness will increase directly with the skill level and as the square root of the breadth. The breadth allows for diversification among the active bets so that the overall level of aggressiveness ω* can increase. The skill increases the possibility of success; thus, we are willing to incur more risk, since the gains appear to be larger.
The value a manager can add depends on the information ratio [Eq. (5.12)]. If we express the manager’s ability to add value in terms of skill and breadth, we see
The value added by a strategy (the risk-adjusted return) will increase with the breadth and with the square of the skill level.
The fundamental law is designed to give us insight into active management. It isn’t an operational tool. A manager needs to know the trade-offs between increasing the breadth of the strategy BR—by either covering more stocks or shortening the time horizons of the forecasts—and improving skill IC. Thus we can see that a 50 percent increase in the strategy breadth (with no diminution in skill) is equivalent to a 22 percent increase in skill (maintaining the same breadth). A quick calculation of this sort may be quite valuable before launching a major research project. Operationally, it will prove difficult in particular to estimate BR accurately, because of the requirement that the forecasts be independent.
Figure 6.1 shows the trade-offs between breadth and skill for two levels of the information ratio.
We can see the power of the law by making an assessment of three strategies. In each strategy, we want an information ratio of 0.50. Start with a market timer who has independent information about market returns each quarter. The market timer needs an information coefficient of 0.25, since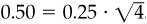 
. As an alternative, consider a stock selecter who follows 100 companies and revises the assessments each quarter. The stock selecter makes 400 bets per year; he needs an information coefficient of 0.025, since 
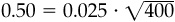. As a third example, consider a specialist who follows two companies and revises her bets on each 200 times per year. The specialist will make 400 bets per year and require a skill level of 0.025. The stock selecter achieves breadth by looking at a large number of companies intermittently, and the specialist achieves it by examining a small group of companies constantly. We can see from these examples that strategies with similar information ratios can differ radically in the requirements they place on the investor.
We can give three very straightforward examples of the law in action. First, consider a gambling example. Since we want to be successful active managers, we will play the role of the casino. Let’s take a roulette game where bettors choose either red or black. The roulette wheel has 18 red spots, 18 black spots, and 1 green spot. Each of the 37 spots has probability 1/37 of being selected at each turn of the wheel. The green spot is our advantage.
If the bettor chooses black, the casino wins if the wheel stops on green or red. If the bettor chooses red, the casino wins if the wheel stops on green or black. Consider a $1.00 bet. The casino puts up a matching $1.00; that’s the casino’s investment. The casino will end up with $2.00 (a plus 100 percent return) with probability 19/37, and with zero (a minus 100 percent return) with probability 18/37. The casino’s expected percentage return per $1.00 bet is
The standard deviation of the return on that single bet is 99.9634%.1 If there is one bet of $1.00 in a year, the information ratio for the casino will be 0.027038 = 2.7027/99.9634. In this case, our skill is 1/37 and our breadth is one. The formula predicts an information ratio of 0.027027. That’s pretty close.
We can see the dramatic effect breadth has by operating like a real casino and having 1 million bets of $1.00 in a year. Then the expected return will remain at 2.7027 percent, but the standard deviation drops to 0.09996 percent. This gives us an information ratio of 27.038. The formula predicts 
We could (American casinos do) add another green spot on the wheel and increase our advantage to 2/38. Then our expected return per bet will be 5.263 percent, and the standard deviation will be 99.861 percent. For 1 million plays per year, the expected return stays at 5.263 percent, and the standard deviation drops to 0.09986 percent. The information ratio is 52.70. The formula with IC = 2/38, and BR = 1,000,000 leads to an information ratio of 52.63. Owning a casino beats investment management hands down.
As a second example, consider the problem of forecasting semiannual residual returns on a collection of 200 stocks. We will designate the residual returns as θn. To make the calculations easier, we assume that
■ The residual returns are independent across stocks.
■ The residual returns have an expected value of zero.
■ The standard deviation of the semiannual residual return is 17.32 percent—that’s 24.49 percent annual for each stock.
Our information advantage is an ability to forecast the residual returns. The correlation between our forecasts and the subsequent residual returns is 0.0577. One way to picture our situation is to imagine the residual return itself as the sum of 300 independent terms for each stock, θn,j for j = 1,2,..., 300:
where each θn,j is equally likely to be +1.00 percent or −1.00 percent. Each θn,j will have a mean of 0 and standard deviation of 1.00 percent. The standard deviation of 300 of these added together will be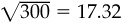 
.
Our forecasting procedure tells us θn,1 and leaves us in the dark about θn,2 through θn,300. The correlation of θn,1 with θn will be 0.0577.2 There are 300 equally important things that we might know about each stock, and we know only 1 of them. We don’t know very much.
Since we are following 200 stocks, we will have 200 pieces of information twice a year, for a total of 400 per year. Our information coefficient, the correlation of θn,1 and θn, is 0.0577. According to the fundamental law, the information ratio should be 0.0577 ·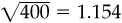 
.
Can we fashion an investment strategy that will achieve an information ratio that high? In order to describe a portfolio strategy to exploit this information and calculate its attributes easily, we need a simplifying assumption. Assume that the benchmark portfolio is an equal-weighted portfolio of the 200 stocks (0.50 percent each). In each 6-month period, we expect to have about 100 stocks with a forecasted residual return for the quarter of + 1.00 percent and 100 stocks with a forecasted residual return of −1.00 percent. This is akin to a buy list and a sell list. We will equal-weight the buy list (at 1.00 percent each), and not hold the sell list.
The expected active return will be 1.00 percent per 6 months with an active standard deviation of 1.2227 percent per 6 months.3 The 6-month information ratio is 0.8179. To calculate an annual information ratio, we multiply the 6-month information ratio by the square root of 2, to find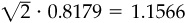 
. This is slightly greater than the 1.154 predicted by the formula, since the formula does not consider the slight reduction in uncertainty resulting from the knowledge of θn,1.4
We can also consider a third example, to put the information coefficient in further context. Suppose we want to forecast the direction of the market each quarter. In this simple example, we care only about forecasting direction. We will model the market direction as a variable x(t) = ±1, where x has mean 0 and standard deviation 1. Our forecast is y(t) = ± 1, also with mean 0 and standard deviation 1. Then the information coefficient—the correlation of x(t) and y(t)—depends on the covariance of x(t) and y(t):
where we observe N bets on market direction.
If we correctly forecast market direction (x = y) N1 times, and incorrectly forecast market direction (x =−y) N — N1 times, then the information coefficient is
Equation (6.6) provides some further intuition into the information coefficient. For example, we saw that an information coefficient of 0.0577 can lead to an information ratio above 1.0 (top decile, according to Chap. 5). Using Eq. (6.6), an IC = 0.0577 corresponds to correctly forecasting direction only 52.885 percent of the time—a small edge indeed.
These examples not only show the formula at work, but also show how little information one needs in order to be highly successful. In fact, an information coefficient of 0.02 between forecasted stock return and realized return over 200 stocks each quarter [with an implied accuracy of only 51 percent according to Eq. (6.6)] will produce a highly respectable information ratio of 0.56.
The fundamental law is additive in the squared information ratios. Suppose there are two classes of stocks. In class 1 you have BR1 stocks and a skill level of IC1. Class 2 has BR2 stocks and a skill level IC2. The information ratio for the aggregate will be
assuming optimal implementation of the alphas across the combined set of stocks.5 Notice that this is the sum of the squared information ratios for the first class and second class combined. Suppose the manager currently follows 200 stocks with semiannual forecasts; the breadth is 400. The information coefficient for these forecasts is 0.04. The information ratio will be 
. How would the information ratio and value added increase if the manager was to follow an additional 100 stocks (again with two forecasts per year) with information coefficient 0.03? The manager’s value added will be proportional to 0.64 + (0.03)2 · 200 = 0.64 + 0.18 = 0.82. There will be a 28 percent increase in the manager’s ability to add value. The information ratio will increase from 0.8 to 
.
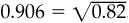The additivity works along other dimensions as well. Suppose a manager follows 400 equities and takes a position on these on the average of once per year. The manager’s information coefficient is 0.03. This yields an information ratio of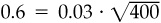 
. In addition, the manager makes a quarterly forecast on the market. The information coefficient for the market forecasts is 0.1. The information ratio for the market timing is 
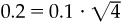. The overall information ratio will be the square root of the sum of the squared information ratios for stock selection and market timing: 0.63.
We can even carry this notion to an international portfolio. Figure 6.2 shows the breakdown of return on an international portfolio. The active return comes from three main sources: active currency positions, active allocations across countries, and active allocations within country markets.
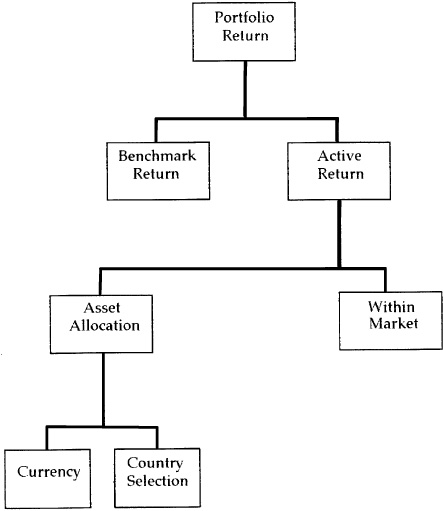
Assume that we are based in London, and that we invest in four countries: the United States, Japan, Germany, and the United Kingdom. There are three currency bets available to us;6 we revise our currency position each quarter, and so we make 12 independent bets per year. We also make active bets across countries. These bet on the local elements of market return (separated from the currency component). We revise these market allocations each quarter. In addition we select stocks in each of the markets. We follow 400 stocks in the United States, 300 in Japan, 200 in the United Kingdom, and 100 in Germany. We revise our forecasts on these stocks once a year. Suppose our skill levels are ICC for currency, ICM for market allocation, and ICUS, ICJ, ICUK, and ICG for the national stocks. The overall information ratio will be
To make things simple, suppose that ICUS = ICJ = ICUK = ICG = 0.02. Then the squared information ratio contribution from the stocks will be 0.40 = 1000 · (0.02)2. For the timing component to contribute equally, we would need ICC = ICM = 0.129, since 0.40 = 24 · (0.129)2. Consider a more realistic (although still optimistic) information coefficient of 0.075 for the currency and market allocation decisions. That would make the contribution from currency and market allocation 0.135. The total squared information ratio would be 0.535 = 0.40 + 0.135. The total information ratio is 
.
The additivity holds across managers. In this case, we must assume that the allocation across the managers is optimal. Suppose a sponsor hires three equity managers with information ratios 0.75, 0.50, and 0.30. Then the information ratio that the sponsor can obtain is 0.95,7 since (0.95)2 = (0.75)2 + (0.50)2 + (0.30)2.
There are other applications of the law. Most notable is its use in scaling alphas; i.e., making sure that forecasts of exceptional stock returns are consistent with the manager’s information ratio. That point will be discussed in Chap. 14, “Portfolio Construction.”
The law, like everything else, is based on assumptions that are not quite true. We’ll discuss some of those assumptions later. However, the basic insight we can gain from the law is clear: It is important to play often (high BR) and to play well (high IC).
The forecasts should be independent. This means that forecast 2 should not be based on a source of information that is correlated with the sources of forecast 1. For example, suppose that our first forecast is based on an assumption that growth stocks will do poorly, and our second is based on an assumption that high-yield stocks will do well. These pieces of information are not independent; growth stocks tend to have very low yields, and not many high-yield stocks would be called growth stocks. We’ve just picked out two ways to measure the same phenomenon. In example of independent forecasts is a quarterly adjustment of the portfolio’s beta from 1.00 to either 1.05 or 0.95 as a market timing decision based on new information each quarter.
In a situation where analysts provide recommendations on a firm-by-firm basis, it is possible to check the level of dependence among these forecasts by first quantifying the recommendations and then regressing them against attributes of the firms. Analysts may like all the firms in a particular industry: Their stock picks are actually a single industry bet. All recommended stocks may have a high earnings yield: The analysts have made a single bet on earnings-to-price ratios. Finally, analysts may like all firms that have performed well in the last year; instead of a firm-by-firm bet, we have a single bet on the concept of momentum. More significantly, the residuals of the regression will actually be independent forecasts of individual stock return. Thus the regression analysis gives us the opportunity both to uncover consistent patterns in our recommendations and to remove them if we choose.
The same masking of dependence can occur over time. If you reassess your industry bets on the basis of new information each year, but rebalance your portfolios monthly, you shouldn’t think that you make 12 industry bets per year. You just make the same bet 12 times.
We can see how dependence in the information sources will lower our overall skill level with a simple example. Consider the case where there are two sources of information. Separately, each has a level of skill IC; that is, the forecasts have a correlation of IC with the eventual returns. However, if the two information sources are dependent, then the information derived from the second source is not entirely new. Part of the second source’s information will just reinforce what we knew from the first source, and part will be new or incremental information. We have to discover the value of the incremental information. As one can imagine, the greater the dependence between the two information sources, the lower the value of the incremental information. If γ is the correlation between the two information sources, then the skill level of the combined sources, IC(com), will be
If there is no correlation between sources (γ = 0), then IC2(com) = 2 · IC2—the two sources will add in their ability to add value. As γ increases toward 1, the value of the second source diminishes.
For example, recall the case earlier in this chapter where the residual return θn on stock n was made up of 300 nuggets of return θn,j for j = 1,2,..., 300. Suppose we have two information sources on the stocks. Source 1 knows θn,1 and θn,2 and source 2 knows θn,2 and θn,3. The information coefficient of each source is 0.0816. In this situation, the information coefficient of the combined sources will be 0.0942, since the information supplied by source 2 is correlated with that supplied by source 1; γ = 0.5. The formula gives 
, which you can confirm by a direct calculation.
The law is based on the assumption that each of the BR active bets has the same level of skill. In fact, the manager will have greater skills in one area than another. We can see from the additivity principle, Eq. (6.7), that the square of the information ratio is the sum of the squares of the information ratios for the particular sources. Figure 6.3 demonstrates this phenomenon. If we order the information sources from highest skill level to lowest, then the total value added is just the area under the “skill” curve. Notice that the law assumes that the skill curve is horizontal; i.e., we replace the sum of the skill levels by an average skill level.
The strongest assumption behind the law is that the manager will accurately gauge the value of information and build portfolios that use that information in an optimal way. This requires insight and humility, a desirable combination that is not usually found in one individual.
A few investment professionals interpret the fundamental law of active management as a version of the statistical law of large numbers. This is a misinterpretation of one law or both. The law of large numbers says that sample averages for large samples will be very close to the true mean, and that our approximation of the true mean gets better and better as the sample gets larger.
The fundamental law says that more breadth is better if you can maintain the skill level. However, the law is just as valid with a breadth of 10 as with a breadth of 1000. The information ratio is still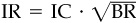 
.
This confusion stems from the role of breadth. More breadth at the same skill level lets us diversify the residual risk. This is analogous to the role of large sample sizes in the law of large numbers, where the large sample size allows us to diversify the sampling error.
The fundamental law is a guideline, not an operational tool. It is desirable that we have some faith in the law’s ability to make reasonable predictions. We have conducted some tests of the law and found it to be excellent in its predictions.
The tests took the following form: Each year we supply alphas for BR stocks. The alphas are a mixture of the residual return on the stock over the next year and some random noise. The mixture can be set8 so that the correlation of the forecasts with the residuals will be IC. That gives us a prediction of the information ratio that we should realize with these alphas.
The realized information ratios for optimal portfolios based on these forecasts are statistically indistinguishable from the forecasts of the fundamental law. When we then impose institutional constraints limiting short sales, the realized information ratios drop somewhat.
The law encourages managers to have an eclectic style. If a manager can find some independent source of information that will be of use, then he or she should exploit that information. It is the manager’s need to present a clear picture of his or her style to clients that inhibits the manager from adopting an eclectic style. At the same time, the sponsor who hires a stable of managers has an incentive to diversify their styles in order to ensure that their bets are independent. The way investment management is currently organized in the United States, the managers prepare the distinct ingredients and the sponsor makes the stew.
We have shown how the information ratio of an active manager can be explained bytwo components:the skill (IC)ofthe investment manager and the breadth (BR) of the strategy. These are related to the value added by the strategy by a simple formula [Eq. (6.3)].
Three main assumptions underlie this result. First and foremost, we assumed that the manager has an accurate measure of his or her own skills and exploits information in an optimal way. Second, we assumed that the sources of information are independent; i.e., the manager doesn’t bet twice on a repackaged form of the same information. Third, we assumed that the skill involved in forecasting each component, IC, is the same. The first assumption, call it competence or hypercompetence, is the most crucial. Investment managers need a precise idea of what they know and, more significantly, what they don’t know. Moreover, they need to know how to turn their ideas into portfolios and gain the benefits of their insights. The second two assumptions are merely simplifying approximations and can be mitigated by some of the devices mentioned above.
The message is clear: you must play often and play well to win at the investment management game. It takes only a modest amount of skill to win as long as that skill is deployed frequently and across a large number of stocks.
1. Manager A is a stock picker. He follows 250 companies, making new forecasts each quarter. His forecasts are 2 percent correlated with subsequent residual returns. Manager B engages in tactical asset allocation, timing four equity styles (value, growth, large, small) every quarter. What must Manager B’s skill level be to match Manager A’s information ratio? What information ratio could a sponsor achieve by employing both managers, assuming that Manager B has a skill level of 8 percent?
2. A stock picker follows 500 stocks and updates his alphas every month. He has an IC = 0.05 and an IR = 1.0. How many bets does he make per year? How many independent bets does he make per year? What does this tell you about his alphas?
3. In the example involving residual returns θn composed of 300 elements θn,j, an investment manager much choose between three research programs:
a. Follow 200 stocks each quarter and accurately forecast θn,12 and θn,15.
b. Follow 200 stocks each quarter and accurately forecast θn,5 and θn,105.
c. Follow 100 stocks each quarter and accurately forecast θn,5, θn,12, and θn,105.
Compare the three programs, all assumed to be equally costly. Which would be most effective (highest value added)?
Divecha, Arjun, and Richard C. Grinold. “Normal Portfolios: Issues for Sponsors, Managers and Consultants.” Financial Analysts Journal, vol. 45, no. 2, 1989, pp. 7-13.
Ferguson, Robert. “Active Portfolio Management.” Financial Analysts Journal, vol. 31, no. 3, 1975, pp. 63-72.
——. “The Trouble with Performance Measurement.” Journal of Portfolio Management, vol. 12, no. 3, 1986.
Fisher, Lawrence. “Using Modern Portfolio Theory to Maintain an Efficiently Diversified Portfolio.” Financial Analysts Journal, vol. 31, no. 3, 1975, pp. 73-85.
Grinold, Richard. “The Fundamental Law of Active Management.” Journal of Portfolio Management, vol. 15, no. 3, 1989, pp. 30-37.
Jacobs, Bruce I., and Kenneth N. Levy. “The Law of One Alpha.” Journal of Portfolio Management, vol. 21, no. 4, 1995, pp. 78-79.
Rosenberg, Barr. “Security Appraisal and Unsystematic Risk in Institutional Investment.” Proceedings of the Seminar on the Analysis of Security Prices (Chicago: University of Chicago Press, November 1976), pp. 171-237.
Rudd, Andrew. “Business Risk and Investment Risk.” Investment Management Review, November-December 1987, pp. 19-27.
Sharpe, William F. “Mutual Fund Performance.” Journal of Business, vol. 39, no. 1, January 1966, pp. 66-86.
Treynor, Jack, and Fischer Black. “How to Use Security Analysis to Improve Portfolio Selection.” Journal of Business, vol. 46, no. 1, 1973, pp. 66-86.
In this appendix we derive the fundamental law. The derivation includes three steps:
■ Measuring the impact of the information on the means and variances of the returns
■ Solution for the optimal policy
■ Calculation and approximation of the information ratio
To facilitate the analysis, we will introduce orthogonal bases for both the residual returns and the information signals. We require these independent bases in order to isolate the independent bets driving the policy.
We can express the excess returns on the universe of N securities as
where β = the asset’s betas with respect to the benchmark
θ = the residual returns
rB = the excess return on the benchmark
We will model the residual returns θ as
where x = a vector of N uncorrelated standardized random variables, each with mean 0 and standard deviation 1
A = an N by N matrix equal to the square root of the residual covariance matrix of r; i.e.,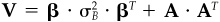 
Note that A has rank N — 1, since the benchmark holdings hB will satisfy AT · hB = 0.
If the residual returns are uncorrelated, then A is simply a diagonal matrix of residual risks. More generally, A linearly translates between the correlated residual returns and a set of uncorrelated movements.
Our information arrives as BR signals z. With very little loss of generality, we can assume that these signals z have a joint normal distribution with mean 0 and standard deviation equal to 1. We write z as
y = J · zT
where y = a vector of BR uncorrelated random variables, each with mean 0 and standard deviation equal to 1
E = the square root of the covariance matrix of z; i.e., Var{z} = E · ET
J = the inverse of E
So our signals may be correlated. The matrix E, like the matrix A, translates to an equivalent set of uncorrelated signals. At one extreme, our signals may contain stock-specific information. Then E is the identity matrix. But for industry momentum signals, for example, E may separate industry-specific information from sector and marketwide information.
Let Q = Cov{θ,z} be the N by BR covariance matrix between the residual returns θ and signals z, and let P = Corr{x,y} be the N by BR correlation matrix between the vectors x and y. It follows that Q = A · P · ET. The items of interest to the active manager are the mean and variance of θ conditional on the signal z. These are9
Note:
■ The unconditional expectation of α(z) is 0.
■ The conditional variance of the residual returns is independent of the value of z.
■ The unconditional variance of the alphas is Var{α(z)} A · P · PT · AT.
The active manager’s objective is to maximize the value added through stock selection, as derived in Chap. 4. We are ignoring the benchmark timing component, although that will reappear in a later chapter devoted to benchmark timing.
The objective is: Given z, choose a residual position (i.e., β = 0) h*(z) to solve the optimization problem
This is the standard optimization, here conditional on particular information z. We will not impose the full investment condition, but rather the residual condition of zero beta.
The first-order conditions for the maximization problem, Eq. (6A.6), are
or, using Eqs. (6A.4) and (6A.5),
The additional restriction that h*(z) is a residual position, i.e., βT · h*(z) = 0, will uniquely determine h*(z). With some manipulation, we find
with
We have derived the optimal holdings, conditional on z. From here, we will need to calculate the information ratio conditional on z, and then take the expectation over the distribution of possible values of z.
The optimal portfolio’s alpha is
while the optimal portfolio’s residual variance is
where the matrix calculations in Eqs. (6A.11) and (6A.12) are identical. Therefore, the squared information ratio conditional on the knowledge z, will be
The unconditional squared information ratio is
where Tr{•} is the trace (sum of the diagonal elements) and we have taken the expectation of the uncorrelated N[0,1] random variables y. (Note that E{y2} = 1.)
We complete our analysis by approximating Tr{PT · D · P}. We can write D as
so
With typical correlations being extremely close to zero, and the most optimistic being close to 0.1, we can safely ignore all but the first term in Eq. (6A.16). In effect, we are ignoring the reduction in variance due to knowledge of z. The trace of PT · P is therefore
where we are summing the correlations between orthonormal basis elements x of the residual returns and independent signals y over all assets and signals.
To achieve the form of the fundamental law requires two more steps. First, sum the correlation of each signal with the basis elements, over the basis elements:
which already exhibits the additivity of the fundamental law. Finally, by assuming that all the signals have equal value,
we find the desired result:
For the following exercises, consider the following model of a stock picker’s forecast monthly alphas:
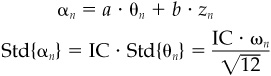
where αn is the forecast residual return, θn is the subsequent realized residual return, and zn is a random variable with mean 0 and standard deviation 1, uncorrelated with θn and with zm (m ≠ n).
1. Given that a = IC2, what coefficient b will ensure that
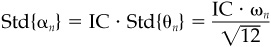
2. What is the manager’s information coefficient in this model?
3. Assume that the model applies to the 500 stocks in the S&P 500, with a = 0.0001 and ωn = 20 percent. What is the information ratio of the model, according to the fundamental law?
4. Distinguish this model of alpha from the binary model introduced in the main part of the chapter.
Consider the performance of the MMI versus the S&P 500 over the past 5 years.
1. What are the active return and active risk of the MMI portfolio over this period? What is its information ratio (based on active risk and return)?
2. What is the t-statistic of the active return? How does it compare to the information ratio? Distinguish what the IR measures from what the t-statistic measures.
