Valuation is the central concept of active management. Active managers must believe that their assessment of value is better than the market or consensus assessment. In this chapter, we describe a basic theory of valuation. The following chapters will illustrate practical valuation procedures and any links that these might have with theory.
This chapter contains three important messages:
■ The modern theory of valuation connects stock values to risk-adjusted expected cash flows.
■ The theory is closely related to the theory of option pricing, and is consistent with the CAPM and the APT.
■ Valuation (and misvaluation) is connected to expected returns.
The modern theory of asset valuation is general, esoteric, and worth studying. The theory provides a framework for judging more ad hoc and practical valuation methods.
We start with the important premise that a stock’s value is derived from the cash flows an investor can obtain from owning the stock. These cash flows arise as dividends or as the future value of the stock realized by selling the stock.1 The key to the theory will be discounting these uncertain cash flows back to the present. This is the same task required for option pricing, and readers familiar with option pricing theory will recognize the similarities (which we will make more explicit in the technical appendix).
In the simplest case, the investor will obtain a certain cash flow cf(t) at future time t. To make it even simpler, we assume a constant risk-free interest rate that applies over all maturities. Let iF be the (annual) return on a risk-free investment. When interest rates are 6 percent annually, then iF = 0.06. The present value of a promised $1.00 in 1 year is 1/(1 + iF). The promise of $1.00 in t years is 1/(1 + iF)t and the present value of cf(t) dollars in t years is
Equation (8.1) is the basis for valuing fixed-income instruments with certain cash flows. Given a stream of cash flows, e.g., cf(1) in 1 year, cf(2) in 2 years, etc., the valuation formula becomes
For example, if we have a promise of 6 dollars in 1 year and 10 dollars in 3 years and iF = 0.06, we find
Equation (8.1) fails when the cash flows are uncertain. Uncertainty means that there is more than one possible value for the future cash flows. We need a way to describe those possibilities. We do this by listing the possible outcomes at time t and determining the probability of each outcome. This is easier said than done in practice, but remember, this is the theory chapter. Let’s push on bravely and ask what we would do next if we could define both the possible future cash flows and the probability of each outcome.
We can index the possible outcomes at time t by s (for states). Let π(t,s) be the probability of outcome s at time t, and let cf(t,s) be the uncertain cash flow at time t in state s. The probabilities are nonnegative and sum to 1; i.e., 
for every t.
As an example, consider a 1-month period, t = 
, and a stock currently valued at 50. In 1 month its value (sale price plus any dividend paid in the month) will be either cf(t,1) = 49 or cf(t,2) = 53. The outcomes are equally likely; π(t,1) = π(t,2) = 0.5. The risk-free interest over the year is 6 percent. The expected cash flow is 51, and the standard deviation is 2.
Given this information, how should we value these uncertain cash flows? The simplest and most tempting way is to generalize Eq. (8.1), replacing certain cash flows with expected cash flows:
Unfortunately, this doesn’t work. Expectations generally overestimate the stock’s value. When the cash flows are uncertain, we usually find
In our example, the discounted expected cash flows lead to a value of 50.75, but the current price is 50. The problem is that expected cash flows do not take account of risk. An instrument with an expected but uncertain cash flow of 51 should not have the same price as an instrument with a certain cash flow of 51. The two have the same expected cash flows, but one is certain and one is not. We must dig deeper to find a valuation formula.
Before we present a valuation formula, we can list the properties that a reasonable formula should display. There are several.2
1. If all future cash flows are nonnegative, the value is nonnegative.
2. If we double (or triple or halve) the cash flows, the value should change in the same proportion.
3. If we add two sets of cash flows, the value of the total cash flow should be the sum of the values of each separately.
4. The valuation formula should reduce to Eq. (8.1) in the case of certain cash flows.
5. The formula should agree with the market value of securities.
Property 1 is certainly sensible; if we can’t lose and we might gain, the opportunity should be worth something. Property 2 says that the price of six shares is six times the price of one share. Property 3 combined with property 2 says that our valuation rule works for portfolios. We can value each stock in the portfolio and know that the portfolio’s value is simply the weighted sum of the values for each stock separately. Property 3 not only lets us combine stocks into portfolios, but also allows us to value each cash flow in a stream of cash flows separately. Thus we could value next quarter’s dividend separately from the dividend the quarter following. The cash flows for the 3-month and 6-month dividends may be highly correlated, but that doesn’t matter; the valuation formula should still get each right.
Property 3 also lets us see the flexibility of this valuation notion. Suppose we have a stock that pays a quarterly dividend and the next dividend occurs in 3 months. Rather than consider an indefinite sequence of dividends, we can always consider the stock as the promise of the next four dividends plus the price of the stock in 1 year. The price in 1 year is the final cash flow that we receive. The 1 year was arbitrary. We could have used the price in 1 month, before the first dividend, or in 2 years, after eight dividends. The valuation formula should give us the same answer no matter how we represent the cash flows!
Property 4 says that we can value a certain cash flow of any maturity. This is clearly a prerequisite to valuing uncertain cash flows of any maturity. Equation (8.1) is based on a constant interest rate. We can easily generalize it to allow for risk-free rates that depend on maturity.
Property 5 says that the valuation formula works. This is where the active manager and the economist part company. The active manager is interested in using the concept to find stocks for which the formula is not working. In practice, property 5 can be used to say that the valuation is correct on average or within certain groups. The active manager is free to look within those groups for under-and overpriced stocks.
We know the properties that we want. How do we get them?
There are two ways to modify the right side of Eq. (8.5) in order to get a straightforward relationship like Eq. (8.1). One possibility is to introduce a risk-adjusted interest rate. Then we could discount the expected cash flows at the higher (one presumes) rate of interest and therefore lower their value. This seems like a good idea, and, as we’ll see in the next chapter, it is used in practice. It is just a straightforward extension of the CAPM and the APT, which state
where cf(t) is the stock value in 1 year, and so
Here the risk-adjusted interest rate is based on the asset’s beta and the expected excess return to portfolio Q. The term 
is sometimes called the equity cost of capital.
While this risk-adjusted interest rate is simple and easy to understand, this valuation approach can break down. In particular, imagine a coin-toss security worth $100,000 (if heads) or -$100,000 (if tails). The expected cash flow is zero. Any attempt to value this by adjusting the discount rate will still get zero.3
The modern theory of valuation employs the alternative modification of Eq. (8.5): risk-adjusted expectations E*{cf(t)}. As we will see, this approach will go far beyond Eq. (8.7) in providing insight into valuation and unifying concepts from the CAPM, the APT, and options pricing. By introducing a unique risk-adjusted probability distribution, we will be able to consistently discount all adjusted expected cash flows at the same risk-free rate.
We obtain the risk adjustment by introducing value multiples4 υ(t,s), so the modified expectation can be written as
where υ(t,s)is
■ Positive
■ With expected value 1
■ A function of the return to portfolio Q and proportional to the total return on a portfolio S, the portfolio with minimum second moment of total return (see appendix)
In the technical appendix, we will show that these valuation multiples exist as long as there are no arbitrage opportunities in the valuation scheme. Arbitrage can occur if we can start with a nonpositive amount of money at t = 0 and have all outcomes nonnegative with at least one outcome positive.
With this definition of the risk-adjusted expectations, we obtain our valuation formula:
All modern valuation theories, including option theory, the CAPM, and the APT, use valuation formulas that have the form of Eq. (8.9). The technical appendix will discuss this in more detail.
Let’s check that Eq. (8.9) has the required valuation properties. Since υ(t) is positive, property 1 will hold: Nonnegative cash flows will lead to nonnegative risk-adjusted expectations E*{cf(t)} and, by Eq. (8.9), nonnegative values.
The valuation rule is linear, so properties 2 and 3 have to hold. That means that Eq. (8.9) has the portfolio property. If stock n has uncertain cash flows cfn(t), and the weight of stock n in portfolio P is hPn, then the portfolio’s cash flow is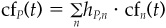 
, and the value of portfolio P is
where
is the value of stock n valued in isolation.
If the cash flow cf(t) is certain, then
The first equality follows from the definition of E*, the second equality because cf(t) is certain, and the third equality because v(t) has expected value of 1. This means that property 4 is true: Eq. (8.9) will agree with Eq. (8.1) when the cash flows are certain.
We hope that property 5 holds, at least on average. If property 5 held for all stocks, the active manager would not find any opportunities in the marketplace.
The value multiples υ(t,s) help define a new set of probabilities 
. The risk-adjusted expectation E* uses the modified set of probabilities.
In the simple example used previously, the outcomes cf(t,1) = 49 and cf(t,2) = 53 are equally likely, π(t,1) = π(t,2) = 0.5, and the risk-free interest over the year is 6 percent, iF = 0.06. We find (see the appendix) that υ(t,1) = 1.38 and υ(t,2) = 0.62. This is consistent with properties 1 through 5. The altered probabilities are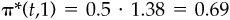 
and π*(t,2) = 0.5 · 0.62 = 0.31. The valuation for the risky stock works out correctly:
The definition of covariance and the fact that E{υ(t)} = 1, can be used to link the true and risk-adjusted expectations of cf(t):
Equations (8.5) and (8.9) imply that the covariance term will, in general, be negative; in our example, we have E*{cf(t)} = 50.24 and E{cf(t)} = 51, and so the covariance term is −0.76. This is the explicit penalty for the risk. Its present value is −0.756.
An alternative interpretation of the valuation formula is that the value multiples modify the cash flows. The value multiples υ(t,s) change the cash flows by amplifying some, if υ(t,s) > 1, and reducing others, if υ(t,s) < 1. Since the value multiples have expected value equal to 1, they are on average unbiased. For our example, the rescaled cash flows are 67.62 = 1.38 · 49 and 32.86 = 0.62 · 53.
Suppose that cfM(t) is proportional to the total return on the market portfolio. Then, the negative covariance indicates that υ(t,s) will tend to be less than 1 when the market is doing better than its average (good times) and υ(t,s) will tend to be larger than 1.0 when the market is below its average. The expectations E* makes the risk adjustment by placing a lower value on good-time cash flows as compared to bad-time cash flows. There is no great surprise here. This means that the marginal amount of cash flow is worth more when cash flow in general is scarce.
According to the modern theory of valuation, the key elements of Eq. (8.9), both the risk-free rate of interest and the value multipliers υ(t,s), are market-dependent and not stock-dependent. The only stock information needed is the potential cash flows cf(t,s). We use the same υ(t,s) and the same iF for all instruments: for IBM stock, for GM puts, or for the S&P 500 portfolio. This critical property arises in all modern asset valuation theories, including the CAPM and the APT, which assert that only systematic risks are priced.
The APT frames this issue in the context of arbitrage-free pricing: that assets with identical exposures to nondiversifiable risks should have identical returns. This notion of arbitrage-free pricing is critical to proving that the value multiples cannot depend on individual stock returns, but only on portfolio Q returns.
We have discovered a simple formula for the value of a stock providing a sequence of uncertain cash flows. The formula uses adjusted expectations of the cash flows and discounts those adjusted expectations at market rates of interest to obtain a present value for the stock. In some cases, such as option valuation and variants of the CAPM, explicit formulas allow us to calculate the modified cash flows. In other cases, such as the APT, these modified expectations exist, although we don’t have specific information for calculating them.5 The appendix includes examples of these applications.
We can now link formulas for expected return, i.e., the CAPM and the APT, and the valuation formula just described. Consider a stock currently priced at p(0), paying a dividend d at the end of 1 year, and with an uncertain price p(1) at the end of the year. Assume that the stock is fairly valued now and will be fairly valued at the end of the year. If we sell the stock at the end of the year, the cash flow will be the dividend plus the sale price: cf(1) = d + p(1). The valuation formula over one period is
If p(0) ≠ 0, then we can convert Eq. (8.15) to an expected return equation. Define total return R = [d + p(1)]/p(0). Divide Eq. (8.15) by p(0), and multiply by 1 + iF. Then recall that E{υ(1)} = 1. The net result is
and
Equation (8.16) says that the expected excess return on all stocks is determined by their covariance with υ. This result is suspiciously close to the CAPM and the APT results, that the expected excess return on every stock is determined by its covariance with portfolio Q (which for the CAPM is the market). The technical appendix will show, in fact, that υ is a function of the return to portfolio Q and proportional to the return to a portfolio S, which is a combination of the risk-free asset and portfolio Q. So we will relate Eq. (8.16) to the CAPM and the APT. And, not only can we derive Eq. (8.16) from Eq. (8.15), we can also derive Eq. (8.15) from Eq. (8.16). Our previously derived expected return formulas imply valuation as in Eq. (8.15).
Equation (8.17) also demonstrates that under the modified probabilities, the expected return on the risky investment is equal to the return on the risk-free investment. In fact, under the modified expectations, all stocks have (modified) expected returns equal to the risk-free return.
What if the market price and the model price don’t agree? Suppose we start with an asset that has a market value p(0,mkt) that is not equal to zero and is not properly valued:
and
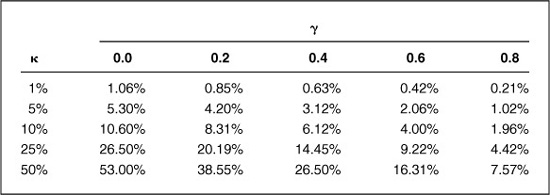
The parameter κ measures the extent of misvaluation of the stock; it is the percentage difference between the fitted and market prices at time 0. The parameter 7 measures the persistence of the misvaluation: how long it will take for the market to learn what we know. Presumably 0 ≤ γ ≤ 1. If this is a “slow idea,” then 7 will be close to 1.0; much of the mispricing will remain. If this is a “fast idea,” then 7 will be close to 0. We can think of −0.69/ln{γ} as the half-life of the misvaluation, the number of years it will take for half the misvaluation to disappear.
Equations (8.16), (8.19), and (8.20) yield6
where α is
Equation (8.22) breaks the expected return into what we would expect if the stock were fairly valued and a second term that corrects for the market’s incorrect valuation of the stock. Notice that α = 0 if either κ = 0 or γ = 1; it is no good if the world never learns that this stock is improperly valued. Also, if γ = 0, then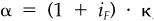 
we realize the full benefit, plus interest, over the period.
Table 8.1 shows the alphas we get for different levels of κ and γ. It assumes a 6 percent annual interest rate.
The modern theory of valuation prices uncertain future cash flows by risk-adjusting the expected cash flows and discounting them to the present using the risk-free rate. This theory is consistent with the CAPM and APT models, which forecast expected returns; and in fact the risk-adjusting procedure is related to portfolio Q.
If the market doesn’t currently price the asset fairly, then the asset’s expected return comprises two components: the return expected if the asset were fairly priced, and a correction term based on the market price’s approaching fair value.
1. In the simple stock example described in the text, value a European call option on the stock with a strike price of 50, maturing at the end of the 1-month period. The option cash flows at the end of the period are Max{0,p(t,s) −50}, where p(t,s) is the stock price at time t in state s.
2. Compare Eq. (8.16) to the CAPM result for expected returns, to relate υ to rQ. Impose the requirement that E{υ} = 1 to determine υ exactly as a function of rQ.
3. Using the simple stock example in the text, price an instrument which pays $1 in state 1 [cf(t,1) = 1] and $−1 in state 2 [cf(t,2) = −1]. What is the expected return to this asset? What is its beta with respect to the stock? How does this relate to the breakdown of Eq. (8.7)?
4. You believe that stock X is 25 percent undervalued, and that it will take 3.1 years for half of this misvaluation to disappear. What is your forecast for the alpha of stock X over the next year?
Arrow, Kenneth J. Essays in the Theory of Risk-Bearing (Chicago: Markham Publishing Company, 1971).
Bar-Yosef, Sasson, and Hayne Leland. Risk Adjusted Discounting. University of California, Berkeley Research Program in Finance working paper #134, December 1982.
Black, Fischer, and Myron Scholes. “The Pricing of Options and Corporate Liabilities.” Journal of Political Economy, vol. 81, no. 3, 1973, pp. 637-654.
Chamberlain, Gary, and M. Rothschild. “Arbitrage, Factor Structure and Mean-Variance Analysis on Large Asset Markets.” Econometrica, vol 51, no. 5,1983, pp. 1281-1304.
Cox, John C., and Mark Rubinstein. Options Markets (Englewood Cliffs, N.J.: Prentice-Hall, 1985).
Debreu, Gerard. Theory of Value (New York: John Wiley & Sons, 1959).
Garman, Mark B. “A General Theory of Asset Valuation under Diffusion State Processes.” University of California, Berkeley Research Program in Finance working paper #50, 1976.
Garman, Mark B. “Towards a Semigroup Pricing Theory.” Journal of Finance, vol. 40, no. 3, 1985, pp. 847-861.
Grinold, Richard C. “The Valuation of Dependent Securities in a Diffusion Process,” University of California, Berkeley Research Program in Finance working paper #59, April 1977.
______. “Market Value Maximization and Markov Dynamic Programming.” Management Science, vol. 29 no. 5, 1983, pp. 583-594.
______. “Ex-Ante Characterization of an Efficient Portfolio.” University of California, Berkeley Research Program in Finance working paper #59, September 1987.
Harrison, Michael J., and David M. Kreps. “Martingales and Arbitrage in Multiperiod Securities Markets.” Journal of Economic Theory, vol 20, 1979, pp. 381-408.
Hull, John. Options, Futures, and Other Derivative Securities (Englewood Cliffs, N.J.: Prentice-Hall, 1989).
Ohlson, James A. “A Synthesis of Security Valuation Theory and the Role of Dividends, Cash Flows, and Earnings.” Columbia University working paper, April 1989.
Ross, Stephen. “Return, Risk, and Arbitrage.” In Risk and Return in Finance, edited by I. Friend and J. Bicksler (Cambridge, Mass.: Ballinger, 1976).
Rubinstein, Mark. “The Valuation of Uncertain Income Streams and the Pricing of Options.” Bell Journal of Economics, vol 7, 1976, pp. 407-425.
Sharpe, William F. “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk.” Journal of Finance, vol. 19, no. 3, 1964, pp. 425-442.
Williams, John Burr. The Theory of Investment Value (Amsterdam: North-Holland Publishing Company, 1964).
This appendix derives some of the results used in the text. In particular,
■ We derive the basic valuation result in the case of a finite number of outcomes.
■ We illustrate the basic valuation result using option pricing.
■ We apply the CAPM (or really mean/variance theory) to valuation.
■ We introduce portfolio S as a more general portfolio approach to valuation.
Consider a finite number of assets indexed by n = 0, 1,..., N over a finite number of periods T. Start at time t = 0, and observe the prices of the assets at times t = 1, 2,..., T. The prices evolve along paths. The collection of paths determines the possible outcomes. At time t = T, we will know what path we have followed. At time t = 0, we know only the set of possible paths. At intermediate times, 0 < t < T, we have partial knowledge of the eventual path we will follow.
Specifying the state of knowledge at each intermediate point in time determines the system. Knowledge is refined through time, as the collection of possible paths shrinks. At time t, we can be in one of S(t) states, where a state indicates a collection of possible paths we might be following. As time moves on, this set of possible paths is reduced, until at time T we know what path we have been following. Figure 8A.1 illustrates a case in which there are 3 time periods and 11 possible paths.
We can make this more precise. At time t > 1 in state s, we will know the unique time t − 1 state that preceded state s; the predecessor is denoted Φ(s,t). We will also know the possible successors to (s,t) at time t + 1. That collection of possible successors is denoted Ω(s,t). For every possible successor z ∈ Ω(s,t), we must have (s,t) as a predecessor; i.e., if z ∈ Ω(s,t), then Φ(z,t+1) = s. Similarly, if z ∈ Ω(s,t), then Φ(z,t+1) ≠ s. The set of all possible states at time t is denoted Φ(t.
We have probabilities π{s,t} of being in state s at time t. We require only that these probabilities be positive.
Asset prices are given by pn(s,t), the price of asset n if state s occurs at time t. Since there is only one state at time t = 0, we have pn(1,0) as the initial prices.
One of the assets, call it asset n = 0, is risk-free. At time t in state s, a positive risk-free rate of interest iF(s,t) will prevail from time t until time t + 1. We start with p0(1,0) = 1. At time t + 1, we have
for every z∈ Ω(s,t). This assumption allows future rates of interest to be uncertain, although we will always know what rate of interest obtains over the next period.
To make life simple, we will ignore dividends. This means that we can assume either that all dividends are paid at time T or that pn(s,t) includes accumulated dividends.
An investment strategy is determined by the N+1-element vector NS(s,t) = {NS0(s,t),NS1(s,t)...,NSN(s,t)} for each state, time, and asset. It describes the number of shares of that asset in the portfolio at that state and held from time t to time t + 1. The value of the portfolio at time t in state s using strategy NS is denoted W(s,t). The value W(s,t) is
To conserve value, we impose a self-financing condition: The value of the portfolio at the end of period t-1 must exactly match the value of the portfolio at the start of period t. Mathematically, for t ≥ 1 and s ∈Φ(t),
The value of the portfolio before it is revised is the same as the value of the portfolio after it is revised.
An arbitrage opportunity is available if we can find an investment strategy that starts with a nonpositive amount of money, W(1,0) ≤ 0; is guaranteed not to lose money, W(s,t) ≥ 0 for s∈Φ(T); and makes money in at least one outcome, 
.
If there are no arbitrage opportunities, we can find positive valuation multiples υ(s,t) > 0 such that for any asset n = 0, 1, 2,.., N and any time t = 1, 2,.. , T,
Proof Consider the following linear program:
for s∈Φ(T).
The linear program maximizes the sum of the end-period wealths across the possible states, subject to the constraints of initial wealth nonpositive [Eq. (8A.6)], self-financing strategies [Eq. (8A.7)], end-period wealth definition [Eq. (8A.8)], and nonnegative end-period wealth in each possible state [Eq. (8A.9)].
Given the constraints of initial wealth nonpositive and final wealth nonnegative, this linear program has a feasible solution: NSn(s,t) = 0 for all n, s, and t. By the no-arbitrage condition, this is an optimal solution as well; i.e., no solution will exhibit positive value for the objective.
The duality theorem of linear programming then implies that there will be an optimal solution q(s,t) to the dual problem. The dual problem is
subject to
for all n = 0,..., N; 0 ≤ t < T; s∈Φ(t), and
Let q(s,t) be an optimal dual solution. Equation (8A.13) guarantees that q(s,T) are positive, and in fact greater than 1. We can further show, by successive applications of Eq. (8A.11), that each q(s,t) is positive, using the risk-free asset:
Define the conditional probabilities π*(z,t + 1 | s,t) by
This definition, along with Eq. (8A.11), leads to the intertemporal valuation formula
This formula requires probabilities in states (z,t+1) conditional on predecessor states (s,t) We would like to rewrite these in terms of unconditional probabilities, which we can derive starting with π(1,0) - 1. Then, using the laws of probability and the fact that state s at time t+1 has a unique predecessor Φ(s,t+1) at time t,
The valuation multipliers are then
Repeated application of Eqs. (8A.16) through (8A.18) will demonstrate Proposition 1, Eq. (8A.4).7,8
The most familiar context for the modern theory of valuation is in options pricing. Here is an example, which we also used in the main text of the chapter. Consider a single stock and a single 1-month period with two equally likely outcomes. The stock can go either up, the UP event, or down, the DN event. The risk-free asset increases in value from 1.00 to RF = (1 + iF)1/12 = 1.00487, corresponding to an annual interest rate of 6 percent. The stock’s initial price is p = 50, and its final value is equally likely to be pUP = 53 or pDN = 49. The outcomes UP and DN are equally likely: πUP = πDN = 0.5.
Now let’s calculate the valuation measure in the UP and DN states. Following Eq. (8A.11), the dual linear program in this simple case is
with q0 ≥ 0 and qUP, qDN ≥ 1. Solving for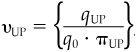 
, 
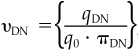we find 0.62 and 1.38, respectively.
We can check that these valuation multiples correctly value both the risk-free asset and the stock. These multiples will be non-negative9 as long as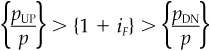 
, and their expected value will always be 1.0.
Of course, options pricing theory was developed to price options, and given these valuation multiples, we can price any claim contingent on the stock price. For this simple case in particular, we can price options maturing at the end of the period, with payouts dependent on the ending stock value. The payout for a call option would have the form Max[0, S(T) − K], where K is the strike price.
We can easily expand this framework to multiple periods. For a more substantial treatment, see the texts by Cox and Rubinstein and by Hull.
The main body of the chapter discussed the connection between valuation and expected returns. We revisit that topic here. Let pn be the initial value of stock n, dn the dividends paid on the stock (at the end of the month), and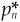 
the final value. Let Rn, RF, and RQ be the total returns on the stock, the risk-free asset, and portfolio Q. The excess returns are rn and rQ. In the CAPM, portfolio Q is the market.
The valuation function υ depends only on the return to portfolio Q, according to
with
Proof Define the return on asset n with outcome s as
Since portfolio Q defines expected excess returns,
The definition of covariance implies
Now, Eq. (8A.25), in combination with Eqs. (8A.24) and (8A.21), leads to
This is the desired result.
Notice that υ depends only on portfolio Q’s return. The expected value of υ is 1 and, since κ > 0, υ decreases as the market return increases. Reasonable estimates of κ are between 1.5 and 2.00; as an example, we’ll choose 1.75. Hence υ is negative if rQ > fQ + 0.57. If the expected annual excess return to the market was approximately 6 percent, this would be a 63 percent excess market return: more than a three standard deviation event. In fact, the largest two annual S&P 500 returns since 1926 have been a 54 percent return in 1933 and a 53 percent return in 1954.
Proposition 2 relates the valuation multipliers υ to the excess return to portfolio Q. Alternatively, we can introduce a new portfolio, portfolio S, which also explains excess returns and whose total returns are directly proportional to the valuation multipliers. For the purpose of this technical appendix, portfolio S provides simply another view of excess returns and valuation. We introduce portfolio S because (although we will not make use of this property) it is also a more robust approach to excess returns and valuation than portfolio Q. We require very few assumptions to determine that portfolio S exists and explains excess returns. For example, while we require that the expected excess return to portfolio C be positive for the existence of portfolio Q, portfolio S exists and explains expected excess returns even without that assumption.
We define a portfolio S as the portfolio containing both risky and riskless assets with the minimum second moment of total return. We will investigate the properties of portfolio S, including its relation to excess returns, portfolio Q, and the valuation multipliers.
The total return for any portfolio P is given by Rp = 1 + iF + rP. Portfolio S solves the problem
where portfolio P contains both risky and risk-free assets. The risk-free portfolio would give us second moment 
. Portfolio S has even less.
For any portfolio P, we have
Proof Consider a portfolio P(w) with fraction (1 − w) invested in portfolio S and fraction w invested in portfolio P. The total return on this mixture will be
Define gP(w) as the expected second moment of the return on the mixture:
Since Rs is the portfolio that has minimum second moment, the derivative of gP(w) at w = 0 must be zero. Hence
for any portfolio P. We can expand this to
Equation (8A.33) holds for any portfolio P, including the risk-free portfolio F, and so
Combining Eqs. (8A.33) and (8A.34) leads to Proposition 3, Eq. (8A.28).
Proposition 3 demonstrated the connection between portfolio S and expected returns. We also know the connection between portfolio Q and expected returns. And so, there is a link between portfolio S and portfolio Q.
If
■ Portfolio S solves Eq. (8A.27)
■ Portfolio Q is the fully invested portfolio with maximum Sharpe ratio11
then portfolio S is a mixture of portfolio F and portfolio Q:
where
Proof Given an arbitrary starting fully invested portfolio P, consider a portfolio P(w) composed of a fraction w invested in portfolio P and a fraction (1 — w) invested in portfolio F. Its total return is
Now choose w to minimize the expected second moment,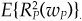 
, of the return. The optimal w is
with associated optimal expected second moment
As long as SRP is not zero, we can do better than just the risk-free portfolio. In fact, the larger SRP is in absolute value, the better we can do. We achieve the minimum second moment over all portfolios (risky plus risk-free) by choosing the fully invested portfolio P that maximizes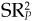 
: portfolio Q. This proves Proposition 4, Eq. (8A.35).
Our final task is to express the valuation multiples in terms of portfolio S.
The valuation multiples are
Proof Combining Proposition 3 [Eq. (8A.28)], which explains expected excess returns using portfolio S, and Proposition 2 [Eq. (8A.21)], which expresses the valuation multiples in terms of portfolio Q, we can derive
where
Since Φ = −1/E{Rs}, this simplifies to Proposition 5, Eq. (8A.40).
1. Using the definitions from the technical appendix to Chap. 2, what is the characteristic associated with portfolio S?
2. Show that the portfolio S holdings in risky assets satisfy
3. Show that portfolio S exists even if fC < 0, and that if fC = 0, then portfolio S will consist of 100 percent cash plus off setting long and short positions in risky assets.
4. Prove the portfolio S analog of Proposition 1 in the technical appendix of Chap. 7, i.e., that the factor model (X, F, Δ) explains expected excess returns if and only if portfolio S is diversified with respect to (X, F, Δ).
1. If portfolio Q is the MMI and μQ = 6 percent, what is portfolio S? Use Proposition 4 of the technical appendix, which expresses portfolio S in terms of portfolio Q.
2. Using the result from the first applications exercise, what is the valuation multiple in the state defined by rQ = 5 percent? Use Proposition 5 of the technical appendix. If interest rates are 6 percent, what is the value of an option which pays $1 in 1 year only in the state defined by rQ = 5 percent? Assume that the probability of that state occurring is 50 percent.
