ANALYTIC CONTINUATION
74. ELEMENTS AND CHAINS
By the problem of analytic continuation of a single-valued function f(z) defined on a set E we mean the problem of finding a domain D containing E and a function φ(z) defined on D such that
1. φ(z) is analytic on D;
2. φ(z) = f(z) for all z ∈ E;
3. D is as large as possible.1
The function φ(z) is then said to be an analytic continuation of f(z) from E into D. If E has a limit point z0 ∈ D, it follows from Theorem 10.8 that φ(z) is unique.
Remark. Two other definitions of analytic continuation will be encountered below, but they can both be interpreted as variants of this basic definition.2
Example 1. Let E be the real line z = x(y = 0), and let f(x) = ex. Then
and the function
obtained by replacing x by z in (16.1) is the unique analytic continuation of f(x) into the whole finite plane. In fact, instead of the approach used in Sec. 29, we could have defined the complex exponential by the series (16.2). However, the treatment in Sec. 29 has the advantage of not requiring previous knowledge of complex series and the uniqueness theorem for analytic functions.
Example 2. Let E be the unit disk |z| < 1, and let
Then the function
is the analytic continuation of f(z) into the domain D consisting of the whole plane minus the point z = 1.
Example 3. Let E be the unit disk |z| < 1, and let
Then, as will be shown in Example 2, p. 355, there is no analytic continuation of f(z) into a domain larger than E. This fact is summarized by saying that the circle |z| = 1 is the natural boundary of the series (16.3).
Next we consider the case where D intersects E but does not necessarily contain E. At the same time, we assume that E is itself a domain, there by insuring that E ∪ D is a domain.
DEFINITION 1. A set {G, f(z)} consisting of a domain G and a single-valued analytic function defined on G is called an element, and G is called the domain of the element. Two elements {G, f(z)} and {D, φ(z)}} are equal if and only if G = D, f(z) ≡ φ(z).
DEFINITION 2. Each of two elements {G, f(z)} and {D, φ(z)} is said to be a direct analytic continuation of the other if G ∩ D ≠ 0 and if there exists a domain g ⊂ G ∩ D such that f(z) = φ(z) for all z ∈ g.
Remark 1. Let {G, f(z)}, {D, φ(z)} and g be the same as in Definition 2, and let g’ be the connected component of G ∩ D containing g (see p. 40). Then, by Theorem 10.8, f(z) and φ(z) coincide on g′, and hence on G ∩ D if G ∩ D is connected. However, f(z) and φ(z) may not coincide on the other components of G ∩ D if G ∩ D is not connected.
Remark 2. Let {G2, f2(z)} be a direct analytic continuation of {G1, f1(z)} in the sense of Definition 2, and let
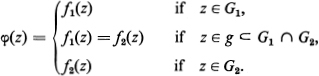
Then φ(z) is an analytic continuation of f(z) from G1 (or G2) into G1 ∪ G2 in the sense of the definition on p. 341 if G1 ∩ G2 is connected (see Prob. 4).
Example 1. Let G be the domain bounded by the ray – ∞ < x ≤ 0, y = 0 and D the domain bounded by the ray 0 ≤ x < + ∞, y = 0. Let
where θ is the value of Arg z satisfying the condition –π < θ < π and α is the value satisfying the condition 0 < α < 2π. Each of the functions (16.4) is single-valued and analytic on its domain of definition. The set G ∩ D is nonempty and consists of two components, the upper half-plane ∏U and the lower half-plane ∏L. Moreover α = θ in ∏U while α = θ+ 2π in ∏L, and hence f(z) = φ(z) if z ∈ ∏U but f(z) ≠ φ(z) if z ∈ ∏L. Therefore {G, f(z)} and {D, φ(z)} are direct analytic continuations of each other (with ∏U as the domain g figuring in Definition 2).
Example 2. Let G, D, f(z) and φ(z) be the same as in Example 1, and consider another function
defined on D, where β is the value of Arg zsatisfying the condition – 2π < β < 0. Then α = β + 2π at every point of D, and hence φ(z) ≠ 
if z ∈ D. Therefore {D, φ(z)} and {D, } are not direct analytic continuations of each other. On the other hand, β = θ in the lower half-plane ∏L and hence f(z) = if z ∈ ∏L, so that {G, f(z)} and {D, } are direct analytic continuations of each other.
Definition 3. Let
be a set of elements such that{Gk, fk(z)} is a direct analytic continuation of {Gk-1, fk-1(z)} for ever k = 1,…, n. Then (16.5) is called a chain of elements joining {G0, f0(z)} and{Gn, fn(z)}. Each of the elements{G0, f0(z)} and {Gn, fn(z)} is called an analytic continuation of the other.3
Definition 3 immediately implies
THEOREM 16.1. The relation leading from an element {G, f(z)} to any of its analytic continuations is reflexive, symmetric and transitive.4More exactly,
1. {G, f} is an analytic continuation of itself;5
2. If {D, φ} is an analytic continuation of {G, f}, then {G, f} is an analytic continuation of{D, φ};
3. If {D, φ} is an analytic continuation of {G, f} and if{E, ψ} is an analytic continuation of{D, φ}, then{E, ψ} is an analytic continuation of {G, f}.
Example. Let Gk be the domain
and let fk(z) be the function
where θk = θk(z) is the value of Arg z satisfying (16.6). Then any two elements {Gm, fm} and {Gn, fn} are analytic continuations of each other. In fact, suppose n = m + p, where p > 0 (say). Then {Gm, fm},…, {Gn, fn} is a chain of p + 1 elements joining {Gm, fm} and {Gn, fn}.
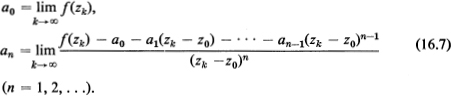
Problem 1. Suppose f(z) can be continued analytically from a set E ⊂ D with a limit point z0 ∈ D into the domain D itself. Let
be the power series expansion of f(z) at z0, where Δ0 is the distance from z0 to the boundary of D, and let {zk} be a sequence of points of E converging to z0 (recall Sec. 9, Prob. 8). How can the coefficients a0, al…, an,…be deduced from a knowledge of f(z) on the set E?
Ans. Use the inductive formula
Problem 2. Let f(z), z0, D and Δ0 be the same as in the preceding problem, and let z’ be a point in the disk |z – z0| < Δ0. Then
where Δ′ is the distance from z′ to the boundary of D. Relate the coefficients b0, bl,…, bn,…to the coefficients a0, al,…, an,…figuring in (16.7).
Ans.
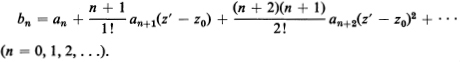
Problem 3. Interpret the proof of the uniqueness theorem for analytic functions (Theorem 10.8) from the standpoint of analytic continuation.
Problem 4. Generalize Remark 2, p. 343 to the case where G1 ∩ G2 is not connected.
Hint. Recall footnote 1, p. 341.
Problem 5. Verify that the relation leading from a domain G to any of its conformal images (see p. 323) is an equivalence relation.
75. GENERAL AND COMPLETE ANALYTIC FUNCTIONS
Let F be a nonempty (finite or infinite) set of elements {G, f}. Then F is said to be connected if every pair of elements in F can be joined by a chain of elements all belonging to F. In particular, if F is connected, every element of F is an analytic continuation of every other element of F.
THEOREM 16.2. Let F be a connected set of elements, and let D be the union of the domains of all the elements in F. Then D is itself a domain.
Proof. Since F is nonempty, so is D. Moreover, if z0 ∈ D, then z0 belongs to at least one domain G such that {G, f} ∈ F. Therefore z0 has a neighborhood contained in G and hence in D, i.e., D is open. To prove that D is connected, let z0 and z* be two distinct points of D. Then there are two elements {G0, f0}, {G*, f*} ∈ F such that z0 ∈ G0, z* ∈ G*. Furthermore, F contains a chain
joining {G0, f0} and {G*, f*}. Since {Gk-1, fk-1} and {Gk, fk} are direct analytic continuations of each other, the set Gk-1 ∩ Gk is nonempty (k = 1,…, n). Let zk be any point of Gk-1 ∩ Gk, and let γk be a continuous curve contained in Gk joining zk to zk+1 (k = 1,…, n-1). Then joining z0 to z1 by any curve γ0 ⊂ G0, z0 to z1 by any curve γ1 ⊂ Gl, zn-1 to zn by any curve γn-1 ⊂ Gn-1, and finally zn to z* by any curve γn ⊂ Gn, we obtain a continuous curve contained in D joining z0 to z* (draw a picture!). Therefore D is connected as well as nonempty and open, and the proof is complete.
The following definitions form the basis for a rigorous theory of multiple valued analytic functions:
DEFINITION 1. A nonempty connected set of elements is called a general analytic function, said to be generated by any of its elements. The union of the domains of all the elements of a general analytic function F is called the domain of F.
DEFINITION 2. Given a general analytic function F, let z0 be any point in the domain of F. Then by a value of F at z0, written F(z0), is meant any value f(z0) where{G, f(z)} ∈ F, z0 ∈ G.6
DEFINITION 3. A general analytic function which contains all analytic continuations of any of its elements is called a complete analytic function. The domain of a complete analytic function F is often called the domain of existence of F, and the elements of F are often called single-valued(analytic) branches of F.
Remark. Roughly speaking, a complete analytic function is the result of unrestricted analytic continuation of some originally given sample of the function, and the domain of existence of a complete analytic function is the largest domain into which the given sample can ever be continued.
Example 1. Let G be a domain, and let f(z) be single-valued and analytic on G. Then the set of all elements {K, f(z)}, where K is a disk contained in G, is a general analytic function F, with domain G. Moreover, F(z) is single-valued and F(z) = f(z).
Example 2. Let G be any simply connected domain not containing the origin. Then the complete analytic function generated by the element {G, In z}, where In z is the principal value of the logarithm, is the multiple valued function.
whose domain of existence is the whole plane minus the origin.7
Example 3. Let F be a general analytic function whose domain is simply connected. Then, according to the monodromy theorem, 8 F must be single-valued.
Problem 1. Prove that every element belongs to a unique complete analytic function.
Problem 2. Find the complete analytic function generated by the element {G, f(z)}, where G is the unit disk |z| < 1 and f(z) is the function (16.3). What is the domain of existence of F?
Problem 3 (M3, Sec. 39). Given a meromorphic function f(z), let G be any domain containing no poles of f(z). What is the complete analytic function F(z) generated by (G, f(z)}?
Ans. F(z) = f(z).
76. ANALYTIC CONTINUATION ACROSS AN ARC
Given a domain G with boundary Γ, suppose every point z0 ∈ G can be joined to a point ζ ∈ Γ by a curve 
, i.e., by a curve entirely contained in G except for the end point ζ. Then ζ is said to be an accessible point of Γ. A set E ⊂ Γ is said to be accessible if every point of E is accessible.
Example 1. Let G be the interior of a closed Jordan curve. Then it can be shown (see M3, Sec. 8) that every boundary point of G is accessible.
Example 2. Suppose we draw infinitely many line segments
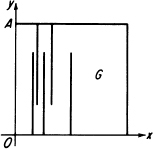
FIGURE 16.1
and
in the closed square 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, and then take G to be the domain whose boundary Γ consists of these segments together with the four sides of the square, as shown in Figure 16.1. Then no point of the segment OA is accessible, but every other point of Γ is accessible.
We now consider the problem of analytic continuation based on the use of “adjacent elements” sharing an appropriate boundary arc:
THEOREM 16.3. Let{G1, f1} and {G2, f2} be two elements whose domains are disjoint but share an accessible Jordan boundary arc δ, where δ is open and rectifiable.9 Supposef1(z) is analytic on G1 and continuous on G1 ∪ δ, while f2(z) is analytic on G2 and continuous on G2 ∪ δ. Moreover, suppose f1(z) and f2(z) coincide on δ, so that
Then there exists a function φ(z) analytic on D = G1 ∪ δ ∪ G2 such that
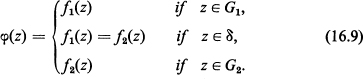
Proof. The proof involves Morera’s theorem (Theorem 8.6) and the generalized Cauchy integral theorem,10 which states that if G is the interior of a closed rectifiable Jordan curve L and if φ(z) is analytic on G and continuous on 
, then
First we note that D is a domain (here the accessibility of δ is vital!). Let L be an arbitrary closed rectifiable Jordan curve contained in D and traversed in the positive direction. If L ∩ δ =0, then L ⊂ G1 or L⊂ G2, and hence, by the ordinary form of Cauchy’s integral theorem, 16.10) holds with φ(z) given by 16.9). If L ∩ δ ≠ 0, we divide L into two arcs L1 and L2 with end points ζ1, ζ2 ∈ δ, as in Figure 16.2 (verify that this figure is sufficiently general for our purposes). It follows from the generalized Cauchy integral theorem that
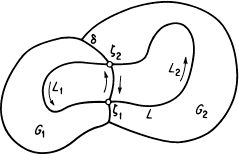
FIGURE 16.2
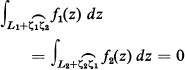
, and hence
since (16.8) implies
But then, according to (16.9),
and hence, by Morera’s theorem, φ(z) is analytic on D, as asserted.
DEFINITION. Either of the elements{G1, f1} and {G2, f2} figuring in Theorem 16.3 is called a direct analytic continuation of the other(across the arc δ).
Remark. Let {G2, f2} be a direct analytic continuation of {G1, f1} in the sense of the above definition, and let φ(z) be given by (16.9). Then φ(z) is an analytic continuation of f(z) from G1(or G2) into G1 ∪ δ ∪ G2, in the sense of the definition on p. 341.
Problem 1. Give an example where G1 and G2 share an arc such that (16.8) fails to hold as well as an arc δ satisfying (16.8).
Problem 2. Generalize Theorem 16.3 to the case where δ is unbounded.
Hint. Assume that every finite subarc of δ is rectifiable.
Problem 3. Generalize Theorem 16.3 to the case where G1 and G2 overlap.
Hint. The function φ(z) can now be double-valued on G1 ∩ G2.
77. THE SYMMETRY PRINCIPLE
The following technique of analytic continuation is of great practical importance:
THEOREM 16.4 (Symmetry principle).11 Let G be a domain whose boundary contains an accessible open line segment δ, and let w= f(z) be analytic on G and continuous on G ∪ δ. Let G* be the domain symmetric to G with respect to δ, 12 and suppose G and G* are disjoint. Moreover, suppose Δ = f(δ) is itself a line segment, and let f*(z) be the function defined on G* ∪ δ by the conditions
1. f*(z) = f(z) for all z ∈ δ;
2. f*(z*) and f(z) are symmetric with respect to Δ for all z* ∈ G*, where z* is the point symmetric to z ∈ G with respect to δ.
Then the elements {G, f} and {G*, f*} are direct analytic continuations of each other across δ.
Proof. There is no loss of generality in assuming that δ and Δ are both segments of the real axis, as shown in Figure 16.3. In fact, this configuration can always be achieved by making suitable preliminary entire linear transformations in both the z and w-planes, and such transformations (and their inverses) preserve continuity, analyticity, accessibility and symmetry (recall Sec. 27). Thus we can write
on δ and
FIGURE16.3
on Δ. Then the points z* and z symmetric with respect to δ are just complex conjugates of each other, and the same is true of the points w* and w symmetric with respect to Δ:
Given any point z0 ∈ G, suppose G contains the neighborhood |z – z0| < ρ (see Figure 16.3). Being analytic on G, f(z) has an expansion at z0 of the form
from
But then
i.e.,
Therefore f* is analytic on G*,13 since the point z0 ∈ G (and hence the point z0* ∈ G*) is arbitrary.
Next we show that f* is continuous on G* ∪ δ (it is obviously continuous on G*). Let z = x0 be any point on δ. Then
since f(z) = u(x, y) + iv(x, y) is real on δ and continuous on G ∪ δ, and hence
It follows that
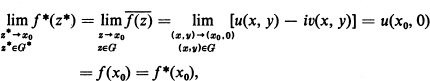
i.e., f* is continuous on G* ∪ δ, as asserted [how about the case where z* approaches x0 along δ itself?]. The rest of the proof is an immediate consequence of Theorem 16.3.
Example. Let G be the interior of the triangular contour ABC shown in Figure 16.4(a), and let f(z) be analytic on G and continuous on . Suppose
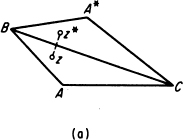
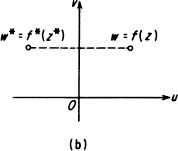
FIGURE 16.4
f(z) takes purely imaginary values on the segment BC. Then f(z) can be continued analytically across BC into the quadrilateral ABA*C which is “twice as big” as the original domain G. Moreover, if z* and z are symmetric with respect to BC, i.e., if z* is the reflection of z in BC, then the image points w = f(z) and w* = f*(z*) are symmetric with respect to the imaginary axis, as shown in Figure 16.4(b).
Remark. There is a natural generalization of the symmetry principle to the case where δ is a circular arc (see M3, Sec. 46).
Problem 1. Generalize Theorem 16.4 to the case where δ is an infinite line segment.
Problem 2. Generalize Theorem 16.4 to the case where the domains G and G* overlap.
Problem 3. Prove that the function (15.5) maps the lower half-plane onto the rectangle with vertices –K, K, K – iK′, –K – iK′, where K and K′ have the same meaning as in Sec. 72.
78. MORE ON SINGULAR POINTS
Given an element {G, f(z)}, let Γ be the boundary of the domain G. Then every point of Γ falls into one of the following two classes (a priori, either class can be empty):
1. Points ζ ∈ Γ for which there can be found a neighborhood 
(ζ) and a function φζ(z) analytic on (ζ), i.e., an element {(ζ), φζ(z)} such that φζ(z) = f(z) for all z in (ζ) ∩ G; such points are called regular points [of {G, f(z)}, or simply of f(z)].
2. Points ζ ∈ Γ for which no such neighborhood and analytic function can be found; such points are called singular points [of {G, f(z)}, or simply of f(z)].
It follows from the definition of a regular point that if ζ ∈ Γ is a regular point, then so is every point ζ′ ∈(ζ) ∩ Γ. In fact, for (ζ′) we need only choose any disk with center ζ′ which is contained in (ζ), while for φζ′(z) we need only choose the function φζ(z) which is analytic on(ζ) and coincides with f(z) on (ζ) ∩ G14. In particular, this means that if f(z) has one regular point, then f(z) has infinitely many regular points. On the other hand, f(z) can have just one singular point.
It should be noted that every point ζ ∈ G has the characteristic property of a regular point, i.e., there exists a neighborhood (ζ) [in fact, any neighborhood of ζ contained in G] and a function φζ(z) analytic on (ζ)[in fact, f(z) itself] which coincides with f(z) on (ζ) ∩ G. Therefore, extending our definition of a regular point to include interior points of G, we shall henceforth regard the points of the domain G itself as regular points of f(z).
Example 1. Let G be the deleted neighborhood 0 < |z – ζ| < R, and let f(z) be a function analytic on G. Then f(z) has a regular point or a singular point at ζ in the sense of the above definition if and only if f(z) has a regular point or a singular point in the sense of the definition on p. 234. The new definition is more general and will allow us to consider the case of nonisolated singular points (see Example 2, p. 355).
Example 2. Let G be the unit disk |z| < 1, and let
For every point ζ ≠ 1 lying on the boundary of G (i.e., on the unit circle |z| = 1), we can find a neighborhood (ζ): |z – ζ| < |1 – ζ| and a function
analytic on (ζ) such that φζ(z) = f(z) on (ζ) ∩ K. Therefore, every point ζ≠ 1 is a regular point of f(z). On the other hand, the point ζ = 1 is a singular point of f(z), since otherwise there would be a neighborhood (1) and an analytic function φ(z) coinciding with f(z) on E = (1) ∩ K. But then the limit
would have to be finite, which is impossible.
Example 3. Given any element {G, f(z)}, let Γ be the boundary of G and suppose f(z) → ∞ as z ∈ G approaches an accessible point ζ ∈ Γ. Then ζ is a singular point of f(z) by exactly the same argument as in Example 2.
THEOREM 16.5. Given a disk K: |z – z0| < R and an element{K, f(z)}, suppose every point of the circle Γ:|z – z0| = R is a regular point. Then there is a disk K1:|z – z0| < R1 and another element {K1, φ(z)} such that R1 > R and φ(z) = f(z) on K, i.e., f(z) can be continued analytically into a larger concentric disk.15
Proof. Let D be the union of K and all the neighborhoods (ζ), ζ ∈ Γ, where (ζ) is any neighborhood figuring in the definition of the regular point ζ. Then D is obviously nonempty. Since K and all the (ζ) are open, so is D (recall Sec. 9, Prob. 5a). Moreover, D is connected, since any two points of D can be joined by a curve contained in D (why?). Therefore D is a domain.
Next let φζ(z) have the same meaning as in the definition of the regular point ζ, and define the following function on D:
As we now show, φ(z) is single-valued and analytic on D. Since D contains points which simultaneously belong to a neighborhood (ζ) and to K, and also points which simultaneously belong to two neighborhoods (ζ') (ζ″), and we must verify that the definition (16.11) is consistent, in the sense that a point z ∈ D will always be assigned the same value φ(z) whether z is regarded as belonging to K, (ζ), (ζ′) or (ζ″). There are basically two cases to be considered:
1. Let G = (ζ) ∩ k. Then φζ(z) = f(z) on G, by the very definition of the regular point ζ.
2. Let G = (ζ’) ∩ (ζ″) ≠ 0 and let E = G ∩ K [see Figure 16.5, which illustrates the situation where neither neighborhood(ζ’), (ζ″) is a subset of the other]. Then φζ’(z) = f(z) = φζ″(z) on E, and hence by the uniqueness theorem for analytic functions (Theorem 10.8), φζ’(z)= φζ″(z) on the whole set G, since E ⊂ G obviously contains a limit point of G.
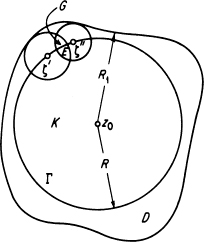
FIGURE 16.5
Thus the function φ(z) defined by (16.11) is single-valued on D. Moreover φ(z) is analytic on D, since, by construction, φ(z) coincides with an analytic function [either f(z) or some φζ(z)] in a neighborhood of every point of D [note that if z ∈ D, then there is a neighborhood ζ such that (z)⊂ K or (z) (ζ) for some ζ ∈ Γ].
Finally let R1 be the distance between z0 and the boundary of D. Since every point is an interior point of D, R1 must exceed the radius R of the original disk K. Therefore D contains the disk K1:|z – z0| < Rl and the theorem is proved.
Given a power series
with radius of convergence R, the disk K: |z – z0| < R and the sum function f(z) constitute a circular element {K, f(z)}. For simplicity, a regular or singular point of {K, f(z)} will be called a regular or singular point of the series (16.12) or of its sum f(z).
THEOREM 16.6. The power series (16.12) has at least one singular point on its circle of convergence Γ: |z – z0| = R.
Proof. If the element {K, f(z)}, where K is the interior of Γ, has no singular points on Γ, it follows from Theorem 16.6 that f(z) can be continued analytically into a larger disk K1:|z – z0| < R1. But then the series (16.12) has a radius of convergence larger than R (why?), contrary to hypothesis.
Example 1. The geometric series
has circle of convergence Γ:|z| = 1 and sum 1/(1 – z). As required by Theorem 16.6, there is a singular point on Γ, namely, the point z = 1 (see Example 2, p. 352).
Example 2. We now show that every point on the circle of convergence Γ: |z| = 1 of the power series
is a singular point. Suppose first that z → 1 along the segment 
, i.e., along the radius of Γ contained in the nonnegative real axis. Then, since the nth partial sum
approaches n + l as x → l –, there is a δ(n) > 0 such that
if x > 1 — δ(n). Therefore
if x > 1 — δ(n), which implies
But then z = 1 is a singular point of f(z) [recall Example 3, p. 353].
Next we note the identity
Since the term in brackets differs from the original series only by having z2n instead of z, we have
for any positive integer n. Consider all the 2nth roots of unity, i.e., all the numbers
which correspond to the vertices of a regular 2n-gon inscribed in the unit circle. If ζ is one of these roots and if z → ζ along the radius 
, then z2n obviously lies on the radius 
and z2n → 1 — as z → ζ. It follows that
and therefore
Thus every root (16.13) is a singular point of f(z), for all n = 1, 2,…. Consequently, the set of singular points of f(z) is everywhere dense in the unit circle Γ (i.e., every arc of Γ, however small, contains a singular point). But this means that every point of Γ is a singular point, since if ζ′ ∈ Γ were a regular point, then, as on p. 352, some arc (ζ’) ∩ Γ would consist only of regular points. In particular, f(z) cannot be continued analytically into any domain larger than the unit disk, as already noted in Example 3, p. 342.
Finally we generalize the concept of a singular point even further:
DEFINITION. Let F(z) be a complete analytic function.16 Then by a singular point of F(z) is meant a singular point of any element of F(z).
Example 1. If
then z = 1 is a singular point of F(z), since it is a singular point of the single-valued branch of F(z) for which z½ = — 1. On the other hand, z = 1 belongs to the domain of existence of F(z) [see Definition 3, p. 346], since z = 1 is a regular point of the single-valued branch of F(z) for which l½ = +1.
Example 2. Suppose ζ is an isolated singular point of a complete analytic function F(z), so that F(z) is defined on some annulus G:0 < |z — ζ| < R. If F(z) is single-valued on G, then ζ is an isolated singular point of single-valued character, as already studied in Sec. 56 (also recall Example 1, p. 352). More generally, F(z) is multiple-valued on G, and then ζ is called an isolated singular point of multiple-valued character. Let D be the domain obtained from the disk |z — ζ| < R by deleting the line segment joining the origin to the point z = R (thus D is a “slit disk”). Then it can be shown (see M3, Sec. 42) that there are just two possibilities:
1. F(z) has precisely n distinct single-valued branches
on D such that
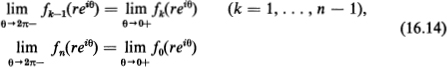
for every positive r < R. In this case, ζ is called a branch point of order n — 1 (cf. p. 76).
2. F(z) has a countably infinite set of distinct single-valued branches
on D (and no others) such that
for every positive r < R. In this case, ζ is called a logarithmic branch point (cf. p. 129).
Example 3. Let F(z) be a complete analytic function with a branch point ζ of order n — 1. Then ζ is called an algebraic branch point if F(z) approaches a limit (finite or infinite) as z → ζ (cf. p. 76). Otherwise ζ is called a transcendental branch point. For example, each of the functions z1/n and exp (z1/n) has an algebraic branch point of order n — 1 at the origin, while the function exp (z-1/n) has a transcendental branch point of order n — 1 at the origin.
Example 4. The considerations given in Example 2 and 3 are easily generalized to the case of branch points at ∞ by taking G to be the domain |z| > R and D the domain obtained from G by deleting the infinite line segment joining the point z = R to the point at infinity. For example, the function exp (z–1/n) has an algebraic branch point of order n — 1 at ∞.
Problem 1. Let G be the interior of a closed Jordan curve Γ. Prove that ζ ∈ Γ is a regular point of {G, f(z)} if and only if f(z) can be continued analytically across an arc δ ⊂ Γ containing ζ.
Problem 2 (Ml, p. 387). Given a power series
with radius of convergence R, let ζ be a point of the circle Γ: |z — z0| = R and let z1 be a point of the radius 
distinct from z0 and ζ. Prove that ζ is a singular point of f(z) if
and a regular point if
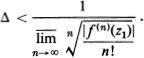
Problem 3 (Ml, p. 389). Prove the following result known as Pringsheim’s theorem: Given a power series
with radius of convergence 1, suppose the coefficients an are all nonnegative real numbers. Then z = 1 is a singular point of f(z).
Problem 4. Prove that the circle |z| = 1 is the natural boundary (see p. 342) of the series
Problem 5 (Ml, p. 393). Prove that the point z = 1 is a singular point belonging to the domain of existence of the complete analytic function
Problem 6. Discuss the branch points considered in Secs. 20 and 32 from the standpoint of the general definition of branch points in Examples 2–4.
Problem 7. Find the singular points of the following functions:
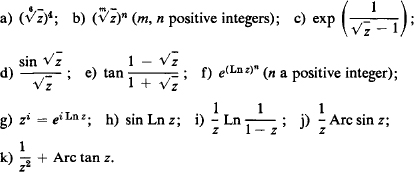
Ans.
a) Algebraic branch points of order 2 at z = 0, ∞;
c) Algebraic branch points of order 1 at z = 0, ∞; one of the branches has an essential singular point at z = 1;
e) Algebraic branch points of order 1 at z = 0, ∞; one of the branches has a limit point of poles at z = 1;
g) Logarithmic branch points at z = 0, ∞;
i) Logarithmic branch points at z = 1, ∞; every branch except one has a pole of order 1 at z =0;
k) Logarithmic branch points at z = ±i; every branch has a pole of order 2 at z = 0.
79. RIEMANN SURFACES
Finally we consider the problem of finding a “generalized domain” on which a given complete analytic function F is single-valued. This is done by the following simple construction: Let {G, f} and {D, φ} be any two elements of F such that G ∩ D ≠ 0 and think of G and D as being cut out of separate pieces of paper. Then “ paste together” the components of G ∩ D on which f(z) and φ(z) coincide, while “ leaving unpasted ” the components on which f(z) and φ(z) differ (see Prob. 1). Doing this for every pair of elements of F, we obtain a “layered surface” covering every point z0 in the domain of existence of F a number of times (possibly infinite) equal to the number of values F takes at z0. This “ many-sheeted structure” is called the Riemann surface of F.
Clearly, the effect of the construction just described is to make F single-valued on its Riemann surface. More precisely, a “point” on the Riemann surface can be interpreted as an ordered pair (z, F(z)), where z lies in the ordinary complex plane and F(z) is a value of F at z. But equality of two such points (zl, F(z1)) and (z2, F(z2)) means not only that z1 = z2 but also that F(z1) = F(z2)!
More generally, we can define a complete analytic function F by using the definition of a direct analytic continuation given on p. 349 instead of that given on p. 342, or by using both definitions simultaneously (supply the details). Then in general two elements {G, f}, {D, φ} ∈ F share suitable boundary arcs and overlap as well. Correspondingly, the prescription for constructing the Riemann surface of F involves pasting the boundaries of G and D together along every common arc δ on which f(z) and φ(z) coincide,17 as well as pasting together those portions of the domains themselves on which f(z) ≡ φ(z).
Remark. These heuristic considerations can be supported by perfectly rigorous mathematics, and in fact much of the modern theory of analytic functions is concerned with Riemann surfaces and related topics. The mathematical tools needed to pursue the subject in proper depth are rather sophisticated. From the standpoint of the advanced theory, the entities constructed here are “topological models of Riemann covering surfaces” (see M3, Sec. 35).
Example 1. Suppose F has a branch point of order 2 at a point ζ. To construct the Riemann surface of F in the vicinity of ζ, we start from three “replicas” D0, Dl, D2 of the slit disk figuring in Example 2, p. 356, all cut along the segment joining the points z = 0 and z = R. These domains have the appearance shown in Figure 16.6(a), where the upper and lower edges of the cut are suitably labelled in each case. Next we paste δ0– to δ1+, then δ1– to δ2+ and finally δ2– to δ0+(this has the effect of joining D0 to Dl, then D1 to D2 and finally D2 back to D0).18 As a result, we obtain the “three-sheeted domain” shown in Figure 16.6(b). The intersections which come about as a result of “ pasting D2 back to D0” have no mathematical meaning and should be disregarded.
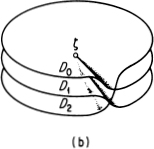
FIGURE 16.6
Example 2. Next we construct the Riemann surface of the function
starting from n replicas D0, D1,…, Dn−1 of the finite plane cut along the nonnegative real axis. Let δk+ and δk− denote the upper and lower edges of the nonnegative real axis regarded as the boundary of Dk, and let
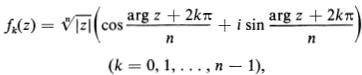
so that every {Dk, fk(z)} is an element of F(z).19 We now paste δ0− to δ1+, δ1−to δ2+,…, δn−2−to δn−1+ and finally δn−1−to δ0+, corresponding to the fact that {Dk, fk(z)} is a direct analytic continuation of {Dk−1, fk−1(z)} for every k = 1,…, n [with {Dn, fn(z)} = {D0, f0(z)}]. The result is an n−sheeted Riemann surface, shown schematically in Figure 16.7 for the case n = 4. All n sheets come together at the branch points z = 0 and z = ∞.20
FIGURE 16.7
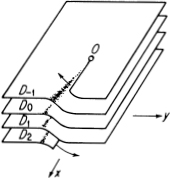
FIGURE 16.8
Example 3. Finally we construct the Riemann surface of the function
starting from infinitely many replicas…, D−1, D0, Dl,…of the finite plane cut along the nonnegative real axis. The construction is the same as that given in the preceding example, except that now there is no “first sheet” and no “last sheet” which are pasted together at the end of the construction, and instead we obtain the infinite−sheeted Riemann surface shown schematically in Figure 16.8.
Problem 1. Can a complete analytic function F(z) take the same value at several points of a Riemann surface all lying over the same point ζ in the z−plane? If so, how many such points are allowed?
Hint. Consider the function
Comment. In constructing a Riemann surface we do not paste together separate points of the domains G and D of two elements {G, f} and {D, φ}, but only common boundary arcs of G and D or whole domains (components of G ∩ D).
Problem 2. Construct the Riemann surface of the function
which is the inverse of the Joukowski function of Sec. 22.
Problem 3. Construct the Riemann surface of the function
Problem 4. Discuss the notion of a domain of univalence (see p. 73) from the standpoint of Riemann surfaces.
1 Ultimately we will purse this last condition even to the extent of allowing φ(z) to be a multiple−valued functions and D to be a “many−sheeted domain” (see Sec. 79).In this case, condition2 is replaced by the requirement that some single−valued analytic branch φ(z) coincide with f(z)on E.
2 See Remark 2, p. 343 and the remark on p. 349.
3 The absence of the adjective “direct” is crucial here.
4 Such a relation is called an equivalence relation (see e.g., G.Birkhoff and S.MacLane, op.cit., p. 30).
5 {G, F} is shorthand for {G, f(z)},and similarly for {D, φ} and {E, ψ}.
6 Obviously, F is in general multiple−valued.
7 Of course, single−valued branches of Ln z can also be defined on appropriate multiply connected domains.
8 For the proof, see M3, Sec. 40.
9 we call δ an arc emphasize that its end points are distinct. By an open arc is meant an arc minus its end points (rectifiability of an open arc is defined in the obvious way, i.e., by including the end points).
10 This result has already been mentioned in Sec. 37, Prob. 6. For the proof, see M3 sec. 12.
11 Often called Schwarz’s reflection principle.
12 More exactly, symmetric with respect to the straight line containing δ.
13 This is a situation where confusion can be avoided by omitting the argument of the function f*(cf. p. 14).
14 In a context like this, (ζ) will denotes one of the neighborhoods figuring in the defination of the regular point ζ
15 Elements like {K, f} and {k1, φ}, whose domains are disks, are often called circular elements.
16 We revert to the notation which does not distinguish between a function and its values at a point(cf. p. 14).
17 Here, as in Theorem 16.3, it is assumed that f(z)is analytics on G and continuous on G ∪δ, while φ(z)is analytics on D and continuous on D ∪ δ. It is also assumed that δ has the propertices needed to invoke Theorem 16.3 or one of its generalizations(see Sec. 76, probs. 3, 4).
18 The justification for this construction stems, of course, from the formulas(16.14) and Theorem 16.3
19 In writing {Dk, fk(z)}, there is really no need to distinguish between domains Dk with different subscripts.
20 It is customary to include these points on the Riemann surface, although they do not belong to any of the domains Dk.
