18

IMPLICATIONS OF
SPECIAL RELATIVITY

J. RICHARD GOTT

Einstein’s theory of special relativity revolutionized our ideas of space and time. It implied that time could be regarded as a fourth dimension—added to the three dimensions of space. Interestingly, it was Einstein’s teacher Hermann Minkowski, using Einstein’s work in special relativity, who developed this geometric picture of space and time, publishing his results in 1907. Einstein immediately adopted this view. We live in a four-dimensional universe. What do I mean by that? We say that the surface of Earth is two-dimensional. It takes two coordinates, latitude and longitude, to locate a point on Earth’s surface. If you know your latitude and longitude, you know your location on the surface of Earth. But the universe is four-dimensional, meaning it takes four coordinates to tell you where you are. If I want you to come to a party, I will have to tell you where in latitude and longitude on Earth’s surface to go. I must also tell you the altitude. You wouldn’t want to show up on the fourth floor, if the party was on the twelfth floor! And I must tell you at what time you should arrive. If you come at the wrong time, you will miss the party just as surely as if you went to the wrong floor. Every event, such as a New Year’s Eve party on the fifty-fourth floor, at 5th Avenue, and 34th Street, requires four coordinates to locate it: two coordinates to tell you where to go on Earth’s surface, the altitude, and the time of the event. Since four coordinates are needed, we know that we live in a four-dimensional universe.

We can use this idea to draw spacetime diagrams. You have undoubtedly seen a picture in a book of Earth orbiting the Sun. The Sun is a big white dot in the center, and Earth’s orbit is shown as a dashed circle surrounding it (because Earth’s elliptical orbit is nearly circular). Earth can be shown as a small blue dot at the 12 noon position on the circle, representing its position on January 1. If we wanted to show Earth circling the Sun, we could have a sequence of pictures, with Earth working its way counterclockwise around the circle. By February 1, it will have reached about 11 o’clock on the circle, by March 1, it will reach 10 o’clock, and so forth. You could make a movie of this by making each picture in the sequence a frame of the movie. As the frames were played, you would see Earth circling the Sun.

Now imagine taking that film, cutting it up into individual frames, and stacking those frames on top of one another to form a vertical stack. Each frame would represent an instant of time, and frames that were higher in the stack would represent later times. In this way, you could make a spacetime picture of how Earth orbits the Sun. Time is the vertical dimension of the stack—the future is toward the top and the past is toward the bottom. The two horizontal directions represent two dimensions of space (as you would see them in a two-dimensional picture of Earth’s orbit around the Sun). The Sun is not moving—it’s always in the center; therefore, all these images of the Sun form a white rod extending vertically up the stack. In each frame, however, Earth has moved to a new position as it keeps advancing counterclockwise in its orbit around the Sun, which makes Earth in the stack appear as a blue helix winding around the white rod. The radius of this blue helix is 8 light-minutes—the radius of Earth’s orbit. Vertically, the helix winds around the Sun once a year. The blue helix winding around the vertical white rod represents a spacetime diagram. We can add the orbits of Mercury, Venus, and Mars to the diagram by adding helixes for them that also wind around the vertical rod representing the Sun. This diagram is three-dimensional; I am leaving out one of the spatial dimensions to allow you to visualize the diagram. You couldn’t visualize this diagram if it were four dimensional—you can only see three dimensions. We are showing the diagram in 3D in this book using a stereo pair (figure 18.1). You can either enjoy it as two photographs of a three-dimensional model from slightly different viewpoints or follow the instructions (appearing in the text near figure 4.2) for using both eyes to see it in its full three-dimensional glory.

The vertical white rod is called the worldline of the Sun—its path through space and time. It’s white because, as we learned in chapter 4, the Sun is white (not yellow). The blue helix is the worldline of Earth—its path through spacetime. Notice how blue helix passes alternately in front of and behind the vertical worldline of the Sun. The orange helix winding tightly around the Sun is the worldline of Mercury. It orbits the Sun once every 88 days. The grey helix is Venus, and the red helix is Mars. The farther out a planet is, the less tightly its helix is wound around the Sun. If you think four-dimensionally, you should not think of Earth as a sphere, but as a long piece of spaghetti, a helix wound around the Sun. Earth has an extension in time.

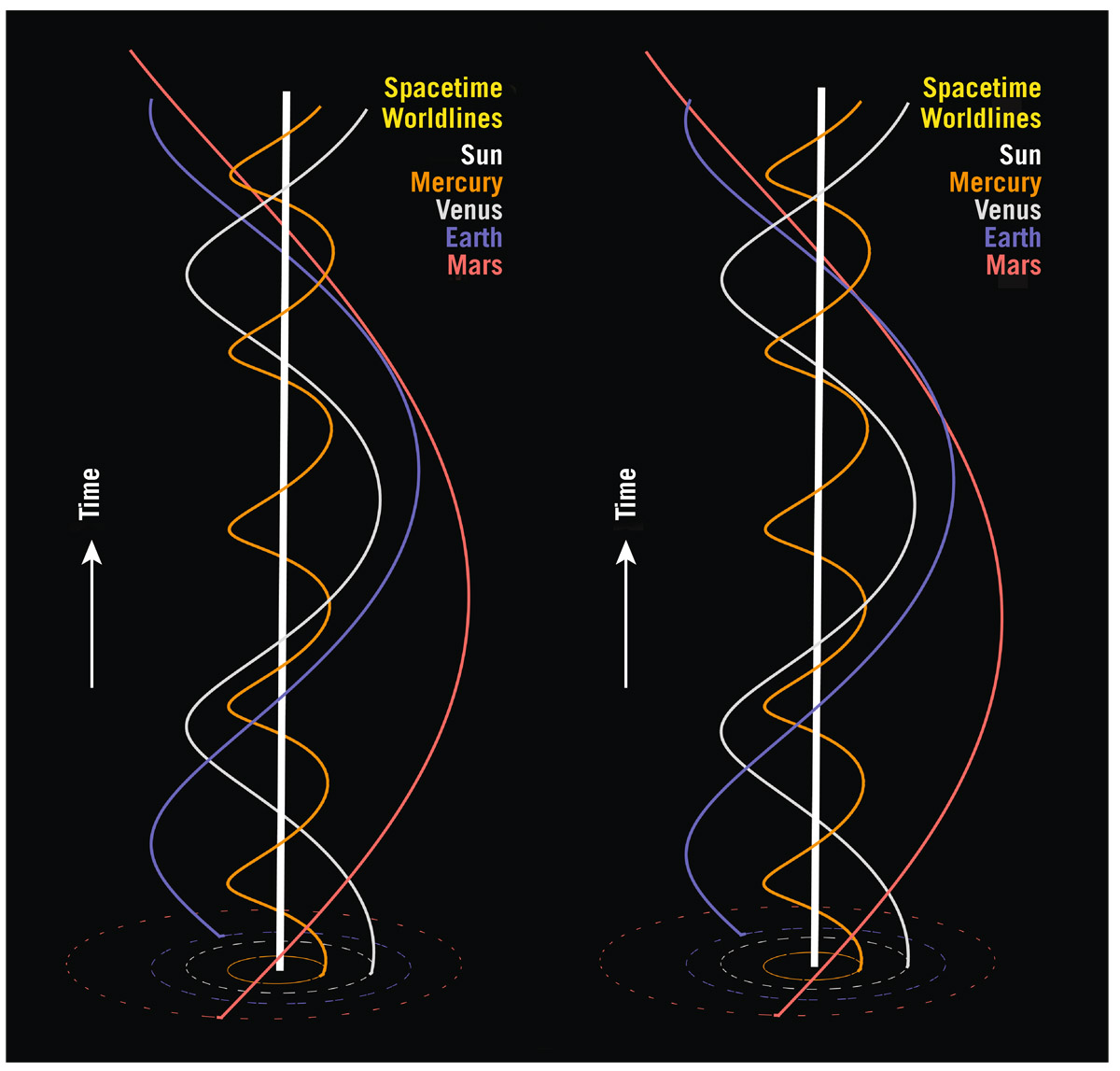
FIGURE 18.1. Spacetime diagram of the inner solar system. Time is vertical, and two dimensions of space are shown horizontally. This is a three-dimensional picture, so we have produced a cross-eyed stereo pair. Follow the same instructions for stereo viewing as for figure 4.2. The worldline of the Sun is the vertical white line in the middle. Earth, orbiting counterclockwise, circles first in front of the Sun and then passes behind it later (further up in the diagram). Mercury, Venus, Earth, and Mars have successively larger orbital periods and therefore successively more loosely wound helixes. Photo credit: Robert J. Vanderbei and J. Richard Gott

You have a worldline too. It starts at your birth, snakes through all the events of your life, and ends at your death. Your worldline is about 1 foot, front to back; about 2 feet wide; 6 feet tall; and if you are lucky, maybe 80 years in duration. These are spacetime diagrams where motionless worldlines intertwine in a static four-dimensional spacetime sculpture.

We can draw spacetime diagrams of some of the thought experiments that Einstein proposed on the concept of simultaneity. Suppose I am sitting in the center of my lab, and it is 30 feet wide. I’m an Earthling. My lab is stationary with respect to Earth, and I am stationary in the center of my lab. In the spacetime diagram, the horizontal coordinate represents space, and the vertical coordinate represents time. Because I am advancing in time but not moving in space (left to right, or right to left), my worldline goes vertically upward. The front of my lab is not moving; it likewise has a vertical worldline, as does the back of my lab. The worldlines of the back of the lab, me (the Earthling), and the front of the lab are three parallel vertical lines. The future is toward the top, and the past is toward the bottom. The front of my lab is the vertical line to the right, and the back of my lab is the vertical line to the left. To make the horizontal and vertical scales, I am going to use units of feet and nanoseconds. Light moves through empty space at 1 foot per nanosecond. In the diagram (figure 18.2), light beams will be diagonal lines tipped at 45° with respect to vertical.

FIGURE 18.2. Spacetime diagram of my lab and an astronaut’s rocket.

Credit: Adapted from J. Richard Gott (Time Travel in Einstein’s Universe, Houghton Mifflin, 2001)

Let’s say at time t = 0 (Earth time, ET; shown by the little clock on my worldline with its hand pointing vertically) I send out two laser beams, to the right and to the left, which hit mirrors on the front and back walls, respectively, of my lab. The worldlines of these two light beams are diagonal lines tipped at 45°. They reach the front and back of the lab simultaneously (traveling equal distances of 15 feet) at time 15 nanoseconds (ET). Two little 60-nanosecond clocks each reading 15 nanoseconds (ET) are shown at the points where the two light beams intersect the front and back walls of the lab. The Earthling’s (my) worldline also has a little clock on it that reads 15 nanoseconds (ET). A horizontal dashed line connects those three little clocks reading 15 nanoseconds. That horizontal line connects simultaneous events according to me. After the laser beams bounce off the mirrors at the front and back of my lab, they return to me. And they both arrive back at the same time, 30 nanoseconds after the start. When the laser beams arrive back to me, my clock reads 30 nanoseconds, because the laser beams traveling at the speed of light have traveled out 15 feet and back 15 feet, traveling a total distance of 30 feet in 30 nanoseconds. So far, so good.

But then following Einstein’s argument, consider an astronaut traveling at 80% of the speed of light in a rocket ship (going from left to right). The astronaut’s worldline must therefore be tilted. For every 4 feet to the right he moves, he moves 5 nanoseconds upward in time. He is traveling at 4/5 (or 80%) of the speed of light. The front of his rocket is moving at the same speed and has the same tilt, as does the back of his rocket. The worldline of the back of the rocket, the worldline of the astronaut, and the worldline of the front of the rocket are all parallel. They are not moving relative to one another. Now that astronaut sitting at the center of his rocket sends laser beams toward the front and back of his rocket, just as I do in my lab. I measure the length of his rocket to be 18 feet. I will say more about that later. The light beam he sends to the left hits the back of his rocket, which starts out 9 feet away (that’s half of 18 feet). I’m watching this experiment through a window of the rocket. I see the back of the rocket move 4 feet to the right in 5 nanoseconds, while the laser beam travels 5 feet to the left in those same 5 nanoseconds. Now 4 feet plus 5 feet is 9 feet, so it takes 5 nanoseconds for the astronaut’s laser beam to hit the back of the rocket, closing that original distance of 9 feet. The astronaut’s laser beam hits the back of the rocket at 5 nanoseconds Earth time (ET), according to me. The laser beam going to the left and the rocket going to the right are closing on each other and so collide quickly, according to me (that is, from my viewpoint).

The laser beam that the astronaut sends out to the right has to catch up with the front end of the rocket, which is moving away, and therefore it takes longer to catch up and meet it, according to me. While the laser beam travels 45 feet in 45 nanoseconds (ET; according to Einstein’s second postulate, light travels at a constant speed of 1 foot per nanosecond), the front of the rocket travels just 36 feet (or 4/5 of 45 feet). In 45 nanoseconds, the light beam travels 45 feet, while the rocket travels 36 feet, or 9 feet less, but the front of the rocket had a 9-foot head start. Thus, the astronaut’s laser beam hits the front of his rocket 45 nanoseconds (ET) later. This means that I observe the laser beam that is headed toward the back of his rocket hitting the back before the other laser beam headed toward the front hits the front. The events in which the laser beams hit the front and back of his rocket are not simultaneous, according to me.

What does the astronaut see? The astronaut is traveling at constant speed in a constant direction; by virtue of Einstein’s first postulate, the astronaut is entitled to think of himself at rest. He does think he is at rest. He sits in the center of his rocket, which is also at rest with respect to him, and sends out laser beams toward the front and back of his rocket. Since he sits in the middle of his rocket and his rocket is not moving, he must think that the two laser beams traveling at the speed of light must take equal amounts of time to get to the front and back. From his perspective, he must see the two events, in which one laser beam hits the back of the rocket and the other laser beam hits the front of the rocket, as simultaneous events. I (the Earthling) do not think they are simultaneous events: I see the lasers hit in succession—the back of the rocket gets hit first, then the front. We do not agree on which events are simultaneous. This is counter to common sense, but it is a direct result of the postulates of special relativity.

Interestingly, when Einstein formulated this thought experiment, he did not use an astronaut on a rocket with mirrors at the front and back of his rocket, but a man on a train with mirrors at the front and back of the train. In 1905, the fastest vehicles we had were trains—about 120 miles per hour!

I slice spacetime differently from the astronaut. Think of four-dimensional spacetime as a loaf of bread. I slice the loaf in slices like those of American bread. Set a loaf of American bread on its end, so the individual slices are horizontal. These horizontal slices show individual instants of Earth time (ET), and each slice of bread contains simultaneous events according to me. The astronaut slices spacetime differently. Let us call him Jacques (he is French). He slices the loaf of spacetime on a slant, like French bread. His slanted slices measure instants of astronaut time (AT). Jacques and I do not agree on simultaneous events, that is, on which events we say are in the same slice. We slice the loaf differently, but we see the same loaf. According to Einstein, the things that are real are those that are observer-independent. Space and time as separate entities are not real. I say the present is a horizontal American-bread slice, but Jacques says the present is a slanted French-bread slice. Since he is moving with respect to me, we do not agree on what the present is. We therefore disagree on which events lie in the past and the future. But we can agree on the spacetime loaf. It is the entire four-dimensional spacetime that is real.

Now let’s return to my view of Jacques’s rocket. After Jacques’s laser beam reflects off the mirror at the front of his rocket, it takes only 5 nanoseconds to get back to him, according to me. I see the light beam and the astronaut closing on each other. It only takes 5 nanoseconds for the light beam to move back 5 feet, while the rocket moves forward 4 feet, to close the distance of 9 feet. According to me, the front laser beam takes a total of 45 nanoseconds + 5 nanoseconds = 50 nanoseconds to go out and back. The laser beam that has hit the back mirror takes 45 nanoseconds to catch up with the astronaut. To go out and back takes 5 + 45 = 50 nanoseconds Earth Time (ET), according to me. I thus see both laser beams return to the astronaut at the same time. He must also see them returning at the same time, because they return at the same time and the same place.

I see 50 nanoseconds elapse between when he sent the laser beams out and when they returned. I see him moving at 80% of the speed of light (v/c = 0.8), so I must see his clocks ticking at 60% (or √[1 – (v²/c²)]) of the speed of my clocks. If I see 50 nanoseconds elapse, I must see the astronaut age only 30 nanoseconds. When the astronaut sees his laser beams return, he must say that that event occurs at 30 nanoseconds astronaut time (AT), because he is 30 nanoseconds older when they get back. The laser beams must have hit the front and back of the rocket simultaneously at 15 nanoseconds AT. Note the French-bread-tilted slice labeled “15 ns AT.” This connects simultaneous events according to the astronaut. The astronaut thinks he is at rest, and the situation looks to him exactly like what I see in the lab on Earth. Since the laser beams go out and back in 30 nanoseconds according to him, he must deduce that his rocket is 30 feet long.

The events where the astronaut’s two laser beams hit the front and back of the rocket are events that I see as separated in space by 50 feet and in time by 40 nanoseconds. Using the speed of light (1 foot per nanosecond) to compare distances in space with distances in time, I see these two distant events as being separated by more distance in space than distance in time. Any two events that I see separated by more distance in space than distance in time have what we call a spacelike separation. There is always some astronaut traveling at high speed (but lower than the speed of light) who will see those two events as simultaneous. He or she will see those events as having a separation in space but no separation in time. Einstein showed that what the two observers can agree on is the square of the separation in space of the two events minus the square of the separation in time of the two events; we refer to this quantity as ds². Using units where the speed of light is 1 (i.e., where 1 foot = 1 nanosecond), I find the separation in space of the two events to be 50 and the separation in time of the two events to be 40, so I calculate ds² to be 50² – 40² = 2,500 – 1,600 = 900. The astronaut Jacques, however, sees the time difference between the two events to be 0 and the spatial separation between the two events to be 30 (remember he judges his rocket to be 30 feet long); but when he calculates ds², he gets 30² – 0², or 900, just as I do. We may disagree on both distances and times, yet surprisingly, we will still agree on some important things.

Consider now the separation between the astronaut’s sending of the light signal and its arrival at the back of his rocket. The separation I measure in space between these two events is 5 feet, and the time between these two events I measure to be 5 nanoseconds. So I calculate ds² = (separation in space)² – (separation in time)² to be 5² – 5² = 0. The astronaut measures a separation in space of 15 feet between the two events and a separation in time of 15 nanoseconds between the two events, so he calculates ds² = 15² – 15² = 0, just as I do. Events connected by a light ray (called a null separation) always have ds² = 0 as seen by any observer. Einstein’s second postulate states that all observers must see a light beam traveling at a constant speed of 1 in these units (1 foot per nanosecond); thus, the separation in space must equal the separation in time, and ds² must be zero. Indeed, the minus sign in the ds² formula connected with the difference in time is designed to guarantee that the second postulate is always obeyed.

The Pythagorean theorem tells you that in a plane with an (x, y) Cartesian coordinate system, if two points are separated by distances dx and dy, then their (separation in space)² = dx² + dy². The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. In three-dimensional space with x, y, and z Cartesian coordinates, the Pythagorean theorem generalizes to (separation in space)² = dx² + dy² + dz². That’s high-school Euclidean solid geometry. But Einstein is saying that ds² = (separation in space)² – (separation in time)². Substituting, we find ds² = dx² + dy² + dz² – (separation in time)². But separation in time is just dt. So substituting for that, we have: ds² = dx² + dy² + dz² – dt². So that’s the difference between the dimension of time t and any one of the three dimensions of space (x or y or z): there is a minus sign in front of the dt². It is that little minus sign that makes all the difference. That minus sign makes the time we know different from an ordinary dimension of space—all just to make the speed of light a constant.

Whew! That’s a lot of arithmetic—but it gets us to an important point, the difference between time and the dimensions of space.

Remember that I began by noting that I measured the astronaut’s rocket to be 18 feet long. So I say that his rocket is shorter than the astronaut thinks it is (which is 30 feet). I think his rocket is only √[1 – (v²/c²)] as long as he does. Our clocks do not agree and our rulers do not agree—once again ensuring that we observe the speed of light always to be 1 (foot per nanosecond). How can we differ on the width of the worldline of his rocket? It results from our taking different “slices” through it. I am measuring its width at a particular instant of Earth time (ET), and he is measuring its width at a particular instant of astronaut time (AT). I am taking a horizontal American-bread slice through his rocket’s worldline, and he is taking a tilted French-bread slice. To use a different metaphor, it is as if I were to saw through a tree trunk horizontally and then say “the trunk is 6 inches wide.” If someone else saws through it on a slant, he may conclude it is 10 inches wide, but the trunk itself is the same. We are just making different cuts through it. The astronaut and I are simply taking different cuts through the rocket’s worldline.

Why is this important? Take an extreme case where an astronaut passes by me on Earth traveling at 99.995% the speed of light: then the magic factor √[1 – (v²/c²)] is 1/100. I see the astronaut fly out to the star Betelgeuse, 500 light-years away. I will see him take about 500 years to get there. After all, he is traveling at nearly the speed of light, and Betelgeuse is 500 light-years away—so it should take him about 500 years (ET) to get there. I observe him to age only 1/100 × 500 years, or 5 years, during the trip. I see his clocks ticking very slowly, because he is moving so fast. Everything he does looks slow to me—I see him take 100 hours to finish breakfast! When he reaches Betelgeuse, he will indeed be only 5 years older.

How does the trip look to him? He thinks he is at rest, and he sees Earth and Betelgeuse fly past him at 99.995% the speed of light. First he sees Earth pass him—whish, and then 5 years later, he sees Betelgeuse pass him—whish. Earth and Betelgeuse are basically at rest with respect to each other, on parallel worldlines. The Earth + Betelgeuse system looks to him like a long rocket with Earth at the front end and Betelgeuse at the back end. Since this rocket is moving at nearly the speed of light past him, and it takes 5 years to pass, he must deduce that the length of the Earth + Betelgeuse rocket is 5 light-years. Thus he must deduce that the distance between Earth and Betelgeuse is only 5 light-years. He thus judges the distance between Earth and Betelgeuse to be 1/100 of the distance I see. He sees my lengths compressed: he sees them to be 1/100 as long as I do. The factor of length compression he observes, √[1 – (v²/c²)], must be the same as the factor by which I see him aging more slowly. This is certainly one of the most remarkable results of special relativity, beautiful in its symmetry and ironclad logic.

The fact that different observers have different ideas of simultaneity explains a paradox. Suppose my original astronaut Jacques, traveling at 80% of the speed of light, is instead a pole vaulter and carries a 30-foot-long pole with him pointing in the direction he is going. I will see his pole as only 18 feet long as it passes me. Suppose I have a barn 30 feet wide. Its front door is open, and its back door is closed. Jacques comes in the open front door; when he is in the center of my barn, I can close the front door, and his 18-foot-long pole will be trapped inside my 30-foot-wide barn. Then I open the back door and let him go on out the back. But how does it look to Jacques? He must think he is at rest holding a 30-foot-long pole. He sees my barn traveling toward him at 80% of the speed of light; he must think it is only 18 feet wide. When he is in the middle of my barn, he must see his 30-foot pole sticking out both the front and the back ends of my 18-foot-wide barn. Both doors can’t be closed around it simultaneously trapping it inside. It looks like a paradox. But here is the answer. I close both doors around the pole at the same time—simultaneously according to me. But those events are not simultaneous to Jacques. He slices spacetime differently, on a slant. He sees me close those two barn doors at different times, one after the other, according to him. Because he never sees both barn doors closed simultaneously, he can see his pole sticking out both ends as he passes through the barn with both doors open.

It is a tribute to Einstein that he was able to work through all his thought experiments correctly. No one had ever tried doing thought experiments based on postulates in the way Einstein did. It was one of the most original features of his work.

Now we come to another apparent paradox, the famous Twin Paradox. In this paradox, the first twin—we will call her Eartha—stays home on Earth, while her twin sister Astra voyages to Alpha Centauri, 4 light-years away, at 80% of the speed of light, then turns around and comes back at 80% of the speed of light. Eartha sees Astra going at 4/5 of the speed of light, so she sees Astra taking 5 Earth years to get out to Alpha Centauri, and 5 Earth years to get back. When Astra gets back, Eartha is 10 years older. Because Eartha sees Astra moving at 80% of the speed of light, according to our formula √[1 – (v²/c²)], Eartha must see Astra aging slowly, at 60% of the rate Eartha ages. When Astra returns, Eartha expects Astra to have aged only 6 years. So far so good. But what does Astra see? Since motion is relative, why doesn’t Astra think Eartha has gone away and come back at 80% of the speed of light, and why doesn’t she expect Eartha to be the younger one when Eartha returns? The answer is that Astra has accelerated during her trip; she has slammed on the brakes at Alpha Centauri to stop and start back. All her stuff would have hit the front windshield of her spacecraft. She has changed her velocity; she has reversed its direction. She no longer obeys the first postulate’s requirement for an observer to be in uniform motion in the same direction without turning (figure 18.3.)

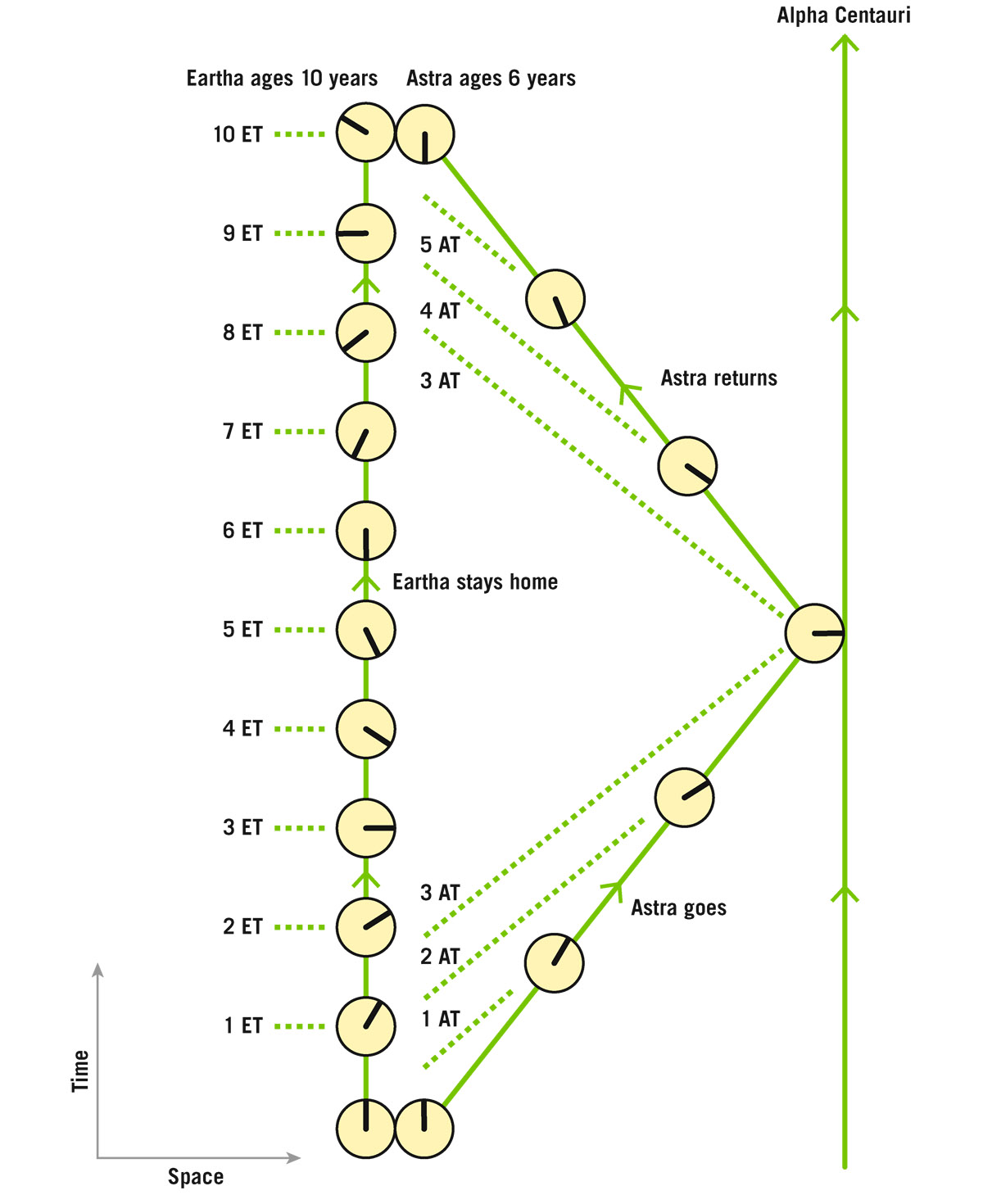
FIGURE 18.3. The Twin Paradox spacetime diagram of twins Eartha and Astra. Eartha stays home. Her worldline is straight. Astra goes to Alpha Centauri and returns—her worldline is bent. Astra ages less than Eartha does. Clocks show time measured by each in years. Dashed lines show Eartha Time (ET) and Astra Time (AT).

Credit: J. Richard Gott

During the first half of her trip, Astra is traveling away from Earth, and slices of Astra Time (AT) are tilted like slices of French bread. Just as she is arriving at Alpha Centauri, her clock reads 3 years (AT), telling her how much she has aged. But the line of simultaneous events “3 AT” is tilted, so it intersects Earth only 1.8 years after the start. As she is arriving at Alpha Centauri, Astra thinks she is simultaneous with Eartha 1.8 years after the start. Astra says she has aged 3 years in the time Eartha has aged only 1.8 years. Now 1.8 years is 60% of 3 years. Therefore, Astra sees Eartha aging slowly, since Astra thinks of herself at rest and sees Eartha receding from her at 80% of the speed of light. At this point, Astra thinks Eartha has aged less. But wait! Now Astra slams on the brakes, stops, and reverses course. Astra’s worldline is bent at this point. She has changed velocity, and therefore her notion of simultaneity changes radically as well. Just as she is leaving Alpha Centauri, her clock still reads “3 AT,” but now, because she is moving in the opposite direction, the slice “3 AT” marking simultaneous events is tipped in the opposite direction and intersects Earth 8.2 years after the start. Once she is on the way back, Astra thinks that her departure from Alpha Centauri is simultaneous with Eartha being 8.2 years older than at the start. During the trip back, Astra sees Earth age another 1.8 years while she, Astra, ages another 3 years. That makes Eartha a total of 8.2 + 1.8 = 10 years older than at the start, while Astra is 3 + 3 = 6 years older than at the start. So Astra agrees with Eartha, as she must, that Astra is younger than Eartha when they meet again. Eartha has traveled on a straight worldline, whereas Astra’s worldline is bent. This is the solution to the Twin Paradox. The idea of simultaneity is very important here.

The Twin Paradox enables you to visit the future. If you want to visit Earth a thousand years from now, all you have to do is get on a rocket ship and travel at 99.995% of the speed of light out to the star Betelgeuse, 500 light-years away. Your clock ticks 1/100 as fast as one on Earth. It will take you 500 years to get there, according to clocks on Earth. But you will only age 5 years. Come back at 99.995% the speed of light and you will age another 5 years on the way back. But when you get back, you will find Earth 1,000 years older. You will have time-traveled into the future. A trip such as this would be a lot more expensive than the current NASA budget (!), and of course the technology for building such a fast spacecraft doesn’t exist yet, but we know it is possible under the laws of physics. We send protons in our particle accelerators at speeds faster than this, so we know such speeds are possible. It’s just a matter of money and engineering—NASA, take note.

You might complain that the high acceleration at the turn-around point would kill you. But it turns out that you can arrange the same trip with only a comfortable 1 g acceleration, such as you experience on the surface of Earth. Your feet would be pressed to the floor, because your rocket was accelerating, just as they are pressed to the floor now because of gravity. Your trip would take you longer this way, but it would be comfortable. You would accelerate outward toward Betelgeuse for 6 years and 3 weeks of spaceship time, reaching a peak velocity of 99.9992% the speed of light. At that point, you are halfway to Betelgeuse. Then you decelerate at 1 g for another 6 years, 3 weeks of spaceship time to bring yourself to a halt at Betelgeuse. Accelerate back toward Earth for 6 years, 3 weeks, and finally decelerate for another 6 years, 3 weeks to bring yourself to a stop at Earth. You will age 24 years, 12 weeks during the trip, but when you get back, Earth will be 1,000 years older. You just have to invest a little more of your time (24 years versus 10 years) to do it comfortably. It took Marco Polo 24 years to make his famous visit to China and return to Europe. You would just need to invest as much of your time in your trip as Marco Polo did in his, and you could visit the future. You could visit Earth a millennium from now.

Gennady Padalka, a Russian cosmonaut, is our greatest time traveler to date. By orbiting Earth at high speed for a total of 879 days during visits to the Russian space station Mir and the International Space Station, he aged 1/44 of a second less than he would have if he had stayed home. (This calculation also includes some smaller general relativity effects due to his high altitude.) When he returned, he found Earth 1/44 of a second to the future of where he expected it to be. He has time traveled 1/44 of a second into the future. I know you’re laughing. It’s not a big trip, but it is a trip into the future. I was once interviewed on National Public Radio, and they asked why it was so easy to travel in space and so difficult to travel in time. I replied that the truth is we have not gone very far in space either! Einstein showed us that when comparing distances in space with distances in time, we should use the velocity of light. Thus, astronomers know to say that Alpha Centauri is 4 light-years away, because it takes light 4 years to come from it to us. The farthest our astronauts have gone is to the Moon. The Moon is only 1.3 light-seconds away. Humans have traveled as far as 1.3 light-seconds in space, and have time traveled 1/44 of a second into the future. These are roughly comparable.

Interestingly we have actual identical twin astronauts today to illustrate the twin paradox. Mark Kelly has spent 54 days in low Earth orbit, while his identical twin brother Scott Kelly has spent 519 days in low Earth orbit. Because Scott spent more time traveling at high speed in low Earth orbit, he is now about 1/87 of a second younger than his twin brother Mark.

I have pointed out that if we sent an astronaut to the planet Mercury and she lived there for 30 years before returning to Earth, she would be about 22 seconds younger than if she had stayed home. Clocks on Mercury tick more slowly than those on Earth both because Mercury circles the Sun at a faster speed (a special relativity effect) and because Mercury is deeper in the Sun’s gravitational field (a general relativity effect).1

In 1905, Einstein showed that time travel to the future was possible. This is just 10 years after H. G. Wells proposed the idea, in 1895, in his book The Time Machine. In Newton’s laws of physics, you could forget it—everyone agreed on time, everyone agreed on what “now” was, and time travel to the future was impossible. But Einstein showed that observers did not always agree on what was happening “now”; time was flexible—moving clocks ticked more slowly. Einstein gave us an entirely new picture of the universe, a universe with three dimensions of space and one dimension of time.

Now I am going to derive Einstein’s famous equation E = mc². Suppose you had a laboratory with a particle moving slowly from left to right inside it with velocity v much, much less than c (i.e., v << c). Newton’s laws will apply, and if the particle has a mass m, it will have, according to Newton, a momentum P = mv pointed toward the right. The particle gives off two photons each of energy E = hν₀ in opposite directions: one to the right and one to the left. We are using Einstein’s famous equation for the energy of photons, where h is Planck’s constant and ν₀ (Greek letter nu) is the frequency of the photons as measured by the particle. The particle loses an amount of energy ΔE = 2hν₀, equal to the energy the particle sees carried off by the two photons. Einstein showed that photons carry not only energy but momentum. The momentum of a photon is equal to its energy divided by the speed of light c. The particle sees the two photons carry away equal amounts of momentum but in opposite directions, making the total momentum carried off by the two photons zero as seen by the particle. The particle “thinks” it is at rest (by the first postulate), and it gives off two equal photons in opposite directions. By symmetry, a particle at rest that gives off two equal-frequency photons in opposite directions stays at rest. The recoils from the two photons on the particle cancel out. The particle’s worldline remains straight: it does not change in velocity (figure 18.4).

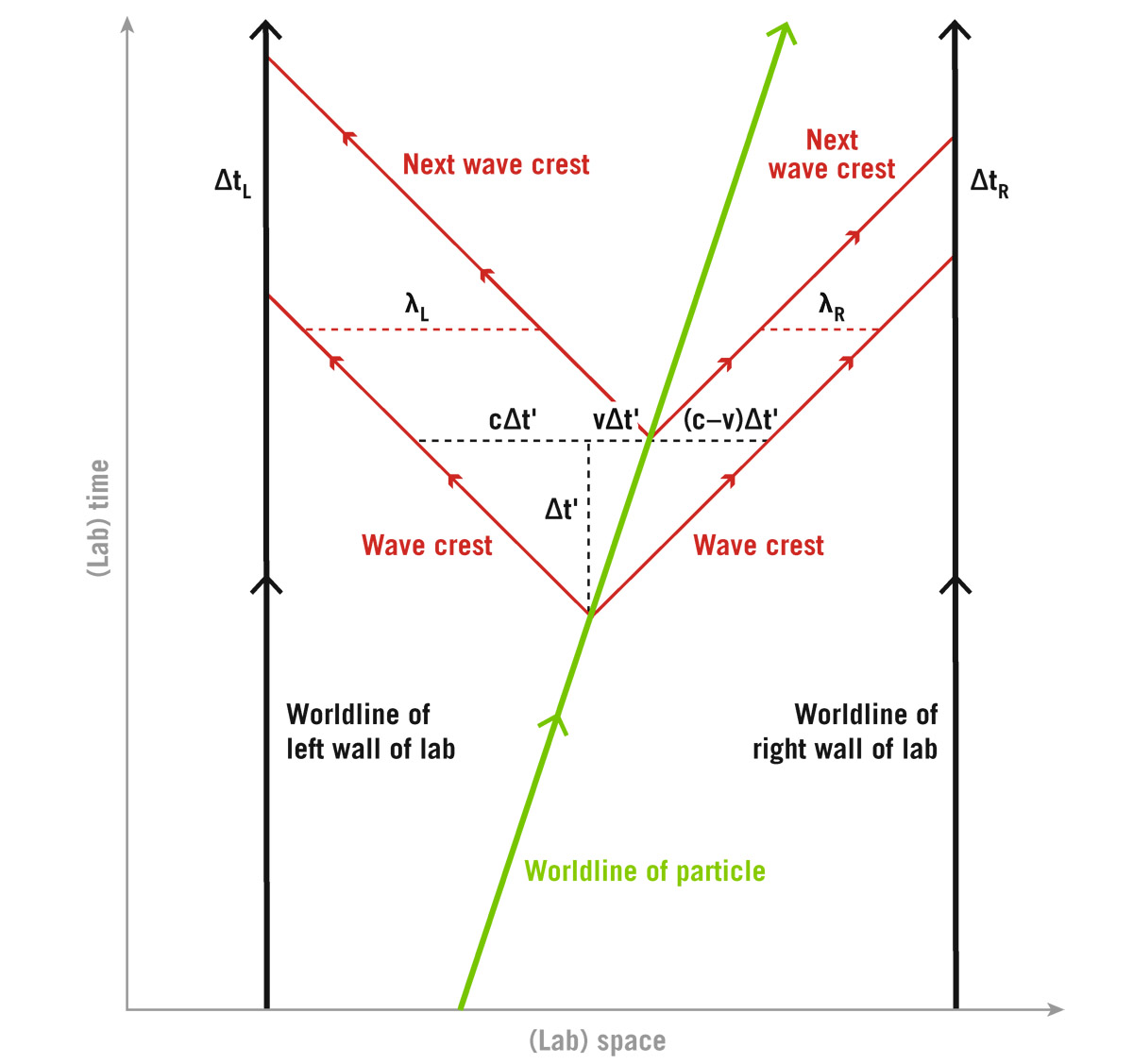
FIGURE 18.4 Spacetime diagram of E = mc² thought experiment. Stationary walls of the lab have vertical worldlines. The particle moves from left to right with velocity v, its worldline is tipped. It emits a photon to the left (whose wave crests move at 45° to the upper left) and an equivalent photon to the right (whose wave crests move at 45° to the upper right). The lab time between the particle’s emission of the two sets of wave crests is Δt', shown by the vertical dashed line. In that time the first leftward wave crest moves a distance cΔt' to the left, while the particle moves a distance v Δt' to the right as shown. The wavelength (distance between wave crests) of the leftward-moving photon is shown: λ_L = (c + v)Δt'. The wavelength of the rightward-moving photon is shorter: λ_R = (c – v)Δt' due to the Doppler shift. Credit: J. Richard Gott

Now consider what happens to those two photons. The one going to the right will eventually slam into the right wall of the lab. It hits the wall, and the wall is pushed a tiny bit toward the right. Einstein showed that a photon carries a momentum equal to its energy divided by the speed of light. This is the effect of radiation pressure: the wall absorbs the momentum of the photon, and this pushes the wall to the right. An observer sitting on the right wall will see the photon headed to the right hitting the right wall with a frequency that is higher than the emitted frequency, because the particle is approaching the right wall. This is an instance of the Doppler effect, which you will recall from previous chapters. In contrast, an observer sitting on the left wall of the lab will see a redshifted photon traveling to the left hit the left wall with a lower frequency than emitted, because the particle is going away from him. A higher frequency (bluer) photon carries a larger momentum than a lower frequency (redder) photon does. So, the right wall receives a harder kick (to the right) than the left wall receives (to the left). The two kicks do not cancel out, and the lab receives an overall kick to the right. The lab has received some momentum. There must be conservation of momentum, as Newton supposed (otherwise one could construct various unphysical levitating devices!), and therefore, this momentum must come from someplace. The only place it can come from is the particle itself.

Now the velocity of the particle is v << c, so the momentum of the particle should be given by Newton’s formula: mv. Since the lab has gained momentum, the particle must have lost momentum. But the particle’s worldline is not bent—it remains straight (see spacetime diagram in figure 18.4). Its velocity does not change. If the particle’s momentum mv decreases while its velocity v remains the same, its mass m must have decreased. It gave up some energy (in the form of two photons) and it lost some mass. Some of its mass was turned into energy! Whoa! That’s a remarkably bold conclusion. What is the relation between the amount of energy given off and the amount of mass lost? This just requires you to calculate the Doppler shifts of the two photons. The total rightward momentum gained by the walls of the lab is 2hν₀(v/c²). I show the full calculation of these in appendix 1. The energy given off by the particle in the form of the two photons is ΔE = 2hν₀, so the total rightward momentum gained by the walls is ΔE(v/c²). The factor v/c² comes from a factor v/c due to the Doppler shifts and a factor of 1/c due to the ratio of momentum to energy carried by photons. The total rightward momentum gained by the walls, ΔE(v/c²), in turn, must equal the momentum lost by the particle: (Δm)v. So we have ΔE(v/c²) = (Δm)v. Divide both sides of the equation by v. (The velocity of the particle cancels out!) We get ΔE/c² = Δm. Now multiply both sides of the equation by c². That gives ΔE = Δmc². Get rid of the Δ signs. The answer is E = mc².

In the thought experiment, the particle loses some energy by emitting two photons, and it loses some mass. A particle that loses mass emits energy. The emitted energy is related to the mass that is lost by the formula E = mc². It’s as simple, yet as powerful, as that. The c² appears in the equation because all the Doppler shift and momentum calculations involve light, and c is its speed.

As you know, c is a very large number (300,000 km/sec in ordinary units), enabling a tiny amount of mass to be converted into a huge amount of energy. Newton’s laws show us that the kinetic energy of a truck is ½mv², where m is the mass of the truck, and v is its velocity. That’s accurate as long as v << c. A truck going at a velocity of 100 miles per hour has a velocity of 0.045 km/sec (that’s only 0.00000015c). If two trucks each going 100 miles per hour collide head on, all that kinetic energy—2 times (½ mv²)—will be released in a giant explosion. Pieces of the trucks will fly all over. But now suppose a truck made of matter would hit a truck made of antimatter. These two trucks would annihilate each other, converting all their mass into energy—an extreme case. That would cause an explosion releasing 2 × (mc²) worth of energy, which is a lot bigger than mv² for the normal trucks. How much bigger? By a factor of 2/(0.00000015)² = 89 trillion! That matter–antimatter explosion would be 89 trillion times as energetic as the explosion caused by two normal trucks hitting each other at 100 miles per hour. There is a tremendous amount of energy locked up in the mass of ordinary matter.

That is the secret of the atomic bomb. Uranium or plutonium atoms can fission to create decay products that weigh slightly less than the original atoms, releasing an enormous amount of energy. In the Sun, four hydrogen nuclei fuse to become one slightly lighter helium nucleus, releasing energy. This is what has powered the Sun for the past 4.6 billion years. Chemists have measured accurate masses for different elements, which show slight differences in the mass per nucleon in different elements. Consequently, one can calculate how much nuclear energy could be produced by fusing light elements or by splitting heavy ones. Iron has the lowest mass per nucleon—there is no getting nuclear energy out of it, as we discussed in chapter 7.

Einstein realized, along with other physicists, that his equation implied that atomic bombs, from splitting atoms, could be made, and he wrote the crucial letter to President Franklin D. Roosevelt on August 2, 1939, urging him to build an atomic bomb before Hitler did. Thus, the Manhattan Project was born, and American and European refugee physicists developed a working atomic bomb. As the Americans later learned, Germany did have an atomic bomb program just as Einstein had feared, but it was ineffectual and did not succeed. Germany had already surrendered by the time the first U.S. atomic bomb was tested in New Mexico. But ultimately, two atomic bombs were dropped on Japan. Japan surrendered a short time later, ending World War II. The devastation was horrendous: approximately 200,000 people were killed by the bombs and their aftermath, including radiation exposure. Robert Oppenheimer, who led the Manhattan Project, later said the first test of the atomic bomb reminded him of lines from the Bhagavad Gita: “now I am become Death destroyer of worlds.” President Truman took full responsibility for the decision to drop the bomb. He felt its use was necessary to end World War II as swiftly as possible. But Truman said, “I realize the tragic significance of the atomic bomb.” Years later, in Truman’s private library, a book on the atomic bomb was found where he had underlined words from Horatio’s last speech in Hamlet: “Let me speak to the unknowing world. So shall you hear of carnal, bloody and unnatural acts, of accidental judgments, casual slaughters, of deaths put on by cunning and forced cause, and, in this upshot, purposes mistook fall’n on the inventors’ heads.” After the war, Einstein devoted himself to the cause of nuclear disarmament.

By thinking about traveling near the speed of light, which was far from practical in his day, Einstein nevertheless discovered a principle that would change the course of history. Einstein’s work in his miracle year of 1905 would catapult him into the first rank of scientists, along with Marie Curie and Max Planck, but his greatest work was yet to come.