14.3 Thinking Recursively

There are two kinds of people in the world: those who divide the world into two kinds of people and those who do not.

ANONYMOUS

Recursive Design Techniques

When defining and using recursive functions you do not want to be continually aware of the stack and the suspended computations. The power of recursion comes from the fact that you can ignore that detail and let the computer do the bookkeeping for you. Consider the example of the function power in Display 14.3. The way to think of the definition of power is as follows:

power(x, n) returns power (x, n − 1) * x

Since xⁿ is equal to x^n–1 * x, this is the correct value to return, provided that the computation will always reach a stopping case and will correctly compute the stopping case. So, after checking that the recursive part of the definition is correct, all you need check is that the chain of recursive calls will always reach a stopping case and that the stopping case always returns the correct value.

Criteria for functions that return a value

When you design a recursive function, you need not trace out the entire sequence of recursive calls for the instances of that function in your program. If the function returns a value, all that you need do is confirm that the following three properties are satisfied:

1. There is no infinite recursion. (A recursive call may lead to another recursive call and that may lead to another and so forth, but every such chain of recursive calls eventually reaches a stopping case.)

2. Each stopping case returns the correct value for that case.

3. For the cases that involve recursion: If all recursive calls return the correct value, then the final value returned by the function is the correct value.

For example, consider the function power in Display 14.3:

1. There is no infinite recursion: The second argument to power(x,n) is decreased by 1 in each recursive call, so any chain of recursive calls must eventually reach the case power(x,0), which is the stopping case. Thus, there is no infinite recursion.

2. Each stopping case returns the correct value for that case: The only stopping case is power(x,0). A call of the form power(x,0) always returns 1, and the correct value for x⁰ is 1. So the stopping case returns the correct value.

3. For the cases that involve recursion—if all recursive calls return the correct value, then the final value returned by the function is the correct value: The only case that involves recursion is when n>1. When n>1, power(x,n) returns

   power(x, n − 1) * x

   To see that this is the correct value to return, note that: if power(x,n−1) returns the correct value, then power(x,n−1) returns xⁿ⁻¹ and so power(x,n) returns

   xn−1 * x, which is xn

   and that is the correct value for power(x,n).

That’s all you need to check in order to be sure that the definition of power is correct. (This technique is known as mathematical induction, a concept that you may have heard about in a mathematics class. However, you do not need to be familiar with the term in order to use this technique.)

We gave you three criteria to use in checking the correctness of a recursive function that returns a value. Basically, the same rules can be applied to a recursive void function. If you show that your recursive void function definition satisfies the following three criteria, then you will know that your void function performs correctly:

Criteria for void functions

1. There is no infinite recursion.

2. Each stopping case performs the correct action for that case.

3. For each of the cases that involve recursion: If all recursive calls perform their actions correctly, then the entire case performs correctly.

Case Study Binary Search—An Example of Recursive Thinking

In this case study we develop a recursive function that searches an array to find out whether it contains a specified value. For example, the array may contain a list of numbers for credit cards that are no longer valid. A store clerk needs to search the list to see if a customer’s card is valid or invalid. In Chapter 7 (Display 7.10) we discussed a simple method for searching an array by simply checking every array element. In this section we will develop a method that is much faster for searching a sorted array.

The indexes of the array a are the integers 0 through finalIndex. In order to make the task of searching the array easier, we assume that the array is sorted. Hence, we know the following:

a[0] <= a[1] <= a[2] <= … <= a[finalIndex]

When searching an array, you are likely to want to know both whether the value is in the list and, if it is, where it is in the list. For example, if we are searching for a credit card number, then the array index may serve as a record number. Another array indexed by these same indexes may hold a phone number or other information to use for reporting the suspicious card. Hence, if the sought-after value is in the array, we will want our function to tell where that value is in the array.

Problem Definition

We will design our function to use two call-by-reference parameters to return the outcome of the search. One parameter, called found, will be of type bool. If the value is found, then found will be set to true. If the value is found, then another parameter, called location, will be set to the index of the value found. If we use key to denote the value being searched for, the task to be accomplished can be formulated precisely as follows:

Precondition: a[0] through a[finalIndex] are sorted in increasing order.
Postcondition: if key is not one of the values a[0] through a[finalIndex], then found == false; otherwise, a[location] == key and found == true.

Algorithm Design

Now let us proceed to produce an algorithm to solve this task. It will help to visualize the problem in very concrete terms. Suppose the list of numbers is so long that it takes a book to list them all. This is in fact how invalid credit card numbers are distributed to stores that do not have access to computers. If you are a clerk and are handed a credit card, you must check to see if it is on the list and hence invalid.

How would you proceed? Open the book to the middle and see if the number is there. If it is not and it is smaller than the middle number, then work backward toward the beginning of the book. If the number is larger than the middle number, you work your way toward the end of the book. This idea produces our first draft of an algorithm:

Algorithm—first version

found = false; //so far.
mid = approximate midpoint between 0 and finalIndex;
if (key == a[mid])
{
    found = true;
    location = mid;
}
else if (key < a[mid])
    search a[0] through a[mid − 1];
else if (key > a[mid])
    search a[mid + 1] through a[finalIndex];

Since the searchings of the shorter lists are smaller versions of the very task we are designing the algorithm to perform, this algorithm naturally lends itself to the use of recursion. The smaller lists can be searched with recursive calls to the algorithm itself.

Our pseudocode is a bit too imprecise to be easily translated into C++ code. The problem has to do with the recursive calls. There are two recursive calls shown:

search a[0] through a[mid − 1];

and

search a[mid + 1] through a[finalIndex];

More parameters

To implement these recursive calls, we need two more parameters. A recursive call specifies that a subrange of the array is to be searched. In one case it is the elements indexed by 0 through mid-1. In the other case it is the elements indexed by mid+1 through finalIndex. The two extra parameters will specify the first and last indexes of the search, so we will call them first and last. Using these parameters for the lowest and highest indexes, instead of 0 and finalIndex, we can express the pseudocode more precisely as follows:

Algorithm—first refinement

To search a[first] through a[last] do the following:
found = false; //so far.
mid = approximate midpoint between first and last;
if (key == a[mid])
{
    found = true;
    location = mid;
}
else if (key < a[mid])
    search a[first] through a[mid − 1];
else if (key > a[mid])
    search a[mid + 1] through a[last];

To search the entire array, the algorithm would be executed with first set equal to 0 and last set equal to finalIndex. The recursive calls will use other values for first and last. For example, the first recursive call would set first equal to 0 and last equal to the calculated value mid-1.

Stopping case algorithm—final version

As with any recursive algorithm, we must ensure that our algorithm ends rather than producing infinite recursion. If the sought-after number is found on the list, then there is no recursive call and the process terminates, but we need some way to detect when the number is not on the list. On each recursive call, the value of first is increased or the value of last is decreased. If they ever pass each other and first actually becomes larger than last, then we will know that there are no more indexes left to check and that the number key is not in the array. If we add this test to our pseudocode, we obtain a complete solution as shown in Display 14.5.

Display 14.5 Pseudocode for Binary Search

int a[Some_Size_Value];
Algorithm to search a[first] through a[last]
 1    //Precondition:
 2    //a[first]<= a[first + 1] <= a[first + 2] <= … <= a[last]

To locate the value key:

 1    if (first > last) //A stopping case
 2        found = false;
 3    else
 4    {
 5        mid = approximate midpoint between first and last;
 6        if (key == a[mid]) //A stopping case
 7        {
 8            found = true;
 9            location = mid;
10        }
11        else if key < a[mid] //A case with recursion
12            search a[first] through a[mid − 1];
13        else if key > a[mid] //A case with recursion
14            search a[mid + 1] through a[last];
15    }

Coding

Now we can routinely translate the pseudocode into C++ code. The result is shown in Display 14.6. The function search is an implementation of the recursive algorithm given in Display 14.5. A diagram of how the function performs on a sample array is given in Display 14.7.

Display 14.6 Recursive Function for Binary Search

 1    //Program to demonstrate the recursive function for binary search.
 2    #include <iostream>
 3    using namespace std;
 4    const int ARRAY_SIZE = 10;
 5     
 6     
 7    void search(const int a[], int first, int last,
 8        int key, bool& found, int& location);
 9    //Precondition: a[first] through a[last] are sorted in increasing order.
10    //Postcondition: if key is not one of the values a[first] through a[last],
11    //then found == false; otherwise, a[location] == key and found == true.
12      
13     
14    int main( )
15    {
16        int a[ARRAY_SIZE];
17        constint finalIndex = ARRAY_SIZE − 1;
18     
< This portion of the program contains some code to fill and sort the array a. The exact details are irrelevant to this example.>
19        int key, location;
20        bool found;
21        cout << "Enter number to be located: ";
22        cin >> key;
23        search(a, 0, finalIndex, key, found, location);
24     
25        if (found)
26            cout << key << " is in index location "
27                 << location <<endl;
28        else
29            cout << key << " is not in the array." <<endl;
30     
31        return 0;
32    }
33    void search(const int a[], int first, int last,
34                             int key, bool& found, int& location)
35    {
36        int mid;
37        if (first > last)
38        {
39            found = false;
40        }
41        else
42        {
43            mid = (first + last)/2;
44     
45            if (key == a[mid])
46            {
47                found = true;
48                location = mid;
49            }
50            else if (key < a[mid])
51            {
52                search(a, first, mid −1, key, found, location);
53            }
54            else if (key > a[mid])
55            {
56                search(a, mid + 1, last, key, found, location);
57            }
58        }
59    }

Display 14.7 Execution of the Function search

Figure 14.7 Full Alternative Text

Solve a more general problem

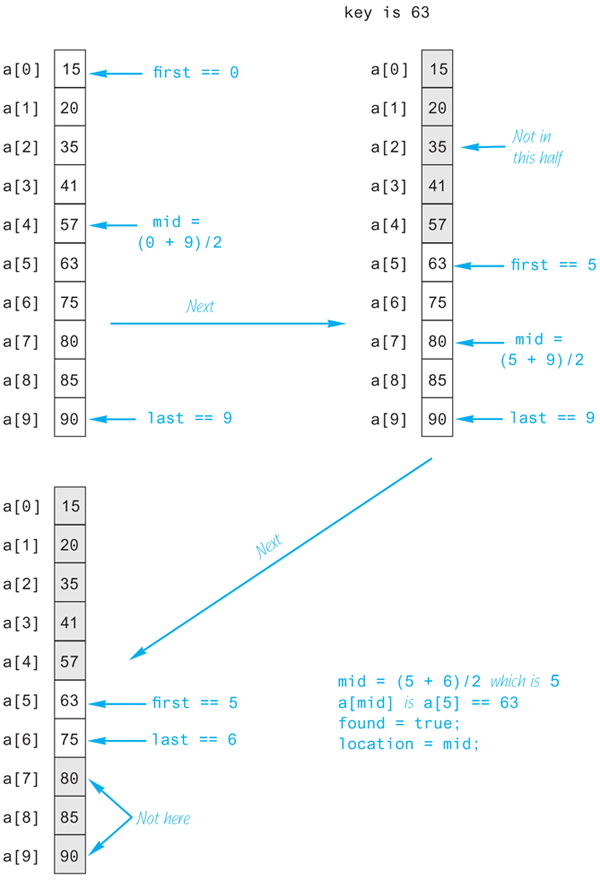
Notice that the function search solves a more general problem than the original task. Our goal was to design a function to search an entire array. Yet the function will let us search any interval of the array by specifying the index bounds first and last. This is common when designing recursive functions. Frequently, it is necessary to solve a more general problem in order to be able to express the recursive algorithm. In this case, we only wanted the answer in the case where first and last are set equal to 0 and finalIndex. However, the recursive calls will set them to values other than 0 and finalIndex.

Checking the Recursion

In the subsection entitled “Recursive Design Techniques,” we gave three criteria that you should check to ensure that a recursive void function definition is correct. Let’s check these three things for the function search given in Display 14.6.

1. There is no infinite recursion: On each recursive call, the value of first is increased or the value of last is decreased. If the chain of recursive calls does not end in some other way, then eventually the function will be called with first larger than last, and that is a stopping case.

2. Each stopping case performs the correct action for that case: There are two stopping cases: when first > last and when key==a[mid]. Let’s consider each case.

   If first > last, there are no array elements between a[first] and a[last], and so key is not in this segment of the array. (Nothing is in this segment of the array!) So, if first > last, the function search correctly sets found equal to false.

   If key==a[mid], the algorithm correctly sets found equal to true and location equal to mid. Thus, both stopping cases are correct.

3. For each of the cases that involve recursion, if all recursive calls perform their actions correctly, then the entire case performs correctly: There are two cases in which there are recursive calls: when key < a[mid] and when key > a[mid]. We need to check each of these two cases.

   First suppose key < a[mid]. In this case, since the array is sorted, we know that if key is anywhere in the array, then key is one of the elements a[first] through a[mid−1]. Thus, the function need only search these elements, which is exactly what the recursive call

   search(a, first, mid − 1, key, found, location);

   does. So if the recursive call is correct, then the entire action is correct.

   Next, suppose key > a[mid]. In this case, since the array is sorted, we know that if key is anywhere in the array, then key is one of the elements a[mid+1] through a[last]. Thus, the function need search only these elements, which is exactly what the recursive call

   search(a, mid + 1, last, key, found, location);

   does. So if the recursive call is correct, then the entire action is correct. Thus, in both cases the function performs the correct action (assuming that the recursive calls perform the correct action).

The function search passes all three of our tests, so it is a good recursive function definition.

Efficiency

The binary search algorithm is extremely fast compared to an algorithm that simply tries all array elements in order. In the binary search, you eliminate about half the array from consideration right at the start. You then eliminate a quarter, then an eighth of the array, and so forth. These savings add up to a dramatically fast algorithm. For an array of 100 elements, the binary search will never need to compare more than 7 array elements to the key. A simple serial search could compare as many as 100 array elements to the key and on the average will compare about 50 array elements to the key. Moreover, the larger the array is, the more dramatic the savings will be. On an array with 1000 elements, the binary search will need to compare only about 10 array elements to the key value, as compared to an average of 500 for the simple serial search algorithm.

Iterative version

An iterative version of the function search is given in Display 14.8. On some systems, the iterative version will run more efficiently than the recursive version. The algorithm for the iterative version was derived by mirroring the recursive version. In the iterative version, the local variables first and last mirror the roles of the parameters in the recursive version, which are also named first and last. As this example illustrates, it often makes sense to derive a recursive algorithm even if you expect to later convert it to an iterative algorithm.

Display 14.8 Iterative Version of Binary Search

Function Declaration

 1    void search(const int a[], int lowEnd, int highEnd,
 2    int key, bool& found, int& location);
 3    //Precondition: a[lowEnd] through a[highEnd] are sorted in increasing
 4    //order.
 5    //Postcondition: If key is not one of the values a[lowEnd] through
 6    //a[highEnd], then found == false; otherwise, a[location] == key and
 7    //found == true.

Function Definition

 1    void search(const int a[], int lowEnd, int highEnd,
 2        int key, bool& found, int& location)
 3    {
 4        int first = lowEnd;
 5        int last = highEnd;
 6        int mid;
 7     
 8        found = false; //so far
 9        while ( (first <= last) && !(found) )
10        {
11            mid = (first + last)/2;
12            if (key == a[mid])
13            {
14                found = true;
15                location = mid;
16            }
17            else if (key < a[mid])
18            {
19                last = mid − 1;
20            }
21            else if (key > a[mid])
22            {
23                first = mid + 1;
24            }
25        }
26    }

Programming Example A Recursive Member Function

A member function of a class can be recursive. Member functions can use recursion in the same way that ordinary functions do. Display 14.9 contains an example of a recursive member function. The class BankAccount used in that display is the same as the class named BankAccount that was defined in Display 10.6, except that we have overloaded the member function name update. The first version of update has no arguments and posts one year of simple interest to the bank account balance. The other (new) version of update takes an int argument that is some number of years. This member function updates the account by posting the interest for that many years. The new version of update is recursive; has one parameter, called years; and uses the following algorithm:

• If the number of years is 1, then //Stopping case:

  • call the other function named update (the one with no arguments).

• If the number of years is greater than 1, then //Recursive case:

  • make a recursive call to post years-1 worth of interest, and then call the other function called update (the one with no arguments) to post one more year’s worth of interest.

Display 14.9 A Recursive Member Function

Figure 14.9 Full Alternative Text

14.3-7 Full Alternative Text

It is easy to see that this algorithm produces the desired result by checking the three points given in the subsection entitled “Recursive Design Techniques.”

1. There is no infinite recursion: Each recursive call reduces the number of years by 1 until the number of years eventually becomes 1, which is the stopping case. So there is no infinite recursion.

2. Each stopping case performs the correct action for that case: The one stopping case is when years==1. This case produces the correct action, since it simply calls the other overloaded member function called update, and we checked the correctness of that function in Chapter 10.

3. For the cases that involve recursion, if all recursive calls perform correctly, then the entire case performs correctly: The recursive case—that is, years>1—works correctly, because if the recursive call correctly posts years-1 worth of interest, then all that is needed is to post one additional year’s worth of interest and the call to the overloaded zero-argument version of update will correctly post one year’s worth of interest. Thus, if the recursive call performs the correct action, then the entire action for the case of years>1 will be correct.

Overloading

In this example, we have overloaded update so that there are two different functions named update: one that takes no arguments and one that takes a single argument. Do not confuse the calls to the two functions named update. These are two different functions that, as far as the compiler is concerned, just coincidentally happen to have the same name. When the definition of the function update with one argument includes a call to the version of update that takes no arguments, that is not a recursive call. Only the call to the version of update with the exact same function declaration is a recursive call. To see what is involved here, note that we could have named the version of update that takes no argument postOneYear(), instead of naming it update(), and then the definition of the recursive version of update would read as follows:

void BankAccount::update(int years)
{     if (years == 1)
    {
        postOneYear();
    }     else if (years > 1)
    {
        update(years − 1);
        postOneYear();
    }
}

Recursion and Overloading

Do not confuse recursion and overloading. When you overload a function name, you are giving two different functions the same name. If the definition of one of these two functions includes a call to the other, that is not recursion. In a recursive function definition, the definition of the function includes a call to the exact same function with the exact same definition, not to some other function that coincidentally uses the same name. It is not too serious an error if you confuse overloading and recursion, since they are both legal. It is simply a question of getting the terminology straight so that you can communicate clearly with other programmers and so that you understand the underlying processes.

Self-Test Exercises

15. Write a recursive function definition for the following function:

    int squares(int n); //Precondition: n >= 1
    //Returns the sum of the squares of numbers 1 through n.

    For example, squares(3) returns 14 because 1² + 2² + 3² is 14.

16. Write an iterative version of the one-argument member function Bank-Account::update(int years) that is described in Display 14.9.