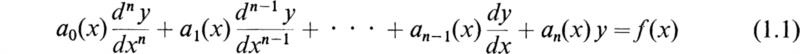
The analysis of any type of linear system generally leads to a mathematical model in the form of a differential equation. In applied mathematics the most important and frequently occurring differential equations are linear. A linear differential equation of order n is one of the form
where a0, a1 , . . . , an and f are functions of the independent variable x and a0 ≠ 0.
If n = 1, we have the linear equation of the first order; this is written in the form
This equation is called a homogeneous linear differential equation of the first order. It may be put in the form
In this form the variables are said to be separated, and we may therefore integrate both members and obtain
where c is an arbitrary constant of integration. Therefore we have
but since ec is an arbitrary constant, we may denote it by K. Hence the solution of (1.3) is
To solve the more general differential equation (1.2), let us place
where u and v are functions of x to be determined. Placing this form for y in (1.2), we obtain
This may be written in the form
Since u and v are at our disposal, let us place the term in brackets equal to zero. We then obtain
and
However, (1.11) is of the same form as (1.3), and therefore its solution is
If we substitute this value of u into (1.12), we obtain
Since the right-hand member is a function of x alone, we may integrate both sides and thus obtain
where C1 is an arbitrary constant.
Substituting these values of u and v into (1.8), we obtain
This may be written in the form
where C is an arbitrary constant.
We thus see that the solution of Eq. (1.2) consists of two parts. One part is the solution of the homogeneous equation with the right-hand member equal to zero. This is called the complementary function; it contains an arbitrary constant. The other part involves an integral of the right-hand member Q(x). This is called the particular integral. The general solution is the sum of these two parts and is given by (1.17).
In the last section the solution of the general linear differential equation with variable coefficients of the first order was obtained. Equation (1.17) gives a formula by means of which the solution may be obtained, provided the indicated integrations may be performed.
If the linear differential equation with variable coefficients is of order higher than the first, it is not possible to obtain an explicit solution in closed form in the general case. In general a series solution must be resorted to in this case. Fortunately a great many of the problems of applied mathematics such as the study of small-amplitude mechanical oscillations and the analysis of electrical networks lead to the solution of linear differential equations with constant coefficients. Accordingly in this chapter we shall study methods of solution of this type of equation.
If the various coefficients ar(x),r = 0, 1, 2, . . . ,n of (1.1) are constants, we may write this equation in the form
provided a0 = 1.
It is convenient to introduce the symbol of operation
We may then write (2.1) in the form
This may also be written in the form
where the significance of the term in parentheses of the left-hand member is that it constitutes an operator that when operating on y(x) leads to the left-hand member of (2.3).
To save writing, we may condense our notation further by letting
We may then write (2.4) concisely in the form
If F(x) in (2.6) is placed equal to zero, we obtain the equation
This is called the reduced equation.
It will now be shown that the general solution of (2.6) consists of the sum of two parts yc and yP. yc is the solution of the reduced equation and is called the complementary function. It then satisfies
The particular integral yP satisfies the equation
If we add (2.8) and (2.9), we obtain
But this may be written in the form
If we now let
we thus obtain
This proves the proposition.
It thus follows that the general solution of a linear differential equation with constant coefficients is the sum of a particular integral yP and the complementary function yc, the latter being the solution of the equation obtained by substituting zero for the function F(x).
We have seen that the general linear differential equation with constant coefficients may be written in the form
The expression Ln(D) is known as a linear differential operator of order n. It is not an algebraic expression multiplied by y but a symbol that expresses the fact that certain operations of differentiation are to be performed on the function y.
Consider the particular linear operator
We shall also write this in the factorized form
factorizing the expression in D as if it were an ordinary algebraic quantity. Is this justifiable?
The operations of multiplication performed in ordinary algebra are based upon three laws:
1. The distributive law
![]()
2. The commutative law
![]()
3. The index law
![]()
Now D satisfies the first and third of these laws, for
As for the second law,
is true if c is a constant, but not if c is a variable. We also have
if m and n are positive integers.
Thus D satisfies the fundamental laws of algebra except in that it is not commutative with variables. It follows that we are justified in performing any operations depending on the fundamental laws of algebra on the linear operator.
In view of this, the solution of the general linear differential equation with constant coefficients may be written symbolically in the form
We must now investigate the interpretation of the symbol 1/Ln(D) when operating on F(x). Let us consider the case n = 1. That is,
This is the solution of the equation
This is a special case of the general linear equation of the first order (1.2) with P(x) = a1, Q(x) = F(x). Accordingly the solution of this equation is given by (1.17) with the above values for P(x) and Q(x). The solution is
We see that the solution consists of two parts. One part is the solution of Eq. (3.11) if F(x) = 0. This is the complementary function, so that, using the notation of Sec. 2, we have
This part contains the arbitrary constant C. The second part, which involves F(x), is the particular integral; so we have
for the operator 1/(D – a) operating on F(x).
Let us return to the general problem of interpreting 1/Ln(D)F(x), where Ln(D) is a linear operator of the nth order. Consider the equation
regarding Ln(D) as a polynomial in D. Now, if this equation has n distinct roots (m1,m2, . . . , mn), it is known from the theory of partial fractions that we may decompose 1/Ln(D) into the simple factors
This is an algebraic identity, and the Ar (r = 1, 2, . . . , n) quantities are constant, given by
It should be noted that Ar is the residue of 1/Ln(z) at mr.
In this case the solution of the equation becomes
But by (3.15) we have
Hence the general solution is
where the Kr quantities are arbitrary constants and the Ar quantities are given by (3.18).
If the equation Ln(D) = 0 has repeated roots, then the above partial-fraction expansion of 1/Ln(D) is no longer possible. Let us first consider the case in which all the roots of Ln(D) are repeated. Let the multiple root be equal to m. In this case the equation to be solved is
To solve this equation, let us assume a solution of the form
where v(x) is a function of x to be determined. Let us consider the effect of operating with the operator D – m on emx0(x). We have
If we operate again with D – m, we obtain
If we repeat this procedure n times, we obtain
In view of this, we see that Eq. (3.22), because of the assumption (3.23), becomes
In order to satisfy this, we must have
If we integrate Eq. (3.28) n times, we obtain
where the factor e–mx F(x) must be integrated n times and the quantities Cr (r = 1, 2, . . . , n) are arbitrary constants.
We thus see from (3.22) that the result of the operator 1/(D – m)n operating on F(x) may be written in the form
Here the term involving the integrals is the particular integral of Eq. (3.22), and the term involving the arbitrary constants is the complementary function.
Let us consider the case in which the operator Ln(D) is such that (D – m)r is a factor of Ln(D) and that D – m1, D – m2, etc., are simple factors of Ln(D). To solve the equation Ln(D)y = F(x), we must expand
where s = n – r, into partial fractions. In this case the partial-fraction expansion is of the form
The coefficients AP (P= 1, 2, . . . , r) are given by
where
and
The coefficients Br (r = 1, 2, . . . s) are given by
We thus see that the solution of the equation
when the equation
has multiple roots, contains terms of the form
as in the solution of (3.21). The term involving the repeated roots gives rise to terms of the form given by (3.30).
We thus have an explicit solution for the general linear differential equation of the nth order with constant coefficients. The difficulties that arise in using the general formulas are due to the difficulties in evaluating the integrals involved in various special cases.
As an example of the general theory, consider the equation

![]()
Here

Accordingly the two roots are

By (3.18) we have
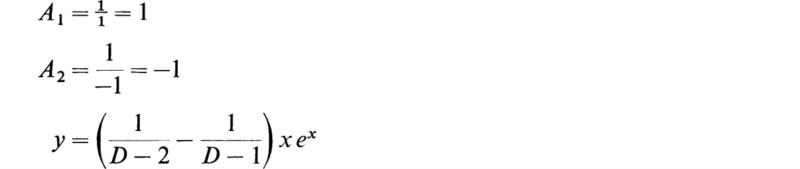
By (3.21) we then have
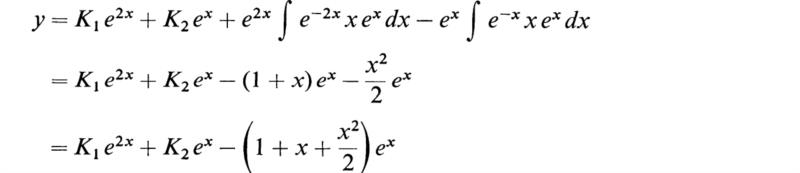
As another example, consider

or
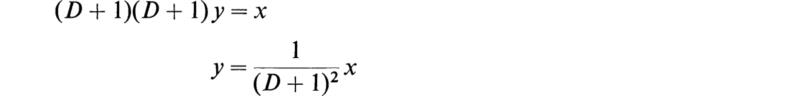
This is a special case of (3.30), for
![]()
We therefore have
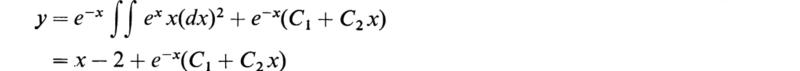
Before we continue with the discussion of differential equations it will be instructive to derive the partial-fraction relations stated in the last section. It should be noted that the results of this section apply whether the roots are real or complex.
First let us consider the case in which the linear operator contains only distinct roots; that is,
As indicated it is desired to decompose 1/Ln(D) into partial fractions:
To determine the coefficients we shall derive the relation for the kth coefficient Ak. Equation (4.2) is multiplied by the term D – mk to obtain
Now if we allow D → mk the right-hand side of (4.3) →Ak, we are left with the relation
The ratio (D – mk)/Ln(D) is indeterminant and may be evaluated by means of L’Hospital’s rule. The result is
where

which was previously stated in (3.18).
As an example consider
The roots are 1, 2, and 3. To apply (4.5) we have
Hence
![]()
From (4.2) we have
Now let us consider the case of a multiple root; that is, we shall let
and attempt to determine the expansion
The coefficients Bk of the simple poles may be determined by the method described above. To determine Ak multiply both sides of (4.11) by (D – m)r:
Differentiating both sides k – 1 times, we have
where O(D – m) denotes terms of order (D – m) and higher. Taking the limit of both sides as D → m and solving for Ak, we have
which agrees with (3.33), (3.34), and (3.35) in Sec. 3.
As an illustrative example let us consider the operator
From (4.11) we have
To evaluate B we apply (4.5):
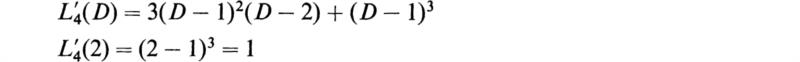

Now if we apply (4.14) to evaluate A1, A2, and A3, we find
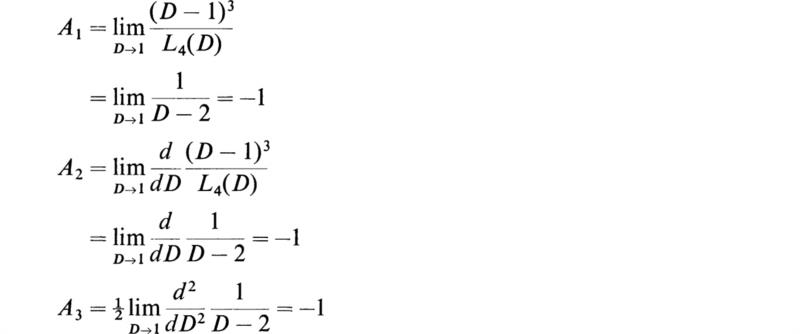
Thus we finally have
which the reader may verify as being the correct partial-fraction expansion of the inverse of (4.15).
As a concluding note it should be realized that this method is not restricted to operational polynomials but may be applied to polynomials of any type where it is desired to obtain partial-fraction expansions. To accomplish this the operator D in the above relations may be replaced by any variable that appears in the polynomial.
At this point in our discourse it is convenient to discuss the concept of linear dependence of a set of functions, say fn(x). Linear dependence is formally defined as follows. If for a given set of functions fn(x) a set of constants cn can be found that satisfy the relation
then the set of functions is said to be linearly dependent. If, on the other hand, the only set of constants that will satisfy (5.1) is
![]()
then the set of functions are said to be linearly independent. In terms of only two functions f(x) and g(x) this implies that if
then f(x) and g(x) are linearly dependent. Conversely if
then the two functions are linearly independent.
A convenient tool for testing for linear dependence of a set of functions is the Wronskian. The development of this test function proceeds as follows. Equation (5.1) is differentiated a total of n – 1 times, yielding the following system of n homogeneous equations for the n unknown coefficients ci:
Using matrix notation, this system may be written as follows:
where
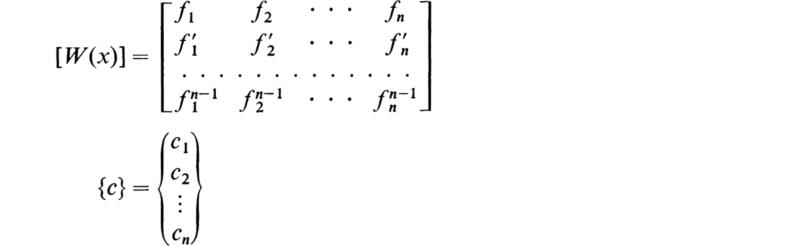
From Sec. 18 of Chap. 3 it is seen that a nontrivial solution for {c} exists only when |W| =0. It may thus be stated that the set of functions fn(x) are linearly dependent whenever |W| = 0. †
The determinant |W| is called the Wronskian of the system of functions
The labor involved in performing the integrations in the general method to obtain the particular integral may sometimes be avoided by the use of a method known as the method of undetermined coefficients.
This may be illustrated by an example. Consider the differential equation
To obtain the particular integral, let us assume a general polynomial of the third degree of the form
Substituting this into (6.1), we obtain
Equating coefficients of like powers of x, we obtain
Solving these equations, we obtain
Substituting these values into (6.2), we obtain the particular integral
The substitution (6.2) was successful because it did not give in the first member of (6.1) any new types of terms. Both members are linear combinations of the functions x3, x2, x, and 1; hence we could equate coefficients of like powers of x.
The method of undetermined coefficients for obtaining the particular integral is particularly well adapted when the function F(x) is a sum of terms such as sines, cosines, exponentials, powers of x, and their products whose derivatives are combinations of a finite number of functions. In this case we assume for y a linear combination of all terms entering with undetermined coefficients and then substitute it into the equation and equate coefficients of like terms.
As another example, consider the equation
In this case we assume
Substituting this into the equation, we obtain
We equate coefficients of like terms and obtain
Solving for a and b and substituting them into (6.8), we obtain
Whenever the driving function f(x) contains terms that appear in the homogeneous solution, the method must be altered in the following manner. The term or family of terms that are included in the assumed particular integral which are also contained in the homogeneous solution must be multiplied by xm, where m is of large enough order so that all of these particular terms are of the form xyh.
As an example consider the following differential equation:
If the standard procedure were followed, the particular integral would be assumed to have the form
However, since the homogeneous solution is
![]()
the assumed particular integral must be modified according to the proceeding rule; that is,
The reason for this modification is to render the assumed particular integral linearly independent of the homogeneous solution. Substituting (6.14) into (6.12) and equating like coefficients yields
![]()
The complete solution to (6.12) may now be written as
If (6.13) had been used instead of (6.14), it would have turned out that A = 0 and E and B would be undetermined. This would mean that the terms x2 and xe–x would not have been found as part of yp.
In the analysis of electrical networks or mechanical oscillations we are usually interested in finding the particular integral of an equation of the type
We can obtain the particular solution in this case by replacing the right-hand member by a complex exponential. The success of the method depends on the following theorem:
Consider the equation
where F1(x) and F2(x) are real functions of x and j = –1. Then the particular integral of (7.2) is of the form
where y1 satisfies
and y2 satisfies
To prove this, it is necessary only to substitute (7.3) into (7.2), and, on equating the real and imaginary coefficients, we obtain (7.4) and (7.5). To illustrate the method, let us solve (6.7) by making the substitution
where Re denotes the “real part of.” We thus replace the right-hand member of (6.7) by e(2+j3)x and take the real part of the solution; that is, we have
instead of (6.7).
To solve this, assume
where A is a complex constant to be determined. Substituting this into (7.7) and dividing both members by the common factor e(2+j3)x, we obtain
We therefore have
Substituting this into (7.8), we have
If we take the real part of this expression, we have
This is the required particular integral.
To solve the equation
we replace sin ωx by ejωx and consider
We now assume a solution of the form
We note that, if we operate on A ejωx with D, we have the result
and
We therefore note that the result of these operations merely replaces D by jω; accordingly we have
Hence, on substituting (7.15) into (7.14), we have
provided Ln(jω) ≠ 0.
Now Ln(jω) is in general a complex number and may be written in the form
where
and Im denotes the “imaginary part of.” Hence A may be written in the form
Substituting this into (7.15), we have
The solution of (7.13) is obtained by taking the imaginary part of (7.25) to correspond to B0 sin ωx. Hence
is the required particular integral.
If we had taken the real part, we would obtain the solution of the equation
This method is of extreme importance in the field of electrical engineering and mechanical oscillations and forms the basis of the use of complex numbers in the field of alternating currents. These matters will be discussed more fully in Chaps. 5 and 6.
Linear second-order differential equations with variable coefficients are probably the most frequently encountered differential equations in applied mathematics next to those with constant coefficients. The first type of equation we will consider is the homogeneous equation, which is typified by the form
This equation may be transformed to the so-called “normal” form by the transformation†
Applying this transformation to (8.1) yields
where
If r(x) happens to be a constant, then the solution to (8.3) is easy to obtain. If r(x) does not happen to be a constant, then (8.3) may be transformed into other possible forms. One may also recognize (8.1) as one of the standard equations that are well known in applied fields and readily obtain the solution. Equations of this type are Bessel’s equation and Legendre’s equation, which, among others, are discussed in Appendix B.
A theorem which is of great use for solving equations of the form of (8.3) is the comparison theorem. This theorem states that if a solution to (8.3) is oscillatory, then the solution to any similar equation, say
will be oscillatory as long as
![]()
for all values of x within the interval of interest. For example, consider the equation
This equation has an oscillatory solution of the form
The comparison theorem states that as long as
![]()
then (8.5) will have an oscillatory solution.
The most common method of solving homogeneous linear second-order differential equations is the method of Frobenius. This method is a power-series method by which solutions to
near the origin, that is, x = 0, are found. ‡
To apply the method of Frobenius to (9.1), it is assumed that the coefficients p(x) and q(x) are in the form of polynomials or may be expanded as such by means of a Taylor’s series expansion. For the moment we will assume that
where the constants an and bn are known.
The method proceeds by assuming a solution of the form
substituting it into (9.1), and then expanding and equating coefficients of like powers of x. This procedure will provide a method of determining the successive constants cn in terms of the prior ones. Because Eq. (9.1) is a second-order equation, two of these coefficients will remain as arbitrary constants. As an example, consider the equation
Substituting (9.3) and equating the coefficients of like powers of x yields
![]()
hence
If the coefficients in (9.1) are regular at x = 0, then this point is called an ordinary point of the differential equation. The point is termed a regular singular point if

The point x = 0 is an irregular singular point whenever

With this classification of singular points for (9.1) the following general rules may be stated.
1. If p(x) and q(x) have no singular points, then (9.1) possesses two distinct solutions of the form given by (9.3).
2. If (9.1) has only regular singular points, then there will always be at least one solution of the form
3. If (9.1) has an irregular singular point, then regular solutions may or may not exist and no general method exists for determining these solutions.
If rule 2 applies to (9.1), it may then be written in the following form:
where f(x) and g(x) are both regular at x = 0. Assuming that f(x) and g(x) have the following expansions
![]()
Eq. (9.6) may be substituted into (9.1) and the coefficients of like powers of x equated. This procedure yields the indicial equation as the coefficient of the lowest power of x:
The remaining coefficients yield the standard recursion relations to evaluate the succeeding powers of x.
The indicial equation yields the possible values of α for which a solution to (9.1) of the form given by (9.6) will exist. There are three distinct cases for the roots of (9.8) that must be examined further.
1. The roots are distinct and do not differ by a real integer. This includes the case of complex conjugate roots. In this case the solutions are
2. Equation (9.8) has a double root. In this case the solutions to (9.1) are
3. The roots differ by an integer. In this case one solution is given by
where a1 is the root with the largest real part. The second solution is given by
where the constant A may or may not vanish depending upon the original form of (9.1).
Of the equations that are classified under rule 2, a few common types occur frequently in applied mathematics. These are Legendre’s, Bessel’s, and the hypergeometric differential equations (cf. Appendix B).
In Sec. 6 the method of undetermined coefficients was introduced for obtaining particular integrals of linear differential equations. This method is most useful for equations with constant coefficients. The method of variation of parameters, to be presented in this section, is more general in that it may be applied to linear differential equations with variable coefficients. However, it should be remembered that the method of undetermined coefficients is easier to apply in the case of equations with constant coefficients.
The method of variation of parameters may be illustrated by considering the following linear differential equation:
This method assumes that the general homogeneous solution is known a priori; that is,
A particular integral to (10.1) is now assumed to have the form of (10.2), except the arbitrary constants c1 and c2 are replaced by arbitrary functions A(x) and B(x):
At this point we must evaluate the first and second derivatives of (10.4):
The last two terms in this expression are arbitrarily set to zero:
Applying (10.6) to (10.5) and differentiating again yields
Substituting Eqs. (10.4), (10.5), (10.6), and (10.7) into (10.1) gives
Equations (10.6) and (10.8) constitute two simultaneous differential equations for A and B. Solving these two equations by Cramer’s rule yields
where | W | is the Wronskian of the homogeneous solution. Integrating (10.9) and substituting into (10.4) yields the complete general solution:
As a first example consider the equation
For this equation
Substituting these values into (10.10) and performing the indicated integrations yields the general solution
For the second example let us consider the problem of obtaining a solution to the equation
Thus, substituting into (10.10) and again performing the indicated integrations results in the following general solution:
An equation that occurs with great frequency in applied mathematics is the Sturm-Liouville differential equation. This equation is generally written in the form
In this equation μ is a real constant. Instead of initial conditions, this equation is usually subjected to the boundary conditions
where a, b, c, and d are constants.
In finding solutions to (11.1) subject to the general boundary conditions (11.2), it turns out that nontrivial solutions exist only for specific values of the constant μ. These values have been defined as the characteristic or eigenvalues of the equation (11.1). The nontrivial solutions to (11.1) corresponding to the eigenvalues are likewise termed eigenfunctions or characteristic functions. The common notation is that μi represents the ith eigenvalue and yi the ith eigenfunction which is the solution to (11.1) when μ = μi.
An important property of the eigenfunctions may now be demonstrated by considering the special case in which b = 0, and d = 0 in (11.2); that is, the boundary conditions become
We now consider two distinct eigenvalues and their associated eigenfunctions, say μi μj, yi and yj where μi ≠ μj. Since these are solutions to (11.1) we may write
Multiplying the first equation by yj and the second by —yi and adding the two equations yields
Integrating from x1 to x2 gives
If the two integrals on the right-hand side of (11.6) are integrated by parts, the result is
Imposing the boundary conditions given by (11.3), we have
since μi ≠ μj.
It may thus be stated that the eigenfunctions yi and yj are orthogonal with respect to the weighting function r(x) over the interval x1 to x2.
Frequently r(x) = 1 and (11.8) becomes
This is a common definition of orthogonal functions. We have thus shown that the eigenfunctions of the Sturm-Liouville differential equation† are either orthogonal functions or weighted orthogonal functions.
The theory of orthogonal functions is quite important in applied mathematics, and the interested reader is referred to any of the references listed at the end of this chapter.
Problems characterized by (11.1) are commonly referred to as eigenvalue problems or boundary value problems. The usual method of solution is to apply the method of Frobenius unless the equation is recognized to be one of the more common forms to which solutions are readily found. Examples would be differential equations with constant coefficients or Legendre’s or BessePs equations.
Solve the equations:
5. Show that the equation dy/dx + Py = Qyn is reduced to a linear equation by the substitution v = y1–n.
7. Solve the equation d4y/dx4 + ky = 0 subject to the initial conditions that y = y0 at x = 0 and that the first three derivatives of y are zero at x = 0.
8. Find the general solution of (D — a)ny = sinbx, where D = d/dx, n is a positive integer, and a and b are real and unequal.
Find the solution of the following equations which satisfy the given conditions:
15. Find the general solution of the equation (D2n+1 – 1) y = 0, where n is a positive integer.
16. Solve d2 x/dt2 + 4x = sin2x subject to the conditions

17. Solve d2 x/dt2 + b2 x = k cos bt, if

18. Solve the following first-order differential equations:
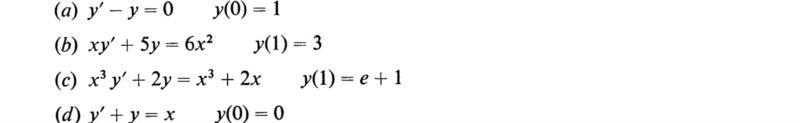
(Hochstadt, 1964)
19. Solve the following homogeneous equations:
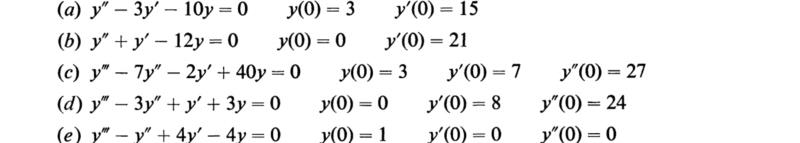
(Hochstadt, 1964)
20. Solve the following differential equations:
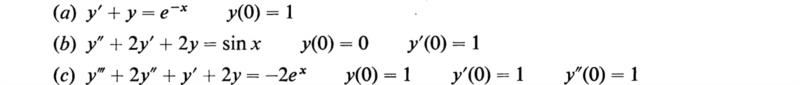
(Hochstadt, 1964)
21. Using (5.1) show that (5.2) does in fact guarantee that f1(x) and f2(x) are linearly independent.
22. Solve (9.4) by reducing it to normal form; that is, apply (8.2).
23. Show how (10.8) results from (10.1) by the indicated substitutions.
24. In the method of undetermined coefficients a special modification must be applied whenever one or more of the terms in the forcing function are contained in the homogeneous solution. Why is it that a similar modification does not have to be made in the method of variation of parameters?
25. In Sec. 10 the method of variation of parameters is presented as a general method for computing a particular integral for a differential equation. However, the solution, as given by (10.10), is the complete general solution. Why?
26. Solve the following differential equations:
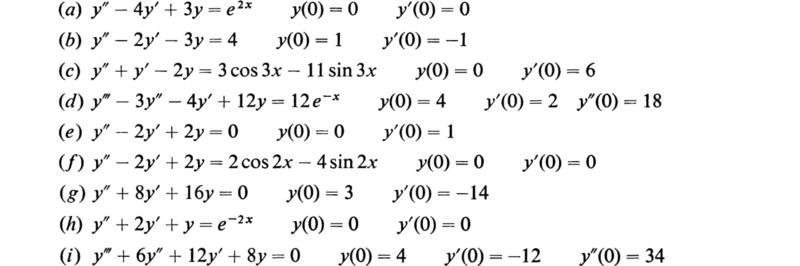
(Kreyszig, 1962)
27. In each case, show that the given set is orthogonal on the given interval I with respect to the weighting function r(x) = 1:
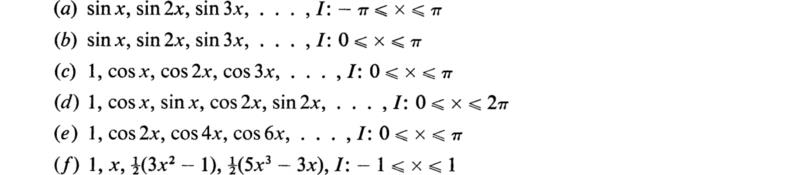
(Kreyszig, 1962)
28. Find the eigenvalues and eigenfunctions to the following Sturm-Liouville differential equations:
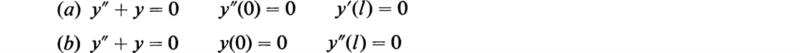
(Kreyszig, 1962)
1927. Jeffreys, H.: “Operational Methods in Mathematical Physics,” Cambridge University Press, New York.
1929. Forsythe, A. R.: “A Treatise on Differential Equations,” The Macmillan Co., New York.
1929. Piaggio, H. T. H.: “An Elementary Treatise on Differential Equations and their Applications,” G. Bell & Sons, Ltd., London.
1933. Cohen, A.: “An Elementary Treatise on Differential Equations,” 2d ed., D. C. Heath and Company, Boston.
1933. Ford, L. R.: “Differential Equations,” McGraw-Hill Book Company, New York.
1939. McLachlan, N. W.: “Complex Variable and Operational Calculus with Technica Applications,” Cambridge University Press, New York.
1939. Pipes, L. A.: The Operational Calculus, Journal of Applied Physics, vol. 10, pp. 172–180.
1941. Carslaw, H. S., and J. C. Jaeger: “Operational Methods in Applied Mathematics,” Oxford University Press, New York.
1949. Hildebrand, F. B.: “Advanced Calculus for Engineers,” Prentice-Hall, Inc., Englewood Cliffs, N.J.
1953. Bellman, R.: “Stability Theory of Differential Equations,” McGraw-Hill Book Company, New York.
1956. Ince, E. L.: “Ordinary Differential Equations,” Dover Publications, Inc., New York.
1958. Kaplan, W.: “Ordinary Differential Equations,” Addison-Wesley Publishing Company, Inc., Reading, Mass.
1959. Kamke, E.: “Differentialgleichungen: Lösungemethoden und Lösungen,” 2d ed., Akademische Verlagsgesellschaft, Leipzig.
1962. Kreyszig, E.: “Advanced Engineering Mathematics,” John Wiley & Sons, Inc., New York.
1964. Hochstadt, H.: “Differential Equations,” Holt, Rinehart and Winston, Inc., New York.
† Note that for |W| to exist, the functions fn(x) must be differentiate at least n – 1 times, which means that this definition is more restrictive than (5.1). However, since the Wronskian is used mainly with differential equations, this restriction does not affect the situation because the same order of differentiability is required for the existence of solutions.
† Cf. Bellman, 1953, p. 108 ff., or Kamke, 1959, p. 119 (see References).
† For a good detailed discussion of this method, see either Hildebrand, 1949, p. 132 ff., or Kreyszig, 1962, p. 180 ff. (see References).
‡ This method may be used to determine solutions of (9.1) about any point x0 by expanding in terms of x – x0. Throughout the remainder of this section it will be assumed that x0 = 0.
† This has been shown only for the special boundary conditions given by (11.3). The results are also true for the general case, and the interested reader may refer to Kreyszig, 1962, p. 513 ff., for the proof of the general case (see References).