A large part of the analysis in engineering and physics is concerned with the study of vibrating systems. The electrical circuit is the most common example of a vibrating system. By analogy the electrical circuit serves as a model for the study of mechanical and acoustical vibrating systems. Historically the equations of motion of mechanical systems were developed a long time before any attention was given to the equations for electrical circuits. It was because of this that in the early days of electrical-circuit theory it was natural to explain the action in terms of mechanical phenomena. At the present time electrical-circuit theory has been developed to a much higher state than the theory of corresponding mechanical systems. Mathematically the elements in an electrical network are the coefficients in the differential equations describing the network. In the same way the coefficients in the differential equations of a mechanical or acoustical system may be looked upon as mechanical or acoustical elements. Kirchhoff’s electromotive-force law plays the same role in setting up the electrical equations as D’Alembert’s principle does in setting up the mechanical and acoustical equations. Therefore a mechanical or acoustical system may be represented by an analogous electrical network, and the problem may be solved by electrical-circuit theory.
The differential equations for electrical circuits with lumped parameters are of the same form as the equations for mechanical systems. Kirchhoff’s first law is the application of the conservation-of-electricity principle to the circuit and may be stated in the following form:
1. The algebraic sum of all the currents into the junction point of a network is zero.
Kirchhoff’s second law is a statement concerning the conservation of energy in the circuit and is usually stated in the following form:
2. The algebraic sum of the electromotive forces around a closed circuit is zero.
Let us apply the above Kirchhoff laws to the simple series circuit of Fig. 2.1. The parameters R, L, and S of the circuit are expressed symbolically in the diagram below and are called the resistance, inductance, and elastance coefficients, respectively. From basic principles, we have
Where q is the charge on the capacitor whose elastance is S, it is related to the current i by the equation
The capacitance of the capacitor C is related to S by the equation
Fig. 2.1
Applying Kirchhoff’s second law to the circuit, we have
or, in terms of q, it is written in the form
where 
and 
If R = 0 and S = 0, the above equation reduces to
This equation has the same form as that governing the displacement x of a mass M when it is acted upon by a force F, as shown in Fig. 2.2. In the mechanical case, we have by Newton’s law (F= Ma) the equation
If the mass is attached to a linear spring as shown in Fig. 2.3, we have by Newton’s law
where k is the spring constant of the spring. This is analogous to Eq. (2.5) if we place R = 0. If in addition to the spring the mass of Fig. 2.3 were retarded by a force proportional to its velocity of the form 
, then its equation of motion would be given by
This equation has exactly the same form as Eq. (2.5); we therefore see that we have the following equivalence between electrical and mechanical quantities:
This correspondence between electrical and mechanical quantities is the basis of the electrical and mechanical analogies.
Fig. 2.2
Fig. 2.3
The energy of an oscillating electrical or mechanical system is of importance in studying the behavior of the system. The potential energy stored in the spring of Fig. 2.3 when the mass has been displaced by a distance x is given by
In the electrical case the energy involved in charging the capacitor plays the same role as the elastic energy in the mechanical case. This is given by
The kinetic energy of motion of the mass is given by
where v = 
is the velocity of the mass.
In the electrical case we have
The power dissipated in friction in the mechanical case is given by
and the power dissipated in the electrical circuit is
We have seen in Sec. 2 that the equation governing the current of the general series circuit of Fig. 2.1 is given by
where
This is a linear differential equation with constant coefficients, and we may solve it by the methods discussed in Chap. 2 or 4. The Laplace-transform method is particularly well suited for solving this equation. To do this, we let
NOTE: In order to avoid confusion with the inductance parameter, the Laplace transforms will be denoted by a script 
.
We therefore have from Chap. 4
From (4.2) we have
where i0 is the initial current flowing in the circuit and q0 is the initial charge on the capacitor. From (4.5) we obtain
Equation (4.1) is transformed to
Eliminating Q, we obtain
Solving for I, we obtain
Let us first consider the case when there is no external electromotive force applied to the system. In this case e(t) is equal to zero. To simplify the equation, let
In this case we have
To obtain the inverse transform of this expression, we use Nos. 2.22 and 2.23 of our table of transforms (Appendix A). There are three cases to consider:
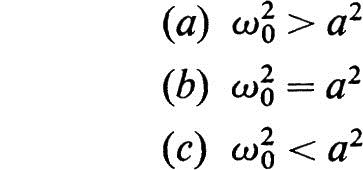
Case a is called the oscillatory case. For this case we obtain from the table
where
We thus see that the current is given as a damped oscillation, where i0 and q0are the initial current and charge of the system.
If ω0 = a, we have case b. This is called the critically damped case. We then obtain
In this case there are no oscillations, and the current dies down in an exponential manner.
Case c is the overdamped case, and the solution for this case may be easily obtained from Nos. 2.22 and 2.23 of the table of transforms.
If there is no resistance present in the circuit, then a = 0 and our transform becomes
We may compute the inverse transform of this equation by the use of transform No. 2.6 of the table of transforms. We then have
where now
The foregoing equations give the velocity of the mass of the analogous mechanical system. In this case q0 corresponds to the initial displacement x0, and i0 corresponds to the initial velocity of the mass of the mechanical system. The quantity 
in the case where we have no resistance is called the natural angular frequency of the electrical system. This corresponds to
for the mechanical system. Here k is the spring constant, and M is the mass of the system.
If e(t) is not equal to zero, we must add to the preceding expressions the transform of
The inverse transform of (4.19) gives the current in a general series circuit that has no initial current and no initial charge but has impressed on it an electromotive force e(t) at t = 0. Let us compute this for the case in which e(t) is an alternating potential of the form
By No. 2.4 of the tables we obtain
Substituting this into (4.19), we obtain
The inverse transform of this expression may be most simply computed by the use of No. T.17 of the table of transforms. For this case, we have
The roots of D(s) are
We also have
Hence, substituting into No. T.17 of the table of transforms, we obtain
Since the roots s1 and s2 have a negative real part, the expression within the brackets vanishes ultimately as time increases. The second expression may be denoted by is. It may be easily transformed to the form
This term persists with the passage of time and is called the steady-state term. If R is zero so that the circuit is devoid of resistance, this becomes
If 
the denominator of (4.28) vanishes and the steady-state current amplitude becomes indefinitely great. This is the phenomenon of resonance and occurs when the impressed electromotive force has a frequency equal to that of the natural frequency of the circuit. If the circuit has resistance, then the denominator of (4.27) does not vanish and we do not have true resonance.
It may be noted that the steady-state current may be obtained more simply directly from the differential equation of the circuit
by the method of undetermined coefficients explained in Chap. 2, Sec. 6. The steady-state current is the particular integral of this equation. We replace the right-hand member of (4.29) by Im E0ejωt, where “Im” means the “imaginary part of.”
We let
where A is a complex number to be determined by (4.22). Suppressing the Im symbol and realizing that
Substitution into (4.29) gives
where we have divided both sides by the common factor ejωt. Hence we have
It is convenient to introduce the notation
This complex number is called the complex impedance of the circuit. It may be written in the polar form
where
We thus have
The steady-state current is now given by (4.30) in the form
This is the steady-state current given in (4.27) obtained more directly. The solution (4.26), however, contains both the steady-state solution and the transient response of the system produced by the sudden application of the potential E0 sin ωt on the system at t = 0.
An interesting application of the differential equations governing the distribution of charges and currents in electrical networks is the following one.
Consider the electrical circuit of Fig. 5.1. Let a charge q0 be placed on the capacitor, and let the switch S be closed at t = 0. Let it be required to determine the charge on the capacitor at any instant later.
When the switch is closed, we have, by Kirchhoff’s law, the equation
To solve this, let us introduce the transform
Fig. 5.1
The initial conditions of the problem are
Hence we have
Hence Eq.(5.1) transforms to
or
As before, let
We, therefore, have
By the use of transforms Nos. 2.22 and 2.23 of the table of transforms, we obtain
where 
and 
Let us consider the circuit of Fig. 5.2. In this case, at t = 0, the switch is closed and the potential E of the battery is impressed on the circuit. It is required to determine the manner in which the charge on the capacitor behaves.
The equation satisfied by the charge is now
Fig. 5.2
To solve this equation, we again let
and since E is a constant, we have
The initial conditions are now
Hence we have
Equation (5.10) transforms to
and hence
To obtain the inverse transform of (5.16), we must use transform No. 3.23 of the table of transforms and thus obtain
where β and ωs are as defined in (5.9).
In each case, the charging current is given by 
The analogous mechanical problem is that of determining the motion of a mass when it has been given an initial displacement and is acted upon by a spring and retarded by viscous friction or if the mass has a sudden force applied to it.
Let us consider the circuits of Fig. 6.1. In this case we have two circuits coupled magnetically. The coefficient L12 is termed the mutual inductance coefficient. It is positive if the magnetic fields of i1 and i2 add. If they are opposed, then the coefficient L12 is negative. In any case the equations governing the currents in the two circuits are given by applying Kirchhoff’s laws to the two loops and are
We wish to determine the currents i1 and i2 on the supposition that at t = 0 the switch s is closed and the initial currents are zero. Let us introduce the transforms
Now since we have
and also E is a constant, Eq. (6.1) transforms to
We now solve these two algebraic equations by using Cramer’s rule
and obtain
Fig. 6.1
If we let
and
we then have
In this case
Using the transforms Nos. 2.23 and 3.23 of the table of transforms, we obtain after some algebraic reductions
for the transforms of I1 and I2. We see that, as time elapses, i2 approaches its final value E/R11. If we set di2/dt = 0 and solve for t, we find that i2 rises to a maximum value when
and then approaches zero asymptotically. An interesting special case is the symmetrical one. In this case the resistances of each mesh are equal, and the self-inductances are equal. We then have
Equations (6.4) then become
If we add the two equations, we obtain
If we subtract the second equation from the first one, we have
If we now let
we have
Hence
If we let
we obtain
Using transform No. 2.1 of the table of transforms, we have
Hence
and adding the two equations we obtain
Subtracting the second equation from the first equation, we obtain
These are the currents in the symmetrical case.
Let us consider the circuit of Fig. 7.1. In this case, we have two coupled circuits. The coupling element is now a capacitor. Let the switch S be closed at t = 0, and let it be required to determine the current in the system. We write Kirchhoff’s law for both meshes. We then obtain
where
Let us introduce the transforms
If we assume
Eqs. (7.1) transform into
Fig. 7.1
We now solve these equations algebraically for the transforms I1 and I2. We thus obtain
Expanding the determinants, we obtain the transforms I1 and I2 as the ratios of polynomials in s. The inverse transforms of I1and I2 give the currents in the system. In this case, the determinant in the denominator of (7.6) of the system is a polynomial of the fourth degree in s. The inverse transforms may now be calculated by the use of No. T.17 in the table of transforms. This entails the solution of a quartic equation in s. If numerical values are given, this may be done by the Graeffe root-squaring method described in Appendix D. The trend of the general solution may be determined by solving the symmetrical case in which we have
In this case Eqs. (7.5) reduce to
If we add the two equations, we obtain
If we subtract the second equation from the first, we have
If we let
we obtain
If we let
the two equations become
The inverse transforms of x1 and x2 may now be calculated by No. 2.22 in the table of transforms. In the case
we have
Hence, adding the two equations (7.16), we have
If there is no resistance in the circuit, then a = 0 and the current oscillate without loss of amplitude with the angular frequencies ω1 and ω2
It frequently happens that the response of an electrical circuit is desired when a potential pulse is applied to it. The general procedure may be illustrated by the following example.
Consider the circuit of Fig. 8.1. Let e(t) be a pulse of the form given by Fig. 8.2. It is required to find the current in the circuit. For generality, let us assume that the capacitor has an initial charge q0 at t = 0. The current satisfies the equation
We introduce the transforms
We now have
Hence
The transforms of the potential e(t) is given by
Accordingly, Eq. (8.1) is transformed:
If we let
Fig. 8.1
Fig. 8.2
To obtain the inverse transform of, we use Nos. 1.1 and T.6 of the table of transforms. We thus obtain
This example illustrates the general procedure.
In this section the analysis of a general n-mesh network will be considered. Given a network, we can draw n independent circulating currents so that they permit a different current in each branch of the network. We shall use the following notation:
a. The resistance coefficients: Rrs is the resistance common to the ir and is circuits. Rrr is the total resistance in the ir circuit.
b. The inductance coefficients: The inductance notation is complicated by the possibility of mutual inductance. If L1rs is the total self-inductance common to ir and is, and Mrs is the mutual inductance between the ir and is circuits, then we define Lrs to be
The negative sign is used if Mrs opposes L1rs. We define Lrr as the total self-inductance in the ir circuit.
c. The elastance coefficients: In the circuits that we are considering, every capacitor will be traversed by one or more circulating currents. For a given current, capacitors appear in series but not in parallel. It is convenient if we write the equations in terms of the elastance coefficients rather than in
terms of the capacitance coefficients. The elastance coefficients are the reciprocals of the capacitance coefficients and are denoted by the symbol S.
Let us denote by Srs the elastance common to the ir and is circuits. We shall denote by Srr the sum of the elastances in the ir circuit.
With the notations defined above, we have
These coefficients are called the mutual parameters of the network and Srr, Lrr, and Rrr are called the mesh parameters.
The set of differential equations describing the behavior of the general n-mesh networks may be written conveniently if we introduce the operators
If now (e1,e2, . . . , en) denote the potentials impressed on the contours of the meshes 1, 2, . . . , n, and (i1,i2, . . . ,in) are the mesh currents of the corresponding n meshes, we have
A concise form of these equations may be obtained by the use of matrix notation, as explained in Chap. 4. To do this, we introduce the following square matrices:
In terms of the matrices we construct the square matrices [Z(D)] by
We also introduce the column matrices
The set of differential equations (9.4) may then be written concisely in the form
In the usual network problem we are given the various mesh charges and mesh currents of the system at t = 0, and the various mesh potentials (e1 e2 . . . en) are assumed impressed on the system at t = 0. We desire to find the subsequent distribution of currents in the system.
Let us introduce a column matrix {E(s)} whose elements are the transforms of the elements of the matrix (e). That is,
In the same way introduce the column matrix {I(s)}.
If we now introduce the column matrices
where 
are the initial currents of the corresponding meshes of the system at t = 0 and 
are the corresponding initial mesh charges of the system at t = 0, then the set of differential equations (9.8) transforms into
If we now premultiply both sides of this equation by the inverse matrix [Z(s)]–1, we obtain
We now obtain the various mesh currents from the equation
This formally completes the solution of the problem. In general the above algebraic procedure will give the elements of the matrix I as the ratios of polynomials in s. The inverse transforms of these elements must be evaluated by using transform No. T.17 of the table of transforms. The procedure involves the computation of the roots of the polynomial equation
In the general case this polynomial cannot be factored, and it is of the 2nth degree. The roots may be determined by the Graeffe root-squaring method of Appendix D.
If there are no initial mesh charges and mesh currents in the system, we have
and we have
The solution in this case is that of a system initially at rest that has the potentials {e} impressed on it at t = 0.
The equations of the last section give the complete solution of a system having initial charges and potentials and also impressed electromotive forces of arbitrary form at t = 0.
There is one case of extreme practical importance in electrical engineering. This is the case where it is desired to find the so-called “steady-state current distribution” when the various mesh electromotive forces have the form
This is the case that occurs in alternating-current theory. For generality, we shall assume that the various mesh potentials have the same frequency but differ in phase. To determine the steady-state mesh currents, it is necessary to determine the particular integral of the set of equations
It is convenient to write
where Im denote of the “imaginary part of and
where {I}a is a column matrix whose elements are the unknown complex amplitudes of the steady-state currents to be determined by Eq. (10.1). Substituting (10.4) into (10.1) and suppressing the Im symbol, we obtain
Hence we have
The steady-state currents are now given by (10.4). The elements of the column matrix {I}a are called the complex currents of the system. The above procedure is a generalization of the method of Sec. 4 for the single-mesh case. We have
This is called the impedance matrix. The terms
are called the mesh impedances, and the terms
are called the mutual impedances.
A special form of the general network discussed in Sees. 9 and 10 is one that has a pair of input and a pair of output terminals. It is customary to refer to such a network as a four-terminal network or a two-terminal-pair network. A four-terminal network is illustrated schematically by Fig. 11.1 as a box with two pairs of terminals.
The reference directions for voltage and current will be taken as those shown in Fig. 11.1. The four-terminal network will be supposed to consist
Fig. 11.1
of an n-mesh network having two pairs of accessible terminals as shown. The potentials E1 and E2 are complex potentials produced by sources external to the network, and the currents I1 and I2 are the complex currents in the corresponding meshes. The internal structure of the four-terminal network will be assumed to be quite general, and the n meshes will be supposed to have impedances Zkk and complex mutual impedances Zks between the meshes. The restrictions on the component elements of the network are that they be linear and constant. It is further assumed that the network is passive; that is, the only sources of electromotive force are Ex and E2 produced by external agencies. It can be shown that, as a consequence of the general equations (10.5), we have the following linear relations:
The coefficients A, B, C, D of Eqs. (11.1) are called general four-terminal-network parameters. It can be seen that as a consequence of the form of (11.1) A and D are in general complex numbers and that B has the dimension of an impedance and C the dimension of an admittance, or reciprocal impedance. As a result of Eq. (10.9) it can be shown that the following relation between the network parameters exists:
For many purposes it is convenient to express the pair of equations (11.1) as the following matrix equation:
where [T] is the square matrix
The square matrix [T] is usually called the transmission matrix of the network. The determinant of [T] is equal to unity as a consequence of the relation (11.2). The transmission matrix [T] has the following inverse:
Fig. 11.2
If two four-terminal networks of transmission matrices T1 T2 are connected in cascade as shown in Fig. 11.2, then the over-all relations between the input and output quantities are given by
where [T] is the transmission matrix of the over-all network. It is given by
It is thus seen that, in the cascade connection of several four-terminal networks, the over-all transmission matrix of the network is the matrix product of the transmission matrices of the individual networks taken in the order of connection. If a four-terminal network is symmetrical so that its input and output terminals may be interchanged without altering the current and potential distribution of the network, it may be shown that its transmission matrix has the property that A = D.
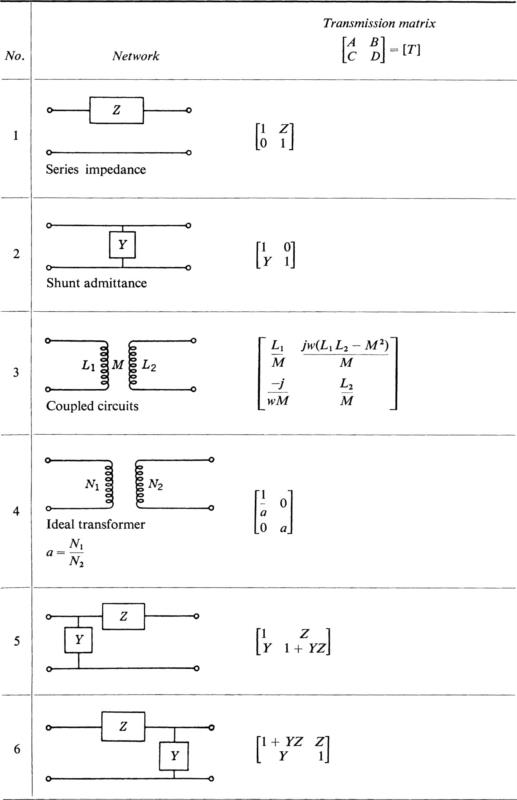
If the transmission matrices of several fundamental types of electrical circuits are known, then by matrix multiplication it is easy to obtain many useful properties of more complex structures formed by a cascade connection of fundamental circuits. The transmission matrices [T] of several basic electrical circuits are listed in Table 1.
Many important problems of electrical-circuit theory such as those involving electric filters, delay lines, and transducers involve the determination of the nature of the current and potential distribution along a chain of identical symmetric four-terminal networks. Consider the cascade of n identical four-terminal networks as shown in Fig. 11.3. Let each of the four-terminal networks be a symmetrical one with the following transmission matrix:
Table 1 Transmission matrices of fundamental four-terminal structures
Since each of the structures of the chain has the same matrix, the output potential and current En and In„ of the nth structure are related to the input potential and current E0 and I0 of the first structure by the following equation:
Fig. 11.3
In order to obtain a form for the transmission matrix [T] that is convenient for computing powers of [T], introduce the new variables a and Z0 by the equations
and
With this notation the transmission matrix [T] takes the following form:
If the matrix [T] is multiplied by itself, the following result is obtained:
Similarly, by direct multiplication and by the use of the identities of hyperbolic trigonometry, it can be shown that
The result (11.14) is very useful in the study of the behavior of four-terminal networks and associated structures. By means of (11.14) Eq. (11.9) may be written in the form
The potential Ek and the current lk along the chain of four-terminal structures of Fig. 11.3 are given by the equation
If the chain of four-terminal networks is terminated by an impedance equal to Z0, then
Then the impedance Z looking into the chain of structures may be obtained from (11.15) in the form
The quantity Z0 is called the characteristic impedance of the chain of four-terminal networks. Hence, if the cascade of networks is terminated by the characteristic impedance Z0, the impedance Zi looking into the cascade is also equal to the characteristic impedance. In this case the input current of the chain is
The potential and currents along the cascade may be obtained by the use of (11.17) if I0 is eliminated by (11.20). The results are
The quantity a is the propagation function of the chain of four-terminal structures of Fig. 11.3.
In general the propagation function a is a complex function of the angular frequency ω. It has the form
The quantity α is called the attenuation function, and β is the phase function of the cascade. β gives the change of phase per section as one progresses along the cascade. If the cascade of four-terminal networks is to pass a certain band of frequencies without attenuation, the real part of the propagation function must be zero and hence the propagation function a must be a pure imaginary quantity. Therefore for a passband it is necessary that
The relation (11.10) is then
It follows that the network constant A of the fundamental four-terminal network of the cascade must satisfy the two following conditions for a passband,
and since cos β can vary only between –1 and +1, the following inequality must be satisfied:
A very important class of circuits are those which are devoid of resistance. Circuits of this class are called dissipationless circuits. It can be shown that the parameter A is a real number if the fundamental circuit in the box is dissipationless so that (11.25) is always satisfied for circuits of this class. If the inequality (11.26) is satisfied, the cascade passes currents and potentials without attenuation. If the inequality is not satisfied, the currents and potentials are attenuated along the cascade. In general the parameter A is a function A(ω) of the angular frequency of the applied alternating potential. The ranges in frequencies that are attenuated or passed without attenuation may be determined by the use of the inequality (11.26). This relation is fundamental in the theory of electrical filter circuits.
A very important type of circuit is the transmission line shown schematically in Fig. 12.1.
Fig. 12.1
This figure depicts a two-wire transmission line. In the alternating steady state this transmission line may be regarded as a continuous distribution of series impedance Z and shunt admittance Y per unit length, defined by the equations
where R is the resistance of the line per unit length, L the inductance per unit length, C the capacitance per unit length, and G the leakage conductance per unit length.
Consider a length dx of the transmission line at a distance x from the sending end as shown in Fig. 12.1. This length of line contains a shunt admittance Y dx and a series impedance Z dx. Let dl be the complex current that flows from one conductor to the other through the admittance Y dx, and let dE be the change in the complex potential difference between the conductors caused by the current I(x) flowing in the impedance Z dx. If higher-order infinitesimals are neglected, it is seen that, by an application of Kirchhoff’s laws to a section of the line of length, dx, we obtain the following equations:
The complex current I(x) and the complex potential E(x) therefore satisfy the following two differential equations:
If these two simultaneous first-order differential equations are solved subject to the boundary conditions that E = E1 and I = I1 at x = 0, the result is
where
and
The quantity a is the propagation function of the line. The real part of a, α, is the attenuation function, and the imaginary part of a, β, is the phase function of the line. The impedance Z0 is the characteristic impedance of the line.
If S is the length of the line and I2 and E2 the output complex current and potential of the line, Eqs. (12.4) yield the following values for E2 and I2:
The two equations (12.7) may be written in the convenient matrix form
Equation (12.8) may also be written in the alternative form
It is thus evident from (12.9) that the transmission matrix of the two-wire line of Fig. 12.1 is given by
The matrix has the following inverse
Calculations involving transmission lines may be greatly simplified by the use of the matrices (12.10) and (12.11). The quantity θ = aS is called the angle of the line and is, in general, a complex number. As an example of the use of the transmission matrix [T], consider a transmission line short-circuited at the end x = S. In this case E2 = 0, and from Eq. (12.9) we have the relation
Hence the current at the short-circuited end is given by the equation
If, on the other hand, the end x = S is open-circuited, I2 = 0 and (12.9) give E2 = E1/cosh θ for the open-circuit potential.
1. What is the analogous electrical circuit for a mechanical pendulum that is subjected to very small displacements?
2. A circuit consisting of an inductance L in series with a capacitance C has impressed on it at / = 0 a potential e(t) = E0 t/T0 (0 < t < T0) and e(t) = 0, t > T0. Find the current in the system.
3. Two circuits are coupled with a mutual inductance M. One contains an impressed potential E0, R, L1 and a switch in series; the other circuit has L2 and C in series. For what value of the circuit constants are oscillations possible?
4. Each side of an equilateral triangular circuit contains a capacitance C, and each vertex is connected to a common central point by an inductance L. Show that the possible oscillations of this circuit have the period 
.
5. Two points are connected by three branches, two of which contain both a capacitance C and an inductance L, and the third only a capacitance C. Show that the angular frequencies of oscillation of the network are 
and 
.
6. Two circuits L1, R1 and L2, R2 are coupled by a mutual inductance M, where M2 = L1L2. A constant electromotive force E is applied at t = 0 in the primary circuit. The initial currents are zero. Determine the currents in the circuits.
7. An electromotive force E cos(ωt + θ) is applied at t = 0 to a circuit consisting of capacitance C and inductance L in series. The initial charge and current are zero. Find the current at time t.
8. An electromotive force E sin ωt, where 
, is applied at t = 0 to a circuit consisting of capacitance C and inductance L in series. The initial current and charge are zero. Find the current. (This is the case of resonance.)
9. Show that a combination of capacitance C shunted by resistance R in series with a combination of inductance L shunted by resistance R behaves as a pure resistance for all forms of applied electromotive force if L = CR2.
10. Two resistanceless circuits L1 C and L2, C2 are coupled by mutual inductance M. If at t = 0, when the currents and charges are zero, a battery of electromotive force E0 is applied in the primary, find the current in the secondary.
11. A circuit consists of a resistance, an inductance, and a capacitance in series. An electromotive force e = E1 cos ω1t + E2 cos ω2t is impressed on the circuit. Find the steady-state current.
12. A series circuit consisting of an inductance capacitance and resistance has an electromotive force e(t) of the “meander” type, as shown in the figure, impressed on it. Find the steady-state current.
Fig. P 12
13. Two transmission lines of series impedances Z1 and Z2 per length and shunt admittances Y1 and Y2 are connected in cascade. The transmission lines have lengths S1 and S2, respectively. Find the over-all transmission matrix of the combination. The receiving end of the second transmission line is short-circuited. Find the current at this end in terms of the complex potential applied to the sending end of the first transmission line.
14. A circuit is composed of a cascade connection of n four-terminal networks. All the four-terminal networks of the cascade are identical and contain the structure shown in Fig. P 14. Obtain the over-all transmission matrix of the cascade, and determine the range in o» that gives the passband and the stopband.
Fig. P 14
15. The same as Prob. 14 for the case in which all four-terminal networks contain the structure shown in Fig. P 15.
Fig. P 15
16. The cascade of four-terminal networks of Prob. 14 is short-circuited at the receiving end. A potential E0 sin a > t is impressed at the sending end of the cascade. Determine the instantaneous value of the receiving current when co lies in a stopband and when to lies in a passband.
17. Using (11.1) and the standard short- and open-circuit test conditions, derive
(a) Transmission matrix No. 1, Table 1
(b) Transmission matrix No. 2, Table 2
(c) Transmission matrix No. 5, Table 2
(d) Transmission matrix No. 6, Table 2
(e) Transmission matrix No. 7, Table 2
(f) Transmission matrix No. 8, Table 2
18. Using transmission matrices Nos. 1 and 2 in Table 1 and matrix multiplication, derive
(a) Transmission matrix No. 5
(b) Transmission matrix No. 6
(c) Transmission matrix No. 7
Transmission matrix No. 8
Bode plots are plots of amplitude ratio (in decibels) and the phase angle (in degrees) versus the logarithm (base 10) of the frequency. In terms of voltages, the amplitude ratio is given by 20 log magnitude of output/input voltage (decibels), and the phase angle is the angle by which the output voltage leads (+angle) or lags (-angle) the input voltage. To solve the following problems, assume that the input voltage Ex is E0 sin cot, and that the output is an open circuit, that is, I2 = 0.
19. Draw Bode plots for the transmission matrix No. 1, Table 2, when
20. Draw Bode plots for the transmission matrix No. 6, Table 2, for 
when
In the following problems, use matrix methods to solve for the indicated circulating steady-state currents.
Fig. P 21
R1 = 5 R2 = 2 R3 = 3
Fig. P 22
R = 10 
L = 15
Fig. P 23
R = 10 
L = 10
Fig. P 24
L = 1 R1 = 1 R2 = 2
Fig. P 25
R1 = 1 R2 = 3 R3 = 1 R4 = 2 R5 = 4
Fig. P 26
R1 = 2 R2 = 1 
In the following problems assume that all the initial conditions are zero and solve for the transient and steady-state currents when the switch S is closed at t = 0.
Fig. P 27
Fig. P 28
Fig. P 29
Fig. P 30
Fig. P 31
Fig. P 32
Fig. P 33
1920. Carson, J. R.: “Electric Circuit Theory and the Operational Calculus,” McGraw-Hill Book Company, New York.
1920. Pierce, G. W.: “Electric Oscillations and Electric Waves,” McGraw-Hill Book Company, New York.
1929. Berg, E. J.: “Heaviside’s Operational Calculus,” McGraw-Hill Book Company, New York.
1929. Bush, V.: “Operational Circuit Analysis,” John Wiley & Sons, Inc., New York.
1931. Guillemin, E. A.: “Communication Networks,” John Wiley & Sons, Inc., New York.
1939. Pipes, L. A.: The Operational Calculus, Journal of Applied Physics, vol. 10, Nos. 3–5.
1940. Pipes, L. A.: The Matrix Theory of Four-terminal Networks, Philosophical Magazine, ser. 7, vol. 30, pp. 370–395, November.
1943. Jackson, L. S.: “Wave Filters,” John Wiley & Sons, Inc., New York.
1943. Kerchner, R. M., and F. Corcoran: “Alternating Current Circuits,” John Wiley & Sons, Inc., New York.
1945. Bode, H. W.: “Network Analysis and Feedback Amplifier Design,” D. Van Nostrand Company, Inc., Princeton, N.J.
1946. Josephs, H. J.: “Heaviside’s Electric Circuit Theory,” John Wiley & Sons, Inc., New York.
1952. LePage, W., and S. Seely: “General Network Analysis,” McGraw-Hill Book Company, New York.
1955. IRE Transactions on Circuit Theory, vol. CT-2, no. 2, June.
1963. Paskusz, G. F., and B. Bussel: “Linear Circuit Analysis,” Prentice-Hall, Inc., Engle-wood Cliffs, N.J.
1963. Pipes, L. A.: “Matrix Methods for Engineering,” Prentice-Hall, Inc., Englewood Cliffs, N.J.
1965. Skilling, H. H.: “Electrical Engineering Circuits,” John Wiley & Sons, Inc., New York.
1965. Toro, V. D.: “Principles of Electrical Engineering,” Prentice-Hall, Inc., Englewood Cliffs, N.J.
