Chapter Three
Fundamental Principles of a Theory of Gambling
Decision Making and Utility
The essence of the phenomenon of gambling is decision making. The act of making a decision consists of selecting one course of action, or strategy, from among the set of admissible strategies. A particular decision might indicate the card to be played, a horse to be backed, the fraction of a fortune to be hazarded over a given interval of play, or the time distribution of wagers. Associated with the decision-making process are questions of preference, utility, and evaluation criteria, inter alia. Together, these concepts constitute the sine qua non for a sound gambling-theory superstructure.
Decisions can be categorized according to the relationship between action and outcome. If each specific strategy leads invariably to a specific outcome, we are involved with decision making under certainty. Economic games may exhibit this deterministic format, particularly those involving such factors as cost functions, production schedules, or time-and-motion considerations. If each specific strategy leads to one of a set of possible specific outcomes with a known probability distribution, we are in the realm of decision making under risk. Casino games and games of direct competition among conflicting interests encompass moves whose effects are subject to probabilistic jurisdiction. Finally, if each specific strategy has as its consequence a set of possible specific outcomes whose a priori probability distribution is completely unknown or is meaningless, we are concerned with decision making under uncertainty.
Conditions of certainty are, clearly, special cases of risk conditions where the probability distribution is unity for one specific outcome and zero for all others. Thus a treatment of decision making under risk conditions subsumes the state of certainty conditions. There are no conventional games involving conditions of uncertainty1 without risk. Often, however, a combination of uncertainty and risk arises; the techniques of statistical inference are valuable in such instances.
Gambling theory, then, is primarily concerned with decision making under conditions of risk. Furthermore, the making of a decision—that is, the process of selecting among n strategies—implies several logical avenues of development. One implication is the existence of an expression of preference or ordering of the strategies. Under a particular criterion, each strategy can be evaluated according to an individual’s taste or desires and assigned a utility that defines a measure of the effectiveness of a strategy. This notion of utility is fundamental and must be encompassed by a theory of gambling in order to define and analyze the decision process.
While we subject the concept of utility to mathematical discipline, the nonstochastic theory of preferences need not be cardinal in nature. It often suffices to express all quantities of interest and relevance in purely ordinal terms. The essential precept is that preference precedes characterization. Alternative A is preferred to alternative B; therefore A is assigned the higher (possibly numerical) utility; conversely, it is incorrect to assume that A is preferred to B because of A’s higher utility.
The Axioms of Utility Theory
Axiomatic treatments of utility have been advanced by von Neumann and Morgenstern originally and in modified form by Marschak, Milnor, and Luce and Raiffa (Ref.), among others. Von Neumann and Morgenstern have demonstrated that utility is a measurable quantity on the assumption (Ref.) that it is always possible to express a comparability—that is, a preference—of each prize (defined as the value of an outcome) with a probabilistic combination of other prizes. The von Neumann–Morgenstern formal axioms imply the existence of a numerical scale for a wide class of partially ordered utilities and permit a restricted specific utility of gambling.
Herein, we adopt four axioms that constrain our actions in a gambling situation. To facilitate formulation of the axioms, we define a lottery L as being composed of a set of prizes A1, A2, …, An obtainable with associated probabilities p1, p2, …, pn (a prize can also be interpreted as the right to participate in another lottery). That is,
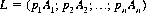
And, for ease in expression, we introduce the notation p to mean “is preferred to” or “takes preference over”, e to mean “is equivalent to” or “is indifferent to”, and q to mean “is either preferred to or is equivalent to.” The set of axioms delineating Utility Theory can then be expressed as follows.
Axiom I(a). Complete Ordering: Given a set of alternatives A1, A2, …, An, a comparability exists between any two alternatives Ai and Aj. Either Ai q Aj or Aj q Ai or both.
Axiom I(b). Transitivity: If Ai q Aj and Aj q Ak, then it is implied that Ai q Ak. This axiom is requisite to consistency. Together, axioms I(a) and I(b) constitute a complete ordering of the set of alternatives by q.
Axiom II(a). Continuity: If Ai p Aj p Ak, there exists a real, nonnegative number rj, 0 < rj < 1, such that the prize Aj is equivalent to a lottery wherein prize Ai is obtained with probability rj and prize Ak is obtained with probability 1 − rj.
In our notation, Aj e [rj Ai; (1 − rj)Ak]. If the probability r of obtaining Ai is between 0 and rj, we prefer Aj to the lottery, and contrariwise for rj < r ≤ 1. Thus rj defines a point of inversion where a prize Aj obtained with certainty is equivalent to a lottery between a lesser prize Ai and a greater prize Ak whose outcome is determined with probabilities rj and (1 − rj), respectively.
Axiom II(b). Substitutability: In any lottery with an ordered value of prizes defined by Ai p Aj p Ak, [rj Ai; (1 − rj)Ak] is substitutable for the prize Aj with complete indifference.
Axiom III. Monotonicity: A lottery [rAi; (1 − r)Ak] q [rjAi; (1 − rj)Ak] if and only if r ≥ rj. That is, between two lotteries with the same outcome, we prefer the one that yields the greater probability of obtaining the preferred alternative.
Axiom IV. Independence: If among the sets of prizes (or lottery tickets) A1, A2, …, An and B1, B2, …, Bn, A1 q B1, A2 q B2, etc., then an even chance of obtaining A1 or A2, etc. is preferred or equivalent to an even chance of obtaining B1 or B2, ….
This axiom is essential for the maximization of expected cardinal utility.
Together, these four axioms encompass the principles of consistent behavior. Any decision maker who accepts them can, theoretically, solve any decision problem, no matter how complex, by merely expressing his basic preferences and judgments with regard to elementary problems and performing the necessary extrapolations.
Utility Functions
With Axiom I as the foundation, we can assign a number u(L) to each lottery L such that the magnitude of the values of u(L) is in accordance with the preference relations of the lotteries. That is, u(Li) ≥ u(Lj) if and only if Li q Lj. Thus we can assert that a utility function u exists over the lotteries.
Rational behavior relating to gambling or decision making under risk is now clearly defined; yet there are many cases of apparently rational behavior that violate one or more of the axioms. Common examples are those of the military hero or the mountain climber who willingly risks death and the “angel” who finances a potential Broadway play despite a negative expected return. Postulating that the probability of fatal accidents in scaling Mt. Everest is 0.10 if a Sherpa guide is employed and 0.20 otherwise, the mountain climber appears to prefer a survival probability of 0.9 to that of 0.8, but also to that of 0.999 (depending on his age and health)—or he would forego the climb. Since his utility function has a maximum at 0.9, he would seem to violate the monotonicity axiom. The answer lies in the “total reward” to the climberas well as the success in attaining the summit, the payoff includes accomplishment, fame, the thrill from the danger itself, and perhaps other forms of mental elation and ego satisfaction. In short, the utility function is still monotonic when the payoff matrix takes into account the climber’s “gestalt.” Similar considerations evidently apply for the Broadway “angel” and the subsidizer of unusual inventions, treasure-seeking expeditions, or “wildcat” oil-drilling ventures.
Since utility is a subjective concept, it is necessary to impose certain restrictions on the types of utility functions allowable. First and foremost, we postulate that our gambler be a rational being. By definition, the rational gambler is logical, mathematical, and consistent. Given that all x’s are y’s, he concludes that all non-y’s are non-x’s, but does not conclude that all y’s are x’s. When it is known that U follows from V, he concludes that non-V follows from non-U, but not that V follows from U. If he prefers alternative A to alternative B and alternative B to alternative C, then he prefers alternative A to alternative C (transitivity). The rational being exhibits no subjective probability preference. As initially hypothesized by Gabriel Cramer and Daniel Bernoulli as “typical” behavior, our rational gambler, when concerned with decision making under risk conditions, acts in such a manner as to maximize the expected value of his utility.
Numerous experiments have been conducted to relate probability preferences to utility (Ref. Edwards, 1953, 1954). The most representative utility function, illustrated in Figure 3-1, is concave for small increases in wealth and then convex for larger gains. For decreases in wealth, the typical utility function is first convex and then concave, with the point of inflection again proportional to the magnitude of present wealth. Generally, u(W) falls faster with decreased wealth than it rises with increased wealth.
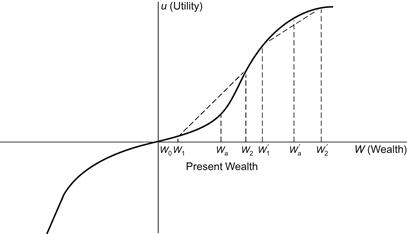
Figure 3-1 Utility as a function of wealth.
From Figure 3-1, we can determine geometrically whether we would accept added assets Wa or prefer an even chance to obtain W2 while risking a loss to W1. Since the line 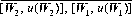 passes above the point [Wa, u(Wa)], the expected utility of the fair bet is greater than u(Wa); the lottery is therefore preferred. However, when we are offered the option of accepting W′a or the even chance of obtaining W′2 or falling to W′1, we draw the line
passes above the point [Wa, u(Wa)], the expected utility of the fair bet is greater than u(Wa); the lottery is therefore preferred. However, when we are offered the option of accepting W′a or the even chance of obtaining W′2 or falling to W′1, we draw the line 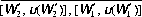 , which we observe passes below the point u(W′a). Clearly, we prefer W′a with certainty to the even gamble indicated, since the utility function u(W′a) is greater than the expected utility of the gamble. This last example also indicates the justification underlying insurance policies. The difference between the utility of the specified wealth and the expected utility of the gamble is proportional to the amount of “unfairness” we would accept in a lottery or with an insurance purchase.
, which we observe passes below the point u(W′a). Clearly, we prefer W′a with certainty to the even gamble indicated, since the utility function u(W′a) is greater than the expected utility of the gamble. This last example also indicates the justification underlying insurance policies. The difference between the utility of the specified wealth and the expected utility of the gamble is proportional to the amount of “unfairness” we would accept in a lottery or with an insurance purchase.
This type of utility function implies that as present wealth decreases, there is a greater tendency to prefer gambles involving a large chance of small loss versus a small chance of large gain (the farthing football pools in England, for example, were patronized by the proletariat, not the plutocrats). Another implication is that a positive skewness of the frequency distribution of total gains and losses is desirable. That is, Figure 3-1 suggests that we tend to wager more conservatively when losing moderately and more liberally when winning moderately. The term “moderate” refers to that portion of the utility function between the two outer inflection points.
The Objective Utility Function
From the preceding arguments it is clear that the particular utility function determines the decision-making process. Further, this utility function is frequently subjective in nature, differing among individuals and according to present wealth. However, to develop a simple theory of gambling, we must postulate a specific utility function and derive the laws that pertain thereto. Therefore we adopt the objective model of utility, Figure 3-2, with the reservation that the theorems to be stated subsequently must be modified appropriately for subjective models of utility.
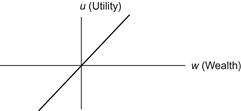
Figure 3-2 The objective utility function.
It has been opined that only misers and mathematicians truly adhere to objective utilities. For them, each and every dollar maintains a constant value regardless of how many other dollars can be summoned in mutual support. For those who are members of neither profession, we recommend the study of such behavior as a sound prelude to the intromission of a personal, subjective utility function.
The objective model assumes that the utility of wealth is linear with wealth and that decision making is independent of nonprobabilistic considerations. It should also be noted that in subjective models, the utility function does not depend on long-run effects; it is completely valid for single-trial operations. The objective model, on the other hand, rests (at least implicitly) on the results of an arbitrarily large number of repetitions of an experiment.
Finally, it must be appreciated that, within the definition of an objective model, there are several goals available to the gambler. he may wish to play indefinitely, gamble over a certain number of plays, or gamble until he has won or lost specified amounts of wealth. In general, the gambler’s aim is not simply to increase wealth (a certainty of $1 million loses its attraction if a million years are required). Wealth per unit time or per unit play (income) is a better aim, but there are additional constraints. The gambler may well wish to maximize the expected wealth received per unit play, subject to a fixed probability of losing some specified sum. Or he may wish with a certain confidence level to reach a specified level of wealth. His goal dictates the amount to be risked and the degree of risk. These variations lie within the objective model for utility functions.
Prospect Theory
Developed by cognitive psychologists Daniel Kahneman2 and Amos Tversky (Ref.), prospect theory describes the means by which individuals evaluate gains and losses in psychological reality, as opposed to the von Neumann-Morgenstern rational model that prescribes decision making under uncertainty conditions (descriptive versus prescriptive approaches). Thus Prospect Theory encompasses anomalies outside of conventional economic theory (sometimes designated as “irrational” behavior).
First, choices are ordered according to a particular heuristic. Thence (subjective) values are assigned to gains and losses rather than to final assets. The value function, defined by deviations from a reference point, is normally concave for gains (“risk aversion”), convex for losses (“risk seeking”), and steeper for losses than for gains (“loss aversion”), as illustrated in Figure 3-3.
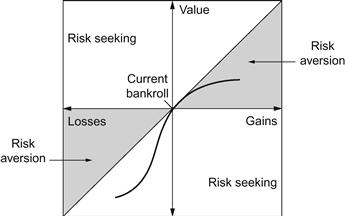
Figure 3-3 A Prospect Theory value function.
Four major principles underlie much of Prospect Theory:
 People are inherently (and irrationally) less inclined to gamble with profits than with a bankroll reduced by losses.
People are inherently (and irrationally) less inclined to gamble with profits than with a bankroll reduced by losses.
 If a proposition is framed to emphasize possible gains, people are more likely to accept it; the identical proposition framed to emphasize possible losses is more likely to be rejected.
If a proposition is framed to emphasize possible gains, people are more likely to accept it; the identical proposition framed to emphasize possible losses is more likely to be rejected.
 A substantial majority of the population would prefer $5000 to a gamble that returns either $10,000 with 0.6 probability or zero with 0.4 probability (an expected value of $6000).
A substantial majority of the population would prefer $5000 to a gamble that returns either $10,000 with 0.6 probability or zero with 0.4 probability (an expected value of $6000).
 Loss-aversion/risk-seeking behavior: In a choice between a certain loss of $4000 as opposed to a 0.05 probability of losing $100,000 combined with a 0.95 probability of losing nothing (an expected loss of $5000), another significant majority would prefer the second option.
Loss-aversion/risk-seeking behavior: In a choice between a certain loss of $4000 as opposed to a 0.05 probability of losing $100,000 combined with a 0.95 probability of losing nothing (an expected loss of $5000), another significant majority would prefer the second option.
One drawback of the original theory is due to its acceptance of intransitivity in its ordering of preferences. An updated version, Cumulative Prospect Theory, overcomes this problem by the introduction of a probability weighting function derived from rank-dependent expected Utility Theory.
Prospect Theory in recent years has acquired stature as a widely quoted and solidly structured building block of economic psychology.
Decision-Making Criteria
Since gambling involves decision making, it is necessary to inquire as to the “best” decision-making procedure. Again, there are differing approaches to the definition of best. For example, the Bayesian solution for the best decision proposes minimization with respect to average risk. The Bayes principle states that if the unknown parameter θ is a random variable distributed according to a known probability distribution f, and if FΔ(θ) denotes the risk function of the decision procedure Δ, we wish to minimize with respect to Δ the average risk
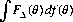
We could also minimize the average risk with respect to some assumed a priori distribution suggested by previous experience. This latter method, known as the restricted Bayes solution, is applicable in connection with decision processes wherein maximum risk does not exceed minimum risk by more than a specified amount. A serious objection to the use of the restricted Bayesian principle for gambling problems lies in its dependence on subjective probability assignments. Whenever possible, we wish to avoid subjective weightings.
Another method of obtaining a best decision follows the principle of “mini-mization of regret.” As proposed by Leonard Savage (Ref. 1951), this procedure is designed for the player who desires to minimize the difference between the payoff actually achieved by a given strategy and the payoff that could have been achieved if the opponent’s intentions were known in advance and the most effective strategy adopted. An obvious appeal is offered to the businessman whose motivation is to minimize the possible disappointment deriving from an economic transaction. The regret matrix is formed from the conventional payoff matrix by replacing each payoff aij with the difference between the column maximum and the payoff—that is, with 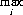 (aij) − aij. For example, consider the payoff matrix,
(aij) − aij. For example, consider the payoff matrix,
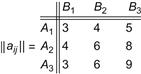
which possesses a saddle point at (A2, B1) and a game value of 4 to player A under the minimax criterion. The regret matrix engendered by these payoffs is
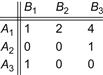
While there now exists no saddle point defined by two pure strategies, we can readily solve the matrix (observe that we are concerned with row maxima and column minima since A wishes to minimize the regret) to obtain the mixed strategies (0, 1/4, 3/4) for A and (3/4, 0, 1/4) for his opponent B. The “regret value” to A is 3/4; the actual profit to A is
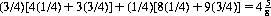
compared to a profit of 4 from application of the minimax principle.
Chernoff (Ref.) has pointed out the several drawbacks of the “minimization of regret” principle. First, the “regret” is not necessarily proportional to losses in utility. Second, there can arise instances whereby an arbitrarily small advantage in one state of nature outweighs a sizable advantage in another state. Third, it is possible that the presence of an undesirable strategy might influence the selection of the best strategy.
Other criteria include the Hurwicz pessimism–optimism index (Ref.), which emphasizes a weighted combination of the minimum and maximum utility numbers, and the “principle of insufficient reason,” credited to Jacob Bernoulli. This latter criterion assigns equal probabilities to all possible strategies of an opponent if no a priori knowledge is given. Such sophistry leads to patently nonsensical results.
The objective model of utility invites an objective definition of best. To the greatest degree possible, we can achieve objectivity by adopting the minimax principle—that is, minimization with respect to maximum risk. We wish to minimize the decision procedure Δ with respect to the maximum risk sup θ FΔ(θ)—or, in terms of the discrete theory outlined in Chapter 2, 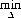
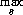 FΔ(θ).
FΔ(θ).
The chief criticism of the minimax (or maximin) criterion is that, in concentrating on the worst outcome, it tends to be overly conservative. In the case of an intelligent opponent, the conservatism may be well founded, since a directly conflicting interest is assumed. With “nature” as the opposition, it seems unlikely that the resolution of events exhibits such a diabolical character. This point can be illustrated (following Luce and Raiffa, Ref.) by considering the matrix
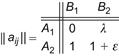
Let λ be some number arbitrarily large and ε some positive number arbitrarily small. The minimax principle asserts that a saddle point exists at (A2, B1). While an intelligent adversary would always select strategy B1, nature might not be so inconsiderate, and A consequently would be foolish not to attempt strategy A1 occasionally with the possibility of reaping the high profit λ.
Although this fault of the minimax principle can entail serious consequences, it is unlikely to intrude in the great preponderance of gambling situations, where the opponent is either a skilled adversary or one (such as nature) whose behavior is known statistically. In the exceptional instance, for lack of a universally applicable criterion, we stand accused of conservatism. Accordingly, we incorporate the minimax principle as one of the pillars of gambling theory.
The Basic Theorems
With an understanding of utility and the decision-making process, we are in a position to establish the theorems that constitute a comprehensive theory of gambling. While the theorems proposed are, in a sense, arbitrary, they are intended to be necessary and sufficient to encompass all possible courses of action arising from decision making under risk conditions. Ten theorems with associated corollaries are stated.3 The restrictions to be noted are that our theorems are valid only for phenomena whose statistics constitute a stationary time series and whose game-theoretic formulations are expressible as zero-sum games. Unless otherwise indicated, each theorem assumes that the sequence of plays constitutes successive independent events.
Theorem I: If a gambler risks a finite capital over a large number of plays in a game with constant single-trial probabilities of winning, losing, and tying, then any and all betting systems lead ultimately to the same mathematical expectation of gain per unit amount wagered.
A betting system is defined as some variation in the magnitude of the wager as a function of the outcome of previous plays. At the ith play of the game, the player wagers βi units, winning the sum kβi with probability p (where k is the payoff odds), losing βi with probability q, and tying with probability 1 − p − q.
It follows that a favorable (unfavorable) game remains favorable (unfavorable) and an equitable game (pk = q) remains equitable regardless of the variations in bets. It should be emphasized, however, that such parameters as game duration and the probability of success in achieving a specified increase in wealth subject to a specified probability of loss are distinct functions of the betting systems; these relations are considered shortly.
The number of “guaranteed” betting systems, the proliferation of myths and fallacies concerning such systems, and the countless people believing, propagating, venerating, protecting, and swearing by such systems are legion. Betting systems constitute one of the oldest delusions of gambling history. Betting-system votaries are spiritually akin to the proponents of perpetual-motion machines, butting their heads against the second law of thermodynamics.
The philosophic rationale of betting systems is usually entwined with the concepts of primitive justice—particularly the principle of retribution (lex talionis), which embodies the notion of balance. Accordingly, the universe is governed by an eminently equitable god of symmetry (the “great CPA in the sky”) who ensures that for every Head there is a Tail. Confirmation of this idea is often distilled by a process of wishful thinking dignified by philosophic (or metaphysical) cant. The French philosopher Pierre-Hyacinthe Azaïs (1766–1845) formalized the statement that good and evil fortune are exactly balanced in that they produce for each person an equivalent result. Better known are such notions as Hegelian compensation, Marxian dialectics, and the Emersonian pronouncements on the divine or scriptural origin of earthly compensation. With less formal expression, the notion of Head–Tail balance extends back at least to the ancient Chinese doctrine of Yin-Yang polarity.
“Systems” generally can be categorized into multiplicative, additive, or linear betting prescriptions. Each system is predicated on wagering a sum of money determined by the outcomes of the previous plays, thereby ignoring the implication of independence between plays. The sum βi is bet on the ith play in a sequence of losses. In multiplicative systems,
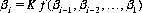
where K is a constant ≥ 1 and plays i − 1, i − 2, …, 1 are immediately preceding (generally, if play i − 1 results in a win, βi reverts to β1).
Undoubtedly, the most popular of all systems is the “Martingale”4 or “doubling” or “geometric progression” procedure. Each stake is specified only by the previous one. In the event of a loss on the i − 1 play, β1 = 2βi−1. A win on the i − 1 play calls for βi = β1. (With equal validity or equal misguided intent, we could select any value for K and any function of the preceding results.)
To illustrate the hazards of engaging the Martingale system with a limited bankroll, we posit an equitable game (p = q = 1/2) with an initial bankroll of 1000 units and an initial wager of one unit, where the game ends either after 1000 plays—or earlier if the player’s funds become insufficient to wager on the next play. We wish to determine the probability that the player achieves a net gain—a final bankroll exceeding 1000 units.
Consider an R × C matrix whose row numbers, R = 0 to 10, represent the possible lengths of the losing sequence at a particular time, and whose column numbers, C = 0 to 2000, represent the possible magnitude of the player’s current bankroll, BC. That is, each cell of the matrix, P(R, C), denotes the probability of a specified combination of losing sequence and corresponding bankroll. Matrices after each play are (computer) evaluated (Ref. Cesare and Widmer) under the following criteria: if C < 2R, then BC is insufficient for the next prescribed wager, and the probability recorded in P(R, C) is transferred to the probability of being bankrupt, PB; otherwise, 1/2 the probability record-ed in P(R, C) is transferred to P(R + 1, C − 2R) and the remaining 1/2 to P(0, C + 2R), since p = q = 1/2 for the next play.
The results for BF, the final bankroll, indicate that
It is perhaps surprising that with a bankroll 1000 times that of the individual wager, the player is afforded only a 0.6 probability of profit after 1000 plays. Under general casino play, with p < q, this probability, of course, declines yet further.
Another multiplicative system aims at winning n units in n plays—with an initial bet of one unit. Here, the gambler wagers 2n − 1 units at the nth play. Thus every sequence of n − 1 losses followed by a win will net n units:
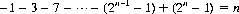
In general, if the payoff for each individual trial is at odds of k to 1, the sequence of wagers ending with a net gain of n units for n plays is
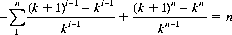
Thenth win recovers all previous n − 1 losses and nets n units.
Additive systems are characterized by functions that increase the stake by some specific amount (which may change with each play). A popular additive system is the “Labouchère5 or “cancellation,” procedure. A sequence of numbers a1, a2, …, an is established, the stake being the sum of a1 and an. For a win, the numbers a1 and an are removed from the sequence and the sum a2 + an−1 is wagered; for a loss, the sum a1 + an constitutes the an+ 1 term in a new sequence and a1 + an+ 1 forms the subsequent wager. Since the additive constant is the first term in the sequence, the increase in wagers occurs at an arithmetic rate. A common implementation of this system begins with the sequence 1, 2, 3—equivalent to a random walk with one barrier at +6 and another at −C, the gambler’s capital.
In a fair game, to achieve a success probability Ps equal to 0.99 of winning the six units requires a capital:
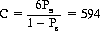
On the other hand, to obtain a 0.99 probability of winning the gambler’s capital of 594, the House requires a capital of 6 m, where
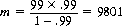
and 6 m = 58,806. Of course, the House can raise its winning probability as close to certainty as desired with sufficiently large m. For the gambler to bankrupt the House (i.e., win 58,806), he must win 9801 consecutive sequences.
Note that g gamblers competing against the House risk an aggregate of 594 g, whereas the House risks only 6 g. For unfavorable games, this imbalance is amplified, and the probability of the House winning approaches unity.
Linear betting systems involve a fixed additive constant. A well-known linear system, the “d’Alembert” or “simple progression” procedure, is defined by
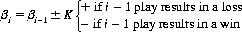
It is obviously possible to invent other classes of systems. We might create an exponential system wherein each previous loss is squared, cubed, or, in general, raised to the nth power to determine the succeeding stake. For those transcendentally inclined, we might create a system that relates wagers by trigonometric functions. We could also invert the systems described here. The “anti-Martingale” (or “Paroli”) system doubles the previous wager after a win and reverts to β1 following a loss. The “anti-Labouchère” system adds a term to the sequence following a win and decreases the sequence by two terms after a loss, trying to lose six (effecting a high probability of a small loss and a small probability of a large gain). The “anti-d’Alembert” system employs the addition or subtraction of K according to a preceding win or loss, respectively.
Yet other systems can be designed to profit from the existence of imagined or undetermined biases. For example, in an even-bet Head–Tail sequence, the procedure of wagering on a repetition of the immediately preceding outcome of the sequence would be advantageous in the event of a constant bias; we dub this procedure the Epaminondas system in honor of the small boy (not the Theban general) who always did the right thing for the previous situation. The “quasi-Epaminondas” system advises a bet on the majority outcome of the preceding three trials of the sequence. Only the bounds of our imagination limit the number of systems we might conceive. No one of them can affect the mathematical expectation of the game when successive plays are mutually independent.
The various systems do, however, affect the expected duration of play. A system that rapidly increases each wager from the previous one will change the pertinent fortune (bankroll) at a greater rate; that fortune will thereby fall to zero or reach a specified higher level more quickly than through a system that dictates a slower increase in wagers. The probability of successfully increasing the fortune to a specified level is also altered by the betting system for a given single-trial probability of success.
A multiplicative system, wherein the wager rises rapidly with increasing losses, offers a high probability of small gain with a small probability of large loss. The Martingale system, for example, used with an expendable fortune of 2n units, recovers all previous losses and nets a profit of 1 unit—insofar as the number of consecutive losses does not exceed n − 1. Additive systems place more restrictions on the resulting sequence of wins and losses, but risk correspondingly less capital. The Labouchère system concludes a betting sequence whenever the number of wins equals one-half the number of losses plus one-half the number of terms in the original sequence. At that time, the gambler has increased his fortune by 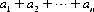 units. Similarly, a linear betting system requires near equality between the number of wins and losses, but risks less in large wagers to recover early losses. In the d’Alembert system, for 2n plays involving n wins and n losses in any order, the gambler increases his fortune by K/2 units. Exactly contrary results are achieved for each of the “anti” systems mentioned (the anti-d’Alembert system decreases the gambler’s fortune by K/2 units after n wins and n losses).
units. Similarly, a linear betting system requires near equality between the number of wins and losses, but risks less in large wagers to recover early losses. In the d’Alembert system, for 2n plays involving n wins and n losses in any order, the gambler increases his fortune by K/2 units. Exactly contrary results are achieved for each of the “anti” systems mentioned (the anti-d’Alembert system decreases the gambler’s fortune by K/2 units after n wins and n losses).
In general, for a game with single-trial probability of success p, a positive system offers a probability p′ > p of winning a specified amount at the conclusion of each sequence while risking a probability 1 − p′ of losing a sum larger than β1 n, where β1 is the initial bet in a sequence and n is the number of plays of the sequence. A negative system provides a smaller probability p′ < p of losing a specified amount over each betting sequence but contributes insurance against a large loss; over n plays the loss is always less than β1 n. The “anti” systems described here are negative. Logarithmic (βi = log βi−1 if the i − 1 play results in a loss) or fractional [βi = (βi−1)/K if the i − 1 play is a loss] betting systems are typical of the negative variety.For the fractional system, the gambler’s fortune X2 n after 2n plays of n wins and n losses in any order is
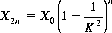
The gambler’s fortune is reduced, but the insurance premium against large losses has been paid. Positive systems are inhibited by the extent of the gambler’s initial fortune and the limitations imposed on the magnitude of each wager. Negative systems have questionable worth in a gambling context but are generally preferred by insurance companies. Neither type of system, of course, can budge the mathematical expectation from its fixed and immutable value.
Yet another type of system involves wagering only on selected members of a sequence of plays (again, our treatment is limited to mutually independent events). The decision to bet or not to bet on the outcome of the nth trial is determined as a function of the preceding trials. Illustratively, we might bet only on odd-numbered trials, on prime-numbered trials, or on those trials immediately preceded by a sequence of ten “would have been” losses. To describe this situation, we formulate the following theorem.
Theorem II: No advantage accrues from the process of betting only on some subsequence of a number of independent repeated trials forming an extended sequence.
This statement in mathematical form is best couched in terms of measure theory. We establish a sequence of functions Δ1, Δ2(ζ1), Δ3(ζ1, ζ2), …, where Δi assumes a value of either one or zero, depending only on the outcomes ζ1, ζ2, …, ζi−1 of the i − 1 previous trials. Let ω:(ζ1, ζ2, …) be a point of the infinite-dimensional Cartesian space Ω∞ (allowing for an infinite number of trials); let F(n, ω) be the nth value of i for which Δi = 1; and let ζ′n = ζF. Then (ζ′1, ζ′2, …) is the subsequence of trials on which the gambler wagers. It can be shown that the probability relations valid for the space of points (ζ′1, ζ′2, …) are equivalent to those pertaining to the points (ζ′1, ζ′2, …) and that the gambler therefore cannot distinguish between the subsequence and the complete sequence.
Of the system philosophies that ignore the precept of Theorem II the most prevalent and fallacious is “maturity of the chances.” According to this doctrine, we wager on the nth trial of a sequence only if the preceding n − 1 trials have produced a result opposite to that which we desire as the outcome of the nth trial. In Roulette, we would be advised, then, to await a sequence of nine consecutive “reds,” say, before betting on “black.” Presumably, this concept arose from a misunderstanding of the law of large numbers (Eq. 2-25). Its effect is to assign a memory to a phenomenon that, by definition, exhibits no correlation between events.
One final aspect of disingenuous betting systems remains to be mentioned. It is expressible in the following form.
Corollary: No advantage in terms of mathematical expectation accrues to the gambler who may exercise the option of discontinuing the game after each play.6
The question of whether an advantage exists with this option was first raised by John Venn, the English logician, who postulated a coin-tossing game between opponents A and B; the game is equitable except that only A is permitted to stop or continue the game after each play. Since Venn’s logic granted infinite credit to each player, he concluded that A indeed has an advantage. Lord Rayleigh subsequently pointed out that the situation of finite fortunes alters the conclusion, so that no advantage exists.
Having established that no class of betting system can alter the mathematical expectation of a game, we proceed to determine the expectation and variance of a series of plays. The definition of each play is that there exists a probability p that the gambler’s fortune is increased by α units, a probability q that the fortune is decreased by β units (α ≡ kβ), and a probability r = 1 − p − q that no change in the fortune occurs (a “tie”). The bet at each play, then, is β units of wealth.
Theorem III: For n plays of the general game, the mean or mathematical expectation is n(αp − βq), and the variance is n[α2 p + β2 q − (αp − βq)2].
This expression for the mathematical expectation leads directly to the definition of a fair or equitable game. It is self-evident that the condition for no inherent advantage to any player is that
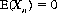
For the general case, a fair game signifies
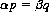
To complete the definition we can refer to all games wherein E(Xn) > 0 (i.e., αp > βq) as positive games; similarly, negative games are described by E(Xn) < 0 (or αp<βq).
Comparing the expectation and the variance of the general game, we note that as the expectation deviates from zero, the variance decreases and approaches zero as p or q approaches unity. Conversely, the variance is maximal for a fair game. It is the resulting fluctuations that may cause a gambler to lose a small capital even though his mathematical expectation is positive. The variance of a game is one of our principal concerns in deciding whether and how to play. For example, a game that offers a positive single-play mathematical expectation may or may not have strong appeal, depending on the variance as well as on other factors such as the game’s utility. A game characterized by p = 0.505, q = 0.495, r = 0, α = β = 1, has a single-play expectation of E(X) = 0.01. We might be interested in this game, contingent upon our circumstances. A game characterized by p = 0.01, q = 0, r = 0.99, α = β = 1, also exhibits an expectation of 0.01. However, our interest in this latter game is not casual but irresistible. We should hasten to mortgage our children and seagoing yacht to wager the maximum stake. The absence of negative fluctuations clearly has a profound effect on the gambler’s actions.
These considerations lead to the following two theorems, the first of which is known as “the gambler’s ruin.” (The ruin probability and the number of plays before ruin are classical problems that have been studied by James Bernoulli, de Moivre, Lagrange, and Laplace, among many.)
Theorem IV: In the general game (where a gambler bets β units at each play to win α units with single-trial probability p, lose β with probability q, or remain at the same financial level with probability r = 1 − p − q) begun by a gambler with capital z and continued until that capital either increases to α ≥ z + β or decreases to less than β (the ruin point), the probability of ruin Pz is bounded by
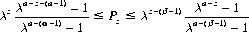
where λ is a root of the exponential equation 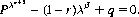 . For values of a and z large with respect to α and β, the bounds are extremely tight.
. For values of a and z large with respect to α and β, the bounds are extremely tight.
If the game is equitable—a mathematical expectation equal to zero—we can derive the bounds on Pz as
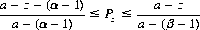 (3-1)
(3-1)
With the further simplification that α = β = 1, as is the case in many conventional games of chance, the probability of ruin reduces to the form
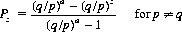 (3-2)
(3-2)
And the probability, 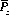 , of the gambler successfully increasing his capital from z to a is
, of the gambler successfully increasing his capital from z to a is
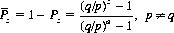 (3-3)
(3-3)
For a fair game, p = q, and we invoke l’Hospital’s rule to resolve the concomitant indeterminate form of Eqs. 3-2 and 3-3:
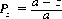
and
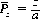 (3-4)
(3-4)
We can modify the ruin probability Pz to admit a third outcome for each trial, that of a tie (probability r). With this format,
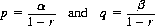
And Eq. 3-2 takes the form
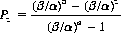
It is interesting to note the probabilities of ruin and success when the gambler ventures against an infinitely rich adversary. Letting α → ∞ in the fair game represented by Eq. 3-1, we again observe that Pz→ 1. Therefore, whenever αp ≤ βq, the gambler must eventually lose his fortune z. However, in a favorable game as (a − z) → ∞, λ < 1, and the probability of ruin approaches
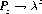
With the simplification of α = β =1, Eq. 3-2 as α → ∞ becomes
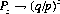
for p > q. Thus, in a favorable game, the gambler can continue playing indefinitely against an infinite bank and, with arbitrarily large capital z, can render his probability of ruin as close to zero as desired. We can conclude that with large initial capital, a high probability exists of winning a small amount even in games that are slightly unfavorable; with smaller capital, a favorable game is required to obtain a high probability of winning an appreciable amount.
As an example, for p = 0.51 and q = 0.49, and betting 1 unit from a bankroll of 100 units, the ruin probability is reduced to 0.0183. Betting 1 unit from a bankroll of 1000 confers a ruin probability of 4.223 × 10−18.
Corollary: The expected duration Dz of the game is equivalent to the random-walk probability of reaching a particular position x for the first time at the nth step (Chapter 2, Random Walks). Specifically,
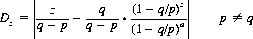 (3-5)
(3-5)
For p = q, Eq. 3-5 becomes indeterminate as before—and is resolved in this case by replacing z/(q − p) with z2, which leads to
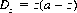
Illustratively, two players with bankrolls of 100 units each tossing a fair coin for stakes of one unit can expect a duration of 10,000 tosses before either is ruined. If the game incorporates a probability r of tying, the expected duration is lengthened to
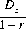
Against the infinitely rich adversary, an equitable game affords the gambler an infinite expected duration (somewhat surprisingly). For a parallel situation, see Chapter 5 for coin tossing with the number of Heads equal to the number of Tails; see also Chapter 2 for unrestricted symmetric random walks, where the time until return-to-zero position has infinite expectation.
These considerations lead directly to formulation of the following theorem.
Theorem V: A gambler with initial fortune z, playing a game with the fixed objective of increasing his fortune by the amount a − z, has an expected gain that is a function of his probability of ruin (or success). Moreover, the probability of ruin is a function of the betting system. For equitable or unfair games, a “maximum boldness” strategy is optimal—that is, the gambler should wager the maximum amount consistent with his objective and current fortune. For favorable games, a “minimal boldness” or “prudence” strategy is optimal—the gambler should wager the minimum sum permitted under the game rules.
The maximum-boldness strategy dictates a bet of z when z ≤ a/(k + 1) and (a − z)/k when z > a/(k + 1). For k = 1 (an even bet), maximum boldness coincides with the Martingale, or doubling, system. (Caveat: If a limit is placed on the number of plays allowed the gambler, maximum boldness is not then necessarily optimal.) For equitable games, the stakes or variations thereof are immaterial; the probability of success (winning the capital a − z) is then simply the ratio of the initial bankroll to the specified goal, as per Eq. 3-4.
Maximizing the probability of success in attaining a specified increase in capital without regard to the number of plays, as in the preceding theorem, is but one of many criteria. It is also feasible to specify the desired increase a − z and determine the betting strategy that minimizes the number of plays required to gain this amount. Another criterion is to specify the number of plays n and maximize the magnitude of the gambler’s fortune after the n plays. Yet another is to maximize the rate of increase in the gambler’s capital. In general, any function of the gambler’s fortune, the desired increase therein, the number of plays, etc. can be established as a criterion and maximized or minimized to achieve a particular goal.
In favorable games (p > q), following the criterion proposed by John L. Kelly (Ref.) leads in the long run to an increase in capital greater than that achievable through any other criterion. The Kelly betting system entails maximization of the exponential rate of growth G of the gambler’s capital, G being defined by
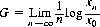
where x0 is initial fortune and xn the fortune after n plays.
If the gambler bets a fraction f of his capital at each play, then xn has the value
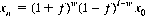
for w wins and l losses in the n wagers. The exponential rate of growth is therefore
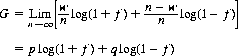
where the logarithms are defined here with base 2. Maximizing G with respect to f, it can be shown that
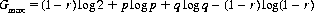
which, for r = 0 (no ties), reduces to 1 + p log p + q log q, the Shannon rate of transmission of information over a noisy communication channel.
For positive-expectation bets at even odds, the Kelly recipe calls for a wager equal to the mathematical expectation. A popular alternative consists of wagering one-half this amount, which yields 3/4 the return with substantially less volatility. (For example, where capital accumulates at 10% compounded with full bets, half-bets still yield 7.5%.)
In games that entail odds of k to 1 for each individual trial with a win probability Pw, the Kelly criterion prescribes a bet of
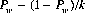
Illustratively, for k equals 3 to 1 and a single-trial probability Pw = 0.28, the Kelly wager is 0.28 − 0.72/3 = 4% of current capital.
Breiman (Ref.) has shown that Kelly’s system is asymptotically optimal under two criteria: (1) minimal expected time to achieve a fixed level of resources and (2) maximal rate of increase of wealth.
Contrary to the types of systems discussed in connection with Theorem I, Kelly’s fractional (or logarithmic or proportional) gambling system is not a function of previous history. Generally, a betting system for which each wager depends only on present resources and present probability of success is known as a Markov betting system (the sequence of values of the gambler’s fortune form a Markov process). It is heuristically evident that, for all sensible criteria and utilities, a gambler can restrict himself to Markov betting systems.
While Kelly’s system is particularly interesting (as an example of the rate of transmission of information formula applied to uncoded messages), it implies an infinite divisibility of the gambler’s fortune—impractical by virtue of a lower limit imposed on the minimum bet in realistic situations. There also exists a limit on the maximum bet, thus further inhibiting the logarithmic gambler. Also, allowable wagers are necessarily quantized.
We can observe that fractional betting constitutes a negative system (see the discussion following Theorem I).
Disregarding its qualified viability, a fractional betting system offers a unity probability of eventually achieving any specified increase in capital. Its disadvantage (and the drawback of any system that dictates an increase in the wager following a win and a decrease following a loss) is that any sequence of n wins and n losses in a fair game results in a bankroll B reduced to
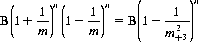
when the gambler stakes 1/m of his bankroll at each play.
When the actual number of wins is approximately the expected number, proportional betting yields about half the arithmetic expectation. However, when the actual number of wins is only half the expectation, proportional betting yields a zero return. Thus the Kelly criterion acts as insurance against bankruptcy—and, as with most insurance policies, exacts a premium.
For favorable games replicated indefinitely against an infinitely rich adversary, a better criterion is to optimize the “return on investment”—that is, the net gain per unit time divided by the total capital required to undertake the betting process. In this circumstance we would increase the individual wager β(t) as our bankroll z(t) increased, maintaining a constant return on investment, R, according to the definition
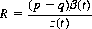
A more realistic procedure for favorable games is to establish a confidence level in achieving a certain gain in capital and then inquire as to what magnitude wager results in that confidence level for the particular value of p > q. This question is answered as follows.
Theorem VI: In games favorable to the gambler, there exists a wager β defined by
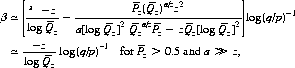 (3-6)
(3-6)
such that continually betting β units or less at each play yields a confidence level of 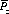 or greater of increasing the gambler’s fortune from an initial value z to a final value a. (Here,
or greater of increasing the gambler’s fortune from an initial value z to a final value a. (Here, 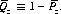 )
)
Figure 3-4 illustrates Eq. 3-6 for z = 100, a = 1000, and four values of the confidence level 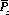 . For a given confidence in achieving a fortune of 1000 units, higher bets cannot be hazarded until the game is quite favorable. A game characterized by (q/p) = 0.64 (p = 0.61, q = 0.39, r = 0), for example, is required before ten units of the 100 initial fortune can be wagered under a 0.99 confidence of attaining 1000. Note that for a
. For a given confidence in achieving a fortune of 1000 units, higher bets cannot be hazarded until the game is quite favorable. A game characterized by (q/p) = 0.64 (p = 0.61, q = 0.39, r = 0), for example, is required before ten units of the 100 initial fortune can be wagered under a 0.99 confidence of attaining 1000. Note that for a 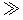 z, the optimal bets become virtually independent of the goal a. This feature, of course, is characteristic of favorable games.
z, the optimal bets become virtually independent of the goal a. This feature, of course, is characteristic of favorable games.
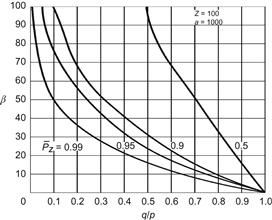
Figure 3-4 Optimal wager for a fixed confidence level.
Generally, with an objective utility function, the purpose of increasing the magnitude of the wagers in a favorable game (thereby decreasing the probability of success) is to decrease the number of plays required to achieve this goal.
We can also calculate the probability of ruin and success for a specific number of plays of a game:
Theorem VII: In the course of n resolved plays of a game, a gambler with capital z playing unit wagers against an opponent with capital a − z has a probability of ruin given by
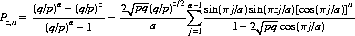 (3-7)
(3-7)
where p, and q are the gambler’s single-trial probabilities of winning, and losing, respectively.
As the number of plays n → ∞, the expression for Pz, n approaches the Pz of Eq. 3-2. Equation 3-7 is illustrated in Figure 3-5, which depicts Pz, n versus n for an initial gambler’s capital of z = 10, an adversary’s capital a − z = 10, and for several values of q/p.
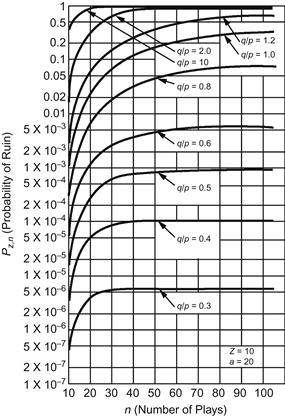
Figure 3-5 Ruin probability in the course of n plays.
An obvious extension of Theorem VII ensues from considering an adversary either infinitely rich or possessing a fortune such that n plays with unit wagers cannot lead to his ruin. This situation is stated as follows.
Corollary: In the course of n resolved plays of a game, a gambler with capital z, wagering unit bets against an (effectively) infinitely rich adversary, has a probability of ruin given by
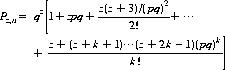 (3-8)
(3-8)
where 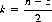 or
or 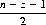 , as
, as  n − z
n − z is even or odd.
is even or odd.
Figure 3-6 illustrates Eq. 3-8 for z = 10 and p = q = 1/2. For a large number of plays of an equitable game against an infinitely rich adversary, we can derive the approximation
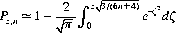 (3-9)
(3-9)
which is available in numerical form from tables of probability integrals. Equation 3-9 indicates, as expected, that the probability of ruin approaches unity asymptotically with increasing values of n.
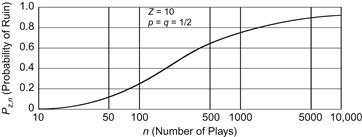
Figure 3-6 Ruin probability in the course of n plays of a “fair” game against an infinitely rich adversary.
Equations 3-8 and 3-7 are attributable to Lagrange. A somewhat simpler expression results if, instead of the probability of ruin over the course of n plays, we ask the expected number of plays E(n)z prior to the ruin of a gambler with initial capital z:
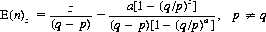 (3-10)
(3-10)
For equitable games, p = q, and this expected duration simplifies to
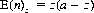
For example, a gambler with 100 units of capital wagering unit bets against an opponent with 1000 units can expect the game to last for 90,000 plays. Against an infinitely rich opponent, Eq. 3-10, as a → ∞, reduces to
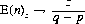
for p < q. In the case p > q, the expected game duration versus an infinity of Croesuses is a meaningless concept. For p = q, E(n)z→ ∞.
We have previously defined a favorable game as one wherein the single-trial probability of success p is greater than the single-trial probability of loss q. A game can also be favorable if it comprises an ensemble of subgames, one or more of which is favorable. Such an ensemble is termed a compound game. Pertinent rules require the player to wager a minimum of one unit on each subgame; further, the relative frequency of occurrence of each subgame is known to the player, and he is informed immediately in advance of the particular subgame about to be played (selected at random from the relevant probability distribution). Blackjack (Chapter 8) provides the most prevalent example of a compound game.
Clearly, given the option of bet-size variation, the player of a compound game can obtain any positive mathematical expectation desired. He has only to wager a sufficiently large sum on the favorable subgame(s) to overcome the negative expectations accruing from unit bets on the unfavorable subgames. However, such a policy may face a high probability of ruin. It is more reasonable to establish the criterion of minimizing the probability of ruin while achieving an overall positive expectation—i.e., a criterion of survival. A betting system in accord with this criterion is described by Theorem VIII.
Theorem VIII: In compound games there exists a critical single-trial probability of success p* > 1/2 such that the optimal wager for each subgame β*(p), under the criterion of survival, is specified by
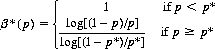 (3-11)
(3-11)
As a numerical illustration of this theorem, consider a compound game where two-thirds of the time the single-trial probability of success takes a value of 0.45 and the remaining one-third of the time a value of 0.55. Equation 3-11 prescribes the optimal wagers for this compound game as
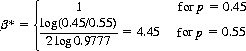
Thus the gambler who follows this betting prescription achieves an overall expectation of
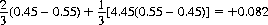
while maximizing his probability of survival (it is assumed that the gambler initially possesses a large but finite capital pitted against essentially infinite resources).
Much of the preceding discussion in this chapter has been devoted to proving that no betting system constructed on past history can affect the expected gain of a game with independent trials. With certain goals and utilities, it is more important to optimize probability of success, number of plays, or some other pertinent factor. However, objective utilities focus strictly on the game’s mathematical expectation. Two parameters in particular relate directly to mathematical expectation: strategy and information. Their relationship is a consequence of the fundamental theorem of game theory, the von Neumann minimax principle (explicated in Chapter 2), which can be stated as follows.
Theorem IX: For any two-person rectangular game characterized by the payoff matrix 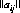 , where A has m strategies A1, A2, …, Am selected with probabilities p1, p2, …, pm, respectively, and B has n strategies B1, B2, …, Bn selected with probabilities q1,q2, …, qn, respectively (∑pi = ∑qj = 1), the mathematical expectation E[SA(m),SB(n)] for any strategies SA(m) and SB(n) is defined by
, where A has m strategies A1, A2, …, Am selected with probabilities p1, p2, …, pm, respectively, and B has n strategies B1, B2, …, Bn selected with probabilities q1,q2, …, qn, respectively (∑pi = ∑qj = 1), the mathematical expectation E[SA(m),SB(n)] for any strategies SA(m) and SB(n) is defined by
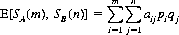
Then, if the m × n game has a value γ, a necessary and sufficient condition that SA*(m) be an optimal strategy for A is that
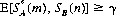
for all possible strategies SB(n). Similarly, a necessary and sufficient condition that SB*(n) be an optimal strategy for B is that
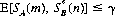
Some of the properties of two-person rectangular games are detailed in Chapter 2. If it is our objective to minimize our maximum loss or maximize our minimum gain; the von Neumann minimax theorem and its associated corollaries enable us to determine optimal strategies for any game of this type.
Further considerations arise from the introduction of information into the game format since the nature and amount of information available to each player can affect the mathematical expectation of the game. In Chess, Checkers, or Shogi, for example, complete information is axiomatic; each player is fully aware of his opponent’s moves. In Bridge, the composition of each hand is information withheld, to be disclosed gradually, first by imperfect communication and then by sequential exposure of the cards. In Poker, concealing certain components of each hand is critical to the outcome. We shall relate, at least qualitatively, the general relationship between information and expectation.
In the coin-matching game matrix of Figure 2-2, wherein each player selects Heads or Tails with probability p = 1/2, the mathematical expectation of the game is obviously zero. But now consider the situation where A has in his employ a spy capable of ferreting out the selected strategies of B and communicating them back to A. If the spy is imperfect in applying his espionage techniques or the communication channel is susceptible to error, A has only a probabilistic knowledge of B’s strategy. Specifically, if p is the degree of knowledge, the game matrix is that shown in Figure 3-7, where (i, j) represents the strategy of A that selects i when A is informed that B’s choice is H (Heads) and j when A is informed that B has selected T (Tails). For p > 1/2, strategy A2 dominates the others; selecting A2 consistently yields an expectation for A of
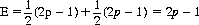
With perfect spying, p = 1, and A’s expectation is unity at each play; with p = 1/2, spying provides no intelligence, and the expectation is, of course, zero.

Figure 3-7 Coin-matching payoff with spying.
If, in this example, B also has recourse to undercover sleuthing, the game outcome is evidently more difficult to specify. However, if A has evidence that B intends to deviate from his optimal strategy, there may exist counterstrategies that exploit such deviation more advantageously than A’s maximin strategy. Such a strategy, by definition, is constrained to yield a smaller payoff against B’s optimal strategy. Hence A risks the chance that B does not deviate appreciably from optimality. Further, B may have the option of providing false information or “bluffing” and may attempt to lure A into selecting a nonoptimal strategy by such means. We have thus encountered a circulus in probando.
It is not always possible to establish a precise quantitative relationship between the information available to one player and the concomitant effect on his expectation. We can, however, state the following qualitative theorem.
Theorem X: In games involving partnership communication, one objective is to transmit as much information as possible over the permissible communication channel of limited capacity. Without constraints on the message-set, this state of maximum information occurs under a condition of minimum redundancy and maximum information entropy.
Proofs of this theorem are given in many texts on communication theory.7 The condition of maximum information entropy holds when, from a set of n possible messages, each message is selected with probability 1/n. Although no conventional game consists solely of communication, there are some instances (Ref. Isaacs), where communication constitutes the prime ingredient and the principle of this theorem is invoked. In games such as Bridge, communication occurs under the superintendence of constraints and cost functions. In this case, minimum redundancy or maximum entropy transpires if every permissible bid has equal probability. However, skewed weighting is obviously indicated, since certain bids are assigned greater values, and an ordering to the sequence of bids is also imposed.
Additional Theorems
While it is possible to enumerate more theorems than the ten advanced herein, such additional theorems do not warrant the status accruing from a fundamental character or extensive application in gambling situations. As individual examples requiring specialized game-theoretic tenets arise in subsequent chapters, they will be either proved or assumed as axiomatic.
For example, a “theorem of deception” might encompass principles of misdirection. A player at Draw Poker might draw two cards rather than three to an original holding of a single pair in order to imply a better holding or to avoid the adoption of a pure strategy (thereby posing only trivial analysis to his opponents). A bid in the Bridge auction might be designed (in part) to minimize the usefulness of its information to the opponents and/or to mislead them.
There are also theorems reflecting a general nature, although not of sufficient importance to demand rigorous proof. Illustrative of this category is the “theorem of pooled resources”:
If g contending players compete (against the House) in one or more concurrent games, with the ith player backed by an initial bankroll zi (i = 1, 2, …, g), and if the total resources are pooled in a fund available to all, then each player possesses an effective initial bankroll zeff given by
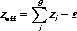 (3-12)
(3-12)
under the assumption that the win–loss–tie sequences of players i and j are uncorrelated.
The small quantity ε is the quantization error—that is, with uncorrelated outcomes for the players, the g different wagers can be considered as occurring sequentially in time, with the proviso that each initial bankroll zi can be replenished only once every gth play. This time restriction on withdrawing funds from the pool is a quantization error, preventing full access to the total resources. As the correlation between the players’ outcomes increases to unity, the value of zeff approaches 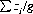 .
.
Another theorem, “the principle of rebates,” provides a little-known but highly useful function, the Reddere integral,8 E(c), which represents the expected excess over the standard random variable (the area under the standard normal curve from 0 to c):
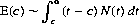
where N(t) is the pdf for the standard normal distribution. E(c) can be rewritten in the form
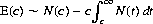
which is more convenient for numerical evaluation. (This integral is equivalent to 1 minus the cumulative distribution function [cdf] of c.) According to the rebate theorem, when the “standard score” (the gambler’s expectation after n plays of an unfavorable game divided by 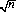 ) has a Reddere-integral value equal to itself, that value, Re, represents the number for which the player’s break-even position after n plays is Re standard deviations above his expected loss.
) has a Reddere-integral value equal to itself, that value, Re, represents the number for which the player’s break-even position after n plays is Re standard deviations above his expected loss.
The Reddere integral is evaluated in Appendix Table A for values of t from 0 to 3.00. Applicable when the gambler is offered a rebate of his potential losses, examples for Roulette and Craps are detailed in Chapters 5 and 6, respectively.
Finally, while there are game-theoretic principles other than those considered here, they arise—for the most part—from games not feasible as practical gambling contests. Games with infinite strategies, games allowing variable coalitions, generalized n-person games, and the like, are beyond our scope and are rarely of concrete interest.
In summation, the preceding ten theorems and associated expositions have established a rudimentary outline for the theory of gambling. A definitive theory depends, first and foremost, on utility goals—that is, upon certain restricted forms of subjective preference. Within the model of strictly objective goals, we have shown that no betting system can alter the mathematical expectation of a game; however, probability of ruin (or success) and expected duration of a game are functions of the betting system employed. We have, when apposite, assumed that the plays of a game are statistically independent and that no bias exists in the game mechanism. It follows that a time-dependent bias permits application of a valid betting system, and any bias (fixed or varying) enables an improved strategy.
Statistical dependence between plays also suggests the derivation of a corresponding betting system to increase the mathematical expectation. In Chapter 7we outline the theory of Markov chains, which relates statistical dependence and prediction.
Prima facie validation of the concepts presented here is certified by every gambling establishment in the world. Since the “House” is engaged in favorable games (with the rarest of exceptions), it wishes to exercise a large number of small wagers. This goal is accomplished by limiting the maximum individual wager; further, a limit on the lowest wager permitted inhibits negative and logarithmic betting systems. In general, casino games involve a redistribution of wealth among the players, while the House removes a certain percentage, either directly or statistically. In the occasional game where all players contend against the House (as in Bingo), the payoff is fixed per unit play. The House, of course, has one of the most objective evaluations of wealth that can be postulated. No casino has ever been accused of subjective utility goals.
REFERENCES
Anscombe FJ, Aumann Robert J, (1963). A Definition of Subjective Probability. Annals of Mathematical Statistics.34(1):199–205.
Bellman Richard, (1954). Decision Making in the Face of Uncertainty I, II. Naval Research Logistics Quarterly.1:230–232 [327–332.]
Blackwell David, (1954). On Optimal Systems. Annals of Mathematical Statistics.25(2):394–397.
Blackwell David, Girshick MA, (1954). Theory of Games and Statistical Decisions. John Wiley & Sons.
Borel Emile, (1953). On Games That Involve Chance and the Skill of the Players. Econometrica.21:97–117.
Breiman, Leo, “Optimal Gambling Systems for Favorable Games,” Proceedings of Fourth Berkeley Symposium on Mathematical Statistics and Probability, pp. 65–78, University of California Press, 1961.
Breiman, Leo, “On Random Walks with an Absorbing Barrier and Gambling Systems,” Western Management Science Institute, Working Paper no. 71, University of California, Los Angeles, March 1965.
Cesare Guilio, Widmer Lamarr, (1997). Martingale. Journal of Recreational Mathematics.30(4):300.
Chernoff Herman, (1954). Rational Selection of Decision Functions. Econometrica.22:422–441.
Chow YS, Robbins H, (1965). On Optimal Stopping in a Class of Uniform Games. [Mimeograph Series no. 42] Department of Statistics, Columbia University [June].
Coolidge JL, (1908–1909). The Gambler’s Ruin. Annals of Mathematics, Second Series.10(1):181–192.
Doob JL, (1971). What Is a Martingale?”. American Mathematics Monthly.78(5):451–463.
Dubins, Lester E., and Leonard J. Savage, Optimal Gambling Systems Proceedings of the National Academy of Science, p. 1597, 1960.
Edwards Ward, (1953). Probability Preferences in Gambling. American Journal of Psychology.66:349–364.
Edwards Ward, (1954). Probability Preferences among Bets with Differing Expected Values. American Journal of Psychology.67:56–67.
Epstein, Richard A., “An Optimal Gambling System for Favorable Games,” Hughes Aircraft Co., Report TP-64-19-26, OP-61, 1964.
Epstein, Richard A., “The Effect of Information on Mathematical Expectation,” Hughes Aircraft Co., Report TP-64-19-27, OP-62, 1964.
Epstein, Richard A., “Expectation and Variance of a Simple Gamble,” Hughes Aircraft Co., Report TP-64-19-30, OP-65, 1964.
Ethier Stewart N, Tavares S, (1983). The Proportional Bettor’s Return on Investment. Journal of Applied Probability.20:563–573.
Feller William, (1957). An Introduction to Probability Theory and Its Applications. 2nd ed. John Wiley & Sons.
Ferguson, Thomas S., “Betting Systems Which Minimize the Probability of Ruin,” Working Paper no. 41, University of California, Los Angeles, Western Management Science Institute, October 1963.
Griffin Peter, (1999). The Theory of Blackjack. Huntington Press.
Hurwicz, Leonid, “Optimality Criteria for Decision Making under Ignorance,” Cowles Commission Discussion Paper, Statistics, no. 370, 1951.
Isaacs Rufus, (1955). A Card Game with Bluffing. American Mathematics Monthly.42:94–108.
Kahneman Daniel, Tversky Amos, (1999). Prospect Theory: An Analysis of Decision Under Risk. Econometrika.47:263–291.
Kelly John L, (1956). A New Interpretation of Information Rate. Bell System Technical Journal.35(4):917–926.
Kuhn Harold W, (1953). Contributions to the Theory of Games. [“Extensive Games and the Problem of Information,”] Princeton University Press [Vol. 2, Study No. 28, pp. 193–216].
Luce RDuncan, Raiffa Howard, (1957). Games and Decisions. John Wiley & Sons.
Marcus, Michael B., “The Utility of a Communication Channel and Applications to Suboptimal Information Handling Procedures,” I.R.E. Transactions of Professional Group on Information Theory, Vol. IT-4, no. 4 (1958), 147–151.
Morgenstern Oskar, (1949). The Theory of Games. Scientific American.180:22–25.
Sakaguchi, Minoru, Information and Learning,” Papers of the Committee on Information Theory Research, Electrical Communication Institute of Japan, June 1963.
Samuelson Paul A, (1952). Probability, Utility, and the Independence Axiom. Econometrica.20:670–678.
Savage, Leonard J., “The Casino That Takes a Percentage and What You Can Do About It,” The RAND Corporation, Report P-1132, Santa Monica, October 1957.
Savage Leonard J, (1951). The Theory of Statistical Decision. Journal of American Statistical Association.46:55–67.
Snell JL, (1952). Application of Martingale System Theorems. Transactions of American Mathematical Society.73(1):293–312.
von Neumann John, Oskar Morgenstern, (1953). Theory of Games and Economic Behavior. Princeton University Press.
Warren Michael G, (1981–1982). Is a Fair Game Fair—A Gambling Paradox. Journal of Recreational Mathematics.14(1):35–39.
Wong, Stanford, What Proportional Betting Does to Your Win Rate www.bjmath.com/bjmath/paper1/proport.htm.
Bibliography
Byrns, Ralph, “Prospect Theory,” www.unc.edu/depts/econ/byrns_web/Economicae/Figures/Prospect.htm.
Dubins Lester E, Savage Leonard J, (1965). How to Gamble If You Must. McGraw-Hill.
Gottlieb Gary, (1985). An Optimal Betting Strategy for Repeated Games. Journal of Applied Probability.22:787–795.
Halmos Paul R, (1939). Invariants of Certain Stochastic Transformations: The Mathematical Theory of Gambling Systems. Duke Mathematical Journal.5(2):461–478.
Hill Theodore P, (1999). Goal Problems in Gambling Theory. Revista de Matemàtica.6(2):125–132.
Isaac Richard, (1999). Bold Play Is Best: A Simple Proof. Mathematics Magazine.72(5):405–407.
Rayleigh Lord, (1899). On Mr. Venn’s Explanation of a Gambling Paradox. Scientific Papers of Lord Rayleigh.50(1):1869–1881 [Cambridge University Press].
1 For decision making under conditions of uncertainty. Bellman (Ref.) has shown that one can approach an optimum moderately well by maximizing the ratio of expected gain to expected cost.
2 Daniel Kahneman shared the 2002 Nobel Prize for Economics.
3 Proofs of the theorems were developed in the first edition of this book.
4 From the French Martigal, the supposedly eccentric inhabitants of Martigues, a village west of Marseille. The Martingale system was employed in the 18th century by Casanova (unsuccessfully) and was favored by James Bond in Casino Royale.
5 After its innovator, Henry Du Pre Labouchère, a 19th-century British diplomat and member of parliament.
6 In French, the privilege of terminating play arbitrarily while winning has been accorded the status of an idiom: le droit de faire Charlemagne.
7 For example, Arthur E. Laemmel, General Theory of Communication, Polytechnic Institute of Brooklyn, 1949.
8 Developed by Peter Griffin (Ref.) as the unit normal linear loss integral.