Chapter two
Mathematical Preliminaries
The Meaning of Probability
The word “probability” stems from the Latin probabilis: “truth-resembling”; thus the word itself literally invites semantic imprecision. Yet real concepts exist and are applicable in resolving or ordering certain questions. For our purpose, which is to categorize gambling phenomena, we adopt an operational definition of probability that avoids philosophic implications and Bergsonian vagueness and constrains the area of application. This restricted definition we term “rational probability” and credit it as the only valid mathematical description of likelihood or uncertainty.
Rational probability is concerned only with mass phenomena or repetitive events that are subject to observation or to logical extrapolation from empirical experience.
That is, we must have, either in space or in time, a practically unlimited sequence of uniform observations or we must be able to adapt correlated past experience to the problem for it to merit the attention of rational probability theory.
The extension of probability theory to encompass problems in the moral sciences, as ventured in the rampant rationalism of the 18th century, is not deemed invalid, but simply another field of endeavor. The views of de Morgan and Lord Keynes we classify as “philosophic probability.” Questions of ethics, conduct, religious suppositions, moral attributes, unverifiable propositions, and the like are, in our assumed context, devoid of meaning.
Similarly, “fuzzy logic,” an offshoot of set theory that deals with degrees of truth, lies outside the domain of gambling theory.1 Degrees of truth are not probabilities, although the two are often conflated.
Three principal concepts of probability theory have been expressed throughout the sensible history of the subject. First, the classical theory is founded on the indefinable concept of equally likely events. Second, the limit-of-relative-frequency theory is founded on an observational concept and a mathematical postulate. Third, the logical theory defines probability as the degree of confirmation of an hypothesis with respect to an evidence statement.
Our definition of rational probability theory is most consistent with and completed by the concept of a limiting relative frequency. If an experiment is performed whereby n trials of the experiment produce n0 occurrences of a particular event, the ratio n0/n is termed the relative frequency of the event. We then postulate the existence of a limiting value as the number of trials increases indefinitely. The probability of the particular event is defined as
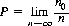(2-1)
The classical theory considers the mutually exclusive, exhaustive cases, with the probability of an event defined as the ratio of the number of favorable cases to the total number of possible cases. A weakness of this perspective lies in its complete dependence upon a priori analysis—a process feasible only for relatively unsophisticated situations wherein all possibilities can be assessed accurately; more often, various events cannot be assigned a probability a priori.
The logical theory is capable of dealing with certain interesting hypotheses; yet its flexibility is academic and generally irrelevant to the solution of gambling problems. Logical probability, or the degree of confirmation, is not factual, but L-determinate—that is, analytic; an L concept refers to a logical procedure grounded only in the analysis of senses and without the necessity of observations in fact.
Notwithstanding this diversity of thought regarding the philosophical foundations of the theory of probability, there has been almost universal agreement as to its mathematical superstructure. And it is mathematics rather than philosophy or semantic artifacts that we summon to support statistical logic and the theory of gambling. Specifically in relation to gambling phenomena, our interpretation of probability is designed to accommodate the realities of the situation as these realities reflect accumulated experience. For example, a die has certain properties that can be determined by measurement. These properties include mass, specific heat, electrical resistance, and the probability that the up-face will exhibit a “3.” Thus we view probability much as a physicist views mass or energy. Rational probability is concerned with the empirical relations existing among these types of physical quantities.
The Calculus of Probability
Mathematics, qua mathematics, is empty of real meaning. It consists merely of a set of statements: “if …, then … .” As in Euclidean geometry, it is necessary only to establish a set of consistent axioms to qualify probability theory as a rigorous branch of pure mathematics. Treating probability theory, then, in a geometric sense, each possible outcome of an experiment is considered as the location of a point on a line. Each repetition of the experiment is the coordinate of the point in another dimension. Hence probability is a measure—like the geometric measure of volume. Problems in probability are accordingly treated as a geometric analysis of points in a multidimensional space. Kolmogorov has been largely responsible for providing this axiomatic basis.
Axioms and Corollaries
A random event is an experiment whose outcome is not known a priori. We can state
Axiom I: To every random event A there corresponds a number P(A), referred to as the probability of A, that satisfies the inequality
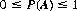
Thus the measure of probability is a nonnegative real number in the range 0 to 1.
Now consider an experiment whose outcome is certain or whose outcomes are indistinguishable (tossing a two-headed coin). To characterize such an experiment, let E represent the collection of all possible outcomes; thence
Axiom II: The probability of the certain event is unity. That is,
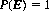
The relative frequency of such events is (cf. Eq. 2-1) n0/n = 1.
Lastly, we require an axiom that characterizes the nature of mutually exclusive events (if a coin is thrown, the outcome Heads excludes the outcome Tails, and vice versa; thus, Heads and Tails are mutually exclusive). We formulate this axiom as follow:
Axiom III: The theorem of total probability. If events A1, A2, …, An are mutually exclusive, the probability of the alternative of these events is equal to the sum of their individual probabilities. Mathematically,
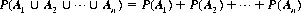
where A1 
A2 denotes the union of events A1, and A2. Axiom III expresses the additive property of probability. It can be extended to include events not mutually exclusive. If A1 and A2 are such events, the total probability (A1, and/or A2 occurs) is
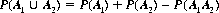(2-2)
whereP(A1 A2) is defined as the joint or compound probability that both A1 and A2 occur.
Generalizing, the probability of occurrence, P1, of at least one event among n events, A1, A2, …, A n, is given by
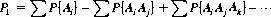
And Eq. 2-2 can be extended to any number of independent events:
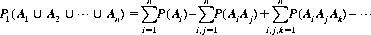
From these axioms several logical corollaries follow.
Corollary I: The sum of the probabilities of any event A and its complement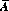 
is unity. That is,
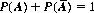
The complement of an event is, of course, the nonoccurrence of that event.
Characterizing an impossible event O, we can state the following:
Corollary II: The probability of an impossible event is zero, or
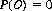
It is worth noting that the converse of Corollary II is not true. Given that the probability of some event equals zero, it does not follow that the event is impossible (there is a zero probability of selecting at random a prespecified point on a line).
Another important concept is that of “conditional probability.” The expression P(A2
A1) refers to the probability of an event A2, given (or conditional to) the occurrence of the event A1. We can write, for P(A1) > 0,
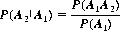(2-3)
By induction from Eq. 2-3, we can obtain the multiplication theorem (or the general law of compound probability):
Corollary III: The probability of the product of n events A1, A2, …, An is equal to the probability of the first event times the conditional probability of the second event, given the occurrence of the first event, times the conditional occurrence of the third event given the joint occurrence of the first two events, etc. In mathematical form,
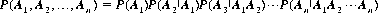
It can be demonstrated that conditional probability satisfies Axioms I, II, and III. A special case of Corollary III occurs when the events A1, A2, …, An are independent; then the law of compound probability reduces to
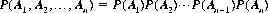
Thus the necessary and sufficient condition for n events to be independent is that the probability of every n-fold combination that can be formed from the n events or their complements be factorable into the product of the probabilities of the n distinct components.
Finally, the concept of complete (or absolute) probabillity is expressed by
Corollary IV: If the random events A1, A2, …, An are pairwise exclusive, then the probability P(X) of any random event X occurring together with one of the events Ai is given by
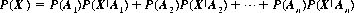
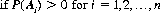
Combining the principles of complete and conditional probabilities leads to the following statement:
Corollary IV(a): If the independent events A1, A2, …, An satisfy the assumptions of the complete probability theorem, then for an arbitrary event X associated with one of the events Ai we have, for P(X) > 0,
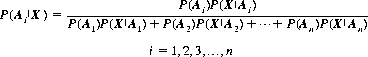(2-4)
Equation 2-4 is known as Bayes theorem, or the formula for a posteriori probability. It should be noted that no assumptions as to the probabilities of the respective Ai’s are implied (a common error is to interpret Bayes theorem as signifying that all Ai’s are equal).
Together, the preceding axioms and corollaries constitute the foundation of the theory of probability as a distinct branch of mathematics.
An example may aid in clarifying these concepts. Given that the probability P(K) of drawing at least one king in two tries from a conventional deck of 52 cards is 396/(52 × 51) = 0.149, that the probability P(Q) of drawing a queen in two tries is also 0.149, and that the joint probability (drawing both a king and a queen) is 32/(52 × 51) = 0.012, what is the conditional probability P(KQ) that one of the two cards is a king, given that the other is a queen?2 What is the total probability P(KQ) that at least one card is either a king or a queen? Are the two events—drawing a king and drawing a queen—independent?
Applying Eq. 2-3 directly.
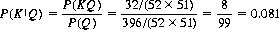
and of course, the probability P(Q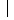K) of one of the two cards being a queen, given the other to be a king, is also 0.081. From Eq. 2-2, the total probability (drawing a king and/or a queen) is
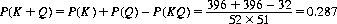
It is evident that the two events are not independent, since P(KQ) ≠ P(K)P(Q).
Permutations and Combinations
Gambling phenomena frequently require the direct extension of probability theory axioms and corollaries into the realm of permutational and combinatorial analysis. A permutation of a number of elements is any arrangement of these elements in a definite order. A combination is a selection of a number of elements from a population considered without regard to their order. Rigorous mathematical proofs of the theorems of permutations and combinations are available in many texts on probability theory. By conventional notation, the number of permutations of n distinct objects (or elements or things) considered r at a time without repetition is represented by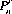 
. Similarly, 
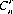represents the number of combinations of n distinct objects considered r at a time without regard to their order.
To derive the formula for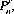 
consider that we have r spaces to fill and n objects from which to choose. The first space can be filled with any of the n objects (that is, in n ways). Subsequently, the second space can be filled from any of (n − 1) objects (n − 1) ways, the third space in (n − 2) ways, etc., and the rth space can be filled in [n − (r − 1)] ways. Thus
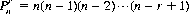(2-5)
For the case r = n, Eq. 2-5 becomes
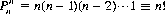(2-6)
Combining Eqs. 2-6 and 2-5, the latter can be rewritten in the form
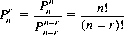
It is also possible, from Eq. 2-5, to write the recurrence relation
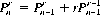
Similar considerations hold when we are concerned with permutations of n objects that are not all distinct. Specifically, let the n objects be apportioned into m kinds of elements with n1 elements of the first kind, n2 elements of the second, etc., and n = n1 + n2 + … + nm. Then the number of permutations Pn of the n objects taken all together is given by
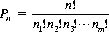(2-7)
Illustratively, the number of permutations of four cards selected from a 52-card deck is
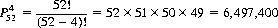
Note that the order is of consequence. That is, the A, 2, 3, 4 of spades differs from, say, the 2, A, 3, 4, of spades. If we ask the number of permutations of the deck, distinguishing ranks but not suits (i.e., 13 distinct kinds of objects, each with four indistinct elements3), Eq. 2-7 states that
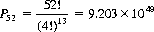
To this point we have allowed all elements of a population to be permuted into all possible positions. However, we may wish to enumerate only those permutations that are constrained by prescribed sets of restrictions on the positions of the elements permuted. A simple example of a restricted-position situation is the “problème des ménages,”4 which asks the number of ways of seating n married couples around a circular table with men and women in alternate positions and with the proviso that no man be seated next to his spouse. This type of problem is equivalent to that of placing k rooks on a “chessboard”—defined by mathematicians as an arbitrary array of cells arranged in rows and columns—in such a way that no rook attacks any other (the rook is a Chess piece that moves orthogonally). Applications of these concepts lie in the domain of combinatorial analysis. As noted briefly in Chapter 7, they are particularly useful and elegant in the solution of matching problems.
Turning to r combinations of n distinct objects, we observe that each combination of r distinct objects can be arranged in r! ways—that is r! permutations. Therefore, r! permutations of each of the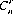 
combinations produce 
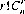permutations:
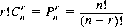
Dividing by r!, we obtain the expression for the number of combinations of n objects taken r at a time:
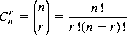(2-8)
where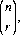
the symbol for binomial coefficients, is the (r + 1)st coefficient of the expansion of (a + b)n. For values of r less than zero and greater than n, we define 
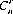to be equal to zero. (Eq. 2-8 can also be extended to include negative values of n and r; however, in our context we shall not encounter such values.) It is also apparent that the number of combinations of n objects taken r at a time is identical to the number of combinations of the n objects taken n − r at a time. That is,
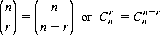
We can also derive this equivalence in the format
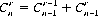(2-9)
Equation 2-9 is known as Pascal’s rule. By iteration it follows that
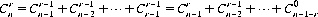
As an example, we might ask how many Bridge hands of 13 cards are possible from a 52-card population. Equation 2-8 provides the answer:
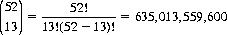
Note that the ordering of the 13 cards is of no consequence. If it were, the resulting number of permutations would be greater by a factor of 13!
Probability Distributions
With a nonhomogeneous population (n objects consisting of m kinds of elements with n1 elements of the first kind, n2 elements of the second kind, etc.), the number of permutations of the n objects taken all together is given by Eq. 2-7. We can also determine the number of combinations possible through selection of a group of r elements from the n objects. Thence it is feasible to ask the probability Pk1,k2,…, km that if a group of r elements is selected at random (without replacement and without ordering), the group will contain exactly k1 ≤ n1elements of the first kind, k2 ≤ n2 elements of the second kind, etc., and km ≤ nm elements of the mth kind. Specifically, it can be shown that
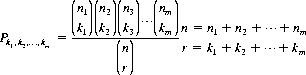(2-10)
Equation 2-10 represents the generalized hypergeometric distribution, the probability distribution for sampling without replacement from a finite population. It should be noted that in the limit (for arbitrarily large populations) sampling with or without replacement leads to the same results.
As an illustration of the hypergeometric distribution, we compute the probability that a Bridge hand of 13 cards consists of exactly 5 spades, 4 hearts, 3 diamonds, and 1 club. According to Eq. 2-10,
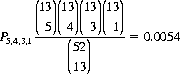
since the order of the cards within the Bridge hand is irrelevant.
Another distribution of consequence in practical applications of probability theory is the binomial distribution. If an event has two alternative results, A1 and A2, so that P(A1) + P(A2) = 1, and the probability of occurrence for an individual trial is constant, the number of occurrences r of the result A1 obtained over n independent trials is a discrete random variable, which may assume any of the possible values 0, 1, 2, …, n. A random variable is simply a variable quantity whose values depend on chance and for which there exists a distribution function. In this instance the number r is a binomial variate, and its distribution P(r) defines the binomial distribution.5 Letting p = P(A1) and q = P(A2) = 1 − p, we can readily derive the expression
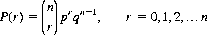(2-11)
Equation 2-11 is also referred to as the Bernoulli distribution, since it was first derived by Jacob Bernoulli in Ars. Conjectandi. An application to the Kullback matching problem is noted in Chapter 7.We can readily generalize from two possible outcomes of an event to the case of m mutually exclusive outcomes A1, A2, …, A m, each A i occurring with probability pi = P(Ai) ≥ 0 for each individual trial. The probability of obtaining r1 instances of A1, r2 instances of A2, etc. with n independent trials is known as the multinomial distribution and is determined in a fashion similar to Eq. 2-11:
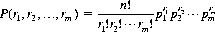(2-12)
where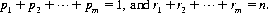 
Equation 2-12 specifies the compound or joint distribution of the number of outcomes for each A i.
When a chance event can occur with constant probability p on any given trial, then the number of trials r required for its first occurrence is a discrete random variable that can assume any of the values 1, 2, 3, …, ∞. The distribution of this variable is termed the geometric distribution. If the first occurrence of the event is on the rth trial, the first r − 1 trials must encompass nonoccurrences of the event (each with probability q = 1 − p). The compound probability of r − 1 nonoccurrences is qr−1; hence r − 1 nonoccurrences followed by the event has probability qr−1p. Accordingly, the geometric distribution is defined by
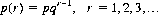(2-13)
By implication from this distribution, the expected number of trials is equal to the reciprocal of the constant probability p (cf. Eq. 6-18).
For the situation where events occur randomly in time, let P(r, T) denote the probability that exactly r events occur in a specified time interval T. Defining α as the probability that one event occurs in the incremental interval ΔT (so the average number of events in the interval T isαT), we can determine P(r, T) as
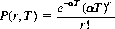(2-14)
Equation 2-14 defines the Poisson distribution; it serves as an approximation to the binomial distribution when the number of trials is large.
Illustratively, if a gambler can expect five successes in ten trials, the probability that he will win at least twice is then
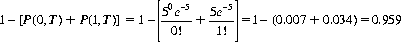
Note that the single-trial probability of success does not enter the computation—only the average number of successes pertains.
The Poisson distribution provides substantial benefit in representing the time sequence of random independent events. Whereas a binomial distribution is symmetric and bounded at both ends, the Poisson distribution is asymmetric, being bounded at the lower end but not at the top.
Consider a telephone service that receives an average of one call per minute from a pool of millions of customers. The Poisson distribution then specifies the probability of receiving r calls in any particular minute. Since we are dealing here with only a single parameter, αT, knowledge of the average (mean) is sufficient in itself to describe the pertinent phenomenon.
Applications of the several probability distributions are multifold. The following numerical example is representative. From a deck of 52 cards, ten are dealt at random. The full deck is then reshuffled, and 15 cards are selected at random. We ask the probability P(r) that exactly r cards are common to both selections (r = 0, 1, 2, …, 10). From the 52 cards, 15 can be selected in 
distinct ways. If r of these have been selected on the previous deal, then 15 − r are in the nonoccurring category. Obviously, there are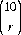 
distinct ways of choosing r of the cards from the first deal and 
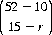ways of selecting the remaining cards. Thus, according to Eq. 2-10 for the hypergeometric distribution,
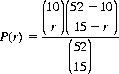
For no matching cards, r = 0, P(0) = 0.022, and for r = 5, P(5) = 0.083. The most probable number of matches is 3 − P(3) = 0.296.
Mathematical Expectation
A parameter of fundamental value in the evaluation of games of chance is the mathematical expectation. Its definition is straightforward: If a random variable X can assume any of n values x1, x2, …, xn with respective probabilities p1, p2, …, pn, the mathematical expectation of X, E(X), is expressed by
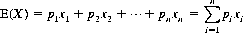(2-15)
The mathematical expectation of the number showing on one die is accordingly
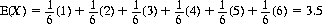(2-16)
since the possible values of X, the number showing, are 1, 2, 3, 4, 5, and 6, each with probability 1/6. For two dice, X can range between 2 and 12 with varying probabilities:
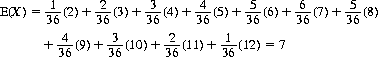(2-17)
A useful theorem states that the mathematical expectation of the sum of several random variables X1, X2, …, Xn is equal to the product of their mathematical expectations. That is,
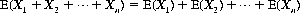(2-18)
Thus the mathematical expectation of the total showing on n dice is 3.5n. (The result of Eq. 2-17 is directly obtainable by letting n = 2.)
Similarly, the theorem can be proved that the mathematical expectation of the product of several independent variables X1, X2, …, Xn is equal to the product of their expectations. That is,
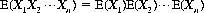(2-19)
(Note that Eq. 2-19 appertains to independent variables, whereas Eq. 2-18 is valid for any random variable.) It can also be shown in simple fashion that
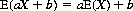
for any numerical constants a and b.
The condensed description of probability theory presented here cannot, of course, include all those tools required for the solution of gambling problems. However, most of the requisite information has been covered briefly and is of propaedeutic value; more comprehensive developments can be found by consulting the References and Bibliography at the end of this chapter.
Statistics
Statistics6 and probability theory cannot always be separated into water-tight compartments. Statistics may be considered as the offspring of the theory of probability, as it builds on its parent and extends the area of patronymic jurisdiction. In this sense, probability theory enables us to deduce the probable composition of a sample, given the composition of the original population; by the use of statistics we can reverse this reasoning process to infer the composition of the original population from the composition of a properly selected sample. Frequently, however, the objective of a statistical investigation is not of a purely descriptive nature. Rather, descriptive characteristics are desired in order to compare different sets of data with the aid of the characteristics of each set. Or we may wish to formulate estimates of the characteristics that might be found in related sets of data. In either case, it is evident that description is a preliminary stage, and further analysis is our principal goal.
As in the theory of probability, the meaning and end result of a statistical study are a set of conclusions. We do not predict the individual event, but consider all possible occurrences and calculate the frequency of occurrences of the individual events. Also, like probability theory, statistics is an invention of men rather than of nature. It, too, has a meaning ultimately based on empirical evidence and a calculus established on an axiomatic foundation. Attributing to statistics the inherent ability to describe universal laws leads to a profusion of artful and provocative fallacies.7 As per G.K. Chesterton, we caution against using statistics as a drunk uses a lamppost for support rather than illumination.
Mean and Variance
Analysis of the conventional games of chance involves only the more elementary aspects of statistical theory, primarily those related to the concepts of variance, estimation, hypothesis testing, and confidence limits. Our treatment of the subject is therefore correspondingly limited.
The mathematical expectation of a random variable X is also known as the mean value of X. It is generally represented by the symbol μ; that is, μ = E(X). Thus E(X − μ) = 0. Considering a constant c instead of the mean μ, the expected value of X − c [that is, E(X − c)] is termed the firstmoment of X taken about c. The mean (or center of mass of the probability function) depicts the long-run average result for an experiment performed an arbitrarily large number of times. This type of average refers to the arithmetical average of a distribution, defined according to Eq. 2-15. It should not be confused with the mode (that value of the distribution possessing the greatest frequency and hence the most probable value of the distribution), the weighted average (wherein each value of the random variable X is multiplied by a weighting coefficient before the arithmetical averaging process), the median (the sum of the frequencies of occurrence of the values of X above and below the median are equal; for symmetrical distributions, the mean and the median are identical), or the geometric mean (the positive nth root of the product of n random variables), among others.8
In addition to the mean, another parameter is required to describe the distribution of values: a measure of spread or variability comparing various results of the experiment. The most convenient and commonly used measure of spread is the variance. Let X be a random variable assuming any of the m values xi (i = 1, 2, …, m) with corresponding probabilities p(xi) and with mean μ = E(X). The variance, Var(X), then is defined by
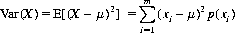
Note that the units of Var(X) are squares of the units of x. Therefore, to recover the original units, the standard deviation of X, σ(X), is defined as
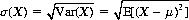
An invaluable theorem formulates the variance of X as the mean of the square of X minus the square of the mean of X—that is,
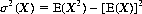(2-20)
The mean value of the up-face of a die, as per Eq. 2-16, equals 7/2. The mean of this value squared is
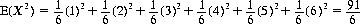
Thus the variance of the number showing on the die is, according to Eq. 2-20,
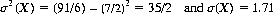
For two dice, E(X) = 7 and E(X2) = 329/6. Therefore the variance of the sum of numbers on two dice is
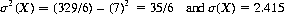
The expected total showing on two dice is occasionally stated as 7 ± 2.415.
We can readily compute the mean and variance for each well-known probability distribution. The hypergeometric distribution (Eq. 2-10), with but two kinds of elements, simplifies to
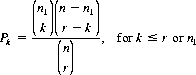(2-21)
Consider a deck of n cards—n1 red and n − n1 black. Then if r cards are drawn without replacement, the probability that the number X of red cards drawn is exactly k is given by Eq. 2-21. The mean of X is expressed by
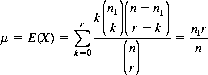
and the mean of X2 is
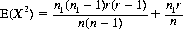
Eq. 2-20 specifies the variance:
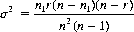
For the binomial distribution (Eq. 2-11), we can compute the mean as
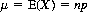
and the mean of X2 as
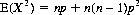
Thus the variance associated with the binomial distribution is
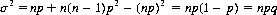(2-22)
The Poisson distribution (Eq. 2-14) can be shown to possess both mean and variance equal to the average number of events occurring in a specified time interval T. That is,
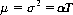
Consequently, the Poisson distribution is often written in the form
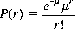
The Law of Large Numbers
Another highly significant theorem can be deduced from the definition of the variance by separating the values of the random variable X into those that lie within the interval μ − kσ to μ + kσ and those that lie without. The sum of the probabilities assigned to the values of X outside the interval μ ± kσ is equal to the probability that X is greater than kσ from the mean μ and is less than or equal to 1/k2. Thus
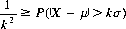(2-23)
This expression, known as Tchebychev’s theorem, states that no more than the fraction 1/k2 of the total probability of a random variable deviates from the mean value by greater than k standard deviations.
A notable application of Tchebychev’s inequality lies in determining the point of stochastic convergence—that is, the convergence of a sample probability to its expected value. If, in Eq. 2-23, we replace the random variable X by the sample probability p′ (the ratio of the number of occurrences of an event to the number of trials attempted) and the mean μ by the single-trial probability of success p, Tchebychev’s inequality becomes
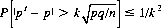(2-24)
since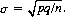 
Specifying the value of k as 
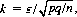where ε is some fraction greater than zero, Eq. 2-24 assumes the form
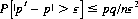(2-25)
which is the law of large numbers. It declares that no matter how small an ε is specified, the probability P that the sample probability differs from the single-trial probability of success by more than ε can be made arbitrarily small by sufficiently increasing the number of trials n. Thus for an unbiased coin, the probability of the ratio of Heads (or Tails) to the total number of trials differing from 1/2 by greater than a specified amount approaches zero as a limit. We conventionally express this fact by the statement that the sample probability converges stochastically to 1/2.
The law of large numbers has frequently (and erroneously) been cited as the guarantor of an eventual Head–Tail balance. Actually, in colloquial form, the law proclaims that the difference between the number of Heads and the number of Tails thrown may be expected to increase indefinitely with an increasing number of trials, although by decreasing proportions. Its operating principle is “inundation” rather than “compensation” (cf. Theorems I and II of Chapter 3).
Confidence
In addition to a measure of the spread or variability of a repeated experiment, it is desirable to express the extent to which we have confidence that the pertinent parameter or specific experimental result will lie within certain limits. Let the random variable X possess a known distribution, and let us take a sample of size r(x1, x2, …, xr) with which we will estimate some parameter θ. Then, if θ1 and θ2 are two statistical estimations of θ, the probability ξ that θ lies within the interval θ1 to θ2 is called the confidence level—that is,
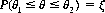
The parameter θ, it should be noted, is not a random variable. It represents a definite, albeit unknown, number. However, θ1 and θ2 are random variables, since their values depend on the random samples.
As an example, consider a random variable X that follows a normal distribution with a known standard deviation σ but with an unknown expectation μ. We ask the range of values of μ that confers a 0.95 confidence level that μ lies within that range. From the definition of the normal distribution (Eq. 2-26), the probability that μ lies between
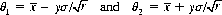
is given by
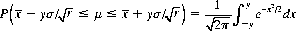
From tables of the normal probability integral we find that this probability is equal to 0.95 for y = 1.96. Thus, for an estimate 
of μ from a small sample of size r, we can claim a 0.95 confidence that μ is included within the interval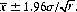 
Let us postulate a Bridge player who, having received ten successive Bridge hands, nine of which contain no Aces, complains that this situation is attributable to poor shuffling. What confidence level can be assigned to this statement? The probability that a hand of 13 cards randomly selected contains at least one Ace is
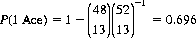
The binomial distribution (Eq. 2-11) provides the probability that of ten hands, only one will contain at least one Ace:
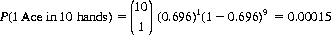
Thus, with a confidence level of 99.985%, the Bridge player can justly decry the lack of randomness and maintain that as a consequence the null hypothesis [P(1 Ace) = 0.696] does not hold in this game.
Estimation
In the field of economics, one aspect of mathematical statistics widely applied is that of estimation from statistical data. Statistical inference is a method of educing population characteristics on the basis of observed samples of information.9 For example, we might be ignorant of the probability p that the throw of a particular coin will result in Heads; rather we might know that in 100 trials, 55 Heads have been recorded and wish to obtain from this result an estimate of p. In general, the parameter to be estimated can be a probability, a mean, a variance, etc.
There are several “good” estimates of unknown parameters offered by the discipline of statistics. A common procedure is that of the method of moments. To estimate k unknown parameters, this procedure dictates that the first k sample moments be computed and equated to the first k moments of the distribution. Since the k moments of the distribution are expressible in terms of the k parameters, we can determine these parameters as functions of the sample moments, which are themselves functions of the sample values.
Assuredly, the most widely used measure is the maximum likelihood estimate—obtainable by expressing the joint distribution function of the sample observations in terms of the parameters to be estimated and then maximizing the distribution function with respect to the unknown parameters. Solutions of the maximization equation yield the estimation functions as relations between the estimated parameters and the observations. Maximum likelihood estimates are those that assign values to the unknown parameters in a manner that maximizes the probability of the observed sample.
Statistical Distributions
Of the various distributions of value in statistical applications, two are summoned most frequently: the normal or Gaussian distribution and the chi-square distribution. The former constitutes a smooth-curve approximation to the binomial distribution (Eq. 2-11) derived by replacing factorials with their Stirling approximations10 and defining a continuous variable X:
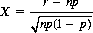
which is the deviation of the distribution measured in terms of the standard deviation [for the binomial distribution,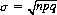 
(cf. Eq. 2-22)]. We then obtain
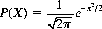(2-26)
for the normal distribution of the random variable X with zero mean and unit variance (x signifies the values assumed by X).
Related to the normal distribution and readily derived therefrom, the chi-square (χ2) distribution is defined as the distribution of the sum of the squares of n independent unit normal variates (and is sometimes referred to as Helmert’s distribution, after F.R. Helmert, its first investigator). For n degrees of freedom (i.e.,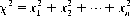 
), we can determine that
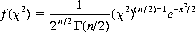(2-27)
where Γ(n) is the gamma function. Γ(n) = (n − 1)! for integral values of n, and Γ(1/2) =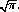 
11 Values of χ2 are tabulated in mathematical handbooks and computer packages.
In those instances where it is desired to measure the compatibility between observed and expected values of the frequency of an event’s occurrence, the χ2 statistic is particularly useful. For n trials, let ri represent the number of times the event xi is observed, and let si be the expected number of occurrences in n trials (si = pin, where pi is the single-trial probability of xi); then χ2 is defined by
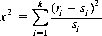(2-28)
for the k events x1, x2, …, xk (in actuality, Eq. 2-28 represents a limiting distribution valid for large n; empirically, we usually require si > 5 for all i). A value of zero for χ2 corresponds to exact agreement with expectation. If the n-trial experiment is repeated an arbitrarily large number of times, we obtain a distribution of χ2 identical to that expressed by Eq. 2-27 with m − 1 degrees of freedom.
The χ2 test for goodness of fit is one of the most widely used methods capable of testing an hypothesis for the mathematical form of a single distribution, for a difference in the distribution of two or more random variables, and for the independence of certain random variables or attributes of variables. Its ready application to discrete distributions is not shared by other tests for goodness of fit, such as the Kolmogorov-Smirnov test (which applies as a criterion of fit the maximum deviation of the sample from the true distribution function).
Other distributions—some with widespread uses in statistical studies—can be derived by considering diverse functions of random variables. For example, if only a small sample of the total population is available, the sample standard deviation is not an accurate estimate of the true standard deviation σ. This defect can be circumvented by introducing a new variable based on the sample standard deviation. This new variate is defined as the quotient of two independent variates and results in the Student’s t-distribution,12 an offshoot of the chi-square distribution. Its importance stems from the fact that it is functionally independent of any unknown population parameters, thus avoiding dubious estimates of these parameters.
In connection with elementary statistical logic and gambling theory, those distributions stated ut supra encompass the majority of significant developments. We shall introduce additional distributions only as required for special applications.
Game Theory
Nomenclature
The theory of games, instituted by John von Neumann, is essentially a mathematical process for the analysis of conflict among people or such groups of people as armies, corporations, or Bridge partnerships. It is applicable wherever a conflicting situation possesses the capability of being resolved by some form of intelligence—as in the disciplines of economics (where it commands a dominating authority), military operations, political science, psychology, law, and biology, as well as in games of Chess, Bridge, Poker, inter alia. Hence the word “game” is defined as the course (playing) of a conflicting situation according to an a priori specified set of rules and conventions. Games are distinguished by the number of contending interests, by the value of the winner’s reward, by the number of moves required, and by the amount of information available to the interests.
Care should be exercised to avoid confusion with the colloquial meaning of the word game. Ping-Pong and sumo wrestling are “games” but lie outside the domain of game theory since their resolution is a function of athletic prowess rather than intelligence (despite the fact that a minimum intelligence is requisite to understand the rules). For social conflicts, game theory should be utilized with caution and reservation. In the courtship of the village belle, for example, the competing interests might not conform to the rules agreed upon; it is also difficult to evaluate the payoff by a single parameter; further, a reneging of the promised payoff is not unknown in such situations. Game theory demands a sacred (and rational) character for rules of behavior that may not withstand the winds of reality. The real world, with its emotional, ethical, and social suasions, is a far more muddled skein than the Hobbesian universe of the game theorist.
The number of players or competitors in a game are grouped into distinct decision-making units, or interests (Bridge involves four players, but two interests). With n interests, a game is referred to as an n-person game. It is assumed that the value of the game to each interest can be measured quantitatively by a number, called the payoff. In practice, the payoff is usually in monetary units but may be counted in any type of exchange medium. If the payoff is transferred only among the n players participating, the game is designated a zero-sum game. Mathematically, if ρi is the payoff received by the ith player (when the ith player loses, ρi is negative), the zero-sum game is defined by the condition that the algebraic sum of all gains and losses equals zero:
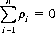
Instances where wealth is created or destroyed or a percentage of the wealth is paid to a nonparticipant are examples of non–zero-sum games.
Tic-tac-toe (which involves a maximum of nine moves) and Chess (a maximum possible 5950 moves) describe a type of game wherein only a finite number of moves are possible, each of which is chosen from a finite number of alternatives. Such games are termed finite games, and obviously the converse situation comprises infinite games.
The amount of information also characterizes a game. Competitions such as Chess, Checkers, or Shogi, where each player’s move is exposed to his opponent, are games of complete information. A variant of Chess without complete information is Kriegspiel (precise knowledge of each player’s move is withheld from his or her opponent). Bridge or Poker with all cards exposed would considerably alter the nature of that game. A variant of Blackjack with the dealt cards exposed is Zweikartenspiel (double exposure), proposed in Chapter 8.
Strategy
A system of divisions that selects each move from the totality of possible moves at prescribed instances is a strategy. A strategy may consist of personal moves (based solely on the player’s judgment or his opponent’s strategy or both), chance moves (determined through some random Bernoulli-trial method with an assessment of the probability of the various results), or, as in the majority of games, by a combination of the two. If player A has a total of m possible strategies, A1, A2, …, Am, and player B has a total of n strategies, B1, B2, …, Bn, the game is termed an m × n game. In such a game, for A’s strategy Ai parried against B’s strategy Bj, the payoff is designated by aij (by convention, A’s gain is assigned a positive sign and B’s a negative sign). The set of all values of aij is called the payoff matrix and is represented by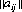 
—expressed as a paradigm in Figure 2-1.
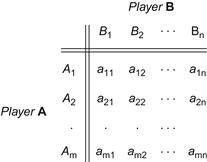
Figure 2-1 The general payoff matrix.
As an elementary illustration, consider A and B selecting either Heads or Tails simultaneously; if the two selections match, A wins one unit and conversely. This coin-matching payoff matrix is elaborated in Figure 2-2. It is evident that if A employs a pure strategy [e.g., selecting A1 (Heads) continually], his opponent, B, can gain the advantage by continually selecting Tails. Intuitively, A’s (and B’s) best course of action is a mixed strategy—that is, alternating among the possible strategies according to some probability distribution. For the coin-matching payoff matrix, A’s optimal strategy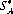 
is to select A1 or A2 with probability 1/2. In mathematical form,
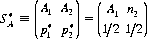(2-29)
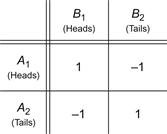
Figure 2-2 Coin-matching payoff matrix.
In general, A’s optimal strategy for a given payoff matrix can be determined from the minimax principle, the quintessential statement of the theory of games (see Chapter 3). For each row of the matrix of Figure 2-1, aij will have a minimum value αi. That is, for all possible values of j (with a given i), αi is the lowest value in the ith row of the matrix:
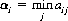
Player B can always prevent A from winning more than αi. Thus, A’s best strategy is to select the maximum value of αi. Denoting this maximum by α, we have
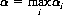
Combining these two equations,
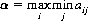
which states that the maximum of the minimum yield, or maximin, is A’s optimal strategy. The quantity α is the lower value of the game, since a profit of not less than α is ensured to A regardless of B’s strategy.
Considerations from the viewpoint of B are similar. The maximum value of αij for each column in Figure 2-1 is defined as
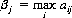
and the minimum over all the βjs is
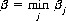
so that β can be written in the form
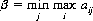
which states that the minimum of the maximum yield, or minimax, is B’s optimal strategy. The quantity β is the upper value of the game, since a loss of not more than β is guaranteed to B regardless of A’s strategy.
Clearly, every payoff matrix has a value—and that value can be achieved by at least one optimal strategy for each player.
Solutions of Games with Saddle Points
In the example of Figure 2-2, α1 = α2 = −1. Therefore the lower value of the game is α = −1. Similarly, β = +1. Any strategy of A’s is a maximin strategy, since A can never lose more than one unit, and similarly for B. If both A and B adhere to a mixed strategy, the average value γ of the game lies between the upper and lower values:
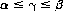
For the case considered here, γ = 0 if the mixed strategies are unpredictable.
In some instances, the lower value of the game is equal to the upper value:
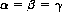
and the game is said to possess a saddle point. Every game with a saddle point has a solution that defines the optimal strategies for all the players; the value of the game is simultaneously its lower and upper values. Further, if any player deviates from the indicated optimal strategy, while the other players adhere to theirs, the outcome of the game for the deviating player can only be less than the average value. A proven theorem of game theory states that every game with complete information possesses a saddle point and therefore a solution.
These considerations can be summarized as follows: For every finite game matrix 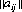, a necessary and sufficient condition
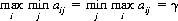
is that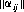 
possesses a saddle point. That is, there exists a pair of integers i0 and j0 such that 
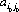is simultaneously the minimum of its row and the maximum of its column. Thus, if a game matrix possesses a saddle point, the solution of the game is evident and trivial.
A 2 × 2 game has a saddle point if and only if the two numbers of either diagonal are not both higher than either of the other two numbers—a situation that occurs with probability 2/3. With a 3 × 3 game, the probability of encountering a saddle point decreases to 3/10. The probability Pm,n that a randomly selected m × n game matrix exhibits a saddle point is
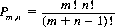
Solutions of Games without Saddle Points
In the Heads–Tails matching game of Figure 2-2, let A select his strategies via a random device that assigns a probability p to Heads and 1 − p to Tails. Further, let us assume that B has secured knowledge of the nature of A’s random device. Then the mathematical expectation of A, when B selects strategy B1 (Heads), is
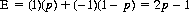
For B’s choice of strategy B2 (Tails),
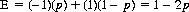
Clearly, if p > 1/2, B will select strategy B2, and A’s expectation is negative. Conversely, for p < 1/2, B selects strategy B1 and wins 1 − 2p units per game. It follows that if A selects A1 and A2 with equal probabilities 1/2, the expectation of both A and B is zero regardless of B’s strategy. Thus, A’s optimal strategy is to let p = 1/2 (as indicated in Eq. 2-29).
In general, for m × n game matrices, let A have a mixed strategy
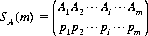
which is interpreted to mean that strategy Ai is selected with probability pi, where the pis sum to 1. Similarly, a mixed strategy for B is designated by
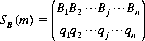
where the qjs sum to 1.When A and B employ the mixed strategies SA(m) and SB(n), respectively, the mathematical expectation of A is given by
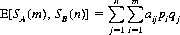
If it occurs that strategies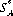 
(m) and 
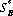(n), exist for A and B, respectively, such that
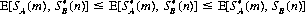
then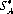 
(m) and 
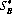(n) are optimal strategies, and 
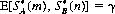is the value of the game.
In solving games without saddle points, a preliminary step is to eliminate from the game matrix all duplicate strategies as well as those strategies that are totally unfavorable with respect to another strategy. If the remaining game generates an m × n matrix, the necessary and sufficient condition for γ to be the value of the game and for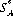 
(m) and 
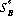(n) to be the optimal strategies of A and B, respectively, is that
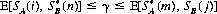
for 1 ≤ i ≤ m and 1 ≤ j ≤ n. Thus, for the solution of the game matrix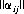 
, there must exist values of pi, qj, and γ that satisfy the conditions
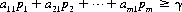
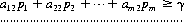
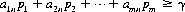(2-30)
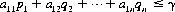
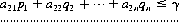
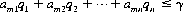
To illustrate the preceding concepts, consider the 4 × 4 matrix:
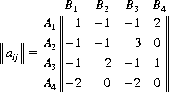
Here, A would assign zero probability to strategy A4, since, regardless of B’s strategy, A’s gain by selecting A3 is always greater than the yield from A4. Thus, A3 dominates A4, and we can eliminate A4. Similarly, B4 can be eliminated because it is dominated by B1. The remaining game matrix is
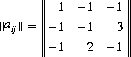
Applying Eqs. 2-30 with the equality signs,
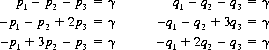
Combining these equations with the conditions p1 + p2 + p3 = 1 and q1 + q2 + q3 = 1, elementary algebraic methods provide the solution:
Thus, A’s optimal strategy is to select A1, A2, and A3 with probabilities 6/13, 4/13 and 3/13, respectively, thereby guaranteeing to A a loss of no more than 1/13.
Solving game matrices without saddle points often involves computational messiness. In some instances, a geometrical interpretation is fruitful, particularly for 2 × n games. In general, geometrical (or graphical) solutions of m × n game matrices pose exceptional mathematical difficulties. More advanced analytic techniques exist but are unlikely to be required in connection with any of the conventional competitive games.
Equilibria
It is possible to generalize (to multiperson games) the concept of the solution of a two-person, zero-sum game by introducing the notion of an equilibrium point (John Nash is responsible for this idea, although it had been previously applied in the field of economics under the terminology of Cournot’s duopoly point.) A Nash equilibrium (Ref: Nash, 1950) is a set of strategies and corresponding payoffs such that no player can benefit by changing his strategy while the strategies of all other players are held invariant. Every game with a finite number of players and a finite set of strategies has at least one mixed-strategy Nash equilibrium. For zero-sum games, the Nash equilibrium is also a minimax equilibrium.
A “weakness” of the Nash equilibrium is that it rests on the foundation of rational behavior (each player restricted to rational choices). Outside the rigid and enforced rules of formal games, more realistic behavior conforms to the quantal response equilibrium (QRE), which entertains the notion that players’ responses to differences in expected payoffs are more orderly for large differences and more random for small differences (Ref. Nash, 1951).
In addition, a large body of work has developed to deal with infinite games, games with infinitely many strategies, continuous games, and “nonrational” games such as the prisoner’s dilemma.13 However, these situations lie beyond our scope of interest; here, we have outlined only the basic mathematical tools useful for solving problems in applied gambling theory and statistical logic.
Random Walks
One-Dimensional
Most practical gambling situations can be formalized as sequences of Bernoulli trials wherein the gambler wins one unit for each success and loses one unit for each failure—with respective probabilities p and q = 1 − p. We represent the gambler’s capital x by a point on the real line; then from an initial capital x = x0, x moves along the line at each play either to x0 + 1 (probability p) or to x0 − 1 (probability q). After an indefinite number of plays, the random walk terminates either at x = 0 or at x = C, where C is the adversary’s capital. With a casino as the adversary, C is effectively infinite.
This construct describes the classic random walk and leads to the gambler’s ruin theorem (Chapter 3).
To determine the probability that the gambler’s capital returns to its initial value x0, we note that this event can occur only at an even-numbered play. After 2n plays, it is both necessary and sufficient for the gambler to have experienced n wins and n losses. Therefore,
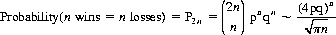
(see footnote 10). For p = q = 1/2,
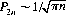
Note that the series ΣP2n diverges, but that the probability P2 n→0 with increasing n. Consequently, the return to initial capital x0 is a certain recurrent event, while the mean recurrence time is infinite.
Defining rj as the probability that a return to x0 occurs at the jth play (not necessarily for the first time), then the recurrent event x = x0 is uncertain if and only if
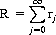
is finite. In this case the probability r that x = x0 ever recurs is given by
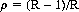
For p ≠ 1/2, we have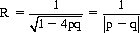 
Hence the probability that the accumulated numbers of successes and failures will ever be equal is expressed by
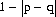(2-31)
Equation 2-31 also represents the probability of at least one return to x0.
Biased Walks
Let u and v denote the relative frequencies of moving left or right (failure or success) at each play. We can then write the generating function f(x) as
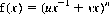
for n plays. With u = 1, v = 5, and n = 3 for example, the generating function is
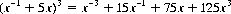
Thus there is one possible outcome at − 3, 15 outcomes at −1, 75 at +1, and 125 at + 3, with respective probabilities [dividing by (1 + 5)3] 1/216, 5/72, 25/72, and 125/216.
Walk, Don’t Walk
To the Biased Walk, we can add the possibility, with frequency w, of remaining in place (a tie game). Let w = 3 as an example; then our generating function (with n = 3) becomes
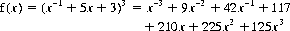
Table 2-1 displays the seven possible outcomes for the three-plays walk, don’t walk game.
Table 2-1. Outcomes for Three-Plays Walk, Don’t Walk
The number of outcomes for which success (unit moves rightward) minus failure (unit moves leftward) has the value j − n is
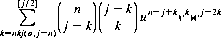
where [j/2] denotes the largest integer less than j/2. Designating the summand as Q, the number of successes can be expressed as
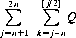
And the number of failures as
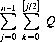
The number of times the position remains unchanged is
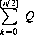
Several modifications to the random walk can be implemented. One example: a random walk with persistence, wherein the direction of moves taken by the gambler is correlated with previous moves. Another modification correlates the extent of each move (rather than +1 or −1). With a little ingenuity, games can be concocted to embody these rules.
While random walks in higher dimensions offer no insights into classical gambling theory, it is of interest to note that, quite surprisingly, a two-dimensional random walker (on a lattice) also has unity probability of reaching any point (including the starting point) in the plane and will reach that point infinitely often as the number of steps approaches infinity. A three-dimensional random walker, on the other hand, has less than unity probability of reaching any particular point; his probability of returning to the starting point is ∼0.34, and his expected number of returns ∼0.538. In the fourth dimension, the (hyper)random walker will revisit his starting point with probability ∼0.193. With yet higher dimensions, the (hyper)random walker will experience decreasing probabilities of returning to his starting point; in an n-dimensional hypercube, that probability is ∼1/2(n − 1) for n ≥ 8.
Change in capital
Of equal concern is the amount Δn that the gambler’s capital has increased or decreased after n plays. It can be shown, with adroit mathematical manipulations (Ref: Weisstein), that
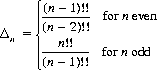
where n!! is the double factorial.14The first several values of Δn for n = 0, 1, 2, … are 0, 1, 1, 3/2, 3/2, 15/8, 15/8, 35/16, 35/16, 315/128, 315/128, ….
Quantum Games
While quantum game theory explores areas closed off to its classical counterpart, it does not always secure a foothold in reality.
In classical game theory, a mixed strategy different from the equilibrium strategy cannot increase a player’s expected payoff. Quantum strategies transcend such limitations and can prove more successful than classical strategies. A quantum coin, in contrast to a real coin that can be in one of only two states (Heads or Tails), enjoys the property of existing in a state that superimposes both Heads and Tails, and thus can be in an infinite number of states.
It has been shown that with quantum strategies available to both players, a two-person, zero-sum game does not necessarily possess an equilibrium solution, but does (always) have a mixed-strategy solution.
Quantum decoherence15 often precludes implementing such strategies in the real world—although two-state quantum systems exist that are consonant with the superposition of states necessary for a quantum strategy.
Parrondo’s principle (Chapter 4), Tic-Tac-Toe, Duels, and Truels, and the Monty Hall problem (Chapter 5) are examples of games amenable to the introduction of quantum theory.
REFERENCES
Feller William, (1957). An Introduction to Probability Theory and Its Applications. 2nd ed. John Wiley & Sons.
Fisher Sir Ronald A, (1956). Statistical Methods and Scientific Inference. Oliver and Boyd.
Flitney AP, Abbott Derek, (2002). An Introduction to Quantum Game Theory. Fluctuation and Noise Letters.2(4):R175–R187.
McKelvey Richard D, Palfrey Thomas R, (1995). Games and Economic Behavior.10:6–38.
Nash John, (1950). Equilibrium Points in N-Person Games. Proceedings of the National Academy of Sciences.36:48–49.
Nash John, (1951). Non-Cooperative Games. Annals of Mathematics.54(2):286–295.
Rapoport Anatole, (1967). Escape from Paradox. Scientific American.217(1):50–56.
Reichenbach Hans, (1949). The Theory of Probability. University of California Press.
Riordan John, (1958). An Introduction to Combinatorial Analysis. John Wiley & Sons.
Savage Leonard J, (1950). The Role of Personal Probability in Statistics. Econometrica.18:183–184.
Uspensky JV, (1937). Introduction to Mathematical Probability. McGraw-Hill.
Von Neumann John, Morgenstern Oskar, (1953). Theory of Games and Economic Behavior. Princeton University Press.
Weisstein, Eric W., “Random Walk–1-Dimensional,” http://mathworld.wolfram.com/RandomWalk1-Dimensional.html.
Bibliography
Bewersdorff, Jörg, Luck, Logic, and White Lies, A.K. Peters, Ltd., 2004.
Birnbaum Allan W, (1962). Introduction to Probability and Mathematical Statistics. Harper & Brothers.
Birnbaum Allan W, (1962). On the Foundations of Statistical Inference. J. American Statistical Assoc..57(298):269–326.
Borel Émile, (1948). Le Hasard. Presses Universitaires de France [New Edition].
Brown G Spencer, (1957). Probability and Scientific Inference. Longmans, Green and Co.
Cameron Colin F, (2003). Behavioral Game Theory: Experiments in Strategic Interaction. Princeton University Press.
Carnap Rudolf, (1950). Logical Foundations of Probability. Routledge and Kegan Paul Ltd.
Ching, W. K., and M. S. Lee, “A Random Walk on a Circular Path,” Journal of Mathematical Education in Science and Technology, 36, No. 6 (2005).
de Finetti, Bruno, “Recent Suggestions for the Reconciliation of Theories of Probability,” Proceedings of Second Berkeley Symposium on Mathematical Statistics and Probability, pp. 217 − 225, University of California Press, 1951.
Everett Brian, (1999). Chance Rules: An Informal Guide to Probability, Risk, and Statistics. Springer-Verlag.
Goeree, Jacob K., and Charles A. Holt, “Ten Little Treasures of Game Theory and Ten Intuitive Contradictions,” Working Paper, University of Virginia, 1999.
Goeree Jacob K, Holt Charles A, (1999). Stochastic Game Theory: For Playing Games, Not Just for Doing Them. Proceedings of the National Academy of Science.96:10564–10567 [September].
Good IJ, (1950). Probability and the Weighing of Evidence. Charles Griffin and Co.
Kendall MG, (1949). On the Reconciliation of Theories of Probability. Biometrika.36:101–106.
Kolmogorov AN, (1956). Foundations of the Theory of Probability. Chelsea Publishing Co.
Kyburg Henry E, Smokler Howard E, eds. Studies in Subjective Probability. New York: John Wiley & Sons;.
Markowitz H, (1952). The Utility of Wealth. Journal of Political Economy.60(2):151–158.
McKinsey JCC, (1952). Introduction to the Theory of Games. McGraw-Hill.
Mosteller Frederick, Rourke Robert, Thomas George, (1961). Probability and Statistics. Addison-Wesley.
Nisan Noam, Roughgarden Tim, Tardos Eva, Vazirani Vijay, eds. Algorithmic Game Theory. Cambridge University Press.
Smith John Maynard, (1982). Evolution and the Theory of Games. Cambridge University Press.
Venn John, (1876). The Logic of Chance. 2nd ed. Macmillan.
Von Mises Richard, (1957). Probability, Statistics, and Truth. George Allen and Unwin.
Williams JD, (1954). The Compleat Strategyst. McGraw-Hill.
Zadeh Lotfi, (1965). Fuzzy Sets. Information and Control.8:338–353.
1 Fuzzy logic has, in fact, been applied to Backgammon computers (q.v. Chapter 6).
2 Note that either of the two cards may be the postulated queen. A variation asks the probability of one card being a King, given the other to be a non-King (
). In this case,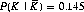 
).
3 Observe that if we distinguish suits but not ranks (four distinct kinds of objects, each with 13 indistinct elements), we obtain a considerably smaller number of permutations: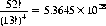 
4 So named by E. Lucas in Théorie des Nombres, Paris, 1891.
5 An apparatus that generates the binomial distribution experimentally is the quincunx (named after a Roman coin valued at five-twelfths of a lira), described by Sir Francis Galton in his book, Natural Inheritance (1889). It consists of a board in which nails are arranged in rows, n nails in the nth row, the nails of each row being placed below the midpoints of the intervals between the nails in the row above. A glass plate covers the entire apparatus. When small steel balls (of diameter less than the horizontal intervals between nails) are poured into the quincunx from a point directly above the single nail of the first row, the dispersion of the balls is such that the deviations from the center-line follow a binomial distribution.
6 The word “statistics” derives from the Latin status, meaning state (of affairs).
7 For a fascinating compendium of statistical traps for the unwary, see Darrell Huff, How to Lie with Statistics, W.W. Norton and Co., 1954.
8 Any type of average is known to statisticians as a “measure of central tendency.” Its etymological ancestor is the Latin word havaria, which originally described compensation funds paid to owners of cargo sacrificed to lighten the ship during heavy storms. Those whose merchandise survived transit provided indemnification to those less fortunate. Thus the concept of “average” arises from a type of primitive insurance.
9 The dangers of statistical inference are well known in certain commercial situations. Consider the proposition: “Statistics demonstrate that cancer-prone individuals tend toward cigarette smoking.”
11 Generally,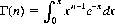 
for all n > 0.
12 The distribution of the quotient of two independent variates was first computed by the British statistician William Sealy Gosset who, in 1908, submitted it under the pseudonym “Student” (he was an employee of a Dublin brewery that did not encourage “frivolous” research).
13 Originally formulated in 1950 by Princeton mathematician Albert W. Tucker, the issue is framed by two prisoners, A and B, who, under separate police interrogation, must either confess—and implicate the other—or dummy up (remain silent). If both confess, each is sentenced to five years. If one confesses, while the other dummies up, the implicating prisoner goes free, while the silent prisoner receives a sentence of ten years. If both dummy up, each is sentenced to one year.A reasons that, should B confess, A would serve ten years if he dummies up and five years if he too confesses. On the other hand, should B dummy up, A would serve one year if he likewise dummies up, but will go free if he confesses. Ergo, his superior strategy is to confess. B will reason similarly. “Rational” decision making will therefore prompt both A and B to confess—and to serve five years in prison. Yet if both reached “irrational” conclusions and dummied up, each then would serve only one year.The dilemma arises from the fact that these individually rational strategies lead to a result inferior for both prisoners compared to the result if both were to remain silent. No solution exists within the restricted confines of classical game theory.
14 An extension of the conventional factorial,
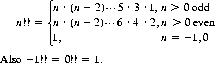
15 Decoherence is the mechanism whereby quantum systems interact with their environments to produce probabilistic behavior.