Chapter Seven

The Play of the Cards

Origins and Species

The invention of playing cards has been variously credited to the Indians, Arabs, and Egyptians. Chinese records claim that the first modern pack was shuffled in the reign of Sèun-ho,1 about A.D. 1120, and that cards became commonplace by the reign of Kaou-tsung, who ascended the Dragon throne in 1131; however, card games per se date back more than two millenia, preceding the invention of paper.²

Card playing was introduced into Europe through the Crusades (the Arabs endured lengthy sieges with cards and other gambling paraphernalia) and gained currency in Western society during the 14th century. In 1423, the Franciscan friar St. Bernardino of Siena preached a celebrated sermon against cards (Contra Alearum Ludos) at Bologna, attributing their invention to the devil. Despite such ecclesiastic interdiction, Johannes Gutenberg printed playing cards the same year as his famous Bible (1440). The pack struck by Gutenberg’s press consisted of Tarot cards, from which the modern deck is derived. Initially there were 78 cards: 22 “atouts” (literally: “above all,” later known as “triumph” or “trump”) including a Joker (le Fou) and four denominations of 14 cards each (ten numbered ranks plus a King, Queen, Cavalier or Knight, and a Valet or Knave). The four denominations, or suits, represented the four major divisions of medieval society: Swords symbolized the nobility; Coins, the merchant class; Batons or Clubs, the peasants; and Cups or Chalices, the Church. These suits are still reflected in the contemporary playing cards of Italy, Spain, Andorra, and Portugal.

About 1500, the French dropped the 22 atouts and eliminated the Knight, leaving a deck of 4 × 13 = 52 cards. They also transformed Swords, Coins, Batons, and Cups into Piques (soldiers’ pikes), Carreaux (building tiles, lozenge- or diamond-shaped), Trèfles (trefoils or clover leaves), and Coeurs (hearts). In 16th-century Spain, Swords were Espados; Coins were square pieces of currency, Dineros; Batons, Clubs, or Cudgels were Bastos; and Cups or Chalices were Copas. Hence, we have adopted the French symbols, translated the names of two (Hearts and Diamonds) into English and applied to the other two English translations of Spanish names for different symbols. Such is the illogic of language.

Despite a number of coincidences, no firm connection has been found between the structure of the deck and the calendar. It seems palpable to link the four suits with the seasons and the 13 ranks with the lunar months (corresponding to one card per week of the year). Further, if we assign a weight of 13 to the Kings, 12 to the Queens, 11 to the Jacks, and so forth, the 52-card pack totals 364; adding 1 for the Joker equals the number of days in a (nonbissextile) year. Such is the treachery of numerology.

Initially, the court cards3 were designed as portraits of actual personages, and stylistic vestiges of the individuals remain today. The four original kings (invested in 14th-century Europe) were Charlemagne (Hearts), the biblical David (Spades), Julius Caesar (Diamonds), and Alexander the Great (Clubs). Distaff royalty included Helen of Troy as the Queen of Hearts, Pallas Athena as the Queen of Spades (the only queen to be armed), and the biblical Rachel as the Queen of Diamonds. Regal ladies passingly honored as card monarchs were Joan of Arc, Elizabeth I, Elizabeth of York (wife of Henry VII), Roxane, Judith, Hecuba, Florimel, and Fausta, among many. Famous Jacks were frequently renowned warriors, such as Hogier La Danois, one of Charlemagne’s lieutenants (Spades); Etienne de Vignoles, a soldier under Charles VII of France (Hearts); Roland, Charlemagne’s nephew (Diamonds); and the gallant knight Sir Lancelot (Clubs).

Many cultures have evolved decks partitioned in other ways. The Hindus employ a deck with ten denominations, representing the ten incarnations of Vishnu. The Italians use, generally, a 40-card deck, and the Spanish use a 48-card deck. The French play games with both the 52-card pack and the 32-card Piquet pack (omitting twos through sixes). Clearly, the number of cards comprising a deck is arbitrary and could be selected to satisfy the needs of a particular game. However, we shall consider, unless otherwise specified, the 52-card pack partitioned into 4 denominations and 13 ranks.

Randomness and Shuffling

Bias

The question of the “fairness” of a deck of cards is distinct from questions of bias relating to coins, dice, or roulette. Intuitively, a deck of cards is fair if each outcome is enumerated and is represented identically as all others. Experimenters have conducted tests to establish the veracity of this intuition. Most notably, the statistician C.V.L. Charlier performed 10,000 drawings (with replacement) from a conventional deck, recording 4933 black cards and 5067 red cards for a deviation of 67 from the expected value. The standard deviation is

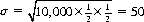
assuming red and black cards to be equiprobable. A result with a 1.34σ deviation is hardly unusual.

Cut and Shuffle Operations

Rather than bias, the appropriate parameter for cards is randomness. Since the ordering of a deck is neither random nor nonrandom in itself (every possible ordering is equiprobable a priori), we must adopt a dynamic concept of randomness. That is, the question of randomness is meaningful only when the ordering is being changed by some process such as shuffling. We consider here five types of processes that transform one ordering of a deck into another.

A simple cut c translates the top card of the deck to the bottom; thus the power cⁱ of this operation separates the deck after the ith card and is merely a phase shift transforming the order 1, 2, 3, …, i, j, k, …, 2n into the order j, k, …, 2n, 1, 2, 3, …, i.

The perfect shuffle (or “out shuffle”) operation s on a 2n-card deck separates the top n cards from the bottom n cards and precisely interleaves them, the top and bottom cards remaining unchanged in position. Functionally,

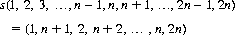
From this equation it follows that if the card in position a₀ is moved to position a₁ by the perfect shuffle s, then

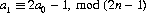
noting that a₁ = 1 for a₀ = 1, and a₁ = 2n for a₀ = 2n. After k iterations of s, the card originally in position a₀ has moved to position a_k. Thus,

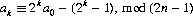
The modified perfect shuffle (or “in shuffle”) s′ constitutes the same operation, but with the (n + 1)st card moving to the top and the nth card to the bottom.

Defining this operation:

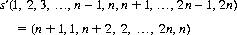
and if the card in position b₀ is moved to position b₁ by the modified perfect shuffle s′,

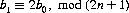
In general, after k iterations of s′,

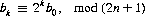
One mildly interesting characteristic of the modified perfect shuffle is that, for the standard deck, each shuffle interchanges cards in the 18th and 35th position. Also, the 52-card deck reverses its order after 26 such shuffles.

A curious phenomenon arising from the mixing of successive operations s and s′ (Out and In shuffles) was discovered by Alex Elmsley (Ref. Gardner) who found that card c₁ would be moved to position c_x by a sequence of shuffles that spells out x–1 in binary form. For example, to move the card in first position to the 15th position, perform three In shuffles followed by an Out shuffle: IIIO, the binary representation of 14. Further, reversing this sequence of shuffles reverses the card movement. Thus an Out shuffle followed by three In shuffles (OIII) moves card c₁₅ to position c₁.

The amateur shuffle operation s_a divides the deck approximately into two groups of n cards and interleaves them singly or in clusters of 2, 3, or 4 according to some probability distribution. An amateur shuffle operation, wherein the probability of the ith card in the final sequence originating in either half of the deck is 1/2, provides 2⁵² possible sequences. hence, the maximum amount of information associated with this shuffling process is log₂2⁵² = 52 bits. With a known probability distribution constraining the s_a operator, the information required to specify s_a is evidently less than 52 bits.

Finally, we define the random shuffle s_r as an operation equivalent to having each card selected in turn by a blindfolded inebriate. Since the random shuffle renders equiprobable all possible orderings of the 52 cards, it is associated with the greatest amount of information. Specifically, log₂52! = 225.7 bits of information are required to describe this operation.

(A perfect shuffle is completely deterministic and therefore is not accompanied by an information parameter.)

Randomness and Cycling

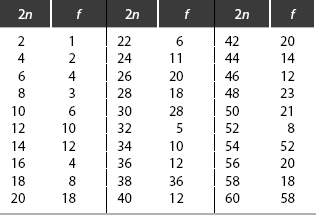
It can be shown that to randomize the deck, the amateur shuffle operation must be repeated at least five times. Typical forms of s_a dictate 20 to 30 replications to achieve randomization.If the perfect shuffle operation s is iterated f times on a 2n-card deck, where f is the exponent of 2, mod (2n – 1), the deck is restored to its original ordering. Specifically, eight perfect shuffles cycle the 52-card pack to its original ordering,⁴ since 2⁸ = 1, mod 51. Table 7-1 tabulates the values of f for decks up to 2n = 60 cards.

Table 7-1. Deck Cycles with Perfect Shuffles

For the modified perfect shuffle operation s′, 52 iterations are necessary to cycle the deck, since 2 is primitive, mod 53—that is, f′ = 52 is the lowest solution to 2^f′ = 1, mod 53. Thus, f and f′ are the orders of s and s′, respectively. The operation c has order 2n, since c is a primitive cyclic permutation on 2n cards. The operations c and s together (cut and shuffle) generate the entire symmetric group S_{2 n} of permutations on the 2n cards (c and s′ also generate an entire symmetric group of permutations). The order of the product operation cs assumes one of two values. If the deck size is such that 2n – 1 is a power p^m of a prime p, where n is any positive integer, and 2 is primitive, mod p^m—that is, f = ϕ(p^m) = p^m−1(p − 1), where ϕ is Euler’s function—then the order of cs, O(cs), is

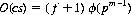
If, on the other hand, either 2n − 1 has two or more distinct prime factors or, although 2n − 1 is a power of a prime, 2 is not primitive, mod(2n − 1), then the order of cs is given by

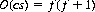
as is the case for the conventional deck (n = 26).

A proof of the theorem that the operations c and s (or c and s′) applied to a deck of 2n cards generate the entire symmetric group S_{2 n} of permutations on the 2n cards has been published by S.W. Golomb (Ref.). This theorem expresses the equivalence between the operations cⁱs^k and s_r—that is, the perfect shuffle and single-cut operations sufficiently iterated can produce complete randomness.

For decks of 2n − 1 cards, we adjust our definition of the perfect shuffle as an operation that separates the bottom n cards from the top n − 1 cards and precisely interleaves the two sets, the bottom card remaining invariant, and the nth card emerging on the top. The operation has order f (the exponent of 2, mod [2n − 1]), and the simple-cut operation is definable as with an even-numbered deck and has order 2n − 1. A theorem developed by Golomb states that the operations and applied iteratively to a deck of 2n− 1 cards generate a subgroup of the symmetric group S_2n−1 of order

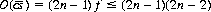
This subgroup is proper for n > 2. Therefore the operation cⁱs^k can never be made equivalent to the random shuffle operation s_r, since not all permutations of odd-sized decks are obtained by the cutting and perfect shuffling operations.

Characteristics of the Amateur Shuffle

Of more practical concern is the amateur shuffle operation s_a. Experiments undertaken by the author indicate that neophyte shufflers tend to interleave cards in clusters at the beginning and end of each shuffle; intermediate positions are generally alternated singly or by twos. More proficient shufflers appear to overcome the clustering tendency, which is caused by the first and final cards of the new sequence adhering to the fingers. Indeed, postgraduate shufflers, such as dealers in Las Vegas casinos, exhibit a uniform type of card interleaving with quite small variances. The nature of the s_a operator was investigated by recording the sound waves produced by shuffling a deck of cards (a flat-response microphone and sharp-skirted high-pass filters were used with a fast-response sonograph). Duration of a beginner’s shuffle is about 700 milliseconds, while virtuoso shufflers average about 1/2 second for a shuffle.

It was found that highly expert shufflers create sequences with single-card interlacings approximately eight times more frequently than two-card interlacings; a group of three cards appears less than once per shuffle. Thus, to an excellent approximation, the geometric distribution (Eq. 2-13)

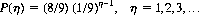(7-1)

represents the probability that a sequence consists of η cards. It is evident from this equation that a large measure of orderliness is preserved for a small number of shuffles. This fact suggests the feasibility of predicting the position of a card following the s_a operation. However, the problem of prediction is subsequent to the question of the correlation between successive card sequences.

Correlation of Card Sequences; Markov Chains; Entropy

The shuffling operation evidently is not a function of the order of the deck on which it operates nor of the past history of the deck. Hence, successive operations correspond to independent trials with fixed transition probabilities. The sequence of cards is therefore said to form a Markov chain, and the matrix of transition probabilities from one of the 52! states of the deck to another is doubly stochastic (both the row sums and the column sums are unity).

As a measure of the relationship between the initial state S_j and the state S_k that results after n shuffles, the concept of entropy logically suggests itself (connected, as it is, to Markov processes). In statistical mechanics, Boltzmann’s hypothesis, which relates it to probability. Therein, p_i is defined as the probability of a system being in cell (or state) i of its phase space. The entropy H of the set of probabilities p₁, p₂, …, p_n is

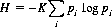
Entropy, then, is a measure of uncertainty or of disorder; the greater the entropy, the less the preservation of order. (The constant K simply specifies the unit of measure; it is expedient to set K = 1.)

Applying the entropy concept to the phenomenon of card shuffling, we define

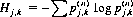
as the desired measure. Here, p_j,k^{( n)} denotes the probability of finding the deck in state S_k at step t + n, given that at step t it was in state S_j.

To compute numerical values of entropy for a conventional deck imposes a Herculean burden of arithmetical labor. The transition probabilities form a 52! × 52! matrix (52! 10⁶⁸); evaluations of H_j,k are thus far beyond the reach of any practical computer. Fortunately, since the ultimate goal is to develop a useful prediction function, there exists a pragmatic simplification that dispenses with excessive computational chores.

Prediction

We can state the problem of prediction as follows: Given the deck of cards in state S_j, and, following n shuffles, given the first m cards of the new sequence represented by state S_k, what predictions can be made concerning the (m + 1)st card? Note that since we are applying the prediction to the goal of increasing the probability of success at some game, we wish a probability distribution of this (m + 1)st card; that is, we wish to obtain a maximum-expectancy decision rather than a maximum-likelihood prediction. Rigorously, we should now examine all those states reachable from state S_j after n shuffles whose sequences begin with the m cards specified. The corresponding transition probabilities for each allowable state are then tabulated according to the possible cards that can occur in the (m + 1)st position—and the probability distribution of the (m + 1)st card is obtained. However, we now invoke our pragmatic observation that

given the original sequence and the first m cards of the final sequence, the (m + 1)st card must be one of 2ⁿ cards, n shuffles having transformed one sequence into the other.

To apply this observation practically, we consider only those transition processes comprising one, two, or three shuffles; for n equal to six or more shuffles, the statement is virtually useless with a conventional deck. First, we must specify for the shuffling process a probability distribution that is applicable to a finite-length deck (Eq. 7-1 implies an infinite deck). From experience, an expert shuffling operation interleaves alternate packets of cards where each packet consists of one, two, or three cards (with amateur shuffling the packets may comprise four or more cards).

Accordingly, we let r₁, r₂, and r₃ represent the probabilities that a packet selected at random is composed of one, two, or three cards, respectively (where r₁ + r₂ + r₃ = 1), Or, equivalently, we can define p₁ as the probability that a packet ends with the first card. Given that the packet does not end with the first card, the (conditional) probability that it ends with the second card is designated by p₂. And, given that the packet does not end with the second card, the (conditional) probability that it ends with the third card is p₃ = 1. Thus,

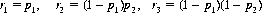
If three consecutive cards of the new sequence are observed, one of four patterns must occur: AAA, AAB, ABA, or ABB, where A represents a card from one section of the divided deck and B represents a card from the other section. The probability of occurrence of each of these four patterns is readily calculated as

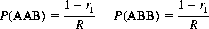
where R = r₁ + 2r₂ + 3r₃.

We can now compute the transition probabilities between packets after observing one of the four allowable patterns. Let P_t(X) be the probability of a transition, given the event X, and let Q_t(X) be the probability of no transition. Then it is elementary to demonstrate that

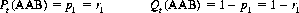
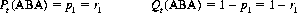
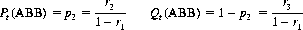
For a second shuffle, consider the A cards to be divided into C and E cards and the B cards to be divided into D and F cards, depending on the deck partitioning. The first test is to apply these equations for transition probabilities between members of the CD set and those of the EF set. Second, we apply the same equations to determine the conditional transition probabilities for the C set versus the D set and the E set versus the F set. The next card in sequence within each set occurs with the probability accorded that set. This procedure can evidently be generalized to three or more shuffles; for n shuffles, there are 2ⁿ sets of cards.

A numerical example will clarify these concepts. Observations of professional card dealers indicate a shuffling operation described by

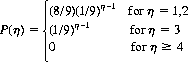(7-2)

(which approximates Eq. 7-1). In terms of packet lengths, r₁ = 8/9, r₂ = 8/81, and r₃ = 1/81. Thus, assuming an equipartition of the deck, the probability of successive cards of the post-shuffle sequence alternating between members of the opposing halves of the original sequence is 8/9; at any point in the new sequence, the probability of obtaining two consecutive members of the original sequence is 8/81; and the probability of obtaining, at any point, three consecutive members of the original sequence is 1/81.

With this probability distribution for the shuffling process, the prediction function for the (m + 1)st card is readily obtained. Consider the initial state S_j defining the sequence of cards c₁, c₂, …, c₅₂. A single shuffle is performed according to Eq. 7-2 (with equipartition of the deck and the first card remaining invariant). The first m cards forming the new state are then composed of α cards of one half and m − α cards of the other half. Thus, the (m + 1)st card is either the (α + 1)st card of the first half (the A set) or the (m − α + 1)st card of the second half (the B set), with respective probabilities corresponding to Eq. 7-2 as a function of the (m − 2)nd (m − 1)st, and mth cards. As an example, let m = 10, and let the first ten cards of the new sequence following one shuffle be c₁, c₂, c₂₇, c₃, c₂₈, c₄, c₂₉, c₅, c₃₀, c₃₁. The 11th card must be either c₃₂ or c₆ with probabilities 1/9 and 8/9, respectively, as seen from the equations for Q_t(ABB) and P_t(ABB).

Continuing the example: After two shuffles (we assume that results of the first shuffle are not disclosed) with the first ten cards of the new state forming the sequence c₁, c₂₇, c₁₃, c₂, c₃₉, c₄₀, c₂₈, c₁₄, c₁₅, c₃, the 11th card must be c₄, c₂₉, c₁₆, or c₄₁. Let the A set initially encompass cards c₁, c₂, …, c₂₆, and the B set cards c₂₇, c₂₈, …, c₅₂. Then, following two shuffles, the classification of the first ten cards of the new sequence is

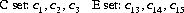
The first test, as described above, is to distinguish between the CD and EF sets. Referring to the new sequence, the last three cards form an AAB pattern; then, from the equations for P_t(AAB) and Q_t(AAB),

(7-3)

Equations 7-3 represent the probabilities that the eleventh card is a member of the EF or CD set, respectively. Now, given that the eleventh card belongs to the EF set, we test for E versus F by noting that the last three cards of the EF set (c₄₀, c₁₄, c₁₅) form an ABB pattern. Hence, applying the equations for P_t(ABB) and Q_t(ABB),

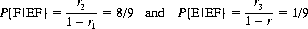(7-4)

Similarly, in testing for C versus D, we note that the last three cards of the CD set (c₂, c₂₈, c₃) form an ABA pattern. Thence, from the equations for P_t(ABA) and Q_t(ABA),

(7-5)

The probability that the 11th card is c₄, c₂₉, c₁₁, or c₄₁ is then determined by Eqs. 7-3 through 7-5 in the following manner:

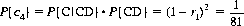
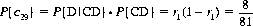
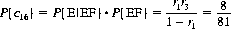
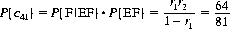
Continuation of this procedure for three shuffles is straightforward, albeit hampered by arithmetical drudgery. Practical applications of card prediction, even with our pragmatic theorem, invite the aid of a modest computer.

Monge’s Shuffle

There are other methods of card shuffling apart from the alternate interleaving of card packets.5 Each method might be associated with one or more convenient theorems for card prediction, depending on the regularities involved in the shuffling procedure. As one example, consider a pack of cards arranged in the order c₁, c₂, c₃, …; we shuffle this pack by placing c₂ above c₁, c₃ under c₁, c₄ above c₂, c₅ under c₃, etc.—an operation known as Monge’s shuffle.⁶ Then, illustratively, if the pack contains 6n − 2 cards, the 2nth card always retains its original position. With 22 cards (n = 4) shuffled repeatedly by this process, the eighth card never changes place; the fifth and 16th cards oscillate, exchanging positions at each shuffle; and the third, 13th, and 18th cards circulate in an independent cycle, regaining their original positions every third shuffle. Cyclic periods of the full deck are generally longer with Monge’s method as compared with the perfect shuffle (interleaving alternate cards).

There exists a theorem stating that the cyclic period ρ resulting from Monge’s shuffle on a 2n-card deck is equal to the smallest root of the congruence

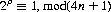
and if this congruence possesses no solutions, ρ equals the smallest root of the congruence:

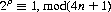
With 52 cards (n = 26), Monge’s shuffle operations cycle the deck after 12 shuffles (2¹² ≡ 1, mod 105), compared to eight for the perfect shuffle. For a 16-card deck, the original order returns after five Monge shuffles, compared to four perfect shuffles needed for cycling.

Monge’s shuffle, as well as other shuffling operations considered here, are examples of binary shuffling, wherein the deck is divided into two parts that are then interleaved. It is quite feasible, of course, to divide the deck into three or more parts and then perform a shuffling operation (Ref. Medvedoff and Morrison); however, in practical terms, such shuffles are inconvenient.

Card Probabilities

Sampling without Replacement

Combinations and permutations of cards generally involve the hypergeometric distribution (Eq. 2-10)—as opposed to dice or coin combinations, which are governed by the binomial distribution. Card statistics, then, involve the principle of sampling without replacement. An elementary illustration of this principle, which demonstrates the considerable difference from sampling with replacement, is that of drawing two cards at random from a complete deck. The probability of both cards being Aces (say) is (4/52) · (3/51) = 0.0045, whereas if the first card is replaced before drawing the second, the probability of obtaining two Aces is (4/52)² = 0.0059, a 31% change.

Another example supplies greater emphasis: A single red card is removed from the deck. Then 13 cards are drawn and found to be the same color; the (conditional) probability that they are black is

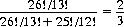
a greater difference than might be expected from the corresponding probability of 1/2 for sampling with replacement. Of course, if the population size (52, initially) is large compared with the sample size (4, for the example of the card ranks), the binomial and hypergeometric distributions produce approximately the same results. The striking differences occur as cards are withdrawn from the deck. If we consider the number of cards drawn without replacement until a Spade appears (at the mth draw), then

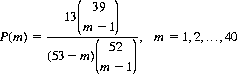
constitutes the probability distribution over m. Clearly, P(m) becomes quite small as more cards are drawn without a Spade appearing. For m = 11, P(m) has decreased to 0.0124 from its value of 0.25 at m = 1. For m = 40, P(40) = 1.575 × 10⁻¹².

Similarly, the number of cards drawn without replacement until an Ace appears is

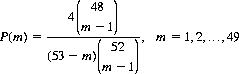
For m = 11, P(11) is 0.0394 as compared with P(1) = 1/13. For m = 49, P(49) = 3.694 × 10⁻⁶.

An example demanding careful distinction between a priori and a posteriori probabilities in sampling without replacement concerns a deck of cards from which one card has been removed. Two cards are then drawn at random and found to be Spades. We wish to determine the probability that the missing card is also a Spade. A priori, this probability is 1/4. The joint probability that the missing card and the two drawn cards are Spades is

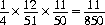
while the joint probability that the missing card is a non-Spade and two Spades are drawn is

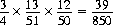
Hence, applying Bayes theorem, Eq. 2-4, to determine the a posteriori probability of the missing card being a Spade, we obtain

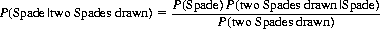
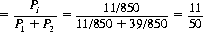
Expected Number of Cards to Achieve Success

An important consideration in card probabilities is the expected number of cards drawn without replacement to achieve a particular success; we could ask, for example, the expected number of cards drawn to uncover the first Ace, or the first Spade, etc. The solution of this type of problem is obtained from the discrete analog to the nonparametric technique used in order statistics. An equivalent to the density function of ordered observations can be derived directly. With a deck composed of a kinds of cards and b of each kind (a total of n = ab), the probability P_i(r), i < a, that none of the i kinds is represented in a random sample of r cards is given by

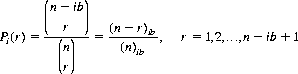
Now, if we define p_i(r) as the probability of failure through the first r − 1 cards times the probability of success on the rth card, we have

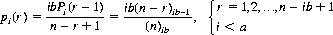(7-6)

For i = a, p_a(1) = 1.

The expected number of cards to achieve the event specified by the probability p_i(r) is defined by

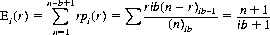(7-7)

with the expression for p_i(r) substituted from Eq. 7-6. By extension, the expected number of cards E_i^m(r) to uncover the mth number of one of i groups of b cards is

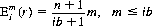(7-8)

[If the cards are drawn with replacement, E_i^m(r) is expressed by nm/ib.]

We can now answer the questions posed. The expected number of cards to uncover the first Ace is, from Eq. 7-7 with n = 52, i = 1, and b = 4,

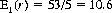
The expected number of cards until the appearance of the first Spade is also given by Eq. 7-7 with i = 1 and b = 13:

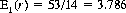
And, according to Eq. 7-8, it is expected that

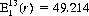
cards are required to expose all Spades in the deck. It also follows that the expected number of cards between successive Spades remains unchanged. That is, if A deals from the pack until a Spade appears, then passes the remainder of the deck to B, who deals until a second Spade appears and then passes the remainder of the deck to C, who deals cards until the appearance of the third Spade, the expectations of the number of cards dealt by A, B, and C are identical.

From Eq. 7-7, we can also answer the following question: What is the expected number of cards drawn without replacement until at least one card of each suit is exposed? With four suits, S, H, D, and C, we can write this expectation in the form

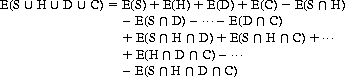
After appropriate substitutions,

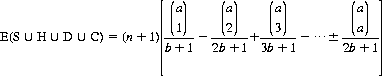
For the conventional deck (a = 4, b = 13),

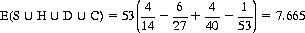(7-9)

This figure suggests the following game: The House deals out eight cards, winning one unit from the Player if all four suits are represented; otherwise the Player is paid two units. The probability of this event is expressed by

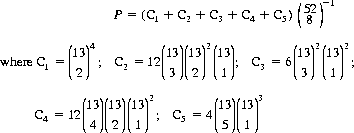
Thus P = 0.685, and the House Take is 3P − 2 = 5.63%.

Interestingly, replacement of the cards creates a problem easier to solve. Drawing until each suit is exposed at least once represents four exclusively ordered events. The probability of obtaining the first suit at the first card is p₁ = 1. The probability that the second card is a suit other than the first is p₂ = 3/4. Subsequently, p₃ = 1/2 and p₄ = 1/4 by the same reasoning. Thus, by applying Eq. 6-18, we have

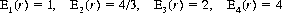
The sum of these expectations produces

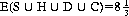
which, as might well be anticipated, is greater than the value obtained by sampling without replacement (Eq. 7-9).

Combinations

The number of combinations of n objects taken r at a time is given by Eq. 2-10 as . Thus, the number of distinct Poker hands totals

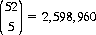(7-10)

and the number of different hands possible at cribbage is = 20,358,520.

An extension of this combinatorial formula considers the probability P that, in a random sample of size r selected without replacement from a population of n elements, all of N given elements are contained in the sample. It is straightforward to prove that

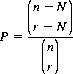
Illustratively, the probability that a Poker hand contains all four Aces is

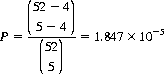
Similar combinatorial formulae can answer most of the elementary probability questions that arise in games of cards.

Dividing the Deck

A conventional deck of cards is divided, at random, into two parts—that is, the dividing point is randomly distributed and, therefore, is equally likely to be in the left half as in the right half of the deck. Thus, on average it will be at one-half of that half or one-fourth of the deck length, the deck being divided into segments of 39 and 13 cards.⁷

To determine the average ratio of the smaller segment to the larger, let the dividing point be in the right half of the deck. Then (1 −x)/x is the ratio, and, since x is evenly distributed from 1/2 to 1, the average value is

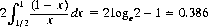
rather than the intuitive 1/3. Thus there will be 14.48 cards rather than 13 in the smaller segment.

It can be shown that when the deck is randomly divided into three parts, the average lengths of the segments form the proportions 1/9, 5/18, and 11/18. (For a 54-card deck [two Jokers added], the three segments comprise 6, 15, and 33 cards.)

Positions of the Aces

Cards from a standard deck are turned over one by one. We ask the most likely positions for the two black Aces.

The probability that the first black Ace turns up in position p₁ (1 ≤ p₁ ≤ 51) is

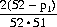
which has its maximum value at p₁ = 1; therefore the most likely position for the first black Ace is on top. By symmetry, the probability that the second Ace turns up in position p₂(2 ≤ p₂ ≤ 52) is

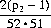
which has its maximum value at p₂ = 52; thus the most likely position for the second black Ace is on the bottom.

If we inquire as to the probability of the first of the four Aces being in position p₁^′, we can derive the expression

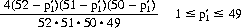
which has its maximum value (1/13) at p₁^′ = 1. The probability that an Ace appears in the first eight cards is close to 1/2 (more precisely, 0.4986).

Higher Card

Two cards are drawn successively from a standard deck. We are interested in the probability that the second card is higher in rank than the first card.

SinceP(higher) + P(lower) + P(same) = 1; since P(higher) = P(lower); and since P(same) = 3/51, we can immediately write

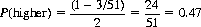
Sens Dessus-Dessous (Ref. Nick’s Mathematical Puzzles)

A standard deck is thrown into a high-velocity wind tunnel—so that each card, independently and equiprobably, lands face up or face down. The numerical rankings of the face-up (or face-down) cards are summed, with Ace = 1 through King = 13. We ask the probability P that this sum is divisible by 13.

First, we establish the generating function

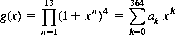
Each exponent in g(x) represents a total value, and each corresponding coefficient a_k represents the number of ways of obtaining that value. Thus, we can write for P:

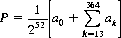
since there are 2⁵² configurations of the deck.

To express this summation, let t be a complex primitive root of 1. Then t¹³ = 1, and 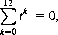which leads to

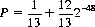
That P differs from 1/13 is counterintuitive. That it differs by such a minute amount (in the 18th decimal place) is a further surprise.

Matching Problems (Rencontres)

In the simplest form of card matching, a deck of n distinct cards numbered 1, 2, …, n is randomized and dealt out. If the number of a card coincides with its position in the deck, that circumstance is designated a match. We inquire as to the probability of one or more matches occurring.8

Let P_n equal the number of permutations without a match. Then

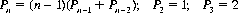
Since the total number of permutations is n!, the probability of no matches is P₀ = P_n/n! Table 7-2 shows that P₀ converges rapidly for even relatively small decks.

Table 7-2. Probability of No Matches versus Deck Size

The probability of at least one match, therefore, equals 0.632⁺. For n = 52, P₀ = 0.368⁻. As n increases, P₀→ 1/e = 0.36788⁻ (a value—surprisingly—virtually independent of n).

The probability P_m of exactly m matches among n events (e.g., a deck of n cards) was calculated by Montmort. Specifically,

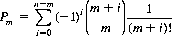(7-11)

As an example, for three matches with decks of any length greater than 6, P₃ = 0.0613⁺. Note that P_n−1 = 0 since exactly n − 1 matches are not possible, and P_n= 1/n! for the case where both decks are in the same order.

Equation 7-11 can further be applied to evaluate the validity of “psychic” perceptions (see Chapter 11).

A matching problem credited to Levene⁹ consists of shuffling together the Hearts and Spades of a conventional deck. The 26 cards are then divided into two piles of 13 and matched against each other; a match is recorded if the ith of Spades and the ith of Hearts occur at the same position in the two piles. We wish to determine the probability of exactly r matches. The probability distribution of r can be derived as

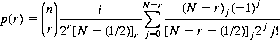
where N is the number of cards in each pile. For N = 13, the probability of no matches is p(0) = 0.5948. For r = 1, p(1) = 0.3088; also p(2) = 0.0804, and p(3) = 0.0140. As N→ ∞, the number of matches assumes a Poisson distribution, and p(r) approaches the values 0.6065, 0.3033, 0.0758, and 0.0126 for r= 0, 1, 2, 3, respectively.

Oddly, Levene’s problem assumes a simpler form (suggested by Kullback¹⁰) if the compositions of the two piles are determined by random, independent drawings from two populations. Let the first pile be composed by drawing cards from a population containing a_i cards of the ith kind, i = 1, 2, …, k, where p_i is the constant probability that a card of the ith kind is drawn. Similarly, let the second pile be formed by drawing cards from a second population containing b_i cards of the ith kind, i = 1, 2, …, k, and let p′_i be the constant probability of drawing a card of the ith kind from this population. Each pair of cards in the same position in the two piles constitutes an independent event; thus the probability p of a match is simply

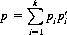
The probability of r matches therefore forms a binomial distribution (Eq. 2-11):

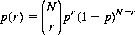
As N and k both increase indefinitely, p(r) becomes Poisson-distributed.

A more difficult matching problem, not readily handled by conventional means, is the matching of two n-card decks, each of which comprises a suits and b cards in each suit. A match is now defined as the coincidence of two cards of the same rank without regard to suit (we could, obviously, interchange rank and suit and inquire as to matching by suits).

This problem is best attacked through the application of rook and hit polynomials. The former is defined as the generating function of the number of ways of placing non-mutually-attacking rooks on a chessboard. Thus to formulate the rook polynomial R(x), we envision the equivalent n x n chessboard as containing n rooks, no two in the same row or column; i rooks on the negatively sloped diagonal correspond to i matches. The rook polynomial is then expressible as

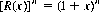
Further, we define a hit as the occurrence of an element of a permutation in a forbidden position. Thus the hit polynomial N_n(t) engenders the permutations by enumerating the number of hits. That is,

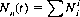
where N_i is the number of permutations of n distinct elements, i of which are in restricted positions. Clearly, the rook polynomial determines the hit polynomial, and vice versa.

To determine the rook polynomial for a = 4 and b = 13, consider a 4 × 4 chessboard. There are 4² = 16 ways of placing a single rook on such a board; two mutually nonattacking rooks can be placed in (4² × 3²)/2! = 72 ways; three nonattacking rooks can be placed on this board in (4² × 3² × 2²)/3! = 96 ways; and four rooks allow (4² × 3² × 2² × 1²)/4! = 24 ways. It is clearly impossible to place five or more nonattacking rooks on a 4 × 4 chessboard. The rook polynomial is therefore written as

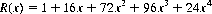
We are specifically concerned with the polynomial [R(x)]¹³ arising from the 13 cards in each suit. The corresponding hit polynomial assumes the form

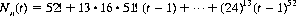
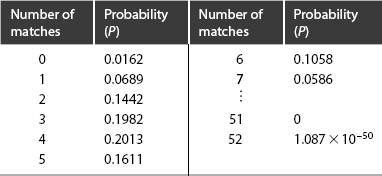
and the quantity N_n(0)/n! is the probability of no matches. The probabilities of exactly i matches are displayed in Table 7-3. Hence the probability of at least one match is 1 − P(0) = 0.984, somewhat higher than might be expected intuitively.

Table 7-3. Probability of i Matches

We can also calculate the expected number of matches as

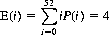
which is also the most probable number. The standard deviation is .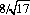

Rook polynomials are not restricted to square chessboards; rectangular, triangular, and trapezoidal chessboards have also been called on to solve problems in combinatorics.

Rank Matching

Cards are dealt out one at a time from a standard deck. We inquire as to the expected number of cards, E, to realize a match—that is, two cards of the same rank. This expectation11 can be expressed as

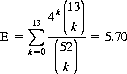(7-12)

The probability P(n) that a match occurs for the first time with the nth card, 2 ≤ n ≤ 14, is given by

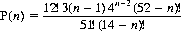
For n = 2, 3, 4, 5, Eq. 7-12 yields

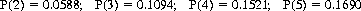
for a cumulative total of 0.4893. Thus the wager that a match (of ranks) will occur by the fifth card dealt has an expected gain of −0.0214.

Rank Color Matching

Here, we define n distinct pairs of same-colored cards: n/2 Red pairs and n/2 Black pairs. With the cards exposed one at a time, the expected number to realize a matched pair is

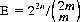
For the standard deck, n = 26, and

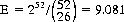
The probability that the first rank-and-color match occurs at the exposure of the nth card, 2 ≤n ≤ 27, is expressed by

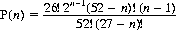(7-13)

Evaluating Eq. 7-13 for values of n between 2 and 9:

for a cumulative total of 0.5102. Wagering that a match occurs by the ninth card dealt therefore entails a positive expectation of 0.0204.

Suit Matching

Dealing cards one by one from a standard deck, the probability of obtaining a suit match on the nth card, 2 ≤ n ≤ 5, can be written as

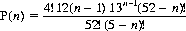
which yields

With a payoff of 3 to 1 for achieving a match at the second card dealt, the bettor on that event is faced with an expected gain of −0.0588.

Color Matching

Considerably more complex is a particular problem of color matching. From a deck of 4n cards, 2n red and 2n black, cards are dealt out in pairs. If a pair is matched by color, it is placed in Pile 1. Pairs of mismatched colors are retained, shuffled, and then dealt out again in twos, this time with color-matched pairs deposited in Pile 2. This process is continued until the deck is depleted. We wish to determine E(n), the expected number of piles resulting (including piles containing zero cards).

For any n, there are ways of pair-matching on the first round. Noting that for every matched red pair there must be a matched black pair (since a mismatched pair consists of one red and one black card), there will be 2k pairs, 2n ≥ k ≥ 0, discarded in each round. After the first round there will be 2n − 2k pairs remaining—having discarded 2k pairs in 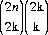2^{2( n− k)} ways (2k out of 2n pairs are same-colored, and k out of these 2k pairs are red, leaving 2^{2( n− k)} possible ways for the remaining unmatched 2n − 2k pairs). The number of pairs retained is therefore 2n − 2k, and the expected number of further rounds required to discard them is E(n − k). We can then write

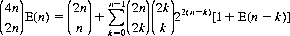
The k = 0 component can be expressed distinctly, reconstituting this equation to

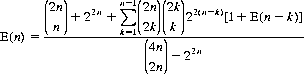(7-14)

For n = 1 (a deck of 2 red and 2 black cards), we can immediately write

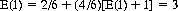
Then, from Eq. 7-14,

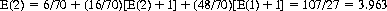
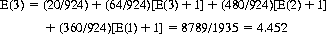
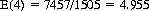
For the conventional deck, E(13) = 6.653. With increasing n, E(n) slowly edges toward infinity.

The probability P(n) that the deck will be depleted on or before the nth deal is tabulated as follows:¹²

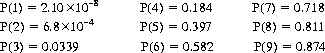
Thus, for example, a wager (at even odds) that the deck will be depleted by the sixth deal entails an expected gain of +0.164.

Selected Sidelights

Highest Rank in a Sample

It is informative to consider a game wherein the cards of a pack are exposed one by one until all four suits are represented, with the first-drawn card of each suit set aside. Of the four cards so collected, we inquire as to the probability P_m that m is the highest rank (Ace = 1, King = 13). Clearly, the probability P that the highest rank does not exceed m is P = P₁ + P₂ + … + P_m, which is equivalent to (m/13)⁴, since the probability that each suit contributes a rank m or less is m/13. Therefore, replacing m by m − 1, we can write

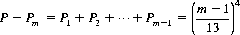
Combining the expressions for P and P − P_m,

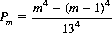
which is monotonically increasing with m. For m = 1 (Ace), P₁ = 3.5 × 10⁻⁵; for Queen and King, P₁₂ = 0.211 and P₁₃ = 0.274.

Information: The Exposed Ace

It is enlightening to consider an example that illustrates the effect of information on card probabilities. Suppose that in a random sample of five cards, one is known to be an Ace. Then the probability P that the remaining four cards comprise at least one additional Ace is

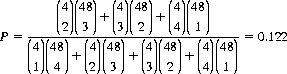
Now suppose that of the five-card sample, one is known to be the Ace of Spades. The probability P′ that the remaining four cards include at least one more Ace is then determined to be

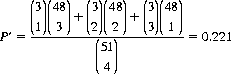
In this instance the knowledge of the specific Ace has increased the probability of one or more additional Aces in the sample.

Knowledge of color-only results in an intermediate value of the probability for additional Aces. Specifically, the probability P″ of the four unknown cards comprising one or more Aces, given the first card to be a red Ace, is

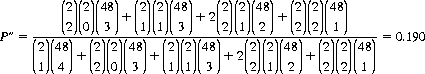
This probability is closer to the specified-Ace value than to the value for the case of an unspecified Ace. In order to avoid semantic confusion, each case should be considered as a distinct dichotomy—the particular condition (red Ace, for example) is either specified or not; alternations between color and suit produce equal probabilities for all cases.

Informal Card Games

In addition to the conventional card games that have evolved throughout the centuries, many rudimentary games can be invented spontaneously to illustrate certain principles.

First Ace Wins

Consider the simple game wherein first A and then B alternately draw cards from a deck, the winner being that player who first draws an Ace. A wins the game immediately with probability

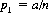
where a is the number of aces and n the total number of cards. A also wins on his second try if the first two cards are non-Aces and the third is an Ace. The probability p₂ of this occurrence, by the theorem of compound probabilities, is expressed in the form

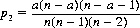
Similarly, the probability p₃ of A winning on his third try (the first four cards drawn being non-Aces and the fifth an Ace) is

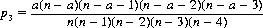
And the probability P_A that A wins the game is the sum p₁ + p₂ + p₃ + … + p_{( n− a)/2}:

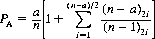
Analogously, B’s probability P_B of winning the game is

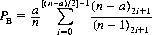
For a = 4 and n = 52, we have, numerically,

Thus, A gains a 4% advantage by being first to draw.

With three players A, B, and C competing in that order to draw the first Ace, we can derive the expressions

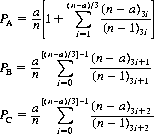
For a = 4 and n = 52, these equations are evaluated numerically as

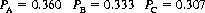
Obviously, as the number of players increases, the greater becomes the advantage of drawing first.

Polish Bank

Several players contend against the banker who deals three cards, face up, to each player and a single card, face up, to himself—from a deck of 32 cards with four suits ranked 7 to Ace. A player wins—at 2 to 1 odds—only if one of his cards is of a higher rank than the banker’s card and in the same suit. A hand of three 7s or of 7, 8, 9 in the same suit is declared non avenu and replaced with another three cards.

Let n₁, 0 ≤ n₁ ≤ 21, denote the number of cards the player can beat, and n₂ the number of different hands that can beat n₁ cards. Then eliminating the non-avenu hands, the total number of possible games, N_t, is

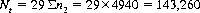
while the number of games, N_p, that the player can win is

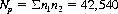
Therefore, the winning probability P_w for the player is

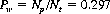
Thus, with 2-to-1 odds, the player’s expectation is −0.109.

Stein’s Game13

From a deck of cards numbered from 1 to n, cards are turned over in random sequence. Whenever the rank of the turned-over card exceeds the highest rank of those cards preceding it, the player receives X units from the House, which charges an entry fee for the game.

The probability that the player wins on a particular card is 1/n. Therefore, his expectation is simply

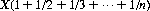
With n = 10, an entry fee of 2.93X units would constitute a fair game. With n = 52, a fair game would require an entry fee of 4.54X, and for n = 100, the fee rises only to 5.187X. For large n, the player’s expectation asymptotically approaches

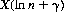
where γ = 0.577 … is Euler’s constant.

Odds and Evens

Invented by Richard Cowan (Ref. 1), Odds and Evens is a two-person game played with n cards numbered 1 through n. A and B each receives (n −2)/2 cards. Simultaneously, each selects and turns over one of his cards. A wins if the sum of the two exposed cards is odd, B wins if the sum is even.

Table 7-4 shows the payoff matrix for n = 8, along with the card played (odd or even) and the probabilities for each three-card hand.

Table 7-4. Payoffs and Probabilities for Odds and Evens

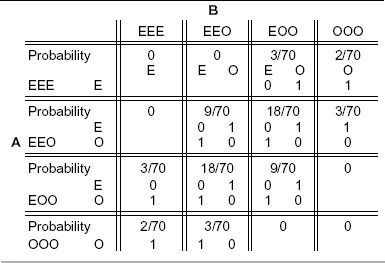
In this instance, A’s optimal strategy is to play E (or O) with a probability inversely proportional to the ratio of Es (or Os) in his hand. Thus, from hand EOO, A should play E with probability 2/3 and O with probability 1/3. A’s probability of winning with this strategy is readily computed as 18/35 (game value of +1/35).

For n = 10, 12, 14 cards, A retains winning probabilities of 11/21, 39/77, 229/429, respectively. (From hand E000, as another example, A should play E with probability 3/4 and 0 with probability 1/4.)

With the number of cards dealt to each player fixed at three, A’s winning probabilities for n = 10, 12, and 14 cards are 85/168, 83/165, and 287/572, respectively. As n → ∝, the winning probability → 1/2.

Further analysis of odds and Evens is available in Cowan (Ref., 2007).

Red and Black

From a deck of R red and B black cards, where R ≥ B ≥ 0, player A at each step guesses the color of the top card—which is then exposed and discarded (Ref. Knopfinacher und Prodinger), To maximize the number of correct guesses, he chooses that color corresponding to the majority of cards remaining in the deck.

Let p(R,B;k) be the probability of guessing k cards correctly:

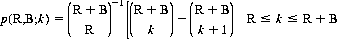
And the expected number of correct guesses E(R, B) is expressed by

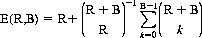
For a standard (symmetric) deck, R = B = 26, and

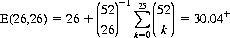
A second player, B, using a random strategy, has a probability of guessing k cards correctly given by

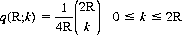
with, of course, an expectation equal to R. The probability P_A that A wins in competition against B’s random strategy is

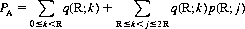
which can be expressed as

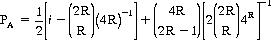
For R = 26, P_A = 0.793. And the game has a value to A of 0.586.

More Red and Black

Two cards are selected at random from a deck of R red and B black cards. The probability P_s that the two cards show the same color is

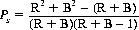(7-15)

For B = R, Eq. 7-15 reduces to

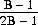
which, for a conventional deck (B = 26), equals 25/51 = 0.490.

Somewhat curiously, if B = R − 1, the same result ensues—owing to the fact that we are dealing, in this case, with a deck comprising an odd number of cards.

The Kruskal Count

Devised by Martin Kruskal (while at Rutgers University), this mathematical “trick” consists of a subject who selects a card according to a prescribed counting procedure and a “magician” who then identifies the selected card without having observed the procedure. Underlying the mathematics is a principle related to coupling models for Markov chains.

A deck of N cards is shuffled and spread out face up. The subject then chooses—privately—an integer j, 1 ≤ j ≤ 10, and counts from one end of the deck to the jth card, referred to as the first key card. The rank of this card—with Aces equal to 1, each face card assigned the value 5, and each other card contributing its numerical value—defines the number to be counted to the second key card, whose rank, in turn, specifies the number to be counted to the third key card, and so forth. The final key card before exhausting the deck is designated the chosen one and is noted by the subject (and revealed by the magician).

It can be proved that, for most orderings of the cards, all the numbers 1 through 10 will lead to the same chosen card. (Setting face card values at 5 rather than 10 increases the number of key cards in an average chain and thereby increases the success rate by ∼16%.)

The proof relies on the ensemble success probability averaged over the set of all possible permutations of the deck. Although this procedure is a non-Markovian stochastic process, it can be approximated by a geometric distribution.

Lagarius, Rains, and Vanderbei (Ref.) have determined that the optimal first key card is the first card of the deck (i.e., j = 1, which also increases slightly the expected number of key cards in the chain and affords a concomitant increase in the probability of success; ergo, the magician is best advised to select j = 1 as his first key card), and the expected key card size is 70/13. Thus we have a geometric distribution GP defined by

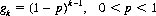
and let GN(p) define the deck distribution induced on a deck of N cards.

Further, letP[t > N] denote the probability that the subject and the magician have no key card in common (i.e., the probability of failure, P_F). For GN(p) with initial geometric value distributions, Gp, we have

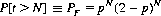
Choosing j = 1 reduces the failure probability by 1/(2 −p) to

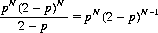
For p = 1 − 1/(70/13) = 57/70 and N = 52,

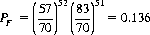
Thus the probability that the magician’s final key card will match the subject’s chosen card is 1 − 0.136 = 0.864⁺.

Using two decks, N = 104, and the probability of matching equals 0.978. As the deck size increases, the probability that both final key cards are identical approaches one.

In the Kruskal count, any two Markov chains, as defined here, tend to become coupled, after which they lead, of course, to the same chosen card.

Two-Card Hi-Lo

Two cards, marked Hi and Lo, are randomly dispensed, one to each of two players. A looks at his card and may either pass or bet. If he passes, he pays B an amount a > 0. If he bets, B, without looking, has the option of (1) passing, whereby he pays a units to A, or (2) calling, whereby A or B receives an amount b > a from his opponent according to whether A’s card is Hi or Lo. It is readily seen that if A’s card is Hi, he bets with unity probability, whereas if he draws the Lo card, he should bet with probability P₁:

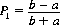
B’s strategy is to call with probability P₂:

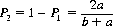
and the value γ of the game (to A) is

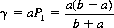
Formal Card Games

Literally tens of thousands of formalized card games have evolved or have been invented over the past few centuries. The majority of them have vanished into a well-deserved oblivion. Of the remainder, only a very few entail greater complexity than a pure or simple mixed strategy. Many games possess only a rudimentary structure, but have strategies involving selection among an astronomical number of alternatives. Bridge and Poker are generally nominated as the two card games demanding the highest level of skill—particularly the former, which is recognized by international competition.

A partial enumeration of the more popular card games might include Bézique, with its variations of Pinochle, Rubicon Bézique, and Chinese Bézique; Hearts, with its variations of Black Lady, Cancellation Hearts, Omnibus Hearts, Polignac, and Slobberhannes; the diverse forms of Poker; Conquian (a corruption of the Spanish con quien?), the direct ancestor of all Rummy games, which bred the Canasta family (including Samba, Bolivia, and Oklahoma) and the Gin Rummy family (including Seven-Card Rummy, Kings and Queens, Five-Hundred Rummy, Persian Rummy, Contract Rummy, Continental Rummy, Brelan—a 15th-century French rummy game—and Panguingue or “Pan”); All Fours, with its derivatives of Seven Up, Auction Pitch, and Cinch; Skat (which has inspired a World Congress of Skat players) with its variations of Schafkopf, Calabrasella, and Six Bid Solo; Klaberjass or Kalabriasz (among many spellings); Cribbage, invented by Sir John Suckling (1609–1642), who based it on the contemporarily popular game of Noddy; the Cassino family; the Whist family, with its offshoots of Black Maria, Mort, Cayenne, Boston, Preference, and Vint; Whist’s successors: Auction Bridge, Contract Bridge, Brint, Calypso, and Towie (originated by J. Leonard Replogle), inter alia.

Further the many Solitaire games, including Klondike, Canfield, Spider, Forty Thieves, Golf, and the varieties of Patience; Bassette (a predecessor of Faro devised by Pietro Cellini at the end of the 16th century); Primero (Cardano’s favorite game); Primero’s descendants: Brag and Loo; Gilet, a French version of Primero; Michigan; the varieties of Euchre; Handicap; Muggins; Gleek; Ecarté; Belote (a relative of this French game, Jo-Jotte, was created by Ely Culbertson in 1937); Monte and its many variations; Svoyi Kozin; Durachki; Tresillo; Quadrille (or Cuartillo); Ombre; “66”; Tablanette; Hasenpfeffer; Spoil Five (the national game of Ireland); Manilla; Quinze; Angel–Beast; and innumerable others. The procedures for these games can be found in rule books for card games, such as those listed at the end of this chapter.

Recently, a number of card games have been devised with the intent of embedding more sophisticated analytic techniques than those required by games surviving the evolutionary filter. For example, the game of “Eleusis,” invented by Robert Abbott, involves principles of pattern recognition similar to those discussed (Chapter 5) for coin-matching phenomena. Each of n − 1 players attempts to analyze a card-acceptance rule established by the nth player, thus permitting the successful analyzer to contribute the most cards from his hand in accordance with that rule. The appeal of Eleusis and its siblings has been confined, thus far, to an eclectic minority of game fanciers.

Poker

Of the considerable multitude of card games, likely the most widespread among Americans is that of Poker. Derived from the ancient Persian pursuit called Nâs or Dsands, the game was played with 20 cards¹⁴ during its popularity in 18th-century Paris. A variation known as Poque arrived in the United States with the French colonists of New Orleans, whence arose the word “Poker” from the American mispronunciation of Poque. An English version of the game is Brag, and another French offshoot is named Ambigu. The full 52-card deck was adapted around 1830, although the form of the game remained essentially that of straight Poker. Draw Poker was not introduced until the early 1860s during the Civil War.

Embodying psychological elements as well as being a game of imperfect information, Poker is not amenable to the deep-search techniques that have proved successful for Chess, Checkers, etsimilia. Further, developing an optimal strategy lies beyond the scope of current game theory owing to the large number of (often ill-defined) tactical alternatives that present themselves. For these reasons plus, Poker may be described as something of a black art.

Parallels between Poker and political/economic/military concerns are frequently drawn. Chance, deceit, and cost-effectiveness form some of the basic elements of Poker. It is axiomatic that the best hand may not win the pot—strong players with weak hands can deploy bluffing techniques to finagle pots from weak players with strong hands. Bluffing, in particular, qualifies Poker as a useful model for nations with opposing aims and ideals.

Elementary combinatorial formulae enable us to calculate the probabilities of all subdivisions of the 2,598,960 five-card Poker hands (Eq. 7-10). Ten categories are defined, and within each category the winning hand is that composed of the highest rank or suit. In ascending order of value:

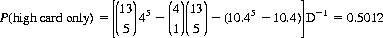
where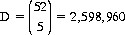

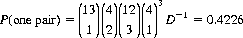
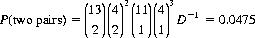
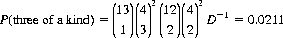
P(straight)15 =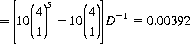

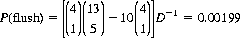
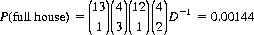
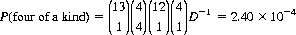
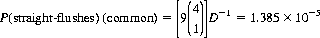
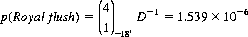
These results are summarized in Table 7-5. The relative values of the hands are, logically, ordered inversely to their probabilities.

Table 7-5. Poker-Hand Probabilities

Hand	Probability
High card	0.5012
One pair	0.4226
Two pairs	0.0475
Three of a kind	0.0211
Straighta	0.00392
Flusha	0.00199
Full house	0.00144
Four of a kind	2.40 × 10−4
Straight-flush (common)	01.385 × 10−5
Royal flush	1.539 × 10−6
Four flush	0.043
Four straight (open)	0.035
Four straight (middle)	0.123
Four straight (end)	0.0087
Four straight-flush	1.23 × 10−4

^a Excluding straight-flushes.

Each of the figures in this table is strictly applicable only to independent hands. As an illustration of the change in probability associated with a second, dependent hand, consider the probability of obtaining a straight, given another hand composed of A, 2, 3, 4, 5. For this case, P = 137/32,637 = 0.00420 compared with 0.00392 for the probability of a straight in a singular hand—a 7⁺% increase.

In diverse forms of Poker, the player is permitted to replace one, two, or three cards in his hand with an equivalent number drawn from the remainder of the deck. The probabilities of achieving certain improvements are enumerated in Table 7-6.

Table 7-6. Draw Possibilities

It does not follow that optimal play can be derived directly from the probabilities of Tables 7-5 and 7-6. There exist strategies such as “bluff” or “inverse bluff” that, in some circumstances, might create an advantage to drawing two cards rather than three to a pair, as an example, although the latter drawing effects an improvement of 0.287 compared with 0.260.

The next sensible step in Poker analysis is that which provides the probable ranking of all possible hands, before and after the draw, as a function of the number of players contending (and of the number of cards each has drawn). Knowing the wager risked on each hand, it is then theoretically possible to calculate the expectation and devise an optimum strategy. However, because of the formidable computational labor attendant to the large number of hands, such a description is rendered inaccessible to precise mathematical treatment.

For games that permit increasing the initial bet (ante) during the course of playing out a hand–Poker being the prime example—element of risk offers a better measure than House Edge to evaluate comparative bets. Element of risk is defined as the ratio of expected gain to the total sum wagered on a particular hand.

Countless varieties of Poker have evolved over the past two centuries, and more will undoubtedly be invented. Some, such as Stud Poker (five cards per hand, one hidden and four exposed successively, no draw) or Seven-Card Stud,16 are tight games, almost purely strategic. Others, such as those with certain cards or groups of cards declared “wild” (allowed to assume any value desired), tend to increase the variance and decrease the strategic content of the basic game.

Table 7-7 lists the probabilities for the 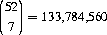possible seven-card hands.

Table 7-7. Seven-Card Hand Probabilities

Hand	Probability
High card	0.174
One pair	0.438
Two pair	0.235
Three of a kind	0.0483
Straight	0.0462
Flush	0.0303
Full house	0.0260
Four of a kind	0.00168
Straight-flush	0.000311

Texas Hold’em

Currently the most popular and most strategically complex Poker variant, Texas Hold’em,17 holds a virtual monopoly in high-stakes poker tournaments and dominates as the main event in the World Series of Poker. Touted by its advocates as “the brightest star in the Poker universe,” it has largely displaced its predecessors in casinos, Poker parlors, and informal home gatherings.

Terminology peculiar to Texas Hold’em is provided in numerous works on the subject (e.g., Ref. Yao).

Of the = 1326 possible two-card combinations, there are three distinct groupings of starting hands: 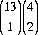= 78 pairs, 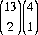= 312 same-suited cards, and 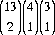= 936 unsuited cards. The value of the two hole cards—and the concomitant strategy—can vary markedly with the player’s position (with respect to the “designated dealer”) and over subsequent developments—such as the composition of the five community cards, the betting structure of each round, pot size at each round, the number of opponents and their actions, implied strategies, and inferred characteristics, inter alia. Ergo, the game is notably path-dependent, making it difficult to specify a priori the probability of a particular hand leading to a winning combination (the best poker hand composed of the two hole cards and three community cards) in the showdown.

As a general rule, however, proficient Hold’em players advocate folding with most unsuited cards and some same-suited cards as soon as the rules permit—i.e., in the preflop round except for the mandatory blind bets—and as a function of position and the number of opponents remaining. The following two-card hands, under the qualifications stated, are recommended as playable [Refs. Shackleford (1); Galfond]:

In early position:

Pairs: 7 and higher
Suited Ace and T-K	Unsuited Ace and T-K
K and T-Q	K and J, Q
Q and T-J
T and 9

There are 170 such hands (12.8% of the total number).

In later positions, additional hands may be engaged in play—particularly if the pot has not been raised.

Additional hands:

Pairs: 5, 6
Suited Ace and 6-9	Unsuited K and T
K and 8, 9	Q and T, J
Q and 8, 9	J and T
J and 8, 9
T and 8
9 and 8

There are 168 such hands (12.7% of the total number). Thus, a conservative player will enter the flop stage less than 25.5% of the time. In last (or next-to-last) position—again with no pot raise and with fewer opponents remaining—the player might hazard continuing in the game with a pair of 4s; Suited A,5, K,8, J,7, T,7; and Unsuited K,9, Q,9, J,9, T,9—for a further 5.3% participation (a positive return dependent on a favorable flop).

Regardless of these considerations, any deterministic strategy is, ipso facto, ill advised; an intelligent opponent could then readily devise an effective counter- strategy. Indeed, a corollary to this statement warrants that it may prove advantageous at times to play incorrectly to advertise a false pattern.

For each player’s hand, the three-card flop entails = 19,600 possible combinations. Independent of the hand, the probabilities for the flops are readily calculated as follows:

	Probability
No pair	0.828
One pair	0.169
Three of the same suit	0.0518
Three in sequence	0.0347
Three of a particular suit	0.0129
Three of a kind	0.00235

Computer simulations indicate that the best hand after the flop wins the pot with a probability greater than 0.7.

To estimate the probability of winning after each card of the flop has been dealt, a parameter widely applied is the number of “outs” (defined as the number of cards remaining in the deck that will improve the hand to best in the game, referred to as “the nut hand”). Since the opponents’ cards are unknown, it may be impossible to compute the precise number of outs.18 It should be noted that the unseen cards do not exhibit a uniform density, but are somewhat more likely to be skewed toward low-ranking values since those hands still contending are more likely to contain high-valued cards (this effect is minimal, however, except when all—or most—players remain). Further, clues to those cards are often revealed in the opponents’ betting (or nonbetting) actions and in their “tells” (indiscreet body or facial movements). As with most Poker strategies, counting outs is an amalgam of art and science.

Texas Hold’em Computers

The history of Hold’em computer programs extends back more than three decades (Ref. Findler). The most notable—and successful—programs have issued from the Computer Poker Research Group (CPRG) at the University of Alberta, Canada:

LOKI—a probabilistic formula-based program.

POKI—incorporates opponent-modeling to adjust its hand evaluations. Based on enumeration, simulation techniques, and expert knowledge, POKI, designed for a ten-player game, performs well against weak opposition.

PsOPTI (for pseudo-optimal Poker program)—a range of programs that apply Nash equilibrium game-theoretic methods. However, computation of a true Nash equilibrium solution for Hold’em lies beyond the foreseeable future.

Polaris—a composite Artificial Intelligence program consisting of ten differ-ent bots, each with a distinct playing style, and a number of other fixed strategies. Development of Polaris began in 1991. Matched against human experts in July 2007 (the first Man–Machine Poker Championship), the program was narrowly defeated. For the rematch, July 2008, a component of learning was added, enabling Polaris to identify which common Hold’em strategy its opponents were using and to switch its own strategy in counteraction. Further, the model size was enlarged—thus more closely approximating a realistic game. Polaris gained the victory with three wins, two losses, and a tie.19

Despite the admirable success of Polaris, considerable further development is required before Poker programs master the game well enough to surpass all human players.

Although more ingenious and challenging card games may be proposed by gamblers or mathematicians, it is improbable that any game will so inspire game theorists and analysts or will achieve the public success and addiction as that gained by the pastime of Poker.

Poker Models

Simplified Poker models are frequently called upon to illustrate certain fundamental principles since they present the right degree of challenge—neither impossibly difficult as many real games nor trivial as most games of pure chance. To date, these models have shed little light on the actual game—although certain analogies to business, war, and politics have proved rewarding.

For example, Rhode Island Hold’em, a model for Texas Hold’em, reduces each hand and the flop to a single card. Its underlying structure differs markedly from the actual game. Poker models have been analyzed by Borel (Ref.), von Neumann, H.W. Kuhn, Bellman and Blackwell, and Goldman and Stone, among others.

Red dog

A realistic model, Red Dog (or High Card Deal) is played with the standard deck. Each of N players receives a hand of five cards (or four as N exceeds 8). Following an ante of 1 unit, each player in turn may either fold or bet an amount ranging from 1 unit to the size of the pot that his hand contains a card of greater value in the same suit than one to be drawn from the remainder of the deck.

An analysis of this game, results in a strategy dictating that the player should wager the maximum stake (the entire pot) when his hand falls in the region

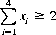(7.16)

where x_i is the relative ranking in the ith suit of the highest card in that suit (Ace is ranked high). A minimum bet should be risked when the hand is described by

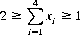
and the folding region is defined by

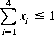
As an illustration, consider a hand consisting of the Ace of Spades (x₁ = 13/13), the Queen and Three of Hearts (x₂ = 11/13 for the Queen), the Four of Diamonds (x₃ = 3/13), and the Nine of Clubs (x₄ = 8/13). (Ace is ranked high.) Thus

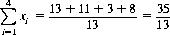
which, being greater than 2, the value specified by Eq. 7-16, advises that we should bet the maximum that a card in this hand can exceed, in its suit, the rank of any card exposed from the remainder of the deck.

One-Card Poker (Ref. Beasley)

Player A draws a card randomly from a conventional deck (concealed from player B) and wagers either 1 unit or 5 units that it is a face card (J, Q, K). B then concedes or doubles the wager. If he concedes, he pays A the amount of the wager. If he doubles, the card is turned over, and the wager resolved (with either 2 or 10 units at stake from each of the players).

An initial impression might suggest that the game retains a negative expectation for A, since he draws a face card with probability 3/13. However, applying the proper mixed strategy proves the contrary. Specifically:

A bets 5 units whenever he draws a face card; when drawing an Ace through 10, he bets 5 units with probability 1/10 and 1 unit otherwise—that is, he bluffs randomly with probability 1/10. (This strategy is simple to implement by wagering the higher sum whenever the drawn card is J, Q, K, or A.)

B responds by always doubling a bet of 1 unit, with a tentative bet of 5 units, he doubles at random with probability 7/15 and concedes with probability 8/15.

The game therefore has a value to A of (4/13)5 + (9/13)(−2) = 2/13.

Note that if A bluffs with a probability less than 1/10, B can then gain a positive expectation by conceding all bets of 5; if A bluffs with probability greater than 1/10, B gains by doubling all bets of 5.

Similarly, if B doubles bets of 5 with probability less than 1/3, A gains by bluffing on every card; if B doubles with probability greater than 1/3, A gains by never bluffing.

More One-Card Poker

A and B are each dealt one card face down. A may keep his card or exchange it for B’s card. B’s options are to retain his card (be it the original one or the one given him in exchange) or trade it for the next card in the deck. The higher-ranking card wins the stake. Ties are “no bets” [Ref. Shackleford (1)].

A’s optimal strategy is to switch with a 7 or lower. B will then maximize his expectation by trading (for the next card in the deck) with an 8 or lower. The game is favorable to A with an expectation of 0.082.

Steve Shaefer (Ref.) has proposed a variation wherein B wins the ties unless A and B have just exchanged cards of equal rank, in which case he must draw a new card (or flip a coin) to break the tie. A’s optimal pure strategy is, as before, to switch with 7 or less. Then, if A hasn’t switched, B will again draw to 8 or lower—resulting in a positive expectation for B of 3/13³. However, if A hazards a mixed strategy, trading 8s with probability p₁, he compels B also to adopt a mixed strategy p₂ for drawing to a 9—so that B’s expectation becomes

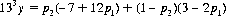
For each player to maximize his expectation against his opponent’s optimal strategy, the two partial derivatives, ∂y/∂p₁ and ∂y/∂p₂, must be zero:

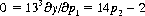
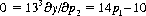
Thus

So A should trade an 8 with probability 5/7. Then, when A does not trade, B should draw to a 9 with probability 1/7. The game is slightly favorable to B with an expectation of (11/7)/13³ = 0.000715.

Le Her

An 18th-century card game whose solution was first sought by N. Bernoulli and de Montmort, Le Her is played between two persons, Dealer and Receiver, with the standard 52-card deck. Dealer dispenses one card to Receiver and one to himself. If receiver is dissatisfied with his card, he may exchange it for dealer’s—unless Dealer has a King, which he is permitted to retain (le droit de refuser). If Dealer is then dissatisfied with his original card or that obtained in exchange from Receiver, he may replace it with a third card selected from the deck; however, if the new (third) card is a King, the replacement is canceled, and Dealer must retain his undesired card. The object of the game is to conclude with the higher-valued card (Ace equals 1). In the event of a tie, Dealer wins.

Three moves comprise the game: a chance move, which selects the first two cards; a personal move by Receiver; and a personal move by Dealer. Since cards of 13 ranks can be either held or exchanged, there are 2¹³ strategies available to both contenders. It is straightforward to demonstrate that two strategies dominate all others. Obviously, Receiver will retain cards with a value of 8 or greater, and he will exchange cards of value 6 or lower. His decision relates to rank 7. As a consequence, Dealer’s decision relates to rank 8. The payoff matrix of Le Her is therefore a 2 × 2 matrix; its elements are displayed in Figure 7-1.

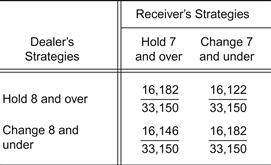
Figure 7-1 Le Her payoff matrix.

Applying the minimax principle, we can determine that optimal strategy for Dealer dictates mixing his two strategies in the ratio of 3:5. Receiver’s optimal strategy is (5/8, 3/8). Probability of success for Dealer is 0.487 and therefore 0.513 for Receiver, an expectation (for Dealer) of −0.026. Although it may appear that the advantage lies with Dealer since he wins the ties, the reverse is true owing to the greater ability of Receiver to influence the game’s outcome.

Casino Games

Despite the plethora of card games, only a few have flourished in the major gambling emporia. Trente et quarante, Baccarat, Poker in specialized settings, and Blackjack comprise the contemporary card games available to the gambling public. [Blackjack offers sufficient depth and interest to warrant a chapter (8) of its own.] Faro, once the dominant card game in 19th-century Western America (virtually every saloon in the Old West featured at least one Faro Bank), has now all but vanished from the scene.20

Trente et Quarante

Trente et Quarante is a game of pure chance found in virtually all French casinos (there are more than 160 state-licensed gambling establishments in the Gallic republic), although rarely offered in the United States. It is played with six decks of cards shuffled together, forming a total pack of 312 cards. Suits are of no significance; each card is assigned a value equal to its rank (Ace = 1), with Jacks, Queens, and Kings set equal to 10. Dealer representing the House lays out two rows of cards, the first row corresponding to Noir and the second to Rouge, until the cumulative total of the card values in each row reaches or exceeds 31. Thus, Noir and Rouge are each associated with a number that ranges between 31 and 40. Players may place wagers according to the diagram of Figure 7-2.

Figure 7-2 The Trente et Quarante layout.

A bet on Rouge wins if the cumulative total of the second row is lower (closer to 31) than that of the first row (Noir). If the two totals are equal, the bet is a tie unless the equality exists at 31, in which case the House pockets one-half of all stakes. Similarly, a wager on Noir wins if the first-row total is the lesser. The payoff for a winning bet is at even odds. Couleur is determined by the first card dealt. If Rouge (Noir) wins and the first card is red (black), Couleur wins; otherwise, Inverse wins. A player betting on Couleur or Inverse also ties if the two totals are equal at 32 through 40 and loses one-half the stake if the two totals are 31.

Probabilities for the totals 31 through 40 were first computed by Denis Poisson and subsequently by Joseph Bertrand with the assumption of sampling with replacement (equivalent to an infinite deck); the concomitant error is extremely small with a pack of six conventional decks. Table 7-8 summarizes the pertinent probabilities—from which it is readily calculated that the game of Trente et Quarante offers the player an expected return of 0.989 (a House Take of 1.1%) since the probability of a tie at 31 equals (0.148)² = 0.0219. Other ties (at 32 through 40) occur with a frequency of 8.783%. A reduction to a House Take of 0.9% is available through an “insurance” bet, permitting the player to wager an additional 1% stake (quantized to the higher 1-euro level) that cancels the loss in the event of a tie at 31; the insurance bet is garnered by the House in all instances except ties at 32 through 40.

Table 7-8. Trente et Quarante Probabilities

Total	Probability
31	0.148
32	0.138
33	0.128
34	0.117
35	0.106
36	0.095
37	0.084
38	0.072
39	0.061
40	0.052

Baccarat

Introduced into France from Italy where it originated ca. 1490, Baccarat was devised by a gambler named Felix Falguiere, who based it on the old Etruscan ritualism of the “Nine Gods.”²¹ According to legend, 26 centuries ago in “The Temple of Gold Hair” in Etruscan Rome, the Nine Gods prayed standing on their toes to a golden-tressed virgin who cast a novem dare (nine-sided die) at their feet. If her throw was 8 or 9, she was crowned a priestess. If she threw a 6 or 7, she was disqualified from further religious office and her vestal status summarily transmuted. And if her cast was 5 or under, she swam resolutely out to sea. Baccarat was designed with similar partitions (albeit less dramatic payoffs) of the numbers, modulo 10.

Three accepted versions of the game have evolved: Baccarat Banque (wherein the casino as the Banker opposes the Player), Baccarat Chemin de Fer (a Player assumes the role of Banker), and Punto Banco (the casino banks the game, and no strategic choice is involved). Chemin de Fer became the dominant version in the United States in 1920; more recently, it has been supplanted by Punto Banco, a game of lesser interest.

Eight decks are employed in Punto Banco; thus, most probability calculations can be performed under the assumption of independence (sampling with replacement) with small error. Each card from Ace through Nine is assigned the face value of its rank; Tens, Jacks, Queens, and Kings contribute zero.

From a shoe of eight decks, Banker and Player are initially dealt two cards each, which are turned face up. The two cards are summed mod 10. If either hand totals 8 or 9, no further cards are drawn. With a total of 0 to 5, Player must draw an additional card; with a total of 6 or 7, he must stand. Banker then draws or stands according to the schedule presented in Table 7-9.

Table 7-9. Punto Banco Rules for Drawing

Player Draws	Banker Draws with Total	Banker Stands with Total
No card	0–5	6 or 7
2 or 3	0–4	5–7
4 or 5	0–5	6 or 7
6 or 7	0–6	7
8	0–2	3–7
A, 9, T	0–3	4–7

The hand with the higher total wins. Equal totals for both hands (ties) are “no bets.” Any participant at the Baccarat table may wager on either Banker or Player, with a payoff of 1 to 1 for the latter and 0.95 to 1 for the former (a 5% House commission). A bet on Player entails an expectation of −0.0124⁻; and a bet on Banker an expectation of −0.0106 (after commission). A bet on ties (Égalité) pays 8 to 1, for an expectation of −0.144⁻. (Some casinos pay 9 to 1 on a tie bet—increasing the expectation to −0.0484⁺.)

In Chemin de Fer, Player’s sole decision is whether to stand or draw on 5, his optimal strategy being (1/2, 1/2). Banker’s fixed response is as follows:

Stand on 6 when Player stands (on 5)

Stand on 4 when Player draws a 1

Draw on 5 when Player draws a 4

Draw on 3 when Player draws a 9

Under this rule, the value of the game is −0.0137 for a bet on Player, and −0.0116 for a bet on Banker (after the 5% commission).

A 4-5-6 side bet is sometimes available—i.e., a wager that the final number of cards in the two hands totals 4, 5, or 6, as illustrated in Table 7-10.

Table 7-10. Baccarat Side Bet

Another side bet pays 9 to 1 that Banker’s (or Player’s) two cards will total 9 (or 8). Knowledge of the remaining 9s and non-9s in the eight decks thus enables occasional positive-expectation wagers. Thorp has calculated that for a deck composition of n cards remaining, t of which are 9s, the probability P_n,t of Banker receiving a two-card total of 9 is

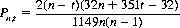
The side bet yields a positive expectation whenever P_n,t > 0.1—i.e., whenever there is at least one or more 9s among 12 remaining cards, two or more 9s among 26 remaining cards, or three or more 9s among 40 remaining cards.

However, for the principal bets at Baccarat, no positive expectation can be derived even with an exact knowledge of the remaining cards. The effect on the expectation from the removal of one card of a given rank (Ref. Thorp, 1984) can be shown to be about one-ninth of the equivalent effect in Blackjack (Ref. Griffin).

Reddere Baccarat

With a 10% rebate on losses, the Punto Banco player has a positive expectation, 0.0035, for coups of 13 or fewer. At 14 coups, the expectation drops to −0.0087; at 3 coups, it reaches a maximum of 0.0417.

Card Conundra

1. Consider a game with m winning and n losing cards, m + n players, and a banker who pays out and takes in the wagers. Each player is dealt a single card, receiving a units from the banker if it is one of the m winners, and paying b units to the banker if it is one of the n losers. If the amount won is equal to the amount lost—i.e., ma = nb—and if m and n are relatively prime, show that the probability of the banker always having sufficient funds to pay the winners is 1/(m + n). Show that the probability of a bankrupt banker at any particular point in the game is also 1/(m + n).

2. Cards are dealt from a deck of R red and B black cards until the first red card appears. Show that the expected number of black cards preceding the first red card is B/(R+1). For a conventional deck, this expectation is 26/27.Let B = R + 1 (one more black card). Then the number of black cards preceding the first red card is 1 for any deck of finite length.

3. A Three-Person Money Game. Three players simultaneously expose either a $1, $5, $10, or $20 bill. If all three expose the same denomination, the game is a draw. If the three bills are all different, that player with the middle value wins the money shown by the other two. If two of the bills are equal, that player with the different denomination wins from the other two. Determine the optimal (mixed) strategy. Note: For a simpler version, the problem can be formulated with $1 and $5 bills only, deleting the middle-man-wins possibility.

4. Hi-Lo Forehead Poker. Three players ante one unit apiece, and each receives a random integer ≤ N. Without looking at the integer, it is exposed on the forehead for the other two players to observe. Simultaneously, each player announces for either “Hi” or “Lo.” The pot is split between the two winners of Hi and Lo. If all declare for Hi (Lo), a single winner is determined by the highest (lowest) integer. Compute the optimal strategy.A modification of this game permits the players to draw lots to determine the order of announcing for Hi or Lo.

REFERENCES

Abbott, Robert., Abbott’s New Card Games, Stein and Day, 1963.

Battin IL, (1942). On the Problem of Multiple Matching. Annals of Mathematical Statistics.13(3):294–305.

Beasley John D, (1990). The Mathematics of Games. Oxford University Press.

Borel, Emile, Traité du Calcul des Probabilités et ses Applications, Vol IV, Part 2, pp. 105-113, Gathier villars.

Chatto William, (1848). Facts and Speculations on the Origin and History of Playing Cards. J. R. Smith.

Cowan (1), Richard, “Game Theory,”www.maths.usyd.edu.au/u/richardc/gametheory.html.

Cowan, Richard, “Some Solutions for the Game Odds & Evens,” November 2007, www-personal.usyd.edu.au/~rcowan/professional/Odds%20and%20Evens.pdf.

Epstein, Richard A., Card Prediction for a Shuffled Deck, Hughes Aircraft Co., Report TP-64-19-11, OP-68, July 1964.

Findler Nicholas V et al, (1972). Studies on Decision Making Using the Game of Poker, Information Processing. [71] North Holland Publishing Company.

Fréchet M, (1936). Traité du Calcul des Probabilités. Gauthiers-Villars and Cie [tome 1, fasc. 3, 2e livre].

Galfond, Phil, “G-Bucks Conceptualizing Money Matters,” April 2007, www.bluffmagazine.com/online feature/gbucks.asp.

Gardner Martin, (1977). Mathematical Carnival. Vintage Books.

Gillies DB, Mayberry JP, von Neumann J, (1953). Contributions to the Theory of Games. [“Two Variants of Poker,” Study 28] Princeton University Press [2, pp. 13–50].

Golomb Solomon W, (1960). Permutations by Cutting and Shuffling. [Jet Propulsion Laboratory Technical Release no. 34-3] California Institute of Technology [February].

Griffin Peter, (1999). The Theory of Blackjack. 6th ed. Huntington Press.

Johnson Paul B, (1956). Congruences and Card Shuffling. American Mathematical Monthly.63:718–719 [December].

Joseph AW, Bizley MTL, (1960). The Two-Pack Matching Problem. Journal of the Royal Statistical Society.22(Series B):114–130.

Knopfmacher Arnold, Prodinger Helmut, (2001). A Simple Card Guessing Game Revisited. The Electronic Journal Combinatorics.8(2):1–9.

Lagarius Jeffrey C, Eric Rains, Vanderbei Robert J, (2009). The Kruskal Count. In: Brams Steven J, Gerlein William V, Roberts Fred S, eds. The Mathematics of Preference, Choice and Order. Springer Berlin Heidelberg: 371–391. .

Lemyre G, (1935). Le Baccara. Hermann and Compagnie.

Medvedoff Steve, Morrison Kent, (1987). Groups of Perfect Shuffles. Mathematics Magazine.60(1):3–14.

Nick’s Mathematical Puzzles, 2004, www.byte.org/puzzles/puzzle11.html.

Poisson Denis, (1825). Mémoire sur L’Avantage du Banquir au Jeu de Trente et Quarant. Annals Mat. Pures Appl..xvi(vi):173–208.

Riordan John, (1958). An Introduction to Combinatorial Analysis. John Wiley & Sons.

Schaefer, Steve, “High Card wins,” 2003, www.mathrec.org/old/2003mar/index.html.

Shackleford (1), Michael, “Problem 60 Solution,”www.mathproblems.info/prob60s.htm.

Shackleford, Michael, “Texas Hold’em,”http://wizardofodds.com/holdem.

Thorp Edward O, (1984). The Mathematics of Gambling. Gambling Times Books.

Thorp Edward O, Walden William E, (1973). The Fundamental Theorem of Card Counting with Applications to Trente-et-Quarante and Baccarat. International Journal of Game Theory.2(2):109–119.

Wilde Edwin F, Tomandl Daniel A, (1969). On Shuffling Cards. Mathematics Magazine.42(3):139–142.

Yao King, (2005). Weighing the Odds in Poker. Pi Yee Press.

Bibliography

Bellman Richard, (1960). Introduction to Matrix Analysis. McGraw-Hill.

Bellman Richard, (1952). On Games Involving Bluffing. Rendiconti del Circolo Matematico di Palermo.(series 1, 2):139–156 [May–August].

Bellman Richard, Blackwell D, (1949). Some Two-Person Games Involving Bluffing. Proceedings of the National Academy of Science, USA.35:600–605.

Billings, Darse., “Algorithms and Assessment in Computer Poker,” doctoral thesis, University of Alberta, Edmonton, 2006.

Billings Darse, Papp Denis, Peña Lourdes, Schaeffer Jonathan, Szafron Duane, (1999). Using Selective-Sampling Simulations in Poker. Department of Computing Science, University of Alberta.

Bluff Magazine, Atlanta, GA 30319.

Bolle, Das Knochspiel der Alten, Wismar, 1886.

Breitkopf, J. G. L., Versuch den Ursprung der Spielkarten, die Einführung des Keinenpapiers und den Anfang der Holzschneidekunst in Europa zu Erforschen, Leipzig, 1784.

Burton Bill, (2005). Get the Edge at Low Limit Texas Hold’em. Bonus Books.

Cutler WH, (1975). An Optimal Strategy for Pot-Limit Poker. American Mathematics Monthly.82(4):368–376.

Deloche Régis, Oguer Fabienne, (2007). A Game-Theoretic Analysis of the Card Game Le Her. In: Stewart Ethier, Eadington William, eds. Optimal Play, Mathematical Studies of Games and Gambling. Institute for the Study of Gambling and Commercial Gaming, University of Nevada: 175–193. .

Deloche Régis, Oguer Fabienne, (2007). Baccarat and Perfect Bayesian Equilibrium. In: Stewart Ethier, Eadington William, eds. Optimal Play, Mathematical Studies of Games and Gambling. Institute for the Study of Gambling and Commercial Gaming, University of Nevada: 195–210. .

Gilpin, Andrew, and Tuomas Sandholm, “A Competitive Texas Hold’em Poker Player via Automated Abstraction and Real-Time Equilibrium Computation,” in National Conference on Artificial Intelligence, 2006.

Gilpin, Andrew, and Tuomas Sandholm, “Optimal Rhode Island Hold’em Poker,” inProceedings 20th National Conference Association for the Advancement of Artificial Intelligence AAAI, pp. 1684–1685, 2005.

Glazer Andrew, (2004). The Complete Idiot’s Guide to Poker. Alpha Books.

Grosjean James, (2007). Much Ado about Baccarat. In: Stewart Ethier, Eadington William, eds. Optimal Play, Mathematical Studies of Games and Gambling. Institute for the Study of Gambling and Commercial Gaming, University of Nevada: 143–173. .

Harrington Dan, Robertie Bill, (2005). Harrington on Hold’em. [1: Strategic Play] Two Plus Two Publishing.

Kuhn HW, (1950). Contributions to the Theory of Games. [“A Simplified Two-Person Poker,” Study 24] Princeton University Press [Vol. 1 97–103.]

Morehead Albert H, Mott-Smith Geoffrey, (1946). Hoyle’s Rules of Games. [A Signet Key Book] New American Library.

Nash John F, Shapley Lloyd S, (1950). Contributions to the Theory of Games. [“A Simple Three-Person Poker Game,” Study 24] Princeton University Press [Vol. 1 105–116.]

Noble, Jason., Finding Robust Texas Hold’em Poker Strategies Using Preto Coevolution and Deterministic Crowding, pp. 233–239, International Conference on Machine Learning and Applications, Informatics Research Institute, School of Computing, University of Leeds, 2002.

Petrev Mike, (1996). Hold’em Odds Book. Objective Observer Press.

Phillips Hubert, (1960). The Pan Book of Card Games. Pan Books Ltd.

Rive, Jean-Joseph, Eclaircissements historiques et Critiques sur l’ Invention des Cartes a Jouer, De l’Imprimerie de Fr. Ambr. Didot, 1780, 40 pp.

Sklansky David, Miller Ed, (2006). No Limit Hold’em: Theory and Practice. Two Plus Two Publishing.

Thorp Edward O, (1973). Nonrandom Shuffling with Applications to the Game of Faro. Journal of the American Statistical Association.68(344):842–847.

Thorp Edward O, (1970). Solution of a Poker Variant. Information Sciences.2(2):299–301.

Van Rensselaer JK, (1890). The Devil’s Picture Books. Dodd, Mead, and Co.

Ken Warren, (1996). The Winner’s Guide to Texas Hold’em Poker. Cardoza Publishing.

Yardley Herbert C, (1957). The Education of a Poker Player. Simon and Schuster.

Zadeh Norman, (1977). Computation of Optimal Poker Strategies. Operations Research.25(4):541–562.

¹ According to the Chinese dictionary, Ching-tsze-tung, compiled by Eul-koung and first published in 1678.

² The word “card” stems from the Greek word for paper, χα´ρτησ. Similarly, the Hebrew term for playing, card, qlaf, is equivalent to “parchment.”

³ A corruption of coat cards, so called because they bear the representation of a clothed or coated figure (not because the King, Queen, and Knave may be considered as members of a royal court).

⁴ It is worth noting that two perfect shuffles of a “fresh” deck (arranged customarily by suits in ascending ranks) followed by simple cuts order the cards for a deal of four perfect hands at bridge (all 13 cards of a suit comprising each hand). This fact may account partially for the astounding number of perfect hands reported each year.

⁵ For more esoteric studies of shuffling phenomena, the reader is referred to the works of Henri Poincaré and Jacques Hadamard on probability chains.

⁶ Analyzed by Casper Monge, Comte de Péluse.

⁷ In practice, cutting the deck is not a random process since the cutter usually aims for a point about midway.

⁸ First proposed and solved by Montmort, 1708.

⁹ Howard Levene, Department of Mathematics, Statistics, and Genetics, Columbia University, New York.

¹⁰ Solomon Kullback, 1903–1999, cryptologist, Chief Scientist, National Security Agency.

¹¹ Contributed by Stewart Ethier.

¹² Simulation courtesy Norman Wattenberger, Casino Vérité.

¹³ Suggested by E.P. Stein.

¹⁴ The deck consisted of four suits, each of five ranks: Lion, King, Lady, Soldier, and Dancing Girl.

¹⁵ For straights and straight flushes, the Ace is permitted to rank either high or low.

¹⁶ Featured by “The Thanatopsis Literary and Inside Straight Club,” Seven-Card Stud was extremely popular but little understood during the 1920s. It was also celebrated at Charles Steinmetz’s famed Poker gathering, “The Society for the Equalization and Distribution of Wealth.”

¹⁷ The game was born a century ago in Robstown, Texas.

¹⁸ Online computer programs are available to estimate the value of any particular hand against a range of opponent hands.

¹⁹ Polaris is credited with showing a perfect poker-face.

²⁰ Whatever its fate in the world’s casinos, Faro will be remembered from Pushkin’s classic short story, “The Queen of Spades.”

²¹ Macaulay, Horatius at the Bridge: “Lars Porsena of Clusium/By the Nine Gods he swore/…”