Chapter Six
Coups and Games with Dice
A Brief Chronicle
The casting of knuckle bones for amusement, profit, or divination dates from the dawn of civilization. As bones were marked and evolved into dice, cleromancy (divination by dice) and gambling became intimately intermingled—the gods of old shaped human destiny by rolling dice and then used the same dice in games among themselves. One of the oldest mythological fables tells of Mercury playing at dice with Selene and winning from her the five days of the epact (thus totaling the 365 days of the year and harmonizing the lunar and solar calendars). In the same vein, it was reported by Herodotus that the Egyptian Pharaoh Rhamsinitus regularly rolled dice with the goddess Ceres. The entire world in the great Sanskrit epic, the Mah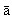
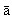bhrata,1 is treated as a game of dice in which Siva (god of a thousand names) gambles with his queen, the numbers thrown determining the fate of mankind.
Both Greeks2 and Romans were enthusiastic dice devotees, casting the tessera (cube) and talus (elongated cube) in their games (in the Far East, the teetotum, or spinning die, was more common); the talus was occasionally numbered 1, 3, 4, 6, leaving the ends unassigned. Regal and passionate dice players in ancient Rome included Nero, Augustus, Caligula, Claudius I,3 Domitian, and Julius Caesar. Dice served for sortilege, divination, or judicial decision, one renowned example being Caesar’s tossing a die to resolve his indecision over crossing the Rubicon (“alea jacta est”). During the Middle Ages, dicing stood as a favored pastime of knights and ladies. Dicing schools and guilds of dicers prospered, all despite repeated interdiction. Charles V of France in 1369 forbade the play of certain games of chance, and an edict of the provost of Paris in 1397 prohibited the proletariat from playing at “tennis, bowls, dice, cards, or nine-pins on working days.”
In the late 18th century, a popular pastime for some composers entailed the creation of melodies by rolling a pair of dice to select the 16 bars of a Viennese minuet. The most famous of these compositions is the Musikalishes Würfelspiel, often (but erroneously) attributed to Mozart. (All 11 outcomes of a two-dice throw were—quite naïvely—considered equiprobable.)
For a die to be fair (all sides having equal probability of turning up), it must be isohedral (all faces exhibiting the same shape, the same relationship with the other faces and with the same center of gravity). There are 25 such isohedra (plus five infinite classes).
The Greek geometers focused on the five regular polyhedra (the Platonic solids). The tetrahedron, with four equilateral triangles as faces, does not roll well nor does it offer much variety; the hexahedron, or cube, with six square faces, appears to satisfy both the desired motion and number requirements; the octahedron, with eight faces in the form of equilateral triangles, has greater variety, but rolls a bit too smoothly; the dodecahedron, with 12 pentagons as faces, and the icosahedron,4 with 20 equilateral triangles as faces, roll too fluidly for control in a restricted area and have more possibilities than can be comprehended by the unsophisticated mind (fittingly, these polyhedra are often used for fortune-telling). Hence, the adoption of the hexahedron as a die appears to be a natural selective process, although the octahedron could be pressed into service by some enterprising casino (cf. “Sparc,” Casino Games section). For more sophisticated gamblers, the use of irregular polyhedra might provide a provocative challenge.
The earliest dice were imprinted with consecutive numbers on opposite faces: 1 opposite 2, 3 opposite 4, and 5 opposite 6. However, as far back as the 18th dynasty of Egypt (ca. 1370 B.C.), the present standardized format was introduced whereby the two-partitions of 7 are ensconced on opposing faces. Under this constraint there are two topologically distinct constructions for a die. [the three two-partitions of 7 define three axes; a well-known geometric theorem states that there exist two three-dimensional coordinate systems—left-handed and right-handed—that remain distinct under rotation (and constitute mirror images of each other.)] Most American casinos employ right-handed dice—the values 1, 2, and 3 progress counterclockwise around their common corner. Only in China are left-handed dice favored.
In four-dimensional Euclidean space there are regular convex “polytopes,” such as the hypercube (eight cubes combined) and the hypertetrahedron (five tetrahedra combined). Polytope games are enjoyed exclusively by four-dimensional mathematicians.
The word “die” retains an obscure provenance. A possible etymology suggests that the expression jeu de dé is derived from juis de dé = judicium dei (judgment of God). Alternatively, dé may stem from datum, which initially signified chance—that is, that which is given or thrown.
Detection of Bias
Dice problems contributed the initial impetus to the development of probability theory. Cardano, Pascal, and Fermat enunciated the concept of equally likely outcomes for the six faces of a die; thus, by definition, the probability that any one side will face upward is 1/6 (more rigorously, one must establish the necessary and sufficient conditions for the applicability of the limiting ratio of the entire aggregate of possible future throws as the probability of any one particular throw).
Many experimenters have attempted to confirm (or dispute) this figure empirically. The most widely published dice data were compiled by the English zoologist and biometrician W.F.R. (Rafael) Weldon who (in 1894) recorded the frequencies of 5s and 6s in 26,306 throws of 12 dice.
Yet more tedious experiments were carried out by the Swiss astronomer Rudolph Wolf toward the second half of the 19th century. Wolf’s feat of stamina—100,000 throws of a single die—is notable for furnishing the data that led, several decades later, to the Principle of Maximum Entropy (Ref. Jaynes). Given testable data, this procedure (more sophisticated than the χ2 test) consists of seeking the probability distribution that maximizes information entropy, subject to the constraints of the information—that is, comparing predicted entropies to the entropies of the data.
Wolf’s experiment produced 16,632 1s, 17,700 2s, 15,183 3s, 14,393 4s, 17,707 5s, and 18,385 6s. The validity of the hypothesis that the probability of each side facing up is 1/6 may be checked by the χ2 test (Eq. 2-28):
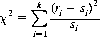
where ri is the actual number of times the ith side appears, si the predicted number, and k the number of possible outcomes. If χ2 = 0, exact agreement is evidenced. As χ2 increases for a given number of trials, the probability of bias increases. Applying the χ2 test to Wolf’s data, we obtain
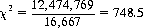
To comprehend the significance of this value, we note from Eq. 2-27 that repeating this experiment theoretically should yield a distribution of χ2 given by
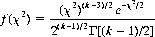(6-1)
with k−1 degrees of freedom. (A die evidently exhibits five degrees of freedom.)
We now wish to designate a value of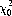 
such that the probability of χ2 exceeding 
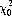represents the significance level of the experimental results. Selecting a significance level of 0.01, we can, from Eq. 6-1, find a value 
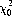such that
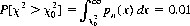
where pn is the probability density function. It can be established5 that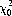 
= 15.1 appertains for the case under consideration. That is, if the die were perfect, 100,000 throws would result less than 1% of the time in a value of χ2 greater than 15.1. Since χ2 = 748.5, we may conclude that the probability of Wolf’s die being unbiased is vanishingly small. We might have suspected this fact, since all faces of the die except the 1 differ by considerably more than the standard deviation, σ = 117.8, from the expected value of 16,667.
Weldon’s data recorded the event that of 12 × 26,306 = 315,672 possibilities, the numbers 5 or 6 appeared on the dice 106,602 times—resulting in a one-degree-of-freedom χ2 value of 27.1 (the equivalent figure from Wolf’s data is 342.5). A reasonable conclusion is that a die of poor quality (such as those manufactured in the 19th century) is highly susceptible to bias with continued use. The dice employed by the major gambling casinos are now machined to tolerances of 1/2000 inch, are of hard homogeneous material, and are rolled only a few hundred times on a soft green felt surface before being retired. Thus, the probability of finding an unintentionally biased die in a casino—and determining wherein lies the bias—is tantamount to zero.
A final question concerning biased dice relates to the number of throws of a die necessary to ascertain the existence of a bias (we assume throughout that the rolls of a die comprise a stationary statistic—though the bias is not altered with time). Although a bound to the number of throws required is given by Bernoulli’s form of the law of large numbers, such a bound, applicable to any distribution, is extremely conservative. When dealing with a binomial distribution, a better estimate of the requisite number of throws to ascertain a bias is provided by the Laplace-Gauss theorem (a special case of the central limit theorem). The probability that the outcome 6 occurs between np1 and np2 times in n throws of a die, where p is the estimated single-trial probability of a 6, is approximated by
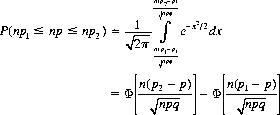(6-2)
where Φ(x) is the cumulative probability function (cpf). Thus, the probability that, for a perfect die, p differs from 1/6 by not more than 0.01 with 0.95 confidence is expressed by
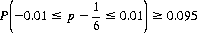
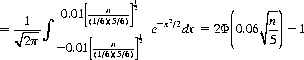
since Φ(−x) = 1 − Φ(x). Hence, the requirement on the number of throws n is governed by the relation
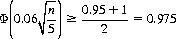
and, from tables of the cumulative probability function, we find that n = 5335 throws of the die suffice to obtain a relative frequency of 1/6 ± 0.01 with a confidence level of 0.95 (Bernoulli’s rule suggests 27,788 throws).
Similarly, if we suspect the die of bias and assign an unknown value p to the probability of an outcome, we wish to find the number of throws n sufficient to determine p within a tolerance of 0.01 with 0.95 confidence. The Laplace-Gauss theorem states that
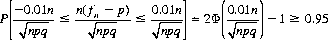
or
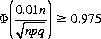
From tables of the cumulative probability function, this condition is fulfilled for
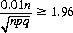(6-3)
and, since the maximum value of pq is 1/4, Eq. 6-3 indicates that a bound occurs at n ≥ 9604. Therefore, 9604 throws of a suspect die can test for bias to within 1% with 0.95 confidence (a value less than one-fifth that suggested by the Bernoulli rule).
As with coins in the preceding chapter, we proceed under the assumption that the dice referred to are fair and that successive throws of a die are independent. Fairness implies that the possible outcomes are equiprobable. Independence of successive events signifies that if the events A1, A2, …, An are independent, the probability of their joint occurrence is the product of the probabilities of their individual occurrences—that is,
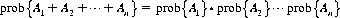
Finally, it follows that successive dice throws constitute an ergodic process: n throws of one die are equivalent to one throw of n dice.
Divers Dice Probabilities
Dice problems generally succumb to straightforward analysis. A few simple formulas encompass virtually all forms of dice play.
De Méré’s Problem
This 17th-century “gambler’s conundrum” (cf. pp. 2 and 131), which contributed to the inception of probability theory, is readily solved by consideration of simple repetitions. If a chance event has a constant probability p of occurrence on any given trial, then the number of trials n required for its first occurrence is a discrete random variable that can assume any of the infinitely many positive integral values n = 1, 2, 3, …. The distribution of n is the geometric distribution (cf. Eq. 2-13)
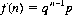
and the cumulative distribution function F(n) is
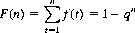
Therefore the probability Pn that the event occurs in n trials is expressed by
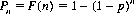(6-4)
De Méré had posed the question of the probability of obtaining at least one 6 in one roll of four dice as compared to the probability of obtaining at least one double-6 in 24 rolls of two dice. His “reason” argued that the two probabilities should be identical, but his experience insisted that the former dice game offered a positive and the latter a negative expected gain.
The single-trial probability of rolling a 6 with one die is defined as p = 1/6, and that of throwing a double-6 with two dice is p = (1/6)2 = 1/36. Thus the probability P4 of obtaining at least one 6 in one roll of four dice (or four rolls of one die) is, from Eq. 6-4,
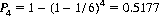
and the probability P24 of obtaining at least one double-6 in 24 rolls of two dice has the value
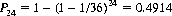
De Méré also inquired as to the number of rolls necessary to ensure a probability greater than 0.5 of achieving the 6 or double-6, respectively. Solving Eq. 6-4 for n,
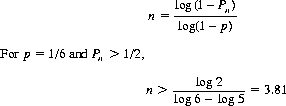
Hence, four rolls of a die are required to obtain a probability greater than 1/2 of rolling a 6. For p = 1/36 and Pn > 1/2,
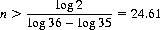(6-5)
Therefore, 25 is the smallest number of rolls of two dice that offers a probability greater than 1/2 of achieving a double-6.
Newton–Pepys Problem
Another contribution to early probability theory was triggered by an exchange of letters between Samuel Pepys and Isaac Newton. Pepys, the 17th-century English diarist, questioned which was most likely:
P1+ = probability of at least one 6 in a fling of six dyse,
P2+ = probability of at least two 6 s in a fling of twelve dyse, or
P3+ = probability of at least three 6 s in a fling of eighteen dyse.
Newton responded that the odds were “in favour of ye Expectation of [ye first chance].”
From the vantage point of more than three centuries, we can express the probability of an outcome of n or more 6s in a cast of 6n dice as
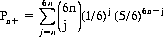
Therefore,
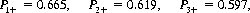
and P1+ is the most likely event. Newton calculated only the probabilities of P1+ and P2+, then contented himself by noting that “in ye third case, ye value will be found still less.” He also neglected to mention that Pn+ → 0.5 as n increases.6
Mean versus Median for Two Dice
P2+ provides an illustration of the difference between mean and median (Ref. Griffin; Chapter 2).
The number n computed in Eq. 6-5 represents the median of the distribution of the number of throws necessary to obtain a pair of 6s—that is, half the values of the distribution are less than or equal to 24, and half are greater or equal to 25.
In a proposed game, A throws the two dice until (6,6) appears—at throw n1. B pays A 30 units initially, and, subsequently, A pays B n1 units. The game would seem favorable to A, who will win 55.85% of the time. However, the expected number of throws, E(n1), or mean, for (6,6) to appear is
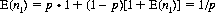
where p is the single-trial probability of throwing (6,6). Ergo, E(n1) = 36, and the value of the game is 36−30=6 to B, though B will win only 42.93% of the time (1.22% of the time n1 = 30, and a tie will result). (A’s gain is limited to 29 units, whereas B’s gain is theoretically unlimited.)
Note that, for standard dice, the mean is greater than the median (since the probability distribution is skewed leftward).
Probability of a Particular Outcome
Analogous reasoning to that leading to the formula for simple repetition will conclude that the probability of achieving a particular outcome exactly m times in n throws is the binomial expression
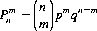(6-6)
Thus, the probability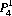 
of exactly one 6 in four rolls of a die is computed to be
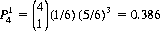
and for the probability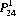 
of obtaining exactly one double-6 in 24 rolls of two dice,
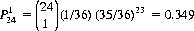
Similarly, if a chance event has constant single-trial probability p, and n denotes the number of trials up to and including the rth success, the distribution of n has the form
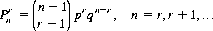(6-7)
which is recognizable as the negative binomial distribution,7 aka Pascal’s distribution.
By extension from Eq. 6-7 we can also determine the probability Pn that, in n throws of a die, a particular outcome occurs between n/6 − t and n/6 + t times:
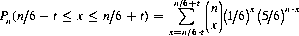
Applying the normal approximation to the binomial distribution,
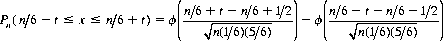
akin to Eq. 6-2. With n = 6000 and t = 50 as an example, tables of the cpf result in
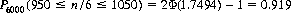
A perfect die, then, will produce a particular outcome 1000 ± 50 times 91.9% of the time over 6000 trials.
Expected Sum of Single-Die Outcomes
A die is thrown repeatedly until a 6 appears. We inquire as to the expected sum of all outcomes of the die prior to the first 6.
Let x equal the sum at any given throw. The expected sum, E(x), can then be written as
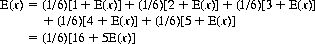
Probability of a Particular Sum
A general formula, useful for the solution of many dice games, provides the probability P(s) of obtaining a given sum s of the outcomes of n dice (or n throws of one die). Of the 6n different configurations of n dice, the number of configurations whereby the n outcomes sum to a number s is equivalent to the number of solutions of the equation
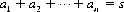(6-8)
where each of the ai’s are integers between 1 and 6. A theorem of the discipline of number theory states that the number of solutions of Eq. 6-8 for any n corresponds to the coefficient of xs in the expansion of the polynomial
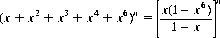
Applying the binomial theorem,
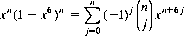(6-9)
and
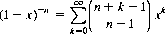(6-10)
Multiplying the two series of Eqs. 6-9 and 6-10 and dividing by 6n, the total number of configurations, we obtain
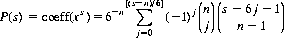(6-11)
for the probability of a total of s points on n dice, where [(s − n)/6] is the largest integer contained in (s − n)/6. Two-dice probabilities are displayed in Table 6-1.
Table 6-1. Two-Dice Probabilities
The most common outcome for n dice is 7n/2 for n even, and (7n ± 1)/2 for n odd. Thus 7, 10 & 11, 14, 17 & 18, 21, … are the most common outcomes for n = 2, 3, 4, 5, …, with respective probabilities 1/6, 1/8, 73/648, 65/648, 361/3888, … .
The game of Razzle-Dazzle is played (in Havana) with eight dice. Pertinent is the probability that a throw of all eight totals 30 or higher. Eq. 6-11 indicates that
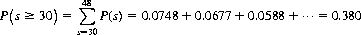
Probability of All Possible Outcomes
We can also inquire as to the probability that one throw of n dice (n≥6) will produce each of the outcomes, 1, 2, …, 6 at least once. By extending the theorem of total probability (Eq. 2-2), we can state that the probability of m events, A1, A2, …, Am, occurring simultaneously is
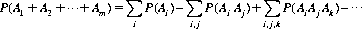(6-12)
For the m = 6 events possible from the throw of a die, Eq. 6-12 leads to
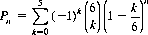
for the probability that all outcomes of a die are represented in a throw of n dice.
Numerically, for n = 8, P8 = 0.114. With ten dice, P10 = 0.272, and, with the minimum of six dice, P6 has the value 0.0154 (equivalent to 6!/66). Thirteen dice (the median number) are required to obtain a probability greater than 1/2 for the occurrence of all six outcomes (P13 = 0.514).
Occurrence of All Possible Outcomes
The expected number of throws for all outcomes to appear at least once is
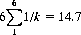
which represents the (arithmetic) mean.
The mode, the most likely number of throws following which all outcomes are represented, is determined by defining P(n, m) as the probability that, out of n ≥ 6 throws, there are m distinct outcomes, n ≥ m ≥ 1. Then (Ref. Nick's Mathematical Puzzles),
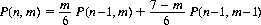
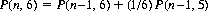
From these probabilities the mode is calculated as 11, since
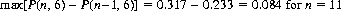
Further, the minimum number of times a die must be thrown for at least an even chance that all outcomes occur is 13 [P(12, 6) + 0.438; P(13, 6) = 0.514].
Potpourri
1. In 6q throws of a die, the probability that each of the six numbers will appear exactly q times is immediately determined from the multinomial distribution (Eq. 2-12):
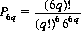
With 6 throws (q = 1), P6 = 0.0154+ (as per Eq. 6-12 with six dice). With 12 throws (q = 2), P12 = 0.00344−. With 18 throws (q = 3), P18 = 1.359 × 10−3. And with 24 throws (q = 4), P24 = 8.879 × 10−4.Applying Stirling’s formula for larger values of q,
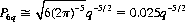
2. With n dice, the expected value, E n, of the highest outcome k ≤ 6 is expressed by
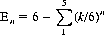
For n = 6 dice, En = 5.560+; for n = 12, En = 5.880−. Obviously, as n increases, En → 6.
3. Let N(n, m) denote the number of ways of throwing n dice, each with m faces. We can readily derive this number as
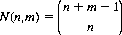
For two conventional dice, N(2, 6) = 21; and for three conventional dice, N(3, 6) = 56.
4. Eq. 6-11 can be generalized to specify the probability of obtaining the sum s from n dice, each with m faces:
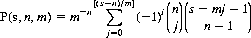
5. We wish to determine the expected number of throws of n dice for the appearance of two consecutive all-1s.Let X represent the state that the last throw of the n dice did not show all-1s for the second consecutive time (and is also the state at the first throw). Let Y represent the state that the last throw of the n dice did show all-1s for the second consecutive time. After the first throw there is probability 1 − (1/6)n that state X still pertains and probability (1/6)n that state Y pertains. Then the expected values of X and Y can be written as
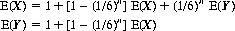
Solving for E(X):
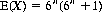
Thus with a single die, the expected number of throws to obtain two consecutive 1s is 6 · 7 = 42. With two dice, the expected number of throws to obtain consecutive “snake eyes” is 36 · 37 = 1332; and, for n = 3, E(X) = 216 · 217 = 46,872.
6. With a k-sided die, numbered 1, 2, …, k, the probability P2 of obtaining a particular number twice in m rolls is
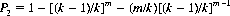
For six rolls of a conventional die,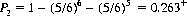 
and with 12 rolls,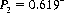 
Structured Dice Games
First or Second or Third or Time Up
In one of the oldest formal dice games, a single die is thrown until a particular number appears (or, in alternative versions, until it appears twice or three times). If p is the single-trial probability of that event, and n is the number of throws until it occurs for the rth time, Eq. 6-7 applies (the parameter n − r obeys the negative binomial distribution), and with p = 1/6 and r = 1, yields
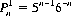(6-13)
To obtain the probability, Pn(r), that the particular outcome occurs for the rth time by the nth throw of the die, we sum Prn from r to n:
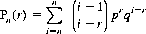(6-14)
For r = 2, this event occurs by the seventh throw with a probability greater than 0.5 (specifically, 0.536). For r = 3, Eq. 6-14 indicates a probability greater than 0.5 (specifically, 0.513) that the third occurrence of this outcome appears by the 16th throw.
Nicolas Bernoulli’s Game—Expected Number of Throws to Achieve a Particular Outcome
A nearly identical problem posed by Nicolas Bernoulli can be considered the forerunner of the St. Petersburg game. Bernoulli inquired as to the expected value of n in a game consisting of rolling a die until a 6 appears for the first time at the nth throw, with a payoff of n units.
Evidently, the largest value of Pn1 in Eq. 6-13 occurs for n = 1. Therefore, the most probable number of throws to obtain a 6 is 1. The expected number is expressed by
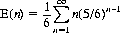(6-15)
Using the identity 1 + 2x + 3x2+ … = (1 − x)−2, Eq. 6-15 becomes
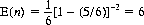(6-16)
and, as we would have anticipated, six throws are expected for obtaining one particular outcome of the die. This value should be clearly distinguished from the number of throws (four) required to obtain a 6 with probability greater than 1/2.
The specific example of Eq. 6-16 can be generalized by the following theorem.
In any series of trials where the probability of occurrence of a particular event X is constantly p, the expected number of trials E(X) to achieve that event is the reciprocal of the probability of its occurrence.
We can prove this statement by noting that if p is constant, the probability of X first occurring at the ith trial follows the geometric distribution (Eq. 2-13)
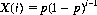
The expected number of trials is then defined by
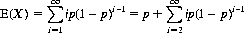(6-17)
With the substitution j = i − 1, Eq. 6-17 is rewritten in the form
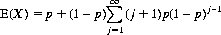
Therefore
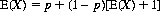
and
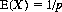(6-18)
As an example, since the probability of rolling the sum of 9 with two dice is 4/36, the expected number of rolls of two dice to achieve a 9 is nine. (Eq. 6-18 also specifies the expected length of a sequence of throws of a biased coin until the first occurrence of Heads [single-trial probability = p].)
James Bernoulli’s Game
To illustrate one of the pitfalls inherent in skewed distributions, consider the following dice game initially propounded by James Bernoulli. Let a solitary player perform one throw of a single die, securing the result i (i = 1, 2, …, 6). He then selects i dice from a set of six and throws them once (or throws the single die i times), obtaining the sum si. If si > 12, he receives one unit payment; if si < 12, he loses one unit; and if si = 12, the game is declared a tie. The total number of outcomes is 6 × 66; enumerating those that contribute a sum greater than, equal to, or less than 12:
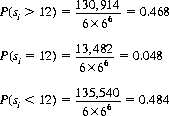
Comparing these values, it is apparent that the player is burdened with a negative mathematical expectation (specifically, 0.468(1) − 0.484(−1) = −0.016). Yet, the expected sum obtained from throwing i dice according to the game rules is
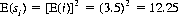
for which the player receives a unit payment. Were the distribution about 12.25 symmetrical rather than skewed, the game would be favorable to the player.
A Maximization Game
A dice game popular among military personnel consists of throwing five dice simultaneously, declaring one or more to be “frozen,” then repeating the process with the remaining dice until all five are frozen (in five or fewer throws). Objective: to maximize the sum of the points on the five frozen dice. By obtaining a total of s points, a player receives s − 24 units from each of the other players (24 − s units are paid to each other player if s < 24). We wish to determine an optimal strategy and its corresponding mathematical expectation.
The expected sum arising from a throw of one die is, as per Eq. 2-16,
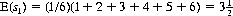
With two dice plus the option of rethrowing one, the mathematical expectation of the sum of the pips on the two dice is given by
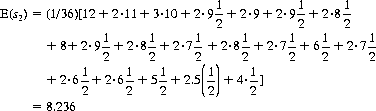
With three dice plus the option of rethrowing two, one of which may be thrown for the third time, the expectation of the sum can be calculated as
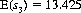
Similarly, throwing four dice with rethrow options according to the stated rule produces an expectation of the sum of
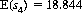
and, with five dice, according to the game rules, the mathematical expectation of the sum has the value
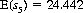
Optimal strategy is specified by these expectations. Thus, the option of rethrowing one die should be exercised if its outcome is 3 or less, since the expectation of the rethrow is higher (3.5). With the option of rethrowing two dice, combinations totaling 9 or less should be (at least partially) rethrown. For example, 4-4 is rethrown, and 5-4 declared frozen; with the combination 5-3, only the 3 should be rethrown, resulting in an expectation of 5 + 3½ = 8.5 (rethrowing the 5 and the 3 results, in the lower expectation of E(s2) = 8.236). With the option of rethrowing three dice, all combinations totaling 15 or less should be examined to determine whether rethrowing one, two, or three dice maximizes the expectation. As examples, with 5-5-3 we freeze the two 5s and rethrow the 3 [10 + E(s1) is the maximum value], and with 5-4-4 we rethrow all three dice [E(s3) is maximum].
Following the first roll of the game, we have the option of rethrowing four dice. Here we examine all combinations totaling 21 or less to determine whether rethrowing one, two, three, or four dice maximizes the expectation. Illustratively, with 5-5-5-3, we would rethrow all four dice [resulting in E(s4)], and with 6-5-4-4 we would rethrow the 5-4-4 [resulting in 6 + E(s3)]. Clearly, a 6 is never rethrown; 5 and 4 are rethrown or not, depending on the number of dice remaining with rethrow options; and 3, 2, and 1 are always rethrown whenever permitted by the rules. The expected gain E(G) of the game is the sum of the products of each possible payoff by its corresponding probability, P(s):
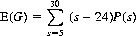(6-19)
where s can range from 5 (all 1s on the five dice) to 30 (all 6s). The values of P(s) are computed by delineating the various combinations of dice that total each value of s; the results are presented in Table 6-2. Substituting the appropriate numerical values into Eq. 6-19, we obtain
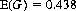
Table 6-2. Maximization Game Probabilities
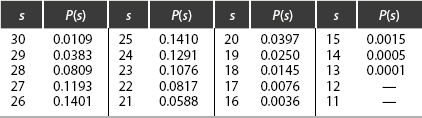
The game is thus highly favorable to the player rolling the dice since 25 is the most probable sum achieved by optimal play. Prevailing opinion that the game is nearly equitable likely rests on the assumption of nonoptimal strategies.
All Sixes
A game similar in its mechanics, although not in its computations, consists of rolling n (usually five) dice, attempting to achieve the outcome 6 on all n. Following each throw of the dice, those showing a 6 are set aside and the remainder rethrown; this process is then continued indefinitely until all n dice exhibit a 6. We wish to determine the expected number of throws En(N) to obtain all 6s.
The classical method of solving this problem proceeds by computing Pn(N), the probability of achieving the goal with n dice by the Nth throw, and then summing the product NPn(N) over all values of N and n (from 1 to ∞)—thus prescribing a large number of tedious calculations. Fortunately, there exists a clever insight leading to a direct solution of this problem.
The probability of throwing at least one 6 in a roll of n dice is 1 − (5/6)n; hence, from Eq. 6-18, the expected number of rolls to obtain at least one 6 is 6n/(6n−5n). If the throw that achieves the first 6 contains no other 6s, the probability of which is n5n−1/(6n − 5n), the problem reduces to one with n − 1 dice. If the throw achieving the first 6 contains exactly one additional 6, the probability of which is
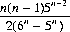
then the problem reduces to one with n − 2 dice. Proceeding by induction, we are subsequently led to the expression
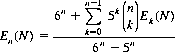(6-20)
where E0(N) = 0. For n = 5 dice, Eq. 6-20 is evaluated as
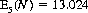
Thus, slightly more than 13 throws are expected to obtain all 6s on five dice with repeated throws of those dice exhibiting non-6s.
Turn the Die
A simple strategic dice game suggested by Martin Gardner involves a single die that is initially thrown by A and then rotated a quarter-turn by B and A as alternating moves, recording a running sum of the numbers facing up. The object of the game is to maneuver the cumulative sum of the up-faces exactly to a specified goal.
Strategy for either player dictates the attempt to force the running sum to a value equal to the residue of the goal, mod 9, or to prevent the opponent from achieving that value. For example, if the goal is set at 31 (4, mod 9), and A throws a 4, he strives to include the totals 4-13-22-31 in the running series. Thus, if B plays 6 or 5, A counters with 3 or 4, respectively (totaling 13); if B plays 1 or 2, A shows 4 or 3, respectively, which totals 9 and prevents B from reaching 13 (the 4 is not available). In general, letting r be the residue of the goal, mod 9, one should play to r − 5, leaving the 5 on the top or bottom of the die, and to r − 3, r − 4, or r + 1, leaving the 4 unavailable.
Except for r = 0, a win for A exists for at least one roll of the die. Table 6-3 indicates the winning rolls for each residue of the goal, mod 9. Clearly, if the first player is afforded the option, he chooses a goal with residue 7, mod 9, thereby obtaining a fair game.
Table 6-3. Winning Numbers for Turn-the-Die Game
Roller Coaster Dice
A game found on the Internet and in a few unpretentious casinos, Roller Coaster Dice pits a single player against the House. To begin, following a unit wager, the player rolls two conventional dice and then predicts whether a second roll will produce a sum greater or less than the first. If correct, he repeats this procedure for a third, a fourth, and a fifth roll (if he continues to predict successfully).
Obviously for any sum ≤6, he will predict a higher number for the next roll; and, for any sum ≥8, he will predict a lower number. For an initial outcome of 7, his two choices are equivalent.
A single incorrect prediction loses the wager. With four correct choices, the player may end the game and gain a sum from the House equal to three times his wager. He also has the option of proceeding under the same rules—risking his stake of 4 units. Two more consecutive correct predictions (a total of six) will increase his net gain to 6 units. He may then end the game or opt to continue—whence yet two more correct predictions (for a total of eight) will raise his net gain to 12 units. Finally, he may either end the game at this stage or continue, striving for yet two more correct predictions (for a total of ten) and a net gain of 29 units.
Appropriate arithmetic shows the player to have a probability of 0.2324 of achieving four correct predictions—for an expected return of 4(0.2324) − 1 = −0.0704.
If the fifth dice roll has shown 4 through 10, he should end the game. With a 2 or 12 (3 or 11), he has a probability of 891/1296 or (825/1296), respectively, of reaching the sixth stage—and should therefore continue. His expected return is thereby increased by
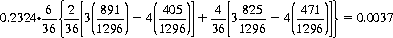
After six correct predictions, the player should end the game if the (seventh) roll shows a 5 through 9. With a 2 or 12, 3 or 11, 4 or 10, he should continue, similar calculations indicating an additional expected return of 0.0026. After eight correct predictions, he should stop if the (ninth) roll shows a 6 through 8. With a 2 or 12, 3 or 11, 4 or 10, 5 or 9, he should continue—accruing a further expected return of 0.00608.
Thus, with optimal strategy, the game entails a value of −0.0704 + 0.0037 + 0.0026 + 0.0061 = −0.0580.
La Queue Circulaire Aux Dés
Each of six players in a ring rolls a die in sequence; the first to roll a 6 wins. With a non-6, the die is passed on to the next player, seriatim; the first player regains a turn if no 6 has been rolled by his five competitors, and so forth.
Eq. 5-39 indicates that the first player’s probability of success, P1,6, is
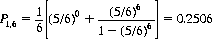
Similarly, for players 2 to 6,
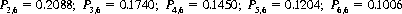
With a large number of competitors, the first player’s probability of success approaches 1/6, since it is unlikely he will have further opportunities with the die. A player in 25th position along a ring of 50 persons has a probability of success of 0.013, and a player midway around a 100-person ring faces a dismal probability success of 0.00014.
A Parrondo-Type Dice Game
Although Parrondo’s principle (Chapter 4) is illustrated with biased coins, it can also be applied to a game with fair dice (or a fair coin) (Ref. Astumian). Consider the five-square Astumian diagram of Figure 4-3 with a checker at the START position. We then define two games as follows.
Game I: The player rolls two dice, moving the checker to the RIGHT square if the dice total 11, to the LEFT square for a total of 2, 4, or 12. With any other total, the dice are rolled again. With the checker positioned at LEFT or RIGHT, a roll of 7 or 11 moves it one square rightward; a roll of 2, 3, or 12 moves it one square leftward. When the checker reaches WIN or LOSE, the game is over.The probability of reaching WIN non-stop is (2/7)(8/12) = 4/21, and of reaching LOSE non-stop is (5/7)(4/12) = 5/21. Ergo, Game I is losing.
Game II: Here the player follows a prescription reversing the Game I rules, moving right from START with a roll of 7 or 11, and left from START with a roll of 2, 3, or 12. With the checker at LEFT or RIGHT, he moves rightward with 11, and leftward with 2, 4, or 12.His probability of reaching WIN non-stop is therefore (8/12)(2/7) = 4/21, and of reaching LOSE non-stop is (4/12)(5/7) = 5/21. Thus Game II is also losing.
Since both games continue after the dice mandate a non-move, the probability of ending with WIN is 4/9, and of ending with LOSE is 5/9, whence both games entail an expectation of −1/9.
Now, in accordance with the Parrondo principle, we mix the two games in random fashion, flipping a fair coin prior to each move: with Heads, Game I is played; with Tails, Game II. Then the probability of reaching WIN is the product of the average number of rightward moves: [(2 + 8)/2] · [(8 + 2)/2] = 25. Similarly, the probability of reaching LOSE is the product of the average number of leftward moves: [(5 + 4)/2] · [(4 + 5)/2] = 20.25.
The combined game, therefore, offers an expectation of +0.105.
The Racing Game
The general racing game is defined by two players, A and B, alternately throwing m dice, the winner being that player whose cumulative total reaches or exceeds T points.
The mean number of points gained by throwing the m dice is m7/2 with a standard deviation of
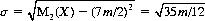
where M2(X) is the second moment (the binomial distribution pertains).
Let ta and tb represent the number of points short of the goal T for A and B, respectively. After n throws, n = 2(ta + tb)/7 m, and the standard deviation in terms of the number of throws becomes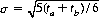 
(independent of m).
The advantage of having the next throw is equal to 1/2 the average number of points to be gained: ta − tb + 7 m/4.
We wish to determine the probability P(x) that the player’s opponent fails to gain this number of points in 2(ta − tb)/7 m throws. Accordingly, we set
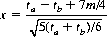
and find P(x) from the tables of standard normal distribution. More directly, for small x, we can apply the approximation
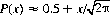(6-21)
To illustrate this general formula, consider ta = tb = t, as is the case at the beginning of the game or at some stage where the two players are tied. For a single die (m=1) and a goal of T = 100 points, the probability Pt that the player who next throws will win the game is (Eq. 6-21):
With m = 2 dice and a goal of 100 points,
And for a goal of 200 points,
The racing game can be rendered more equitable by awarding the second player a handicap of 7 m/2 points.
Of Piglets, Pigs, and Hogs
Jeopardy race games define a class of probabilistic and strategic contests wherein a player’s fundamental decision is (1) whether to jeopardize previous gains by continuing to play for potentially greater gains; or (2) surrender his turn voluntarily and thereby safeguard his gains accumulated to date. In general, the objective is to be first to reach a specified goal.
In the jeopardy game Piglet, a player rolls a single die; the sum of the points obtained at each roll is added to the sum achieved on previous rolls. The player continues to roll the die until either the outcome 1 appears or he voluntarily ends his turn—whereby his accumulated sum is designated a “plateau.” In subsequent turns, the appearance of a 1 reverts his sum to the previous plateau. objective: to reach a cumulative total of 100.
Optimal strategy is a function of the previous plateau, the current score, the opponents’ plateaus, and the number of opponents. To simplify, consider the solitaire form of piglet (Ref. Humphrey, 1979, 1980) with the objective of reaching 100 in as few turns as possible. Let k equal the optimal number of accumulated points at which to declare a plateau. Then, given k points, the expected number at the next roll is
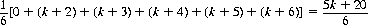
Therefore, optimal strategy dictates ending a turn whenever
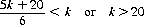
that is, whenever the player has accumulated a total more than 20 points above his previous plateau (at k = 20, the expected gain from continuing is identical to that from stopping).
One Piglet variation scores the squares of the outcome appearing on the die. In this case, the expected number at the next roll is
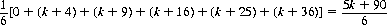
and optimal strategy declares a plateau whenever k > 90. An ultimate goal of 400 or 500 is more consonant with this game.
With one or more opponents, it can be difficult to quantify an optimal strategy. For example, against an opponent holding a wide lead in points, it is advisable to continue a turn for lower values of k. The same argument pertains when competing against a large number of opponents who may not be adhering to the optimal policy.
Pig differs from Piglet in its use of two dice—a difference that engenders immensely greater complexity. Here, the outcome 1 on either die again reverts the player’s score to the previous plateau; in addition, a 1 on both dice reduces the score to zero.
As with Piglet, we consider a simplified solitaire Pig whose objective is to reach 24 points. In this elementary case, the player pays one unit for each turn at the dice—that is, until a 1 appears on either die or a plateau is declared (here, “snake eyes” adds no further penalty).
We wish to determine the strategy that minimizes the expected number of units paid (plus some fixed payoff for reaching 24).
Let (a, b) represent the position of the player with current score a and plateau b. To prove that the optimal strategy for this game is never to declare a plateau, it is sufficient to examine this strategy for the case of a = 23 and b = 0.
Let V be the expected additional cost under a strategy of declaring a plateau at (23, 0) and paying one unit. Two events can subsequently occur: The player can throw a 1 on either die, remaining at (23, 23), or he can obtain an outcome without a 1 on either die, in which case the game is concluded. The probability of this latter event is 25/36. Thus in the (23, 23) case, the expected cost is 1/(25/36) = 36/25. As a consequence we can write for V,
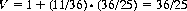(6-22)
Now, if we let W be the expected number of units paid in the (0, 0) case under a strategy of never declaring a plateau, and V1 be the expected cost at (23, 0) under this strategy, we have
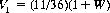(6-23)
To prove that the optimal strategy is never to declare a plateau, we must show that V1 < V—i.e., from Eqs. 6-22 and 6-23, that
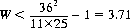
The quantity W is the expected number of times a 1 is thrown on either die before achieving a continuous run (without 1s) adding up to 24 or greater. Further, W = 1/P, where P is the probability of accumulating a score of 24 or more without the appearance of a 1 (Eq. 6-18).
Enumerating all possible combinations, we can calculate the probabilities, pi, of reaching 24 with i rolls of two dice without a 1 appearing (i can assume the values 2, 3, 4, 5, 6). Numerically, p2 = 7.7 × 10−4, p3 = 0.186, p4 = 0.100, p5 = 2.5 × 10−3, and p6 = 3.3 × 10−6.
Thus, P = 0.289, and W = 3.465, which is less than the critical value of 3.71. Hence, no plateau should be declared in this game.
If this solitaire version of Pig is played with a goal of 100, it appears that the first plateau should be declared at about the level of 25.
The unpruned version of Pig has been analyzed by Neller and Presser (Ref.), exploiting the didactic technique of value iteration.
Of several Pig mutations extant, Hog (Ref. Neller and Presser) can claim the most interesting facets. Players are restricted to one roll per turn, but with as many dice as desired. If no 1s occur, the sum of the dice is scored. With one or more 1s, no points are scored for that turn. As customary, the first player to reach 100 points wins. (Hog is equivalent to a version of Piglet where the player must commit beforehand to a specific number of rolls in his turn.)
Let P(n, k) be the probability that rolling n dice results in a turn score of k points, k ≥ 0 and 0 < n ≤ nm, where nm is the number of dice beyond which the optimal policy remains unchanged. Here, nm ≥ 26. Feldman and Morgan (Ref.) have shown that the probability of winning, Pi,j, is expressible as
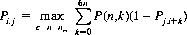
where i is the player’s score, and j the opponent’s, 0 ≤ i,j < 100. This probability can be computed with dynamic programming. Results indicate an optimal strategy akin to that of Pig. And, as with Pig, the first player wins with probability ∼0.53. The maximum expected score per turn (8.04) occurs with either five or six dice—and that number should be rolled on the first turn.
Other variants include Piggy Sevens (throwing a 7 with the two dice loses the turn), Big Pig (the player’s turn continues after throwing two 1s), and Hog Wild, a variant devised by the author wherein the sum of the two numbers rolled (2 through 12) is multiplied by their difference (0 through 5), with the product added to the player’s score.
Yahtzee®
Sometimes described as “poker with dice,” Yahtzee8 entails five standard dice and from two to several players. Each player, in turn, is allowed a maximum of three throws of the dice with the option of “fixing” any non-zero subset of the outcomes of each throw and then rethrowing the remaining dice (if any). The configuration showing after the final throw constitutes the player’s score for that turn—see Table 6-4. Further, an additional 35 points are awarded if the player’s total score from the first six categories exceeds 62. Additional yahtzees after the first are rewarded with 100 points each.
Table 6-4. Yahtzee Scoring
| Outcome | Point Score |
| Aces (1s) | Sum of 1s |
| Twos | Sum of 2s |
| Threes | Sum of 3s |
| Fours | Sum of 4s |
| Fives | Sum of 5s |
| Sixes | Sum of 6s |
| Three of a Kind | Sum of all 5 dice |
| Four of a Kind | Sum of all 5 dice |
| Full House | 25 |
| Small Straight (four consecutive numbers) | 30 |
| Straight | 40 |
| Yahtzee (five of a kind) | 50 |
| Chance (any outcome) | Sum of all 5 dice |
Each player’s objective is to maximize his score.
At the end of his turn, the player applies his configuration to one of the 13 scoring categories. Each category may be selected only once (if the player’s configuration does not fit any unused category, he receives a 0 for that turn). Thus, a game consists of 13 turns.
The maximum score achievable is 375 (without Yahtzee bonuses); the expected score, employing optimal decisions, is 255.
Phil Woodward (Ref.) has evaluated all 1.27 × 109 possible outcomes of the game to determine the optimal playing strategies—detailed in Appendix Table B (Ref. Verhoeff and Scheffers.). To illustrate the use of this table, consider the combination 3 3 4 5 6 obtained with the first throw. Optimal strategy dictates fixing 3 3 and rethrowing the remaining three dice. If this configuration occurs after the second throw, optimal strategy calls for fixing 3 4 5 and rethrowing the other two dice. If this configuration occurs after the third throw, it should be scored as 30 in the Small Straight (SS) category.
Applying this optimal strategy yields an expected final score of 254.59− (with a standard deviation of 59.61−).
Of the 13 categories, Large Straight (LS) proves to be the greatest contributor to the final score, followed by Small Straight (SS) and Full House (FH). Each contribution is enumerated in Table 6-5.
Table 6-5. Yahtzee Categories
| Category | Expectation |
| Large straight | 32.71 |
| Small straight | 39.46 |
| Full house | 22.59 |
| Chance (CH) | 22.01 |
| Three-of-a-kind | 21.66 |
| Sixes | 19.19 |
| Yahtzee (YZ) | 16.87 |
| Fives | 15.69 |
| Four-of-a-kind | 13.10 |
| Fours | 12.16 |
| Threes | 8.57 |
| Twos | 5.28 |
| Aces | 1.88 |
Poker Dice
Analysis of dice games and determination of an optimal strategy are conceptually trivial in most instances. Pig is a notable exception. Liars Dice (where the application of judicious prevarication is the essential ingredient) and Poker Dice (equivalent to conventional Poker played with an infinite number of decks) are two other examples.
Poker Dice (each die admits of six outcomes: Nine, Ten, Jack, Queen, King, and Ace) invokes the theory of partitions. The occupancy problem posed is that of five dice occupying six cells; we therefore consider a partition of the six cells into six subpopulations (0 through 5). A throw of five dice can yield one of seven results whose respective probabilities are obtained by enumerating the partitions for each case:
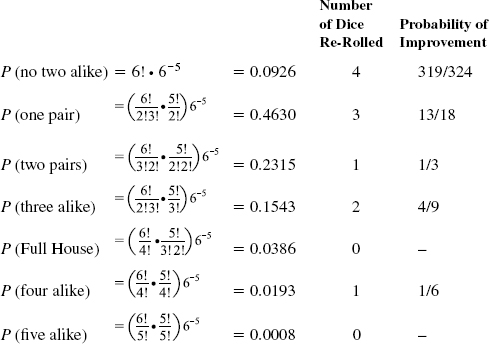
In the standard version of Poker dice, each player has the option of retaining one or more dice after the first throw and rethrowing the others. Probabilities of improving the “poker hand” are listed in the rightmost column.
Nontransitive Dice
Consider two sets of three dice marked as follows:
In a two-person game, the first player selects either A, B, or C. The second player then selects C against A, A against B, and B against C. Each player casts his die, with the higher number winning the stake.
With set I, C wins against A with probability 5/9; A wins against B, and B wins against C, each with probability 2/3. If the first player selects A, B, or C equiprobably, the value of the game is 7/27 to the second player.
With set II, A wins against C with probability 25/36; C wins against B, and B wins against A, each with probability 7/12. If the first player selects A, B, or C equiprobably, the value of the game is 13/54 to the second player.
These two sets constitute the only nontransitive sets wherein no die is marked with a face value higher than 6. Without this constraint, any number of nontransitive sets can be devised. Three such examples are generated by the magic square:
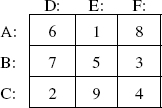
[Rows, columns, and diagonals have the same sum (15).] The three numbers of each row and column define a die with each number marked on two faces.
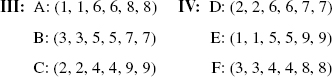
For these two sets, A(D) wins over B(E), B(E) over C(F), and C(F) over A(D), each with probability 5/9. The value of either game is 1/9 to the second player.
A nontransitive set with the same numbers as set III is obtained by interchanging 3 with 4 and 6 with 7.
The same game format, but with each player rolling his selected die twice—and scoring the cumulative total—retains the nontransitivity but reverses the dominance for the cases of sets I and II.
Specifically, for set I, A wins against C with probability 0.613; C wins against B, and B wins against A, each with probability 5/9. The value of the game, with the first player selecting A, B, or C at random, equals 0.150 to the second player.
For set II, C wins over A with probability 0.518; A wins over B, and B wins over C, each with probability 0.590. With the first player selecting A, B, or C equiprobably, the value of the game to the second player is 0.132.
Set III loses its nontransitivity in this game format (each die cast twice)!
With set IV and two rolls of each die, D wins over F with probability 4/9; F wins over E, and E wins over D, each with probability 42/79. (The probability of a tie—the first player choosing D, E, or F equiprobably—is 8/243.) The value of this game is 149/1659 = 0.0898 to the second player.
With each person casting a selected die three times or more and then comparing cumulative totals, the game does not exhibit nontransitivity.
R.P. Savage (Ref.) has constructed a nontransitive set of three dice using the numbers 1, 2, …, 18:
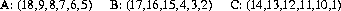
Here, A wins over B, and B wins over C, both with probability 7/12; C wins over A with probability 25/36.
Schwenk’s dice (Ref. Hobbs) constitute yet another three-member nontransitive set:
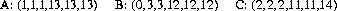
For a single roll of these dice, matched pairwise, A wins over B; B wins over C; and C wins over A, each with probability 7/12. However, when each die is rolled twice, preferences are reversed: C2 now wins over B2 with probability 25/48, while B2 wins over A2, and A2 wins over C2, each with probability 77/144.
Curiously, rolling each die three times returns the order of preference to B3 > C3 (with probability 0.5067), C3>A3, and A3 > B3 (each with probability 0.5028). (For this game, a significant probability of tying exists.)
Bradley Efron9 has devised sets of four dice with nontransitive properties:
In a two-person game, each player selects A, B, C, or D, and then compares the number rolled with their respective dice, the higher number winning the stake.
With sets I or II, the second player wins with A against B, B against C, C against D, and D against A, each with probability 2/3. The value of the game is always 1/3 to the second player.
With set III, the same selection strategy results in a win probability of 11/18 for the second player, for whom the game offers a value of 5/18. (The probability of a tie equals 1/18.)
Another set of four nontransitive dice, notable for using each number 1 through 24 just once, has been devised by Columbia University physicist Shirley Quimby (Ref.):
| A:(3, 4, 5, 20, 21, 22) | C:(10, 11, 12, 13, 14, 15) |
| B:(1, 2, 16, 17, 18, 19) | D:(6, 7, 8, 9, 23, 24) |
Here, A > B > C > D > A. Whichever set the first player selects, the second player then selects the superior set, winning with an average probability of 2/3. (It has been proved that 2/3 is the greatest possible advantage achievable with four dice.)
With three sets of numbers, the maximum advantage is 0.618; however, the sets must contain more than six numbers (thus precluding conventional dice). With more than four sets, the possible advantage approaches a limit of 3/4.
Oskar van Deventer, a Dutch puzzle-maker, devised a three-person game with a nontransitive set of seven dice:
| A:(2, 2, 14, 14, 17, 17) | E:(1, 1, 12, 12, 20, 20) |
| B:(7, 7, 10, 10, 16, 16) | F:(6, 6, 8, 8, 19, 19) |
| C:(5, 5, 13, 13, 15, 15) | G:(4, 4, 11, 11, 18, 18) |
| D:(3, 3, 9, 9, 21, 21) |
The first and second players each select a (mutually exclusive) die from one of the sets A, B, …, G. The third player then wins with a strategy illustrated by a Fano10 plane—defined as a two-dimensional finite projective plane of order 2—an incidence system wherein a set of seven points is partitioned into a family of seven “blocks” in such a way that any two points determine a block with three points, and each point is contained in three different blocks.
The diagram of Figure 6-1 shows the Fano plane with the six points labeled F, A, E, C, B, and G, moving clockwise around the triangle beginning with F at the top vertex. Set A dominates the three pairs along line a (B-C, B-E, and C-E), set B dominates the three pairs along line b, etc., as illustrated in Table 6-6.
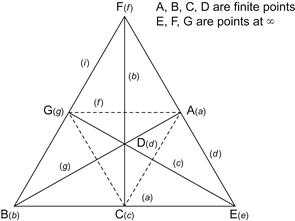
Figure 6-1 The Fano plane.
Table 6-6. Seven-Dice Dominance Pattern
| Dice Set | Dominates |
| A | B-C, B-E, and C-E |
| B | C-D, C-F, and D-F |
| C | D-E, D-G, and E-G |
| D | A-E, A-F, and E-F |
| E | B-F, B-G, and F-G |
| F | A-C, A-G, and C-G |
| G | A-B, A-D, and B-D |
The examples of nontransitivity presented here have been limited to six-sided dice. Sets of n-sided dice that exhibit nontransitivity can also be contrived—see Finkelstein and Thorp (Ref.).
Sicherman’s Dice
The probability distribution of the outcomes 2 through 12 from two conventional dice (Table 6-1) can be duplicated by a second pair with faces not restricted to numbers 1 through 6.11
The two-dice polynomial can be represented by
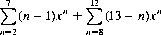
which can be factorized into the form f(x)g(x), with f(0) = g(0) = 0 and f(1) = g(1) = 6. The two factorizations are
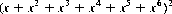(6-24)
and
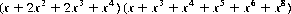(6-25)
where each exponent represents the face of a die, and each coefficient indicates the number of times that face appears on the die.
The expression of 6-24 delineates the two conventional dice, while the two dice represented by that of 6-25 are
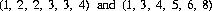
By definition, these are the only two pairs of dice with the standard probability distribution; it is further apparent that n pairs of Sicherman dice have the same probability distribution as 2n conventional dice.12 For n odd, pairs of Sicherman dice plus a conventional die exhibit the same distribution as n conventional dice.13
Casino Games
Craps
Of the various dice games enlisted by the gaming casinos, the most prevalent, by far, is Craps. Its direct ancestor, the game of Hazard, was reputedly (according to William of Tyre, d. 1190) invented by 12th-century English Crusaders during the siege of an Arabian castle. Montmort established formal rules for Hazard (originally: “Hazart”), and it subsequently became very popular in early 19th-century England and France. In the British clubs the casts of 2, 3, or 12 were referred to as “Crabs.” Presumably, the French adaptation involved a Gallic mispronunciation, which contributed the word “Craps,” and since the game immigrated to America with the French colony of New Orleans, its currency became firmly established.14 Adopted by American blacks (the phrase “African dominoes” is often a synonym for dice), Craps spread out from New Orleans across the country. A rather disreputable aura surrounded the game during the latter half of the 19th century, owing to its manipulation by professional “sharpers” frequenting the steamboats and Pullman cars of the era.15However, its widespread popularity among the soldiers of World War I gained it a veneer of social respectability. It was subsequently enshrined in the salons of Monte Carlo and on the green baize table-tops of Las Vegas; today the cabalistic signs of the Craps layout can be seen in every major casino of the world.
Craps is played with two conventional dice. The types of wagers are displayed in the betting layout shown in Figure 6-2 on the next page. The basic bet is the “pass line,” which wins unconditionally when the player initially throws a 7 or 11 (“naturals”) and loses unconditionally when the initial outcome is a 2, 3, or 12 (referred to as “craps”). The remaining outcomes—4, 5, 6, 8, 9, 10—are each known as a “point.” When a point is set, the player continues to roll the dice; the pass-line bettor then wins if that point is rolled again before the appearance of a 7 and loses if the 7 appears first. The latter event, known as a “seven-out,” ends the player’s tenure with the dice.
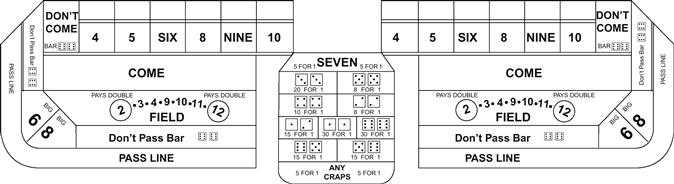
Figure 6-2 Craps layout.
The probabilities of the outcomes 2 through 12 of a throw of two dice are obtainable directly from Eq. 6-14 and are tabulated in Table 6-1. Thence the probability of throwing a 7 is 6/36, of throwing an 11 is 2/36, and of throwing a point is 24/36. Table 6-7 shows the probabilities that a point is repeated before the occurrence of a 7. Thus, the probability of making a pass is
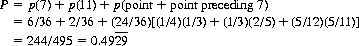(6-26)
Table 6-7. Probabilities of Making a Point
In casino Craps, the opposite of the pass-line bet is the “don’t pass, bar twelve” bet—meaning that a throw of 12 on the first roll of a sequence is deemed a tie. Hence its probability of success is
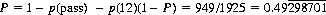
The “come” and “don’t come” bets are identical to pass and don’t pass, respectively, and may be initiated at any time rather than exclusively on the first roll of a sequence.
A “field” bet wagers that the next outcome of the dice is a 2, 3, 4, 9, 10, 11, or 12, with the 2 and 12 each paying 2 to 1—for a winning probability of 0.472 and an expectation of −1/18 (some casinos offer 3 to 1 for a 12, increasing the expectation to −1/36).
Betting the “big 6” or “big 8” constitutes wagering that that outcome will appear before a 7; the probability of this event is (5/36)/[(5/36) + (6/36)] = 5/11. Betting a 7, 11, 2, 12, and 3 are self-evident wagers that the next roll will produce that particular outcome. A “hard-way” bet defines the wager that a specified even-numbered outcome (4, 6, 8, or 10) will occur with the same number of pips showing on each die (sometimes referred to as a double number) before the same outcome with different pips on each die (the “easy way”) or the outcome 7 occurs.
Finally, an “odds” bet is permitted following the establishment of a point during a pass, don’t pass, come, or don’t come wager (events that occur 2/3 of the time). A sum up to 100 times the original bet (depending on individual casino rules) wagers that the point will reappear before the outcome 7. By itself, “taking the odds” constitutes a fair bet and thereby nudges the player’s negative expectation closer to zero.
Some casinos permit different amounts to be wagered for the odds bet on the 4&10, 5&9, and 6&8 points. In general, if the odds bet allows up to x times odds on 4&10, y times odds on 5&9, and z times odds on 6&8, the player’s expectation is
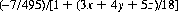
As opposed to taking the odds, the contrary play, combined with a don’t pass (or don’t come) bet, wagers that a 7 appears before the point and is referred to as “laying the odds.” The player’s expectation for this bet is
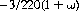
where the player is permitted ω times the odds.
A tabulation of the various wagers for Craps is given in Table 6-8. The overall expectations from combining the pass line (or come) bet with taking the odds and from combining the don’t pass (or don’t come) bet with laying the odds are shown in Table 6-9.
Table 6-8. Probabilities for Craps
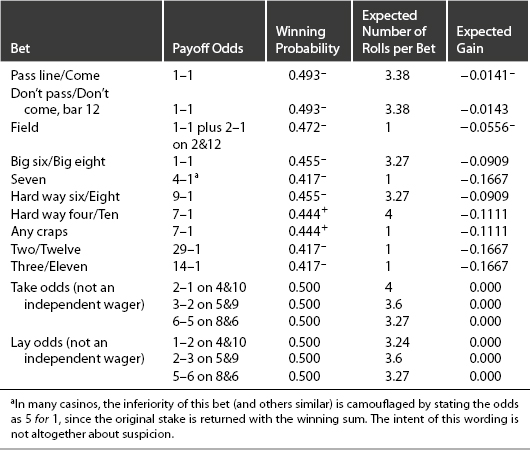
Table 6-9. “Odds” Expectations
| Amount of “Odds” Bet (Times) | Expectation from “Taking the Odds” | Expectation from “Laying the Odds” |
| 1 | −0.0085 | −0.0068 |
| 2 | −0.0061 | −0.0045 |
| 5 | −0.0033 | −0.0023 |
| 10 | −0.0018 | −0.0012 |
| 100 | −0.0002 | −0.0001 |
As is evident, Craps shooters are accorded no significant strategy other than selection of the wager with the least unfavorable odds. Because of its rapid pace, however, the game has attracted a plethora of systems and has developed a small anthology of esoteric machinations, anthropomorphic analogies, and mumbled incantations (“Baby needs a new pair of shoes”). As with Roulette, dice possess “neither conscience nor memory”16 and are democratic to a fault.
Of those determined experimenters who have tested the probabilities of Craps, perhaps the greatest stamina was demonstrated by B.H. Brown (Ref.), who conducted a series of 9900 Craps games, obtaining 4871 successes and 5029 failures compared with the theoretically expected values of 4880 successes and 5020 failures, a discrepancy well within one standard deviation. Although the major gambling casinos do not maintain statistical records, one astounding event has been recorded: on May 23, 2009, at the Borgata Casino in Atlantic City, Patricia Demauro did not seven-out her Craps hand until the 154th roll. The probability for a particular such run is 2.86 × 10−10 (Ref. Ethier and Hoppe).
Proposition (Side) Bets
Associated with Craps are a number of so-called proposition bets. These wagers generally entail the probability of a specified outcome occurring in a specified number of throws or before another particular outcome occurs. six of the more common proposition bets:
1. The probability P5-9 that the outcomes 5 and 9 both appear before a 7. Either 5 or 9 will occur before a 7 with probability (8/36)/(6/36 + 8/36) = 8/14. The probability that the other outcome then occurs before a 7 is (4/36)/(6/36 + 4/36) = 4/10. Therefore,
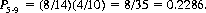
A payoff of 3 to 1 results in a House Take of 8.57%.
2. The probability P4–6 that the outcomes 4 and 6 both appear before a 7. Thorp (Ref.) has shown that
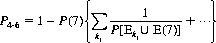
where P(7) is the probability of the event E(7) occurring.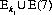 
, the union of preceding events and the event E(7), means that at least one of the events 
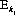and E(7) occurs. Numerically,
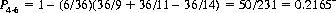
(The unexpected complexity of determining P4–6 lies in the fact that P(4) and P(6) are not equal.) Here, a 3-to-1 payoff leaves a House Take of 13.42%.
3. Thorp has also computed the probability P6p that all six points will appear before a 7 as 0.0622−, and the probability that all numbers other than 7 will appear before a 7 as 0.0053.
4. The probability P12 of rolling 12 before two consecutive rolls of 7 (Ref. Griffin). Player A wagers on the former outcome, B on the latter. We can write immediately
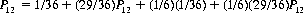
which represents the probability that the first roll is a 12 (first term) plus the probability that the first roll is neither a 12 nor a 7 (second term) plus the probability that the first roll is a 7 and the second roll a 12 (third term) plus the probability that the first roll is a 7 and the second roll is neither a 7 nor a 12 (fourth term). Solving for P12, we have
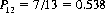
for the probability that 12 appears first. Hence the game offers a positive expectation of 1/13 to A. (The House, of course, accepts only bets that two consecutive 7s appear first.)Fallacious reasoning argues that the two outcomes are equiprobable since 12 occurs with probability 1/36 and two successive 7s with probability (1/6)(1/6). And the game is equitable if it ends immediately upon the occurrence of a second (consecutive) 7 regardless of the number of 12s that precede it.With a continuous sequence of dice rolls (rather than beginning anew as each bet is resolved), A’s probability of success decreases slightly—since the previous roll was either a non-7 (which returns the game to its starting point) or a 7 (whence A’s probability of a win is 6/13). Then, for the continuous sequence,
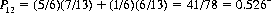
While A’s probability of winning the initial wager is 7/13, his probability of winning the nth wager is (1 + 1/13n)/2, maintaining the game as a positive but diminishing expectation for A.Curiously, if we inquire as to A and B winning specifically on the nth roll of the dice, we find these probabilities to be equal. A’s probability of a win remains (as always) 1/36; for B to win, the nth roll and the n−1st roll must be 7s—that is, (6/36)(6/36) = 1/36. Hence the game is equitable for any wager after the first. Further, if the game is defined for exactly n rolls, A’s expectation is 1/36 = 0.027−, a value that holds for all n.If, on the other hand, the game is defined for exactly nwagers, A’s expectation on the nth wager is 1/13n. A’s total expectation is then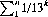 
. For n large, this summation equals (1/13)/(1 − 1/13) = 1/12.
5. The probability P6-8 of rolling 6 and 8 before 7 occurs twice. Note that the probability that a 6 or 8 precedes a 7 is 10/16; the probability that the remaining 8 or 6 precedes a 7 is 5/11; the probability that a 7 precedes the remaining 6 or 8 is 6/11; and the probability that a 7 precedes both 6 and 8 is 6/16. Therefore,
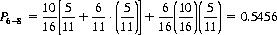
6. A more interesting variation on a proposition bet concerns A and B alternately throwing two dice: A begins the game and wins if he throws a 6 before B throws a 7. B’s successful outcome has probability 6/36 compared to 5/36 for that of A; however, since A throws first, the game is more equitable than would first appear. Specifically, we can show that if the game is limited to n throws, A’s probability pn of winning is
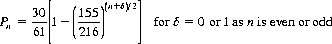
Similarly, B has probability qn of winning, expressed by
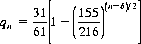
and the probability rn of a tie (no winner after n throws) is
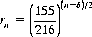
As n increases indefinitely, the probability of a tie declines to zero, and pn and qn approach 30/61 and 31/61, respectively. Hence, the long-term game favors B with an expectation of 0.0164.
Duration of a Craps Hand
It is customary in casino Craps for the shooter to continue rolling the dice until he loses his wager. We ask the expected (mean) number of rolls, E, for a shooter’s turn—that is, before he rolls an initial craps or “sevens out” after establishing a point. Then
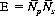
where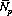 
is the average number of rolls per pass-line decision, and 
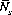is the average number of pass-line decisions per seven out. For 
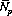we can write
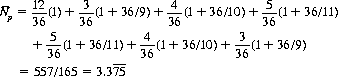
where the first term represents the probabilities of 7, 11, 2, 3, or 12 on the first roll, and the remaining terms represent the probabilities of points 4, 5, 6, 8, 9, and 10, respectively, multiplied by the expected number of rolls to obtain that point. The total probabilities of a seven out for the six points,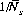 
, can be calculated, analogously to Eq. 6-26, as
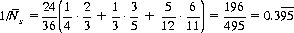
Therefore,
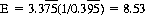
So the shooter can expect to hold the dice for slightly more than 8½ rolls.
A related question asks the median number of rolls—i.e., the number for which the shooter has a probability ≥1/2 of sevening out. We can compute this number from the theorem of complete probability (Eq. 2-6), where Ai are the eight possible states faced by the craps shooter:
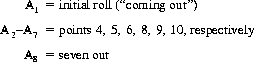
State A8 represents the probability Pn that the shooter will seven out on or before the nth roll. Donald Catlin (Ref., 2002) has computed values of A8, determining that for n = 5, P5 = 0.424−; and for n = 6, P6 = 0.503−.
Thus the probability that the shooter will have sevened out by the sixth roll is slightly greater than 1/2. The probability of the shooter sevening out precisely on the sixth roll is the difference in these two values: 0.079−.
(Some casinos pay a bonus to the shooter who makes all six points before sevening out. The probability of this feat is 1.62− × 10−4.)
Reddere Craps
Analogous to their practice for Reddere Roulette (Chapter 5), major casinos cater to their more affluent clientele by offering a refund of from 10 to 50% of potential losses after n plays. With the pass-line bet, the player’s expected loss is then
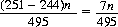
As with any even wager, the standard deviation for n plays is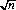 
. Standardizing,
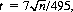
and, setting E(n) equal to t, the Reddere integral (Appendix Table A) has a value of 0.276. Thus,
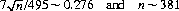
(precise computation yields n = 382). Thus for a sequence of 382 plays or fewer at the pass line, the player retains a positive expectation when half his potential losses are refunded. His greatest expectation occurs at n = 93 (approximately 1/4 the number of plays necessary for the casino to gain a positive expectation) for an expected profit of 0.960.
Other wagers at Reddere Craps with a potential 50% refund after n plays are detailed in Table 6-10.
Table 6-10. Reddere Craps with 50% Rebate
| Bet | Number of Plays or Fewer for Player’s Positive Expectation |
| Any 7 | 9 |
| Any craps | 39 |
| 2 or 12 | 65 |
| 3 or 11 | 32 |
| Big 6 or 8 | 9 |
| Hardway 6 and 8 | 76 |
| Hardway 4 and 10 | 39 |
| Field | 27 |
In general, for a potential refund of r percent, the player’s expectation E (for a single-play probability of winning p and a single-trial probability of losing q = 1 − p) after n plays is given by
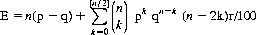
For r = 10, E is positive for nine or fewer plays. The maximum expectation of 0.036+ occurs at n = 1, with a close-to-maximum of 0.035− at n = 3.
5-Count
A distant cousin to the Epaminondas system (Chapters 3 and 5), the 5-count was introduced in 1980 by a gambler identified only as “The Captain.” Designed to uncover any bias—deliberate or not—in the probability distribution of the two-dice outcomes, it kicks in when the shooter first rolls a point. His subsequent three rolls define the 2-count, 3-count, and 4-count (regardless of their outcomes if the shooter has not sevened out). The fifth roll becomes the 5-count only if its outcome is a point; otherwise, the count remains at 4 (assuming a 7 has not been rolled). at this stage, the bettor is advised to wager on the come option.
Simulations run by Donald Catlin (Ref.) indicate that an SRR (Seven-to-Rolls Ratio) of 1 to 7 results in a positive return of 0.18%. with an SRR reduced to 1 to 8, the bettor on pass or come is offerred a 1.15% advantage.
Certain Craps aficionados claim the ability to control the dice sufficiently to reduce the SRR significantly below its unbiased value of 1 to 6. Wagering on 6 or 8, say, the bettor will have an expectation of
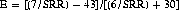
which is positive for SRR <7/43 (Catlin, 2003). An SRR of 1 to 7 offers an expectation of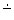 
0.083, while an SRR reduced to 1 to 8 confers an advantage of +0.167 for this wager.
Craps Variations
Four dice are thrown in this variant, with the highest and lowest numbers discarded and the other two employed as in a conventional game of Craps. The probability distribution is displayed in Table 6-11. The mean equals 7, and the probability of winning is
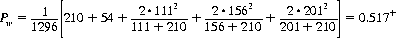
Table 6-11. Craps with Two Middle Dice
As a casino game, if the outcome 11 is classified as a draw rather than a player win, then Pw = 0.497−, an acceptable profit for the House.
In another four-dice variant the highest and lowest numbers are used and the other two discarded; the probability distribution in this case (again with a mean of 7) ensues as shown in Table 6-12. The probability of winning (retaining the standard rules of Craps) is 0.529+.
Table 6-12. Craps with High–Low Dice
When the four dice are used for a game wherein A bets on the sum of the highest and lowest numbers, and B bets on the sum of the two middle numbers, the result is zero expectation. The probability of a tie is 0.1426+, while both A and B share a winning probability of 0.4287−.
Sparc: Craps with Octahedral Dice
The player wins if his opening throw of two octahedral dice (8 sides numbered 1 to 8) shows 9 (the most probable outcome with probability 1/8), 4, 14, 15, or 16 (total probability 17/64). He loses if his opening throw is either 2 or 3 (probability 3/64). All other totals establish points, winning if repeated before a 9 is thrown, losing if a 9 intervenes.
The probability of making a pass (defined similar to conventional Craps) is calculated analogously:
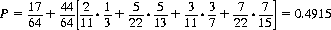
which qualifies Sparc as a casino game. (Side bets generally entail a slightly smaller House edge. For example, Big 8 and Big 10 pay even odds, with an expected gain of −1/15.)
In an alternative Sparc format, the player wins with an initial throw of 9, 14, 15, or 16 (probability 7/32). Totals of 2, 3, or 4 (probability 3/32) are not registered, whence the player throws again. His probability of making a pass now equals 0.4906. The appeal of this variant stems from the fact that the player cannot lose on his first throw.
Chuck-A-Luck
Originally known as “Sweat-Cloth,” Chuck-A-Luck has long been played illegally in British pubs under the name Crown and Anchor—the six sides of the dice are inscribed Clubs, Diamonds, Hearts, Spades, Crown, and Anchor. The game was exported to the United States about 1800. Three dice are agitated inside a double-ended, rotatable cage with an hourglass cross section (the “Bird Cage”). A player may wager upon any of the outcomes 1 through 6. If one (and only one) die exhibits that outcome (p = 75/216), the player wins at even odds; if two dice exhibit that outcome (p = 15/216), the payoff is 2 to 1; if all three dice show the player’s choice (p = 1/216), the payoff is 3 to 1; otherwise (that is, if the specified outcome appears on none of the three dice), the player loses. Elementary calculations indicate a probability of success of 0.461. An equitable game would offer odds of 1 to 1, 2 to 1, and 20 to 1, or of 1 to 1, 3 to 1, and 5 to 1 for the specified outcome occurring once, twice, or three times on the three dice.
Barbotte, Passe-Dix, Counter Dice, and Twenty-Six
Hundreds, if not thousands, of dice games have evolved since the cavemen first cast their knucklebones. In Barbotte, a Canadian version of Craps, the player wins if the two dice produce 3-3, 5-5, 6-6, or 6-5 and loses with the outcomes 1-1, 2-2, 4-4, and 2-1. The remaining values are not registered. In this form, Barbotte is a fair game.
Passe-dix (past ten) is an ancient game that fell into disuse until, in the 17th century, it attracted the attention of Galileo. Three dice are thrown, and the player can wager on manque (an outcome of 10 or lower) or passe (an outcome greater than 10)—whence the name. Passe-dix is also a fair game.
Counter Dice is played occasionally in taverns. The player selects a number 1 through 6 and then rolls ten dice from a cup ten times in all. If the player’s number occurs 20 times, he is paid at odds of 2 to 1; if the number appears 25 times, the payoff is 4 to 1; and if the number occurs 30 or more times, the payoff is 20 to 1. (The expected frequency for each number is, of course,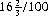 
.)
A version of Counter Dice, well known in Chicago bars, is “Twenty-six.” Here, a player selects a particular outcome of a die as his point; he then rolls ten dice 13 times, recording the total number of occurrences of his point (expected number equals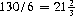 
). There is no standard payoff; however, most establishments pay 4 to 1 if the point occurs 26 times, with increasing odds (usually to about 8 to 1) for 33 or more occurrences. The probability of obtaining 26 particular outcomes in 13 throws of ten dice is given directly by Eq. 6-6:
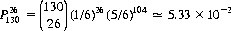
The probability of obtaining 26 or more occurrences of the point is, similar to Eq. 6-2,
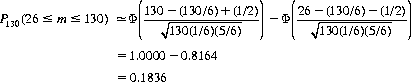
and the probability of achieving 33 or more occurrences of the point is
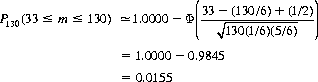
Other dice games that have attained a fleeting popularity in gambling casinos include Cusek (a type of Dice-Roulette in Macao), In-and-In, and Carabino.
Backgammon
A two-person game with complete information and probabilistic moves, backgammon constitutes one of the oldest board games known, originating along the eastern borders of the Persian empire in the third millennium B.C. It is played throughout the world, with numerous tournaments and regular world championship matches (as well as in the International Computer Olympiad). There are likely more professional backgammon players than professional Chess players.
Computer Programs
With 30 checkers and 26 possible locations (including the bar and off-the-board), it is evident that the number of possible configurations of the checkers (>1020) far exceeds the memory capabilities of any currently realizable computer. Further, the game tree has branching ratios of several hundred per “ply” (one player’s turn)—far too many to be amenable to the heuristic search procedures effective in Chess and Checkers.
The first practical backgammon-playing computer, the BKG 9.8,17 functioned by evaluating board positions throughout the course of the game. The program applies techniques of fuzzy logic to smooth over the transitions between phase changes. In 1979, the BKG 9.8 became the first program to defeat a world champion. Ten years later, backgammon-playing software, most notably TD-Gammon (for Temporal Difference learning [Ref. Tesauro]), achieved even greater success using a neural network that trains itself to be a heuristic evaluation function by playing against itself and learning from the outcome.
TD-Gammon incorporates an algorithm to learn complex numerical functions. At each time step, the algorithm is applied to update the network’s “weights” (real-valued parameters for each of the network’s connections), a procedure that has enabled the program to defeat backgammon players of world-class caliber.
Subsequent software programs—such as BGBlitz (2005 World Backgammon Champion), Jellyfish, and Snowie—refined the neural network approach yet further and are superior to the best human players.
Neural networks, it may be noted, are better suited for Backgammon—rather than the alpha-beta search and pruning techniques that have proved more efficient for chess.
Dice Divertissements
Fanciers of dice idiosyncrasies may wish to grapple with the following problems.
1. Removing the restriction that the pips on opposite faces of a die must total 7, show that the number of distinct dice totals 30.
2. Pair O’dice Lost. Prove that no weighting of two conventional dice is possible such that the outcomes of their sums—2 through 12—occur with equal probability (i.e., 1/11).Prove that the sums of two dice, P and Q, weighted as follows:
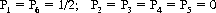
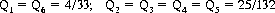
to yield the following distribution:
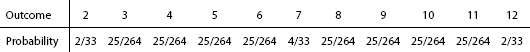
represent the “closest to equality” that can be implemented—that is, with minimal deviations from 1/11.
3. An ancient Chinese dice game entails each of two players casting six dice. Two specific outcomes are noted: any single pair of numbers and any two pairs. Compute their respective probabilities.This wording admits an ambiguity. If we define one pair as not excluding additional but different pairs or three-of-a-kind or four-of-a-kind with the remaining four dice, show that the probability of rolling a pair is 0.7399. And if “two pairs” is similarly defined as not excluding a third pair with the remaining two dice, show that this probability is 0.3445.Compute the probabilities of casting specifically one pair and specifically two pairs (excluding any combinations of the remaining dice that improve the “values” of the six dice cast).Compute the odds of rolling at least one pair and at least two pairs without exclusions for the remaining dice.
4. In a popular children’s game, each of two players casts six dice (or a single die six times). The outcomes are summed, but with the restriction that any number may be used only once. The sum, therefore, can extend from 1 to 21.Compute the probability that each player obtains the same sum (a tie game).
5. In an infinite sequence of dice throws, prove that the probability of the six outcomes ever occurring with equal frequencies is 0.022.
6. Determine the order of preference for n ≥ 4 rolls of Schwenk’s dice.
REFERENCES
Astumian RDean, (2001). Making Molecules into Motors. Scientific American.285:56–64 [July].
Brown Bancroft H, (1919). Probabilities in the Game of Shooting Craps. American Mathematics Monthly.26:351.
Catlin, Donald, “Rhythmic Rolling and the Gambler’s Jamboree,” 2003, http://catlin.casinocitytimes.com/articles/8159.html.
Catlin, Donald, “How Long Is a Roll?,” February 6, 2002, http://catlin.casinocitytimes.com/articles/1232.html.
Diaconis Persi, Keller JB, (1984). Fair Dice. American Mathematics Monthly.96:337–339.
Epstein, Richard A., and Lloyd Welch, “A Generalization of the Banach Match-Box Problem,” Hughes Aircraft Co., Communications Division Report OP-56, September 1963.
Ethier Stewart N, (2000). A Bayesian Analysis of the Shooter’s Hand at Craps. In: Stewart Ethier, William Eadington, eds. Optimal Play: Mathematical Studies of Games and Gambling. Reno: Institute for the Study of Gambling and Commercial Gaming, University of Nevada;: 311–322. .
Ethier Stewart N., and Fred M. Hoppe, “A World Record at an Atlantic City Casino and the Disribution of the Length of the Crapshooter’s Hand,” 2009, www.arXiv.org/abs/0906.1545.
Feldman, Larry, and Fred Morgan, “The Pedagogy and Probability of the Dice Game HOG,” 2003, www.amstat.org/publications/jse/v11n2/feldman.html.
Finkelstein Mark, Thorp Edward O, (2000). Nontransitive Dice with Equal Means. In: Stewart Ethier, William Eadington, eds. Optimal Play: Mathematical Studies of Games and Gambling. Reno: Institute for the Study of Gambling and Commercial Gaming, University of Nevada;: pp. 293–310. .
Fisher RA, (1925). Statistical Methods for Research Workers. Oliver and Boyd.
Gardner, Martin, “Dice,” Chapter 18, in Mathematical Magic Show, Alfred A. Knopf, 1997.
Griffin Peter, (1991). Extra Stuff. Huntington Press.
Hobbs, Clare, “Let 'Em Roll,”http://plus.maths.org/issue41/features/hobbs/index.html.
Humphrey S, (1979). Pig. The Mathematics Gazette.426:256–258 [63].
Humphrey S, (1980). More About Pig. The Mathematics Gazette.429:201–202 [64].
Jaynes ET, (1957). Information Theory and Stastistical Mechanics. Physical Review.106(4):620–630.
Neller Todd W, Presser Clifton, (2004). Optimum Play of the Dice Game Pig. The UMAP Journal.25(1):25–47.
Nick’s Mathematical Puzzles, www.qbyte.org/puzzles/p024s.html.
Pegg, Ed, Jr., “Tournament Dice,” 2005,www.maa.org/editorial/mathgames_07_11_05.html.
Quimby, S., Pallbearer’s Review, January 1971.
Robertson LC, Shortt RM, Landry SG, (1988). Dice with Fair Sums. American Mathematics Monthly.95:316–328.
Savage Richard P, (1994). The Paradox of Nontransitive Dice. American Mathematics Monthly.101(5):42.
Tesauro, Gerald, “Temporal Difference Learning and TD-Gammon,” Communications of the ACM, 38, No. 3 (1995), www.research.IBM.com/massive/tdl.html.
Thorp Edward D, (1964). Repeated Independent Trials and a Class of Dice Problems. American Mathematical Monthly.71(7):778–781.
Verhoeff, Tom, and Erik Scheffers, “Optimal Solitaire Yahtzee Strategies,”www-set.win.tue.nl/~custom/misc/yahtzee/.
Woodward Phil, (2002). Yahtzee®: The Solution. Chance.16(1):17–20.
Bibliography
Jacoby Oswald, (1947). How to Figure the Odds. Doubleday and Co.
Jacoby Oswald, Crawford John R, (1970). The Backgammon Book. Viking Press.
Keeler Emmett B, Spencer Joel, (1969). Proper Raising Points in a Generalization of Backgammon. The RAND Corporation [May P-4078.]
Pegg, Edward Taylor, Jr., “A Complete List of Fair Dice,” Master’s thesis, University of Colorado, 1997.
Rump Christopher M, (2001). Strategies for Rolling the Efron Dice. Mathematics Magazine.74(3):212–216.
Scarne John, Rawson Clayton, (1945). Scarne on Dice. The Military Service Publishing Co.
Schwenk AJ, (2000). Beware of Geeks Bearing Gifts. Mathematics Horizons.7:10–13 [April].
Tenney Richard, Foster Caxton, (1976). Nontransitive Dominance. Mathematics Magazine.49:115–120 [May–June].
Tesauro Gerald, (2002). Programming Backgammon Using Self-Teaching Neural Nets. Artificial Intelligence.134(Nos. 1–2):181.
Weisstein, Eric W., “Dice,” www.mathworld.wolfram.com/Dice.html.
Weisstein, Eric W., “Fano Plane,” www.mathworld.wolfram.com/FanoPlane.html.
1 One tale from the Ma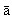hbh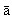rata concerns the pious and righteous King Yudhishthira gambling with Sakuni, an expert with false dice. Yudhishthira lost all.
2 According to post-Homeric legend, the invention of dice is attributed to Palamedes during the Trojan War. On the other hand, Herodotus reports that the Lydians claimed that honor.
3 Claudius (10 B.C.–A.D. 54), grandson of Mark Antony (who whiled away odd moments in Alexandria engaging in dice games), was the author of a book, How to Win at Dice, which, alas, has not survived.
4 The icosahedron offers a simple means of generating random decimal digits since its faces can be numbered (twice) from 0 to 9. Soccer balls are “truncated icosahedra,” constructed with 32 faces—20 regular hexagons and 12 regular pentagons.
5 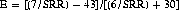is obtained most readily from tables of the χ2 distribution, such as Fisher (Ref.).
6 Newton was not particularly attracted to probability theory; this dice problem marks his sole venture into ye field.
7 For an interesting application of the negative binomial distribution, see Epstein and Welch (Ref.).
8 A corruption of “yacht at sea.”
9 A Stanford University statistician.
10 Gino Fano, 1871–1952, the preeminent precursor of David Hilbert in the field of projective geometry.
11 Noted by Col. George Sicherman of Buffalo, NY.
12 The probability of throwing a double number with a pair of Sicherman dice is 1/9—compared to 1/6 with traditional dice. In games where double numbers are significant (such as Backgammon and Monopoly), the substitution of Sicherman’s dice would alter basic strategies.
13 As an off-beat alternative, a pair of dice, one conventional and the other marked (0, 0, 0, 6, 6, 6), will produce a uniform distribution of outcomes 1 through 12 (the probability of each total equals 3/36).
14 Another plausible legend credits Count Bernard Mandeville Marigny with introducing the game to New Orleans. Marigny was a Creole and as such was known as Johnny Crapaud (French for “toad,” the term was originally applied to Frenchmen by Nostradamus in allusion to the fleur-de-lis pattern of the French national standard that, as altered by Charles VI in 1365, resembled three toadlike flowers; Guillim, in Display of Heraldrie, 1611, refers to the device as “three toads, erect, saltant”—the modern pejorative is “frog”). Thus the game was referred to as Crapaud’s or, finally, Craps.
15 Mis-spotted dice (called “tops”) were often switched in. With the faces of each die marked 1, 1, 3, 3, 5, 5, it becomes impossible to roll a 7 with two dice.
16 Joseph Bertrand, 18th-century French mathematician.
17 Programmed by Hans Berliner, professor of computer science, Carnegie Mellon University, on a PDP-10 in the early 1970s.