Chapter Eleven
Fallacies and Sophistries
Psychology and Philosophy
To Alice’s insistence that “one can’t believe impossible things,” the White Queen demurred: “I daresay you haven’t had much practice. When I was your age, I always did it for half-an-hour a day. Why, sometimes I’ve believed as many as six impossible things before breakfast.”
The White Queen’s sophistry is particularly applicable to gambling—a phenomenon that continues to be associated with superstition and metaphysics. Anthropologists have often commented on the striking resemblance between the uneducated gambler and the primitive. Before declaring war, the primitive consults his crystal ball, tea leaves, buzzard entrails, or other divination media, and if the gods signify success, war follows simply as an administrative action. If, subsequently, the war becomes a losing cause and he flees the battlefield, it is not from cowardice but rather because the “signs” have been erroneously read or interpreted and the gods really favored the opposition. Thus his losses are due to “fate”—a predestined decision from which there is no appeal. Similarly, a gambler assigns his successes to a combination of “luck” and prowess and his failures to the disfavor of the gods of chance. Such a belief is an apparently ineradicable irrationality of the unenlightened gambler.
The ubiquitous belief in luck and numerology is not confined to the unsophisticated gambler. All too many eminent geniuses have, in senility or in moments of sad aberration, succumbed to the irrationalities that beset frailer men.1 Huygen’s faith in “six” as the perfect number led him to the conviction that the planet Saturn could possess but a single moon. Hobbes’s geometry “plussed or minused you to heaven or hell.” Leibnitz applied geometrical principles to ethics and politics, and geometry to the selection of the King of Poland as well as to the deployment of the French army (for Louis XIV). John Craig expounded his “Mathematical Principle of Christian Theology.” Sir James Jeans advocated his conviction that the cosmos was the creation of a divine mathematician. Some of these creeds arise directly from supernaturalism and others from the more sophisticated appeal of the Cartesian image of an admirable science of numbers that would solve all human problems, a doctrine that yet finds ardent devotees in contemporary psychology.
There has been no dearth of attempts to establish axiomatic principles for intuitive mathematics. Perhaps the first such effort emerged from the concept of “moral” expectation as opposed to mathematical expectation. Buffon held that the moral value of any sum varies inversely with the total wealth of the individual who acquires it. Cramer considered it to vary as the square root of total wealth. D. Bernoulli maintained that the moral value of a fortune varies as the logarithm of its magnitude: that is, the personal value of any small monetary increment dx is inversely proportional to the total sum x in the possession of the individual (this idea is familiar to psychophysicists in the form of Fechner’s law).
We have emphasized the advantages of the objective utility function and objective probability for gambling phenomena. The introduction of intuition and morality into the workings of gambling theory is but another trap for the unwary set by the unenlightened.
Fallacies
Without mathematical context, we list here some of the fallacies prevalent in gambling as a result of psychological influences. The uneducated gambler exemplifies, par excellence, the processes of intuitive logic. He is often charged with emotion and directed by passionate, primitive beliefs; thus his acts may often contrast with the dictates of his objective knowledge. He injects a personal element into an impersonal situation.
Culled from many observations and laboratory experiments,2 the following 13 fallacies appear to be most prevalent and most injurious (in terms of profit and loss) to the susceptible gambler:
1. A tendency to overvalue wagers involving a low probability of a high gain and undervalue wagers involving a relatively high probability of low gain. This tendency accounts for some of the “long-shot” betting at race tracks.
2. A tendency to interpret the probability of successive independent events as additive rather than multiplicative. Thus the chance of throwing a given number on a die is considered twice as large with two throws of the die as it is with a single throw.
3. After a run of successes a failure is inevitable, and vice versa (the Monte Carlo fallacy).
4. The psychological probability of the occurrence of an event exceeds its mathematical probability if the event is favorable, and conversely. For example, the probability of success of drawing the winning ticket in a lottery and the probability of being killed during the next year in an automobile accident may both be one chance in 10,000; yet the former is considered much more probable from a personal viewpoint.
5. The prediction of an event cannot be detached from the outcomes of similar events in the past, despite mathematical independence.
6. When a choice is offered between a single large chance and several small chances whose sum is equal to the single chance, the single large chance is preferred when the multiple chances consist of repeated attempts to obtain the winning selection from the same source (with replacement); however, when there is a different source for each of the multiple chances, they are preferred.
7. The value of the probability of a multiple additive choice tends to be underestimated, and the value of a multiplicative probability tends to be over- estimated.
8. When a person observes a series of randomly generated events of different kinds with an interest in the frequency with which each kind of event occurs, he tends to overestimate the frequency of occurrence of infrequent events and to underestimate that of comparatively frequent ones. Thus one remembers the “streaks” in a long series of wins and losses and tends to minimize the number of short-term runs.
9. A tendency to overestimate the degree of skill involved in a gambling situation involving both skill and chance.
10. A strong tendency to overvalue the significance of a limited sample selected from a relatively large population.
11. Short-term outcomes will exhibit the same frequencies as long-term outcomes.
12. The concept of “luck” is conceived as a quantity stored in a warehouse, to be conserved or depleted. A law of conservation of luck is implied, and often “systems” are devised to distribute the available luck in a fortuitous manner. Objectively, luck is merely an illusion of the mind.
13. The sample space of “unusual” events is confused with that of low-probability events. For one example, the remarkable feature of a bridge hand of 13 Spades is its apparent regularity, not its rarity (all hands are equally probable). For another, if one holds a number close to the winning number in a lottery, one tends to feel that a terribly bad stroke of misfortune has caused one just to miss the prize. Bertrand Russell’s remark that we encounter a miracle every time we read the license number of a passing automobile is encompassed by this fallacy. The probability of an unusual occurrence should be equated to the ratio of the number of unusual (by virtue of symmetry or other aesthetic criteria) events to the total number of events.
In addition to those enumerated above, there exist other fallacies more directly associated with superstition than with intuitive logic. For example, there is the belief that the gambler’s “attitude” affects the results of a chance event—a pessimistic frame of mind (I’m going to lose $X) biases the outcome against the gambler. Another example is attributing animistic behavior to inanimate objects: “The dice are hot.” The concept of luck permeates and pervades the experience of the superstitious gambler. He has lucky days,3 lucky numbers, lucky clothes (worn during previous winning sessions), and lucky associates (he firmly believes that certain individuals are inherently more lucky than others and are more likely to achieve gambling success or, perhaps, to contaminate others with their power). He believes in a “sixth sense” that anticipates or compels the direction to success. He may carry amulets, talismans, fascina, charms, or mascots, consult sortes or oracles, and avoid black cats, ladders, or turning his back to the moon while gambling.
It is peculiar that our modern society, having consigned its seers, witches, water diviners, graphologists, geomancers, anthroposophists, astrologers, spiritualists, phrenologists, and pendulum swingers to the dark intellectual limbo, yet preserves a medieval approach to the laws of chance. With the gambler resides the last vestige of codified superstition.
Gobbledygook
“Vibration Science”
A relatively recent concoction, vibration science postulates that “numbers are self-predicting via the parenting relationship of the creative force vibrations and their unions automatically spawn.” Comprehension of this incomprehensible statement, so it is claimed, enables the “prediction of winning numbers.”
Paranormal Phenomena
Throughout our cultural development no social group of substance has failed to evolve a body of beliefs and actions that transcends ordinary experience. The type of noumenon currently fashionable is that encompassed by the field of parapsychology. To its adherents, parapsychology offers the fervor and personal involvement of mysticism and fundamentalist religion; to its detractors it is a beacon for those who prefer certainty to truth, for those prone to consult supernatural powers for the resolution of uncertainties, and for those ignorant of cause-and-effect relationships. Satisfying the Spinozistic yearning for an extra-human quality, it clearly fulfills a need. As Voltaire might have said, “If parapsychology did not exist, it would have been necessary to invent it.”
Various forms of ostensibly paranormal activity have been touted over many centuries. Fire walking, water divining, lycanthropy, shamanism, spiritualism, poltergeists, levitation, alchemy, materialization, faith healing, and oriental thaumaturgy have each experienced periods of popular appeal. In the 17th century, animism was a prevalent doctrine; doctors proclaimed a belief in “animal spirits” as the motive force of blood circulating in the human body. In the Victorian era, psychical “research” emphasized communication with the dead. Nonphysical communication between living persons was a logical extension, and in 1882 the term telepathy was coined by F.W.H. Myers (about seven years earlier Mark Twain had proposed the phrase mental telegraphy). The seeds of parapsychology theory were planted.
Gamblers were now offered the dream of “beating the game” through the exercise of personal, psychic powers. Cards could be read from the back, Roulette numbers predicted, and dice levitated to produce the desired outcome. Fortunes were available to those who possessed the “gift”; the “mind” could now conquer the universe.
The Statistical Approach
Perhaps the most significant turn in the investigation of parapsychology (a term coined in 1889 by psychologist Max Dessoir) was the introduction of the statistical approach. While no reason exists to assume that paranormal phenomena admit of statistical measures, this approach has its ingenious qualities. The obliging nature of the random number tables is well proven. And the field of statistics bows to no master for the ability to furnish subterfuge, confusion, and obscuration.
The first modern statistical experiments to test the existence of telepathic communication were performed in 1912 by J.E. Coover (Ref.) at Stanford University. About 100 students were induced to endure 14,000 trials of divining cards drawn from conventional 52-card decks. The results of the poorly controlled experiments were slightly above chance expectations, although Dr. Coover denied any particular significance.
A similar series of card-guessing trials, sponsored by the Society for Psychical Research, was undertaken by Ina Jephson in London in 1929. Sir Ronald Fisher was consulted to establish the scale of probability for partial successes (e.g., predicting the Ace of Spades instead of the Ace of Clubs). Each day, for a total of five days, 240 people guessed a card at random from the 52-card deck and then, following a shuffling operation, guessed again, the operation being performed five times. Of the 6000 guesses, 245 were correct (chance expectation = 115.4) in addition to many partial successes. Later repeated under more rigidly controlled conditions, the experiments exhibited no obvious paranormality.
In the United States, the first university experiments attempting telepathic communication with a “vocabulary” of playing cards were initiated in 1926 by Dr. G.H. Estabrooks of Harvard. A total of 1660 trials was performed wherein card color was conjectured; 938 successes resulted (expectation = 830).
Dr. and Mrs. J.B. Rhine (Ref.) commenced their experiments in 1927 at the Psychology Laboratory of Duke University. The Rhines replaced the 52-card deck with the 25 Zener cards: five kinds of cards with five of each kind as shown in Figure 11-1. Using these cards, Dr. Rhine conducted or supervised a truly formidable number of experiments (over 10,000 cases) testing for telepathy, clairvoyance, telegnosis (knowledge of distant happenings), precognition (divination of the future), and psychokinesis or PK (mental control over physical objects).
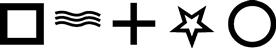
Figure 11-1 The Zener cards.
Rhine was responsible for the term “extrasensory perception” (ESP), which subsumes telepathy, clairvoyance, and precognition. Long-time head of the Duke Parapsychology Laboratory, he established himself as the leading American panjandrum for the existence of paranormal phenomena.
His experiments begin with an “agent” who notes each of the Zener cards sequentially and transmits telepathically to a “percipient” who records his “received signal.” Subsequently, the recorded version of the percipient is compared with the actual order of the cards. Sometimes agent and percipient are in the same room and can communicate verbally; at other times they are separated and communicate by lights or buzzers. The guesses have been attempted with and without the presence of observers, at distances from a few feet to across continents, and with delays ranging up to several years. The same set of cards has been utilized for the investigation of precognition and postcognition by examining the guesses for a possible forward or backward displacement (i.e., the percipient may be guessing one card ahead or one behind the actual card in the sequence being transmitted).
In England, the leading investigator of ESP phenomena for many years was British mathematician S.G. Soal who, despite his academic background, stood accused of altering and faking data. It is noteworthy that the first of Soal’s experimentation (1935–1939), conducted with 160 subjects recording 128,000 guesses, produced results well within predictions from chance alone. Subsequently, following the suggestion of another ESP advocate, Whately Carington, Dr. Soal turned to data mining for evidence of displacement and claimed to unearth significant proof of precognition and postcognition.
ESP experimenters range from those whose working environments are suitable for parlor games to those equipped with highly complex (and expensive) laboratory equipment. Dr. Andrija Puharich (a medical parapsychological researcher) operated a laboratory in Maine where he attempted to analyze the nature of telepathic communication by measuring interference patterns between electric or magnetic fields and ESP waves (the agent or percipient is seated in a Faraday cage!). The Communications Science Laboratory of AFCRL (Air Force Cambridge Research Laboratories) at Hanscom Field, Mass., at one time conducted a government-sponsored program for investigating paranormal phenomena. At SRI International, “remote-viewing” experiments were pursued in the 1970s—subjects attempted to “see” a remote place through the eyes of another person; the CIA initially expressed interest, then backpedaled.
In the Soviet Union, the subject was labeled “biological radio communication”; laboratories devoted to its existence and exploitation were set up in Moscow, Leningrad, and Omsk (with results classified secret).
The world’s first chair of parapsychology was established at the University of Utrecht after the Netherlands Ministry of Education had officially recognized the subject as a branch of psychology. The Princeton Engineering Anomalies Research (PEAR) laboratory gave up the ghost in early 2007 after nearly three decades of PK and ESP experiments that mostly embarrassed the university. And there still exist numerous small concentrations of parapsychology experimenters, each guessing the Zener cards, each rolling dice while concentrating, muscles taut, on directing the outcome, and each publishing their results, however questionable, in receptive journals.
Attitudes to ESP
What reasonable posture can we assume in the face of this overwhelming mass of “evidence”? To skewer the subject with systematic rejection would be hubristic, although we cannot accept it comfortably. As Aristotle declared, in speaking of oracular dreams, “It is neither easy to despise such things, nor yet to believe them.” Yet, were there any credible evidence for the existence of extrasensory perception, scores of reputable scientists would then leap into such a fascinating field. None such has been forthcoming.
The very existence of ESP would revolutionize our understanding of the physical universe and would demand a drastic overhaul of modern philosophy. But scientists and philosophers unquestionably retain a negative view of ESP, many with such intensity that they find it difficult to repress a Nietzschean outburst against determined believers. Likely, their reasoning is similar to Hume’s in his argument regarding miracles:
A miracle is a violation of the laws of nature; and as a firm and unalterable experience has established these laws, the proof against a miracle, from the very nature of the fact, is as entire as any argument from experience can possibly be imagined … [N]o testimony is sufficient to establish a miracle unless the testimony be of such a kind that its falsehood would be more miraculous than the fact which it endeavors to establish.4
Are the miracles of Rhine, Soal, et al., less miraculous than the possibility of fraud, self-deception, or error?
Mathematical Critiques of ESP Experiments
From its inception, the field of ESP has been a magnet for criticism directed at its methods of statistical analysis, its standards of measurement, and/or the integrity and sophistication of is investigators. In the 1930s and 1940s, the statistical techniques employed by Rhine and other ESP researchers were widely but often erroneously disparaged. Indisputably, statistical evaluations of ESP experiments have been of a quality far beyond the standards of the experiments themselves. As a consequence, the mathematical soundness of the analysis of the ESP and PK experiments has been cited to prove the soundness of the experimental procedures (ignoratio elenchi). In addition to the fact that one rigorous element of a structure does not automatically imply a totally sound structure, parapsychologists have shown themselves all too tolerant of worms in their statistical apples.
The first problem in examining the existence of ESP by telepathic transmission of card symbols is to distinguish between prediction and guesswork. A scale must be established that measures the results in terms of their departure from chance occurrences. Following a technique used by psychometrists, ESP investigators have adopted the term critical ratio, which provides a numerical evaluation of the significance of a series of “guesses” in terms of the number of standard deviations above (or below) the expectation resulting from chance. That is,
(Initially, probable error was used instead of the standard deviation; thus the critical ratio would be increased by 0.6745.)
This definition is a convenient and sensible one, particularly if the probability of the various correct guesses follows a binomial distribution, for then the probability that the results are due solely to chance is obtainable directly from tables of the probability integral. Indeed, a binomial distribution is assumed in the evaluation of ESP experiments with card guessing.
Consider a percipient predicting cards drawn (without replacement) from a deck of N cards composed of N/M kinds. Then an implicit assumption in application of the binomial distribution is that each kind may be represented in the deck by any number from zero to N, whence the probability of n correct guesses is expressed by
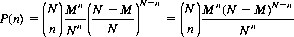(11-1)
Given knowledge of the deck’s composition, it is highly likely that the percipient’s predictions will closely correspond to that composition (i.e., he will tend to guess N/M kinds of cards and M of each kind). the probability distribution of correct guesses for this circumstance can be derived as
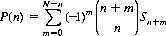(11-2)
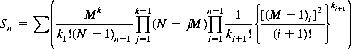(11-3)
with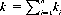 
and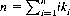 
. The summation in Eq. 11-3 is over those partitions of n restricted by k ≤ N/M and i ≤ M.
Equations 11-1 and 11-2 are evaluated for the Zener pack (N = 25, M = 5) with results tabulated in Table 11-1. The difference between the two distributions is not excessive, the exact distribution being skewed slightly toward the extreme values.
Table 11-1. Probabilities for Guessing Zener Cards
| Number of Correct Guesses | Probability Due to Chance (Binomial Distribution) | Probability Due to Chance (Exact Distributions) |
| 0 | 3.778 × 10−3 | 4.286 × 10−3 |
| 1 | 2.361 × 10−2 | 2.545 × 10−2 |
| 2 | 7.084 × 10−2 | 7.336 × 10−2 |
| 3 | 1.358 × 10−1 | 1.366 × 10−1 |
| 4 | 1.867 × 10−1 | 1.843 × 10−1 |
| 5 | 1.960 × 10−1 | 1.919 × 10−1 |
| 6 | 1.633 × 10−1 | 1.603 × 10−1 |
| 7 | 1.108 × 10−1 | 1.101 × 10−1 |
| 8 | 6.235 × 10−2 | 6.331 × 10−2 |
| 9 | 2.944 × 10−2 | 3.090 × 10−2 |
| 10 | 1.178 × 10−2 | 1.291 × 10−2 |
| 11 | 4.015 × 10−3 | 4.654 × 10−3 |
| 12 | 1.171 × 10−3 | 1.453 × 10−3 |
| 13 | 2.928 × 10−4 | 3.942 × 10−4 |
| 14 | 6.273 × 10−5 | 9.310 × 10−5 |
| 15 | 1.150 × 10−5 | 1.914 × 10−5 |
| 16 | 1.797 × 10−6 | 3.423 × 10−6 |
| 17 | 2.378 × 10−7 | 5.312 × 10−7 |
| 18 | 2.643 × 10−8 | 7.115 × 10−8 |
| 19 | 2.434 × 10−9 | 8.247 × 10−9 |
| 20 | 1.826 × 10−10 | 7.981 × 10−10 |
| 21 | 1.087 × 10−11 | 7.079 × 10−11 |
| 22 | 4.939 × 10−13 | 4.011 × 10−12 |
| 23 | 1.611 × 10−14 | 4.011 × 10−13 |
| 24 | 3.355 × 10−16 | 0 |
| 25 | 3.555 × 10−18 | 1.604 × 10−15 |
Assigning a binomial distribution to card-guessing phenomena results in a platykurtic bias of the probabilities. For the Zener deck, the binomial distribution is characterized by a standard deviation of
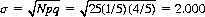
where p = 1/5 is the probability of a correct guess, and q = 1 − p. For the exact distribution of guesses (knowing the composition of the Zener pack), the standard deviation is
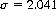
Thus, the assumption of a binomial distribution injects an error of 2% in the critical ratio, favoring the existence of ESP.
R.C. Read (Ref.) examined an ESP experiment wherein each card is exposed to view following the attempt by the percipient to predict its symbol. Under this rule, an intelligent strategy is to select for the next card that symbol (not necessarily unique) represented most frequently among the remaining cards. With an n x n deck (n kinds of cards with n of each kind), the expected number of correct guesses is then
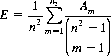(11-4)
where Am is the coefficient of tm in the expression
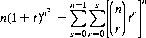
For the Zener deck, Eq. 11-4 results in E = 8.647, an expectation consid-erably greater than that (5) obtained without the sequential exposure of each card.
We could improve the significance of these experiments and their interest—and blunt Read’s criticism—if each of the 25 cards was independently selected with probability 1/5, both agent and percipient remaining uninformed regarding the specific composition of the deck. (The Zener deck would occur with probability 25! (5!)−5 5−25 = 0.00209.)
Another source of error arises from incorrect treatment of the forward or backward displacement of the predictions. Rigorous experimental technique dictates that the object of a series of guesses be established a priori. If the series of trials is sufficiently long, it becomes more feasible to permit a posteriori decisions as to the object of the experiment. However, in a relatively short sequence, the expectation of the number of correct predictions increases with the flexibility of the a posteriori decisions. For example, a series of 25 guesses with the Zener cards, restricted to zero displacement, yields an expectation of
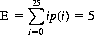
for the number of matches [with either the binomial or exact distribution used for p(i), the probability of guessing exactly i cards correctly].
Now, if we are allowed to decide a posteriori that we will search the recorded data for evidence of a forward displacement of one card (precognition), no displacement (telepathy), or a backward displacement of one card (postcognition), and select that which is maximum, the expected number of correct guesses is expressed by
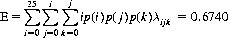
where
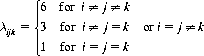
and the exact probability distribution of Table 11-1 is used for p(i), p(j), and p(k). Obviously, if displacements greater than plus or minus one card are allowed, the expected number of correct guesses rises further. On the other hand, as the length of the series of trials increases, the expectation decreases, approaching the value (5) obtained by establishing the data analysis procedure a priori.
Inadequate shuffling of the Zener cards provides yet another potential source of higher scores in telepathic experiments. From the analysis presented in Chapter 7, we can note that more shuffles are required to randomize odd numbered deck lengths than a deck of 2n cards. Thus, special precautions are indicated when employing a 25-card deck. Although the mental feat of predicting cards by estimating the shifts in position after shuffling is a prodigious one, it is not above the ability of some practiced individuals. Further, only a limited success is required to achieve a significant improvement in the results.
Another error common in ESP experimentation arises when the number of trials of card guessing is not established a priori. With the trials concluded at the option of the experimenter (usually when the percipient becomes “tired” and his success rate declines; this circumstance is referred to as the “headache phenomenon”), unusual results can be guaranteed. To illustrate this concept, let us examine the null hypothesis H0 that the mean number of correct guesses in a series of trials is that of chance expectation, as opposed to the hypothesis H1 that the mean number of guesses is greater (say) than chance expectation. Then, if it is assumed that the series of guesses is normally distributed, the conventional statistical test based on a sample of fixed size—n trials—dictates that we must reject H0 in favor of H1 if and only if the number of correct guesses Sn is such that
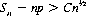(11-5)
where p is the chance probability of achieving a correct guess, and C is some constant. The probability P(C) of rejecting H0 despite its truth is
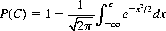
By selecting a suitably large value of C, P(C) can be rendered as small as desired.
Now it follows from the law of the iterated logarithm that with unity probability the inequality of Eq. 11-5 is valid for infinitely many values of n if the sampling is continued indefinitely, regardless of the extent to which P(C) is decreased. Thus, the experimenter must eventually encounter a value of n whereby the inequality holds; terminating the experiment at that point compels us to reject the null hypothesis H0 (and thereby disregard truth). It is evident that when optional stopping is permitted, the usual statistical procedures for hypothesis testing cannot be applied. We should insist on establishing beforehand the sample size or, at least, restraining it to be within reasonable limits. With the flexibility inherent in the option to alter at will the number of trials, it is not surprising that ESP is described (by parapsychologists) as a phenomenon visited upon some people sometimes.
We should note that the consequences of optional stopping are not relevant in games of known probability, as discussed in Chapter 3. In those instances, it is not a statistical hypothesis under examination, but the running sum of a binary sequence, which is automatically concluded if at any time it reaches some preestablished value.
Other Criticisms
It is sometimes difficult to understand how the elementary points expressed here can be ignored by ESP investigators. The accusation of fraud has been raised, notably by Dr. George Price (Ref.) in Science magazine; and, for certain graduate students participating in the experiments, certain soi-disant “psychics,” and certain individuals with vested interests in the existence of ESP, the perpetration of outright fraud likely explains many outstanding results. Several examples of collusion have been uncovered by statistical analyses of the series of correct “guesses” that detected significant periodicities, indicating a high probability of prearranged “guesses” at predetermined positions on a printed form. Subconsciously motivated scoring errors in favor of the basic premise have been detected by hidden cameras. However, in many instances, the unquestionable sincerity and stature of the experimenters must render the possibility of duplicity exceedingly small. Without impugning an experimenter’s integrity, we would be well advised to recall Dicey’s dictum that men’s interests give a bias to their judgments far oftener than they corrupt their hearts. This bias, which can descend to the level of blatant axe-grinding, is often accompanied by incredible naïveté concerning the safeguards necessary to ensure a controlled experiment.
Aside from fraud and bias—conscious or unconscious—workers in the paranormal field appear susceptible to such logic viruses as “the sheep-goat syndrome” and “the decline complaint.” In the former instance, positive results are obtained from believers, while skeptics engender negative results. In the latter case, testing of “successful” subjects is discontinued when the level of “success” declines—attributing the decline to the boring nature of the process rather than to a natural regression toward the mean. Similar is the justification of loose controls on the subject, with the rationale that “controls interfere with the psychic realm.”
Finally, it should be noted that the existence of telepathic ability would enable reliable communication links without transfer of energy (thereby violating the Heisenberg principle). Information theory is unequivocal in demonstrating that any system providing a finite capacity for transmitting information can, with appropriate coding, transmit with any desired degree of accuracy. According to Shannon’s mathematical theory of communication, the capacity C, in bits per trial, of a communication system composed of telepathic transmissions of the five Zener symbols is
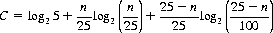
where n (≥ 5) is the mean number of correct guesses per 25 trials (the formula applies only for equiprobability in selecting any of the five symbols). With five correct guesses per 25 trials, C, of course, is zero. For n = 6, C = 0.0069 bits per trial, and for n = 7, C = 0.026 bits per trial. We could consequently realize a communication system with a data rate of several bits per hour—adequate for communicating with submerged Polaris submarines, for example. If the principles of communication theory are admitted, we could increase the data rate by an array of ESP “transmitters” linked for simultaneous emission.
Although but one of many exercises in futility in the search for certainty, ESP has perhaps developed the most convoluted and elaborate illogic.5 The common technique of ESP practitioners, contrary to scientific tradition, is to concoct a speculative thesis and then attempt to confirm its truth. For example, one such hypothesis, propounded to mollify those with a rudimentary knowledge of physical phenomena, is that highly complex organisms (the human brain) do not obey the known laws of physics. The prodigious amount of data accumulated in the pursuit of such speculations serves to demonstrate what sumptuous logical superstructures the human mind can build upon a foundation of shifting sands.
Some Additional ESP Experiments
A limited series of ESP and PK experiments was supervised by the author and a small group of associates.6 Insofar as possible a dispassionate inquiry into the existence of ESP and PK was launched with tabula rasa objectivity; the viewpoint was neither credulous nor incredulous. We were, however, unable to devise a satisfactory methodology for mounting a rational assault on the irrational. Equipment from cooperating engineering laboratories was utilized, as well as a polygraph and an EEG. Since interpretation of results obtained through these two instruments is not rigidly deterministic, their readouts were not accepted without supporting evidence. No religious, psychological, or preternatural overtones were permitted gratuitously in the hypotheses. Those experiments involving statistical elements were checked for possible sources of biased mechanization—in Chapter 6 we have seen the significant deviations from chance occurring from poor-quality dice (cf. Wolf’s and Weldon’s dice data).
The statistical experiments in telepathy and clairvoyance, conducted with the percipient in complete isolation (a soundproof and lightproof chamber), produced results well within one standard deviation of chance expectation. Telepathic trials with the agent and percipient in the same room communicating orally (to signal each card in sequence) yielded, especially with pairs that had worked together for long periods, increasing success with a decreasing number of symbols. That is, binary choices (guessing the color of cards in a conventional deck) were quite successful, five-level choices (the Zener pack) less so, and 26-level and 52-level choices produced only chance results. Of course, as the number of choices increases, the amount of information required from sensory cues increases correspondingly; and it is likely that the subconscious transmission and reception of sensory cues are more efficient when given an established rapport between two individuals closely associated.
For the PK experiments, a cesium-beam atomic clock was requisitioned. Concentrating on the molecular streams, various individuals attempted to change the resonant frequency by altering the vibrations of only a few molecules. The results were negative.
REFERENCES
Bergler Edmund, (1957). The Psychology of Gambling. Hill and Wang.
Cohen John, (1959). The Psychology of Luck. The Advancement of Science.16:197–204 [December].
Cohen John, (1960). Chance, Skill, and Luck. Penguin Books Ltd.
Cohen John, Hansel CEM, (1958). The Nature of Decisions in Gambling. Acta Psychologica.13(5):357–370.
Cohen John, Hansel CEM, (1956). Risk and Gambling. Philosophical Library.
Cohen John, Hansel CEM, (1959). Preference for Different Combinations of Chance and Skill in Gambling. Nature.183(Part 1):841–842.
Coover JE, (1917). Experiments in Psychical Research at Leland Stanford Junior University. Stanford University.
Dale HCA, (1959). A Priori Probability in Gambling. Nature.183(Part 1):842–843.
Diaconis Persi, (1978). Statistical Problems in ESP Research. Science.201:131–136.
Epstein Richard A, (1964). Displacement in Telepathy Experiments. Hughes Aircraft Co. [July Report TP-64-19-12, OP-67].
Epstein Richard A, (1964). Probability Distributions in Card Guessing Experiments. Hughes Aircraft Co. [July Report TP-64-19-13, OP-66].
Gardner Martin, (1952). Fads and Fallacies in the Name of Science. Dover Publications.
Greenwood JH, Stuart EE, (1940). Review of Dr. Feller’s Critique. Journal for Parapsychology.4:298–319.
Gruenberger Fred J, (1964). A Measure for Crackpots. Science.:1413–1415 [September].
Hansel CEM, (1959). Experimental Evidence for ESP. Nature.184(Part 2):1515–1516.
Heinlein CP, Heinlein JH, (1938). Critique of the Premises and Statistical Methodology of Parapsychology. Journal of Psychology.5:135–148.
Herr DL, (1938). Mathematical Analysis of the Experiments in Extra-Sensory Perception. Journal of Experimental Psychology.22:491–495.
McConnell RA, Clark TK, (1991). National Academy of Sciences’ Opinion on Parapsychology. Journal of American Society for Psychical Research.85:333–365.
Price George R, (1955). Science and the Supernatural. Science.122(3165):359–367.
Read Ronald C, (1962). Card-Guessing with Information: A Problem in Probability. American Mathematics Monthly.69(6):506–511.
Rhine Joseph B, (1934). Extra-Sensory Perception. Bruce Humphries.
Robbins Herbert, (1952). Some Aspects of the Sequential Design of Experiments. Bulletin of American Mathematics Society.58(5):527–535.
Rogosin H, (1939). An Evaluation of Extra-Sensory Perception. Journal of General Psychology.21:203–217.
Rogosin H, (1938). Probability Theory and Extra-Sensory Perception. Journal of Psychology.5:265–270.
Soal SG, Bateman F, (1954). Modern Experiments in Telepathy. Yale University Press.
Soal SG, Rhine JB, Meehl PE, Scriven M, Bridgeman PW, (1956). Comments on Science and the Supernatural. Science.123(3184):9–19.
General ReferencesProceedings and journals of the Society for Psychical Research (London), 1884:.
Journal of Parapsychology (Duke University Press), 1937–.
Journal of the Society for Psychical Research, 1932–.
Bibliography
Abramowski, E., Le Subconscient Normal: Nouvelles Recherches Expérimentales, Alcan, 1914.
Alcock James E, (1981). Parapsychology: Science or Magic. Pergamon Press.
Broad CD, (1962). Lectures on Psychical Research. Routledge and Kegan Paul.
Carington , Whately W, (1945). Telepathy: An Outline of Its Facts, Theory, and Implication. 2nd Ed. Methuen & Co.
Cohen John, Dearnaley EJ, Hansel CEM, (1956). The Addition f Subjective Probabilities. Acta Psychologica.12(5/6):371–380.
Cohen John, Hansel CEM, (1955). The Idea of a Distribution. British Journal of Psychology.46(Part 2):111–121.
Cohen John, Hansel CEM, (1955). The Idea of Independence. British Journal of Psychology.46(Part 3):178–190.
Durand Gilbert, (1965). Encyclopédia de la Divination. Paris-Tchou.
Helmer, Olaf., and Nicolas Rescher, “On the Epistemology of the Inexact Sciences,” The RAND Corporation, Report R-353, February 1960.
Huizinga Johan, (1955). Homo Ludens: A Study of the Play Element in Culture. Beacon Press.
Koopman BO, (1940). The Axioms and Algebra of Intuitive Probability. Annals of Mathe-matics, 2nd ser..41:269–292.
Marks David, Kaummann Richard, (1980). The Psychology of the Psychic. Prometheus Books.
Murphy Gardner, Ballou Robert O, eds. William James on Psychical Research. Chatto and Windus.
Myers David G, (2007). Psychology. 8th ed. Worth Publishers.
Park Robert L, (2000). Voodoo Science: The Road from Foolishness to Fraud. Oxford University Press.
Rao KR, ed. Basic Research in Parapsychology. McFarland & Co.
Rhine Joseph B, (1953). New World of the Mind. William Sloane Associates.
Rawcliffe DH, (1959). Illusions and Delusions of the Supernatural and the Occult. Dover Publications.
Thouless Robert H, (1964). Experimental Psychical Research. Pelican.
West DJ, (1962). Psychical Research Today. [rev. ed] Pelican Books.
1 Appropriate is the comment of Frederick the Great, writing of Prince Eugen and Marl- borough: “What a humbling reflection for our vanity (when) the greatest geniuses end up as imbeciles…”
2 A large percentage of these experiments were conducted, curiously, with children. Is it the wage scale or the naïveté of juveniles that accounts for this practice?
3 Indeed, our modern calendar was preceded (before 2000 B.C.) by an astrological list of lucky and unlucky days to mark the occurrence of noteworthy events.
4 From An Enquiry Concerning Human Understanding.
5 A whimsical featherweight contender to ESP is the “science” of pataphysics. Its adherents, including Eugène Ionesco and Raymond Queneau, founded a society, the College of Pataphysics, in Paris. As defined by its creator Alfred Jarry, “Pataphysics is the science of imaginary solutions.”
6 Initially constituted as the Yoknapatawpha Martini and Metaphysical Society, the group was disbanded in the face of persistently nonmystical results.