7. Capture–recapture methods for density estimation
Fridolin Zimmermann and Danilo Foresti
7.1Introduction
Conservation and management of animal populations require making decisions about what actions to take to bring about desired consequences (Nichols 2014). Effective conservation programmes like adaptive management include several key elements such as (i) the development of explicit objectives and targets; (ii) listing of potential management actions to be taken to meet objectives; (iii) a mean for measuring confidence in predictive models (i.e. to project the consequences of different possible actions in order to decide which action represents the ‘best’ choice); and (iv) a monitoring programme that is centred on providing system state variables. Ecological monitoring programmes usually focus on system state variables (i.e. a state variable is a characteristic of the system that reflects the status of the system; Nichols 2014). Commonly selected state variables include abundance, occupancy (see Chapter 6) and species richness (see Chapters 5, 9 and 10). State variables are fundamental for three key steps: (i) decision analysis; (ii) assessment of progress towards the objectives; and (iii) comparison against model predictions for the purpose of discriminating among competing models (Nichols and Williams 2006). Although not always the case, abundance estimates usually require more sampling effort than do estimates of occupancy or species richness. Indeed it is possible to estimate focal species abundance within a small number of specified areas (e.g. Zimmermann et al. 2011) and to use occupancy modelling over much larger areas (e.g. Karanth et al. 2011a; Barber-Meyer et al. 2013), hence allowing inferences to be made about distribution of abundance across the whole area of interest (Royle and Nichols 2003). Once it has been decided that abundance is the appropriate state variable within a given conservation and management programme, it is important to select appropriate abundance estimation methods among the large number of methods that have been developed (e.g. Seber 1982; Borchers et al. 2002; Williams et al. 2002). When choosing a method, careful consideration should be given to whether it deals adequately with geographic (or spatial) variation and detectability. In addition to these basic recommendations, the selection of the method should be tailored to the programme that those methods are designed to serve, with important considerations being the specific roles of estimates in the programme and the logistical issues that accompany the programme (Nichols 2014). This leads to questions such as: ‘For which area are abundance estimates needed?’, ‘Is the entire area easily accessible?’, ‘Is the focal species secretive?’, and ‘What financial and human resources are available?’ (Nichols 2014).
The abundance of elusive animals with individually distinct fur patterns or artificial marks living at low densities is best estimated in the conceptual framework of capture–recapture methods, which can provide estimates of encounter probabilities and abundance along with associated statistical errors (e.g. Karanth 1995; Schwarz and Seber 1999). These models account for the fact that not all animals in the study area are necessarily observed. This methodology has been applied to a range of species, such as common genet (Genetta genetta; Sarmento et al. 2010), striped hyena (Hyaena hyaena; Harihar et al. 2010; Singh et al. 2010), and, in particular, large and small cats with individually distinct coat patterns (e.g. Karanth and Nichols 1998; Silver et al. 2004; Pesenti and Zimmermann 2013).
Several analytical options, which are not universally applicable, have been developed to estimate the abundance and density of species that do not have distinct natural or artificial marks (see Sollmann et al. 2013 for a critical review). These include calibrated (absolute) abundance indices (e.g. relative abundance index, RAI; Carbone et al. 2001; Chapter 5); the random encounter model (REM) by Rowcliffe et al. (2008); the Royle–Nichols model, which is based on species-level detection–non-detection data and makes use of the relationship between the probability of detecting a species at a given site and its site-specific abundance (Royle and Nichols 2003); the spatial capture–recapture model (SCR) without individual identities developed by Chandler and Royle (2013); and mark–resight models, when some tagged or otherwise marked individuals are available for sampling, both non-spatial (White 1996; McClintock et al. 2006, 2009a,b) and spatial (Chandler and Royle 2013). In line with Sollmann et al. (2013) and others we believe that rather than sticking to camera trapping, researchers should sometimes consider alternative survey methods to estimate abundance of species that have no natural marks and cannot easily be tagged. Depending on the study area and target species, non-invasive genetic sampling in combination with capture–recapture models (e.g. Mulders et al. 2007; Wilton et al. 2014), distance sampling (e.g. Wegge and Storaas 2009) or repeated point counts in combination with appropriate models accounting for detection (e.g. N-mixture models; Royle 2004) can provide statistically sound population estimates. Most of these emerging methods have been developed over the past decade, and hence their efficacy is still under study.
In this chapter, we first cover what needs to be considered when planning a camera trapping study to estimate abundance and density by means of capture–recapture models, namely equipment and field practices (i.e. camera traps and related equipment) and survey design considerations (i.e. camera trap site selection, season and survey duration, spatial sampling and assumptions). We briefly discuss the identification of individuals and describe some working steps and useful tools that could ease identification. We then provide an analytical example using camera trapping data for a Eurasian lynx (Lynx lynx) population, introducing the basic SCR model with likelihood inference (using the R package secr; Efford 2015). Subsequently, we present estimates based on conventional (i.e. non-spatial) capture–recapture models.
We refer the readers to Karanth et al. (2011b), O’Brien (2011), Ancrenaz et al. (2012) and Royle et al. (2014) for more detailed background to capture–recapture studies.
7.2Equipment and field practices
7.2.1Camera traps
Camera traps producing high-quality photos in terms of clarity, sharpness (moving objects should not be blurred) and resolution are especially critical for species that do not have easily distinguishable coat patterns and for those that lack individually identifiable natural marks. Currently the ideal camera traps for capture–recapture studies are those with PIR sensors, a xenon white flash and a high trigger speed (see Chapter 2). One exception is represented by a unique cat population of individuals that are almost all melanistic (e.g. leopard Panthera pardus in Malaysia; Hedges et al. 2015), where the identification of individuals is only possible by means of infrared flash camera traps modified to force the traps into night mode. As camera traps should be placed in pairs to photograph both flanks of the passing animal, it is possible to combine the non-overlapping advantages and disadvantages of xenon with infrared LED flash. This combination has proved to be an efficient system for gathering pictures of sufficient quality to enable individual identification while enabling detection of family groups or individuals following each other within short distances and short times (F. Rovero unpublished data). See Chapter 2 for a more detailed overview of critical camera trap features and settings for capture–recapture studies including a list of commercially available camera traps.
7.2.2Focal species and other members of its guild
Ideally, some basic information about the focal species and other members of its guild – and its main prey if the species in question is a predator – should be obtained prior to planning the survey. This information can be obtained from literature searches, from interviews with people knowing the area or from preliminary surveys. Information like this helps to give a general idea about whether the species of interest are rare or abundant and if other species that could potentially interfere with the focal species (via competition, predation or intraguild predation) are present in the area. This information is important for choosing an adequate location for the study area and for selecting optimal camera trap sites.
7.2.3Camera trap sites and camera trap placement
One of the most important aspects of the survey design is to choose camera trap locations that maximise the probability of encountering the focal species. This is even more important when targeting species that live at relatively low densities even in the best habitats, and thus have a very low probability of encountering a camera trap, typically large carnivores. Therefore camera trap sites should be sited on well-used travel routes, near food sources (e.g. fruiting trees in tropical forest) or near water resources – ideally identified based on species signs of presence (e.g. tracks, scent marks and scat deposit when targeting carnivores) – that are more likely to be visited by the focal species and its prey. Depending on the focal species, optimal camera trap sites are along game or hiking trails, roads, junctions between roads or trails, ridgelines, dry river beds, river crossing points, salt licks, mud wallows and water ponds.
In order to identify suitable trap sites, the survey area should be thoroughly explored before the beginning of the session using the best available local knowledge, maps and survey tools (e.g. GIS, GPS). Ideally double the number of trap sites than needed should be identified as this provides flexibility to locate traps optimally in the final survey design without lowering encounter probabilities or compromising on trap-spacing needs (Karanth et al. 2011b). It is recommended that investigators seek assistance from local guides or naturalists for such reconnaissance surveys and/or select optimal sites on maps based on their own experience of the movement behaviour of the focal species (e.g. following trails or other guiding structures such as topographical features). For repeated surveys, camera traps should be deployed using the same sampling design in each survey to minimise potential biases in data collection.
Box 7.1 Use of attractants in capture–recapture studies
In carnivore capture–recapture studies, attractants are sometimes used to entice animals to camera traps with the aim of increasing encounter rates or probability (e.g. Thorn et al. 2009; Braczkowski 2013; du Preez et al. 2014). Such attractants may be lures which include scent such as perfume/cologne (e.g. Thomas et al. 2005), sound or food that is inaccessible to the animal (Gerber et al. 2012) or baits, which entail the use of food rewards (Ariefiandy et al. 2013; du Preez et al. 2014). Lures are generally preferred over baits because they will not be taken by the first animal passing by the camera trap site, which is likely to be a more common species than the target one. Besides enticing animals to walk in front of the camera trap, attractants can cause the focal animal to linger in front of the camera trap, and be subject to multiple exposures. These additional photographs can aid identification of the species or individuals, as well as help to determine the sex. However, relatively few carnivore studies based on photographic capture–recapture estimates have used attractants so far (Trolle and Kéry 2003; Trolle et al. 2007; Gerber et al. 2010, 2012; Garrote et al. 2011, 2012), perhaps because of the various disadvantages they entail. Potential disadvantages include the extra time needed for data processing as memory cards can get filled with many photographs of the same animal if it lingers for a while in front of the camera trap. The use of lures and baits can also be laborious and expensive. For example, under heavy rains scent lures are quickly washed away and thus need to be renewed frequently to be of any use. Good attractants can modify the ranging behaviour of animals and may cause the animals to move beyond their usual home range, potentially violating the assumption of geographic closure (Gerber et al. 2012). Moreover, attractants can introduce a change in the behaviour of an individual in response to the first encounter event, which induces non-independence of encounter probability in the encounter history of that individual (Otis et al. 1978). In addition, attractants can also amplify individual heterogeneity in encounter probability as they might have variable effects on animals depending on age, sex or resident status. When baits are used as attractants, individuals might become habituated, which could expose them to a higher risk of mortality from encounters with humans (e.g. Balme et al. 2014). Baiting may also increase the risk of predation by other larger carnivores, and for some species (e.g. leopard Panthera pardus) it could also artificially elevate rates of infanticide if it increases interaction between females with cubs and males (Balme et al. 2014). Since the use of attractants can have multiple disadvantages, they are only likely warranted in capture–recapture studies if by improving the encounter probabilities, they increase the precision of abundance and density estimates significantly. Attaining a better understanding of the effects of attractants in capture–recapture studies is necessary as the few studies that have so far investigated this issue have produced contrasting results (e.g. Garrote et al. 2012; Gerber et al. 2012; Braczkowski 2013; du Preez et al. 2014). In the study of Gerber et al. (2012) the use of lures did not affect geographic closure, abundance and density estimation of Malagasy civet (Fossa fossana), but did provide more precise population estimates by increasing the number of re-encounters. Likewise Garrote et al. (2012) found that lures increased the efficiency of trail camera trap encounters and consequently increased the accuracy of abundance and density estimates of Iberian lynx (Lynx pardinus). Although the presence of baits near camera traps increased leopard encounters 4-fold in a study by du Preez et al. (2014), there was only a marginal increase in precision (2–4%). This seems a small gain for the increased effort associate with baiting (an additional 314 man-hours per survey; Balme et al. 2014). While in the study of Braczkowski (2013) lures did not affect geographic closure, their use did not, however, increase the number of leopard encounters and accordingly did not provide more precise population estimates. Possible reasons for these contrasting findings are that each study used different forms of attractants, namely lures in the form of either scent (Braczkowski 2013), inaccessible meat (Gerber et al. 2012) or inaccessible live pigeons (Garrote et al. 2012), and baits (du Preez et al. 2014), and species might be attracted to a greater or lesser extent to a given form of attractant depending on the family to which they belong. For example lures might be especially suitable for studying species with superior olfactory senses such as viverrids (Gerber et al. 2012). The use of attractants might also be more warranted in low density populations or for species that are less routine in their movement pattern and thus more difficult to detect by camera traps. Therefore, attractants should only be used after their effects on population and spatial parameters have been adequately assessed and if their associated disadvantages remain within acceptable limits.
It is best to deploy two camera traps per site in order to photograph both flanks of the focal species to maximise the chances of identification. Although setting a single device per site is less optimal, abundance estimation is still possible, and until recently the typical approach when dealing with this situation was to conduct separate analyses using the left- and right-sided photographs and compare the results. However, the additional uncertainty associated with individual identification combined with a small sample size results generally in very imprecise estimates (e.g. Negrões et al. 2012). Nonetheless new analytical methods have recently been developed to take into account bilateral photo-identification in case it is unclear how to link the left- and right-side photos (McClintock et al. 2013). The first applications indicate that these new methods produce abundance estimates that are about twice as precise as those from analogous one-side models. These models have yet to be extended to allow for individual variation in parameters (but see McClintock 2015).
Each camera trap should be placed carefully to maximise image quality and preclude the chance of a ‘skewed’ image that can reduce similarity coefficients (i.e. probability that two photographs of the same individual match) when pattern recognition software is used to identify individuals (see Box 7.2 below). Hence camera traps should be set perpendicular (or only slightly angled) to the trail to obtain a good side image of the passing animal. As the flash of the opposing camera can cause overexposure of the image, it is necessary to avoid setting camera traps exactly facing each other. In steep terrain it is not always easy to find a suitable tree beside the trail that will allow the camera trap to be mounted at approximately the same height as the target. This constraint can be easily solved by using a pole. In some situations natural hurdles (e.g. logs) can be placed on the forest road/hiking trail to ensure that the animals are centred in the camera trap field of view and to avoid overexposed pictures. Alternatively, obstacles can be placed to funnel the route of the animal past the camera trap, preventing animals from being out of flash range and/or very small in the image. Nevertheless, as a rule, the sites should be altered as little as possible to ensure that they remain unnoticed by passing animals, and thus poles or guiding structures should only be used if absolutely necessary.
7.3Survey design
7.3.1Season, survey duration and demographic closure
The season of the survey will be determined jointly by (i) the timing of the decision process of the larger programme (e.g. conservation) that the monitoring is designed to serve; (ii) the natural history of the focal species – for mammalian species with seasonal reproduction, females with young have a lower encounter probability during the period of birth and lactation as they have a reduced mobility, moreover demographic closure is not granted if the study period encompasses the main period of birth or dispersal; (iii) environmental issues (e.g. seasonal snow can help to optimize camera trap sites by revealing tracks of the focal species; temperature to effectively run the camera traps, accessibility of the study area in case of flooding); and (iv) logistical issues (e.g. incidence of human activities and factors such as availability of personnel, permits and equipment; Karanth et al. 2011b). It is usually an advantage to obtain abundance estimates very shortly before the time at which the decision is made and the action taken (Nichols 2014). However, if other biological, environmental or logistical factors are prevailing, these might take precedence over basic considerations of the decision process.
The survey duration is the time required to sample the entire area of interest with camera traps. Abundance estimation assuming demographic closure (Otis et al. 1978; White et al. 1982; Williams et al. 2002) dictates that the duration of capture–recapture surveys should be as ‘short’ as possible in relation to the likely turnover of the focal animal population as a result of recruitment, entry into the sampled population, mortality or exit from the sampled population (Karanth et al. 2011b). With rare and elusive species, there is a need to find a compromise between sampling for long enough to gather sufficient data to provide reliable abundance estimates, but short enough so that the closure assumption is not likely to be violated. Keeping camera traps running for months in the field is likely to break the closure assumption, and requires different types of analyses specific to demographically open populations (Pollock et al. 1990; Kendall et al. 1995; Karanth et al. 2006; Chandler and Clark 2014; Ergon and Gardner 2014).
Investigators usually divide data into discrete sampling occasions, typically 24 h periods, to construct the encounter history in either conventional (i.e. non-spatial) capture–recapture or SCR models. For wide-ranging species living at low densities, this could, however, result in 0-heavy encounter histories in conventional capture–recapture models. Therefore some studies define the occasion length as longer than 24 h (e.g. Dillon and Kelly 2007; Kelly et al. 2008; Zimmermann et al. 2013). Pooling occasions may eliminate more 0s than 1s from the encounter history in conventional capture–recapture models and thus increase the overall encounter probability on any given occasion, which should be ≥0.1 to get reliable abundance (White et al. 1982) or even better ≥0.3, which is safer in the presence of a behavioural response (Tenan et al. 2013). However, such pooling will reduce the number of encounters, potentially making it more difficult to select an appropriate model. Therefore to compensate for the low number of encounters, some investigators increase the length of the survey duration to get enough encounters though this brings the risk that demographic closure is no longer fulfilled. Because aggregating camera trapping data into sampling occasions introduces subjectivity (i.e. the occasion length chosen by the investigator) and discards some information, continuous time models for both conventional capture–recapture (e.g. Hwang et al. 2002) and SCR models (Borchers et al. 2014) have been developed. The continuous-time SCR model developed by Borchers et al. (2014) is unbiased and more precise than discrete occasion estimators based on binary detection data rather than detection frequencies when there is no spatiotemporal correlation. Hence these authors identified the need to develop continuous-time methods that incorporate spatiotemporal dependence in detections.
Few population closure tests have been developed in conventional capture–recapture models mostly because behavioural variation in detection is indistinguishable from violation of demographic closure (Otis et al. 1978; White et al. 1982). Otis et al. (1978) developed a closure test that can handle heterogeneity in encounter probability, but does not perform well in the presence of time or behavioural variation in encounter probability. Stanley and Burnham (1999) developed a closure test for a model allowing time variation in detection, which works well when there is permanent emigration and a large number of individuals migrate. Both tests are implemented in the software CloseTest 3 (Stanley and Richards 2005; http://www.fort.usgs.gov/products/software/clostest/) and in the R package secr with the function closure.test. Like conventional capture–recapture, basic SCR models do not allow for any ongoing demographic processes. However, for the same reasons that violation of other model assumptions cannot necessarily be distinguished from a lack of population closure, there is no closure test in the SCR. Useful solutions to deal adequately with this problem in SCR are provided in Royle et al. (2014). For example, SCR can be expanded to handle open populations, allowing the estimation of demographic parameters such as survival and recruitment (e.g. Gardner et al. 2010a).
7.3.2Spatial sampling and geographic closure
Estimation of animal abundance requires consideration of detectability and spatial variation in abundance (Nichols 2014). Detectability means that even when an individual of the focal species is present in a sample unit that is surveyed, there is some probability that it will be missed during a sampling effort. Individuals may vary in their detectability and detection may vary over time and space (O’Brien 2011). The likelihood of detecting an individual during a sampling occasion provides the key to converting the sample count statistic into an estimate of abundance or density. Spatial variation in abundance is not an issue if the sampling area is sufficiently small that it can be surveyed in its entirety. However, if inferences about large areas are of interest, a subset of sampling areas, representative of the area for which inferences are made, is selected to be surveyed and extrapolation is used to draw inferences about the areas not surveyed (Nichols 2014). Statisticians have long dealt with spatial variation and various approaches to the selection of locations of sampling areas may be used including the rule of stratification or random sampling (see Cochran 1977; Thompson 2012).
Once a sampling area has been defined for a camera trap study, the investigator needs to deal with a number of critical design elements in the context of spatial sampling problems, where populations of mobile animals are sampled by an array of camera trap sites. Three of the most important ones are the spacing of camera trap sites (or sampling devices) relative to individual movement, their configuration within the camera trap array, and the total size and shape of the array (Foster and Harmsen 2011; Royle et al. 2014). Because the number of camera traps available is generally limited, researchers need to compromise between trap spacing, configuration within the camera trap array and the overall trap array.
An important requirement of conventional capture−recapture models is that each individual must have a probability >0 of being detected (although not all individuals may in fact be caught during the survey) and thus there should be at least one sampling site per smallest female home range (usually the smallest home range in the population) (Karanth and Nichols 1998, 2002), resulting in an upper limit to possible camera trap site spacing. The reason why individuals that are not exposed to camera trap sites cause problems in non-spatial models is that they induce heterogeneity in encounter probability. If the entire home range of an individual lies completely or partially in an area that does not contain any camera trap sites, then it will have a different probability of being detected than an individual whose home range is covered with a large number of camera trap sites. Hence the assumption that the encounter probability of every individual be >0 entails strong restrictions with respect to the study design. Although there is no need to cover an area systematically with camera trap sites, there has to be some consistent coverage of the entire area of interest. This is often achieved by dividing the study area in grid cells of a size that approximates the smallest home range recorded for the focal species (in the same or a similar area) and then place at least one camera trap site within each cell. It can be extremely challenging or even impossible to achieve a comprehensive coverage, especially when dealing with wide-ranging species and accordingly large study areas. Even if this is possible, spatial heterogeneity in encounter probability would still exist because individuals with home ranges near the borders of the camera trap site array will have a lower exposure to camera traps compared to individuals that spend all their time within the array. Therefore the geographic closure assumption (i.e. no movement in or off the sampling grid) is likely to be violated in most applications.
To estimate density with conventional capture–recapture models, the area effectively sampled needs to be estimated. This is usually done by obtaining estimates of movement from the camera trapping data itself, such as the mean maximum distance moved (MMDM) between photo-encounters for each individual caught by at least at two different camera trap sites (Soisalo and Cavalcanti 2006; Dillon and Kelly 2008) or half the mean maximum distance moved (1/2MMDM: Karanth 1995; Karanth and Nichols 1998, 2002), or from telemetry data collected simultaneously with the camera trapping session and using this distance to place a buffer around the camera trap array (see section 7.4). The spacing of camera trap sites clearly has an effect on movement estimates, since it determines the resolution of the information on individual movements (Wilson and Anderson 1985; Parmenter et al. 2003). If the camera trap site spacing is too great, most animals will only be detected at a single camera trap site, and little or no information on movement will be gained (Dillon and Kelly 2007). Further, the overall area sampled by camera traps should be large enough to capture the full extent of individual movements. Researchers using conventional capture–recapture models have suggested that the camera trap array size should be at least four times that of individual home ranges (Bondrup-Nielsen 1983; Maffei and Noss 2008) to avoid any positive bias in estimates of density. Moreover, according to White et al. (1982), to obtain reliable abundance estimates with conventional capture–recapture models the overall sample size should be >20 individuals. While this recommendation can be followed for small mammals, with large mammals it may require covering thousands of square kilometers − a logistical and financial challenge that few projects can realistically tackle.
To increase geographical closure regular arrays of traps which maximise the ratio of sampled area size to its perimeter (which corresponds to circular sampled areas) are preferable to reduce the edge effect caused by detected individuals moving in and out of the area surveyed over the course of the study (Foster and Harmsen 2011). However, even such a constraining design cannot fully liberate conventional capture–recapture models from the assumption of geographic closure, especially for mammals with large home ranges.
Efford (2004) and Royle et al. (2009a,b) developed a method that uses location-specific individual encounter histories to construct a SCR model, hence relaxing a number of important assumptions. SCR explicitly models the movement and distribution of individuals in space, relative to the trap array, and thus circumvents the problem of estimating the area effectively sampled that is inherent to conventional (i.e. non-spatial) capture–recapture models, as in SCR studies the trap array is embedded in a large area called the state space. The requirements in terms of spatial study design for SCR models differ markedly from those for conventional capture–recapture. For instance ‘holes’ in the camera trap array are of no concern in SCR studies. Hence some individuals within the study area might have a probability of close to zero of being included in the sample. With SCR models, N (i.e. population size) is explicitly tied to the state space and not to the actual locations of the camera trap sites themselves. Thus, it is possible to make predictions outside the range of data by making inferences from the sample to individuals that live in these holes based on the explicit declaration that the SCR model applies to any area within the state space, even to unsampled areas (Royle et al. 2014). On the contrary, conventional capture–recapture models only apply to individuals that have encounter probabilities that are consistent with the model being considered and individuals with p = 0 are not accommodated in those models. This particularity alone allows for completely new and much more flexible study designs in SCR studies, such as linear designs, camera trap sites tracing the outline of a square, or small clusters of camera trap site grids spread over the landscape (Efford et al. 2005, 2009; Efford and Fewster 2013).
While conventional capture–recapture models are concerned with the number of individuals and re-encounters, SCR models need an additional level of information, namely that some individuals have to be re-encountered at least at several camera trap sites. Therefore, the design of SCR studies needs three pieces of information: (i) the total number of unique individuals encountered; (ii) the total number of re-encounters, which provides information about the baseline encounter rate; and (iii) spatial re-encounters, which provide information about the movement parameter (σ). The ability of SCR models to estimate movement even for relatively small trapping grids lies within the model itself: σ is estimated as a specified function of the ancillary spatial information collected in the survey and the encounter frequencies at those locations (Sollmann et al. 2012). As long as there is enough data across at least some range of distances, this function is able to make predictions across unobserved distances, even when they are larger (within reasonable limits) than the extent of the trap array (Royle et al. 2014). This raises some constraints on how large the overall trap array must be to provide this range of distances (e.g. Marques et al. 2011).
Although potentially time consuming, scenario analysis by Monte Carlo simulations (e.g. Sollmann et al. 2012; Efford and Fewster 2013; Sun et al. 2014; Wilton et al. 2014) is very helpful for evaluating the study design in terms of the ability to generate useful estimates before any field survey is undertaken. Formal model-based strategies have great potential (Royle et al. 2014) and could be an alternative to simulation-based scenarios.
Using a simulation study, Sollmann et al. (2012) investigated how trap spacing and camera trap site array relative to animal movement influence SCR parameter estimates. Their simulation showed that SCR models performed well as long as the extent of the trap array was similar to or larger than the extent of individual movement during the study period, and movement was at least half the distance between traps. SCR models have much more realistic requirements in terms of area coverage than conventional capture–recapture models, which make them particularly suitable for species with large home ranges that are present at low densities. As long as sufficient data are collected, SCR models work well in study areas that are similar in size to an individual’s home range (Marques et al. 2011; Sollmann et al. 2012; Zimmermann et al. 2013). Trap spacing is an essential aspect of design in SCR as long as the study area can be covered uniformly with camera traps. In practice, especially when targeting wide-ranging species, the study area tends to be large relative to the resources available. In such cases other strategies that deviate from a strict focus on camera trap site spacing need to be considered. Two general sampling strategies, which can be used by themselves or combined, have been suggested for sampling large areas (e.g. Sun et al. 2014): (i) sampling based on clusters of camera trap sites (i.e. groups of camera trap sites spaced throughout the larger area of interest; e.g. Efford and Fewster 2013); and (ii) sampling based on moving groups of camera trap sites over the landscape (Karanth and Nichols 2002). Efford and Fewster (2013) looked at the performance of different spatial study designs in an SCR framework, including a clustered design, and found that the latter performed well, although there were indications of a slight positive bias in estimates of N. The distribution of the clusters has to be spatially representative (e.g. systematic with a random origin). In addition, Efford and Fewster (2013) pointed out that if distances among clusters are large, individuals are unlikely to show up in several clusters, and then the method relies on spatial detections within clusters, meaning that spacing of camera trap sites within clusters has to be appropriate to the movement of the species under study. Similarly, Wilton et al. (2014) showed that with limited resources allocating traps to multiple arrays with intensive trap spacing similar in extent to the movement of individuals increased the precision of parameter estimates. In practice, combining clustering and moving traps might be necessary or advantageous (see Royle et al. 2014; Sun et al. 2014).
Generally, however, study design should be tailored to expose as many individuals as possible to sampling and to obtain adequate data on the movement of individuals (Royle et al. 2014). Large amounts of data in terms of numbers of individuals detected and numbers of re-encounters not only improve the precision of parameter estimates (Sollmann et al. 2012) but also allow potentially important covariates (e.g. sex and time effect) to be included in SCR models. In addition, the flexibility in the study design of SCR models also makes it more feasible to collect abundance and density estimates for several species in parallel (Sollmann et al. 2012; Royle et al. 2014).
Although, as we have seen, the basic SCR model relaxes a number of important assumptions compared to conventional models, there are nevertheless some important assumptions besides demographic closure already outlined in section 7.3.1 that need to be considered. Geographic closure is loosened: while the SCR model assumes no permanent immigration or emigration from the state space, it allows for ‘temporary’ movements (‘temporary emigration’, as it is called in the capture–recapture literature, Kendall et al. 1997; Kendall 1999) around the state space and variable exposure to encounters as a result. Further assumptions include the following: (i) activity centres are randomly distributed; (ii) the probability of detection of an individual at a camera trap site declines as a function of distance from that individual’s activity centre; (iii) the encounter of any individual is independent of the encounter of any other individual; and (iv) the encounter of an individual at any site is independent of its encounter at any other site, and on any other subsequent sampling occasion (Royle et al. 2014). However, for some of these core assumptions such as uniformity, and independence of individuals and of encounters, a fair amount of robustness to departures is to be expected (Royle et al. 2014). Moreover it is possible to extend these assumptions in many different ways (see Royle et al. 2014).
Likelihood-based inferences developed by Efford et al. (2009, 2015) can be obtained with the R package secr (see case study in section 7.4), while the software SPACECAP has been developed to implement flexible Bayesian approaches (Gopalaswamy et al. 2012). Many example analyses, including code using likelihood-based and Bayesian methods, can be found in Royle et al. (2014).
Box 7.2 Identification of individuals
Identification of individuals is a key requirement in capture–recapture surveys. While molecular techniques have been used to distinguish individual animals (e.g. Marucco et al. 2009; Janecka et al. 2011), visual identification of individuals conducted either in real time in the field or later based on photographs can be more cost effective and is essential for a variety of ecological and behavioural studies (e.g. Karanth et al. 2006; Zimmermann et al. 2013; Vogt et al. 2014). Either artificially or naturally marked animals can be identified. Non-invasive methods are clearly preferred (e.g. Karanth 1995; Kelly 2001); however, the use of natural markings for individual identification can be labour intensive and problematic in terms of reliability.
For species with easily distinguishable natural markings that remain fairly constant over time (e.g. stripe or spot patterns) identification errors can occur because of lack of clarity in photographs (Yoshizaki et al. 2009) or because of difficulties in comparing photographs with a large set of individual reference photographs. This problem is further complicated when the method is applied to estimate abundance of species that lack clear body patterns but have phenotypic and/or environment-induced characteristics (Noss et al. 2003; Ríos-Uzeda et al. 2007; Kelly et al. 2008). For such species, misidentification can also occur because of the subjectivity involved in identifying individuals, but also because of temporal variability in natural markings (Yoshizaki et al. 2009; Goswami et al. 2012). Moreover, with increasing sample size, it is unlikely that all individuals within the sample have unique markers. Two types of identification errors can be found: false matches (i.e. incorrectly identifying images from multiple individuals as images from one individual), and false mismatches (i.e. incorrectly identifying multiple images of the same individual as images from multiple individuals). When the capture history data contains errors because of misidentification the conventional estimators of population size can be seriously biased (Mills et al. 2000), and methods of analysis that account for this type of error are clearly needed (Yoshizaki et al. 2009). Several frameworks for closed populations have been developed, including a model that can account for temporal variation in detection probability under misidentification due to, for example, variable image quality or genotyping errors (Link et al. 2010; Schofield and Bonner 2015); a generalisation of this approach to account simultaneously for temporal variation, behavioural response and individual heterogeneity (McClintock et al. 2014), which has also been extended to open populations (McClintock 2015); and a model focusing on the situation where errors are due to temporal variability in natural markings (Yoshizaki et al. 2009). These frameworks, with the exception of the one developed by Schofield and Bonner (2015), allow only for bias corrections for false mismatches, not for false matches, which may be common in camera trap studies of species that lack unique natural marks (e.g. Oliveira-Santos et al. 2010). The evolving natural marks model assumes that once a new identity is created the old identity is not subject to re-encounter but the newly false identity is subject to re-encounter; however, for situations where changes in natural marks are not obvious, it is more realistic to assume that both old and new identities of an animal can be re-encountered and the model needs to be extended to incorporate this aspect if possible (Yoshizaki et al. 2009). Moreover the estimator developed by Yoshizaki et al. (2009) should not be used with low encounter probabilities (i.e. ≤0.2), and future research should develop guidelines or criteria to determine whether to use or not the new estimators or a conventional capture–recapture model (Yoshizaki et al. 2009). Modelling misidentification errors requires a detailed understanding of the mechanism and the effect on estimators can be substantial if misidentification is not appropriately modelled (Yoshizaki et al. 2009). Although these models do not require auxiliary information about misidentification probability (i.e. prior information), prior information can be helpful, especially for small data sets, but the models can have prior sensitivity so it is important that the auxiliary information is reliable (e.g. McClintock et al. 2014). When matching photographs to individuals actual identification errors cannot generally be determined solely from non-invasive photos of wild individuals (Ríos-Uzeda et al. 2007; Bashir et al. 2013) but accuracy and precision can be assessed by testing identification assigned blindly to known (i.e. captive) individuals (Oliveira-Santos et al. 2010; Higashide et al. 2012). Care should, however, be taken in using identification error estimates from captive individuals as there could be reasons to suspect that the misidentification rate differs for wild individuals and might differ across populations because of different proportions of individuals with less distinguishable coat patterns in each population (e.g. Eurasian lynx with rosettes, which are more difficult to identify, are represented markedly less in the Jura Mountains than in the population found in the northwestern Swiss Alps).
Following Foster and Harmsen (2011) and Russell et al. (2014), investigators conducting photographic capture–recapture analyses of species that lack clear body pattern should provide enough information to allow for adequate replication of results and an assessment of the reliability of the method. The following recommendations can be made: (i) investigators should indicate which fixed and variable morphological traits were used for identification (e.g. Goswami et al. 2012); (ii) at least two investigators should independently identify the photos (e.g. Kelly et al. 2008); (iii) the level of inter-observer agreement or disagreement should be reported to assess the level of confidence in the result (e.g. Kelly et al. 2008); and (iv) investigators should explain how they dealt with ambiguous photographs, stating how many encounters were unidentifiable and explain whether or how they included them in the abundance estimate (Foster and Harmsen 2011). If the method is not reliable, investigators should consider alternative survey methods (e.g. genetic sampling) to estimate the abundance of species that lack clear body patterns.
When camera trapping studies cover a large temporal and/or spatial extent, the number of comparisons for identification will dramatically increase, especially for long-living species. For species with easily distinguishable natural markings, software that automates the identification process through the use of pattern matching has gained in popularity in recent years (Kelly 2001; Krijger 2002; Hiby et al. 2009 http://www.conservationresearch.co.uk/; Bolger et al. 2012; Bendik et al. 2013; Moya et al. 2015). Although no unsupervised process for the identification of individuals can be completely automated, the strength of such approaches stems from their ability to narrow the pool of potential matches, thereby reducing the time needed for identification and in parallel minimising mismatch errors to a large extent. However, software cannot yet be used to identify species with more complicated coat patterns (e.g. small spots or rosettes in Eurasian lynx) or species that lack clear body patterns (e.g. Kelly et al. 2008; Goswami et al. 2012). In such cases alternative, often imaginative, individual identification strategies are necessary (e.g. Goswami et al. 2012). With appropriate and skilled queries based on individual attributes such as coat patterns, year of birth or morphological traits, as well as spatial and temporal information, the number of comparisons can be significantly reduced. This requires that photographs of individuals with attributes (e.g. coat pattern, date and coordinates) be entered into a picture database (see Chapter 4), incorporated into a GIS that allows for spatial queries (see section 7.4).
7.4Case study: the Eurasian lynx
We present an example of the basic SCR model using likelihood inference (R package secr; Efford 2015) as applied to camera trapping data of Eurasian lynx collected over 60 nights from 29 November 2013 to 28 January 20141 at 61 sites in a 1,051 km2 area in the northwestern Swiss Alps (Figure 7.1; Zimmermann et al. 2014). We also provide estimates using conventional capture–recapture models. Detailed information about the study area, sampling design and timing (in relation to the natural history of the lynx) is found in Pesenti and Zimmermann (2013) and Zimmermann et al. (2013).

Figure 7.1 Study area in the northwestern Swiss Alps. The yellow squares show the camera trap sites, those with black dots indicate lynx detections; the thick black polygon 1,051 km2 delimits the most peripheral camera trap sites. The thin black line shows the area effectively sampled (polygon plus buffer of 1/2MMDM) according to the method described by Karanth and Nichols (1998). Suitable Eurasian lynx habitat 1 × 1 km cells are in light green. A habitat fragment of orthogonally connected suitable habitat cells containing the camera trap sites within the boundaries of the outer rectangle delimiting the area of the state space (or mask in secr) is dark green (= shapefile suitable_habitat_secr). The green and white dots of the mask (= mask_prox; buffer strip of 13 km to the minimum and maximum x,y coordinates of the camera trap sites) show the potential 1,000 m spaced activity centres, within (= habitat_ mask) and outside the suitable habitat fragment, respectively.
7.4.1Analytical steps during field work
If camera traps can be regularly checked (e.g. every 1–2 weeks) it is recommended to keep track of the survey effort, number of individuals and cumulative encounters that are progressively recorded during the survey. This can identify if the survey is running properly in terms of sampling effort and whether the number of individuals detected is reaching a plateau, and makes it possible to intervene to resolve issues by, for example, extending the duration of the survey.
7.4.1.1Sampling effort
In camera trapping studies the sampling effort is usually expressed as the number of camera trap nights or days accumulated (see Chapter 5). When a pair of camera traps is used at each site, one survey night should not be counted as two trap nights but only as one trap night, since under these settings both camera traps together make up one sampling unit and do not accumulate results independently. This also means that working nights need to be subtracted from the sampling effort only if both cameras camera traps did not work simultaneously.
In capture–recapture studies, the greater the effort, the more pictures of (different) individuals are likely to accumulate. A practical way to record effort is to use Excel spreadsheets to report the number of trap nights (Figure 7.2, Figure 7.3 and Appendix 7.1).
After each control the number of realised trap nights in between two controls is entered for each of the two camera traps at each site in the sheet ‘effort’ of the Excel file ‘NWA 2013_2014_eff_trap_nights.xls’. This sheet contains two tables: a basic table with trap nights (or trap days) and a linked table where the values in the cells are automatically computed from the numbers entered in the basic table. The sites and the camera traps are listed in the rows in the basic table (Figure 7.2). Each site has two rows, one for each of the two camera traps. The heads of the columns in the basic table correspond to the date of the days the survey is running. Following the previously described rules, each cell in the basic table gets a value of ‘1’ if the camera trap was working over the 24 h period between noon of the previous day until noon of the date of that given cell; otherwise it has a value of ‘0’.

Figure 7.2 Part of the basic Excel spreadsheet table used to fill in the trap nights of each of the two camera traps at each site. In this example we distinguish between camera traps placed downhill and uphill; as an alternative the camera trap ID number could be used instead. A given cell gets a value of ‘1’ if the camera trap was working from noon of the previous day to noon of the date of the corresponding cell; otherwise it has a value of ‘0’. The first five sites numbered from A1 to A5 were set on 27 November 2013. Both camera traps at site A3 stopped working in the period starting from noon of 6 December 2013 onward and the corresponding cells got a value of ‘0’ and were automatically highlighted in red in the table.
Once all the cells in the basic table have been filled in, the number of trap nights (or trap days) accumulated by a site (row in the table) are automatically summarised in the second table (Figure 7.3). Each cell of a given site and day (column in the table) only gets a value of ‘0’ if both camera traps did not work over the corresponding 24 h period. The information provided in this table will be used to generate the table of trap deployment used in the analyses with secr (see section 7.4.3). During this session, we realized at total of 3,640 of the available 3,660 (60 nights × 61 camera trap sites) trap nights (99.5%). These numbers are shown in the bottom left corner of the second table (light blue cells).

Figure 7.3 The numbers of trap nights accumulated by each camera trap site over the survey are automatically summarised in a table (of which only part is shown here). A cell only gets a value of ‘0’ if both camera traps of the given site did not work over the corresponding 24 h period.
7.4.1.2Individual identification and sex
Lynx are identified visually from photographs by comparing the position of several spots/rosettes relative to each other on the individual’s body (Figure 7.4). A comparison of all lynx photographs taken during a given camera trap survey with all reference photographs of the individuals previously identified is only needed in long-term studies intended to measure demographic parameters (e.g. Karanth et al. 2006), otherwise only the photographs taken during the specific survey are compared to each other.
New lynx photographs are identified over the course of the survey as they are added to the data. To ease the process, we add a recent extract of an Access picture database containing all the relevant information (e.g. individual ID, coat pattern, date, year of birth and mother if available) of the lynx identified so far into a GIS project (ESRI ArcGis 10.1®). Each newly photographed individual is first compared visually with the reference photographs of individuals belonging to the same coat pattern category photographed near the location (i.e. within a given radius) from where the new photographs came from and within a short time window starting from the date when the new photographs were taken. If no matches are found, the temporal and spatial windows are progressively enlarged until a match is found or all photographs of the individuals of the same coat pattern within the database have been checked. A newly identified individual gets a unique identifier composed of a letter and a number. When both flanks are known, it gets the letter B (e.g. B1), when only the left or the right flank are known it gets the letter L or R, respectively. At least two different investigators go through the identification process in order to reduce misidentification errors as much as possible. If no agreement is found between the investigators after more than one trial, it is considered that the individual cannot be identified. This usually happens when the image is of bad quality (e.g. blurred or under/overexposed), not well framed or skewed. In this case the photographs are entered into the picture database as a validated species record (‘hardfact’ C1, SCALP criteria; Molinari-Jobin et al. 2003) but do not get a unique identifier for the individual. Individuals are sexed as males if their scrotums are seen in pictures and as females if they are photographed with juveniles and in some rare occasions based on the genital area if it is clearly visible in pictures.

Figure 7.4 Like all spotted cats, Eurasian lynx have an individual fur pattern. These photos show two individuals with different fur patterns, detected at different locations. (KORA)
7.4.1.3Number of different lynx and cumulative encounters
We use the sheet ‘encounter history’ of the Excel file ‘NWA_2013_14_Lynx_encounter_histories.xls’ provided in Appendix 7.2 to construct the encounter history of each individual pictured during the session. As for the trap nights, this sheet contains two tables: a basic table where the individual encounters need to be filled in (Figure 7.5) and a linked table (Figure 7.6) where the values of most cells are automatically computed (entries in italic) from the entries provided in the basic table. The rows in the table correspond to the individuals and the columns to the dates of the photographs or encounters. Each photographic detection of each individual lynx is entered in the encounter history table. Young lynx (juveniles) are visually distinct from adults and sub-adults in this season and still follow their mother. Because the xenon white flash camera traps used in this study may need up to 1 minute to charge the flash at night depending on the model, most of the time only the first individual of the family group is pictured, the other ones going undetected. For these reasons, following Zimmermann et al. (2013), a picture of any family group member is counted as an encounter of the respective female (if known) in the encounter history (the same procedure is followed to prepare the input files for the spatially explicit capture–recapture model secr; see below). Since independent dispersers cannot be distinguished from resident animals (adults) on the basis of pictures, the abundance estimates refer to ‘independent lynx’, i.e. these are residents plus dispersers, or adults plus sub-adults (Zimmermann et al. 2013). If the individual lynx has not yet been entered in the table, its name is added in the first free row in the column with ‘lynx ID’ as header. If it is already present, we can directly proceed to the second step, which consists in adding the site number of the photographic detection in the appropriate cell. The site number is added in the cell (in the row of the corresponding individual lynx) in the column that corresponds to the 24 h period when the individual lynx was detected, knowing that the date of each column covers the 24 h period between noon of the day before until noon of the date of the given column. For family groups, we add in parenthesis beside the site number if only adult (Ad) or juveniles (Juv) or both (Ad+Juv) were pictured at a given detection. We proceed in the same way for the subsequent encounters until all are entered into the table. If an individual was detected two or more times during the same 24 h period, the number of times is reported in parenthesis beside the site number; if it was detected at different sites, each site number is entered separated by a slash.

Figure 7.5 Detailed encounter history table of each Eurasian lynx showing the first seven individuals (second column) and the first three sampling occasions (first row) defined as five consecutive time frames of 24 h starting at noon (second row). The site number of the photographic detection of each individual is entered in the corresponding cell in the table. In this example lynx B261 was detected four times at site D2 during the 24 h period ending at noon on 30 November 2013 in the first sampling occasion. B196 was detected once and its juvenile B383 was detected twice at site F1 during the 24 h period ending at noon on 10 December 2013 in the third sampling occasion.
Once all the cells in the basic table are filled in, the detailed encounter history of each lynx is automatically summarised into an encounter history table (Figure 7.6). In our case a sampling occasion is defined as five consecutive time frames of 24 h starting at noon, which results in a total of 12 sampling occasions for the duration considered. A ‘1’ is automatically entered if the corresponding lynx is photographed at least once during this sampling occasion or a ‘0’ if it is not photographed at all during this particular sampling occasion. This design of encounter history can be used as an input format for modelling abundance using the CAPTURE module in the program MARK (http://www.phidot.org/software/mark/; see below). The four rows at the bottom of the table (‘encounters’, ‘cumulative encounters’, ‘new individuals encountered’ and ‘individuals in total’; see NWA_2013_14_Lynx_encounter_histories.xls) are automatically updated with the exception of the number of ‘new individuals encountered’ during a given sampling occasion which needs to be filled in by hand by the user. The number of different lynx and the cumulative number of encounters is plotted against the number of sampling occasions in the graph provided in the sheet ‘cumulative encounters’ (Figure 7.7).
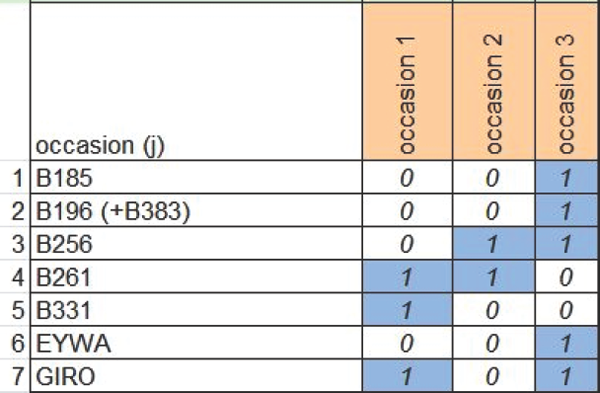
Figure 7.6 Encounter history table showing the first seven individuals (second column) and the first three sampling occasions (first row). The encounter history of each Eurasian lynx consists of a string of 1s and 0s, in which a ‘1’ indicates encounter of the individual during a specific five day long sampling occasion, while a ‘0’ indicates that the individual was not encountered.

Figure 7.7 Cumulative number of Eurasian lynx encounters and different lynx with increasing number of sampling occasions.
In this session the cumulative number of encounters increased almost linearly. At the 9th sampling occasion the number of different lynx stabilised at 22 individuals but a 23rd individual was encountered during the 12th and last sampling occasion. We can conclude that this session worked pretty well, as we detected 23 individuals (6 females, 11 males and 6 of unknown gender), which is more than the minimum of 20 needed to obtain reliable population estimates in the conventional capture–recapture models according to White et al. (1982). In addition, as only one new encounter occurred after the 9th occasion but the cumulative number of encounters increased steadily during the subsequent sampling occasions, we can be confident that we detected a large proportion of the individual present in the area. There were also a fair number of detections of individuals at different trap sites: three individuals were detected at one site, five each at two and three sites, four at four, two each at five and six, and one each at seven and eight sites.
7.4.2Dates and times in R
The software R offers a flexible framework to manage observations from different time zones and summer and winter time notations. The easiest and more reliable way to manage them is to store date, time and time zone of the observations in a unique object of class POSIX. Two basic objects of class POSIX are found: (i) POSIXlt is a list of vectors including year, month, day, hour, etc.; and (ii) POSIXct represents the length of time in seconds that has passed since a given temporal origin as a numerical vector (in R the default origin is 1970-01-01 00:00.00 UTC). Objects of classes POSIXlt and POSIXct can be manipulated by means of the functions as.POSIX* and strptime. These two functions are essentially equivalent for general purposes; we will therefore use preferentially as.POSIX* for clarity.
as.POSIXlt("2015-03-29 01:30:00", format="%Y-%m-%d %H:%M:%S", tz="Europe/Berlin")
[1] "2015-03-29 01:30:00 CET"
as.POSIXct("2015-03-29 01:30:00", format="%Y-%m-%d %H:%M:%S", tz="Europe/Berlin")
[1] "2015-03-29 01:30:00 CET"
The information stored in the two classes looks exactly the same because it is displayed in the same way; however, it is crucial to be aware of the existence of these two classes.
Data sets from different sources, programs or databases store the temporal information in a multitude of different formats in which date and time of the observations may even be located in two separate columns. Moreover, Excel and Access occasionally change the cell content, introducing dummy values to suit certain cell formats. In order to organise this information and create a workable time format, it is suggested to prepare an object − say a vector − with the date and another object with the time in a character format. Hereinafter, we will handle as an example a single observation taken in Central Europe on 29 March 2015 at 1:30 am, as it may be commonly found in a database export sheet:
day<-"29.3.2015 00:00:00"
clocktime<-"30.12.1899 01:30:00"
We can separate the dummy values from the useful temporal information by means of the function strsplit. This function returns a list in which the first element holds the ‘pieces’ that have been separated from each other by means of the character argument split:
strsplit(day, split=" ")
[[1]]
[1] "29.3.2015" "00:00:00"
The different ‘pieces’ can be extracted by double indexing the results. We can therefore overwrite our day and clocktime objects as follows:
day<-strsplit(day, split=" ")[[1]][1]
clocktime<-strsplit(clocktime, split=" ")[[1]][2]
day; clocktime
[1] "29.3.2015"
[1] "01:30:00"
Now we can merge the two objects in a single character string using the general function paste and then transform this latter into an object of class POSIX by means of the functions as.POSIXlt or strptime. The different date and time formats can be accounted for by changing the format parameter of the functions as.POSIX* and strptime. For example "%Y-%m-%d" would be the right choice when reading the date "2015-03-29". The time zone required has to be chosen according to the location of the study area and must be specified correctly in R, otherwise the software will treat all misunderstood entries as UTC (Coordinated Universal Time). In order to find out the exact name of the time zone in which you are located (argument tz of the function as.POSIX*), type Sys.timezone() in the R console. The full list of the possible time zone matches is available by typing OlsonNames().
x<-paste(day,clocktime)
x
[1] "29.3.2015 01:30:00"
xPOSIXlt<-as.POSIXlt(x, format="%d.%m.%Y %H:%M:%S", tz="Europe/Berlin")
xPOSIXlt
[1] "2015-03-29 01:30:00 CET"
The definition of the time zone in objects of class POSIX additionally allows the user to deal with the issue of local time, fractional offsets and daylight savings time conventions. When a few observations are treated, it is straightforward to overcome the problem by adding or subtracting a given amount of minutes to the observation considered, but this can take enormous amount of time and could be subject to errors when bigger data sets are involved. Fortunately, R comes with a powerful set of functions allowing easy and safe manipulation of time objects. For a practical example let us consider three observations: our previous observation in winter time, a second observation on the same date in summer time in the same time zone and a third one on the same date in summer time on the other side of the world:
xPOSIXlt2<-as.POSIXlt("2015-03-29 03:30:00", tz="Europe/Berlin")
xPOSIXlt3<-as.POSIXlt("2015-03-29 03:30:00", tz="Australia/Melbourne")
xPOSIXlt; xPOSIXlt2; xPOSIXlt3
[1] "2015-03-29 01:30:00 CET"
[1] "2015-03-29 03:30:00 CEST"
[1] "2015-03-29 03:30:00 AEDT"
difftime(xPOSIXlt2,xPOSIXlt)
Time difference of 1 hours
difftime(xPOSIXlt2,xPOSIXlt3)
Time difference of 9 hours
The use of POSIX objects forces all computations (here difftime) to take into account the differences in daylight savings notations and time zones, making all conversions straightforward. As a matter of fact, we can easily calculate the corresponding Coordinated Universal Time (UTC) of these observations by means of the function format, which should not, however, be confused with the argument format of the functions used above. Format works with POSIXct objects and returns a character string free from any temporal shift.
xUTC<-format(as.POSIXct(xPOSIXlt),tz="UTC")
xUTC2<-format(as.POSIXct(xPOSIXlt2),tz="UTC")
xUTC;xUTC2
[1] "2015-03-29 00:30:00"
[1] "2015-03-29 01:30:00"
The present character strings already allow to calculate time differences by means of the function difftime, but have to be back-transformed in a POSIX object for any further treatment. We may actually add 60 min to these two observations to get the corresponding UTC+1 local time format in Central Europe. Transforming observations to local time is very important, for instance, in studies investigating the activity pattern of a given species (see Chapter 8). It is crucial to account for all the local time conventions and project the observations back to the right zone in order to obtain something that is meaningful for the biology of the species and readable by researchers.
xUTClocal<-as.POSIXlt(xUTC,tz="UTC") + (60*60)
xUTClocal2<-as.POSIXlt(xUTC2,tz="UTC") + (60*60)
xUTClocal;xUTClocal2
[1] "2015-03-29 01:30:00 UTC"
[1] "2015-03-29 02:30:00 UTC"
Some studies, for example behavioural studies investigating activity patterns in study areas with a strong longitudinal gradient in the same time zone (e.g. China), may need even finer conversions. In such cases, the use of true solar time instead of local time makes more sense. The function local2solar of the package solaR v0.41 (Lamigueiro 2015) can be used for this purpose. In addition to the time of the observation in form of a POSIXct object, this function needs the longitude where the observation was taken and includes two corrections: the difference in longitude between the location and the time zone, and the daylight saving time. In this chapter we are not going to consider corrections due to solar time variations in the same time zone because, given the size of the study area, they can be considered as negligible (<2 min).
7.4.3Analysis with secr
Once the package secr (version 2.10.0 and later) has been loaded in R we can import the data set containing all the lynx encounters from our study area. The following information is required: site number, date and time of the photograph prepared according to the previous section, individual identification, sex, the name of the mother, and the year of birth for juveniles only (only if the investigator would like to take these juveniles into account as an encounter of their respective mothers in the encounter history; see above). The input table and especially the column containing the information about date and time have already been prepared (see section 7.4.2).
library(secr)
lynx_data<-read.delim("Lynx_data.txt", header=T, stringsAsFactors=F)
When data are stored into R dataframes, it is sometimes necessary to specify in detail the class of some variables, since the read.* functions often assign non-numeric values to the classes factor or character. Here we transform a character column into a column of class POSIXct.
lynx_data[,"Time"]<-as.POSIXct(lynx_data$Time)
lynx_data

We then import the table with the coordinates of all sites and add a column with a single numerical identifier for each one of them:
sites<-read.delim("Sites.txt", stringsAsFactors=F)
sites<-data.frame(LOC_ID=1:dim(sites)[1], sites)
sites

Finally, we import the table of the trap deployment details including dates when specific sites were active (this table was prepared from the information in the Excel file ‘NWA 2013_2014_eff_trap_nights.xls’; see Appendix 7.1). This data set is used to correct systematic differences between sites or periods due to, for example, snow falls, battery problems or other technical malfunctions (see above for more details):
trap_nights<-read.delim("Trapnights.txt", header=T, stringsAsFactors=F)
trap_nights

As explained in detail earlier in the present section, we count a photograph of any family group member as an encounter of the respective female (if known) in the encounter history. We therefore replace the names of the juveniles with the name of their corresponding mothers in the table, and make sure that their sex is ‘f’ for females, if the detected juveniles were born in 2013 and their mothers were known. If an investigator does not want to integrate the encounter of juveniles into the analyses, he/she simply needs to delete them prior to the preparation of the data sets.
for (i in 1:dim(lynx_data)[1]){
if(lynx_data$Mother[i]!="" & lynx_data$Year_Born[i]==2013){ lynx_data[i,"Lynx_Name"]<-lynx_data$Mother[i] lynx_data[i,"Sex"]<-"f"}}
We then delete the columns holding the information about motherhood and year of birth, since the detections now refer to independent lynx (i.e. residents plus dispersers, or adults plus sub-adults).
lynx_data<-lynx_data[,-which(names(lynx_data)=="Mother")]
lynx_data<-lynx_data[,-which(names(lynx_data)=="Year_Born")]
In order to automatise the computation of the sampling effort and assign the detections to a given sampling occasion, we need to define the beginning and the end of the session, as well as the length of the sampling occasions (in nights or days). This session started on 29 November 2013 at 12 o’clock, lasted for 60 consecutive nights; the length of a single encounter event was defined as five consecutive nights. In this frame, our data set consists of 12 consecutive sampling occasions with a length of 120 h in a single block.
start_date <- as.POSIXlt("2013-11-29 12:00:00", format="%Y-%m-%d %H:%M:%S", tz="Europe/Berlin")
end_date <- as.POSIXlt("2014-01-28 12:00:00", format="%Y-%m-%d %H:%M:%S", tz="Europe/Berlin")
length_occasion<-5
max_occasions<-as.numeric(difftime(end_date, start_date,unit='days')/length_occasion)
max_occasions
[1] 12
We can then create the table describing the sampling effort by calculating for each sampling occasion of five nights the proportion of trap nights accumulated by a camera trap site (1 if the site worked for five nights, 0.8 if it worked only for four, and so on until 0 if both camera traps at the given site did not work at all).
traps_table<-matrix(nrow=dim(sites)[1], ncol=max_occasions)
for (i in 1:dim(traps_table)[1]){
for (j in 1:max_occasions){
traps_table[i,j]<-sum(trap_nights[i,
(2+length_occasion*(j-1)):(1+length_occasion*j)])/length_occasion}}
traps_table

Similarly, we can automatise the assignment of all the observations to the sampling occasions calculating the difference between the time of the photo and the previously defined start of the session. This time difference is divided by the five nights duration of the sampling occasion and increased by one unit. The function floor returns the largest integer not greater than the giving number, which finally corresponds to the calculated sampling occasion:
captures<-data.frame(SESSION=integer(), ANIMAL_ID=integer(), SO=integer(), LOC_ID=integer(), SEX=integer())
for (i in 1:dim(lynx_data)[1]){
captures[i,"SESSION"]<-1
captures[i,"LOC_ID"]<-sites[sites[,"Site"]== lynx_data$Site[i],"LOC_ID"]
captures[i,"ANIMAL_ID"]<-lynx_data$Lynx_Name[i]
captures[i,"SO"]<-floor(difftime(lynx_data$Time[i], start_date,units='days')/length_occasion)+1
captures[i,"SEX"]<-lynx_data$Sex[i]
if (captures[i,"SEX"]=="") captures[i,"SEX"]<-NA}
captures

Many different detectors can be specified in secr (see the secr overview manual), but principally only two are useful for camera trap studies: ‘count’ and ‘proximity’. Basically, the first detector allows multiple detection events of each individual at a given site on any sampling occasion, whereas the second one restricts the number of detections to at most one. In other words, we have to choose if − within our sampling occasion of five days − we accept only one or eventually more detection events of each individual at a particular site. A ‘count’ detector is more likely to be affected by temporal autocorrelation between consecutive photographs of the same individual at the same site than a ‘proximity’ detector. Therefore, before running the analyses, investigators should address questions about temporal resolution, namely what constitutes an independent record of the same individual at the same site (for more details on subsampling and temporal autocorrelation, refer to Chapter 5). For this case study, we use the ‘proximity’ type of detector and therefore reduce the dimension of our data set by deleting all the repeated observations of the same lynx within the same sampling occasion at a given site simply by means of the function unique. We then reassign the names of the rows from 1 to n by means of the function rownames in order to match the dimensionality of the data frame:
captures_prox<-unique(captures)
rownames(captures_prox)<-1:length(rownames(captures_prox))
captures_prox

We are now ready to create the input datasets for secr. First we create the traps object, which hold all the information about the array of detectors, their type and other additional information. We define a first traps object without any information about the sampling effort (traps_analysis_nousage), and then we integrate the table describing the sampling effort that we calculated previously in a second traps object (traps_analysis).
traps_analysis_nousage<-read.traps(data=sites[,c(1,3:4)], detector="proximity", binary.usage=FALSE)
summary(traps_analysis_nousage)
| Object class |
traps |
| Detector type |
proximity |
| Detector number |
61 |
| Average spacing |
2951.235 m |
| x-range |
567321 618502 m |
| y-range |
137586 173237 m |
| traps_analysis<-traps_analysis_nousage |
| usage(traps_analysis)<-traps_table |
| summary(traps_analysis) |
| Object class |
traps |
| Detector type |
proximity |
| Detector number |
61 |
| Average spacing |
2951.235 m |
| x-range |
567321 618502 m |
| y-range |
137586 173237 m |
Usage range by occasion

Then we create the capthist object, merging the detections that we retained previously and the just-created ‘traps’ object. The capthist objects can additionally carry the covariates that the researcher will eventually test in the model (e.g. sex of individuals), and we therefore specify the gender of the lynx when known. The fact that there are missing values for the gender variable does not represent a major problem for the inference, because among the several ways to incorporate sex effects into models with secr, there is one (see below) that is able to deal with occasional missing values (refer to the secr user manual for possible approaches when the gender is known for all the individuals):
lynx_capthist <-make.capthist(captures_prox, traps_analysis, fmt="trapID", noccasions=max_occasions, covnames="SEX")
summary(lynx_capthist)
| Object class |
capthist |
| Detector type |
proximity |
| Detector number |
61 |
| Average spacing |
2951.235 m |
| x-range |
567321 618502 m |
| y-range |
137586 173237 m |
Usage range by occasion

Counts by occasion
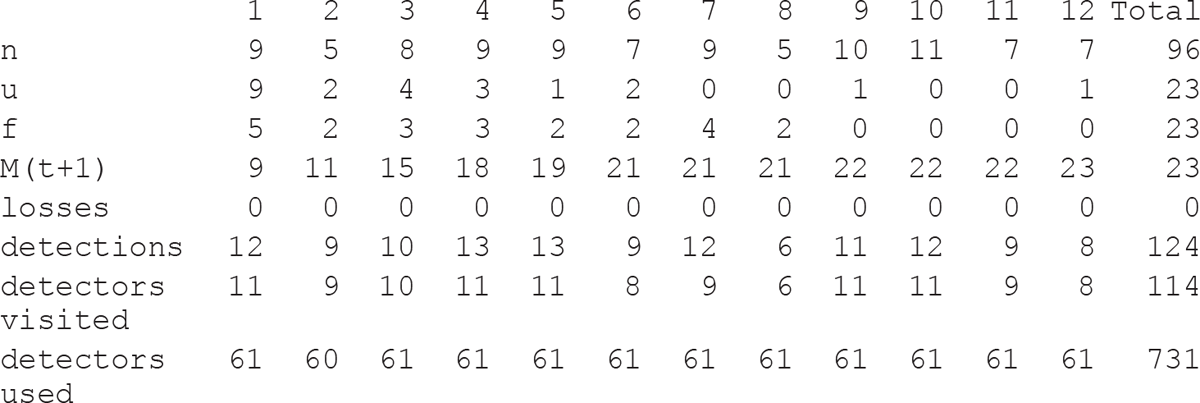
The last object that needs to be created for a secr analysis is the mask to be applied to the array of the camera trap sites. The definition of this object is not strictly necessary for running the model, because it is possible to generate it implicitly by specifying an adequate buffer size with the argument buffer of the function secr.fit. However, it is recommended to create the mask separately by means of make.mask to provide greater control. This function allows different parameters of the state space grid (mask in secr terminology) to be defined, primarily: (i) its shape (argument type) – in this case the ‘traprect’ method is chosen, which constructs a grid of points in the rectangle formed by adding a buffer strip to the minimum and maximum x,y coordinates of the camera trap sites (Figure 7.1); (ii) the spacing between potential activity centres (argument spacing, in this case 1000 m; Figure 7.1); and (iii) its buffer width (buffer, in m). A buffer width that is too narrow is likely to produce inflated density estimates, hence it is critical to determine the buffer width beyond which the density estimates start to stabilise. Following Pesenti and Zimmermann (2013), we create a series of masks for 12 different buffer widths ranging from 1 to 30 km (1, 3, 5, 7, 9, 11, 13, 15, 17, 20, 25 and 30 km) on the smallest grid encompassing the camera trap sites in order to find the minimum buffer width for which the density estimates start to stabilise.
As with all SCR models, secr fits a detection function relating the probability of encounter or the expected number of encounters for an animal to the distance of a detector, in this case the camera trap site, from a point usually thought of as its activity or home range centre. In our case study we use the default ‘halfnormal’ function (commonly called the Gaussian model), which considers that the encounter probability is highest when the camera trap site is placed exactly at the animal’s activity centre and declines as the distance between camera trap site and activity centre increases based on the kernel of a bivariate normal probability distribution function. Additional detection functions can be specified by means of the argument detectfn of the function secr.fit and can be found by calling the help function for the detection function:
?detectfn
Most of the basic detection functions available in secr contain at least two parameters: g0, the baseline encounter probability (i.e. the encounter probability when the distance between the animal’s activity centre and the trap is zero), and some kind of spatial scale parameter that is usually labelled σ. The meaning of this parameter depends on the specific detection model being used, and it should not be directly compared as a measure of home range size across models.
For this series of analyses we use the ‘null model’ formulation, which assumes constant values for animal density D, baseline encounter probability g0 and parameter σ. The corresponding null model formulation in R is implemented specifying ‘~1’ in the parameter list of the model argument in the secr.fit function.
For simplicity, we report only the first analysis with the 1 km buffer width. All the other buffer widths are investigated simply by changing the arguments of these two functions (for the extended script, refer to the supporting material for the present chapter):
mask_1 <-make.mask(traps_analysis, buffer=1000, type="traprec", spacing=1000)
M0_1 <-secr.fit(lynx_capthist, mask=mask_1, model = list(D~1, g0~1, sigma~1))
Checking data
Preparing detection design matrices
Preparing density design matrix
Finding initial parameter values...
Initial values D = 0.00014, g0 = 0.18028, sigma = 3354.50837
Maximizing likelihood...

Completed in 46.51 seconds at 12:42:29 01 nov. 2015
mask_3<- ...
A simple plot of the density estimates resulting from this series of null models suggests that the estimates are fairly stable with a buffer width ≥13 km (Figure 7.8). This value also lies within the range of the buffer width of 2–3σ that should be targeted as a rule of thumb according to Royle et al. (2014) to ensure that no individual animal outside of the area delimited by the corresponding mask has any probability of being detected by the camera traps in the array during the survey.
Figure 7.8 Estimated density (number of individuals per 100 km2) as a function of the mask buffer, based on a null model integrating the sampling effort.
We therefore retain this buffer width in the subsequent analyses:
| mask_prox<-mask_13 |
| summary(mask_prox) |
| Object class |
mask |
| Mask type |
traprect |
| Number of points |
4774 |
| Spacing m |
1000 |
| Cell area ha |
100 |
| Total area ha |
477400 |
| x-range m |
554821 630821 |
| y-range m |
125086 186086 |
| Bounding box |
|
x |
y |
| 1 |
554321 |
124586 |
| 2 |
631321 |
124586 |
| 4 |
631321 |
186586 |
| 3 |
554321 |
186586 |
The secr package easily fits a range of SCR equivalents of conventional capture–recapture models. The package has predefined versions of the classic model Mt where each occasion has its own encounter probability, denoted ‘t’ in secr, as well as a linear trend in baseline encounter probability over occasions, denoted ‘T’. The behavioural response can be either global (Gardner et al. 2010b) or local (Royle et al. 2011). The global trap response model (learned response in secr terminology) and the local trap response model (site-specific learned response in secr terminology) can be fitted in secr using formulae with ‘b’ and ‘bk’, respectively. The site-specific transient response model denoted ‘Bk’ is similar to the site-specific learned response, but only considers the location of the individual at the last occasion it was encountered. This model tests the hypothesis that lynx behaviour changes after being detected at a specific site, but only for that site and not for the duration of the survey. Additional model descriptions can be found in the secr manual or by calling the help function for models for detection parameters:
We now run a series of analyses to investigate the effect of the predefined models on the baseline encounter probability g0 while keeping the parameter σ constant:
M0 <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~1, sigma~1))
Mb <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~b, sigma~1))
Mt <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~t, sigma~1))
Mbt <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~b+t, sigma~1))
MT <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~T, sigma~1))
MB <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~B, sigma~1))
Mbk <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~bk, sigma~1))
MBk <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~Bk, sigma~1))
MK <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~K, sigma~1))
MK_NM <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~K, sigma~1),method="Nelder-Mead")
Mk <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~k, sigma~1))
Mh2 <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~h2, sigma~1))
Mh2_NM <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~h2, sigma~1),method="Nelder-Mead")
Mh2_NM_SL <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~h2, sigma~1),method="Nelder-Mead", start=list(D=0.00012,g0=0.24,sigma=3200))
Mh2_NM_SM0 <-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~h2, sigma~1), method="Nelder-Mead",start=M0)
We encounter problems fitting MK and the finite mixture model (Mh2). While model MK could be fitted by setting the method to ‘Nelder–Mead’, which is less prone to settling in local minima than the default ‘Newton–Raphson’, Mh2 could not be fitted properly with this method even when providing starting values (see ‘Troubleshooting’ in the secr manual). The final result was, however, good enough to include Mh2 in the comparison of models when the non-nested model M0 (Mh2 models have the additional real parameter pmix) was offered in the start ‘argument’. Finite and hybrid mixture models are prone to fitting problems caused by multimodality of the likelihood. There is the risk that the numerical maximisation algorithm will get stuck on a local peak, in which case the estimates are simply wrong. Care is needed as the problem has not been explored fully for secr models (Efford 2014).
Following Royle et al. (2014), we use the AIC because it is not clear what the effective sample size is for most capture–recapture problems. Models are compared by means of the delta AIC (Δi). As a rule of thumb, a Δi < 2 suggests substantial evidence for the model, values between 3 and 7 indicate that the model has considerably less support, whereas a Δi > 10 indicates that the model is very unlikely (Burnham and Anderson 2002).
AIC(M0,Mb,Mt,Mbt,MT,MB,Mbk,MBk,MK_NM,Mk,Mh2_NM_SM0, criterion="AIC")

Model selection reveals substantial evidence for the ‘site-specific learned response’ model Mbk. The two subsequent models, MBk and MB with Δi of 4.192 and 6.239, respectively, have considerably less support. The ‘site-specific learned response’ model incorporates a site-sensitive change of behaviour for individuals after first detection, which implies that if an individual is captured in a specific camera trap site, the probability of a subsequent encounter is increased (i.e. the individual becomes ‘trap happy’) or decreased (i.e. the individual becomes ‘trap shy’) only for that particular camera trap site; secr provides estimates in units of individuals/hectare, and we thus need to multiply the given estimates by 104 in order to have our estimate as individuals/100 km2. The estimated density (SE) from this model corresponds to 1.05 (0.23) independent lynx per 100 km2, with baseline encounter probability g0 (SE) 0.082 (0.015) and sigma σ (SE) 4,736 (336) m. In situations where an individual has the tendency to revisit a camera trap site subsequent to its initial visit (i.e. is ‘trap happy’), as in the present study, the encounter probability is overestimated by the null model and is properly adjusted downward when a behavioural response is added to the model (0.117 vs. 0.082), yielding a corresponding increase in the estimated density (1.03 vs. 1.05 independent lynx per 100 km2). A much more strongly positive site-specific learned response was found in a wolverine (Gulo gulo) SCR density estimation study using baited traps (Royle et al. 2011). Contrary to the wolverine study, our result may seem surprising as the camera trap sites were not baited. Moreover, we would have tended to have expected trap shyness given that lynx tracks bypassing camera trap sites are sometimes found in the snow (although this would only result in trap shyness if the individual avoiding the trap site had previously been detected at this site). Trap shyness has been documented in tiger (Panthera tigris) by Wegge et al. (2004): tigers became trap shy probably because of pad impressions, which provided a cue for the tigers about the presence of camera traps in front of their travel path. Hence, a possible explanation for the slight tendency for an individual to revisit a camera trap site subsequent to its initial visit as observed in this case study may be that in a mountainous landscape such as the Alps, where animal movements are channelled by topographical features, individual lynx have a higher chance of being encountered and subsequently re-encountered at a particular camera trap site within their territory, especially if it is placed at a forced passage at the entrance of a valley regularly used by the lynx. An additional and complementary explanation is that an individual might have killed a larger prey in the vicinity of a camera trap site. This was corroborated during this session by a photograph showing male B333 dragging the carcass of a chamois, which it has just killed, along the trail passing by the camera trap site. As lynx usually feed for several nights (up to seven consecutive nights) on a kill (Jobin et al. 2000), they have a higher chance of being re-encountered at a given site while moving between the day lair and the kill site.
The function region.N is used to produce estimates of N for any given region. In the example here we generate expected (E.N) and realised (R.N) population sizes in the region delimited by the mask_prox by passing the best spatial model (Mbk) and the mask of inference to the function region.N. The area of the mask_prox is 4,774 km2 and was obtained previously by typing summary(mask_prox).
region. N(Mbk, region=mask_prox)

The realised N is simply the number of individuals actually detected plus a model-based estimate of the number of individuals in the region of interest that remain undetected (Johnson et al. 2010). The probability of remaining undetected is a function of location (high at the edges, low near detectors). The expected N is the integral (sum) over the mask of the product of (estimated) local density and the local probability of remaining undetected. The estimates of expected and realised N are generally very similar, or identical, but realised N usually has lower estimated variance, especially if the n detected animals comprise a large fraction (Efford 2015).
There are differences in movement patterns between male and female lynx: resident adult males have larger home ranges than females (Breitenmoser-Würsten et al. 2001), and adult males regularly patrol their territory borders, to deposit scent marks, to defend their territory against potential intruders, and during the mating season to find potential mates (Breitenmoser and Breitenmoser-Würsten 2008). For these reasons, we expect differences between the sexes in the baseline encounter probability (g0) and the parameter σ. We therefore investigate the effect of sex on the detection function parameters g0 and σ using the null and the best model (Mbk) of the previous analysis in order to check which model best explains our data. Because gender was missing for some individuals, the argument hcov in secr.fit is used to fit a hybrid mixture model (Efford 2015). ‘Hybrid’ refers to a flexible combination of latent classes (as for finite mixtures) and known classes (as for classic categorical covariates). A hybrid mixture model automatically estimates the parameter ‘pmix’, which corresponds to the mixing proportion of the different classes and additionally allows more complex model structures in which the detection parameters can be modelled as class specific (~h2). This is particularly useful for investigating sex ratios and sex differences in detection. The argument hcov="SEX" identifies in the corresponding column the individual covariate that should be a factor with two levels, or contain character values that will be coerced to a factor (e.g. ‘female’, ‘male’). Missing values (NA) are used for individuals of unknown class. It is assumed that males and females are equally likely to be sexed from photographs. Models can be compared by means of AIC provided they all have the same hcov covariate in the call to secr.fit, whether or not the h2 notation appears in the model formulation:
M_g0bk_sigma<-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~bk, sigma~1), hcov="SEX")
M_g0sex_sigmasex<-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~h2, sigma~h2), hcov="SEX")
M_g0_sigmasex<-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~1, sigma~h2), hcov="SEX")
M_g0bk_sigmasex<-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~bk, sigma~h2), hcov="SEX")
M_g0bksex_sigma<-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~(bk+h2), sigma~1), hcov="SEX")
M_g0bksex_sigmasex<-secr.fit(lynx_capthist, mask=mask_prox,
model = list(D~1, g0~(bk+h2), sigma~h2), hcov="SEX")
AIC(M_g0_sigmasex,M_g0sex_sigmasex,M_g0bk_sigma,
M_g0bk_sigmasex,M_g0bksex_sigma,M_g0bksex_sigmasex, criterion="AIC")

From the six models we created in secr, the model incorporating the site-specific learned response in the baseline encounter probability g0 and gender in σ is the best model. This is just a bit better than a model incorporating gender in the baseline encounter probability, in addition to the covariates already included in the best model. Following the rule of thumb of Burnham and Anderson (2002) we apply model averaging to the models with Δi < 2:
model.average(M_g0bk_sigmasex,M_g0bksex_sigmasex,criterion="AIC")

Model averaging yields a density estimate (SE) of 1.11 (0.25) individuals per 100 km2 with baseline encounter probability g0 (SE) 0.090 (0.017) and 0.099 (0.028) and σ (SE) 5,138 (407) m and 3,295 (403) m for males and females, respectively. As expected, males have a significantly larger σ than females. However, their baseline encounter probability g0 is slightly lower, but not significantly, compared to females. The estimated sex ratio (SE) of 0.54 (0.13) is slightly skewed towards males, but with a 95% confidence interval (95% CI) including 0.5 does not diverge significantly from a 1:1 ratio. Model-averaged density is almost equal to the one provided by the previous best model Mbk (labelled M_g0bk_sigma according to the new mixture parameterisation), now ranked in sixth and last position with an estimated density of 1.05 (0.23) individuals per 100 km2.
In the previous examples, we considered all potential lynx activity centres of the mask, whether in suitable or unsuitable lynx habitats. However, in secr it is possible to create a habitat mask that can eliminate all potential activity centres falling in non-lynx habitats and which should not be considered in the analyses. In this example we use a previously developed lynx habitat suitability model (Zimmermann 2004) with cut-off point of >20 for habitat suitability (habitat suitability ranges from 0 = unsuitable to 100 = highly suitable habitat) to discriminate suitable habitat fragments of orthogonally connected suitable habitat 1 × 1 km cells in the GIS ArcGis 10.1. Knowing that excluding habitats/areas potentially used by individuals during their movements can potentially bias estimates because this imposes constraints on space usage, we selected a cut-off point to exclude the highly unsuitable areas. These included settlements, intensively used agriculture areas, lakes, large rivers and high mountains peaks above 2,000 m that are not used by resident lynx. We consider only the regions available to resident lynx in our sampling area and thus restrict suitable habitats to the fragment containing the camera trap sites within the state space (dark green area in Figure 7.1). In secr the polygon (argument poly of the function make.mask) may either be a matrix or data frame of two columns interpreted as x and y coordinates, or a SpatialPolygonsDataFrame object. Here we opt for the latter and create the shapefile ‘suitable_habitat_secr’ by intersecting the shapefile delimiting the mask_prox with the shapefile of the suitable lynx habitat fragment containing the camera trap sites in the GIS. The resulting shapefile is then imported into R via the function readShapePoly of the package maptools. The habitat mask can be easily created with make.mask().
library(maptools)
HabitatPol <- readShapePoly("suitable_habitat_secr")
habitat_mask <- make.mask(traps_analysis, spacing=1000, type="polygon", poly = HabitatPol)
Before running further analyses it is useful to draw a map in R (see Figure 7.9) in order to figure out whether the camera trap sites, the potential activity centres and the shapefile of the polygon delimiting the suitable lynx habitat are correctly located relative to each other and if all camera trap sites are within the boundaries of the suitable lynx habitat:
plot(HabitatPol, axes=F)
plot(habitat_mask, pch=20, add=T)
points(traps_analysis[,"x"], traps_analysis[,"y"], pch=20, bg=grey(1), col='black')

Figure 7.9 Map showing the extent of the shapefile delimiting the suitable lynx habitat (polygon), the potential 1 × 1 km spaced activity centres (grey dots) and the camera trap sites (black dots).
We now provide density estimates considering only the potential activity centres lying in lynx habitats in the analyses for the same models as considered in the previous example without the habitat mask:
M_g0bk_sigma_habitat<-secr.fit(lynx_capthist, mask=habitat_mask,
model = list(D~1, g0~bk, sigma~1), hcov="SEX")
M_g0sex_sigmasex_habitat<-secr.fit(lynx_capthist,
mask=habitat_mask, model = list(D~1, g0~h2, sigma~h2), hcov="SEX")
M_g0_sigmasex_habitat<-secr.fit(lynx_capthist, mask=habitat_mask,
model = list(D~1, g0~1, sigma~h2), hcov="SEX")
M_g0bk_sigmasex_habitat<-secr.fit(lynx_capthist,
mask=habitat_mask, model = list(D~1, g0~bk, sigma~h2), hcov="SEX")
M_g0bksex_sigma_habitat<-secr.fit(lynx_capthist,
mask=habitat_mask, model = list(D~1, g0~(bk+h2), sigma~1), hcov="SEX")
M_g0bksex_sigmasex_habitat<-secr.fit(lynx_capthist,
mask=habitat_mask, model = list(D~1, g0~(bk+h2), sigma~h2), hcov="SEX")
AIC(M_g0bk_sigma_habitat, M_g0sex_sigmasex_habitat, M_g0_ sigmasex_habitat, M_g0bk_sigmasex_habitat,
M_g0bksex_sigma_habitat, M_g0bksex_sigmasex_habitat, criterion="AIC")

The model ranks and the two competing models (M_g0bk_sigmasex_habitat and M_g0bksex_sigmasex_habitat) are the same as when models without the habitat mask were compared, though this must not always be the case (e.g. wolverine example, Royle et al. 2014, p. 223). Following the same procedure as before, we use model averaging to obtain unbiased parameter estimates:
model.average(M_g0bk_sigmasex_habitat,
M_g0bksex_sigmasex_habitat,criterion="AIC")

Model-averaged density (SE) corresponds to 1.37 (0.30) individuals per 100 km2 of suitable habitat, with averaged baseline encounter probability g0 (SE) 0.088 (0.017) and 0.096 (0.026) and averaged σ (SE) 5,122 (405) m and 3,316 (409) m for males and females, respectively. As previously, males have significantly larger σ than females and their baseline encounter probability g0 is slightly lower, but not significantly, compared to females. The averaged resulting sex ratio (SE) of 0.54 (0.13) is slightly skewed towards males, but with a 95% CI including 0.5 does not diverge significantly from a 1:1 ratio.
7.4.4Abundance and density estimation in conventional (i.e. non-spatial) capture–recapture models
For the purpose of comparing our results with earlier studies, we also present estimates based on conventional capture–recapture models. The statistical test for population closure of Stanley and Burnham (1999) is conducted with the program CloseTest 3 (Stanley and Richards 2005) and with P = 0.20 supports our assumption that the sampled population is closed (P > 0.05) for the study interval. We use the software MARK 5.1 (White and Burnham 1999) to estimate lynx abundance. The module CAPTURE tests several models that differ in their assumed sources of variation in encounter probability, including: constant encounter probability (M0); variation among individuals (Mh); variation across occasions (Mt); and responses to previous encounters (Mb). It selects the ‘best’ model from a set of eight closed-population models (M0, Mh, Mt, Mb, Mbh, Mth, Mtb and Mtbh; Otis et al. 1978). The overall model selection function scores potential models between 0.0 and 1.0, with a higher score indicating a better relative fit of the model to the specific encounter history data generated by the survey. The heterogeneity model Mh with a score of 1.0 fit our data best. Using the jackknife estimator, the module CAPTURE in MARK estimates the population size (SE) at 25 (3.41) independent lynx, with average encounter probability per sampling occasion of 0.32, yielding a density (SE) of 1.29 (0.19) independent lynx per 100 km2 when a buffer (SE) of 5,829 (664) m based on 1/2MMDM is added to the polygon delimiting the most peripheral camera trap sites (Figure 7.1). The calculation of 1/2MMDM is provided in the sheet ‘distance Pythagoras calculation’ in the Excel file ‘NWA_2013_14_Lynx_encounter_histories.xls’. Following Karanth and Nichols (1998), we use the delta method to calculate the variance of the density estimates. The formula is provided in the sheet ‘options’ in the same Excel file. When only the suitable lynx habitat within the area effectively sampled (polygon plus buffer) is considered, the resulting density (SE) is 1.49 (0.22) independent lynx per 100 km2 suitable habitat.
7.5Conclusions
This chapter has addressed the use of camera trapping to estimate the abundance and density of species with natural marks using spatially explicit and conventional capture–recapture models. We first explained that a monitoring programme for abundance estimation should be tuned to the larger conservation programme that those estimates are intended to serve (Nichols 2014). Then, we describe the steps to select an appropriate sampling area. After that, we discussed survey design considerations (i.e. season, survey duration and spatial sampling) and model assumptions (demographic and geographic closure) of conventional (i.e. non-spatial) capture–recapture and SCR models. Because the latter consider animal movement explicitly (through the parameter σ), they circumvent the problem of estimating the area effectively sampled (inherent to the conventional capture–recapture models) and allow for the estimation of quantities other than density, such as home range size and space usage (Royle et al. 2014). In addition, SCR models are able to make predictions across unobserved distances, even to non-sampled areas. This allows for completely new and much more flexible study designs when compared to conventional capture–recapture models. Moreover, SCR models work well in study areas similar in size to the home range of an individual, which makes them particularly suitable for species with large home ranges occurring at low densities (Sollmann et al. 2012). However, these results should not encourage investigators to choose suboptimal sampling strategies (Royle et al. 2014). Large amounts of data in terms of number of individuals detected and numbers of re-encounters do not only improve the precision of parameter estimates (Sollmann et al. 2012) but also allow for the inclusion of potentially important covariates (e.g. sex and behaviour effects) in SCR models as illustrated by the Eurasian lynx case study. We also stressed that compared to conventional (i.e. non-spatial) capture–recapture models a number of assumptions are relaxed in SCR models. These models also allow these assumptions to be extended in many different ways, e.g. to handle open populations (Royle et al. 2014).
In the case study of Eurasian lynx abundance and density estimation, we highlighted that it is important to track the sampling effort and number of different lynx detected over the course of the sampling and not only at the end. This enables us to recognise if the survey is running properly and potentially modify it. We then showed how to prepare the different input files for secr and fit different likelihood-based SCR models with and without covariates on the baseline encounter probability g0 and the parameter σ. Furthermore, we explained how to construct a mask in order to provide density estimates that take into account only suitable lynx habitats. We finally provided density estimates for all habitats and suitable lynx habitats only using the SCR and conventional capture–recapture models.
The ongoing development of SCR modelling is not merely an extension of previous approaches but also provides a flexible framework for making ecological processes explicit in models of individual encounter history data, and for studying spatial processes such as individual movement, resource selection, space usage, population dynamics and density (Royle et al. 2014).
Appendices
Appendix 7.1 NWA 2013_2014_eff_trap_nights.xls (accumulated trap nights by camera traps and sites)
Appendix 7.2 NWA_2013_14_Lynx_encounter_histories.xls (number of different individuals and cumulative encounters)
Appendix 7.3 Dates and times in R.R (R script used for the data preparation)
Appendix 7.4 Lynx_data.txt (dataset containing all the photographs of lynx taken in our study area)
Appendix 7.5 Sites.txt (table with the coordinates of all sites)
Appendix 7.6 Trapnights.txt (table about the trap deployment details)
Appendix 7.7 suitable_habitat_secr.zip (shapefile of the suitable lynx habitat)
Appendix 7.8 Chapter 7.R (R script for running all the analyses with the package secr)
Appendix 7.9 Chapter_7.RData (R file containing the results)
Acknowledgements
We are grateful to Simone Tenan and Francesco Rovero for valuable comments on previous versions of this chapter, Murray Efford for his help regarding some issues with the R package secr and Brett McClintock for providing useful information regarding methods of analysis that account for misidentifications and bilateral photo-identification.
References
Ancrenaz, M., Hearn, A.J., Ross, J., Sollmann R. and Witting, A. (2012) Handbook for Wildlife Monitoring Using Camera-traps. BBEC II Secretariat, c/o Natural Resources Office, Chief Minister’s Department, Kota Kinabalu, Sabah, Malaysia.
Ariefiandy, A., Purwandana, D., Seno, A., Ciofi, C. and Jessop, T.S. (2013) Can camera traps monitor Komodo Dragons a large ectothermic predator? PLoS ONE 8: e58800.
Balme, G., Hunter, L. and Robinson, H. (2014) Baited camera-trap surveys – marginally more precise but at what cost? A response to du Preez et al. (2014). Biological Conservation 179: 144–145.
Barber-Meyer, S.M., Jnawali, S.R., Karki, J.B., Khanal, P., Lohani, S., Long, B., MacKenzie, D.I., Pandav, B., Pradhan, N.M.B., Shrestha, R., Subedi, N., Thapa, G., Thapa, K. and Wikramanayake, E. (2013) Influence of prey depletion and human disturbance on tiger occupancy in Nepal. Journal of Zoology 289: 10–18.
Bashir, T., Bhattacharya, T., Poudyal, K., Sathyakumar, S. and Qureshi, Q. (2013) Estimating leopard cat Prionailurus bengalensis densities using photographic captures and recaptures. Wildlife Biology 19: 462–472.
Bendik, N.F., Morrison, T.A., Gluesenkamp, A.G., Sanders, M.S. and O’Donnell, L.J. (2013) Computer-assisted photo identification outperforms visible implant elastomers in an endangered salamander, Eurycea tonkawae. PLoS ONE 8: e59424.
Bolger, D.T., Morrison, T.A., Vance, B., Lee, D. and Farid, H. (2012) A computer-assisted system for photographic mark–recapture analysis. Methods in Ecology and Evolution 3: 813–822.
Bondrup-Nielsen, S. (1983) Density estimation as a function of live-trapping grid and home range size. Canadian Journal of Zoology 61: 2361–2365.
Borchers, D.L., Buckland, S.T. and Zucchini, W. (2002) Estimating Animal Abundance: Close Populations. London: Springer.
Borchers, D., Distiller, G., Foster, R., Harmsen, B. and Milazzo, L. (2014) Continuous-time spatially explicit capture–recapture models, with an application to a jaguar camera-trap survey. Methods in Ecology and Evolution 5: 656–665.
Braczkowski, A. (2013) The susceptibility of leopards (Panthera pardus) to trophy hunting. MSc thesis, University of Oxford.
Breitenmoser, U. and Breitenmoser-Würsten, C. (2008) Der Luchs: Ein Grossraubtier in der Kulturlandschaft. Wohlen Bern: Salm Verlag (in German).
Breitenmoser-Würsten, C., Zimmermann, F., Ryser, A., Capt, S., Laass, J., Siegenthaler, A. and Breitenmoser, U. (2001) Untersuchungen zur Luchspopulation in den Nordwestalpen der Schweiz 1997–2000. KORA-Report 9. pp. 88 (in German; summary, tables and figures in English and French).
Burnham, K.P. and Anderson, D.R. (2002) Model Selection and Multimodel Inference: A Practical Information-theoretic Approach, 2nd edn. New York: Springer.
Carbone, C., Christie, S., Conforti, K., Coulson, T., Franklin, N., Ginsberg, J.R., Griffiths, M., Holden, J., Kawanishi, K., Kinnaird, M., Laidlaw, R., Lynam, A., Macdonald, D.W., Martyr, D., McDougal, C., Nath, L., O’Brien, T., Seidensticker, J., Smith, D.J.L., Sunquist, M., Tilson, R. and Wan Shahruddin, W.N. (2001) The use of photographic rates to estimate densities of tigers and other cryptic mammals. Animal Conservation 4: 75–79.
Chandler, R.B. and Royle, A.J. (2013) Spatially-explicit models for inference about density in unmarked populations. Annals of Applied Statistics 7: 936–954.
Chandler, R.B. and Clark, J.D. (2014) Spatially explicit integrated population models. Methods in Ecology and Evolution 5: 1351–1360.
Cochran, W.G. (1977) Sampling Techniques, 3rd edn. New York: John Wiley.
Dillon, A. and Kelly, M.J. (2007) Ocelot activity, trap success and density in Belize: the impact of trap spacing and animal movement on density estimates. Oryx 41: 469–477.
Dillon, A. and Kelly, M.J. (2008) Ocelot home range, overlap and density: comparing radio-telemetry with camera-trapping. Journal of Zoology 275: 391–398.
du Preez, B.D, Loveridge, A.J. and Macdonald, D.W. (2014) To bait or not to bait: a comparison of camera-trapping methods for estimating leopard Panthera pardus density. Biological Conservation 176: 153–161.
Efford, M.G. (2004) Density estimation in live-trapping studies. Oikos 10: 598–610.
Efford, M.G. (2014) Finite mixture models in ‘secr’ 2.9. SECR in R http://www.otago.ac.nz/density/SECRinR.html
Efford, M.G. (2015) Package ‘secr’. The comprehensive R archive network http://cran.r-project.org/
Efford, M.G. and Fewster, R.M. (2013) Estimating population size by spatially explicit capture–recapture. Oikos 122: 918–928.
Efford, M.G., Warburton, B., Coleman, M.C. and Barker, R.J. (2005) A field test of two methods for density estimation. Wildlife Society Bulletin 33: 731–738.
Efford, M.G., Borchers, D.L. and Byrom, A.E. (2009) Density estimation by spatially explicit capture–recapture: likelihood-based methods. In: D.L. Thomson, E.G. Cooch and M.J. Conroy (eds), Modeling Demographic Processes in Marked Populations. New York: Springer. pp. 255–269.
Ergon, T. and Gardner, B. (2014) Separating mortality and emigration: modelling space use, dispersal and survival with robust-design spatial capture–recapture data. Methods in Ecology and Evolution 5: 1327–1336.
Foster, R.J. and Harmsen, B.J. (2011) A critique of density estimation from camera-trap data. Journal of Wildlife Management 76: 224–236.
Gardner, B., Reppucci, J., Lucherini, M. and Royle, J.A. (2010a) Spatially explicit inference for open populations: estimating demographic parameters from camera-trap studies. Ecology 91: 3376–3383.
Gardner, B., Royle, J.A., Wegan, M. T., Rainbolt, R.E. and Curtis, P.D. (2010b) Estimating black bear density using DNA data from hair snares. Journal of Wildlife Management 74: 318–325.
Garrote, G., Perez de Ayala, R., Pereira, P., Robles, F., Guzman, N., García, F., Iglesias, M.C., Hervás, J., Fajardo, I., Simón, M. and Barroso, J.L. (2011) Estimation of the Iberian lynx (Lynx pardinus) population in the Doñana area, SW Spain, using capture–recapture analysis of camera-trapping data. European Journal of Wildlife Research 57: 355–362.
Garrote, G., Gil-Sánchez, J.M., McCain, E.B., de Lillo, S., Tellería, J.L. and Simón, M.A. (2012) The effect of attractant lures in camera trapping: a case study of population estimates for the Iberian lynx (Lynx pardinus). European Journal of Wildlife Research 58: 881−884.
Gerber, B., Karpanty, S.M., Crawford, C., Kotschwar, M. and Randrianantenaina, J. (2010) An assessment of carnivore relative abundance and density in the eastern rainforests of Madagascar using remotely-triggered camera traps. Oryx 44: 219–222.
Gerber, B.D., Karpanty, S.M. and Kelly, M.J. (2012) Evaluating the potential biases in carnivore capture–recapture studies associated with the use of lure and varying density estimation techniques using photographic-sampling data of the Malagasy civet. Population Ecology 54: 43−54.
Gopalaswamy, A.M., Royle, J.A., Hines, J.E., Singh, P., Jathanna, D., Kumar, N.S. and Karanth, K.U. (2012) Program SPACECAP: software for estimating animal density using spatially explicit capture-recapture models. Methods in Ecology and Evolution 3: 1067–1072.
Goswami, V.R., Lauretta, M.V., Madhusudan, M.D. and Karanth, K.U. (2012) Optimizing individual identification and survey effort for photographic capture–recapture sampling of species with temporally variable morphological traits. Animal Conservation 15: 174–183.
Harihar, A., Ghosh, M., Fernandes, M., Pandav, B. and Goyal, S.P. (2010) Use of photographic capture–recapture sampling to estimate density of striped hyena (Hyaena hyaena): implications for conservation. Mammalia 74: 83–87.
Hedges, L., Lam, W.Y., Campos-Arceiz, A., Rayan, D.M., Laurance, W.F., Latham, C.J., Saaban, S. and Clements, G.R. (2015) Melanistic leopards reveal their spots: infrared camera traps provide a population density estimate of leopards in Malaysia. Journal of Wildlife Management 79: 846–853.
Hiby, L., Lovell, P., Patil, N., Kumar, S.N., Gopalaswamay, A.M. and Karanth, K.U. (2009) A tiger cannot change its stripes: using a three-dimensional model to match images of living tigers and tiger skins. Biology Letters 5: 383–386.
Higashide, D., Miura, S. and Miguchi, H. (2012) Are chest marks unique to Asiatic black bear individuals? Journal of Zoology 288: 199–206.
Hwang, W., Chao, A. and Yip, P. (2002) Continuous-time capture–recapture models with time variation and behavioural response. Australian and New Zealand Journal of Statistics 44: 41–54.
Janecka, J.E., Munkhtsog, B., Jackson, R.M., Naranbaatar, G., Mallon, D.P. and Murphy, W.J. (2011) Comparison of non-invasive genetic and camera-trapping techniques for surveying snow leopards. Journal of Mammalogy 92: 771–783.
Jobin, A., Molinari, P. and Breitenmoser, U. (2000) Prey spectrum, prey preference and consumption rates of Eurasian lynx in the Swiss Jura Mountains. Acta Theriologica 45: 243–252.
Johnson, D.S., Laake, J.L. and Ver Hoef, J.M. (2010) A model-based approach for making ecological inference from distance sampling data. Biometrics 66: 310–318.
Karanth, K.U. (1995) Estimating tiger Panthera tigris populations from camera-trap data using capture–recapture models. Biological Conservation 71: 333–336.
Karanth, K.U. and Nichols, J.D. (1998) Estimation of tiger densities in India using photographic captures and re-captures. Ecology 79: 2852–2862.
Karanth, K.U. and Nichols, J.D. (2002) Monitoring Tigers and Their Prey: A Manual for Researchers, Managers and Conservationists in Tropical Asia. Bangalore, Karnataka: Center for Wildlife Studies.
Karanth, K.U., Nichols, J.D., Kumar, N.S. and Hines, J.E. (2006) Assessing tiger population dynamics using photographic capture–recapture sampling. Ecology 87: 2925–2937.
Karanth, K.U., Gopalaswamy, A.M., Kumar, N.S., Vaidyanathan, S., Nichols, J.D. and MacKenzie, D.I. (2011a) Monitoring carnivore populations at the landscape scale: occupancy modelling of tigers from sign surveys. Journal of Applied Ecology 48: 1048–1056.
Karanth, K.U., Nichols, J.D. and Kumar, S.N. (2011b) Estimating tiger abundance from camera trap data: field surveys and analytical issues? In: A.F. O’Connell, J.D. Nichols and K.U. Karanth (eds), Camera Traps in Animal Ecology Methods and Analyses. New York: Springer. pp. 97–117.
Kelly, M.J. (2001) Computer-aided photograph matching in studies using individual identification: an example from Serengeti cheetahs. Journal of Mammalogy 82: 440–449.
Kelly, M.J., Noss, A.J., Di Bitetti, M.S., Maffei, L., Arispe, R., Paviolo, A., de Angelo, C.D. and Di Blanco, Y.E. (2008) Estimating puma densities from camera trapping across three study sites: Bolivia, Argentina, Belize. Journal of Mammalogy 89: 408–418.
Kendall, W.L. (1999) Robustness of closed capture–recapture methods to violations of the closure assumption. Ecology 80: 2517–2525.
Kendall, W.L., Pollock, K.H. and Brownie, C. (1995) A likelihood-based approach to capture–recapture estimation of demographic parameters under the robust design. Biometrics 51: 293–308.
Kendall, W.L., Nichols, J.D. and Hines, J.E. (1997) Estimating temporary emigration using capture–recapture data with Pollock’s robust design. Ecology 78: 563–578.
Krijger, H. (2002) Individual zebra identification: an investigation into image pre-processing, stripe extraction and pattern matching techniques. Unpublished thesis, Rhodes University, Grahamstown, South Africa.
Lamigueiro, O.P. (2015) Package ‘solaR’. The comprehensive R archive network http://cran.r-project.org/
Link, W.A., Yoshizaki, J., Bailey, L.L. and Pollock, K.H. (2010) Uncovering a latent multinomial: Analysis of mark-recapture data with misidentification. Biometrics 66: 178–185.
Maffei, L. and Noss, A. (2008) How small is too small? Camera-trap survey areas and density estimates for ocelots in the Bolivian Chaco. Biotropica 40: 71–75.
Marques, T.A., Thomas, L. and Royle, J.A. (2011) A hierarchical model for spatial capture–recapture data: comment. Ecology 92: 526–528.
Marucco, F., Pletscher, D.H., Boitani, L., Schwartz, M.K., Pilgrim, K.L. and Lebreton, J.-D. (2009) Wolf survival and population trend using non-invasive capture–recapture techniques in the Western Alps. Journal of Applied Ecology 46: 1003–1010.
McClintock, B.T. (2015) Multimark: an R package for analysis of capture-recapture data consisting of multiple ‘noninvasive’ marks. Ecology and Evolution 5: 4920–4931.
McClintock, B.T., White, G.C. and Burnham, K.P. (2006) A robust design mark-resight abundance estimator allowing heterogeneity in resighting probabilities. Journal of Agricultural, Biological, and Environmental Statistics 11: 231–248.
McClintock, B.T., White, G.C., Antolin, M.F. and Tripp, D.W. (2009a) Estimating abundance using mark–resight when sampling is with replacement or the number of marked individuals is unknown. Biometrics 65: 237–246.
McClintock, B.T., White, G.C., Burnham, K.P. and Pryde, M.A. (2009b) A generalized mixed effects model of abundance for mark-resight data when sampling is without replacement. In: D.L. Thomson, E.G. Cooch and M.J. Conroy (eds), Modeling Demographic Processes in Marked Populations. New York: Springer. pp. 271–289.
McClintock, B.T., Conn, P.B., Alonso, R.S. and Crooks, K.R. (2013) Integrated modeling of bilateral photo-identification data in mark-recapture analyses. Ecology 94: 1464–1471.
McClintock, B.T., Bailey, L.L., Dreher, B.P. and Link, W.A. (2014) Probit models for capture–recapture data subject to imperfect detection, individual heterogeneity and misidentification. Annals of Applied Statistics 8: 2461–2484.
Mills, L.S., Citta, J.J., Lair, K.P., Schwartz, M.K. and Tallmon, D.A. (2000) Estimating animal abundance using noninvasive DNA sampling: promise and pitfalls. Ecological Application 10: 283–294.
Molinari-Jobin, A., Molinari, P., Breitenmoser-Würsten, C., Wölfl, M., Stanisa, C., Fasel, M., Stahl, P., Vandel, J.M., Rotelli, L., Kaczensky, P., Huber, T., Adamic, M. and Breitenmoser, U. (2003) Pan-Alpine conservation strategy for lynx. Nature and Environment 130: 1–20.
Moya, O., Mansilla, P.-L., Madrazo, S., Igual, J.-S., Rotger, A., Romano, A. and Tavecchia, G. (2015) APHIS: A new software for photo-matching in ecological studies. Ecological Informatics 27: 64−70.
Mulders, R., Boulanger, J. and Paetkau, D. (2007) Estimation of population size for wolverines Gulo gulo at Daring Lake, Northwest Territories, using DNA based mark-recapture methods. Wildlife Biology 13: 38–51
Negrões, N., Sollmann, R., Fonseca, C., Jácomo, A.T.A., Revilla, E. and Silveira, L. (2012) One or two cameras per station? Monitoring jaguars and other mammals in the Amazon. Ecological Research 27: 639–648.
Nichols, J.D. (2014) The Role of abundance estimates in conservation decision-making. In: L.M. Verdade, M.C. Lyra-Jorge and C.I. Pina (eds), Applied Ecology and Human Dimensions in Biological Conservation. Berlin: Springer. pp. 117–131.
Nichols, J.D. and Williams, B.K. (2006) Monitoring for conservation. Trends in Ecology and Evolution 21: 668–673.
Noss, A.J., Cuéllar, R.L., Barrientos, J., Maffei, L., Cuéllar, E., Arispe, R., Rúmiz, D. and Rivero, K. (2003) A camera trapping and radio telemetry study of lowland tapir (Tapirus terrestris) in Bolivian dry forests. Tapir Conservation 12: 24–32.
O’Brien, T.G. (2011) Abundance, Density and relative abundance: a conceptual framework. In: A.F. O’Connell, J.D. Nichols and K.U. Karanth (eds), Camera Traps in Animal Ecology Methods and Analyses. New York: Springer. pp. 71–96.
Oliveira-Santos, L.G.R., Zucco, C.A., Antunes, P.C. and Crawshaw, P.G. (2010) Is it possible to individually identify mammals with no natural markings using camera-traps? A controlled case-study with lowland tapirs. Mammalian Biology 75: 375–378.
Otis, D.L., Burnham, K.P., White, G.C. and Anderson, D.R. (1978) Statistical inference from capture data on closed animal populations. Wildlife Monograph 62: 1–135.
Parmenter, R.R, Yates, T.L., Anderson, D.R., Burnham, K.P., Dunnum, J.L., Franklin, A.B., Friggens, M.T., Lubow, B.C., Miller, M., Olson, G.S., Parmenter, C.A., Pollard, J., Rexstad, E., Shenk, T.M., Stanley, T.R. and White, G.C. (2003) Small-mammal density estimation: a field comparison of grid-based vs. web-based density estimators. Ecological Monographs 73:1–26.
Pesenti, E. and Zimmermann, F. (2013) Density estimations of Eurasian lynx (Lynx lynx) in the Swiss Alps. Journal of Mammalogy 94: 73–81.
Pollock, K.H., Nichols, J.D., Brownie, C. and Hines, J.E. (1990) Statistical inference for capture–recapture experiments. Wildlife Monographs 107: 1–97.
Ríos-Uzeda, B., Gómez, H. and Wallace, R.B. (2007) A preliminary density estimate for Andean bear using camera-trapping methods. Ursus 18: 124–128.
Rowcliffe, J.M., Field, J., Turvey, S.T. and Carbone, C. (2008) Estimating animal density using camera traps without the need for individual recognition. Journal of Applied Ecology 45: 1228–1236.
Royle, J.A. (2004) N-mixture models for estimating population size from spatially replicated counts. Biometrics 60: 108–115.
Royle, J.A. and Nichols, J.D. (2003) Estimating abundance from repeated presence– absence data or point counts. Ecology 84: 777–790.
Royle, J.A., Karanth, K.U., Gopalaswamy, A.M. and Kumar, N.S. (2009a) Bayesian inference in camera-trapping studies for a class of spatial capture–recapture models. Ecology 90: 3233–3244.
Royle, J.A., Nichols, J.D., Karanth, K.U. and Gopalaswamy, A.M. (2009b) A hierarchical model for estimating density in camera-trap studies. Journal of Applied Ecology 46: 118–127.
Royle, J.A., Magoun, A.J., Gardner, B., Valkenburg, P. and Lowell, R.E. (2011) Density estimation in a wolverine population using spatial capture–recapture models. Journal of Wildlife Management 75: 604–611.
Royle, J.A., Chandler, R.B., Sollmann, R. and Gardner, B. (2014) Spatial Capture–Recapture. Waltham, MA: Academic Press.
Russell, C., Van Horn, R.C., Zug, B., LaCombe, C., Velez-Liendo, X. and Paisley, S. (2014) Human visual identification of individual Andean bears Tremarctos ornatus. Wildlife Biology 20: 291–299.
Sarmento, P., Cruz, J., Eira, C. and Fonseca, C. (2010) Habitat selection and abundance of common genets Genetta genetta using camera capture–recapture data. European Journal of Wildlife Research 56: 59–66.
Schofield, M.R. and Bonner, S.J. (2015) Connecting the latent multinomial. Biometrics 71: 1070–1080.
Schwarz, C.J. and Seber, G.A.F. (1999) Estimating animal abundance: review III. Statistical Science 14: 427–456.
Seber, G.A.F. (1982) The Estimation of Animal Abundance and Related Parameters. New York: Macmillan.
Silver, S.C., Ostro, L.E., Marsh, L.K., Maffei, L., Noss, A.J., Kelly, M.J., Wallace, R.B., Gómez, H. and Ayala, G. (2004) The use of camera-traps for estimating jaguar Panthera onca abundance and density using capture/recapture analysis. Oryx 38: 148–154.
Singh, P., Gopalaswamy, A.M. and Karanth, K.U. (2010) Factors influencing densities of striped hyenas in arid regions of India. Journal of Mammalogy 91: 1152–1159.
Soisalo, M.K. and Cavalcanti, S.M.C. (2006) Estimating the density of a jaguar population in the Brazilian Pantanal using camera-traps and capture–recapture sampling in combination with GPS radio-telemetry. Biological Conservation 129: 487–496.
Sollmann, R., Gardner, B. and Belant, J.L. (2012) How does spatial study design influence density estimates from spatial capture–recapture models? PLoS ONE 7: e34575.
Sollmann, R., Mohamed, A., Samejima, H. and Wilting, A. (2013) Risky business or simple solution – relative abundance indices from camera-trapping. Biological Conservation 159: 405–412.
Stanley, T.R. and Burnham, P.K. (1999) A closure test for time-specific capture–recapture data. Environmental and Ecological Statistics 6: 197–209.
Stanley, T.R. and Richards, J.D. (2005) Software review: a program for testing capture–recapture data for closure. Wildlife Society Bulletin 33: 782–785.
Sun, C.C., Fuller, A.K. and Royle, J.A. (2014) Trap configuration and spacing influences parameter estimates in spatial capture–recapture models. PLoS ONE 9: e88025.
Tenan, S., Vallespir, A.R., Igual, J.M., Moya, O., Royle, J.A. and Tavecchia, G. (2013) Population abundance, size structure and sex-ratio in an insular lizard. Ecological Modelling 267: 39–47.
Thomas, P., Balme, G., Hunter, L. and McCabe-Parodi, J. (2005) Using scent attractants to non-invasively collect hair samples from cheetahs leopards and lions. Animal Keepers Forum 7/8: 342–384.
Thompson, S.K. (2012) Sampling, 3rd edn. New York: Wiley.
Thorn, M., Scott, D.M., Green, M., Bateman, P.W. and Cameron, E.Z. (2009) Estimating brown hyena occupancy using baited camera traps. South African Journal of Wildlife Research 39: 1–10.
Trolle, M. and Kéry, M. (2003) Ocelot density estimation in the Pantanal using capture–recapture analysis of camera-trapping data. Journal of Mammalogy 84: 607–614.
Trolle, M., Noss, A.J., Lima, E.D.S. and Dalponte, J.C. (2007) Camera-trap studies of maned wolf density in the Cerrado and the Pantanal of Brazil. Biodiversity and Conservation 16: 1197–1204.
Vogt, K., Zimmermann, F., Kölliker, M. and Breitenmoser, U. (2014) Scent-marking behaviour and social dynamics in a wild population of Eurasian lynx Lynx lynx. Behavioural Processes 106: 98–106.
Wegge, P. and Storaas, T. (2009) Sampling tiger ungulate prey by the distance method: lessons learned in Bardia National Park, Nepal. Animal Conservation 12: 78–84.
Wegge, P., Pokheral, C.P. and Jnawali, S.R. (2004) Effects of trapping effort and trap shyness on estimates of tiger abundance from camera trap studies. Animal Conservation 7: 251–256.
White, G.C. (1996) NOREMARK: population estimation from mark–resighting surveys. Wildlife Society Bulletin 24: 50–52.
White, G.C. and Burnham, K.P. (1999) Program MARK: survival estimation from populations of marked animals. Bird Study 46: 120–138.
White, G.C., Anderson, D.R., Burnham, K.P. and Otis, D.L. (1982) Capture Recapture and Removal Methods for Sampling Closed Populations. Los Alamos, NM: Los Alamos National Laboratory Publication LA-8787-NERP.
Williams, B.K., Nichols, J.D. and Conroy, M.J. (2002) Analysis and Management of Animal Populations. San Diego: Academic Press.
Wilson, K.R. and Anderson, D.R. (1985) Evaluation of a density estimator based on a trapping web and distance sampling theory. Ecology 66: 1185–1194.
Wilton, C.M., Puckett, E.E., Beringer, J., Gardner, B., Eggert, L.S. and Belant, J.L. (2014) Trap array configuration influences estimates and precision of black bear density and abundance. PLoS ONE 9: e111257.
Yoshizaki, J., Pollock, K.H., Brownie, C. and Webster, R.A. (2009) Modeling misidentification errors in capture–recapture studies using photographic identification of evolving marks. Ecology 90: 3–9.
Zimmermann, F. (2004) Conservation of the Eurasian lynx (Lynx lynx) in a fragmented landscape – habitat models, dispersal and potential distribution. PhD thesis, University of Lausanne.
Zimmermann, F., Molinari-Jobin, A., Ryser, A., Breitenmoser-Würsten, Ch., Pesenti, E. and Breitenmoser, U. (2011) Status and distribution of the lynx (Lynx lynx) in the Swiss Alps 2005–2009. Acta Biologica Slovenica 54: 74–84.
Zimmermann, F., Breitenmoser-Würsten, C., Molinari-Jobin, A. and Breitenmoser, U. (2013) Optimizing the size of the area surveyed for monitoring a Eurasian lynx (Lynx lynx) population in the Swiss Alps by means of photographic capture recapture. Integrative Zoology 8: 232–243.
Zimmermann, F., Foresti, D., Bach, J., Dulex, N., Breitenmoser-Würsten, Ch. and Breitenmoser, U. (2014) Abundanz und Dichte des Luchses in den Nordwestalpen: Fang-Wiederfang-Schätzung mittels Fotofallen im K-VI im Winter 2013/14. KORA-Report 64. pp. 16 (in German with English abstract).
1 The session started when all sites were set and stopped when the first sites were removed from the field
























