

The history of mathematics was not confined to Europe. China, India and the countries of the Middle East each have a tradition rich in the subject, and the flow of mathematical knowledge was, generally speaking, from East to West. As Europe found itself plunged into the Dark Ages, mathematical discoveries in the East ensured the subject continued to go from strength to strength.
CHINESE MATHEMATICS
Chinese history is populated by dynasties – a succession of ruling families, each of whom prioritized eradicating all evidence of the previous incumbent. As such, many important Chinese mathematical works and artefacts have been lost over time.
Much of what we know about Chinese mathematics is attributed to a scholar and bureaucrat called Qin Jiushao (1202–61). He wrote a book called Mathematical Treatise in Nine Sections that discusses practical mathematics in a variety of fields relevant to government officials. Jiushao’s book also contains a detailed history of Chinese mathematics, and sheds light on the country’s mathematicians and their advances in the field.
It All Adds Up
Chinese numbers were based on a system of counting rods: short sticks that, when placed in certain arrangements, denoted various numbers in a decimal system. Their written numerals were simply drawings of the arrangement of these sticks.
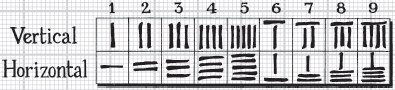
In c. AD 700 the Chinese borrowed the concept of zero from India (see here), which means they were one of the first cultures to have a fully fledged decimal number system.
The I Ching (Book of Changes) is a famous Chinese text that dates from, at the very least, c. 1000 BC, and quite possibly before then. The text allows you to divine your future using trigrams and hexagrams, both of which have their origins in mathematics.
A trigram is a stack of three horizontal lines, which can be either yang (solid) or yin (broken). It is possible to make eight different trigrams using this system, and each trigram has various attributed meanings, including the Chinese elements: earth, mountain, thunder, water, lake, wind, heaven and fire.

Two trigrams could be combined to make a hexagram, and there are 64 (8×8) possible hexagrams to be made from the eight trigrams – which could then be used to predict your future. Soothsayers would need to be familiar with the interpretations of each trigram and hexagram in order to use them to build up your reading.
The German philosopher Gottfried Leibniz (see here) was intrigued by Chinese philosophy and noticed that the trigrams and hexagrams of the I Ching can be written as binary numbers – a system of numbers that has 2 rather than 10 as its base – if the yang is seen as 1 and the yin as 0.

Leaps and bounds
Zu Chongzhi (AD 429–500) was a Chinese astronomer and mathematician whose discoveries lay far ahead of his time. Chongzhi calculated various astronomical constants to extremely high degrees of precision; he also worked out independently a value for π using Archimedes’ method of exhaustion on a polygon with over 12,000 sides. His answer gave a working value of 355/133, which is accurate to six decimal places (see here). Europe would not achieve this level of precision for over 1,000 years.
The Nine Chapters on the Mathematical Art is one of the oldest and most important Chinese mathematical works, compiled over the centuries up to c. AD 100. It gives us a very good idea of the state of Chinese mathematics that existed at approximately the same time as Greek civilization. The chapters covered the following topics:
While the Chinese may have been more concerned than the Greeks with practical matters, we can see that their development in mathematics was on a par.
Court eunuch Jia Xian (AD 1010–70) is credited with being the first individual to investigate what later became known in Europe as Pascal’s triangle (see here). Chinese mathematician Yang Hui (AD 1238–98) published Xian’s findings in 1261, four hundred years before Pascal’s discoveries would be revealed. Xian was also interested in what we call magic squares, which had long fascinated Chinese mathematicians. A magic square is a square of numbers in which all the rows, columns and diagonals add up to a particular number. For example:

In the example above, each row, column and diagonal has a sum of 15. This particular magic square is known as the Lo Shu square because of its connection to a legend in which the River Lo floods and a magic turtle carries the magic square on its shell to aid the afflicted people.
The Chinese Abacus
At some point in c. AD 1000 the Chinese began to use the suanpan (Chinese abacus) in favour of the counting rods, although the suanpan had been around for some time and may have influenced the abacus in the West.
This particular abacus has counters suspended on rods, which are layered on two decks. On the lower deck there are five beads per rod, each of which is worth one; on the top deck there are two beads, each worth five. Each rod represents a decimal column (unit, tens, hundreds, etc.) and pushing the beads towards the separator in the middle signifies the number. For example, 123,456 would look something like this:

The extra bead on each deck can be used for performing calculations.
In 1920 archaeological excavations in north-western India unearthed the Indus Valley civilization, which existed from c. 3500 BC to 2000 BC. These Bronze Age settlements, contemporary to the first urban areas in Egypt and Mesopotamia, indicated the Ancient Indians had a good understanding of basic mathematical concepts, and possessed a standardized system of weights and measures.
Ancient Indian religious texts also contain evidence of mathematical knowledge; in Hinduism, mathematics, astronomy and astrology were considered to be in the same field, and they each had important religious implications. It was a religious requirement that all altars should occupy the same amount of floor space, even if they weren’t the same shape or used different configurations of bricks – all of which required a good knowledge of geometry. Texts from 700 BC show the Ancient Indians possessed knowledge of Pythagoras’ theorem, irrational numbers and methods for calculating them.
Astronomical discoveries
Brahmagupta (AD 598–668), an astronomer, was the first person to treat zero as a number. The Hindu numeral system, predecessor to the Hindu-Arabic numeral system that we use today (see here), developed over time and was fully established by the end of the first millennium AD. Up until Brahmagupta’s treatment of zero as a number, it had been used merely as a place-holder within various number systems in order to show a gap. Brahmagupta, however, thought of 0 simply as a whole number or integer that lies between 1 and -1. He wrote down rules for its use in arithmetic, alongside rules for using negative numbers.
Useful Functions
Aryabhata (AD 475–550) was an astronomer who is credited with being the first person to introduce trigonometry, which we use to work out lengths and angles in triangles, and the concept of the sine, cosine and tangent functions.
Brahmagupta recognized that an equation could have a negative solution and, as a result, that any positive integer would have a positive and negative square root. For example, the square roots of 36 are 6 and -6, because, as Brahmagupta himself stated, a negative multiplied by a negative gives a positive.
Brahmagupta is also famous for developing Brahmagupta’s formula, which tells us the area of a cyclic quadrilateral – a four-sided shape, the corners of which lie on a circle:

Srinvasa Ramanujan (1887–1920) was an Indian mathematical genius. After dropping out of university, he became an accounting clerk at a government office, from where he sent papers to various British mathematicians for consideration. The English mathematician Godfrey Hardy (1877–1947) recognized Ramanujan’s genius and arranged for him to have a research post at the University of Madras.
In 1914 Ramanujan joined Hardy at Cambridge University and remained in England for five years, in which time he became one of the youngest ever members of the Royal Society, had work published and finally gained a degree. However, Ramanujan was often ill.
During one bout of illness, Hardy visited him and mentioned that the number of his taxi, 1729, was ‘rather dull’. Ramanujan replied instantly that 1,729 was the lowest number that could be written as the sum of two cubes in two different ways, and as such, was actually quite interesting:
13 + 123 = 1 + 1728 = 1729
93 + 103 = 729 + 1000 = 1729
There are lower numbers that can be written as the sum of two cubes, but 1,729 is the lowest number that can be written like this in two ways, and Ramanujan’s instant recognition of this was nothing short of miraculous.
In his short life Ramanujan came up with nearly 4,000 theorems, equations and identities that still inspire mathematical research to this day.
If you find half the perimeter of the quadrilateral (let’s call it ‘s’) then the area of the shape can be found using Brahmagupta’s formula:
√(s-a)(s-b)(s-c)(s-d)
Although the Indians were clearly excellent mathematicians, when the British began to take control of the country in the 1700s they assumed the backward pagan Hindus had nothing of worth to contribute beyond vast natural resources and cheap labour. It has only been in the last hundred years that we have come to appreciate the mathematical heritage of the sub-continent.
ISLAMIC MATHEMATICS
Mohammed, the founder of Islam, was born in AD 570. In the two centuries following Mohammed’s birth the Islamic Empire came to dominate all of the Middle East, Central Asia, North Africa and what would become Spain and Portugal. This Islamic Golden Age saw much important mathematical progress emerge from the countries in the empire, while Europe remained still in its Dark Ages.
The Islamic religion itself is particularly open to the idea of science, which contrasted strongly with the ideas prevalent in medieval Europe, where it was often considered heretical to question or investigate the workings of a world made by God.
The Islamic Empire too was committed to gathering the knowledge of the ancient world. Texts in Classical Greek and Latin, Ancient Egyptian, Mesopotamian, Indian, Chinese and Persian were all translated by Islamic scholars, broadening their availability to the empire’s scientists and mathematicians.
AL-KHWARIZMI (c. 790–c. 850)
Mathematician Al-Khwarizmi hailed from an area situated in present-day Uzbekistan, and he is credited with providing several significant contributions to mathematics. Although some of his original works have survived, he is familiar to us through editions of his work translated into Latin for use later in Europe.
The new number system
One of Al-Khwarizmi’s significant legacies was what is now known as the Hindu-Arabic numeral system, which we still use to this day. Derived from his Book of Addition and Subtraction According to the Hindu Calculation, Al-Khwarizmi’s system of numbers, developed over time in India from c. 300 BC and passed through into Persia, revolutionized arithmetic.
Up to this point, no culture had a system of numerals with which it was really possible to use in arithmetic. Numbers would always be converted into letters or symbols (either mentally or using counters, abacuses or other such tools), the calculation performed and the result reconverted back into numerals. Lots of symbols were often needed to show a number, many of which were difficult to decipher at a glance.
The Hindu-Arabic system contains just ten symbols – 0 1 2 3 4 5 6 7 8 9 – that could be used to write any number. It is important to note that these symbols were exactly that – they were not associated with the value they represented through stripes or dots. The zero (from the Arabic zifer, meaning ‘empty’) meant that the symbols could have a different value depending on where they were positioned in the number – which freed people of the difficulty the Mesopotamians had faced. Today, the concept of place-value is taken for granted. But the idea that the 8 in 80 is worth eight tens, and yet could be used, with the help of those friendly zeros, to also mean 800 or 8 million was revolutionary at the time. In fact, some European scholars were deeply suspicious of this heathen method of calculating, despite its advantages.
In the Book of Addition and Subtraction According to the Hindu Calculation Al-Khwarizmi describes how to do arithmetic using these new numbers. His translators referred to him by the Latinized name Algorism. Over time Al-Khwarizmi’s methods of calculation became known as algorithms, a word still in use today and which refers to a set of instructions to perform a calculation – which is exactly what Al-Khwarizmi provided.
Al-Khwarizmi also wrote The Compendious Book on Calculation by Transformations and Dividing, which set out to show how to solve different types of quadratic equations (equations in which the unknown numbers are squared). ‘Transformations’ in Arabic is Al-Jabr, from which we derive (via Latin) the English term algebra. While Al-Khwarizmi himself did not replace unknown numbers with letters, he did pave the way for this to happen.
OMAR KHAYYÁM (1048–1131)
Persian scholar Omar Khayyám is best known for his The Rubaiyat of Omar Khayyám, a selection of poems that were later translated into English in the nineteenth century by the poet Edward Fitzgerald. Multi-talented, Khayyám spent a great proportion of his life as a court astronomer to a sultan, while also working as a scientist and mathematician.
Khayyám’s mathematical works were far-reaching. He expanded on Al-Khwarizmi’s earlier work in algebra, and he was one of the first mathematicians to use the replacement of unknown numbers with letters to make solving equations easier. He also devised techniques for solving cubic equations, where the unknown term has been cubed. Khayyám’s insight enabled him to be one of the first people to connect geometry and algebra, which had until that point been separate disciplines.
Khayyám also investigated something now called the binomial theorem. This has many applications in mathematics, many of which involve rather tricky algebra. One side product of binomial theorem is something called Pascal’s triangle, named after the seventeenth-century French mathematician Blaise Pascal, who borrowed the triangle from Khayyám, who in turn borrowed it from the Chinese (see here). Unlike the binomial theorem, Pascal’s triangle is simple to understand: the number in each cell of a triangle is made by adding together the two numbers above it.

Pascal’s triangle is useful because each horizontal row shows us the binomial coefficients that the binomial theorem spits out. These can tell us how many combinations of two different things it is possible to have.
For example, imagine you have planted a row of four flower bulbs. It says on the packet that the flowers can be blue or pink, with an equal chance of having either.
There is one way for you to grow four blues:
BBBB
There are four ways for you to grow three blues and one pink:
BBBP
BBPB
BPBB
PBBB
There are six ways for you to end up with two of each:
BBPP
BPPB
PBBP
PPBB
BPBP
PBPB
There are four ways for you to have three pinks and one blue:
PPPB
PPBP
PBPP
BPPP
And one way for you to have four pinks:
PPPP
If you look across the fourth row of the triangle, it says 1, 4, 6, 4, 1, which corresponds to the number of ways worked out in the example above. Because there is an equal chance of a flower being either pink or blue, you can also see that you’re most likely to end up with two of each colour because there are 6 out of 16 total ways this could happen.
A new geometry
Khayyám also wrote a book that tackled Euclid’s fifth postulate, which had long rankled a contingent of mathematicians. The fifth postulate Euclid wrote concerned parallel lines, and it is therefore normally referred to as the parallel postulate.
Imagine two lines (PQ and RS) with a third (XY) crossing them. Inside PQ and RS we now have four angles, two on each side of the XY: a, b, c and d:
The parallel postulate suggests that if you add the pairs of angles on the same side of XY together (e.g. a+b and c+d) then PQ and RS will cross on the side of the line where the sum of the angles is less than 180°. If the angles on each side add up to 180° then PQ and RS are parallel and therefore will never cross.
Mathematicians, however, have argued over the ages that this postulate is not quite as obvious as Euclid made out. Khayyám was the first to come up with a counter-example, arguing that Euclid’s parallel postulate does not always work if the surface you are drawing on is curved. Thus Khayyám instigated the ideas of elliptical and hyperbolic geometry, a direct challenge to the simple Euclidean geometry that had gone before. This kind of thinking would eventually help Albert Einstein to come up with his ideas of space-time and gravity.