Were theologians to succeed in their attempt to strictly separate science and religion, they would hill religion. Theology simply must become a branch of physics if it is to survive. That even theologians are slowly becoming effective atheists has been documented …
—Frank Tipler, The Physics of Immortality
God created the natural numbers, and all the rest is the work of man.
—Leopold Kronecker (1823–1891) |

|
In Chapter 20, I alluded to the famous mathematician Kurt Goedel and the fact that he spent the last few years of his life working on a mathematical proof of God’s existence. In this Postscript, I quote colleagues from around the world who have responded to my questions on this subject, and I thank them for permission to reproduce excerpts from their comments. Some of my questions were sent through electronic mail or posted to electronic bulletin boards. Three common sources for such information exchange were “sci.math,” “alt.atheism,” and “soc.religion.christianity”—electronic bulletin boards (or newsgroups) that are part of a large, worldwide network of interconnected computers called Usenet. (The computers exchange news articles with each other on a voluntary basis.)1
Without further ado, I present Kurt Goedel’s proof of God’s existence:
GOEDEL’S MATHEMATICAL PROOF OF GOD’S EXISTENCE
Axiom 1. (Dichotomy) A property is positive if and only if its negation is negative.
Axiom 2. (Closure) A property is positive if it necessarily contains a positive property.
Theorem 1. A positive property is logically consistent (i.e., possibly it has some instance).
Definition. Something is God-like if and only if it possesses all positive properties.
Axiom 3. Being God-like is a positive property.
Axiom 4. Being a positive property is (logical, hence) necessary.
Definition. A property P is the essence of x if and only if × has P and is necessarily minimal.
Theorem 2. If x is God-like, then being God-like is the essence of x.
Definition. NE(x): x necessarily exists if it has an essential property.
Axiom 5. Being NE is God-like.
Theorem 3. Necessarily there is some x such that x is God-like.
Note: I obtained this proof from: Wang, Hao (1987) Reflections on Kurt Goedel. MIT Press: Cambridge, Mass. (page 195).
INTERNET INTERPRETATION OF GOEDEL’S PROOF OF GOD
Christians grossly underestimate the pleasures that will be available in Heaven. They greatly underestimate what a being with literally infinite power can do.
—Frank Tipler, The Physics of Immortality
The appeal of mathematics for artists is precisely the universality of mathematics— universal in the sense of culturally invariant. This is not mathematics as a tool to prove God but rather mathematics as evidence of some universal fabric for existence.
—Anonymous Internet Traveler
You can’t disbelieve something if you don’t even know what it is you’re not believing in. Likewise, you can’t believe in something if you don’t even know what it is you’re believing in. This makes everyone an agnostic until or unless a definition is agreed upon.
—Mark Hopkins
I could not find significant information in the philosophical or mathematical literature regarding the interpretation of Goedel’s proof of God. Author Hao Wang expressed no opinion or help to the reader in interpreting the proof. In fact, he states enigmatically, “I am only including [the proof] for some measure of completeness, and shall, out of ignorance, make no comments on it.” I therefore consulted various mathematicians and philosophers on the Internet for their opinions. If you don’t understand all of their comments, don’t worry. At the least, they will give you the flavor of how current researchers in philosophy and mathematics express their thoughts on complex theomatic areas. I have not eliminated repetitious information so that you can get a feel for the overlap of current, common thinking among respondents.
Ivan Ordonez Reinoso, a doctoral student in Computers and Information Sciences at the Ohio State University, comments:
The proof has an obvious problem in that it only shows the existence of a mathematical object with the property “God-like” as defined in the proof. There is no relation to the real world; it is like proving that there is no last cardinal number. Furthermore, the proof does not exclude the possibility of the existence of an infinite number of disjoint objects all with the property “God-like.”
Mike Miller from Western Illinois University comments:
Here’s the easiest place at which the proof may be ripped apart. Now here is it shown that x has to exist, except by this definition. Thus, we must be shown why this definition is correct before we accept it.
Pertsel Vladimir from the Weizmann Institute of Science’s Computation Center, comments:
I’ve heard the following advanced as a proof of God’s existence:
1. |
“God” is defined as having all qualities in perfection. |
2. |
Existence is a quality. |
3. |
Therefore God must have this quality of existence, and so must exist. |
However, the template for disproving such reasonings was given by A. G. Gein at one of the All-Soviet-Union mathematical competitions:
1 |
Non-existence is a quality. |
2 |
Therefore God must have this quality of non-existence. |
3 |
Therefore God must not exist. |
Kazimir Kylheku from the Computer Science Department of the University of British Columbia, Vancouver comments:
Maybe it was just happy hour in Austria, and Goedel was entertaining a less than erudite gathering.
From an anonymous graduate student in Electrical and Computer Engineering at Rice University in Houston, Texas:
Pascal’s “Pensées” (“Thoughts”) came about because the Church urged him to make some public comment on religion. The following may contain the “ontological argument” for the existence of God:
1 |
Suppose God does not exist. |
2 |
Imagine the most beautiful and perfect place imaginable. |
3 |
Imagine (2) with God. It is more beautiful and perfect than (2) without God. |
4 |
(3) contradicts the supposition that (2) is the most perfect place imaginable. |
5 |
Hence assumption (1) is incorrect. |
This five-step argument is inadequate because of assumptions about the nature and limits of “imagination.” I have generally found “proving” the “existence” of God to be a shallow pursuit. It is much more interesting to lessen the emphasis on “proof” and increase the subtlety of what is meant by “exist.” For example, I believe that my sensible world has incredible order that implies plan and causation. It also has disorder and power which makes me feel weak and small. It is soothing to accept both of these and let the sheer wonderfulness of it comfort my existential worries. When I have an epiphany that the humor in the pose of a cat on a 4000-year-old baked clay sculpture connects, me and the cat in my garage to a person from another time and place, and I open myself to that moment and let it reaffirm my respect for humanity, is that a prayer? There is no question in my mind that Unity is apparent. Some would argue that it is constructed in my mind like a Rorschach test. So what, let them be dour and deterministic. It won’t stop me from stealing those moments of pure joy when I can! For more on this line of reasoning, read Joseph Campbell’s The Inner Reaches of Outer Space and Walker Percy’s The Last Self-Help Book in the Cosmos. The former is short and rigorous with arguments based on semiotics, and the latter is fun, yet profound. People are trained to look for “God” and “religion” outside themselves. Even when they are told that “God is in each of us,” the problem is just that: they are “told.”
On another topic, Walker Percy, in his book The Last Self Help Book, provides a structure by which art can be considered a God-substitute in its role as a conduit between ourselves and the Universal/Infinite. The appeal of math for artists is precisely the universality of mathematics—universal in the sense of culturally invariant. This is not mathematics as a tool to prove God but rather mathematics as evidence of some universal fabric for existence. Perhaps these artists are unaware that all of mathematics is prefixed by the same post-modernist-like disclaimer (authored by Goedel, Russell, and Whitehead) that appears in current art/anthropology/cultural criticism. On the other hand, perhaps they are aware that mathematics has no absolute claim, but nonetheless joins hands with most practicing mathematicians in a willing suspension of disbelief.
Mark Hopkins, a consultant from Milwaukee, comments:
I. Robinson’s Logic. I’ve been considering another proof, somewhat similar in nature, that starts with Robinson’s investigations into idealizations. (Abraham Robinson (1918–1974) was a logician and mathematician famous for his “non-standard analysis.”) Robinson established a mode of inference whereby one could perform the following type of deduction: for all × there exists y such that (x<< y) yields: “there exists y * such that for all × (x<< y*).” The expression y* is called an ideal object, and constraints are imposed on the nature of the relation <*c. My proof seeks to start out with a property that simultaneously identifies an essential aspect of God and satisfies the constraints Robinson placed. As an example (which doesn’t actually work) consider “x is loved by y.” The Prime Mover argument would use the relation “x is caused by y,” but the problem here (apart from the issue of what causality is) is that there may only be a finite number of instances of causal links in the universe. If I understand Robinson correctly, you need an infinite relation. This gets to the heart of the matter.
II. Definition Problem. Here’s another point to consider. People have apparently losttheir common sense when studying proofs of God, and have completely forgotten theidea of Definition Before Proof. One has to define what it is meant by God before tryingto prove existence. Therefore, the lack of resolution over the issue has absolutelynothing to do with the supposed inapplicability of logic here, but rather in the lack ofconsensus over what constitutes a valid definition.
III. Nobody Can be an Atheist. This discussion is the basis for why I argue that nobodycan be an atheist (or a theist). The reason is that in order to be either, you have to knowwhat it is you’re (dis)believing in first. You can’t disbelieve something if you don’t evenknow what it is you’re not believing in. This would be dishonest. Likewise, you can’tbelieve in something if you don’t even know what it is you’re believing in—that’sdelusion (actually, it’s idolatry). This makes everyone an agnostic until or unless adefinition is agreed upon.
Dr. George Markowsky from the University of Maine’s Computer Science Department comments:
I did not find Goedel’s proof very convincing or particularly interesting. Is there good evidence that he put this forward in a serious manner? Perhaps he was just fooling around. One of your respondents suggested that we had to be agnostics rather than atheists. A. J. Ayer, in his book Language, Truth and Logic (Dover, 1946), argues for a fourth position on God. He claims that the standard three positions—believer, atheist, and agnostic—don’t make sense because the concept of God is not well defined. Ayer argues it makes no sense to state a position about God’s existence since the concept makes no sense.
Arturo Magidin is a second year graduate student in the mathematics Ph.D. program at the University of Berkeley. He comments:
1) The first problem arises in Axiom 2 (Closure). What does “necessarily contains” mean? When do we say that a property contains another? If it implies it? Then since a → a is always true, you haven’t really said anything. Note also if you define any property to be positive (and negative), then axioms 1 and 2 are satisfied. 2) The proof up Proof of the to Axiom 3 is “proving by definition.” It is analogous to defining a “Real Loch Ness Monster” as a huge animal that lives in the Loch Ness and that actually exists. Then I claim that a Real Loch Ness Monster necessarily exists. This is indeed true, since I have, in effect, defined a Real Loch Ness monster to exist. However, the possibility that there is no such thing as a Real Loch Ness Monster still holds; i.e., you cannot define things into existence simply by stating that they have the property of existing. 3) In Axiom 4, the term “minimal” is used. Minimal with respect to what? (This is not a critique; this is an honest question; I think I might be missing something.) Theorem 2 also appears to be “defining things into existence.” Finally, by the time we have finished the proof at Theorem 3, it seems that taking every property to be both positive and negative, you have satisfied all axioms. So, if x is God-like, it necessarily exists, but that is not the same as saying that there necessarily exists something which happens to be God-like. You have in essence, paraphrased Descartes’ argument:
Descartes Proof Of God’s Existence
God is a being which by definition possesses all positive properties. Existing is a positive property; therefore, God has the property of existing; hence God exists.
This argument has already been demolished by philosophers. I recommend a perusal of Michael Martin’s Atheism: A Philosophical Justification for a clearer explanation of the “real Loch Ness monster” scenario.
Benjamin J. Tilly, a mathematics graduate student at Dartmouth, comments:
Goedel’s proof of God’s existence seems to have a number of flaws. The main one is that it asserts a number of axioms which are not very reasonable, and the second one is that there is no guarantee that the resulting “God” has any relationship to the ordinary religious notions. 1) Axiom 1 gives a definition. It is fine. However, I would like to know what a “property” is, and what “negative” means. 2) Axiom 2 seems to be missing something since if I define all properties to be both negative and positive then the two axioms are satisfied and the theorem is false. 3) Does the definition, “Something is Godlike if and only if it possesses all positive properties” have any relationship to the usual notions of God? 4) I have no problem with Axioms 3 and 4.5) What does “minimal” mean? Minimal in what sense? 6) Theorem 2, followed by the definition and Axiom 5, essentially asserts the existence of God, as an axiom. Of course if you want to do that then I could just assert that God exists.
Mats Andtbacka, a chemical engineering student from Finland, comments:
All right, so I’m not a logician. But if a property <A> is defined as being something <B> if and only if something else <C>, and then in the next sentence you say that a property <D> is also <B>, provided merely that it contains an instance of <A or D>—well, isn’t that a problem? Or is my expression of this the problem here? Heck, who cares … So there necessarily exists at least one x such that x possesses all positive properties, where a property is positive if its negation is negative. I’m not sure I’d be impressed even if I understood that.
Geoffrey Moore from the University of Maryland comments:
1) Axiom 1 relies on a two way street. What if I said “I am lying”? This is the first paradox which states that Axiom 1 applies to absolutely nothing. 2) In Theorem 2, Goedel is being stupid. He says that a unicorn exists because horns exist. Wrong! 3) Finally look at the definition, “A property P is the essence of x if and only if x has P and P is necessarily minimal.” Is this a circular argument or what? x has P has x? Wrong!
I asked Scott Pallack, a taxi driver in Fort Lauderdale, Florida, “Is there anything you personally would consider mathematical evidence of the existence of a deity?” He responded:
One cannot prove that an omnipotent God does not exist. (Assume you have such a proof. You cannot prove that God has interfered with your mind making you think the proof is valid when it is not.) Of course, this does not prove the existence of God. Personally, I think the question is undecidable in the Goedelian sense. You can assume either G or not-G as an axiom. Just be prepared to accept the consequences of your assumption.
Pascal had a so-called “proof” of God’s existence which contains a statement similar to, “Even if there is a tiny probability that belief in God sends you to heaven and disbelief sends you to hell, one should believe in God, because there’s nothing to lose.” However, this reasoning has a flaw. For example, consider the possibility that only believers go to hell.
Bert Smits is a doctoral student working on dynamical systems in the Limburgs Universitair Centrum, Diepenbeek. He comments:
I’ve attended a talk by a mathematician from Laval University, Canada, who lectured in Europe on “The Existence of the Uncaused Cause.” If you define God to be the uncaused cause, then I think he had a rather convincing proof of God’s existence.
Goran Wicklund works for a subsidiary to Ericsson Telecom as a system designer of switching equipment. He comments:
Some mathematicians consider ei π+ 1 = 0 to be “God’s formula.” It contains the three most important mathematical terms: e, π, and i. It also contains the additive, multiplicative, and exponentiation operator and the two neutral units for these operators (0 and 1). Some believe that this compact formula uniting various facets of mathematics is surely proof of a Creator.
Allan Trojan, an Associate Professor of Mathematics from Atkinson College, York University, comments:
The idea of a mathematical proof of the existence of God does not interest me in the slightest. God is an “energy.” You don’t prove or disprove the existence of an energy, you use it. I am a mathematician (not terribly renowned however), and I am religious. I am a mystic.
St. Anselm (1033–1109) was the Archbishop of Canterbury, and a philosopher famous for his arguments for the existence of God. Langley Muir, a mathematical logician at the Natural Resources Canada, Ottawa, comments:
There is a proof that was first postulated, perhaps by St. Anselm, known as the Ontological argument. It has a very long history in philosophy and is one of the major arguments used by Descartes to prove the existence of God. Shorn of a lot of supporting arguments, it is a simple syllogism in “Barbara.” (Muir explains the term “Barbara” in Appendix 2 of this chapter.)
1 |
Major premise: God is perfect |
2 |
Minor premise: Perfection exists |
3 |
Conclusion: God exists |
There is a long list of books and articles related to this argument which come close to a Proof of the real mathematical proof, if you accept that logic and mathematics are the same thing. For more information, see: Plantinga, A. (1965) The Ontological Argument: From St. Anselm to Contemporary Philosophers, Doubleday-Anchor: New York.
Tim Poston is a researcher at the Institute of Systems Science at the National University of Singapore where he is a principal investigator of a heart project dealing with medical imaging and three-dimensional graphics. He has also published in physics, economics, archeology, and computer vision. He comments on the previous example of St. Anselm’s proof:
The ontological argument is a bit more subtle than explained. It defines God (in modern terminology) as a maximal element in the lattice of good entities, so it needs Zorn’s Lemma to succeed. Thus it depends on the Axiom of Choice. As pointed out in the journal Manifold around 1970, this makes the existence of God equivalent to the Axiom of Choice, since an omnipotent deity could clearly do the choosing.
I’ve often thought that modern mathematics could contribute a lot of pizzazz to numerical theology. The numerology of the religious depends on facts known since Pythagoras. For example, observe that since, according to Revelation, the saints are “a multitude that no man can number,” most saints are clearly not descendants of Adam, who by a simple generation-labelling argument, can be at most a denumerable set, even if Armageddon is [countably] infinitely deferred. Religious reasons do not excuse violence: they accuse religion.
I recommend the following article: “Ontology Revisited” by Vox Fisher, Manifold 6, March 1970. The countability point regarding saints was an exercise in my piece “Aquinas’ God versus Maxwell’s Demon” in Manifold 11.
Paul Swingle, a computer programmer from Boca Raton, Florida, comments:
The responses describing Anselm’s proof of the existence of God remind me of the high point of my philosophical career in school. We were discussing Anselm’s proof, which as I recall was:
1 |
God is defined as, “That than which there is nothing more perfect.” |
2 |
That which exists is more perfect than that which does not exist. |
3 |
Therefore God must exist. |
From this I created Swingle’s Proof of the Existence of the Devil:
1 |
The Devil is defined as, “That than which there is nothing more evil.” |
2 |
That which exists is more evil than that which does not exist. |
3 |
Therefore the Devil must exist. |
I think this rests on the notion of existence being more “something” than nonexistence. A perfect triangle cannot exist; the notion must be debased or harmed in some way by having a concrete example.
David Wilson of Cabletron Systems Inc. comments:
Mathematics effectively amounts to the formal manipulation of symbols. Inasmuch as an idea can be couched in terms of symbols amenable to such formal manipulation, that idea is mathematical, inasmuch as it cannot, it is outside the realm of mathematics. The power of mathematics is derived from the vast store of symbolic manipulations built up over the centuries. In order to benefit from this power, other disciplines often strive to translate their non-symbolic ideas into mathematical symbols, with varying degrees of success. In most cases, the translation is an approximation; in no case is such a translation provably correct. The concepts from many areas of discourse, such as religion, philosophy, social sciences, economics, and politics are at best poorly translated into mathematical symbols, and consequently not amenable to sound mathematical argumentation. Just as within a discipline closely allied to mathematics, such as physics, it would be laughable and demeaning to ask for a mathematical proof of the existence of an electron. Similarly a proof of the existence/nonexistence of God is all the more laughable and demeaning. A mathematical proof of any idea presupposes that that idea can be couched in symbols, which is generally not the case. I, for one, side with Lebesgue on this subject: “In my opinion, a mathematician need not preoccupy himself with philosophy.” (Lesbesgue, as quoted in The Foundations of Geometry and the NonEuclidean Plane, by George E. Martin)
Mating Dance of the Horned Spheres, a visual proof of the existence of God by Tim Poston.
David Joyce from Clark University’s Department of Mathematics and Computer Science comments:
All of this reminds me of an equally circular proof of God. Define God as a perfect being, posit that perfection includes existence, conclude existence of God.
John Baez, a mathematical physicist from the Mathematics Department at the University of California, Riverside, comments:
Here is an old proof of God’s existence. Consider: “If this sentence is true, then God exists.” Call that sentence P for short. Assume for the moment that P is true. Then, since P says if it’s true then God exists, God exists. Of course, we just assumed P was true; we don’t know this. However, look what we have shown: if P is true, then God exists. But that’s just what P says! So we have shown P is true! Therefore God exists. QED.
Oddly enough, this proof works equally well if we change “exists” to “does not exist.” Therefore, the proof is very versatile. Usually I use it to prove that I don’t need to get up in the morning. For more, try reading about provability predicates and Loeb’s theorem in Boolos and Jeffrey’s Computability and Logic, although somehow I suspect Smullyan’s books should have something to say about this one. Sentences that say “this sentence implies this sentence is provable” have an amusing tendency to be provable by an argument similar to the above one.
Tony Davie, a lecturer in computer science specializing in functional programming and programming languages at St. Andrews University (Scotland), makes a comment similar to the previous one:
The following argument, perhaps due to Smullyan, is amusing. Consider the self-referential statement “If this statement is true then God exists.” Let us try to prove it:
1 |
The statement is true. |
2 |
If the statement is true then God exists. |
3 |
God exists. |
So, by the deduction theorem, the hypothesis 1 implies 3, i.e. if 1 then 3. If the statement is true then God exists. Thus the statement is true thus God exists.
Joshua Weiner from Oberlin College’s Department of Physics comments:
There is a problem with the Goedel’s proof of God. “Existing” is not necessarily better than not existing. Consider the field of quantum mechanics. A particle does not exist until observed. Does this make us gods for being able to turn a probability field into a particle? Similarly, by existing and encompassing all, a god must encompass evil as it is better to have all than to have things outside of one’s self. Yet this would contradict the definition of god as being all good. Also there is the quality of being weak and impotent. If god is all encompassing it should have all qualities including weakness, stupidity, anger, hate, and lust. To have less would to be less than perfect. God is a logical contradiction. This isn’t a mathematical proof, it’s just an new wording of an old “proof.”
From an anonymous Internet traveler, software engineer, and mathematician named Sue:
1) Good grief, anyone can make up an axiom like Axiom 3 in Goedel’s proof of God. Maybe being God-like is really a negative property (negative and positive not having been denned in the first place). 2) The meaning of Axiom 4 is unclear. 3) I am not sure how Theorem 2 follows from the definition before it. 4) Regarding Theorem 3, is there a limit on how many such x’s exist? This is a joke, right? This whole proof depends on a set of axioms that I find suspect, to say the least. And the definitions don’t seem to define anything that actually exists. But some poor [expletive deleted] is going to fall for it, and go around saying, “I know God exists, because this really smart guy proved it.”
Joe McCauley, a programmer from Colorado Springs, Colorado, comments:
Being both a religious person and having an analytical personality, I have struggled with the question of how I can really know that God exists. I tend to regard proofs in this chapter as nothing more than clever logical manipulations of words and symbols that provide no real information on the question of whether or not God truly exists. What I would like to see is physical evidence, or something which could be demonstrated experimentally. I do not expect to find this.
After reading some of the works of John Powell (a Jesuit priest at Loyola University), I concluded that it is not possible to know the existence of God in the sense of being able to show a rigorous proof or experimental evidence of God’s existence. Belief in God requires some degree of faith; for those who refuse to accept faith, there will always be room to challenge any alleged proof of God’s existence, and to doubt any alleged divine intervention in anything they observe. And those who have faith don’t need the sort of proof being discussed here. You might say I believe in God because I choose to, and you’d probably be right.
Dan Piatt, an IBM physicist with an interest in religion, comments:
Goedel is spinning wheels. One can define things, postulate axioms about them, and prove theorems about them. The assignment of words such as “God-like” provides a context or connotation to these things. However, it isn’t clear that every theologian would care to describe God in this kind of language. Further, I’ve heard this argument before in slightly different language. There’s possibly a need for the axiom of choice in this (you don’t know what the cardinality of positive properties is). Maybe Goedel is assuming a countable or even finite set.
Timothy Chow, a doctoral student from MIT, comments:
Let Sentence A be the sentence, “If Sentence A is true, then Santa Claus exists.” If we replace truth by theoremhood, can we get something along the lines of Goedel’s theorem by trying to formalize this paradox?
Torkel Franzen, a researcher and philosopher at the Swedish Institute of Computer Science, Kista, comments on Henkin sentences. (Henkin sentences of the form “This sentence is provable,” are automatically true. The key is the relation to the Santa Claus paradox.)
Why are Henkin sentences self-proving? The reasons follows from Loeb’s theorem: if the formula “if A is provable in T, then A” is provable in T (for T satisfying certain conditions), then A is provable in T As far as I know there isn’t any special simpler argument that applies to Henkin sentences in particular.
There are two proofs of Loeb’s theorem. First there is Loeb’s original simple proof which deserves to be well known in wider circles as Goedel’s proof. First note that Loeb’s theorem implies Goedel’s second incompleteness theorem as a special case: taking A to be the formula 0 = 1, we conclude from Loeb’s theorem that the consistency of T is not provable in T unless T is inconsistent. So the reasoning involves some prooftheoretical aspects absent in the proof of Goedel’s first theorem. Understanding the idea of the proof is just as easy as understanding the idea of using the Liar paradox to obtain Goedel’s first theorem. Loeb starts from a variant of the Liar. Where the Liar is “this sentence is false” and the paradoxical reasoning draws a contradictory conclusion, Existence of the present paradox, which we may call the Santa Claus paradox, purports to prove the existence of Santa Claus. Here is the argument: Let p be the statement “if p is true then Santa Claus exists.” Now, if p is true, then if p is true, Santa Claus exists. This means that if p is true, Santa Claus exists. But this is just what p says. So p is in fact true. But then, since if p is true, Santa Claus exists, it follows that Santa Claus exists.
To transform this reasoning into a valid argument in T, we need a provability predicate satisfying certain conditions. So suppose we have a formula Bev (x), formalizing “x is the Goedel number of a variable-free formula provable in T.” We assume that Bev(x) satisfies the following conditions, where $C$ stands for the Goedel number of a formula C. (I) If C is provable in T, Bev($C$) is provable in T. (II) Bev($A → B$) → (Bev(SAS) → Bev(SBS)) is provable in T for all A,B. (Ill) Bev($A$) → Bev($Bev($A$)$) is provable in T for all A.
Now suppose the formula A satisfies the condition that the formula Bev($A$) → A is provable in T In other words, it is provable in T that if A is provable in T, A is true. Now, using a mechanism for self-reference as in Goedel’s proof, we obtain a formula B for which it is provable in T that (2) B $ AL → (Bev($B$)+ A). We now show that A is provable in T, by the following reasoning. From (2) we get that it is provable in T that (3) B → (Bev($B$) → A) and hence, using principles (I) and (II) we get that it is provable in T that (4) Bev(SB$) → Bev($Bev($B$)+ AS) and so by another application of (II) that it is provable in T that (5) Bev($B$) → (Bev($Bev($B$)$)+ Bev($A$)). From (III) and (5) we get that it is provable in T that Bev($B$)4 Bev($A$). But (6) and (1) yield that it is provable in T that (7) Bev($B$) $AR A By (2) and (7) B is provable in T, so by (I), Bev($B$) is provable in T. Hence, by (7), A is provable in T.
Now if you work through this, you’ll see that it mimics the reasoning in the Santa Claus paradox. A funny thing about Loeb’s theorem is that it went unnoticed for years that it actually follows immediately from Goedel’s second theorem. For assume (1) holds but A is not provable in T. Then the theory T+ ~ A is consistent. But in the theory T + ~ A, it is provable that A is not provable in T, i.e., that T+ ~ A is consistent. So, by Goedel’s second theorem, T + ~ A is inconsistent. Hence A is provable in T. Now I like the original proof much better, since it extends the proof of Goedel’s second theorem in a natural way using a refined version of the Liar. Also, the original argument applies to intuitionistic theories as well as classical ones, whereas the second proof applied to an intuitionistic system only shows that ~ ~ A is provable in T.
I recommend a quite readable chapter “The Incompleteness Theorems,” by C. Smorynski, in the Handbook of Mathematical Logic (North-Holland Publishing Company, 1977), edited by Jon Barwise, which contains fascinating information for those who are interested in the subject. See also Smullyan’s books.
Randall Holmes is a professor of mathematics at Boise State University in Boise, Idaho. He is a mathematical logician by training. He teaches and does research on Quine’s set theory “New Foundations” and on computer-assisted reasoning. He comments:
If we try to work by analogy with Goedel, we build a one-place predicate of natural numbers which says, “If one-place predicate n is provable of the number n, then [Santa Claus exists].” This sentence has a Goedel number; let this number be G. Predicate number G holds of G exactly if “if one-place predicate G is provable of the number G, then [Santa Claus exists].” Thus, we have a sentence which says, “If I am provable, then Santa Claus exists.” If Santa Claus exists, this statement is true; it is provable if the existence of Santa Claus is provable, and not provable otherwise. If Santa Claus does not exist, this statement is true but unprovable just as in the case of Goedel’s sentence which asserts that it itself is not provable. Nothing is added to the force of Goedel’s argument by this construction. The point is that the Santa Claus paradox is really exactly the paradox of the Liar (“This statement is false”), and so its translation into the realm of provability is exactly Goedel’s diagonalization.
MANIFOLD AND MATHEMATICAL THEOLOGY
Most theology is more about particular human grammars than about universal truth. “I think, therefore I am” is perfectly paralleled by, “It is raining, therefore it exists,” which clearly tells us nothing at all about “it.”
—Tim Poston, 1994
Manifold—the only journal ever published entirely on the subject of mathematical theology—began as a publication created by half a dozen graduate students at the University of Warwick (UK). The journal started in 1968 and ran for 20 issues, until 1980. Tim Poston, a researcher at the Institute of Systems Science at the National University of Singapore, led me to several interesting articles regarding God and mathematics which appeared in Manifold.
Ontology Revisited
Most theology is word games … getting out of language what was earlier snuck into it; the same is of course true about mathematics.
—Tim Poston, 1994
In Manifold 6 (1970, pp: 48–49), Vox Fisher published “Ontology Revisited,” a fascinating paper on a mathematical proof of God’s existence. The paper starts:
Theorem: The axiom of choice is equivalent to the existence of a unique God. (St. Anselm, Aquinas, and others.)
Proof: Partially order the set of subsets of the set of all properties of objects by inclusion. This set has maximal elements. God is by definition (due to Anselm) a maximal element set:
God ⊆ God ∪ (existence}, so God = God ∪ (existence} ∪ God exists. Uniqueness: if God and God’ are two gods, then God ∪ God’ ⊇ God (due to Aquinas), and ∴ God ⊆ God’ = God, ∴ God ⊇ God’, and similarly God’ ⊇God
∴ God = God’.
Given a set {Aα}α∈R of sets, let the unique God pick xα ∈ Aα for each α∈ A. (He can do so by omnipotence.) Then 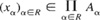 A as required.
A as required.
Aquinas’ God versus Maxwell’s Demon
There cannot be design without a designer, order without choice … Arrangement, Mathematical disposition of parts, and subservience of means to an end imply the presence of intelligence and mind.
—William Paley
In Manifold 11 (1971, pp: 71–72), Tim Poston published “Aquinas’ God versus Maxwell’s Demon,” an unusual paper on thermodynamics and God. As background to the arguments in his paper, the Second Law of Thermodynamics states that in any isolated system, entropy (disorder) must always increase. (The term “isolated” is important because entropy can decrease locally at the expense of greater increase elsewhere.) The Second Law is evident in the shuffling of cards: it is easier to randomly shuffle cards out of a particular sequence than into it. As the cards are shuffled, information is lost.
The following is excerpted with permission from Poston’s paper which attempts to show that God’s omniscience implies the Second Law of Thermodynamics:
We now return to mathematical theology, as follows:
1 |
God is omniscient. |
2 |
Hence, He knows the position of every particle at every time. |
3 |
Hence, He is observing every particle at every time. (Indeed, particle existence depends upon this observation, cf. the writings of Bishop Berkeley.) |
4 |
Hence, He is gaining information about all parts of the Universe at all times and in all places. |
5 |
Hence, he is increasing the entropy of the Universe in all times and in all places. |
6 |
Hence, the entropy of the Universe increases in all times and in all places. (This is the Second Law of Thermodynamics. Q.E.D.) |
Corollary 1. The Axiom of Choice implies the Second Law of Thermodynamics.
Corollary 2. God can raise the dead. Proof: Death and decay involve increase of entropy. God can reverse these processes by means of sacrifice of some of His immense store, accumulated as above, of confidential information.
Corollary 3. God will die. Proof: The Universe will end with a war producing chaos (The Revelation of St. John the Divine), after which God will put it together again as chaos, after which God will put it together again as a whole using all his information. It will then remain perfect (in contrast to the present state). Hence God will cease to observe it, hence He will cease to satisfy the definition of Himself (Summa Contra Gentilla, St. Thomas Aquinas), hence He will cease to exist.
Sanctification and the Hopf Bifurcation
In Manifold 19 (1977, pp: 25–26), Phillip Holmes published the article, “Sanctification and the Hopf Bifurcation,” a thought-provoking paper on the halo (the circle of light surrounding the heads of saints as a symbol of holiness and sanctification). In his paper, Holmes uses chaos theory to suggest that “sanctification consists of the creation of an attracting closed orbit in Hopf bifurcation.”
APPENDIX I OF POSTSCRIPT 1: ST. AUGUSTINE AND THE “CITY OF GOD”
Atheist: “I don’t believe in God.”
Abdu’1-Baha: “I don’t believe in the God that you don’t believe in.”
Interestingly, it seems that the existence of the set of all natural numbers is sanctioned by one of the Fathers of the Church. For example, St. Augustine (see Chapter 6) often speaks of the relationship between numbers and God in his book The City of God. The following is from Book XII, Chapter 19.
The answer to the allegation that even God’s knowledge cannot embrace an infinity of things:
Then there is the assertion that even God’s foreknowledge cannot embrace things which are infinite. If men say this, it only remains for them to plunge into the depths of blasphemy by daring to allege that God does not know all numbers. It is certainly true that numbers are infinite. If you think to make an end with any number, then that number can be increased by the addition of one. More than that, however large it is, however great the quantity it expresses, it can be doubled; in fact, it can be multiplied by any number, according to the very principle and science of numbers.
Every number is defined by its own unique character, so that no number is equal to any other. They are all unequal to one another and different, and the individual numbers are finite, but as a class they are infinite. Does that mean that God does not know all numbers, because of their infinity? Does God’s knowledge extend as far as a certain sum and end there? No one could be insane enough to say that.
Now those philosophers who revere the authority of Plato will not dare to despise numbers and say that they are irrelevant to God’s knowledge. For Plato emphasizes that God constructed the world by the use of numbers, while we have the authority of Scripture, where God is thus addressed, “You have set in order all things by number, measure, and weight.” And the prophet says of God, “He produces the world according to number”; and the Savior says in the Gospel, “Your hairs are all numbered.”
Never let us doubt, then, that every number is known to him “whose understanding cannot be numbered.” Although the infinite series of numbers cannot be numbered, this infinity of numbers is not outside the comprehension of him “whose understanding cannot be numbered.” And so, if what is comprehended in knowledge is bounded within the embrace ofthat knowledge, and thus is finite, it must follow that every infinity is, in a way we cannot express, made finite to God, because it cannot be beyond the embrace of his knowledge.
APPENDIX II OF POSTSCRIPT 1: BARBARA
Langley Muir used the term “Barbara” in his Internet response. “Barbara” refers to the medieval classification of syllogisms. A syllogism is a deductive scheme of a formal argument consisting of a major and minor premise and a conclusion. Example: Every virtue is laudable; kindness is a virtue; therefore kindness is laudable. An odd example from Bob Stong: Hard work is good for you. Stealing refrigerators is hard work. Therefore, stealing refrigerators is good for you. Langley Muir notes that the syllogistic logic allows four types of proposition: 1) A (universal affirmative) subject distributed, predicate undistributed. Example: All men are mortal. 2) E (Universal negative) subject distributed, predicate distributed. 3) I (particular affirmative) subject undistributed, predicate undistributed. 4) O (particular negative) subject undistributed, predicate distributed.
Using these four types of propositions and some rules of argument, all of the valid forms of syllogism may be derived. To remember what they are, one of the more famous sets of memory-lines was given for the first time by Pope John XXI (died 1277): Barbara, Celarent, Darii, Ferioque, prioris; Cesare, Camestres, Festino, Baroko, secundae; tertia, Darapti, Disamis, Datisi, Felapton, Dokardo, Ferison, habet; Bramantip, Camenes, Dimaris, Fesapo, Fresison, quarta insuper addit.
The first, second, third, and fourth refer to the four moods, and the nouns (in upper case) each have three vowels which indicate the form of the propositions making up a valid syllogism, consists of a major premise (first), a minor premise (second), and a conclusion (third). Hence a syllogism is Barbara if a syllogism is made up of major premise A, a minor premise, and a conclusion all using propositions of the form A. Whence: “God is perfect; perfection exists; therefore, God exists” is a syllogism in Barbara. All of this is found in any good book on syllogistic logic that would be used in a first or second year undergraduate philosophy course on logic. (See, for example: Eaton (1959) General Logic: An Introductory Survey, Charles Scribner’s Sons: New York.)


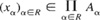 A as required.
A as required.