© The Author(s) 2020
S.-J. Ran et al.Tensor Network ContractionsLecture Notes in Physics964https://doi.org/10.1007/978-3-030-34489-4_5

5. Tensor Network Contraction and Multi-Linear Algebra

Shi-Ju Ran1 , Emanuele Tirrito2, Cheng Peng3, Xi Chen4, Luca Tagliacozzo5, Gang Su6 and Maciej Lewenstein2
(1)
Department of Physics, Capital Normal University, Beijing, China
(2)
Quantum Optics Theory, Institute of Photonic Sciences, Castelldefels, Spain
(3)
Stanford Institute for Materials and Energy Sciences, SLAC and Stanford University, Menlo Park, CA, USA
(4)
School of Physical Sciences, University of Chinese Academy of Science, Beijing, China
(5)
Department of Quantum Physics and Astrophysics, University of Barcelona, Barcelona, Spain
(6)
Kavli Institute for Theoretical Sciences, University of Chinese Academy of Science, Beijing, China
 

Abstract

This chapter is aimed at understanding TN algorithms from the perspective of MLA . In Sect. 5.1, we start from a simple example with a 1D TN stripe, which can be “contracted” by solving the eigenvalue decomposition of matrices. This relates to several important MPS techniques such as canonicalization (Orús and Vidal, Phys Rev B 78:155117, 2008) that enables to implement optimal truncations of the bond dimensions of MPSs (Sect. 5.1.1). In Sect. 5.2, we discuss about super-orthogonalization (Ran et al., Phys Rev B 86:134429, 2012) inspired by Tucker decomposition (De Lathauwer et al., SIAM J Matrix Anal Appl 21(4):1324–1342, 2000) in MLA, which is also a higher-dimensional generalization of canonicalization; it is proposed to implement optimal truncations of the iPEPSs defined on trees. In Sect. 5.3.1, we explain based on the rank-1 decomposition (De Lathauwer et al., SIAM J Matrix Anal Appl 21:1253–1278, 2000) that super-orthogonalization in fact provides the “loopless approximation” of the iPEPSs on regular lattices (Ran et al., Phys Rev B 88:064407, 2013); it explains how the approximations in the simple update algorithm works for the ground-state simulations on 2D regular lattices (Jiang et al., Phys Rev Lett 101:090603, 2008). In Sect. 5.4, we will discuss tensor ring decomposition (TRD) (Ran, Phys Rev E 93:053310, 2016), which is a rank-N generalization of the rank-1 decomposition. TRD naturally provides a unified description of iDMRG (White, Phys Rev Lett 69:2863, 1992; Phys Rev B 48:10345–10356, 1993; McCulloch, Infinite size density matrix renormalization group, revisited, 2008. arXiv:0804.2509) , iTEBD (Vidal, Phys Rev Lett 98:070201, 2007) , and CTMRG (Orús and Vidal, Phys Rev B 80:094403, 2009; Fishman et al., Faster methods for contracting infinite 2D tensor networks, 2017. arXiv:1711.05881) when considering the contractions of 2D TNs .

5.1 A Simple Example of Solving Tensor Network Contraction by Eigenvalue Decomposition

As discussed in the previous sections, the TN algorithms are understood mostly based on the linear algebra, such as eigenvalue and singular value decompositions. Since the elementary building block of a TN is a tensor, it is very natural to think about using the MLA to understand and develop TN algorithms. MLA is also known as tensor decompositions or tensor algebra [1]. It is a highly inter-disciplinary subject. One of its tasks is to generalize the techniques in the linear algebra to higher-order tensors. For instance, one key question is how to define the rank of a tensor and how to determine its optimal lower-rank approximation. This is exactly what we need in the TN algorithms.

Let us begin with a trivial example by simply considering the trace of the product of N number of (χ × χ) matrices M as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{Tr} \mathscr{M} = \text{Tr}(M^{[1]} M^{[2]} \cdots M^{[N]}) = \text{Tr} \prod_{n=1}^{N} M^{[n]}, {} \end{array} \end{aligned} $$
(5.1)
with M [n] = M. In the language of TN , this can be regarded as a 1D TN with periodic boundary condition. For simplicity, we assume that the dominant eigenstate of M is unique.

Allow us to firstly use a clumsy way to do the calculation: contract the shared bonds one by one from left to right. For each contraction, the computational cost is O(χ 3), thus the total cost is O(Nχ 3).

Now let us be smarter by using the eigenvalue decomposition (assume it exists for M) in the linear algebra, which reads
$$\displaystyle \begin{aligned} \begin{array}{rcl} M = U \varLambda U^{\dagger}, {} \end{array} \end{aligned} $$
(5.2)
where Λ are diagonal and U is unitary satisfying UU † = U †U = I. Substituting Eq. (5.2) into (5.1), we can readily have the contraction as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{Tr} \mathscr{M} = \text{Tr} (U \varLambda U^{\dagger} U \varLambda U^{\dagger} \cdots U \varLambda U^{\dagger}) = \text{Tr} (U \varLambda^N U^{\dagger}) = \sum_{a=0}^{\chi-1} \varLambda_a^N. \end{array} \end{aligned} $$
(5.3)
The dominant computational cost is around O(χ 3).
In the limit of N →∞, things become even easier, where we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{Tr} \mathscr{M} = \lim_{N \to \infty} \varLambda_0^N \sum_{a=0}^{\chi-1} \left(\frac{\varLambda_a}{\varLambda_0}\right)^N = \varLambda_0^N, \end{array} \end{aligned} $$
(5.4)
where Λ 0 is the largest eigenvalue, and we have $$\lim _{N \to \infty } (\frac {\varLambda _a}{\varLambda _0})^N = 0$$ for a > 0. It means all the contributions except for the dominant eigenvalue vanish when the TN is infinitely long. What we should do is just to compute the dominant eigenvalue. The efficiency can be further improved by numerous more mature techniques (such as Lanczos algorithm).

5.1.1 Canonicalization of Matrix Product State

Before considering a 2D TN, let us take some more advantages of the eigenvalue decomposition on the 1D TN’s, which is closely related to the canonicalization of MPS proposed by Orús and Vidal for non-unitary evolution of MPS [2]. The utilization of canonicalization is mainly in two aspects: locating optimal truncations of the MPS, and fixing the gauge degrees of freedom of the MPS for better stability and efficiency.

5.1.2 Canonical Form and Globally Optimal Truncations of MPS

As discussed in the above chapter, when using iTEBD to contract a TN , one needs to find the optimal truncations of the virtual bonds of the MPS . In other words, the problem is how to optimally reduce the dimension of an MPS.

The globally optimal truncation can be down in the following expensive way. Let us divide the MPS into two parts by cutting the bond that is to be truncated (Fig. 5.1). Then, if we contract all the virtual bonds on the left-hand side and reshape all the physical indexes there into one index, we will obtain a large matrix denoted as $$L_{\cdots s_n,\alpha _n}$$ that has one big physical and one virtual index. Another matrix denoted as $$R_{s_{n+1}\cdots ,\alpha _n}^{\ast }$$ can be obtained by doing the same thing on the right hand side. The conjugate of R is taken there to obey some conventions.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig1_HTML.png
Fig. 5.1

An impractical scheme to get the global optimal truncation of the virtual bond (red). First, the MPS is cut into two parts. All the indexes on each side of the cut are grouped into one big index. Then by contracting the virtual bond and doing the SVD , the virtual bond dimension is optimally reduced to χ by only taking the χ-largest singular values and the corresponding vectors

Then, by contracting the virtual bond and doing SVD as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{a_n} L_{\cdots s_n,a_n} R_{s_{n+1}\cdots,a_n}^{\ast} = \sum_{a_n^{\prime}} \tilde{L}_{\cdots s_n,a_n^{\prime}} \lambda_{a_n^{\prime}} \tilde{R}_{s_{n+1}\cdots,a_n^{\prime}}^{\ast}, {} \end{array} \end{aligned} $$
(5.5)
the virtual bond dimension is optimally reduced to χ by only taking the χ-largest singular values and the corresponding vectors. The truncation error that is minimized is the distance between the MPS before and after the truncation. Therefore, the truncation is optimal globally concerning the whole MPS as the environment.

In practice, we do not implement the SVD above. It is actually the decomposition of the whole wave-function, which is exponentially expensive. Canonicalization provides an efficient way to realize the SVD through only local operations.

Considering an infinite MPS with two-site translational invariance (Fig. 5.2); it is formed by the tensors A and B as well as the diagonal matrices Λ and Γ as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{\{a\}} \cdots \varLambda_{a_{n-1}} A_{s_{n-1}, a_{n-1} a_{n}} \varGamma_{a_{n}} B_{s_{n}, a_{n} a_{n+1}} \varLambda_{a_{n+1}} \cdots = \text{tTr} (\cdots \varLambda A \varGamma B \varLambda \cdots). \end{array} \end{aligned} $$
(5.6)
This is the MPS used in the iTEBD algorithm (see Sect. 3.​4 and Fig. 3.​5). Note that all argument can be readily generalized to the infinite MPSs with n-site translational invariance, or even to the finite MPSs.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig2_HTML.png
Fig. 5.2

The MPS with two-site translational invariance

An MPS is in the canonical form if the tensors satisfy
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{sa} \varLambda_{a} A_{s, a a'} \varLambda^{\ast}_{a} A^{\ast}_{s, a a''} = I_{a' a''}, {} \end{array} \end{aligned} $$
(5.7)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{sa} A_{s, a' a} \varGamma_{a} A^{\ast}_{s, a'' a} \varGamma^{\ast}_{a} = I_{a' a''}, {} \end{array} \end{aligned} $$
(5.8)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{sa} \varGamma_{a} B_{s, a a'} \varGamma^{\ast}_{a} B^{\ast}_{s, a a''} = I_{a' a''}, {} \end{array} \end{aligned} $$
(5.9)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{sa} B_{s, a' a} \varLambda_{a} B^{\ast}_{s, a'' a} \varLambda^{\ast}_{a} = I_{a' a''}, {} \end{array} \end{aligned} $$
(5.10)
where Λ and Γ are positive-defined (Fig. 5.3). Equations (5.7)–(5.10) are called the canonical conditions of the MPS . Note there will be 2n equations with n-site translational invariance, meaning that each inequivalent tensor will obey to two (left and right) conditions.
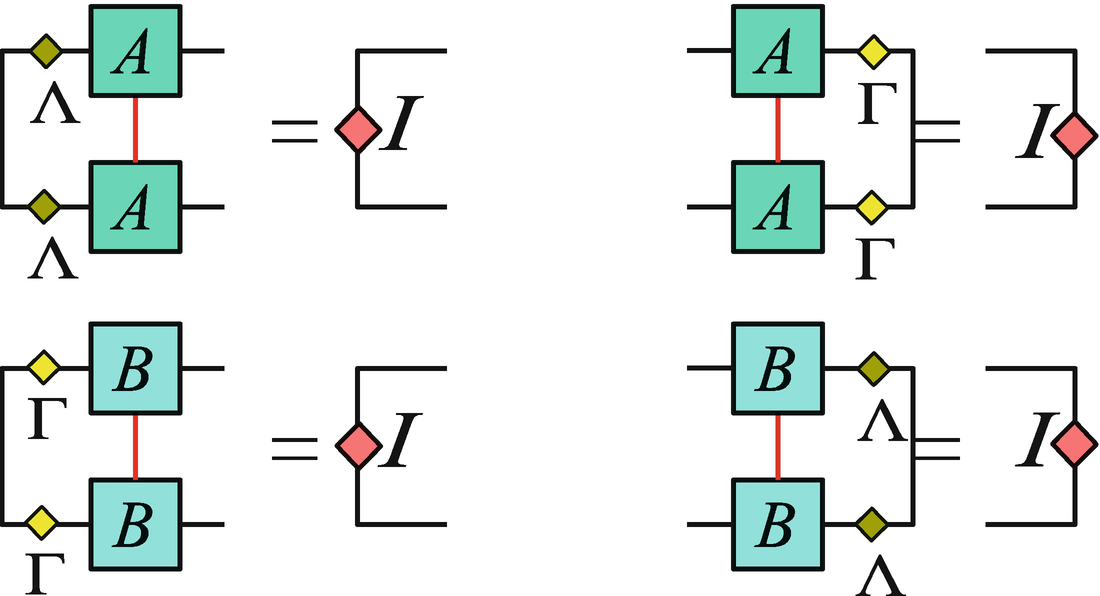
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig3_HTML.png
Fig. 5.3

Four canonical conditions of an MPS

In the canonical form, Λ or Γ directly give the singular values by cutting the MPS on the corresponding bond. To see this, let us calculate Eq. (5.5) from a canonical MPS. From the canonical conditions, matrices L and R are unitary, satisfying L †L = I and R †R = I (the physical indexes are contracted). Meanwhile, Λ (or Γ) is positive-defined, thus L, Λ (or Γ) and R of a canonical MPS directly define the SVD, and Λ or Γ is indeed the singular value spectrum. Then the optimal truncations of the virtual bonds are reached by simply keeping χ-largest values of Λ and the corresponding basis of the neighboring tensors. This is true when cutting any one of the bonds of the MPS. From the uniqueness of SVD , Eqs. (5.7) and (5.8) leads to a unique MPS representation, thus such a form is called “canonical”. In other words, the canonicalization fixes the gauge degrees of freedom of the MPS.

For any finite MPS , the uniqueness is robust. For an infinite MPS, there will be some additional complexity. Let us define the left and right transfer matrices M L and M R of as
$$\displaystyle \begin{aligned} \begin{array}{rcl} M^L_{a_1 a_1^{\prime} a_2 a_2^{\prime}} = \sum_{s} \varLambda_{a_1} A_{s, a_1 a_2} \varLambda^{\ast}_{a_1^{\prime}} A^{\ast}_{s, a_1^{\prime} a_2^{\prime}}, \end{array} \end{aligned} $$
(5.11)
$$\displaystyle \begin{aligned} \begin{array}{rcl} M^R_{a_1 a_1^{\prime} a_2 a_2^{\prime}} = \sum_{s} A_{s, a_1 a_2} \varGamma_{a_1} A^{\ast}_{s, a_1^{\prime} a_2^{\prime}} \varGamma_{a_1^{\prime}}^{\ast}. {} \end{array} \end{aligned} $$
(5.12)
Then the canonical conditions (Eq. (5.7)) say that the identity is the left (right) eigenvector of M L (M R), satisfying
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{a_1 a_1^{\prime}} I_{a_1 a_1^{\prime}} M^L_{a_1 a_1^{\prime} a_2 a_2^{\prime}} = \lambda^L I_{a_2 a_2^{\prime}}, \end{array} \end{aligned} $$
(5.13)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{a_1 a_1^{\prime}} I_{a_2 a_2^{\prime}} M^R_{a_1 a_1^{\prime} a_2 a_2^{\prime}} = \lambda^R I_{a_1 a_1^{\prime}}, \end{array} \end{aligned} $$
(5.14)
with λ L (λ R) the eigenvalue.
Similar eigenvalue equations can be obtained from the canonical conditions associated to the tensor B, where we have the transfer matrices as
$$\displaystyle \begin{aligned} \begin{array}{rcl} N^L_{a_1 a_1^{\prime} a_2 a_2^{\prime}} = \sum_{s} \varGamma_{a_1} B_{s, a_1 a_2} \varGamma^{\ast}_{a_1^{\prime}} B^{\ast}_{s, a_1^{\prime} a_2^{\prime}}, \end{array} \end{aligned} $$
(5.15)
$$\displaystyle \begin{aligned} \begin{array}{rcl} N^R_{a_1 a_1^{\prime} a_2 a_2^{\prime}} = \sum_{s} B_{s, a_1 a_2} \varLambda_{a_1} B^{\ast}_{s, a_1^{\prime} a_2^{\prime}} \varLambda_{a_1^{\prime}}^{\ast}. {} \end{array} \end{aligned} $$
(5.16)
Now the canonical conditions are given by four eigenvalue equations and can be reinterpreted as the following: with an infinite MPS formed by A, B, Λ and Γ, it is canonical when the identity is the eigenvector of its transfer matrices.

Simply from the canonical conditions, it does not require the “identity” to be dominant eigenvector. However, if the identity is not the dominant one, the canonical conditions will become unstable under an arbitrarily small noise. Below, we will show that the canonicalization algorithm assures that the identity is the leading eigenvector, since it transforms the leading eigenvector to an identity. In addition, if the dominant eigenvector of M L and M R (also N L and N R) is degenerate, the canonical form will not be unique. See Ref. [2] for more details.

5.1.3 Canonicalization Algorithm and Some Related Topics

Considering the iTEBD algorithm [3] (see Sect. 3.​4), while the MPO represents a unitary operator, the canonical form of the MPS will be reserved by the evolution (contraction). For the imaginary-time evolution, the MPO is near-unitary. For the Trotter step τ → 0, the MPO approaches to be an identity. It turns out that in this case, the MPS will be canonicalized by the evolution in the standard iTEBD algorithm. When the MPO is non-unitary (e.g., when contracting the TN of a 2D statistic model) [2], the MPS will not be canonical, and the canonicalization might be needed to better truncate the bond dimensions of the MPS.

Canonicalization Algorithm

An algorithm to canonicalize an arbitrary MPS was proposed by Orús and Vidal [2]. The idea is to compute the first eigenvectors of the transfer matrices, and introduce proper gauge transformations on the virtual bonds that map the leading eigenvector to identity.

Let us take the gauge transformations on the virtual bonds between A and B as an example. Firstly, compute the dominant left eigenvector v L of the matrix N LM L, and similarly the dominant right eigenvector v R of the matrix N RM R. Then, reshape v L and v R as two matrices and decompose them symmetrically as
$$\displaystyle \begin{aligned} \begin{array}{rcl} v^R_{a_1 a_1^{\prime}} &\displaystyle =&\displaystyle \sum_{a_1^{\prime\prime}} X_{a_1 a_1^{\prime\prime}}X^{\ast}_{a_1^{\prime} a_1^{\prime\prime}}, \end{array} \end{aligned} $$
(5.17)
$$\displaystyle \begin{aligned} \begin{array}{rcl} v^L_{a_1 a_1^{\prime}} &\displaystyle =&\displaystyle \sum_{a_1^{\prime\prime}} Y_{a_1 a_1^{\prime\prime}}Y^{\ast}_{a_1^{\prime} a_1^{\prime\prime}}. \end{array} \end{aligned} $$
(5.18)
X and Y  can be calculated using eigenvalue decomposition, i.e., v R = WDW † with $$X=W\sqrt {D}$$ .
Insert the identities X −1X and Y Y −1 on the virtual bond as shown in Fig. 5.4, then we get a new matrix $$\mathscr {M} = X \varGamma Y$$ on this bond. Apply SVD on $$\mathscr {M}$$ as $$\mathscr {M} = U \tilde {\varGamma } V^{\dagger }$$ , where we have the updated spectrum $$\tilde {\varGamma }$$ on this bond. Meanwhile, we obtain the gauge transformations to update A and B as $$\mathscr {U}=X^{-1}U$$ and $$\mathscr {V}=V^{\dagger } Y^{-1}$$ , where the transformations are implemented as
$$\displaystyle \begin{aligned} \begin{array}{rcl} A_{s_1,a_1 a_2} \leftarrow \sum_{a} A_{s_1,a_1 a} \mathscr{U}_{a a_2}, \end{array} \end{aligned} $$
(5.19)
$$\displaystyle \begin{aligned} \begin{array}{rcl} B_{s_1,a_1 a_2} \leftarrow \sum_{a} B_{s_1,a a_2} \mathscr{V}_{a_1 a}. \end{array} \end{aligned} $$
(5.20)
Implement the same steps given above on the virtual bonds between B and A, then the MPS is transformed to the canonical form.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig4_HTML.png
Fig. 5.4

The illustration of the canonical transformations

Variants of the Canonical Form
From the canonical form of an MPS, one can define the left or right-canonical forms. Define the follow tensors
$$\displaystyle \begin{aligned} \begin{array}{rcl} A^L_{s, a a'} &\displaystyle =&\displaystyle \varLambda_{a} A_{s, a a'}, \end{array} \end{aligned} $$
(5.21)
$$\displaystyle \begin{aligned} \begin{array}{rcl} A^R_{s, a a'} &\displaystyle =&\displaystyle A_{s, a a'} \varGamma_{a'}, \end{array} \end{aligned} $$
(5.22)
$$\displaystyle \begin{aligned} \begin{array}{rcl} B^L_{s, a a'} &\displaystyle =&\displaystyle \varGamma_{a} B_{s, a a'}, \end{array} \end{aligned} $$
(5.23)
$$\displaystyle \begin{aligned} \begin{array}{rcl} B^R_{s, a a'} &\displaystyle =&\displaystyle B_{s, a a'} \varLambda_{a'}, \end{array} \end{aligned} $$
(5.24)
$$\displaystyle \begin{aligned} \begin{array}{rcl} A^M_{s, a a'} &\displaystyle =&\displaystyle \varLambda_{a} A_{s, a a'} \varGamma_{a'}. \end{array} \end{aligned} $$
(5.25)
The left-canonical MPS is defined by A L and B L as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{tTr} (\cdots A^L B^L A^L B^L \cdots). \end{array} \end{aligned} $$
(5.26)
Similarly, the right-canonical MPS is defined by A R and B R as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{tTr} (\cdots A^R B^R A^R B^R \cdots). \end{array} \end{aligned} $$
(5.27)
The central-orthogonal MPS is defined as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{tTr} (\cdots A^L B^L A^M B^R A^R \cdots). \end{array} \end{aligned} $$
(5.28)
One can easily check that these MPSs and the canonical MPS can be transformed to each other by gauge transformations.

From the canonical conditions, A L, A R, B L, and B R are non-square orthogonal matrices (e.g., $$\sum _{s a} A^L_{s, a a'} A^{L\ast }_{s, a a''} = I_{a' a''}$$ ), called isometries. A M is called the central tensor of the central-orthogonal MPS. This MPS form is the state ansatz behind the DMRG algorithm [4, 5], and is very useful in TN-based methods (see, for example, the works of McCulloch [6, 7]). For instance, when applying DMRG to solve 1D quantum model, the tensors A L and B L define a left-to-right RG flow that optimally compresses the Hilbert space of the left part of the chain. A R and B R define a right-to-left RG flow similarly. The central tensor between these two RG flows is in fact the ground state of the effective Hamiltonian given by the RG flows of DMRG. Note that the canonical MPS is also called the central canonical form, where the directions of the RG flows can be switched arbitrarily by gauge transformations, thus there is no need to define the directions of the flows or a specific center.

Relations to Tensor Train Decomposition

It is worth mentioning the TTD [8] proposed in the field of MLA . As argued in Chap. 2, one advantage of MPS is it lowers the number of parameters from an exponential size dependence to a polynomial one. Let us consider a similar problem: for a N-th order tensor that has d N parameters, how to find its optimal MPS representation, where there are only [2dχ + (N − 2)dχ 2] parameters? TTD was proposed for this aim: by decomposing a tensor into a tensor-train form that is similar to a finite open MPS, the number of parameters becomes linearly relying to the order of the original tensor. The TTD algorithm shares many similar ideas with MPS and the related algorithms (especially DMRG which was proposed about two decades earlier). The aim of TTD is also similar to the truncation tasks in the TN algorithms, which is to compress the number of parameters.

5.2 Super-Orthogonalization and Tucker Decomposition

As discussed in the above section, the canonical form of an MPS brings a lot of advantages, such as determining the entanglement and the optimal truncations of the virtual bond dimensions by local transformations. The canonical form can be readily generalized to the iPEPSs on trees. Can we also define the canonical form for the iPEPSs in higher-dimensional regular lattices, such as square lattice (Fig. 5.5)? If this can be done, we would know how to find the globally optimal transformations that reduces the bond dimensions of the iPEPS, just like what we can do with an MPS. Due to the complexity of 2d TN’s , unfortunately, there is no such a form in general. In the following, we explain the super-orthogonal form of iPEPS proposed in 2012 [9], which applies the canonical form of tree iPEPS to the iPEPS on regular lattices. The super-orthogonalization is a generalization of the Tucker decomposition (a higher-order generalization of matrix SVD ) [10], providing a zero-loop approximation scheme [11] to define the entanglement and truncate the bond dimensions.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig5_HTML.png
Fig. 5.5

The first two figures show the iPEPS on tree and square lattices, with two-site translational invariance. The last one shows the super-orthogonal conditions

5.2.1 Super-Orthogonalization

Let us start from the iPEPS on the (infinite) Bethe lattice with the coordination number z = 4. It is formed by two tensors P and Q on the sites as well as four spectra Λ (k) (k = 1, 2, 3, 4) on the bonds, as illustrated in Fig. 5.5. Here, we still take the two-site translational invariance for simplicity.

There are eight super-orthogonal conditions, of which four associate to the tensor P and four to Q. For P, the conditions are
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_s \sum_{\cdots a_{k-1} a_{k+1} \cdots} P_{s,\cdots a_k \cdots} P_{s,\cdots a_k^{\prime} \cdots}^{\ast} \prod_{n \neq k} \varLambda^{(n)}_{a_n} \varLambda^{(n)\ast}_{a_n} = I_{a_{k} a_{k}^{\prime}}, \ \ (\forall \ k), {} \end{array} \end{aligned} $$
(5.29)
where all the bonds along with the corresponding spectra are contracted except for a k. It means that by putting a k as one index and all the rest as another, the k-rectangular matrix S (k) defined as
$$\displaystyle \begin{aligned} \begin{array}{rcl} S^{(k)}_{s\cdots a_{k-1} a_{k+1} \cdots, a_k} = P_{s,\cdots a_k \cdots} \prod_{n \neq k} \varLambda^{(n)}_{a_n}, {} \end{array} \end{aligned} $$
(5.30)
is an isometry, satisfying S (k)†S (k) = I. The super-orthogonal conditions of the tensor Q are defined in the same way. Λ (k) is dubbed super-orthogonal spectrum when the super-orthogonal conditions are fulfilled.

In the canonicalization of MPS , the vectors on the virtual bonds give the bipartite entanglement defined by Eq. (5.5). Meanwhile, the bond dimensions can be optimally reduced by discarding certain smallest elements of the spectrum. In the super-orthogonalization, this is not always true for iPEPSs. For example, given a translational invariant iPEPS defined on a tree (or called Bethe lattice, see Fig. 5.5a) [12–19], the super-orthogonal spectrum indeed gives the bipartite entanglement spectrum by cutting the system at the corresponding place. However, when considering loopy lattices, such as the iPEPS defined on a square lattice (Fig. 5.5b), this will no longer be true. Instead, the super-orthogonal spectrum provides an approximation of the entanglement of the iPEPS by optimally ignoring the loops. One can still truncate the bond dimensions according to the super-orthogonal spectrum, giving in fact the simple update (see Sect. 4.​3). We will discuss the loopless approximation in detail in Sect. 5.3 using the rank-1 decomposition.

5.2.2 Super-Orthogonalization Algorithm

Any PEPS can be transformed to the super-orthogonal form by iteratively implementing proper gauge transformations on the virtual bonds [9]. The algorithm consists of two steps. Firstly, compute the reduced matrix $$\mathscr {M}^{(k)}$$ of the k-rectangular matrix of the tensor P (Eq. (5.30)) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{M}^{(k)}_{a_{k} a_{k}^{\prime}}=\sum_s \sum_{\cdots a_{k-1} a_{k+1} \cdots} S^{(k)}_{s\cdots a_{k-1} a_{k+1} \cdots, a_k} S^{(k)\ast}_{s\cdots a_{k-1} a_{k+1} \cdots, a_k^{\prime}}. {} \end{array} \end{aligned} $$
(5.31)
Compared with the super-orthogonal conditions in Eq. (5.29), one can see that $$\mathscr {M}^{(k)}=I$$ when the PEPS is super-orthogonal. Similarly, we define the reduced matrix $$\mathscr {N}^{(k)}$$ of the tensor Q.
When the PEPS is not super-orthogonal, $$\mathscr {M}^{(k)}$$ and $$\mathscr {N}^{(k)}$$ are not identities but Hermitian matrices. Decompose them as $$\mathscr {M}^{(k)}=X^{(k)}X^{(k)\dagger }$$ and $$\mathscr {N}^{(k)}=Y^{(k)} Y^{(k)\dagger }$$ . Then, insert the identities X (k)[X (k)]−1 and Y (k)[Y (k)]−1 on the virtual bonds to perform gauge transformations along four directions as shown in Fig. 5.6. Then, we can use SVD to renew the four spectra by $$X^{(k)}\varLambda ^{(k)}Y^{(k)T} = U^{(k)}\tilde {\varLambda }^{(k)}V^{(k)\dagger }$$ . Meanwhile, we transform the tensors as
$$\displaystyle \begin{aligned} \begin{array}{rcl} P_{s,\cdots a_k \cdots} \leftarrow \sum_{a_k^{\prime}a_k^{\prime\prime}} P_{s,\cdots a_k^{\prime} \cdots} [X^{(k)}]^{-1}_{a_k^{\prime}a_k^{\prime\prime}} U^{(k)}_{a_k^{\prime\prime} a_k}, \end{array} \end{aligned} $$
(5.32)
$$\displaystyle \begin{aligned} \begin{array}{rcl} Q_{s,\cdots a_k \cdots} \leftarrow \sum_{a_k^{\prime}a_k^{\prime\prime}} Q_{s,\cdots a_k^{\prime} \cdots} [Y^{(k)}]^{-1}_{a_k^{\prime}a_k^{\prime\prime}} V^{(k)\ast}_{a_k^{\prime\prime} a_k}. \end{array} \end{aligned} $$
(5.33)
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig6_HTML.png
Fig. 5.6

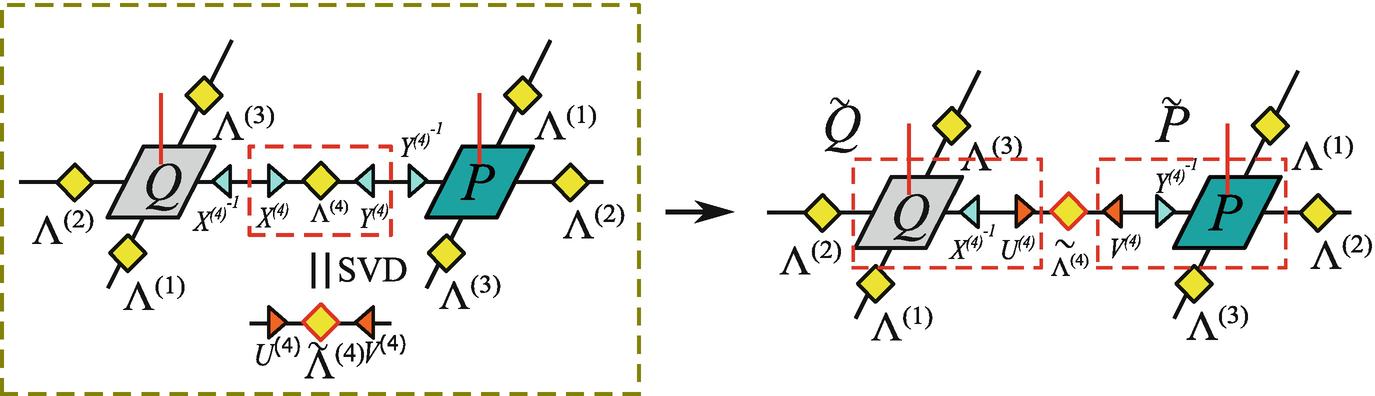
The illustrations of gauge transformations in the super-orthogonalization algorithm

Compared with the canonicalization algorithm of MPS , one can see that the gauge transformations in the super-orthogonalization algorithm are quite similar. The difference is that one cannot transform a PEPS into the super-orthogonal form by a single step, since the transformation on one bond might cause some deviation from obeying the super-orthogonal conditions on other bonds. Thus, the above procedure should be iterated until all the tensors and spectra converge.

5.2.3 Super-Orthogonalization and Dimension Reduction by Tucker Decomposition

Such an iterative scheme is closely related to the Tucker decomposition in MLA [10]. Tucker decomposition is considered as a generalization of (matrix) SVD to higher-order tensors, thus it is also called higher-order or multi-linear SVD. The aim is to find the optimal reductions of the bond dimensions for a single tensor.

Let us define the k-reduced matrix of a tensor T as
$$\displaystyle \begin{aligned} \begin{array}{rcl} M^{(k)}_{a_k a_k^{\prime}} = \sum_{a_1 \cdots a_{k-1} a_{k+1} \cdots} T_{a_1 \cdots a_{k-1} a_k a_{k+1} \cdots} T_{a_1 \cdots a_{k-1} a_k^{\prime} a_{k+1} \cdots}^{\ast}, \end{array} \end{aligned} $$
(5.34)
where all except the k-th indexes are contracted. The Tucker decomposition (Fig. 5.7) of a tensor T has the form as
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1 a_2 \cdots} = \sum_{a_1a_2 \cdots} S_{b_1b_2 \cdots} \prod_{k} U^{(k)}_{a_kb_k}, {} \end{array} \end{aligned} $$
(5.35)
where the following conditions should be satisfied:

  • Unitarity. U (k) are unitary matrices satisfying U (k)U (k)† = I.

  • All-orthogonality. For any k, the k-reduced matrix M (k) of the tensor S is diagonal, satisfying
    $$\displaystyle \begin{aligned} \begin{array}{rcl} M^{(k)}_{a_k a_k^{\prime}} = \varGamma^{(k)}_{a_k} I_{a_k a_k^{\prime}}. \end{array} \end{aligned} $$
    (5.36)

  • Ordering. For any k, the elements of Γ (k) in the k-reduced matrix are positive-defined and in the descending order, satisfying Γ 0 > Γ 1 > ⋯.

../images/489509_1_En_5_Chapter/489509_1_En_5_Fig7_HTML.png
Fig. 5.7

The illustrations of Tucker decomposition (Eq. (5.35))

From these conditions, one can see that the tensor T is decomposed as the contraction of another tensor S with several unitary matrices. S is called the core tensor. In other words, the optimal lower-rank approximation of the tensor can be simply obtained by
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1 a_2 \cdots} \simeq \sum_{a_1a_2 \cdots = 0}^{\chi-1} S_{b_1b_2 \cdots} \prod_{k} U^{(k)}_{a_kb_k}, \end{array} \end{aligned} $$
(5.37)
where we only take the first χ terms in the summation of each index.
Such an approximations can be understood in terms of the SVD of matrices. Applying the conditions of the k-reduced matrix of T, we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} M^{(k)}_{a_k a_k^{\prime}} = \sum_{b_k} U^{(k)}_{a_kb_k} \varGamma^{(k)}_{b_k} U^{(k)\dagger}_{a_k^{\prime}b_k}. \end{array} \end{aligned} $$
(5.38)
Since U (k) is unitary and Γ (k) is positive-defined and in the descending order, the above equation is exactly the eigenvalue decomposition of M (k). From the relation between the SVD of a matrix and the eigenvalue decomposition of its reduced matrix, we can see that U (k) and Γ (k) in fact give the SVD of the matrix $$T_{a_1 \cdots a_{k-1} a_{k+1} \cdots , a_{k}}$$ as
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1 \cdots a_{k-1} a_{k+1} \cdots, a_{k}} = \sum_{b_k} \mathscr{S}_{a_1 \cdots a_{k-1} a_{k+1} \cdots, b_{k}} \sqrt{\varGamma^{(k)}_{b_k}} U^{(k)}_{a_kb_k}. \end{array} \end{aligned} $$
(5.39)
Then, The optimal truncation of the rank of each index is reached by the corresponding SVD . The truncation error is obviously the distance defined as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon^{(k)} = \left|T_{a_1 \cdots a_{k-1} a_{k+1} \cdots, a_{k}} - \sum_{b_k=1}^{\chi} \mathscr{S}_{a_1 \cdots a_{k-1} a_{k+1} \cdots} \varGamma^{(k)}_{b_k} U^{(k)}_{a_kb_k}\right|, \end{array} \end{aligned} $$
(5.40)
which is minimized in this SVD.

For the algorithms of Tucker decomposition, one simple way is to do the eigenvalue decomposition of each k-reduced matrix, or the SVD of each k-rectangular. Then for a K-th ordered tensor, K SVDs will give us the Tucker decomposition and a lower-rank approximation. This algorithm is often called higher-order SVD (HOSVD) , which has been successfully applied to implement truncations in the TRG algorithm [20]. The accuracy of HOSVD can be improved. Since the truncation on one index will definitely affect the truncations on other indexes, there will be some “interactions” among different indexes (modes) of the tensor. The truncations in HOSVD are calculated independently, thus such “interactions” are ignored. One improved way is the high-order orthogonal iteration (HOOI) , where the interactions among different modes are considered by iteratively doing SVDs until reaching the convergence. See more details in Ref. [10].

Compared with the conditions of Tucker decomposition, let us redefine the super-orthogonal conditions of a PEPS as
  • Super-orthogonality. For any k, the reduced matrix of the k-rectangular matrix $$\mathscr {M}^{(k)}$$ (Eq. (5.31)) is diagonal, satisfying
    $$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{M}^{(k)}_{a_k a_k^{\prime}} = \varGamma^{(k)}_{a_k} I_{a_k a_k^{\prime}}. \end{array} \end{aligned} $$
    (5.41)

  • Ordering. For any k, the elements of Γ (k) are positive-defined and in the descending order, satisfying Γ 0 > Γ 1 > ⋯.

Note that the condition “unitary” (first one in Tucker decomposition) is hidden in the fact that we use gauge transformations to transform the PEPS into the super-orthogonal form. Therefore, the super-orthogonalization is also called network Tucker decomposition (NTD) .

In the Tucker decomposition, the “all-orthogonality” and “ordering” lead to an SVD associated to a single tensor, which explains how the optimal truncations work from the decompositions in linear algebra. In the NTD, the SVD picture is generalized from a single tensor to a non-local PEPS. Thus, the truncations are optimized in a non-local way.

Let us consider a finite-size PEPS and arbitrarily choose one geometrical bond (say a). If the PEPS is on a tree, we can cut the bond and separate the TN into three disconnecting parts: the spectrum (Λ) on this bond and two tree brunches stretching to the two sides of the bond. Specifically speaking, each brunch contains one virtual bond and all the physical bonds on the corresponding side, formally denoted as $$\varPsi ^L_{i_1i_2 \cdots ,a}$$ (and $$\varPsi ^R_{j_1j_2 \cdots ,a}$$ on the other side). Then the state given by the iPEPS can be written as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_a \varPsi^L_{i_1i_2 \cdots,a} \varLambda_a \varPsi^R_{j_1j_2 \cdots,a}. {} \end{array} \end{aligned} $$
(5.42)
To get the SVD picture, we need to prove that Ψ L and Ψ R in the above equation are isometries, satisfying the orthogonal conditions as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} \sum_{i_1i_2 \cdots} \varPsi^L_{i_1i_2 \cdots,a} \varPsi^L_{i_1i_2 \cdots,a'} = I_{aa'},\\ \sum_{j_1j_2 \cdots} \varPsi^R_{j_1j_2 \cdots,a} \varPsi^R_{j_1j_2 \cdots,a'} = I_{aa'}. \end{aligned} {} \end{array} \end{aligned} $$
(5.43)
Note that the spectrum Λ is already positive-defined according to the algorithm. To this end, we construct the TN of $$\sum _{i_1i_2 \cdots } \varPsi ^{L(R)}_{i_1i_2 \cdots ,a} \varPsi ^{L(R)}_{i_1i_2 \cdots ,a'}$$ from its boundary. If the PEPS is super-orthogonal, the spectra must be on the boundary of the TN because the super-orthogonal conditions are satisfied everywhere.1 Then the contractions of the tensors on the boundary satisfy Eq. (5.29), which gives identities. Then we have on the new boundary again the spectra to iterate the contractions. All tensors can be contracted by iteratively using the super-orthogonal conditions, which in the end gives identities as Eq. (5.43). Thus, Ψ L and Ψ R are indeed isometries and Eq. (5.42) indeed gives the SVD of the whole wave-function. The truncations of the bond dimensions are globally optimized by taking the whole tree PEPS as the environment.

For an iPEPS , it can be similarly proven that Ψ L and Ψ R are isometries. One way is to put any non-zero spectra on the boundary and iterate the contraction by Eq. (5.31). While the spectra on the boundary can be arbitrary, the results of the contractions by Eq. (5.31) converge to identities quickly [9]. Then the rest of the contractions are exactly given by the super-orthogonal conditions (Eq. (5.29)). In other words, the identity is a stable fixed point of the above iterations. Once the fixed point is reached, it can be considered that the contraction is from infinitely far away, meaning from the “boundary” of the iPEPS. In this way, one proves Ψ L and Ψ R are isometries, i.e., Ψ L†Ψ L = I and Ψ R†Ψ R = I.

5.3 Zero-Loop Approximation on Regular Lattices and Rank-1 Decomposition

5.3.1 Super-Orthogonalization Works Well for Truncating the PEPS on Regular Lattice: Some Intuitive Discussions

From the discussions above, we can see that the “canonical” form of a TN state is strongly desired, because it is expected to give the entanglement and the optimal truncations of the bond dimensions. Recall that to contract a TN that cannot be contracted exactly, truncations are inevitable, and locating the optimal truncations is one of the main tasks in the computations. The super-orthogonal form provides a robust way to optimally truncate the bond dimensions of the PEPS defined on a tree, analog to the canonicalization of MPS .

Interestingly, the super-orthogonal form does not require the tree structure. For an iPEPS defined on a regular lattice, for example, the square lattice, one can still super-orthogonalize it using the same algorithm. What is different is that the SVD picture of the wave-function (generally, see Eq. (5.5)) will not rigorously hold, as well as the robustness of the optimal truncations. In other words, the super-orthogonal spectrum does not exactly give the entanglement. A question rises: can we still truncate iPEPS defined on a square lattice according to the super-orthogonal spectrum?

Surprisingly, numeric simulations show that the accuracy by truncating according to the super-orthogonal spectrum is still good in many cases. Let us take the ground-state simulation of a 2D system by imaginary-time evolution as an example. As discussed in Sect. 4.​2, the simulation becomes the contraction of a 3D TN . One usual way to compute this contraction is to contract layer by layer to an iPEPS (see, e.g., [22, 23]). The contraction will enlarge the virtual bond dimensions, and truncations are needed. When the ground state is gapped (see, e.g., [9, 23]), the truncations produce accurate results, which means the super-orthogonal spectrum approximates the true entanglement quite well.

It has been realized that using the simple update algorithm [23], the iPEPS will converge to the super-orthogonal form for a vanishing Trotter step τ → 0. The success of the simple update suggests that the optimal truncation method on trees still works well for regular lattices. Intuitively, this can be understood in the following way. Comparing a regular lattice with a tree, if it has the same coordination number, the two lattices look exactly the same if we only inspect locally on one site and its nearest neighbors. The difference appears when one goes round the closed loops on the regular lattice, since there is no loop in the tree. Thus, the error applying the optimal truncation schemes (such as super-orthogonalization) of a tree to a regular lattice should be characterized by some non-local features associated to the loops. This explains in a descriptive way why the simple update works well for gapped states, where the physics is dominated by short-range correlations. For the systems that possess small gaps or are gapless, simple update is not sufficiently accurate [24], particularly for the non-local physical properties such as the correlation functions.

5.3.2 Rank-1 Decomposition and Algorithm

Rank-1 decomposition in MLA [25] provides a more mathematic and rigorous way to understand the approximation by super-orthogonalization (simple update) to truncate PEPS on regular lattices [11]. For a tensor T, its rank-1 decomposition (Fig. 5.8) is defined as
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1a_2\cdots a_K} \simeq \varOmega \prod_{k=1}^K v^{(k)}_{a_k}, {} \end{array} \end{aligned} $$
(5.44)
where v (k) are normalized vectors and Ω is a constant that satisfies
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varOmega = \sum_{a_1a_2\cdots a_K} T_{a_1a_2\cdots a_K} \prod_{k=1}^K v^{(k)\ast}_{a_k}. {} \end{array} \end{aligned} $$
(5.45)
Rank-1 decomposition provides an approximation of T, where the distance between T and its rank-1 approximation is minimized, i.e.,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \min_{\left|v^{(k)}_{a_k}\right|=1} \left|T_{a_1a_2\cdots a_K} - \varOmega \prod_{k=1}^K v^{(k)}_{a_k}\right|. {} \end{array} \end{aligned} $$
(5.46)
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig8_HTML.png
Fig. 5.8

The illustrations of rank-1 decomposition (Eq. (5.44))

The rank-1 decomposition is given by the fixed point of a set of self-consistent equations (Fig. 5.9), which are
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{\text{all except } a_k} T_{a_1a_2\cdots a_K} \prod_{j \neq k} v^{(j)}_{a_j} = \varOmega v^{(k)}_{a_k} \ \ (\forall \ k). {} \end{array} \end{aligned} $$
(5.47)
It means that v (k) is obtained by contracting all other vectors with the tensor. This property provides us an algorithm to compute rank-1 decomposition: one arbitrarily initializes the vectors {v (k)} of norm-1 and recursively updates each vector by the tensor and the rest vectors using Eq. (5.47) until all vectors converge.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig9_HTML.png
Fig. 5.9

The illustrations of self-consistent conditions for the rank-1 decomposition (Eq. (5.47))

Apart from some very special cases, such an optimization problem is concave, thus rank-1 decomposition is unique.2 Furthermore, if one arbitrarily chooses a set of norm-1 vectors, they will converge to the fixed point exponentially fast with the iterations. To the best of our knowledge, the exponential convergence has not been proved rigorously, but observed in most cases.

5.3.3 Rank-1 Decomposition, Super-Orthogonalization, and Zero-Loop Approximation

Let us still consider an translational invariant square TN that is formed by infinite copies of the 4th-order tensor T (Fig. 2.​28). The rank-1 decomposition of T provides an approximative scheme to compute the contraction of the TN, which is called the theory of network contractor dynamics (NCD) [11].

The picture of NCD can be understood in an opposite way to contraction, but by iteratively using the self-consistent conditions (Eq. (5.47)) to “grow” a tree TN that covers the whole square lattice (Fig. 5.10). Let us start from Eq. (5.45) of Ω. Using Eq. (5.47), we substitute each of the four vectors by the contraction of T with the other three vectors. After doing so, Eq. (5.45) becomes the contraction of more than one Ts with the vectors on the boundary. In other words, we “grow” the local TN contraction from one tensor plus four vectors to that with more tensors and vectors.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig10_HTML.png
Fig. 5.10

Using the self-consistent conditions of the rank-1 decomposition, a tree TN with no loops can grow to cover the infinite square lattice. The four vectors gathering in a same site give the rank-1 approximation of the original tensor

By repeating the substitution, the TN can be grown to cover the whole square lattice, where each site is allowed to put maximally one T. Inevitably, some sites will not have T, but four vectors instead. These vectors (also called contractors) give the rank-1 decomposition of T as Eq. (5.44). This is to say that some tensors in the square TN are replaced by its rank-1 approximation, so that all loops are destructed and the TN becomes a loopless tree covering the square lattice. In this way, the square TN is approximated by such a tree TN on square lattice, so that its contraction is simply computed by Eq. (5.45).

The growing process as well as the optimal tree TN is only to understand the zero-loop approximation with rank-1 decomposition. There is no need to practically implement such a process. Thus, it does not matter how the TN is grown or where the rank-1 tensors are put to destroy the loops. All information we need is given by the rank-1 decomposition. In other words, the zero-loop approximation of the TN is encoded in the rank-1 decomposition.

For growing the TN , we shall remark that using the contraction of one T with several vectors to substitute one vector is certainly not unique. However, the aim of “growing” is to reconstruct the TN formed by T. Thus, if T has to appear in the substitution, the vectors should be uniquely chosen as those given in the rank-1 decomposition due to the uniqueness of rank-1 decomposition. Secondly, there are hidden conditions when covering the lattice by “growing”. A stronger version is
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1a_2a_3a_4} = T_{a_3a_2a_1a_4}^{\ast} = T_{a_1a_4a_3a_2}^{\ast} = T_{a_3a_4a_1a_2}. {} \end{array} \end{aligned} $$
(5.48)
And a weaker one only requires the vectors to be conjugate to each other as
$$\displaystyle \begin{aligned} \begin{array}{rcl} v^{(1)} = v^{(3)\dagger}, \ \ v^{(2)} = v^{(4)\dagger}. {} \end{array} \end{aligned} $$
(5.49)
These conditions assure that the self-consistent equations encode the correct tree that optimally in the rank-1 sense approximates the square TN.
Comparing with Eqs. (5.29) and (5.47), the super-orthogonal conditions are actually equivalent to the above self-consistent equations of rank-1 decomposition by defining the tensor T and vector v as
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1a_2 \cdots a_K} &\displaystyle =&\displaystyle \sum_s P_{s,a_1^{\prime} a_2^{\prime} \cdots a_K^{\prime}} P_{s,a_1^{\prime\prime} a_2^{\prime\prime} \cdots a_K^{\prime\prime}}^{\ast} \prod_{k=1}^K \sqrt{\varLambda^{(k)}_{a_k^{\prime}} \varLambda^{(k)\ast}_{a_k^{\prime\prime}}}, {} \end{array} \end{aligned} $$
(5.50)
$$\displaystyle \begin{aligned} \begin{array}{rcl} v^{(k)}_{a_k} &\displaystyle =&\displaystyle \sqrt{\varLambda^{(k)}_{a_k^{\prime}} \varLambda^{(k)\ast}_{a_k^{\prime\prime}}}, {} \end{array} \end{aligned} $$
(5.51)
with $$a_k= (a_k^{\prime },a_k^{\prime \prime })$$ . Thus, the super-orthogonal spectrum provides an optimal approximation for the truncations of the bond dimensions in the zero-loop level. This provides a direct connection between the simple update scheme and rank-1 decomposition.

5.3.4 Error of Zero-Loop Approximation and Tree-Expansion Theory Based on Rank-Decomposition

The error of NCD (and simple update) is an important issue. From the first glance, the error seems to be the error of rank-1 decomposition ε = |T −∏kv (k)|. This would be true if we replaced all tensors in the square TN by the rank-1 version. In this case, the PEPS is approximated by a product state with zero entanglement. In the NCD scheme, however, we only replace a part of the tensors to destruct the loops. The corresponding approximative PEPS is an entanglement state with a tree structure. Therefore, the error of rank-1 decomposition cannot properly characterize the error of simple update.

To control the error, let us introduce the rank decomposition (also called CANDECOMP/PARAFAC decomposition) of T in MLA (Fig. 5.11) that reads
$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{a_1a_2 \cdots} = \sum_{r=0}^{R-1} \varOmega_r \prod_k v^{(k,r)}_{a_{k}}, {} \end{array} \end{aligned} $$
(5.52)
where v (k, r) are normalized vectors. The idea of rank decomposition [26, 27] is to expand T into the summation of R number of rank-1 tensors with R called the tensor rank. The elements of the vector Ω can always be in the descending order according to the absolute values. Then the leading term Ω 0∏kv (k, 0) gives exactly the rank-1 decomposition of T, and the error of the rank-1 decomposition becomes $$|\sum _{r=1}^{R-1} \varOmega _r \prod _k v^{(k,r)}_{a_{k}}|$$ .
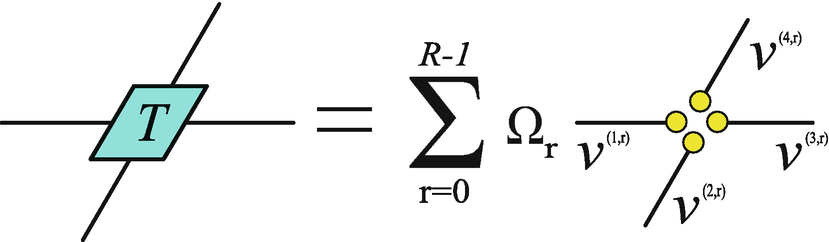
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig11_HTML.png
Fig. 5.11

The illustrations of rank-1 decomposition (Eq. (5.52))

In the optimal tree TN , let us replace the rank-1 tensors back by the full rank tensor in Eq. (5.52). We suppose the rank decomposition is exact, thus we will recover the original TN by doing so. The TN contraction becomes the summation of $$R^{\tilde {N}}$$ terms with $$\tilde {N}$$ the number of rank-1 tensors in the zero-loop TN. Each term is the contraction of a tree TN, which is the same as the optimal tree TN except that certain vectors are changed to v (k, r) instead of the rank-1 term v (k, 0). Note that in all terms, we use the same tree structure; the leading term in the summation is the zero-loop TN in the NCD scheme. It means with rank decomposition, we expand the contraction of the square TN by the summation of the contractions of many tree TN’s.

Let us order the summation referring to the contributions of different terms. For simplicity, we assume R = 2, meaning T can be exactly decomposed as the summation of two rank-1 tensors, which are the leading term given by the rank-1 decomposition, and the next-leading term denoted as T 1 = Ω 1∏kv (k, 1). We dub as the next-leading term as the impurity tensor. Defining $$\tilde {n}$$ as the number of the impurity tensors appearing in one of the tree TN in the summation, the expansion can be written as
$$\displaystyle \begin{aligned} \begin{array}{rcl} Z = \varOmega_0^{\tilde{N}} \sum_{\tilde{n}=0}^{\tilde{N}} \left(\frac{\varOmega_1}{\varOmega_0}\right)^{\tilde{n}} \sum_{\mathscr{C} \in \mathscr{C}(\tilde{n})} Z_{\mathscr{C}}. {} \end{array} \end{aligned} $$
(5.53)
We use $$\mathscr {C}(\tilde {n})$$ to denote the set of all possible configurations of $$\tilde {n}$$ number of the impurity tensors, where there are $$\tilde {n}$$ of T 1s located in different positions in the tree. Then $$Z_{\mathscr {C}}$$ denotes the contraction of such a tree TN with a specific configuration of T 1’s. In general, the contribution is determined by the order of |Ω 1∕Ω 0| since |Ω 1∕Ω 0| < 1 (Fig. 5.12).
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig12_HTML.png
Fig. 5.12

The illustrations of the expansion with rank decomposition. The yellow and red circles stand for $$v^{(k,0)}_{a_k}$$ (zeroth order terms in the rank decomposition) and $$v^{(k,1)}_{a_k}$$ (first order terms), respectively. Here, we consider the tensor rank R = 2 for simplicity

To proceed, we choose one tensor in the tree as the original point, and always contract the tree TN by ending at this tensor. Then the distance $$\mathscr {D}$$ of a vector is defined as the number of tensors in the path that connects this vector to the original point. Note that one impurity tensor is the tensor product of several vectors, and each vector may have different distance to the original point. For simplicity, we take the shortest one to define the distance of an impurity tensor.

Now, let us utilize the exponential convergence of the rank-1 decomposition. After contracting any vectors with the tensor in the tree, the resulting vector approaches to the fixed point (the vectors in the rank-1 decomposition) in an exponential speed. Define $$\mathscr {D}_0$$ as the average number of the contractions that will project any vectors to the fixed point with a tolerable difference. Consider any impurity tensors with the distance $$\mathscr {D}&gt;\mathscr {D}_0$$ , their contributions to the contraction are approximately the same, since after $$\mathscr {D}_0$$ contractions, the vectors have already been projected to the fixed point.

From the above argument, we can see that the error is related not only to the error of the rank-1 decomposition, but also to the speed of the convergence to the rank-1 component. The smaller $$\mathscr {D}_0$$ is, the smaller the error (the total contribution from the non-dominant terms) will be. Calculations show that the convergence speed is related to the correlation length (or gap) of the physical system, but their rigorous relations have not been established yet. Meanwhile, the expansion theory of the TN contraction given above requires the rank decomposition, which, however, is not uniquely defined of an arbitrarily given tensor.

5.4 iDMRG, iTEBD, and CTMRG Revisited by Tensor Ring Decomposition

We have shown that the rank-1 decomposition solves the contraction of infinite-size tree TN and provides a mathematic explanation of the approximation made in the simple update. Then, it is natural to think: can we generalize this scheme beyond being only rank-1, in order to have better update schemes? In the following, we will show that besides the rank decomposition, the tensor ring decomposition (TRD) [28] was suggested as another rank-N generalization for solving TN contraction problems.

TRD is defined by a set of self-consistent eigenvalue equations (SEEs) with certain constraints. The original proposal of TRD requires all eigenvalue equations to be Hermitian [28]. Later, a generalize version was proposed [29] that provides an unified description of the iDMRG [4, 5, 7], iTEBD [3], and CTMRG [30] algorithms. We will concentrate on this version in the following.

5.4.1 Revisiting iDMRG, iTEBD, and CTMRG: A Unified Description with Tensor Ring Decomposition

Let us start from the iDMRG algorithm. The TN contraction can be solved using the iDMRG [4, 5, 7] by considering an infinite-size row of tensors in the TN as an MPO [31–35] (also see some related discussions in Sect. 3.​4). We introduce three third-order variational tensors denoted by v L, v R (dubbed as the boundary or environmental tensors) and Ψ (dubbed as the central tensor). These tensors are the fixed-point solution of the a set of eigenvalue equations. v L and v R are, respectively, the left and right dominant eigenvector of the following matrices (Fig. 5.13a, b)
$$\displaystyle \begin{aligned} \begin{array}{rcl} M^L_{c'b_1^{\prime}b_1,cb_2^{\prime}b_2} = \sum_{aa'} T_{a'c'ac} A^{\ast}_{a'b_1^{\prime}b_2^{\prime}} A_{a b_1b_2}, {} {} \end{array} \end{aligned} $$
(5.54)
$$\displaystyle \begin{aligned} \begin{array}{rcl} M^R_{c'b_1^{\prime}b_1,cb_2^{\prime}b_2} = \sum_{aa'} T_{a'c'ac} B^{\ast}_{a'b_1^{\prime}b_2^{\prime}} B_{a b_1b_2}, {} \end{array} \end{aligned} $$
(5.55)
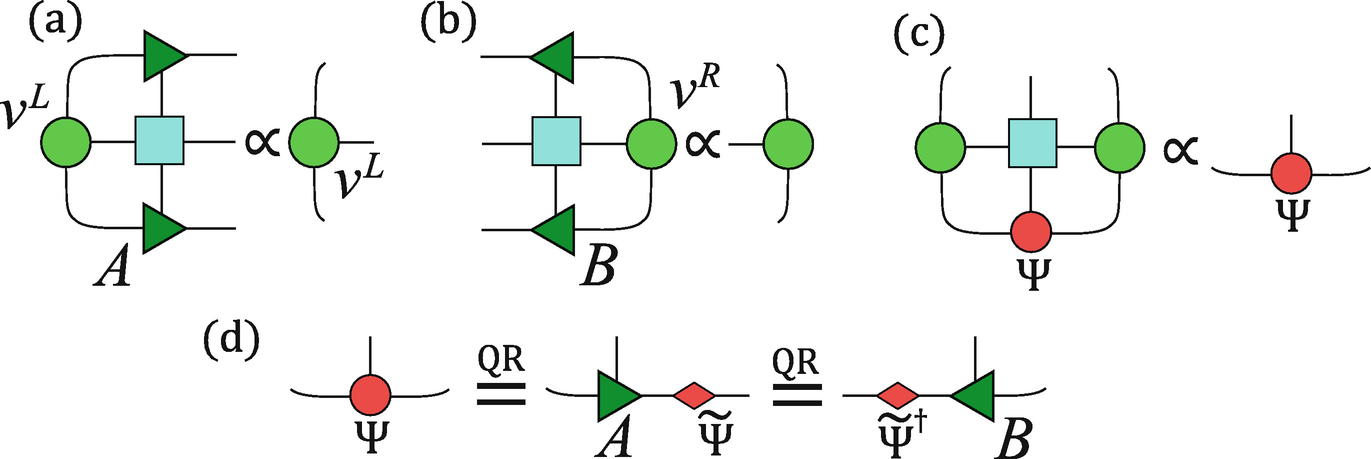
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig13_HTML.png
Fig. 5.13

The (a, b) and (c) show the three local eigenvalue equations given by Eqs. (5.55) and (5.57). The isometries A and B are obtained by the QR decompositions of Ψ in two different ways in Eq. (5.56), as shown in (d)

where A and B are the left and right orthogonal parts obtained by the QR decomposition (or SVD ) of Ψ (Fig. 5.13d) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPsi_{abb'} = \sum_{b''} A_{abb''} \tilde{\varPsi}_{b''b'} = \sum_{b''} \tilde{\varPsi}^{\dagger}_{bb''} B_{ab''b'}. {} \end{array} \end{aligned} $$
(5.56)
Ψ is the dominant eigenvector of the Hermitian matrix (Fig. 5.13c) that satisfies
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{H}_{a'b_1^{\prime}b_2^{\prime},ab_1b_2} = \sum_{cc'} T_{a'c'ac} v^{L}_{c'b_1^{\prime}b_1} v^R_{cb_2^{\prime}b_2}. {} \end{array} \end{aligned} $$
(5.57)

One can see that each of the eigenvalue problems is parametrized by the solutions of others, thus we solve them in a recursive way. First, we initialize arbitrarily the central tensors Ψ and get A and B by Eq. (5.56). Note that a good initial guess can make the simulations faster and more stable. Then we update v L and v R by multiplying with M L and M R as Eqs. (5.54) and (5.55). Then we have the new Ψ by solving the dominant eigenvector of $$\mathscr {H}$$ in Eq. (5.57) that is defined by the new v L and v R. We iterate such a process until all variational tensors converge.

Let us rephrase the iDMRG algorithm given above in the language of TN contraction/reconstruction. When the variational tensors give the fixed point, the eigenvalue equations “encodes” the infinite TN, i.e., the TN can be reconstructed from the equations. To do so, we start from a local representation of Z (Fig. 5.14) written as
$$\displaystyle \begin{aligned} \begin{array}{rcl} Z \leftrightharpoons \sum T_{a'c'ac} \varPsi^{\ast}_{a'b_1b_2} \varPsi_{ab_3b_4} v^{L}_{c'b_1b_3} v^R_{c b_2b_4}, {} \end{array} \end{aligned} $$
(5.58)
where the summation goes through all indexes. According to the fact that Ψ is the leading eigenvector of Eq. (5.57), Z is maximized with fixed v L and v R. We here and below use the symbol “ $$\leftrightharpoons $$ ” to represent the contraction relation up to a difference of a constant factor.
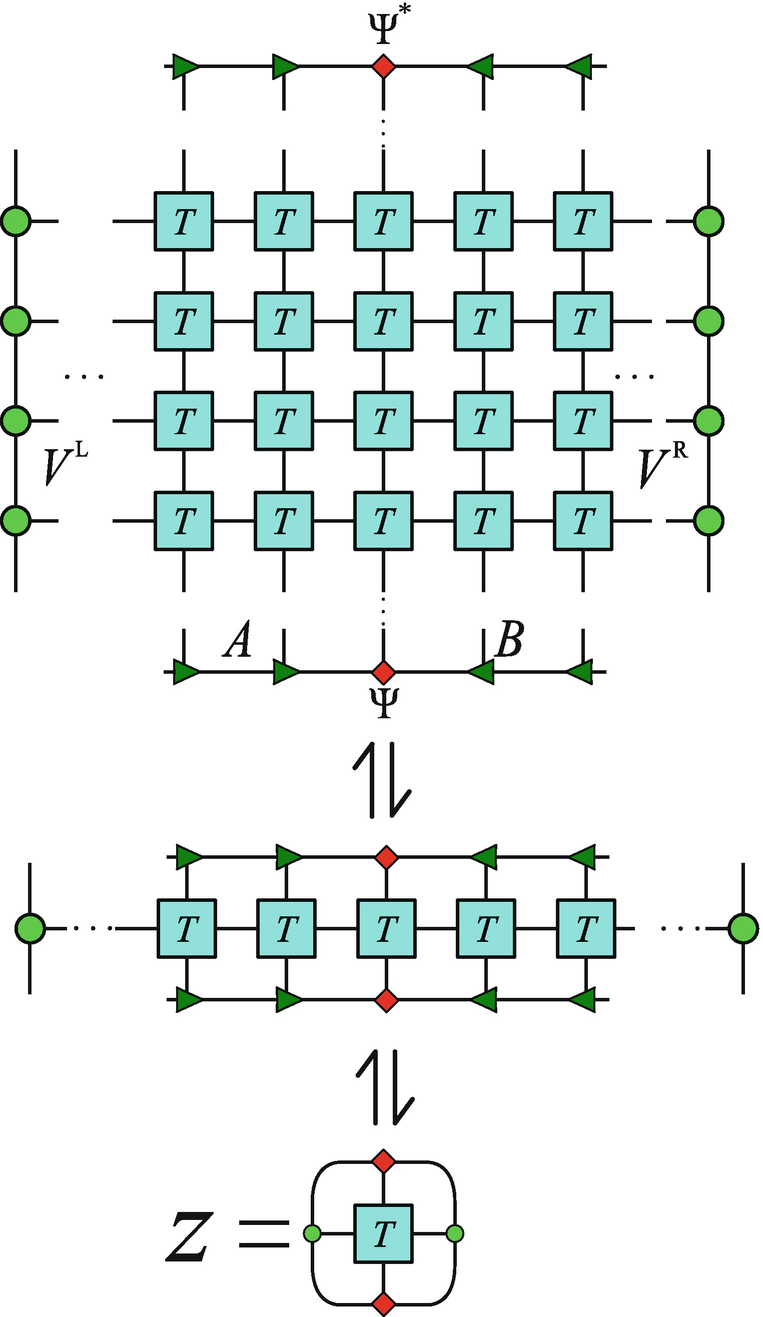
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig14_HTML.png
Fig. 5.14

The eigenvalue equations as illustrated “encode” the infinite TN

Then, we use the eigenvalue equations of v L and v R to add one M L and one M R (Eqs. (5.54) and (5.55)) in the contraction, i.e., we substitute v L by v LM L and v R by M Rv R. After doing so for one time, a finite central-orthogonal MPS appears, formed by A, B and Ψ. Such substitutions can be repeated for infinite times, and then we will have an infinite central-orthogonal MPS formed by Ψ, A and B as
$$\displaystyle \begin{aligned} \varPhi_{\cdots a_n \cdots} = \sum_{\{b\}} \cdots A_{a_{n-2}b_{n-2}b_{n-1}} A_{a_{n-1}b_{n-1}b_{n}} \varPsi_{a_n b_nb_{n+1}} B_{a_{n+1}b_{n+1}b_{n+2}} B_{a_{n+2}b_{n+2}b_{n+3}} \cdots. {} \end{aligned} $$
(5.59)
One can see that the bond dimension of b n is in fact the dimension cut-off of the MPS.
Now, we have
$$\displaystyle \begin{aligned} Z \leftrightharpoons \varPhi^{\dagger} \rho \varPhi, {} \end{aligned} $$
(5.60)
where ρ is an infinite-dimensional matrix that has the form of an MPO (middle of Fig. 5.14) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \rho_{\cdots a_n^{\prime} \cdots, \cdots a_n \cdots} = \sum_{\{c\}} \cdots T_{a_{n}^{\prime}c_{n} a_{n} c_{n+1}} T_{a_{n+1}^{\prime}c_{n+1} a_{n+1} c_{n+2}} \cdots. {} \end{array} \end{aligned} $$
(5.61)
ρ is in fact one raw of the TN . Compared with Eq. (5.58), the difference of Z is only a constant factor that can be given by the dominant eigenvalues of M L and M R.

After the substitutions from Eqs. (5.58)–(5.60), Z is still maximized by the given Φ, since v L and v R are the dominant eigenvectors. Note that such a maximization is reached under the assumption that the dominant eigenvector Φ can be well represented in an MPS with finite bond dimensions. Meanwhile, one can easily see that the MPS is normalized $$|\varPhi _{\cdots a_n \cdots }|=1$$ , thanks to the orthogonality of A and B. Then we come to a conclusion that Φ is the optimal MPS that gives the dominant eigenvector of ρ, satisfying $$\varPhi \leftrightharpoons \rho \varPhi $$ .3 Then, we can rewrite the TN contraction as $$Z \leftrightharpoons \lim _{K \to \infty } \varPhi ^{\dagger } \rho ^K \varPhi $$ , where the infinite TN appears as ρ K (Fig. 5.14).

Now we define the tensor ring decomposition (TRD) 4: with the following conditions

  • Z (Eq. (5.58)) is maximized under the constraint that v L and v R are normalized,

  • Φ †ρΦ is maximized under the constraint that Φ is normalized,

the TRD (Fig. 5.15) of T is defined by $$\tilde {T}$$ as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{T}_{a'c'ac} = \sum_{b_1b_2b_3b_4} \varPsi^{\ast}_{a'b_1b_2} \varPsi_{ab_3b_4} v^{L}_{c'b_1b_3} v^R_{c b_2b_4}, {} \end{array} \end{aligned} $$
(5.62)
so that the TN contraction $$Z = \sum T_{a'c'ac} \tilde {T}_{a'c'ac}$$ (Eq. (5.58)) is maximized. Like the NTD and rank-1 decomposition, TRD belongs to the decompositions that encode infinite TN’s, i.e., an infinite TN can be reconstructed from the self-consistent equations (note the rank decomposition does not encode any TN’s). Comparing with Eq. (5.47), TRD is reduced to the rank-1 decomposition by taking the dimensions of {b} as one.
../images/489509_1_En_5_Chapter/489509_1_En_5_Fig15_HTML.png
Fig. 5.15

The illustrations of the TRD in Eq. (5.62)

It was shown that for the same system, the ground state obtained by iDMRG is equivalent to the ground state by iTEBD , up to a gauge transformation [7, 37]. Different from this connection, TRD further unifies iDMRG and iTEBD. For iTEBD, after combining the contraction and truncation given by Eqs. (3.​34) and (3.​38), we have the equation for updating the tensor there as
$$\displaystyle \begin{aligned} \begin{array}{rcl} A_{s,cc'} \leftrightharpoons \sum_{s'aba'b'} T_{sbs'b'} A_{s',aa'} X_{ab,c} Y_{a'b',c'}. {} \end{array} \end{aligned} $$
(5.63)
Looking at Eqs. (5.55) and (5.55), Eq. (5.63) is just the eigenvalue equation for updating v [L(R)] by $$v^{[L(R)]} \leftrightharpoons M^{[L(R)]} v^{[L(R)]}$$ ; the QR decomposition in Eq. (5.56) guaranties that the “truncations in iTEBD” are implemented by isometries. In other words, one can consider another MPS defined in the vertical direction, which is formed by v [L(R)] and updated by the iTEBD algorithm. It means that while implementing iDMRG in the parallel direction of the TN, one is in fact simultaneously implementing iTEBD to update another MPS along the vertical direction.

Particularly, when one uses iDMRG to solve the ground state of a 1D system, the MPS formed by v [L(R)] in the imaginary-time direction satisfies the continuous structure [29, 38] that was originally proposed for continuous field theories [39]. Such an iTEBD calculation can also be considered as the transverse contraction of the TN [38, 40, 41].

CTMRG [30, 42] is also closely related to the scheme given above, which leads to the CTMRG without the corners. The tensors Ψ, v L and v R correspond to the row and column tensors, and the equations for updating these tensors are the same to the equations of updating the row and column tensors in CTMRG (see Eqs. (3.​27) and (3.​31)). Such a relation becomes more explicit in the rank-1 case, when corners become simply scalars. The difference is that in the original CTMRG by Orús et al. [30], the tensors are updated with a power method, i.e., $$\varPsi \leftarrow \mathscr {H} \varPsi $$ and v [L(R)] ← M [L(R)]v [L(R)]. Recently, eigen-solvers instead of power method were suggested in CTMRG ([42] and a related review [43]), where the eigenvalue equations of the row and column tensors are the same to those given in TRD . The efficiency was shown to be largely improved with this modification.

5.4.2 Extracting the Information of Tensor Networks From Eigenvalue Equations: Two Examples

In the following, we present how to extract the properties of the TN by taking the free energy and correlation length as two example related to the eigenvalue equations. Note that these quantities correspond to the properties of the physical model and have been employed in many places (see, e.g., a review [44]). In the following, we treated these two quantities as the properties of the TN itself. When the TN is used to represent different physical models, these quantities will be interpreted accordingly to different physical properties.

For an infinite TN, the contraction usually gives a divergent or vanishing value. The free energy per tensor of the TN is defined to measure the contraction as
$$\displaystyle \begin{aligned} \begin{array}{rcl} f = -\lim_{N \to \infty} \frac{\ln \mathscr{Z}}{N}, {} \end{array} \end{aligned} $$
(5.64)
with $$\mathscr {Z}$$ the value of the contraction in theory and N denoting the number of tensors. Such a definition is closely related to some physical quantities, such as the free energy of classical models and the average fidelity of TN states [45]. Meanwhile, f can enable us to compare the values of the contractions of two TN’s without actually computing $$\mathscr {Z}$$ .

The free energy is given by the dominant eigenvalues of M L and M R. Let us reverse the above reconstructing process to show this. Firstly, we use the MPS in Eq. (5.59) to contract the TN in one direction, and have $$\mathscr {Z} = (\lim _{K \to \infty } \eta ^K) \varPhi ^{\dagger } \varPhi = \lim _{K \to \infty } \eta ^K$$ with η the dominant eigenvalue of ρ. The problem becomes getting η. By going from Φ †ρΦ to Eq. (5.58), we can see that the eigenvalue problem of Φ is transformed to that of $$\mathscr {H}$$ in Eq. (5.57) multiplied by a constant $$\lim _{\tilde {K} \to \infty } \kappa _0^{\tilde {K}}$$ with κ 0 the dominant eigenvalue of M L and M R and $$\tilde {K}$$ the number of tensors in ρ. Thus, we have $$\eta = \eta _0 \kappa _0^{\tilde {K}}$$ with η 0 the dominant eigenvalue of $$\mathscr {H}$$ . Finally, we have the TN contraction $$\mathscr {Z} = [\eta _0 \kappa _0^{\tilde {K}}]^K = \eta _0^K \kappa _0^{N}$$ with $$K\tilde {K}=N$$ . By substituting into Eq. (5.64), we have $$f = -\ln \kappa _0 - \lim _{\tilde {K} \to \infty } (\ln \eta _0) /K_1 = -\ln \kappa _0$$ .

The second issue is about the correlations of the TN . The correlation function of a TN can be defined as
$$\displaystyle \begin{aligned} \begin{array}{rcl} F\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right) &amp;\displaystyle =&amp;\displaystyle \mathscr{Z}\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right)/\mathscr{Z} - \mathscr{Z}\left(\tilde{T}^{[{\mathbf{r}}_1]}, T^{[{\mathbf{r}}_2]}\right) \\ &amp;\displaystyle &amp;\displaystyle \mathscr{Z}\left(T^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right) / \mathscr{Z}^2,\quad {} \end{array} \end{aligned} $$
(5.65)
where $$\mathscr {Z}(\tilde {T}^{[{\mathbf {r}}_1]}, \tilde {T}^{[{\mathbf {r}}_2]})$$ denotes the contraction of the TN after substituting the original tensors in the positions r 1 and r 2 by two different tensors $$\tilde {T}^{[{\mathbf {r}}_1]}$$ and $$\tilde {T}^{[{\mathbf {r}}_2]}$$ . T [r] denotes the original tensor at the position r.
Though the correlation functions depend on the tensors that are substituted with, and can be defined in many different ways, the long-range behavior share some universal properties. For a sufficiently large distance (|r 1 −r 2|≫ 1), if $$\tilde {T}^{[{\mathbf {r}}_1]}$$ and $$\tilde {T}^{[{\mathbf {r}}_2]}$$ are in a same column, F satisfies
$$\displaystyle \begin{aligned} \begin{array}{rcl} F \sim e^{-|\mathbf{r_1}-\mathbf{r_2}|/\xi}. {} \end{array} \end{aligned} $$
(5.66)
One has the correlation length
$$\displaystyle \begin{aligned} \begin{array}{rcl} \xi = 1/(\ln \eta_0 - \ln \eta_1), {} \end{array} \end{aligned} $$
(5.67)
with η 0 and η 1 the two dominant eigenvalues of $$\mathscr {H}$$ . If $$\tilde {T}^{[{\mathbf {r}}_1]}$$ and $$\tilde {T}^{[{\mathbf {r}}_2]}$$ are in a same row, one has
$$\displaystyle \begin{aligned} \begin{array}{rcl} \xi = 1/(\ln \kappa_0 - \ln \kappa_1), {} \end{array} \end{aligned} $$
(5.68)
with κ 0 and κ 1 the two dominant eigenvalues of M L(R).
To prove Eq. (5.67), we rewrite $$\mathscr {Z}(\tilde {T}^{[{\mathbf {r}}_1]}, \tilde {T}^{[{\mathbf {r}}_2]})/\mathscr {Z}$$ as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{Z}\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right)/\mathscr{Z} = [\varPhi^{\dagger} \rho\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right) \varPhi]/\left(\varPhi^{\dagger} \rho \varPhi\right). \end{array} \end{aligned} $$
(5.69)
Then, introduce the transfer matrix M of Φ †ρΦ, i.e., $$\varPhi ^{\dagger } \rho \varPhi = \mathbf {Tr} M^{\tilde {K}}$$ with $$\tilde {K} \to \infty $$ . With the eigenvalue decomposition of $$\mathscr {M} = \sum _{j=0}^{D-1} \eta _j v_j v_j^{\dagger }$$ with D the matrix dimension and v j the j-th eigenvectors, one can further simply the equation as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{Z}\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right)/\mathscr{Z} = \sum_{j=0}^{D-1} \left(\eta_j/\eta_0\right)^{|{\mathbf{r}}_1 - {\mathbf{r}}_2|} v_0^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_{j} v_{j}^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_0, \\ \end{array} \end{aligned} $$
(5.70)
with $$\mathscr {M}(\tilde {T}^{[\mathbf {r}]})$$ the transfer matrix after substituting the original tensor at r with $$\tilde {T}^{[\mathbf {r}]}$$ . Similarly, one has
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{Z}\left(\tilde{T}^{[{\mathbf{r}}_1]}, T\right)/\mathscr{Z} = v_0^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_0, \end{array} \end{aligned} $$
(5.71)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{Z}\left(T,\tilde{T}^{[{\mathbf{r}}_2]}\right)/\mathscr{Z} = v_0^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_2]}\right) v_0. \end{array} \end{aligned} $$
(5.72)
Note that one could transform the MPS into a translationally invariant form (e.g., the canonical form) to uniquely define the transfer matrix of Φ †ρΦ. Substituting the equations above in Eq. (5.65), one has
$$\displaystyle \begin{aligned} \begin{array}{rcl} F\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right) = \sum_{j=1}^{D-1} \left(\eta_j/\eta_0\right)^{|{\mathbf{r}}_1 - {\mathbf{r}}_2|} v_0^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_{j} v_{j}^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_0.\quad \end{array} \end{aligned} $$
(5.73)
When the distance is sufficiently large, i.e., |r 1 −r 2|≫ 1, only the dominant term takes effects, which is
$$\displaystyle \begin{aligned} \begin{array}{rcl} F\left(\tilde{T}^{[{\mathbf{r}}_1]}, \tilde{T}^{[{\mathbf{r}}_2]}\right) \simeq \left(\eta_1/\eta_0\right)^{|{\mathbf{r}}_1 - {\mathbf{r}}_2|} v_0^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_{1} v_{1}^{\dagger} \mathscr{M}\left(\tilde{T}^{[{\mathbf{r}}_1]}\right) v_0. \end{array} \end{aligned} $$
(5.74)
Compared with Eq. (5.66), one has $$\xi = 1/(\ln \eta _0 - \ln \eta _1)$$ . The second case can be proven similarly.

These two quantities are defined independently on specific physical models that the TN might represent, thus they can be considered as the mathematical properties of the TN. By introducing physical models, these quantities are closely related to the physical properties. For example, when the TN represents the partition function of a classical lattice model, Eq. (5.64) multiplied by the temperature is exactly the free energy. And the correlation lengths of the TN are also the physical correlation lengths of the model in two spatial directions. When the TN gives the imaginary-time evolution of an infinite 1D quantum chain, the correlation lengths of the TN are the spatial and dynamical correlation length of the ground state.

It is a huge topic to investigate the properties of the TN’s or TN states. Paradigm examples include injectivity and symmetries [46–61], statistics and fusion rules [62–65]. These issues are beyond the scope of this lecture notes. One may refer to the related works if interested.

Creative Commons

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.