In this chapter, we’ll spend time getting familiar with how asymmetric encryption is typically used, where it is a critical part of communication privacy, but not responsible for all of it. Typically, asymmetric encryption, also known as “public key cryptography”, is used to establish a trusted session between two parties, and the communication while within that session is protected with much faster symmetric methods.
Let’s dive in with a short example and some code!
Exchange AES Keys with RSA
Armed with their newer cryptography technologies, Alice and Bob have become more brazen in their covert operations. Alice has managed to infiltrate the Snow Den Records Center in West Antarctica and is attempting to steal a document related to genetic experiments to turn penguins completely white, thus creating a perfectly camouflaged Antarctic soldier. WA soldiers are quickly moving on her position, and she decides to risk transmitting the document over a short-wave radio to Bob who is monitoring from outside the building. Eve is certainly listening and Alice does not want her to know which document has been stolen.
The document is nearly ten megabytes. RSA encryption of the entire document will take forever. Fortunately, she and Bob agreed beforehand to use RSA encryption to send AES session keys and then transmit the document using AES-CTR with HMAC. Let’s create the code they will use to make this alphabet soup work.
An AES encryption key, IV, and a MAC key encrypted under Bob’s public key
Alice’s signature over the hash of the AES key, IV, and MAC key
The stolen document bytes, encrypted under the encryption key
An HMAC over the entire transmission under the MAC key
RSA Key Exchange
Hopefully, all of the pieces here are familiar, and if you follow the code paths, it should also be pretty easy to see how things come together. Perhaps you’ve noticed that we are drawing on concepts from Chapter 3, Chapter 4, and Chapter 5! All of these pieces are coming together to shape a more advanced whole.
A few points are worth noting. First, we chose to use AES-CTR, so there is no need for padding. Earlier in the book, we used the term “nonce” to describe the initialization value to the algorithm, as this is what the cryptography library calls it. In other literature it is still called an IV, however, so we use that term here. Either way, the IV (or nonce) is the starting value for the counter.
Note that we are not using Sign-Then-Encrypt as we discussed in Chapter 5. As always, this is an example program not meant to be used for real security. You might want to review the issues we discussed in relation to Sign-Then-Encrypt to see how Eve could strip out the signature, change the keys, and re-sign.
Nevertheless, that’s not the major vulnerability we will discuss. After all, in our scenario, Bob is probably only going to accept data from Alice. The issues of swapping out a signature are more applicable when more than one signature can be accepted.
Like most of the APIs you’ve seen so far, we use update and finalize, but we added a new method called initialize . For transmission, Alice would call initialize first to get the signed and encrypted header with the session keys. Next, she would call update as many times as needed to feed the entire document through. When everything is finished, she would call finalize to get the HMAC trailer over all of the transmitted contents.
Exercise 6.1. Bob’s Receiver
Implement the reverse of this transmitter by creating a ReceiverManager. The exact API might vary a little, but you will probably need at least an update and finalize method. You will need to unpack the keys and IV using Bob’s private key and verify the signature using Alice’s public key. Then, you will decrypt data until it’s exhausted, finally verifying the HMAC over all received data.
Remember, the last bytes of the transmission are the HMAC trailer and are not data to be decrypted by AES. But when update is called, you may not yet know whether these are the last bytes or not! Think through it carefully!
Asymmetric and Symmetric: Like Chocolate and Peanut Butter
Hopefully, Alice’s transmission to Bob in the exercise at the beginning of this chapter gave you a small taste for how asymmetric and symmetric cryptography work together. The protocol we outlined in code works, but lacks some important subtlety, as is often the case with our first attempts. As you might expect by now, the preceding code is not secure and we will demonstrate at least one problem with it shortly. It does illustrate the ideas behind putting the two systems together, though.
Let’s see what we can learn from what we have. We’ll start with session keys.
We first introduced the term session key in Chapter 4 but did not discuss it much. A session key is by nature a temporary thing; it is used for a single communication session and then discarded permanently, never to be reused. In the preceding code, notice that the AES and MAC keys are generated at the beginning of a session by the communications manager. Every time a new communications manager is created, a new set of keys is created. The keys are not stored or recorded anywhere. Once all the data is encrypted, they are thrown away.1
On the receiving end, the session keys are decrypted using the recipient’s private key. Once these keys are decrypted, they are then used to decrypt the rest of the data and process the MAC. Again, after the transmitted data is processed, the keys can—and should—be destroyed.
Symmetric keys make good session keys for multiple reasons. First of all, symmetric keys are easy to create; in our example, we simply generated random bytes. We could also derive symmetric keys from a base secret by using key derivation functions. This is a common approach, and we will see later that you almost always need to derive multiple keys for typical secure communication. Regardless of how they are created, symmetric keys (and IVs) are plain old ordinary bytes, unlike most asymmetric keys that require some additional structure (e.g., public exponents, chosen elliptic curves, etc.).
Second, symmetric keys are good session keys because symmetric algorithms are fast. We have already mentioned this a time or two, but it is worth repeating. AES is typically on the order of hundreds of times faster than RSA, so the more data that can be encrypted by AES, the better. This is another reason that symmetric keys are sometimes called “bulk data transfer” keys.
Finally, let’s also recognize that symmetric keys are good session keys because they are not always good long-term keys! Remember, symmetric keys cannot be private keys because they must always be shared between at least two parties. The longer a shared key is in use, the higher the risk that trust breaks down between the parties and the key should no longer be shared. In the case of Alice’s break-in to the Snow Den archive, she risks capture and the compromise of any keys she has with her. The loss of her asymmetric private key is serious, as we discussed when we talked about certificate revocation, but if Alice and Bob were using the same shared symmetric key for all of their communications, the loss of that key would be even worse as any intercepted communications between them that were encrypted using that key could now be decrypted.
On the other hand, asymmetric keys are very useful for long-term identification. Using certificates, asymmetric keys can establish a sort of proof of identity; once this is done, the shorter-term keys do the work of actually transmitting data between the authenticated parties. That said, sometimes ephemeral (quickly discarded) asymmetric keys are incredibly valuable. We will see this both with key exchanges that have the “forward secrecy” attribute and with how ransomware attackers lock up their victims’ files.
Measuring RSA’s Relative Performance
Even though we’ve hammered home just how much slower RSA is than AES, let’s have some fun and run a few experiments. We’re going to write a tester that will generate random test vectors for encryption and decryption. Then we can compare the performance of RSA and AES for ourselves.
Imports for Encryption Speed Test
Let’s start by creating some algorithms to test. We will define one class for each algorithm, and the instances of the class will build encryption and decryption objects. Builders will be self-contained, providing all keys and necessary configuration. Each will have a name attribute with a human-readable label and a get_cipher_pair() method to create a new encryptor and decryptor. This method must generate new encryption and decryption objects each time it is called.
AES Library Use
The get_cipher_pair() operation creates new keys and nonces each time it is invoked. We could put this in the constructor because we don’t really care if we reuse keys for these speed tests, but the re-generation of a few bytes for a key and a nonce is probably not really a limiting factor for speed.
RSA encryption is a little more complicated. It really wasn’t meant to encrypt arbitrary amounts of data. Unlike AES, which has counter and CBC modes to tie blocks together, RSA must encrypt its data all at once, and the size of data it can manipulate is limited by various factors. An RSA key with a 2048-bit modulus cannot encrypt more than 256 bytes at a time. In fact, once you add in the OAEP (with SHA-256 hash) padding, it’s significantly less: only 190 bytes!2
If we were actually concerned about the security of the encryption, we could thus not use RSA for more than 190 bytes of data. However, what we are really testing here is a hypothetical RSA encryptor that does not exist in the real world. What we want to explore is this: if RSA could encrypt arbitrary amounts of data, how long would it take? For this test, we will encrypt each chunk of 190 bytes one at a time and concatenate the results together. Note that when we encrypt with the OAEP padding, the 190 bytes of plaintext becomes 256 bytes of ciphertext. When we are decrypting, we need to decrypt 256-byte chunks.
Although a truly secure RSA encryption algorithm would have to bind the bytes of the different individual encryption operations together, this version is the fastest it could ever be, so it gives us an upper bound on speed, making for an interesting comparison.
RSA Implementation
Note that we created our encryptor and decryptor to have the same API as the AES encryptor and decryptor. Namely, we provide update and finalize methods . The finalize methods don’t do anything as RSA encryption (with padding) processes each chunk exactly the same way. The chunk-by-chunk encryption takes each 190-byte piece of the input, encrypts it to the 256-byte ciphertext, and returns the concatenation of all of these pieces. The decryptor reverses the processes, taking each 256-byte chunk in for decryption. Our RSAAlgorithm class constructs the appropriate encryptor and decryptor using these classes.
Random Text Generation
Notice that a new random_data_generator contains timing and data specific to each individual test run. So a new object needs to be created for each test.
Encryption Tester
Algorithm Tester
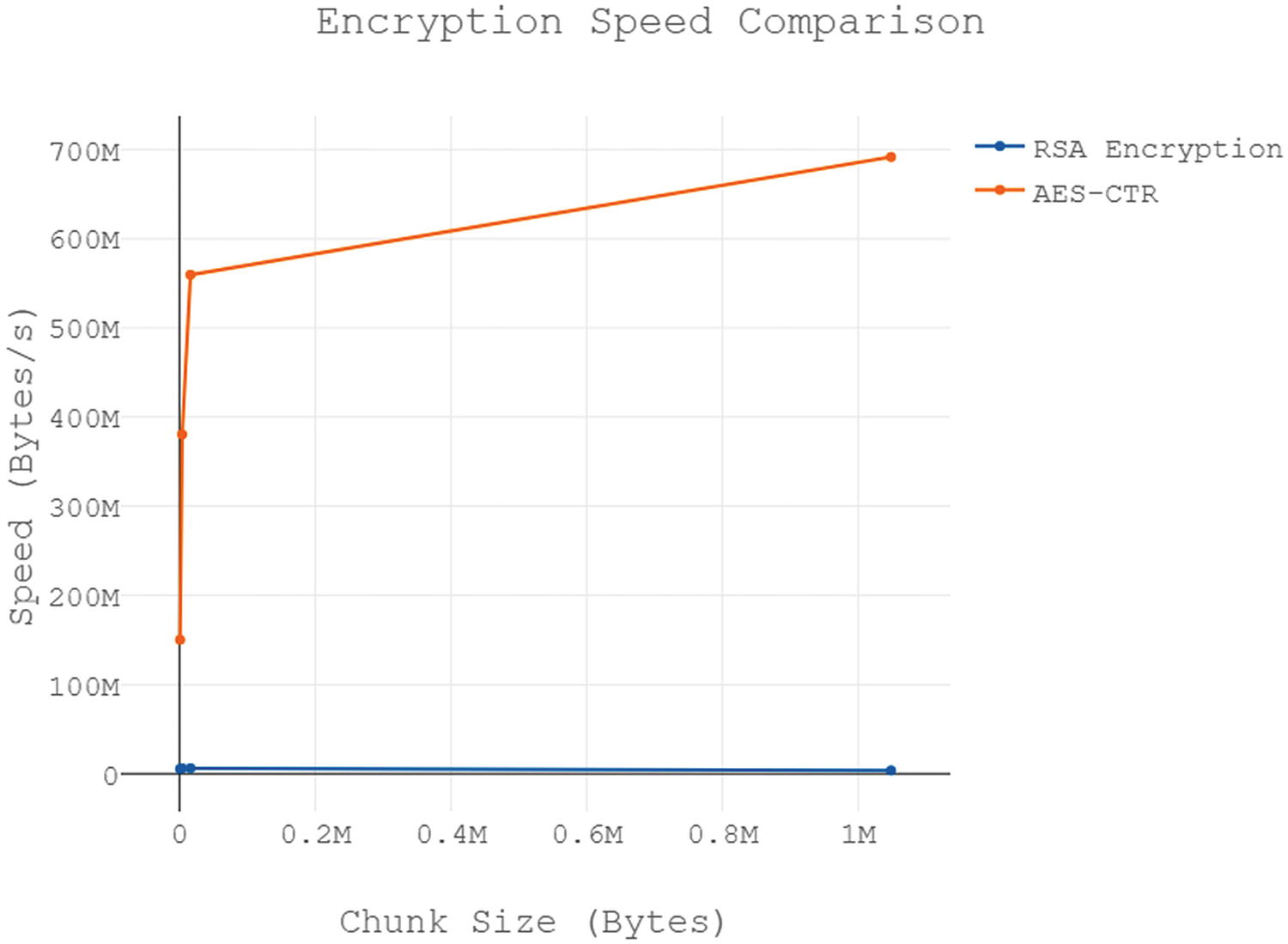
A Comparison of RSA encryption speeds vs. AES-CTR
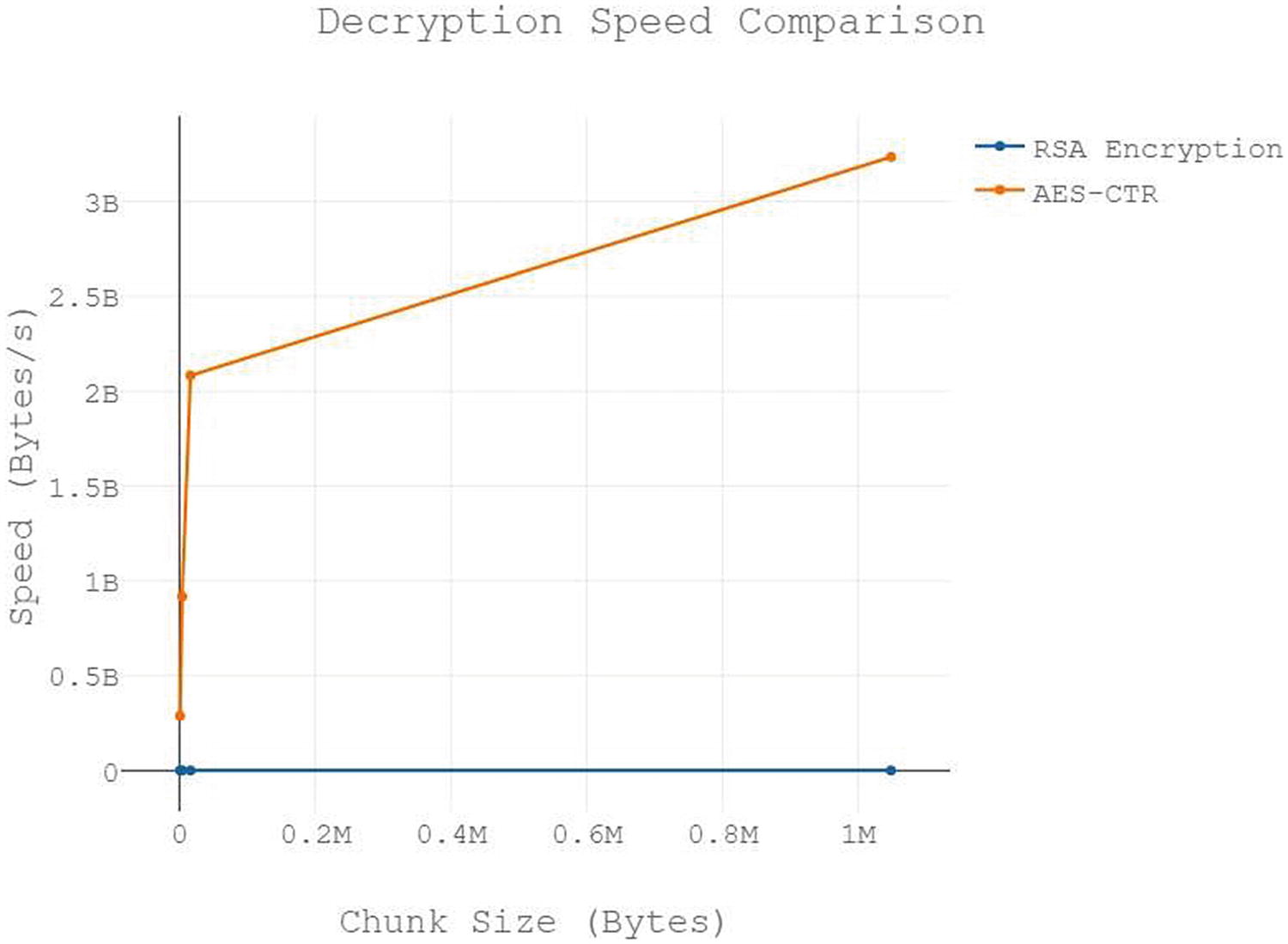
A Comparison of RSA decryption speeds vs. AES-CTR
As you can see, RSA operations are so much slower, it’s not even really a comparison. By the way, if you run the tests we did, RSA encryption over 100 MiB can be slow (about 20 seconds on our computer), but decryption is so bad, it’s just off the charts (about 400 seconds for our tests!). RSA decryption is slower than RSA encryption, so this isn’t a surprise. When you have tests that run this long, make sure to save the statistics in raw, numerical format and then generate graphs from this data. That way you can regenerate graphs quickly and easily without running the entire test again.
Exercise 6.2. RSA Racing!
Use your preceding tester to compare the performance of RSA with a 1024-bit modulus, a 2048-bit modulus, and a 4096-bit modulus. Please note, you will need to change your chunk size to 62 bytes for 1024-bit RSA keys with OAEP (and SHA-256 hashing) and 446 bytes for 4096-bit RSA keys with OAEP (and SHA-256 hashing).
Exercise 6.3. Counters vs. Chains!
Use your tester to compare the performance of AES-CTR against AES-CBC.
Exercise 6.4. MACs vs. Signatures
Modify your algorithms to sign or apply a MAC to the data in the finalize methods. Try disabling encryption (just have the update methods return the unmodified plaintext) so that you can compare only the speed of the MAC and signature. Is the difference as extreme? Can you think why this is so?
Exercise 6.5. ECDSA vs. RSA Signing
In addition to testing the speed of MAC vs. RSA signing, also compare the speed of RSA signing with ECDSA signing. It’s hard to get a fair comparison because it isn’t always obvious what your key size is with ECDSA, but look at the list of supported curves in the cryptography library documentation and try them out to see which ones are faster in general, as well as how they compare to RSA signing using different modulus sizes.
Hopefully, these timed tests have helped to reinforce why, security reasons aside, symmetric ciphers are preferred over asymmetric ciphers for bulk data transfer.
Diffie-Hellman and Key Agreement
For the last couple of sections in this chapter, we will look at another type of asymmetric cryptography known as Diffie-Hellman (or DH) and a more recent variant called Elliptic-Curve Diffie-Hellman (or ECDH).
DH is a little different than RSA. Where RSA can be used to encrypt and decrypt messages, DH is only used for exchanging keys. In fact, it is technically called the Diffie-Hellman key exchange. As we have already explored in this chapter, outside of signatures, RSA encryption is largely used only for transmitting keys, also called “key transport.” This means that if Alice has Bob’s RSA public key, Alice can send Bob an encrypted key that only Bob can decrypt.
Figure 6-3 shows key transport in a TLS 1.2 handshake. We will discuss the TLS 1.2 handshake in more detail in Chapter 8, where this figure will also make an appearance. But notice that the client in this figure can generate a random session key, encrypt it under the server’s public key, and “transport” it back. This process also proves the server is in possession of the certificate because only the server could decrypt the session key and use it to communicate. No signatures are required for the server.3
On the other hand, DH and ECDH actually create a key seemingly out of thin air. No secrets are transmitted between the parties, encrypted or otherwise. Instead, they exchange public parameters that allow them to simultaneously compute the same key on both sides. This process is called key agreement .
To get started, Diffie-Hellman creates a pair of mathematical numbers, one private, one public, for each participant. The DH and ECDH key agreement protocol requires that both Alice and Bob have key pairs. In over-simplistic terms, Alice and Bob share their public keys with each other. The foreign public key and the local private key—when combined—create a shared secret on both sides.
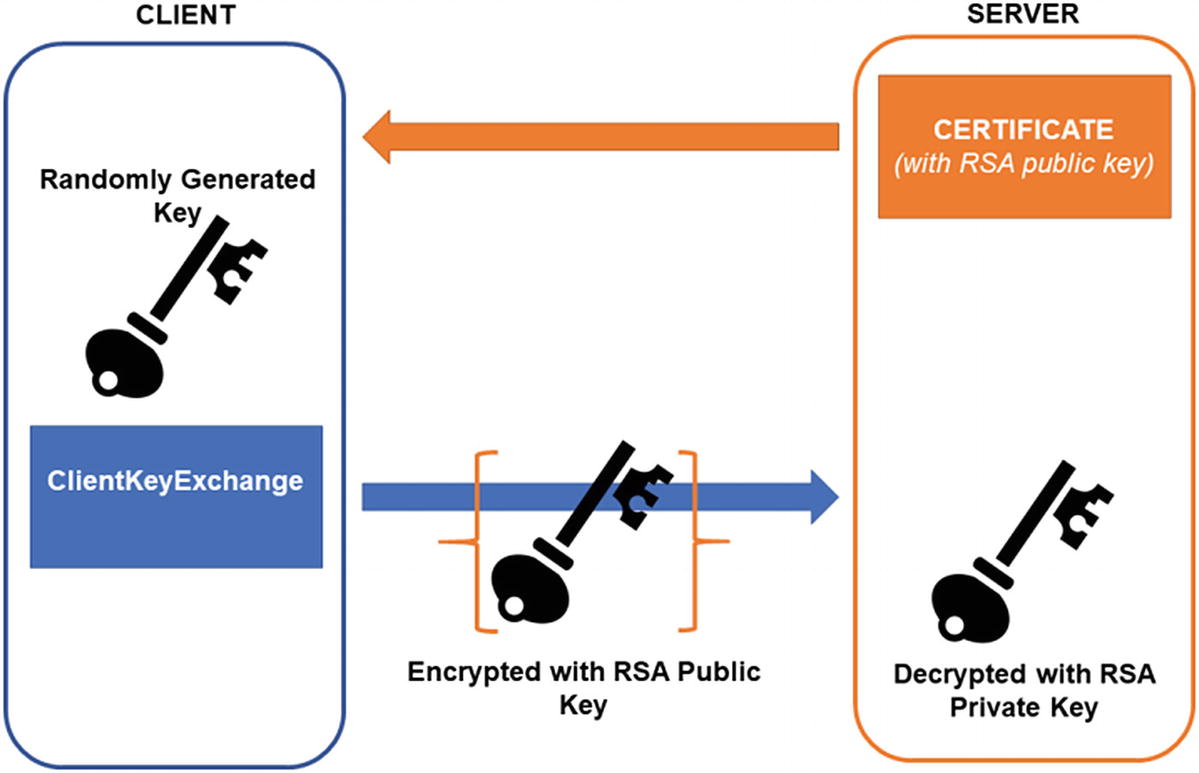
An illustration of key transport using TLS
Please note that, unlike RSA, DH and ECDH do not allow for the transmission of arbitrary data. Alice can send Bob any message she chooses, encrypted under Bob’s RSA public key. Using DH or ECDH, however, all that the two can do is agree upon some random data; they don’t get to choose the message contents. The random data can be, and typically is, used as a symmetric key or for deriving symmetric keys.
In addition to not being able to exchange arbitrary contents, key exchange is also limited in that it requires bidirectional information exchange. In our scenario at the beginning of this chapter, Bob could not transmit for fear of discovery. Were that actually the case, DH and ECDH key exchanges would be impossible and RSA encryption would be the only option. This really isn’t an issue in almost all real-world scenarios. In real Internet applications, we typically assume that both sides are free to communicate with each other.
Diffie-Hellman Key Exchange
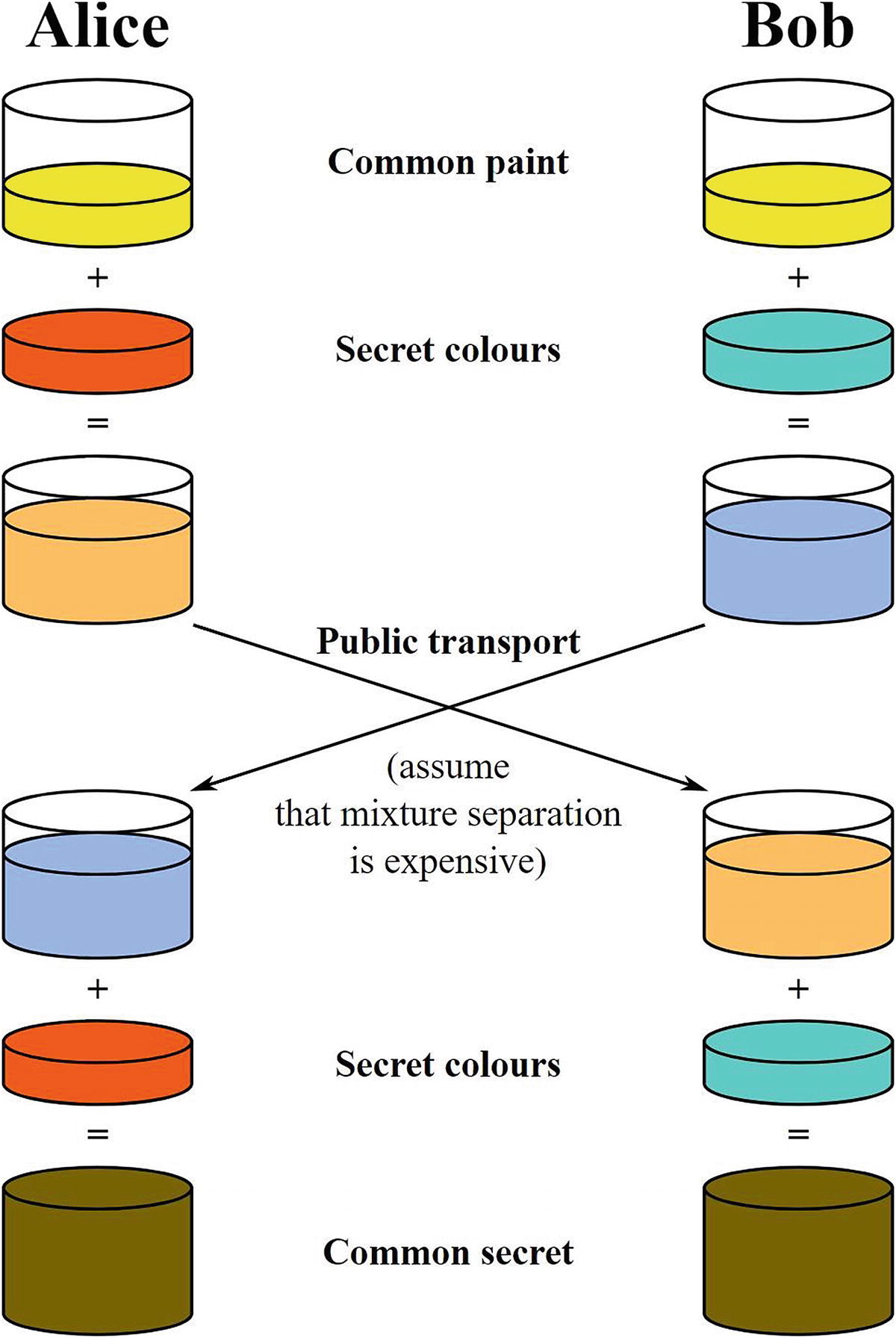
Intuition behind Diffie-Hellman
Unlike RSA there are a lot fewer pitfalls and gotchas.
There are only two parameters to the exchange: the generator and the key size. There are only two legal values for the generator, 2 and 5. Strangely enough, for a cryptographic protocol, the choice of generator doesn’t matter for security reasons but must be the same for both sides of the exchange.
The key size, however, is important and should be at least 2048 bits. Key lengths between 512 and 1024 bits are vulnerable to known attack methods.
Warning: Slow Parameter Generation
Diffie-Hellman is touted as being pretty fast for generating keys on the fly. However, generating the parameters that can generate keys can be pretty slow. We warned you against using key sizes smaller than 2048 and then used 1024 in our own code example. We wanted to give you code that wouldn’t take forever to run to illustrate the basic operations.
So if parameter generation is so slow, why do we say DH is fast? The same parameters can generate many keys so the cost is amortized. So make sure not to regenerate the parameters with every key generation, or DH will run unacceptably slow. Alternatively, use ECDH which is much faster.
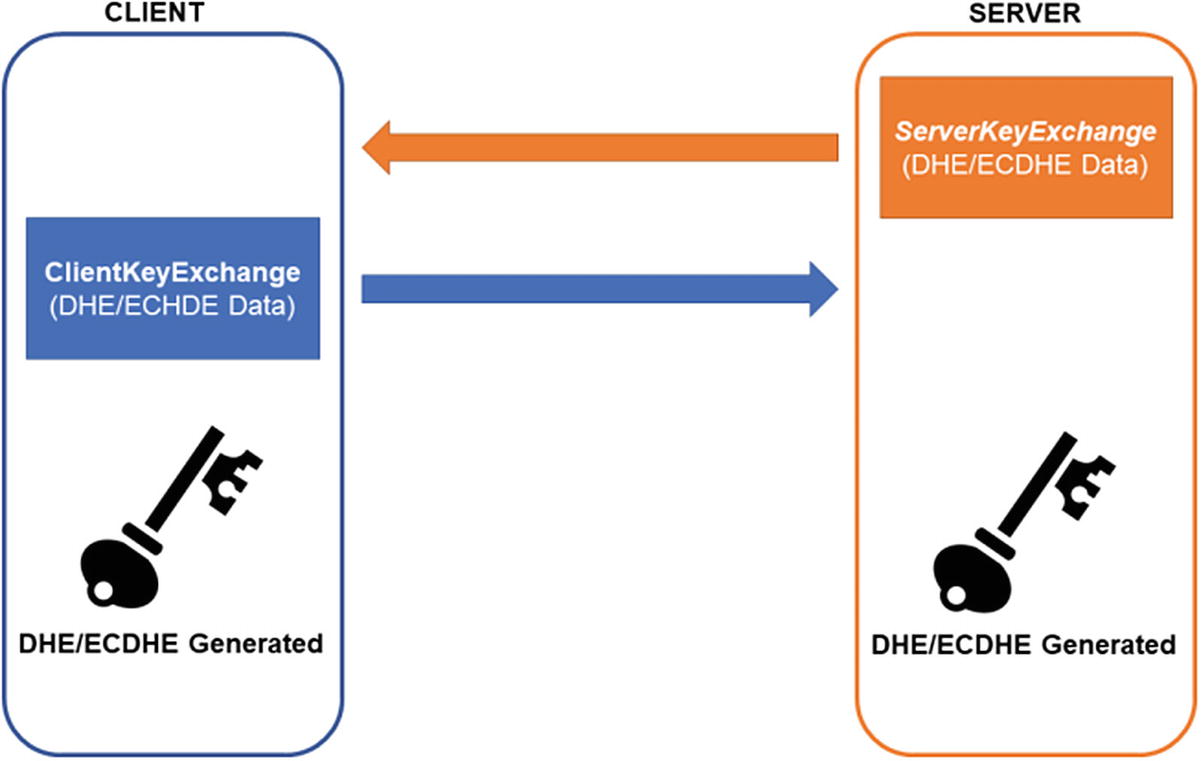
An illustration of key agreement using TLS
The other recommended setting is to derive another key from the shared key rather than using the shared key directly. The key derivation function is similar to the ones we looked at in Chapter 3.
The TLS 1.2 handshake can either do the key transport using RSA encryption or key agreement using DH/ECDH. Again, this will be discussed in Chapter 8 in detail, but Figure 6-5 shows that both sides exchange the public data, derive a key, and can communicate using the agreed-upon keys. Unlike key transport, however, there is no authentication. Either or both sides will have to sign the public data to prove that possession of a public key.
Elliptic-Curve DH
In most circumstances, creating keys with DH or ECDH key agreement is preferred over RSA key exchange. There are a number of reasons but perhaps the biggest one is forward secrecy.
Diffie-Hellman and Forward Secrecy
Using RSA encryption, we can generate a symmetric key, encrypt it under someone’s public key, and send it to them. This allows both parties to share a session key securely, provided that the exchange protocol follows certain rules. There are even ways to have both sides contribute to a key. Each party could send the other some random data, and the concatenation of both could be fed to a hash function to produce the session key.
Unfortunately, RSA key transport does not provide a really fantastic property called forward secrecy. Forward secrecy means that even if a key is eventually compromised, it does not reveal anything about previous communications.
Let’s go back to Alice, Bob, and Eve. Alice and Bob already assume that Eve is recording everything that is transmitted. That’s why they are encrypting the transmission in the first place. So, after the transmission is complete, Eve has a recording of the ciphertext that she cannot yet decrypt. But, rather than toss it aside, Eve files it away in storage.
But also recall that, in our scenario, Alice actually believed she was on the verge of being captured. If the guards capture her and her keys are compromised, what is lost? Fortunately, nothing. Remember that Alice encrypted the session keys under Bob’s public key. Capturing Alice won’t make it any easier to decrypt that data (do you see the advantage of this over shared keys?).
But suppose that Eve finds Bob, perhaps even a long time in the future. Even if it’s years later, if Eve manages to get Bob’s private key, she can go back to her recording of Alice’s previous transmission and decrypt it! Bob’s private key will still decrypt the session keys, and Eve will then be able to decrypt the entire transmission.
Forward secrecy is much stronger than this. If a protocol has forward secrecy, Eve can never recover data from a terminated session no matter what long-term keys she manages to obtain. Forward secrecy is not possible when session keys are sent directly via RSA encryption (in the way we’ve just described) because once the RSA private key is compromised, any recorded data from previous sessions is now vulnerable.
With Diffie-Hellman (DH) and Elliptic-Curve Diffie-Hellman (ECDH), forward secrecy is achieved by the use of ephemeral keys. RSA produces an ephemeral symmetric session key, but DH and ECDH actually produce ephemeral asymmetric keys as well! A new ephemeral key pair is (or should be!) generated with every single key agreement operation and then thrown away. The symmetric key is also ephemeral and thrown away after each session. Because DH and ECDH are typically used in this fashion, an “E” is often tacked onto the end of the acronym (DHE or ECDHE).4
Now that a new key pair is used for every exchange, compromising a single asymmetric key only reveals a single symmetric key and, accordingly, a single communications session. And when the ephemeral DH and ECDH private keys are properly disposed of, there is no key left for Eve to compromise and no way that she could ever decrypt these sessions. In some ways, it is akin to the old spy trope of swallowing the key so the spy’s nemesis can’t unlock the movie’s McGuffin.
Observe that, in theory, Alice and Bob could also do an ephemeral RSA key exchange. They could generate new RSA key pairs for every single key transport, sending each other their new public keys before transmitting the session key, then destroying the key pair after transmission.
The problem is that generating RSA keys is slow in computer terms. You might not have thought it took very long to generate your RSA keys for the examples in this book, but for computers involved in rapid communications (such as setting up a secure connection from your browser to a web site), RSA is mind-numbingly slow. DH and ECDH are much, much faster. Because of the key generation speed, DH and ECDH are the common choices for forward-secrecy-style communications.
This ephemeral mode of operation is the preferred mode for DH and ECDH under almost all circumstances, which is why DH and ECDH often mean DHE and ECDHE.
Exercise 6.6. Off To The Races!
Write a python program to generate a thousand or so 2048-bit RSA private keys and a program to generate a thousand or so DH and ECDH keys. How does the performance compare?
There’s only one other limitation to Diffie-Hellman methods: they have no authentication. Because the keys are completely ephemeral, there is no way to tie them to an identity; you don’t know with whom you are speaking. Remember that beyond communicating confidentially, we need to know with whom we’re communicating confidentially. By itself, DH and ECDH do not provide any such assurances.
For this reason, many DH and ECDH key exchanges also require a long-term public key, such as RSA or ECDSA, and that key is typically protected within a signed certificate. These long-term keys, however, are never used for encryption or key transport and are not used in the actual exchange of key data in any way. Their sole purpose is to establish the identity of the other party, usually by signing some of the ephemeral DH/ECDH data being exchanged, and to ensure freshness via some kind of challenge or nonce.
Remember, to ensure forward secrecy, the Diffie-Hellman parameters must be regenerated for every key exchange. If you take a look through the cryptography library documentation, you’ll notice that they include sample code that, as written, does not provide forward secrecy. This code sample saves what should be a single-use key for later. Make sure that your keys are destroyed after use (never logged).
Unauthenticated ECDH
To use the ECDHExchange , both parties instantiate the class and call the get_public_bytes method to get the data that needs to be sent to the other party. When those bytes are received, they are passed to generate_session_key where they are de-serialized into a public key and used to create a shared key.
So, what’s with HKDF ? This is a key derivation function that is useful for real-time network communications, but should not be used for data storage. It takes the shared key as input and derives a key (or key material) from it. Notice that in our example, we derive both an encryption key and a MAC key. This is done by using HKDF to derive 64 bytes of key material and then splitting it into two 32-byte keys. In reality, we need to derive a lot more data, and we’ll discuss this in the next section. But for now, it demonstrates the basics of the ECDH exchange.
To repeat one last time, notice that ECDH is generating its private key on the fly. This key must be destroyed after every key exchange, along with any session keys created.
Exercise 6.7. Rudimentary ECDH Exchange
Use the ECDHExchange class to create shared keys between two parties. You will need to have two instances of the program running. Each program should write their public key bytes to disk for the other program to load. When they’re finished, have them print out the bytes of the shared key so that you can verify that they both come up with the same key.
Exercise 6.8. Network ECDH Exchange
In the upcoming chapters, we will start using the network to exchange data between two peers. If you already know how to do some client-server programming, modify the previous ECDH exchange program to send the public data over the network instead of saving it to disk.
Our ECDH code so far just does the ECDH ephemeral key exchange. Both sides have a key, but since we aren’t yet doing any authentication, neither side can be certain about whom they’re talking to! Remember, the ephemeral nature of the ECDH keys means that they cannot be used to establish identity.
To remedy this, we are going to modify our ECDHExchange program to also be authenticated. In addition to an ephemeral asymmetric key, it will also use a long-term asymmetric key to sign the data.
Authenticated ECHD
Please note the difference between _private_key, which is generated and is ephemeral, and _auth_private_key. The latter is passed in as a parameter. This persistent key will be used to establish identity. We could use an RSA key here and it would work just fine, but in keeping with the elliptic-curve theme, we will assume this is an ECDSA key.
Authenticated ECDH Signed Public Bytes
When the other side receives our data, they will need to unpack the first four bytes to get the length of the signature before they do anything else. The signature can be verified using the other party’s long-term public key (just like we did with RSA). If the signature works out, we have some confidence that the ECDH parameters we received came from the expected party.
Exercise 6.9. ECDH Left To The Reader
We did not show code for verifying the public parameters received in the AuthenticatedECDHExchange class. Luckily for you, we’ve left it as an exercise to the reader! Update the generate_session_key method to be generate_authenticated_session_key. This method should implement the algorithm previously described for getting the signature length, verifying the signature using a public key, and then deriving the session keys.
The principles in this section are important. You might consider working through this section a couple of times until you are comfortable with both sending a key encrypted under RSA and generating an ephemeral key on the fly using DH or ECDH. Make sure you also understand why the DH/ECDH approach has forward secrecy and the RSA version does not.
Exercise 6.10. Because You Love Torture
To emphasize that RSA technically could be used as an ephemeral exchange mechanism, modify your preceding ECDH program to generate an ephemeral set of RSA keys. Exchange the associate public keys and use each public key to send 32 bytes of random data to the other party. Combine both 32-byte transmissions with XOR to create a “shared key” and run it through HKDF just as the ECDH example does. Once you’ve proved to yourself that this works, review your results from Exercise 6.2 to see why this is too slow to be practical.
Also, creating a shared key with RSA encryption requires a round trip to create the key (transmission of certificate and reception of encrypted key), whereas DH and ECDH only require one transmission from each party to the other. When we learn about TLS 1.3, for example, you’ll see how this can greatly impact performance.
Challenge-Response Protocols
We have briefly introduced challenge-response protocols in Chapter 5. In particular, Alice used challenge-response to validate that the man claiming to be Charlie was the owner of the certificate with the identity “charlie.” At its core, a challenge-response protocol is about one party proving to another that they currently control either a shared secret or a private key. Let’s look at both examples.
First, suppose that Alice and Bob share some key KA,B. If Alice is communicating over a network with Bob, a simple authentication protocol is to send Bob a nonce N (potentially unencrypted) and ask him to encrypt it. For security reasons, it’s a good idea for the response to include the identity of the communicating parties. Accordingly, Bob should reply with {A, B, N}KA,B. If only Alice and Bob share the key KA,B, then only Bob could have responded to Alice’s challenge correctly. Even if Eve overhears the challenge and knows N, she should not be able to encrypt it without the key.
For the asymmetric example, it is more or less the same, but uses signatures generated by private keys. This time, Bob is communicating with Alice over the network and wishes to be sure that he is talking to the real Alice. So he sends a nonce N and asks her to sign it with her public key. As with Bob’s challenge, Alice should also send her name and Bob’s. Her transmission should therefore look like {H(B, A, N)}K –1A (for RSA signatures anyway). Bob verifies with the Alice’s public key that the signature is correct. Only the possessor of the private key could have signed that challenge.
Challenge-response algorithms are relatively simple, but they can go wrong in many ways. For one thing, the nonce must be sufficiently large and sufficiently random to be unguessable, even with knowledge of previous transmissions. In the early days of remote keys for cars, for example, the transmitter used a 16-bit nonce. Thieves only had to record a transmission once and then interrogate the system over and over until it cycled through all the possible nonces and returned to the one they recorded. At that point, they could replay the nonce and gain access to the car.
Another way this can go wrong is via a “(hu)man-in-the-middle” (MITM) attack. Suppose that Eve wants to convince Alice that she is Bob. Eve waits until Bob wants to talk to Alice and then intercepts all of their communications. Then, she initiates communication with Alice pretending to be Bob. Alice responds with a challenge N to prove that the person she is talking to (Eve) is Bob. Eve immediately turns around and sends the challenge to Bob who, wanting to talk to Alice, was already expecting it. Bob happily signs the challenge and sends it back to Eve who forwards it directly on to Alice. (For a fascinating, but probably fictional example, Ross Anderson describes a “MIG-in-the-middle” scenario of this attack [1, Chap. 3].)
One way to defeat this MITM problem is to transmit information that only the true party can use. For example, even if Eve forwards along Bob’s response to the challenge it won’t help her if Alice’s response is to send Bob a session key encrypted under his public key. Eve won’t be able to decrypt it. If all subsequent communication takes place using that session key, Eve is still locked out. Alternatively, Alice and Bob could use ECDH plus signatures to generate a session key. Even if Eve can intercept every transmission between the two of them, Alice and Bob can create a session key that only they can use. The most Eve can do is block the communications.
The point here is to illustrate all the different kinds of considerations that need to go into authenticating the party you’re talking to.
Once the identity of a party has been established, all subsequent communications of the session must be tied to that authentication. For example, Alice and Bob might authenticate one another using challenge-response, but unless they establish a session MAC key and use it to digest all of their subsequent communications, they cannot be sure who is sending the message.
Sometimes, initialization data must be sent in the clear before encrypted communications can be established. All of this data must also be tied together at some point. After session keys have been established, one option is to send a hash of all the unauthenticated data sent so far using the newly established secure channel. If the hash doesn’t match what is expected, then the communicating parties can assume that an attacker, like Eve, has modified some of the initialization data.
In summary, when combining asymmetric and symmetric cryptography, don’t just think about the confidentiality part (encryption). Remember that knowing to whom you are speaking is just as important as, if not more important than, knowing that the communications between the two of you are unreadable to anyone else. You might not want the whole world to read your love poetry, but you definitely don’t want your amorous expressions to be received by the wrong person! Keep in mind that after establishing the other party’s identity, you must ensure that there is a chain of authenticity for all the remaining communications for the rest of the session. If the initial identity is proved with signatures and the remaining data is authenticated by MACs, ensure that there is no break in the chain as you switch from one to the other.
Common Problems
After seeing a bit about how asymmetric and symmetric keys work together, you might be tempted to create your own protocol. Definitely resist that urge. The goal of these exercises is to teach you the principles and to illuminate your understanding, but that alone is not sufficient to prepare you to develop cryptographic protocols. The history of cryptography is littered with protocols that were later found to be exploitable even though they were written by cryptographers with more experience than you or I have.
Let’s take the example we used with Alice sending the encrypted document to Bob. Did you notice that we broke one of our recommendations from previous chapters? Our data has no nonce! This means that Bob has no idea if the message from Alice is “fresh.” What if that data was recorded by Eve from a year ago and is just being replayed now?
Here’s another example. In our derivation of encryption keys, we only generated a single encryption key between both parties. This is only secure for one-way communication! If you want full-duplex communication (the ability to send data in both directions), you will need an encryption key for each direction!
But wait. Why can’t we use the same key to send data from Alice to Bob as we use to send data from Bob to Alice?
Do you remember what you learned about in Chapter 3? You do not reuse the same key and IV to encrypt two different messages! In full-duplex communication, that is exactly what you would be doing. Suppose that AEC-CTR mode is being used for the bulk data transport. If Alice uses a key to encrypt messages she sends to Bob, and Bob uses the same key to encrypt messages to Alice, both data streams could be XORed together to get the XOR of the plaintext messages! As we have seen, that is catastrophic. In fact, if Eve can trick Alice or Bob into encrypting data on her behalf (e.g., by planting “honeypot” data that will certainly be picked up and transmitted), she can XOR that data out leaving the other data as plaintext.
A naive key exchange using RSA encryption could be exploited using this very same principle. Suppose that Alice sends Bob an initial secret K encrypted under Bob’s public key. Alice and Bob correctly derive session keys and IVs for full-duplex communication from K. As an example, Bob has a key KB,A that he uses to send encrypted messages to Alice, and Alice has a key KA,B that she uses to send encrypted messages to Bob. (Bob uses KA,B to decrypt Alice’s messages and Alice uses KB,A to encrypt Bob’s messages.)
But suppose that Eve records all of these transmissions. Then, at a much later date, she replays the initial transmission of K to Bob. Bob doesn’t know that it’s a replay and he uses K to derive KB,A. Now he starts sending data to Eve encrypted under this key.
While it’s true that Eve does not have KB,A and cannot decrypt Bob’s messages directly, she does have the messages Bob sent to Alice under the same key from the earlier transmissions. Again, assuming that Alice and Bob use AES-CTR, the two transmission streams can be XORed together to potentially extract sensitive information. There are ways to solve this (e.g., by reintroducing challenge-response) but there are many ways it can go wrong even still.
It is very difficult to get all the parts of a cryptographic protocol right, even for the experts. In general, do not design your own protocols. Use existing protocols as much as possible and existing implementations whenever feasible. Above all, we want to remind you one more time, YANAC (You Are Not A Cryptographer... yet!).
Exercise 6.11. Exploiting Full-Duplex Key Reuse
In previous exercises, you XORed some data together to see if you could still find patterns, but you didn’t actually XOR the two cipher streams together. Imagine if Alice and Bob used your ECDH exchange and derived the same key for full-duplex communication. Use the same key to encrypt some documents together for Alice to send to Bob and for Bob to send to Alice. XOR the cipher streams together and validate that the result is the XOR of the plaintext. See if you can figure out any patterns from the XORed data.
Exercise 6.12. Deriving All The Pieces
Modify the ECDH exchange program to derive six pieces of information: a write encryption key, a write IV, a write MAC key, a read decryption key, a read IV, and a read MAC key. The hard part will be getting both sides to derive the same keys. Remember, the keys will be derived in the same order. So how does Alice determine that the first key derived is her write key and not Bob’s write key? One way to do this is to take the first n bytes of each side’s public key bytes as an integer and whoever has the lowest number goes “first.”
An Unfortunate Example of Asymmetric and Symmetric Harmony
Most of our examples of cryptography are beneficial in some way, or are at least not inherently evil. Unfortunately, bad guys can use cryptography just as well as the good guys. And given that they can make a lot of money from evil, they can be highly motivated to produce creative, efficient uses of the technology.
One area where bad guys are incredibly good at using cryptography is ransomware. If you’ve been living in a cave in West Antarctica for the past decade and haven’t heard about ransomware, it’s basically software that encrypts your files and refuses to unlock them until you pay the extortionists behind it.
The cryptography behind early ransomware was simplistic and naive. The ransomware encrypted every file with a different AES key, but all of the AES keys were stored on the system in a file. The ransomware’s decryptor could easily find the keys and decrypt the file, but so could security researchers. If you don’t want somebody to unlock a file, it’s bad idea to leave the keys just lying around (under the doormat, so to speak).
Ransomware authors logically turned to asymmetric encryption as a solution. The immediately obvious advantage of asymmetric cryptography is that a public key could be on the victim’s system and a private key could be somewhere else. For all of the reasons you’ve seen in this chapter, the files themselves cannot be encrypted with RSA directly. RSA doesn’t even have the capacity to encrypt data larger than between 190 and 256 bytes, and if it did, it would be too slow. The user might notice their system getting locked down long before the encryption was complete.
Instead, the ransomware could encrypt all of the AES keys individually. After all, an AES key is just 16 bytes for AES-128 and 32 bytes for AES-256. Each key can be easily RSA encrypted before being stored on the victim’s system. RSA encrypts with the public key, so as long as the private key isn’t available to the victim, they won’t be able to decrypt the AES keys.
There are two naive variants of this approach, both of which are problematic. The first approach is to generate the key pair ahead of time and hard-code the public key into the malware itself. After the malware encrypts all the AES keys with the public key, a victim has to pay the ransom to have the private key sent to them for decryption. The obvious flaw in this design is that the same private key would unlock all of the systems attacked by the ransomware, as each copy of the malicious attack file had the same public key baked into it.
The second approach is for the ransomware to generate the RSA key pair on the victim’s system and transmit the private key to the command and control server. Now there is a unique public key encrypting the AES keys, and when the attacker releases the private key for decryption, it only unlocks the specific victim’s files. The problem here is that the system has to be online to get rid of the private key, and many network monitoring systems will detect transmissions to risky IPs where command and control servers often operate. Transmitting the private key might give away the ransomware before it has even started encrypting files on the system. It is stealthier to do everything locally until the system is fully locked.
Modern ransomware solves all of these problems with a pretty clever approach. First, the attacker generates a long-term asymmetric key pair. For our purposes, let’s just assume it is an RSA key pair, and we will call these keys the “permanent” asymmetric keys.
Next the attacker creates some malware and hard-codes the permanent public key into the malware. When the malware activates on a victim’s machine, the first thing that it does is generate a new asymmetric key pair. Again, for simplicity, let’s assume that it is an RSA key pair. We will call it the “local” key pair. It immediately encrypts the newly generated local private key by the attacker’s permanent public key embedded in the malware. The unencrypted local private key is deleted.
Now the malware begins to encrypt the files on the disk using AES-CTR or AES-CBC. Each file is encrypted under a different key, and then each key is encrypted by the local public key. The unencrypted version of the key is destroyed as soon as the file is finished being encrypted.
When the whole process is done, the victim’s files are encrypted by AES keys that are themselves encrypted by the local RSA public key. These AES keys could be decrypted by the local RSA private key, but that key is encrypted under the attacker’s permanent public key, and the private key is not on the computer.
Now the attacker contacts the victim and demands the ransom. If the victim agrees and pays the ransom (usually by way of Bitcoin), the attacker provides some kind of authentication code to the malware. The malware transmits the encrypted local private key to the attacker. Using his or her permanent private key, he or she decrypts the local private key and sends it back to the victim. Now all of the AES keys can be decrypted and the files subsequently decrypted.
What’s clever about this algorithm is that the attacker does not disclose his or her permanent private key. It remains private. A secondary private key is decrypted by the attacker for the victim to use in unlocking the rest of the system.
Warning: Risky Exercise
The upcoming exercise is somewhat risky. You should not do this exercise unless you have a virtual machine that can be restored to a snapshot or a jail (e.g., a chroot jail) with files that can be permanently lost.
Furthermore, this exercise has you create a simplified version of ransomware. We do not condone nor encourage any actual use of ransomware in any form. Don’t be stupid, don’t be evil.
Exercise 6.13. Playing The Villain
Help Alice and Bob create some ransomware to infect WA servers. Start by creating a function that will encrypt a file on disk using an algorithm of your choice (e.g., AES-CTR or AES-CBC). The encrypted data should be saved to a new file with some kind of random name. Before moving on, test encrypting and decrypting the file.
Next, create the fake malware. This malware should be configured with a target directory and the permanent public key. The public key can be hard-coded directly into the code if you wish. Once up and running, it needs to generate a new RSA key pair, encrypt the local private key with the permanent public key, and then delete any unencrypted copies of the local private key. If the private key is too big (e.g., more than 190 bytes), encrypt it in chunks.
Once the local key pair is generated, begin encrypting the files in the target directory. As an extra precaution, you can ask for manual approval before encrypting each file to make sure you don’t accidentally encrypt the wrong thing. For each file, encrypt it under a new random name and store a plaintext metadata file with the original name of the file, the encrypted key, and IV. Delete the original file if you feel that you can do so safely (we will not be held responsible for any mistakes on your part! Use a VM, only operate in a target directory on copies of unimportant files, and manually confirm each deletion!).
The rest should be straightforward. Your “malware” utility needs to save the encrypted private key to disk. This should be decrypted by a separate command and control utility that has access to the permanent private key. Once decrypted, it should be loaded by the malware and used to decrypt/release the files.
While you are hopefully not a malware/ransomware author, this section should also be helpful to you in thinking about how to encrypt “data at rest.” Much of what we talk about in this book is to protect “data in motion,” which is data traveling across a network or in some other way between two parties. The ransomware example illustrates protecting data that stays largely in place, typically to be encrypted and decrypted by the same party.
Utilities that encrypt files on disk have to deal with the wretched key management problem just like they do with data in motion. In general, there will have to be one key per file just like there has to be one key per network communications session; this prevents key reuse. The keys (and IVs) must be stored, or it must be possible to regenerate them. If they are stored, they must be encrypted by some kind of master key and stored along with additional metadata about the algorithm used and so forth. This information can be prepended to the beginning of the encrypted file, or it can be stored somewhere in a manifest.
If the keys are regenerated later, this is typically done by deriving the keys from a password, as we have already discussed in Chapter 2. As there needs to be a different key for each file, a random per-file salt is used in the derivation process to ensure that key’s uniqueness. The salt must be stored with the file, and the loss of the salt would result in a lost file that could never be decrypted.
This is the basic cryptographic concept behind securing data at rest, but production systems are usually far more complicated. NIST, for example, requires that compliant systems have a defined cryptographic key life cycle. This includes a pre-operational, operational, post-operational, and deletion stages as well as an operational “crypto” period for each key. This period is further broken down into an “originator usage period” (OUP) for when sensitive data can be generated and encrypted and a “recipient usage period” (RUP) for when this data can be decrypted and read. Key management systems are expected to handle key rollover (migrating encrypted data from one key to another), key revocation, and many other such functions.
We won’t bother you with another reference to YANAC... but by this point in the book, we hope your own subconscious is starting to do it for us!
That’s a Wrap
The main thrust of this chapter is that you can wrap up a temporary symmetric communication session within an initial asymmetric session establishment protocol. A lot of the world’s asymmetric infrastructure is focused on long-term identification of parties and that infrastructure is useful for establishing identities in some way and based on some model of trust. But once that trust is established, it’s more secure and more efficient to create a temporary symmetric key (well, actually several of them) to handle encrypting and MACing the data going forward.
We reviewed, for example, that you can transport a key from one party to another using RSA encryption. This approach was the primary approach used for a long time. Although still present in many systems, it is being retired for many reasons. More favored these days is using an ephemeral key agreement protocol, such as DH and ECDH (actually, DHE and ECDHE to be precise) to create a session key with perfect forward secrecy.
Either way, whether by key transport or key agreement, the parties can then derive the suite of keys necessary for communications. Or, a single party can derive the keys necessary for encrypting data on a hard drive. In both cases, the asymmetric operations are primarily used to establish identity and get an initial key, while the symmetric operations are used for the actual encryption of data.
If you can understand these principles, you can be conversant about most cryptography systems you’ll find.