In this chapter, we will be talking about “keyed hashes” and how asymmetric cryptography can be used to provide not only message privacy but also message integrity and authenticity via digital signatures. We will also be talking about how certificates differ from keys and why that distinction is important. Let’s dive right into an example and some code!
An Overly Simplistic Message Authentication Code (MAC)
Checking in with Alice and Bob, our East Antarctic espionage duo has had some trouble on their most recent adventure in adversarial territory to the west. Apparently, Eve managed to intercept a few communications sent between them. The messages, encrypted with symmetric encryption, were unreadable, but Eve figured out how to alter them, inserting some false instructions and information. Alice and Bob, acting on false information, were almost trapped in an ambush. Fortunately for them, a bunch of ice melted due to global warming, and they managed to swim home to safety!
Quick to learn from their close call, they spent a little time at headquarters drying off and devising new communication mechanisms to prevent the unauthorized modification of their encrypted data.
Eventually, the East Antarctica Truth-Spying Agency (EATSA) discovered a new concept: “message authentication codes” or “MACs.”
- 1.
The sender computes a code C1 using a function f(M1) for a given message M1.
- 2.
The sender transmits M1 and C1 to the recipient.
- 3.
The recipient receives the data as M and C, but does not know if they have been modified.
- 4.
The recipient recomputes f (M) and compares the output to C to verify that the message is unaltered.
Suppose that Eve intercepts M1 and C1 sent by Alice to Bob. If Eve wants to change the message M1 to M2, she must also recompute C2 = f (M2) and send both M2 and C2 to Bob. Otherwise, Bob will detect that something has been changed because f (M) and C will not match.
If you are asking, “So what? Eve can just recompute the MAC, right?” then you are seeing the problem with our overly simplistic setup. We have to assume that Eve has everything except the key, but this example also assumes she does not have f. We will fix that shortly. Stay tuned!
For now, Alice and Bob are just going to assume that Eve can’t compute, or easily compute, the function f. If this assumption is true (which it isn’t in reality), then just about any mechanism for creating a fingerprint will work. The East Antarctican spying agency decides to send the message hash as an attachment to the message. Thus, the MAC is a hash in this case.
Fake MAC with Symmetric Encryption
Recall that “counter mode” requires no padding and that in our previous examples the “finalize” functions really didn’t do much. But now, when we finalize our manager, it not only finalizes encryption, it also returns the computed hash as the last few bytes to be appended to the encrypted data. Thus, the final encrypted message has our simple MAC tacked onto the end of it.
Exercise 5.1. Trust But Verify
Finish out the code of the simple encryption plus hash system and add a decryption operation. The decryption operation should, upon finalization, recompute the hash of the ciphertext and compare it to the hash that was sent over. If the hashes don’t match, it should raise an exception. Be careful! The MAC is not encrypted and should not be decrypted! If you don’t think carefully about this, you might decrypt data that doesn’t exist!
Exercise 5.2. Ever Evil Eve
Go ahead and “intercept” some of the messages encrypted by the code you wrote in this section. Modify the intercepted messages and verify that your decryption mechanism correctly reports an error.
MAC, HMAC, and CBC-MAC
Alice and Bob were told by their support people that any mechanism for authenticating a message is a message authentication code (MAC). As we hinted, this is not a complete definition. A real MAC also requires a key .1
We’ve used keys for encryption, but so far we haven’t used them for much else. A MAC key, as you might have guessed, isn’t really related to encryption at all. Rather, it ensures that the message authentication code can only be computed by parties that know the key.
In our example, Alice and Bob had to assume that Eve couldn’t compute the function f(M). That, of course, isn’t reasonable. Alice and Bob used SHA-256 to derive a fingerprint, so obviously Eve can use it to compute her own authentication code as well. Assuming that she can deterministically alter the ciphertext, as we saw in the previous chapter that she could under certain circumstances, she could insert a new message and a new fake MAC.
A real MAC, however, which depends on a key, cannot be generated by Eve unless she has compromised the key! Remember, good security means that everything can be known except the key and it still works right.2
A MAC protects the integrity of the message. An attacker without a key cannot undetectably alter the data. Furthermore, if the key remains secret, the MAC also provides authenticity: the receiver knows that only the other person sharing the key could have sent the MAC because only a person with a key could have generated a legal MAC at all.
While there are many MAC algorithms, we will look at two easy-to-understand approaches: HMAC and CBC-MAC. These algorithms do a good job of teaching how and why a MAC works. They are useful in practice as well.
HMAC
An HMAC is a “hash-based message authentication code.” In fact, you already know the most complicated characteristic of an HMAC: hashing. An HMAC is mostly just a hash that is keyed.
What does it mean to be “keyed”? To illustrate, let’s first review standard cryptographic hashes that are not keyed. For such hashes, if the input doesn’t change, neither does the output. They are fully deterministic based only on a single input: the message contents. If you revisit the exercise “GOOGLE KNOWS!” in Chapter 2, you will recall that we can actually enter some hash values into Google and find matching inputs.
The SHA-256 outputs for “hello world” and “happy birthday” are always these values on every computer for the rest of eternity. They will never change. You can verify this by running the code yourself. The SHA-256 definition demands it. You can also try searching for the hashes online.
To repeat, with an unkeyed algorithm the same input always produces the same output.
When an algorithm is keyed, it means that the output is dependent on both the input and a key. But how can a hashing algorithm be keyed?
Conceptually, it is actually pretty easy. Because even a minor change to the input of a hashing algorithm completely changes the output, we can have the key be part of the input itself!
In this example, we used human-readable passwords as the keys. We hashed the input “hello world” two more times, but inserted a different password each time as a prefix. Basically we used the key to change what we were hashing. Each password results in a completely different output, meaning that the only way for someone to recreate the output MAC for the message “hello world” is to also know the password (or break it through brute force). As with any other cryptographic algorithm, the key/password must be both sufficiently large and sufficiently random.
Speaking of size, it is worth noting that the size of the password is not a factor in how effectively it changes the hash output. Do you recall the avalanche principle? Changing a single bit of input to a hash function completely changes the output hash value. You could have a terabyte document, change only a single character of it, and produce a new hash that has no relationship to the unaltered document’s hash. Similarly, your password could be a single character, and it would effectively “scramble” the output for any given input, no matter how large. All you need to worry about is that your password length (and randomness) is sufficiently strong to prevent brute-force attacks.
Exercise 5.3. Brute Force Again
You should already have done some brute-force attacks in previous chapters, but it’s important to repeat the exercise until you develop intuition for the concept. Using our preceding fake HMAC, have the computer generate a random password of specific sizes and use brute-force methods to find out what it is. To be more specific, assume that you already know what the message is (e.g., “hello world,” “happy birthday,” or a message of your choosing). Write a program to create a random password of characters, prepend the password to the message, and then print out the MAC (hash). Take the output and iterate through all possible passwords until you find the right one. Start with a simple test of a single-letter character, then try two characters, and so forth. Mix things up by using different sets of characters such as all lowercase, lowercase and uppercase, either case plus numbers, and so forth.
Exercise 5.4. Brute Force Four-Word Passwords
Repeat the previous exercise. But instead of using letters drawn from a source of letters, use words drawn from a source of words. Find or create a text file with a list of common words. It should be at least 2000 words. Using this dictionary, create passwords by picking n random words. Attempt to brute force this password by trying every possible combination from the dictionary. Start with n = 1 (one-word password) and go up from there.
Even the preceding approach isn’t quite good enough, so let’s talk about the real HMAC. We have repeatedly said that merely prepending the password is not sufficiently secure. “HMAC” is the official name given to an algorithm defined in a standard document called “RFC 2104.” If you haven’t ever looked at an RFC before, these are documents from the Internet Engineering Task Force (IETF) that represent standards, best practices, experiments, and discussions for Internet protocols and algorithms. They are all freely available and can be found online. RFC 2104 can be found at https://tools.ietf.org/html/rfc2104 .
This document describes HMAC, a mechanism for message authentication using cryptographic hash functions. HMAC can be used with any iterative cryptographic hash function, e.g., MD5, SHA-1, in combination with a secret shared key.
That part should already make sense. The experiments we already did used SHA-256 and a secret shared key, but we obviously could have used SHA-1 or MD5. As a reminder, though, those hash algorithms are considered “broken” and should not be used except as necessary with legacy applications.
H(K XOR opad, H(K XOR ipad, text))
Let’s take a look at each of these terms. We already know H; that’s the underlying hash function. The term “text” refers to the input, but does not have to be composed of readable text characters any more than any “plaintext” message needs to be: it can be arbitrary binary data. Oh, and we need to address the commas. Because H is a function, you might be tempted to think that this definition is showing a hashing function that takes two parameters. But in this definition in the RFC, the comma can be thought of as concatenation. As in all of our other examples, a hash function only takes a single input.
The term K refers to the key, but it can’t be just anything. The RFC has a number of requirements for the key that will often require some pre-processing. Most of these requirements are related to the block size of H. Recall from Chapter 3 that we used the term “block size” with block ciphers to describe the size of data that the block cipher operates on at one time. AES, for example, has a block size of 16 bytes (128 bits). Hashing algorithms can hash any size of input, so what is the block size of a hash algorithm?
In actuality, hashing functions typically operate on one block at a time, but feed the hash output from one chunk into the hashing computations of the next. SHA-1, for example, has a 64-byte (512-bit) block size, while SHA-256 has a 128-byte (1024-bit) block size. The RFC refers to the block size of H as B (bytes).
The first requirement for our key is that if it is shorter than the block size B, it has to be padded with zeros until it is B bytes long.
The second requirement is that if the key is longer than B, it is first reduced by hashing the key with H. Don’t let this surprise you. We will use H multiple times in a single HMAC operation.
In summary, if K is too short, it is padded with zeros, and if K is too long, H(K) is used instead.
The eagle-eyed reader will notice that the length of a hash may be also be shorter than the block size. SHA-1’s hash is 20 bytes long and its block size is 64 bytes. SHA-256’s hash is 32 bytes long but its block size is 128 bytes. After reducing the key that is too long with the hashing function, it will generally be too short and will then require padding.
In the end, we should have a key that is exactly B bytes long.
Next, we need to compute K ⊕ ipad (XOR). The term “ipad” stands for “inner padding” because this is the inner hashing operation in the HMAC. The RFC defines ipad as “the byte 0x36 repeated B times” and “opad” as “the byte 0x5c repeated B times.” The values chosen for ipad and opad were picked arbitrarily. What is most important is that they are different.
The reasons for the pads go beyond the scope of this book, but they give HMAC some extra security in case the underlying hash function is broken. So, for example, these paddings made HMAC-MD5 relatively strong even after MD5 was shown to be broken. That’s helpful, but not a good reason to use HMAC-MD5 for new applications. Please don’t. HMAC’s padding means that HMAC-SHA256 will be a reasonably strong MAC even if someone finds a vulnerability in the SHA-256 hashing function, which can help keep existing uses (that might not be easily upgraded to a better hash function immediately) relatively secure.
The computation of K ⊕ ipad is pretty easy because they are the same size. The subsequent value is prepended to the input “text,” and the combined data is hashed by H. We have now computed H(K ⊕ (ipad, text)). Again, this is the inner hash computation.
Now, for the outer hash, we compute K ⊕ opad. The subsequent value is prepended to the output of the inner hash, and the aggregated bytes are hashed again. The hash of the outer function is the HMAC of the input text keyed on K.
Why go to all the trouble of learning how HMAC works on the inside, rather than just learning how to use a supplied library? There are a few reasons. First, it’s good to have at least a little bit of an idea of how things work. It helps with intuition and reasoning about when to use it and why.
Second, and perhaps most important, it is to remind you that YANAC (You Are Not A Cryptographer... yet!). You must remember this principle! Use cryptographic libraries as much as possible and do not try to come up with your own “clever” algorithm. Take a look at HMAC again. It’s built on some of the same concepts as simply prefixing an input with a key, but has much higher complexity. That complexity comes from deeper and subtler goals, including forward security in the event of a broken hash function. That complexity is not arbitrary; the HMAC operation was based on a research paper by cryptographers that mathematically proved certain security properties. Unless you are a cryptographer who publishes your work (often with formal proofs) for public peer scrutiny, test, and debate, then you really should not be creating your own algorithms except for the purposes of education or demonstration.
Exercise 5.5. Test Python’s HMAC
Although you should not roll your own crypto, it doesn’t mean you shouldn’t verify implementations! Create your own implementation of HMAC following the instructions from RFC 2104 and test some inputs and keys with both your implementation and Python’s cryptography library’s implementation. Ensure that they produce the same outputs!
CBC-MAC
HMAC is a very popular MAC and is used, for example, in TLS, but there are other ways to create MACs. For example, we can take what you learned in Chapter 3 about cipher block chaining (CBC) mode as another way to derive a secure MAC.
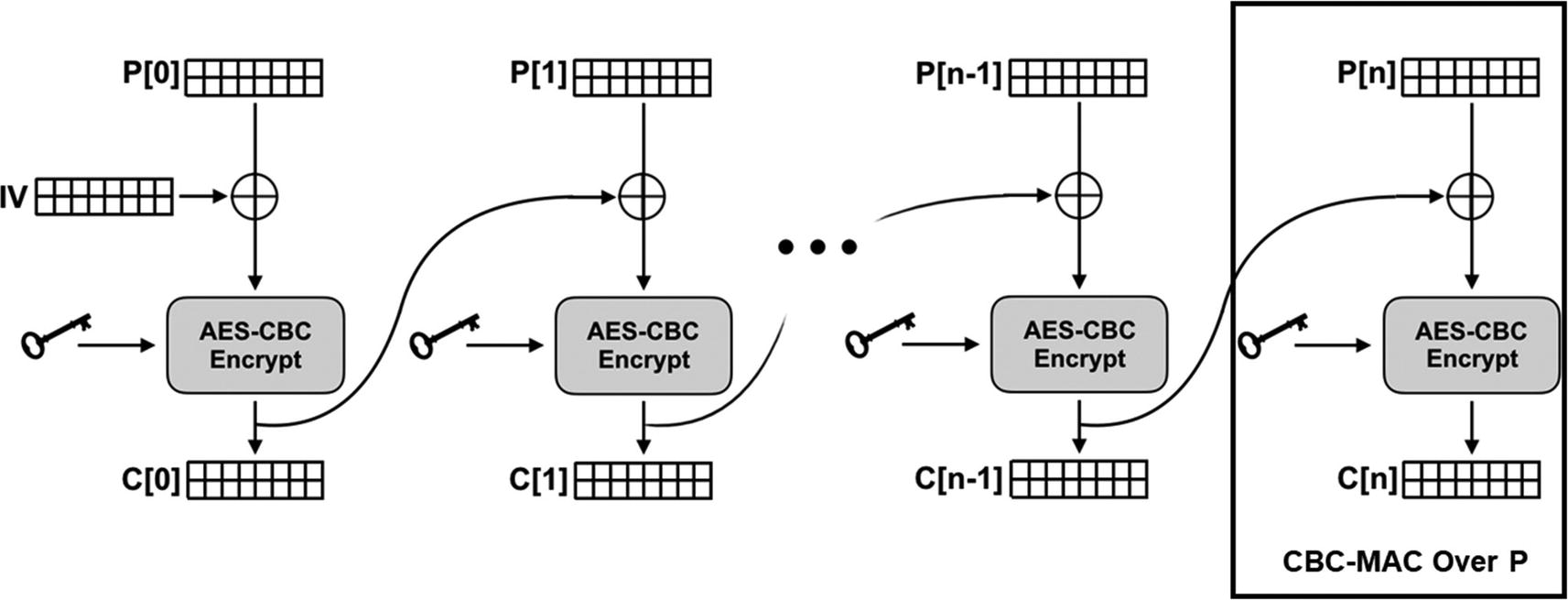
Because all of the message impacts the value of the last encrypted block of data, C[n] is a MAC over all of P... with a few flaws.
Recall that when encrypting with AES, we were limited to encrypting 128 bits at a time. If we encrypted each 128-bit block independently, there was still information that could “leak” through about the overall data. For example, large image features might still be recognizable. One of the solutions to the problem was to “chain” the encryption so that the input from one block carried over and influenced the encryption of the next. In other words, a change in a bit at the beginning would have a cascading effect all the way down to the very last block.
Put another way, the very last block of ciphertext is determined by the value of every other block in the chain: any changes anywhere in the input will be reflected in the last block! That makes the last block of a CBC encryption mode a MAC over the entire data as shown in Figure 5-1.
Hopefully as you have learned by this point in the book, all cryptography comes with limitations and critical parameters. As with HMAC, we will do some naive examples first to see both the basic concepts behind the CBC-MAC algorithm and how naive approaches are exploitable.
Fake MAC with CBC
The code in Listing 5-2, although not secure, does show the basic concept behind the MAC. A piece of data is first padded and then encrypted. No matter how long it is, however, the last block (16 bytes) is determined by all of the preceding input. Change the first letter from an “h” to an “H,” and the MACs are completely different.
Nevertheless, it can be exploited. Recall that a MAC must be unique for a given message and key pair. If an attacker can generate the same MAC for a different message with the same key, the MAC algorithm is broken.
MAC Prepend Attack
The two MACs produced by Listing 5-3 are identical. Our attack prepends another message of our choosing to the original and also corrupts the first block. The only restriction on the prepended message is that it must also have the CBC-MAC value for the prepended message under the same key. We turned off padding for this prepended message to make the attack a little easier, but this is only for our convenience and not a prerequisite for the attack to succeed.
Sadly for the attacker, the original message requires modification to the first block; otherwise, the attack could have been even worse. The attacker could then create messages that say “do not attack the enemy forces at dawn!” The attacker also cannot scrub any of the data beyond the first block. In running the code, you probably noticed that “forces at dawn!” was still readable in the new message. Even so, this is still pretty bad: we added an entirely different message without changing the value of the MAC!
For this simple example, where we assume that a human is reading the output, we hope that our message that says the rest of the data is padding will be enough to convince the sender not to read further. In real attacks, transmitted data lengths and other similar mechanisms can often be used to achieve the same effect. If we are successful, we can basically send arbitrary message with the original MAC.
What went wrong? Before we give you an explanation, see if you can figure it out yourself. You might need to revisit how CBC mode works. If you need an additional hint, remember that A ⊕ B ⊕ B = A.
t = E(mn ⊕ E(mn−1 ⊕ ... E(m2 ⊕ E(m1, k), k) ... , k), k)
Notice that m1, the first block of the message, is encrypted by AES under key k and the output is XORed with m2 before being encrypted.
tP = E(mn ⊕ E(mn−1 ⊕ ... E(m2 ⊕ E(m1 ⊕ E(P, k), k), k) ... , k), k)
t = E(mn ⊕ ... E(m2 ⊕ E(m1 ⊕ C ⊕ E(P, k), k), k) ... , k), k)
t = E(mn ⊕ E(mn−1 ⊕ ... E(m2 ⊕ E(m1 ⊕ C ⊕ C, k), k) ... , k), k)
t = E(mn ⊕ E(mn−1 ⊕ ... E(m2 ⊕ E(m1, k), k) ... , k), k)
This example was just for a single block. But it turns out that no matter how long the prepended message is, we only care about the part that will be XORed with m1 before it is encrypted. In a CBC chain of arbitrary length, the only part that carries over into the next block is the last encrypted block of the chain. In other words, the MAC output of the CBC-MAC operation, t, is the only part of a prepended message that would impact what follows it!
t2 = E(M2,n ⊕ E(M2,n−1 ⊕ ... E(M2,1 ⊕ t1 ⊕ C(M1, k), k) ... , k), k)
As the MAC of M1 is t1, it cancels out with the other t1 and the MAC of what is left is just the MAC of M2.
A visualization of this attack, and the math we just worked through, is depicted in Figure 5-2.
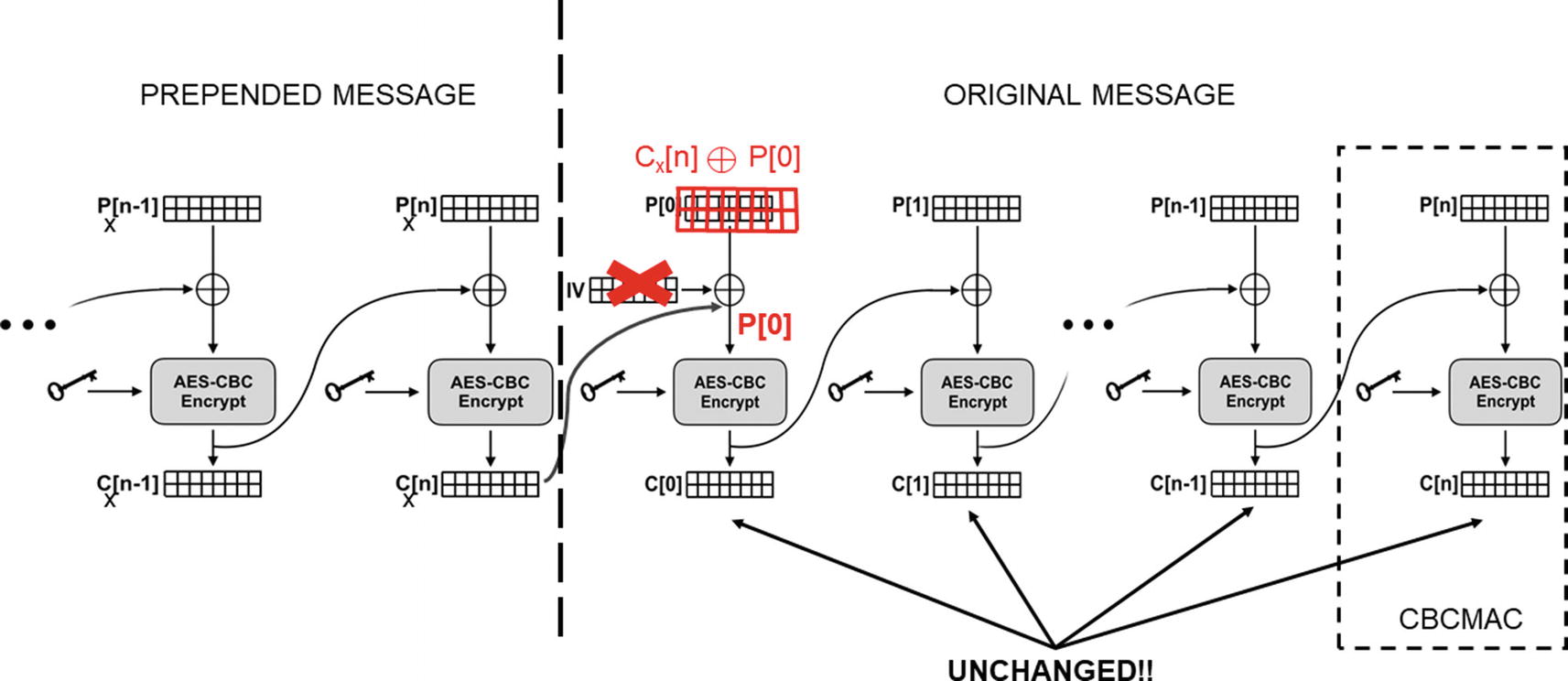
An attacker can prepend a message without changing the (simple) CBC-MAC by corrupting just the first block
But with this attack, an attacker without the key can generate a new message and a falsified tag from two existing messages (e.g., generated by the victim) and corresponding tags.
Prepend Message Length
- 1.
If you are also encrypting the data with AES-CBC, you must not use the same key for both encryption and MAC.
- 2.
The IV should be fixed to zero.
A full explanation of each of these is beyond the scope of this book. Assuming that you follow them, however, the included CBC-MAC code is reasonably secure. We still don’t recommend using it because it is always dangerous to create your own cryptographic algorithms or even your own implementations of known cryptographic algorithms. Instead, always use algorithms in trusted cryptographic libraries.
The Cryptography library that we are using for our example code includes CMAC. This algorithm is an updated and improved CBC-MAC defined in RFC 4493. Either CMAC or HMAC are good choices for a MAC algorithm; HMAC might be faster on most systems without specialized AES encryption hardware.
Encrypting and MACing
In many circumstances a message needs to be encrypted and protected from modification. In the first code example in this chapter, Alice and Bob used an unkeyed hash to protect an encrypted message. Obviously, that doesn’t work because without a key, anyone can generate the corresponding hash. Now that our intrepid (or dastardly) duo know how to use HMAC and CMAC, they can update their code.
Exercise 5.6. Encrypt Then MAC
Update the code from the beginning of the chapter to do a proper MAC by replacing the SHA-256 operation with HMAC or CMAC. Use two keys.
Pay attention to when you use MAC and what you use it on in the previous exercise. You will notice that it is the ciphertext that the MAC is applied to, not the plaintext. As the name of the exercise implied, this is called Encrypt-Then-MAC . There are two other ways of sending an encrypted and authenticated message that have been done in the past.
One is MAC-Then-Encrypt. In this version, the MAC is applied to the plaintext, and then both the plaintext and the MAC are encrypted together. This approach was taken by early versions of TLS (which is used for HTTPS connections).
Another approach is called Encrypt-And-MAC . To take this approach, the MAC is again computed over the plaintext, but the MAC itself is not encrypted. It is sent (unencrypted) along with the ciphertext. If you’ve ever used Secure Shell (SSH or PuTTY), it uses Encrypt-And-MAC.
It is strongly recommended by most cryptographers, with a few dissenters, as there are always some of those, to use Encrypt-Then-MAC3 over these other two approaches. In fact, certain practical vulnerabilities have been found against certain combinations of MAC-Then-Encrypt. You have already demonstrated one! The padding oracle attack against CBC in the previous chapter only works against MAC-Then-Encrypt scenarios.
There’s an even better approach called AEAD (authenticated encryption with additional data) that we will learn about in Chapter 7 that combines encryption and message integrity into a single operation. If, for whatever reason, you need to combine encryption and MAC, make sure you choose Encrypt-Then-MAC (i.e., encrypt the plaintext and then compute a MAC over the ciphertext).
We won’t go into the various arguments for why Encrypt-Then-MAC is generally considered better but one point is worth mentioning. As we have talked about in other circumstances, we generally don’t want bad guys messing around with our ciphertext. It can be unintuitive because we tend to think about the end goal: protecting the plaintext. But bad things happen when the bad guys can change the ciphertext without us being able to detect it. When you do Encrypt-Then-MAC, the ciphertext should be protected against modification.
Exercise 5.7. Know Thy Weakness
Encrypt-Then-MAC is the recommended approach to combining encryption and MACs. However, it is good to understand all three approaches. If nothing else, if you ever have to maintain code you did not write, or have to be compatible with legacy systems, you may encounter this in the future. Modify your (highly recommended) Encrypt-Then-MAC system to create a MAC-Then-Encrypt variant. Finally, create a MAC-And-Encrypt version as well.
Digital Signatures: Authentication and Integrity
Alice and Bob love sending encrypted messages with HMACs (using Encrypt-Then-MAC). On their current assignment in West Antarctica, they each have four keys. One pair allows them to send encrypted and MAC-protected messages to each other (remember, one key for encryption, one key for MAC generation), and the second pair allows them to send and receive encrypted and MAC-protected messages to and from HQ back in East Antarctica.
Unfortunately, one day Alice is captured as she attempts to infiltrate the West Antarctic Snowball Testing Edifice. Instantly, everything is thrown into disarray as Eve now has access to all of her keys.
This is a terrible compromise. Eve is now able to send messages as though they are from Alice or HQ! Trying to mitigate this loss of confidentiality and authentication is a nightmare. Bob’s situation is bad. He needs two new keys to communicate with HQ and perhaps two new keys for communicating with a new partner in the field. This can only be done by returning to HQ, which means pulling him out of the field, potentially wasting time and resources he has spent infiltrating his targets and gathering data. Worse, he can’t even be reliably told about what is going on! If he doesn’t have first-hand knowledge of Alice’s capture, any messages sent by HQ informing him of the event or instructing him to come home can be intercepted and changed.
As bad as things are for Bob, HQ is in far worse shape. They were using the same shared keys for encrypting and tagging all of their messages. Every single agent in the field has the compromised keys lost by Alice. Eve can impersonate HQ to any of them. And Eve can send messages to HQ as any of the agents, because they did not have their own individual keys for communicating with HQ.
The loss of the shared keys sets EATSA back at least 12 months.
As bad as it is that Eve can read the traffic between HQ and their agents using the encryption keys, it might be worse that she can send messages pretending to be any of these parties by using the MAC keys. To repeat one of our earlier comments, when people first start to learn about cryptography, they typically think about “encryption” as its main purpose or characteristic. As our fictional example illustrates, authentication—knowing who sent a message—is at least as important, and arguably more so.
Even once EATSA manages to get all of their agents’ home and is no longer using the old keys (the old keys are thus “revoked”), they have the problem of coming up with a key management system to avoid the same problem in the future. One option they consider is for each agent to have their own individual key. If either HQ or an agent wants to send a message, they use their individual key to tag it.
The problem is MACs require shared keys. The receiver of the message must have the same key as the sender. How will they obtain it? Will every agent have every other agent’s key? If so, an agent’s capture is just as bad as if there was only one key. Worse, nothing keeps an agent from using another agent’s key (impersonating them) either by accident or because they go rogue.
Eventually, one of the scientists remembers asymmetric encryption from Chapter 4, specifically that it can be used for something called a digital signature. Like message authentication codes, digital signatures are designed to provide authenticity (you can tell who sent the message) and message integrity (the message cannot be changed undetectably). Furthermore, because they use asymmetric encryption, there are no shared keys. At the time the EA started playing around with asymmetric encryption, they became very, very focused on encryption of messages (confidentiality) and digital signatures fell off to the side.
It is time to remedy that.
What exactly is a digital signature? First, let’s review how asymmetric encryption works for the RSA algorithm we studied in Chapter 4. Unlike symmetric encryption where there is a single shared key between parties, RSA’s asymmetric encryption involves a pair of keys: the public key and the private key. These keys work as opposites of one other: what one encrypts, the other decrypts. Moreover, the RSA public key can be derived from the private key but not the other way around.
As the name implies, a party should keep the RSA private key private and disclose it to nobody, ever. On the other hand, the RSA public key can and typically should be widely disseminated. This setup enables two very interesting operations.
First, because the RSA public key is held by anyone (and potentially by everyone!), it is easy for anyone in the world to send an encrypted message to the owner of the corresponding RSA private key. Anyone can use the public key to encrypt the message, but only the party with the private key can decrypt it.
This is important! The person that sends the encrypted message knows that only the party possessing the private key can decrypt the message. This is a different kind of reverse authenticity. The recipient of the message has no idea who sent it, but the sender can be certain (if the keys are secure) that only the intended party can read the message. Our introduction to RSA asymmetric encryption in Chapter 4 focused on this use case.
But, the direction of the encryption can be reversed: RSA private keys can also be used to encrypt messages. The party that has the private key can thus use it to encrypt something that can only be decrypted by the public key. What good would that do? Anybody (everybody!) could have the public key. This encryption certainly won’t keep data confidential!
This is true! But, a message sent encrypted under the RSA private key can only have been encrypted by someone who has that private key. Even if everyone can decrypt it, the fact that it can be decrypted by a particular public key is a proof that the sender holds the private key. In other words, if you get a message that you can decrypt using my public key, you know that it came from me; nobody else could have encrypted it. That sounds useful!
Let’s suppose that the EA wants to publish a manifesto of West Antarctica’s crimes to the whole world. First they could disseminate their RSA public key everywhere and then encrypt the document under the associated private key. Now, when they distribute the document, anyone in the world can decrypt it, and that fact proves to them that it came from the EA.
This system is great, but it has a couple of important flaws. First of all, how does the world know that the RSA public key really belongs to the EA (and is not a fake from the WA, for example)? This is a critically important question and we’ll get to it a bit later. For now, we will assume that recipients have a legitimate, trusted RSA public key for the intended party.
Another problem is efficiency. RSA encryption is slow. Decrypting long documents to verify the sender is not a remotely efficient way of doing things. Worse, some asymmetric algorithms do not have any built-in message integrity. Oh, and while we’re talking about RSA’s limitations, it can’t encrypt something as long as a document anyway.
These latter two problems of efficiency and integrity are fortunately easily addressed. Recall that we are not encrypting for confidentiality, but for proof of origin or authenticity. Instead of encrypting the message itself, how about encrypting a hash of the message?
That is the basic idea of an RSA digital signature over arbitrary data. It consists of two steps. First, hash the data. Second, encrypt the hash with the private key. The encrypted hash is the sender’s signature applied to the data. The signature can now be transmitted along with the original (potentially unencrypted) data. When the recipient receives data and a signature, the recipient generates the hash, decrypts the signature with the public key, and verifies that the two hashes (generated and decrypted) are identical.
Here is how cryptographers might represent this. First, for a message M, we generate a hash using a hash function: h = H(M).
Once we have the hash h, we encrypt it under the RSA private key. To depict this operation, we are going to use some notation that is often used in cryptographic protocols. Specifically, we will use {⋅} to indicate RSA-encrypted data. Everything within the braces is plaintext, but the braces indicate that the plaintext is within some cryptographic envelope. The braces will also have a subscript indicating the key. So, for example, the ciphertext C is the plaintext P encrypted under some key K, and this is depicted as C = {P }K.
From this point forward in the book, a shared key between two parties will be depicted with a subscript indicating both parties. So, for example, a key between Alice and Bob can be depicted as KA,B. This would be an example of a symmetric key.
Public keys, such as RSA public keys, will be denoted by a key with just one identifying party. For example, Alice’s public key could be denoted KA and Bob’s would similarly be KB. Because the public key is what is distributed, it is what is named. The private key is denoted instead as the inverse of a public key: K–1A and K–1B).
In this chapter, we will also typically use the letter t to represent RSA signatures because a signature is also sometimes called a tag, just like a MAC is. Thus, we represent an R:
tM = {H(M)}K−1
When another party with possession of the RSA public key K receives M, {H′(M)}K−1, the signature is decrypted by the public key to recover H′(M). The receiving party generates their own H(M), and the signature is considered authentic if H′(M) = H(M).
At the risk of being repetitive, remember that RSA public key encryption is used for different things than private key encryption. Encryption with the RSA public key keeps the message confidential: only the private key owner can read it. Encrypting with the RSA private key proves authenticity: only the owner could have authored it.
In the EA spy agency, this seems miraculous! The agency generates an RSA key pair for itself and also has all of the agents generate an RSA key pair. The agency keeps a copy of all the public keys of all the agents, and every agent takes a copy of the agency’s public key.
When the agency sends an encrypted message to Alice, they encrypt it under her public key and only Alice will be able to decrypt it. They also sign the message with their private key, and Alice can use the agency public key to verify that the message is authentic and uncorrupted. So long as Alice and Bob have a copy of each other’s public keys, they can likewise send encrypted and authenticated messages to each other.
This is a big step forward, and it seems pretty great.
It really is, but as has so often been true with the EA’s cryptographic experiences, there are complications, caveats, and subtleties. Before we get into that, however, let’s help Alice and Bob learn how to send each other some signed communications. For simplicity, we are not going to encrypt them.
Sign Unencrypted Data
There’s probably a bit more in Listing 5-5 than expected, particularly in the padding configuration. Let’s walk through it all.
First, we generate a key pair. For RSA, the public key is derivable from the private key, so generating the private key generates the key pair. The API includes a call to obtain the public key from the private key. In this example, both keys are used. In a real example, the signing and verification code would live in completely different programs, and the verification program would only have access to the public key, not the private key.
In Chapter 4 we also learned how to serialize and de-serialize these kinds of RSA keys from disk.
In the next part of the code, we sign the message. You will notice that we are using padding here just as we did for RSA encryption, but it is a different scheme. The recommended paddings for RSA are OAEP for encryption and PSS for signatures. Perhaps that surprises you given that RSA signatures are generated by encrypting a hash. If it’s all encryption anyway, why do we need different padding schemes?
The answer is that, because signatures are operating on a hash, there are certain characteristics that must be true about the data. The nature of arbitrary data encryption vs. hash encryption drives the two different padding schemes.
Like the OAEP padding used in Chapter 4, PSS padding function also requires the use of a “mask generation function.” At the time of this writing, there is only one such function, MGF1.
Finally, the signature algorithm requires a hashing function. In this example, we are using SHA-256.
The parameters to the verification algorithm should be self-explanatory. Note that the validation function does not return a true or false, rather it raises an exception if the data does not match the signature.
Important
Please pay careful attention to this next paragraph. It is very important and somewhat counter-intuitive.
If you wanted to encrypt and sign, should you sign first and then encrypt, or should you encrypt first and then sign? After the discussion in the previous section on Encrypt-Then-MAC, you might be thinking Encrypt-Then-Sign.
But signatures are not MACs, and you should generally not use Encrypt-Then-Sign. There are two very important reasons.
First, remember that the goal of the signature is not just message integrity but also sender authentication. Suppose that Alice is sending an encrypted message to Bob, and she encrypts the message before signing it. Anyone can intercept the message, strip off the signature, and send the message re-signed under their own key. Oops.
It isn’t clear how practical this attack is because the data was encrypted under the receiver’s public key that everyone already has. The attacker could just send their own encrypted message to Bob (encrypted by Bob’s public key) anyway. The attacker can’t even decrypt Alice’s message to see if he/she wants to take credit for it. But the point is, there is no association between the plaintext and the signature, and there really needs to be: Bob is interested in knowing that the message he can read comes from Alice and not someone else. If the encrypted data is signed instead of the plaintext, when Bob receives the ciphertext and the signature, he cannot reliably determine who authored the original message.
In short, if you sign an encrypted message, it is too easy for it to be intercepted and signed by someone else instead, which compromises its authenticity. The signature should be applied to the plaintext.
Second, and far more important, signatures cannot prevent the bad guys from altering the ciphertext. Remember, the number one reason for using Encrypt-Then-MAC was to prevent undetectable alteration of the encrypted data. With Encrypt-Then-Sign, Eve, for example, could intercept a message from Alice to Bob, strip off Alice’s signature, alter the ciphertext, and then sign the altered data with her own key. What good is this, you might ask? After all, Bob will see that the message is now signed by Eve and not Alice. Why would he trust it?
There are any number of reasons Bob will accept the signature. For example, Eve may have compromised another agent’s key. The whole reason for using RSA encryption was to prevent the compromise of one agent’s key from compromising the communications of another. But if Eve gets a legitimate signing key, she can strip off Alice’s signature, modify the ciphertext, and re-sign with something Bob will accept.
Once this happens, Eve can observe Bob’s behavior to learn things about Alice’s message. As we used in earlier examples, even Bob throwing away a message is information that Eve can use to her advantage (e.g., she knows that the message she sent to him was unreadable).
Does this sound far-fetched? Well, exactly this kind of vulnerability in Apple’s iMessage was discovered by Matt Green. You can read about it on his blog [6]. We won’t discuss his attack in detail here other than to say that this kind of attack is actually very practical.
So please, do not Encrypt-Then-Sign.
Why is this so different from MACs? Why does Encrypt-Then-MAC work? The fundamental difference comes back to the keys. With a MAC, there is a shared key, typically shared between just the two parties. Nobody should be able to replace a MAC created by a key shared between Alice and Bob because nobody else should have the key. The private key used to create a digital signature, however, is not shared and does not bind any parties together.
What should you do? In the first place, there don’t seem to be many crypto systems this applies to. If you are using symmetric encryption, it is usually no problem to include a symmetric MAC. If Apple had done this, the iMessage attack we mentioned wouldn’t have been possible. Asymmetric encryption is not generally used for bulk encryption. When encrypting a lot of data is necessary, the usual approach is to exchange or create a symmetric key using the asymmetric cryptography and then switch to symmetric algorithms. We will talk about this in the next chapter.
If you absolutely must sign and encrypt without the benefit of a symmetric MAC (e.g., RSA encryption plus some signatures), the plaintext message should be signed and both the plaintext and signature should be encrypted (Sign-Then-Encrypt). Although this means that an attacker can try to mess around with the ciphertext, a good RSA padding scheme like OAEP should make this very difficult.
While there are no known attacks against Sign-Then-Encrypt, some of the most paranoid still Sign-Then-Encrypt-Then-Sign-Again. The inner signature is over the plaintext, proving authorship, and the outer signature is over the ciphertext, ensuring the integrity of the message. One other alternative is something called “signcryption.” Because signcryption isn’t supported by the Python cryptography library, we won’t spend any time on it here, but the curious can read this paper about it: www.cs.bham.ac.uk/ ~ mdr/teaching/modules04/security/students/SS3/IntroductiontoSigncryption.pdf .
For now we will stick with the slightly less paranoid Sign-Then-Encrypt strategy. Remember, however, that RSA encryption can only encrypt a very limited number of bytes. When OAEP padding is used with SHA-256, the maximum plaintext that can be encrypted is only 190 bytes! If you start encrypting signatures, there may be very little room left for anything else. If your message is too long, you will have to break it up and encrypt it in 190-byte chunks. This is all the more reason to use the combined asymmetric and symmetric operations we will see in the next chapter.
Exercise 5.8. RSA Returns!
Create an encryption and authentication system for Alice, Bob, and EATSA. This system needs to be able to generate key pairs and save them to disk under different operator names. To send a message, it needs to load a private key of the operator and a public key of the recipient. The message to be sent is then signed by the operator’s private key. Then the concatenation of the sender’s name, the message, and the signature is encrypted.
To receive a message, the system loads the private key of the operator and decrypts the data extracting the sender’s name, the message, and the signature. The sender’s public key is loaded to verify the signature over the message.
Exercise 5.9. MD5 Returns!
In Chapter 2, we discussed some of the ways that MD5 is broken. In particular, we emphasized that MD5 is still not broken (in practice) for finding the preimage (i.e., working backward). But it is broken in terms of finding collisions. This is very important where signatures are concerned because signatures are typically computed over the hash of data and not the data itself.
For this exercise, modify your signature program to use MD5 instead of SHA-256. Find two pieces of data with the same MD5 sum. You can find some examples at or with a quick search of the Internet. Once you have the data, verify that the hashes are the same for the two files. Now, create a signature for both files and verify that they are the same.
Elliptic Curves: An Alternative to RSA
It’s time we told you the truth about asymmetric cryptography. Everything we’ve told you so far has been RSA-specific and quite a bit of what RSA does is actually unique.
When we talk about asymmetric, or public key, cryptography, we are referring to any cryptographic operations that involve a public and private key pair. In Chapter 4 we looked almost exclusively at RSA encryption, and in this chapter, we explored RSA signatures. Conveniently, RSA signatures are also based on RSA encryption (i.e., encrypting a hash of the data to be signed). But most other asymmetric algorithms do not even support encryption as a mode of operation at all and do not use encryption for generating a signature. Other asymmetric algorithms, for example, generate a signature or tag that does not involve any encryption and verify the signature without any kind of reversible operation such as decryption.
This is one reason why we have tried to qualify our conversations about asymmetric cryptography through the book by referring specifically to “RSA public keys,” “RSA encryption,” and “RSA asymmetric operations.” You should not assume that other asymmetric algorithms provide the same operations or do them in the same way.
Why focus so much on RSA encryption? We do this here because RSA has been one of the most popular algorithms for asymmetric operations for decades. It is still found absolutely everywhere, and you will be hard-pressed not to run into it somewhere. DSA (digital signing algorithm) is another asymmetric algorithm, but it is only usable for signatures, not for encryption. For educational and practical purposes, then, RSA is a great place to start.
With that said, RSA is slowly getting phased out. It has been found to have a lot of weaknesses, some of which we have explored already. Cryptography based on “elliptic curves”4 has been used both to sign data and to exchange keys. In this chapter we will look at ECDSA’s signing capabilities. In Chapter 6 we will look at something called Elliptic-Curve Diffie-Hellman (ECDH) that is used to create and agree on session keys. ECDH’s key agreement provides an alternative (arguably a better alternative) to the key transport functionality enabled by RSA encryption.
To sign data with elliptic curves, you make use of the ECDSA algorithm. Just as you must choose parameters for RSA (such as e, the public exponent), you must also choose parameters in EC-based operations. The most obvious of these is the underlying curve. Again, the actual mathematics are not discussed in this book, so we will satisfy ourselves by saying that different elliptic curves can be used in these algorithms.
For ECDSA, the cryptography library provides a number of NIST-approved curves. It should be noted that some cryptographers are wary of these curves because it is possible that the US government recommends curves that it knows can be broken. With that said, these are the only curves currently provided by the library. If you use these in production, you should keep an eye out for additional information about security vulnerabilities and potential replacements.
As with RSA signing, you do have to pick a hash function. Again, we have chosen SHA-256. You will notice that, although it might seem daunting to pick a curve function, once that’s done, the rest of the operation is very straightforward.
ECDSA also has the same pre-hashed API as RSA for processing large amounts of data.
Certificates: Proving Ownership of Public Keys
In our example with Alice and Bob and public keys, we assumed that every interested party had the public key of every other interested party. In our scenario, this might be possible. The HQ could gather all the spies together and have everyone exchange public keys.5
This might not be feasible over time, however.
What if Noel, a new spy, enters the field after everyone else? Assume agent Charlie has been captured and Noel has been sent to take his place. Alice and Bob already had Charlie’s key, but they don’t yet have Noel’s key.
Of course, Noel can’t just show up and hand out a public key. Otherwise, Eve could send in fake agents handing out public keys claiming to be real EA agents. She can create certificates just as easily as HQ. How can Alice and Bob recognize that Noel is a true EATSA agent and is not working for Eve?
One possibility is to have HQ send Alice and Bob a message with the name and public key of the new agent. Alice and Bob already trust HQ and already have HQ’s public key. HQ can act as a trusted third party between them and Noel. In the early days of PKI, this was exactly what was proposed to establish trust. This model was called a “registry.” A registry would be a central repository of identity-to-public-key mappings. The registry’s own public key would be disseminated everywhere: newspapers, magazines, textbooks, physical mailings, and so forth. So long as everyone had a true copy of the registry’s key, they could look up the public key of anyone registered within it.
The problem at the time, although it is less of a problem now, was scale. Although contemporary computing envisions the Googles, Amazons, and Microsofts of the world handling billions of connections from all over the world all the time, such was not the case in the 1990s. It was believed that an online registry was simply not scalable.
In the case of our spies, they have to assume they may be cut off from HQ. They may have to go into deep cover, or they may be on the run from Eve, or maybe the EA wants to disavow any of their activities for a time. For any or all of these reasons, they may not be able to get a timely message from HQ. If they’re on the run from Eve, it would be great if they could tell whether the spy who meets them at the safe house is on their side.
This brings us to certificates. A public key certificate is just data; it generally includes a public key, the metadata related to ownership of the key, and a signature over all of the contents by a known “issuer.” The metadata includes information such as the identity of the owner, the identity of the issuer, an expiration date, a serial number, and so forth. The concept is to bind the metadata, especially for identity, to the public key. The identity can be a name, an email address, a URL, or any other agreed-upon identifier.
Instead of simply handing out public keys to their agents, HQ can now hand out certificates.6 First, the agent generates their own key pair (nobody, not even HQ, should ever have the agent’s private key). Next, HQ takes the agent’s public key and starts creating a certificate by including the identifying information about the agent, such as their code name.7 To complete the certificate, HQ signs it with the HQ private key and becomes the issuer.
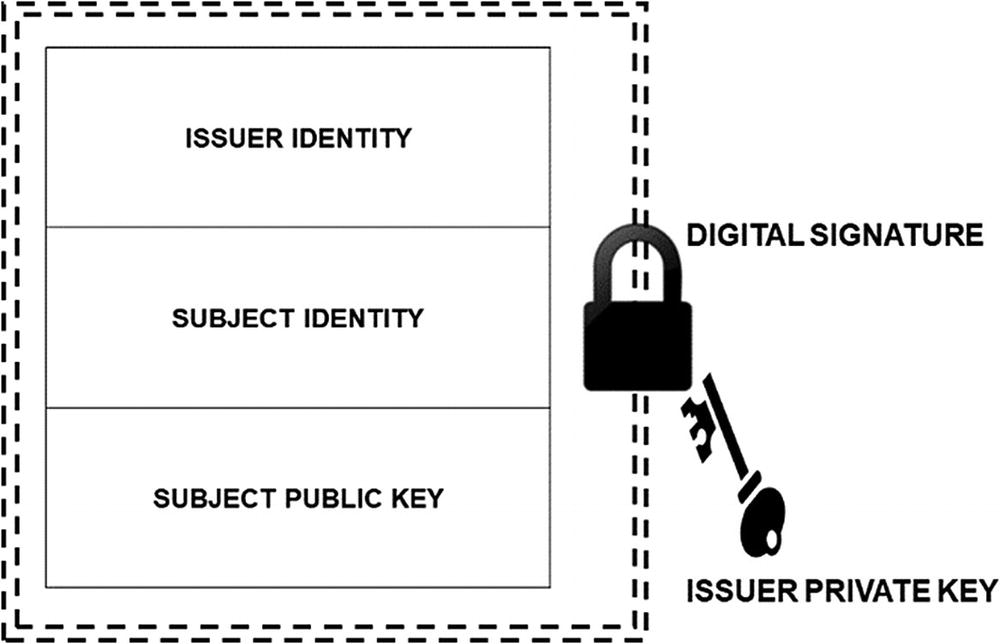
The primary purpose of a certificate is to bind an identity and a public key together. An issuer can sign the certificate data preventing modification and providing trust.
Let’s go back to our scenario where Alice is on the run in West Antarctica with Eve’s agents hot on her trail. She gets to a safe house and sees an agent she’s never met before: Charlie. To prove that he is who he says he is, Charlie presents his certificate. Alice checks that the identity data matches his claim (e.g., that the identity in the certificate is “charlie”). Next, Alice checks that the issuer of the certificate is HQ and then verifies the signature included in the certificate. Remember, the signature in the certificate is signed by the issuer (HQ). Using HQ’s public key issued to her before she left on the mission, Alice’s signature check is successful. Thus, Alice knows that the certificate must have been issued by HQ because nobody else could have generated a valid signature. The certificate is authentic, and Alice now has (and trusts) Charlie’s public key for future communications.
Of course, there is one more wrinkle. Charlie’s certificate is public! There’s nothing to stop Eve from having a copy and present it to Alice herself. How does Alice know that the person at the door that claims to be Charlie, with certificate in hand, really is Charlie?
Charlie must now prove his identity by signing some data for Alice. Alice gives him some kind of test message, and Charlie signs it with his private key. Alice verifies the signature on this data using the public key from his certificate. The signature check passes, so Alice knows that Charlie must be the owner of the certificate. Only the owner has (or should have!) the private key associated with the public key necessary to sign data. Of course, if Charlie were captured and his private key compromised, all bets would be off!
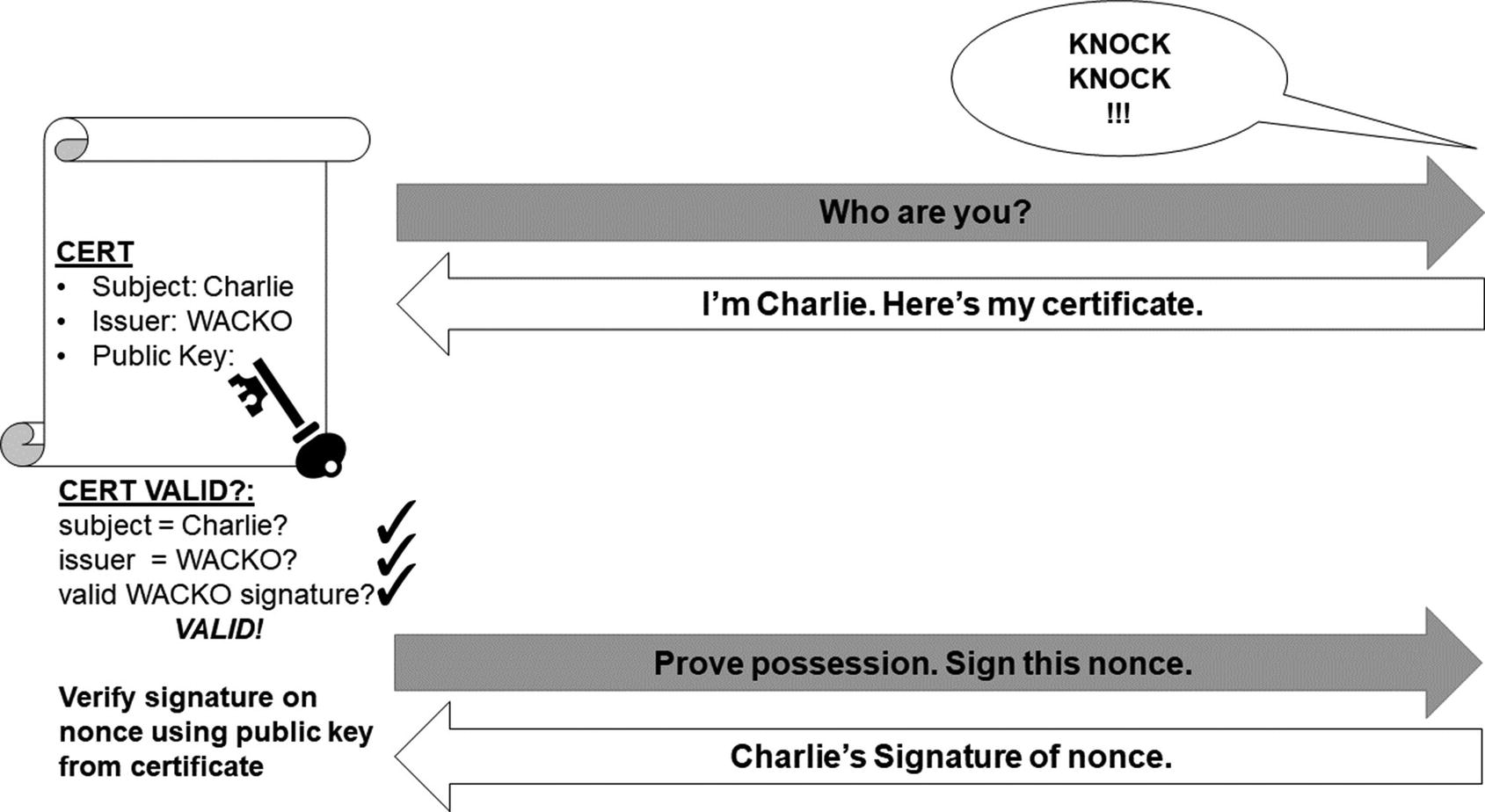
Who’s knocking at the door? Alice would like to know before she lets in whoever it is!
Let’s go through some examples to see how this works. For the first exercise, we are not going to use real certificates, at least not yet. For now, we’re going to use a simple dictionary as our certificate data structure, and we’re going to use the Python json module to convert it to bytes.
Warning: Not for Production Use
My, we do say that “not for production use” thing a lot, don’t we? We kind of have to. Cryptography is uniquely and simultaneously subtle and alluring: the concepts are relatively simple to describe, but tiny details can make the difference between good security and no security. Those details are sometimes hard to discover, and proving that they are correct is hard.
Don’t use any of the non-library implementations from this book in production and do not assume that even our use of libraries is an appropriate solution. Don’t assume that an example has taught you enough to roll your own crypto, and don’t assume that you have mastered the correct use of the libraries. Don’t even assume that our list of things that go wrong is complete!
Remember, YANAC (You Are Not A Cryptographer... yet!). We’ll be saying this again. It’s what we do.
The example we’re going to work has three parties: the party claiming an identity (Charlie), also known as the subject, the party verifying the claim (Alice), and the trusted third party that issued the certificate (HQ). Two of these parties, Charlie and HQ, will need RSA key pairs. You can generate RSA key pairs and save them to disk using the rsa_simple.py script from Chapter 4. For the rest of this exercise, we will assume that HQ’s keys are saved in hq_public.key and hq_private.key and Charlie’s keys are saved in charlie_public.key and charlie_private.key.
Fake Certificate Issuer
Let’s walk through Listing 5-6. There is only one function: create_fake_certificate. We are using the name “fake” not to indicate fraud, but rather that this is not a real certificate. Again, please don’t ever use this in production.9
The function creates a dictionary and loads three fields: a subject name (identity), an issuer name, and a public key. Note that there are (parts of) two key pairs being used in this file. There is an issuer private key and the subject public key. It is the subject’s private key that is being stored in the certificate. This public key in many ways represents the subject as it will be used to prove his or her identity. That is why it is so important that the certificate be signed.10 Otherwise, anyone could create a certificate to claim any identity they like.
Once the dictionary is loaded, we use json to serialize the dictionary to a string. JSON is a common and standard format, but in Python 3.x, it cannot encode bytes directly and it outputs a text string. For compatibility with the Python cryptography library, we load the PEM-encoded keys as binary bytes rather than as text. The public key to be stored in this JSON certificate has to be converted to a string first, but because it is PEM-encoded (i.e., it is already plaintext), we can convert it to UTF-8 safely. Similarly, the entire output of the json.dumps() operation is converted to bytes with a safe UTF-8 conversion.
The bytes are then signed using the issuer’s private key. Only the issuer should have access to this private key because it is the issuer’s way of proving to the world that it (the issuer) has created the certificate. Our final certificate is the raw bytes from json concatenated with the bytes from the signature.
In our hypothetical example, Charlie wants to claim the identity “charlie.” Charlie starts out by generating a key pair. The public key (not the private key) is sent to the HQ certificate-issuing department and a request to make a certificate. The human beings within the issuing department should verify that Charlie has the right to claim the identity “charlie.” For example, the officer in charge might ask to see Charlie’s agency ID, review paperwork from a superior officer, check fingerprints, and so forth to ensure that the real Charlie will be given the certificate.
This will generate a (fake) certificate for Charlie with the claimed identity and associated public key, all signed by HQ.
Now Charlie can prove that he has the identity “charlie” to Alice. He starts by giving her the claimed identity (“charlie”) and providing the certificate.
Verify Identity in a Fake Certificate
Listing 5-7 requires three arguments: the claimed identity of the party, the certificate presented, and the issuer’s public key.
The verification of the claimed identity has to run in two parts. First, it loads the certificate to see if it is signed by HQ’s public key. This is performed by the verify_certificate function . Remember that the signature verification function raises an exception if the signature check fails. You will notice that to get the signature, the script just takes the last 256 bytes of the certificate. Because the signature is concatenated at the end, and because we always use an RSA signature from a 2048-bit key, the signature is always 256 bytes.
If the signature verifies, we take the other bytes and load them into a dictionary using the json module (again converting bytes to string for the JSON operation and then from string to bytes for the public key data).
At this point Alice’s script has given her some information, but it is waiting for more input. What does Alice know right now, at this phase of the process? She knows that she has been presented with a true certificate that was actually signed by HQ. What happens next? She doesn’t yet know if the party presenting the certificate is really Charlie. To do that, she needs to test him or her to see if they have the private key.
She generates a random message and saves it to the file charlie.challenge, which she will ask the person claiming to be Charlie to sign with his private key. The script is waiting for that random message, so Alice provides the name of the file she just created, charlie.challenge.
Prove Identity on a Fake Certificate
Charlie has thus answered Alice’s challenge and put the response into the file charlie.response. Now we can finally finish Alice’s script, which is waiting for the response filename. Enter the filename generated by Charlie (charlie.response) to proceed.
Alice’s script loads the response and verifies it. To do this, Alice’s script now moves to the verify_identity function. It starts by checking that the name in the certificate matches the identity claimed (e.g., “charlie”) and that the issuer is HQ. Next, it loads the public key from the certificate and verifies that the signature on the challenge bytes is valid.
This proves to Alice that not only is the certificate Charlie presented valid, but Charlie is the subject (owner). The person claiming to be Charlie must have the associated private key or he would not have been able to answer her challenge.
Exercise 5.10. Detect Fake Charlies
Experiment with the preceding scripts to check out the various errors from trying to deceive Alice. Create a false issuer and sign the certificate with this private key. Have someone with the wrong private key present Charlie’s certificate. Make sure to understand all the different checks being performed in the code.
Although our certificates are “fake,” they are designed to teach the basic principles behind the certificate concept. Real certificates typically use a format called X.509. We will discuss X.509 in detail in Chapter 8.
Certificates and Trust
One question you might have asked yourself is, why did we name the issuer? After all, if Alice, Bob, and all the other agents are always going to trust HQ, why require the issuer to be named in the certificate?
In our hypothetical world in which Antarctica is locked in its civil cold war, there may be many issuers of certificates. For example, other agencies besides the espionage unit may want to issue certificates. What if the EA military starts to issue certificates? What if the EA Department of Education starts to issue certificates? Should Alice and Bob trust those as well? Maybe they will want to trust military certificates but not education certificates?
In certificate parlance, we also call an issuer a “certificate authority” (CA) , and certificate validators have to decide which certificate authorities they will trust. In fact, CAs also have their own certificates with their identity name and their public key. Thus, the Issuer field of a certificate should be the same identity as the Subject in the CA’s certificate.
If the CA has a certificate, who signs that? There is a concept called an “intermediate” CA. An intermediate CA has its certificate signed by a “higher” CA. In the EA government, perhaps, there might be a top-level CA that signs all other CAs for defense, education, espionage, and so forth. This creates a hierarchical chain of certificates with the highest certificate called a “root” certificate.
Who signs this ultimate root CA?
The answer is: itself. This CA’s certificate is known as a self-signed certificate. Note that anyone can generate a self-signed certificate, so great care must be taken in deciding which self-signed, root certificates to trust. Basically, they become axiomatically trusted along with all of the certificates that they sign!
While this can be a little complicated to visualize, it does make things a little bit easier to manage. The entire EA government could have a single top-level CA. All employees, agents, or even citizens need only have the very top-most, root CA certificate. All other identities can be verified in a chain. For example, Charlie might keep three certificates: his personal certificate, the intermediate certificate for the espionage CA that signed his certificate, and the root EA certificate itself. Charlie can present these three certs to any other EA employee and have him or her verify the chain back to the root.
Things become slightly more complicated (and introduce potential security risks) when there are multiple roots. For example, perhaps the EA government doesn’t have a single, top-level root. After all, do you really want your espionage orders to be signed by a CA that can be traced back to the government? Suppose then that the EA government keeps two roots: one for departments and organizations that operate “visibly” and one for groups and individuals that operate covertly.
Should Charlie and the other agents trust both roots?
Exercise 5.11. The Chains We Forged in Life
Modify the identity validation programs to support a chain of trust. First, create some self-signed certificates for the EA government (at least two as described previously). The existing issuer script can already do this. Just make the issuer private key for the self-signed certificate to be the organization’s own private key. Thus, the organization is signing its own cert, and the private key used to sign the certificate matches the public key in the certificate.
Next, create certificates for intermediate CAs such as “Department of Education,” “Department of Defense,” “Espionage Agency,” and so forth. These certificates should be signed by the self-signed certificates in the previous step.
Finally, sign certificates for Alice, Bob, and Charlie by the espionage CA. Perhaps create some certificates for employees of the defense department and the education department. These certificates should be signed by the appropriate intermediate CA.
Now modify the verification program to take a chain of certificates instead of just a single certificate. Get rid of the command-line parameter for the issuer’s public key and instead hard-code which of the root certificate filenames are trusted. To specify the chain of certificates, have the program take the claimed identity as the first input (as it already does) and then an arbitrary number of certificates to follow. Each certificate’s issuer field should indicate the next certificate in the chain. For example, to validate Charlie, there may be three certificates: charlie.cert, espionage.cert, covert_root.cert. The issuer of charlie.cert should have the same subject name as espionage.cert and so forth. The verify program should only accept an identity if the last certificate in the chain is already trusted.
Certificates are very important to modern cryptography and computer security. In Chapter 8, we will introduce real X.509 certificates and discuss how real CAs operate and additional issues and solutions as part of learning about TLS.
Revocation and Private Key Protection
Certificates and the public keys they contain are very powerful. At the same time, they come with a very dangerous Achilles heel. How do you disable them if the associated private key is compromised?
What we are talking about here is a concept called “revocation.” To revoke a certificate is to reverse the endorsement of the issuer. HQ might have issued a certificate to Charlie, but if Charlie is captured and his private key lost, HQ needs to figure out a way to tell all of the other agents not to trust that certificate anymore.
Unfortunately, this is not easily done. If you recall, one of the reasons why CAs came into existence instead of online registries was the desire for offline verification. How can an offline verification process provide real-time revocation data?
The simple answer is, “It can’t.” There are only two options. Either the verification process must have a real-time component or the revocation cannot be updated in real time. Both options are available for certificates today in the form of the Online Certificate Status Protocol (OCSP) , which checks a certificate’s status on the fly, and Certificate Revocation Lists (CRLs) , which are lists published from time to time with revoked certs. We will review both of these in more detail in Chapter 8.
Because of the difficulty of revoking a certificate, private keys must be protected with the utmost care. When real-time signing is not needed, private keys should be kept offline and in a secure environment. If they must be used in real time, and must be stored on a server, certificates should be stored with the minimum permissions necessary and readable on a strictly need-to-know basis. For end-user keys, such as those used for email and other applications, private keys stored on disk should be adequately protected by symmetric encryption with a strong password. Ideally, avoid storing private keys on desktops and servers altogether (especially in the modern era of continuous backups) and, instead, store private keys in a hardware security module.
It might not be a bad idea to keep certificates with a relatively short expiration date and rotate them as necessary.
Replay Attacks
There is one last security issue to address before moving on from message integrity. It applies equally to both MACs and signatures. The issue is replay attacks.
A replay attack occurs when a legitimate message from a previous communication is used by an attacker at a later time when it should no longer be valid.
Let’s consider the following message: “We attack at dawn!”
We can secure this message from modification and authenticate the sender with either MACs or signatures. But what would prevent Eve from intercepting that message and sending it on a different day? Perhaps she would choose to send it on a day when the EA is not planning an attack? Eve may not be able to change the message contents; perhaps she cannot even read them, but that does not stop her from resending (replaying) the message whenever she wants.
For this reason, almost all cryptographically secured messages typically need some kind of unique component that distinguishes them from all other messages. This piece of data is often referred to as a nonce. In many circumstances a nonce can be a random number. If you take a quick peek back at Chapter 3, you will see that the IV value passed to AES counter mode was called a nonce. Nonces, especially random number nonces, are also used to keep messages from being the same when doing so would introduce security vulnerabilities.
However, to prevent replay attacks, simply using a random number won’t do. In order to detect a replay, the receiver must keep track of the nonces that have been used and reject them when seen a second time.
This can be terribly problematic. How big of a list of nonces should be kept? A hundred? A thousand? Do you remove a nonce from the list after a certain period of time? If you do and the attacker knows it, the attacker can now use it in a replay. For example, if the attacker knows you only keep track of nonces received in the last 5 minutes, the attacker can replay something from 6 minutes ago with a reasonable amount of success.
Some systems use timestamps instead of random nonces. Using a timestamp, a receiver can reject data that is too old. The problem with this approach is that all of the computers have to have synchronized clocks for it to work reliably. Plus, data with an “old” timestamp must be accepted within some window. After all, the message won’t arrive instantaneously. How large a window do you permit? However big it is, the bad guy will figure out a way to use it against you.
It’s possible to combine both approaches together. You can send data with a timestamp and a random number. The timestamp is used to get rid of data that is really old and the nonce is used to prevent replays within the time window permitted. This means that the clocks only need to be relatively close (perhaps even within 24 hours) and that the list of nonces to be stored is bounded.
You have now seen two pieces of metadata that you need to consider sending in a message: the nonce and/or timestamp to prevent replays and the sender/receiver names. In general, you should put all relevant context into the message so that it cannot be used outside of that context.
Exercise 5.12. Replay It Again Sam!
Use either MAC or signatures to send a message from Alice to Bob or vice versa. Include a nonce in the message to prevent replays using all three mechanisms described in this section. Send some replays from Eve and try to get around Alice and Bob’s defenses.
Summarize-Then-MAC
Another chapter, another firehose of information! In this chapter we covered message authentication codes, which are keyed codes computed over a series of data. Without the key, it is impossible to change the data undetectably. Moreover, when two parties share a MAC key, they can be sure that (unless the shared key has been compromised) if one of them received a correctly MACed message, it came from the other party.
Using asymmetric operations, one can use a private key to create a signature over a piece of data (typically over the hash of the data). Unlike MAC operations, which can only ensure correctness and authenticity to those individuals sharing the key, a widely distributed public key can be used theoretically by anyone (that trusts it) to validate the signature over the data.
And we also provided a quick overview of basic certificate operations.
Now you have a way of telling if any corrections or changes were made to this summary by our editors after we submitted it to them!