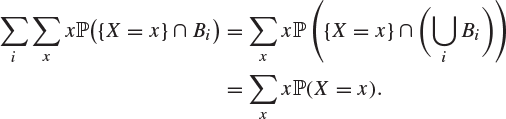Summary. Discrete random variables are studied via their probability mass functions. This leads to the definition of the ‘mean value’ or ‘expectation’ of a random variable. There are discussions of variance, and of functions of random variables. Methods are presented for calculating expectations, including the use of conditional expectation.
2.1 Probability mass functions
Given a probability space ![]() , we are often interested in situations involving some real-valued function X acting on Ω. For example, let
, we are often interested in situations involving some real-valued function X acting on Ω. For example, let ![]() be the experiment of throwing a fair die once, so that
be the experiment of throwing a fair die once, so that ![]() , and suppose that we gamble on the outcome of
, and suppose that we gamble on the outcome of ![]() in such a way that the profit is
in such a way that the profit is
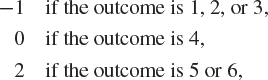
where negative profits are positive losses. If the outcome is ω, then our profit is ![]() , where
, where ![]() is defined by
is defined by
![]()
The mapping X is an example of a ‘discrete random variable’.
More formally, a discrete random variable X on the probability space ![]() is defined to be a mapping
is defined to be a mapping ![]() such that 1
such that 1
(2.1) |
(2.2) |
The word ‘discrete’ here refers to the condition that X takes only countably many values in ![]() .2 Condition (2.2) is obscure at first sight, and the point here is as follows. A discrete random variable X takes values in
.2 Condition (2.2) is obscure at first sight, and the point here is as follows. A discrete random variable X takes values in ![]() , but we cannot predict the actual value of X with certainty since the underlying experiment
, but we cannot predict the actual value of X with certainty since the underlying experiment ![]() involves chance. Instead, we would like to measure the probability that X takes a given value, x say. To this end, we note that X takes the value x if and only if the result of
involves chance. Instead, we would like to measure the probability that X takes a given value, x say. To this end, we note that X takes the value x if and only if the result of ![]() lies in that subset of Ω which is mapped into x, namely the subset
lies in that subset of Ω which is mapped into x, namely the subset ![]() . Condition (2.2) postulates that all such subsets are events, in that they belong to
. Condition (2.2) postulates that all such subsets are events, in that they belong to ![]() , and are therefore assigned probabilities by
, and are therefore assigned probabilities by ![]() .
.
The most interesting things about a discrete random variable are the values which it may take and the probabilities associated with these values. If X is a discrete random variable on the probability space (![]() ), then its image
), then its image ![]() is the image of Ω under X, that is, the set of values taken by X.
is the image of Ω under X, that is, the set of values taken by X.
Henceforth, we abbreviate events of the form ![]() to the more convenient form
to the more convenient form ![]() .
.
Definition
The (probability) mass function (or pmf) of the discrete random variable X is the function ![]() defined by
defined by
(2.4) |
Thus, ![]() is the probability that the mapping X takes the value x. Note that
is the probability that the mapping X takes the value x. Note that ![]() is countable for any discrete random variable X, and
is countable for any discrete random variable X, and
(2.5) |
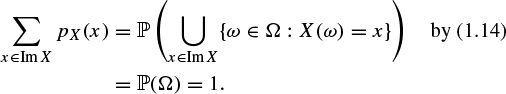
|
(2.6) |
Equation (2.6) is sometimes written as
![]()
in the light of the fact that only countably many values of x make non-zero contributions to this sum. Condition (2.6) essentially characterizes mass functions of discrete random variables in the sense of the following theorem.
Theorem 2.7
Let ![]() be a countable set of distinct real numbers, and let
be a countable set of distinct real numbers, and let ![]() be a collection of real numbers satisfying
be a collection of real numbers satisfying
![]()
There exists a probability space ![]() and a discrete random variable X on
and a discrete random variable X on ![]() such that the probability mass function of X is given by
such that the probability mass function of X is given by
![]()
Proof
Take ![]() ,
, ![]() to be the set of all subsets of Ω, and
to be the set of all subsets of Ω, and
![]()
Finally, define ![]() by
by ![]() for
for ![]() .
.
This theorem is very useful, since for many purposes it allows us to forget about sample spaces, event spaces, and probability measures; we need only say ‘let X be a random variable taking the value si with probability ![]() , for
, for ![]() ’ and we can be sure that such a random variable exists without having to construct it explicitly.
’ and we can be sure that such a random variable exists without having to construct it explicitly.
In the next section, we present a list of some of the most common types of discrete random variables.
Exercise 2.8
If X and Y are discrete random variables on the probability space (![]() ), show that U and V are discrete random variables on this space also, where
), show that U and V are discrete random variables on this space also, where
![]()
Exercise 2.9
Show that if ![]() is the power set of Ω, then all functions which map Ω into a countable subset of
is the power set of Ω, then all functions which map Ω into a countable subset of ![]() are discrete random variables.
are discrete random variables.
Exercise 2.10
If E is an event of the probability space ![]() show that the indicator function of E, defined to be the function
show that the indicator function of E, defined to be the function ![]() on Ω given by
on Ω given by
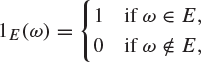
is a discrete random variable.
Exercise 2.11
Let (![]() ) be a probability space in which
) be a probability space in which
![]()
and let U, V, W be functions on Ω defined by
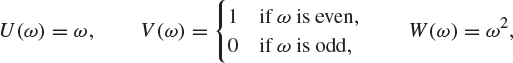
for ![]() . Determine which of U, V, W are discrete random variables on the probability space.
. Determine which of U, V, W are discrete random variables on the probability space.
Exercise 2.12
For what value of c is the function p, defined by
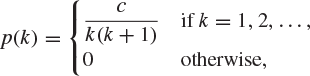
a mass function?
2.2 Examples
Certain types of discrete random variables occur frequently, and we list some of these. Throughout this section, n is a positive integer, p is a number in ![]() , and
, and ![]() . We never describe the underlying probability space.
. We never describe the underlying probability space.
Bernoulli distribution. This is the simplest non-trivial distribution. We say that the discrete random variable X has the Bernoulli distribution with parameter p if the image of X is ![]() , so that X takes the values 0 and 1 only.
, so that X takes the values 0 and 1 only.
Such a random variable X is often called simply a coin toss. There exists ![]() such that
such that
(2.13) |
and the mass function of X is given by
![]()
Coin tosses are the building blocks of probability theory. There is a sense in which the entire theory can be constructed from an infinite sequence of coin tosses.
Binomial distribution. We say that X has the binomial distribution with parameters n and p if X takes values in ![]() and
and
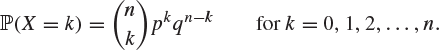
|
(2.14) |
Note that (2.14) gives rise to a mass function satisfying (2.6) since, by the binomial theorem,
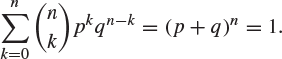
Poisson distribution. We say that X has the Poisson distribution with parameter λ (![]() ) if X takes values in
) if X takes values in ![]() and
and
(2.15) |
Again, this gives rise to a mass function since
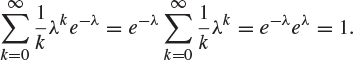
Geometric distribution. We say that X has the geometric distribution with parameter ![]() if X takes values in
if X takes values in ![]() and
and
(2.16) |
As before, note that
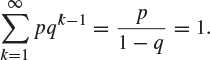
Negative binomial distribution. We say that X has the negative binomial distribution with parameters n and ![]() if X takes values in
if X takes values in ![]() and
and
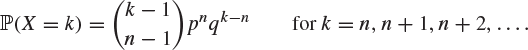
|
(2.17) |
As before, note that
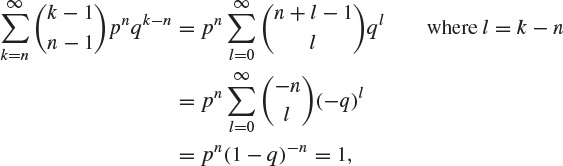
using the binomial expansion of ![]() , see Theorem A.3.
, see Theorem A.3.
Example 2.18
Here is an example of some of the above distributions in action. Suppose that a coin is tossed n times and there is probability p that heads appears on each toss. Representing heads by H and tails by T, the sample space is the set Ω of all ordered sequences of length n containing the letters H and T, where the kth entry of such a sequence represents the result of the kth toss. The set Ω is finite, and we take ![]() to be the set of all subsets of Ω. For each
to be the set of all subsets of Ω. For each ![]() , we define the probability that ω is the actual outcome by
, we define the probability that ω is the actual outcome by
![]()
where ![]() is the number of heads in ω and
is the number of heads in ω and ![]() is the number of tails. Similarly, for any
is the number of tails. Similarly, for any ![]() ,
,
![]()
For ![]() we define the discrete random variable Xi by
we define the discrete random variable Xi by
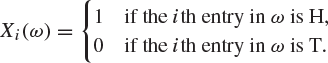
Each Xi takes values in ![]() and has mass function given by
and has mass function given by
![]()
where ![]() is the ith entry in ω. Thus
is the ith entry in ω. Thus
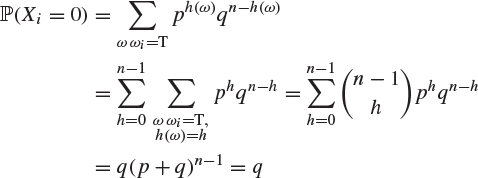
and
![]()
Hence, each Xi has the Bernoulli distribution with parameter p. We have derived this fact in a cumbersome manner, but we believe these details to be instructive.
Let
![]()
which is to say that ![]() . Clearly, Sn is the total number of heads which occur, and Sn takes values in
. Clearly, Sn is the total number of heads which occur, and Sn takes values in ![]() since each Xi equals 0 or 1. Also, for
since each Xi equals 0 or 1. Also, for ![]() we have that
we have that
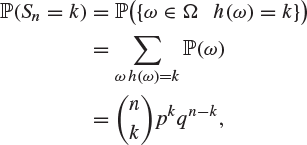
|
(2.19) |
and so Sn has the binomial distribution with parameters n and p.
If n is very large and p is very small but np is a ‘reasonable size’ (![]() , say) then the distribution of Sn may be approximated by the Poisson distribution with parameter λ, as follows. For fixed
, say) then the distribution of Sn may be approximated by the Poisson distribution with parameter λ, as follows. For fixed ![]() , write
, write ![]() and suppose that n is large to find that
and suppose that n is large to find that
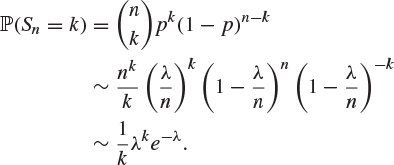
|
(2.20) |
This approximation may be useful in practice. For example, consider a single page of the Guardian newspaper containing, say, ![]() characters, and suppose that the typesetter flips a coin before setting each character and then deliberately mis-sets this character whenever the coin comes up heads. If the coin comes up heads with probability
characters, and suppose that the typesetter flips a coin before setting each character and then deliberately mis-sets this character whenever the coin comes up heads. If the coin comes up heads with probability ![]() on each flip, then this is the equivalent to taking
on each flip, then this is the equivalent to taking ![]() and
and ![]() in the above example, giving that the number Sn of deliberate mistakes has the binomial distribution with parameters
in the above example, giving that the number Sn of deliberate mistakes has the binomial distribution with parameters ![]() and
and ![]() . It may be easier (and not too inaccurate) to use (2.20) rather than (2.19) to calculate probabilities. In this case,
. It may be easier (and not too inaccurate) to use (2.20) rather than (2.19) to calculate probabilities. In this case, ![]() and so, for example,
and so, for example,
![]()
Example 2.21
Suppose that we toss the coin of the previous example until the first head turns up, and then we stop. The sample space now is
![]()
where ![]() represents the outcome of k tails followed by a head, and
represents the outcome of k tails followed by a head, and ![]() represents an infinite sequence of tails with no head. As before,
represents an infinite sequence of tails with no head. As before, ![]() is the set of all subsets of Ω, and
is the set of all subsets of Ω, and ![]() is given by the observation that
is given by the observation that
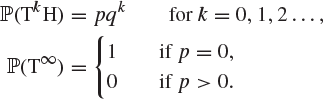
Let Y be the total number of tosses in this experiment, so that ![]() for
for ![]() and
and ![]() . If
. If ![]() , then
, then
![]()
showing that Y has the geometric distribution with parameter p.
Example 2.22
If we carry on tossing the coin in the previous example until the nth head has turned up, then a similar argument shows that, if ![]() , the total number of tosses required has the negative binomial distribution with parameters n and p.
, the total number of tosses required has the negative binomial distribution with parameters n and p.
Exercise 2.23
If X is a discrete random variable having the Poisson distribution with parameter λ, show that the probability that X is even is ![]() .
.
Exercise 2.24
If X is a discrete random variable having the geometric distribution with parameter p, show that the probability that X is greater than k is ![]() .
.
2.3 Functions of discrete random variables
Let X be a discrete random variable on the probability space ![]() and let
and let ![]() . It is easy to check that
. It is easy to check that ![]() is a discrete random variable on
is a discrete random variable on ![]() also, defined by
also, defined by
![]()
Simple examples are
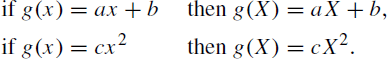
If ![]() , the mass function of Y is given by
, the mass function of Y is given by
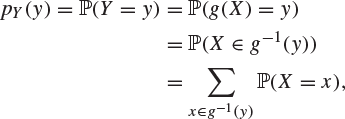
|
(2.25) |
since there are only countably many non-zero contributions to this sum. Thus, if ![]() with
with ![]() , then
, then
![]()
while if ![]() , then
, then
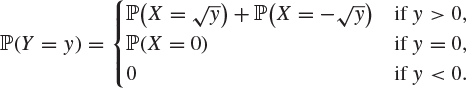
Exercise 2.26
Let X be a discrete random variable having the Poisson distribution with parameter λ, and let ![]() . Find the mass function of Y.
. Find the mass function of Y.
2.4 Expectation
Consider a fair die. If it were thrown a large number of times, each of the possible outcomes ![]() would appear on about one-sixth of the throws, and the average of the numbers observed would be approximately
would appear on about one-sixth of the throws, and the average of the numbers observed would be approximately
![]()
which we call the mean value. This notion of mean value is easily extended to more general distributions as follows.
Definition 2.27
If X is a discrete random variable, the expectation of X is denoted by ![]() and defined by
and defined by
(2.28) |
whenever this sum converges absolutely, in that ![]() .
.
Equation (2.28) is often written
![]()
and the expectation of X is often called the expected value or mean of X.3 The reason for requiring absolute convergence in (2.28) is that the image ![]() may be an infinite set, and we need the summation in (2.28) to take the same value irrespective of the order in which we add up its terms.
may be an infinite set, and we need the summation in (2.28) to take the same value irrespective of the order in which we add up its terms.
The physical analogy of ‘expectation’ is the idea of ‘centre of gravity’. If masses with weights ![]() are placed at the points
are placed at the points ![]() of
of ![]() , then the position of the centre of gravity is
, then the position of the centre of gravity is ![]() , or
, or ![]() , where
, where ![]() is the proportion of the total weight allocated to position xi.
is the proportion of the total weight allocated to position xi.
If X is a discrete random variable (on some probability space) and ![]() , then
, then ![]() is a discrete random variable also. According to the above definition, we need to know the mass function of Y before we can calculate its expectation. The following theorem provides a useful way of avoiding this tedious calculation.
is a discrete random variable also. According to the above definition, we need to know the mass function of Y before we can calculate its expectation. The following theorem provides a useful way of avoiding this tedious calculation.
Theorem 2.29 (Law of the subconscious statistician)
If X is a discrete random variable and ![]() , then
, then
![]()
whenever this sum converges absolutely.
Intuitively, this result is rather clear, since ![]() takes the value
takes the value ![]() when X takes the value x, an event which has probability
when X takes the value x, an event which has probability ![]() . A more formal proof proceeds as follows.
. A more formal proof proceeds as follows.
Proof
Writing I for the image of X, we have that ![]() has image
has image ![]() . Thus
. Thus
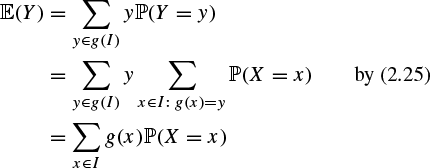
if the last sum converges absolutely.
Two simple but useful properties of expectation are as follows.
Theorem 2.30
Let X be a discrete random variable and let ![]() .
.
(a) If ![]() and
and ![]() , then
, then ![]() .
.
(b) We have that ![]() .
.
Proof
(a) Suppose the assumptions hold. By the definition (2.28) of ![]() , we have that
, we have that ![]() for all
for all ![]() . Therefore,
. Therefore, ![]() for
for ![]() , and the claim follows.
, and the claim follows.
(b) This is a simple consequence of Theorem 2.29 with ![]() .
.
Here is an example of Theorem 2.29 in action.
Example 2.31
Suppose that X is a random variable with the Poisson distribution, parameter λ, and we wish to find the expected value of ![]() . Without Theorem 2.29 we would have to find the mass function of Y. Actually this is not difficult, but it is even easier to apply the theorem to find that
. Without Theorem 2.29 we would have to find the mass function of Y. Actually this is not difficult, but it is even easier to apply the theorem to find that
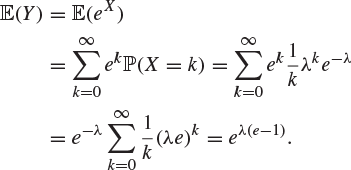
The expectation ![]() of a discrete random variable X is an indication of the ‘centre’ of the distribution of X. Another important quantity associated with X is the ‘variance’ of X, and this is a measure of the degree of dispersion of X about its expectation
of a discrete random variable X is an indication of the ‘centre’ of the distribution of X. Another important quantity associated with X is the ‘variance’ of X, and this is a measure of the degree of dispersion of X about its expectation ![]() .
.
Definition 2.32
The variance ![]() of a discrete random variable X is defined by
of a discrete random variable X is defined by
(2.33) |
We note that, by Theorem 2.29,
(2.34) |
where ![]() . A rough motivation for this definition is as follows. If the dispersion of X about its expectation is very small, then
. A rough motivation for this definition is as follows. If the dispersion of X about its expectation is very small, then ![]() tends to be small, giving that
tends to be small, giving that ![]() is small also; on the other hand, if there is often a considerable difference between X and its mean, then
is small also; on the other hand, if there is often a considerable difference between X and its mean, then ![]() may be large, giving that
may be large, giving that ![]() is large also.
is large also.
Equation (2.34) is not always the most convenient way to calculate the variance of a discrete random variable. We may expand the term ![]() in (2.34) to obtain
in (2.34) to obtain
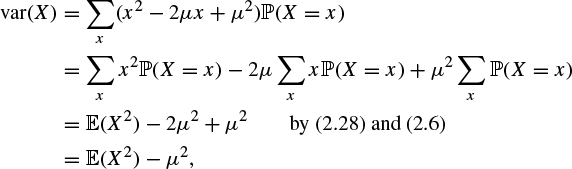
where ![]() as before. Thus we obtain the useful formula
as before. Thus we obtain the useful formula
(2.35) |
Example 2.36
If X has the geometric distribution with parameter p (![]() ), the mean of X is
), the mean of X is
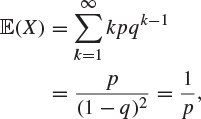
and the variance of X is
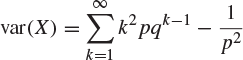
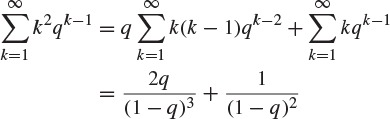
by Footnote 4, giving that
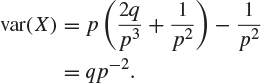
Exercise 2.37
If X has the binomial distribution with parameters n and ![]() , show that
, show that
![]()
and deduce the variance of X.
Exercise 2.38
Show that ![]() for
for ![]() .
.
Exercise 2.39
Find ![]() and
and ![]() when X has the Poisson distribution with parameter λ, and hence show that the Poisson distribution has variance equal to its mean.
when X has the Poisson distribution with parameter λ, and hence show that the Poisson distribution has variance equal to its mean.
2.5 Conditional expectation and the partition theorem
Suppose that X is a discrete random variable on the probability space ![]() , and that B is an event with
, and that B is an event with ![]() . If we are given that B occurs, then this information affects the probability distribution of X. That is, probabilities such as
. If we are given that B occurs, then this information affects the probability distribution of X. That is, probabilities such as ![]() are replaced by conditional probabilities such as
are replaced by conditional probabilities such as ![]() .
.
Definition 2.40
If X is a discrete random variable and ![]() , the conditional expectation of X given B is denoted by
, the conditional expectation of X given B is denoted by ![]() and defined by
and defined by
(2.41) |
whenever this sum converges absolutely.
Just as the partition theorem, Theorem 1.48, expressed probabilities in terms of conditional probabilities, so expectations may be expressed in terms of conditional expectations.
Theorem 2.42 (Partition theorem)
If X is a discrete random variable and ![]() is a partition of the sample space such that
is a partition of the sample space such that ![]() for each i, then
for each i, then
(2.43) |
whenever this sum converges absolutely.
We close this chapter with an example of this partition theorem in use.
Example 2.44
A coin is tossed repeatedly, and heads appears at each toss with probability p, where ![]() . Find the expected length of the initial run (this is a run of heads if the first toss gives heads, and of tails otherwise).
. Find the expected length of the initial run (this is a run of heads if the first toss gives heads, and of tails otherwise).
Solution
Let H be the event that the first toss gives heads and ![]() the event that the first toss gives tails. The pair H,
the event that the first toss gives tails. The pair H, ![]() forms a partition of the sample space. Let X be the length of the initial run. It is easy to see that
forms a partition of the sample space. Let X be the length of the initial run. It is easy to see that
![]()
since if H occurs, then ![]() if and only if the first toss is followed by exactly
if and only if the first toss is followed by exactly ![]() heads and then a tail. Similarly,
heads and then a tail. Similarly,
![]()
Therefore,
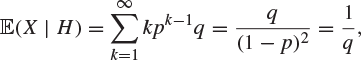
and similarly,
![]()
By the partition theorem, Theorem 2.42,
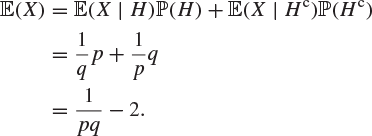
Exercise 2.45
Let X be a discrete random variable and let g be a function from ![]() to
to ![]() . If x is a real number such that
. If x is a real number such that ![]() , show formally that
, show formally that
![]()
and deduce from the partition theorem, Theorem 2.42, that
![]()
Exercise 2.46
Let N be the number of tosses of a fair coin up to and including the appearance of the first head. By conditioning on the result of the first toss, show that ![]() .
.
2.6 Problems
1. If X has the Poisson distribution with parameter λ, show that
![]()
for ![]() .
.
2. Each toss of a coin results in heads with probability p (![]() ). If
). If ![]() is the mean number of tosses up to and including the rth head, show that
is the mean number of tosses up to and including the rth head, show that
![]()
for ![]() , with the convention that
, with the convention that ![]() . Solve this difference equation by the method described in Appendix B.
. Solve this difference equation by the method described in Appendix B.
3. If X is a discrete random variable and ![]() , show that
, show that ![]() . Deduce that, if
. Deduce that, if ![]() , then
, then ![]() , whenever
, whenever ![]() is finite.
is finite.
4. For what values of c and α is the function p, defined by
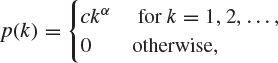
a mass function?
5. Lack-of-memory property. If X has the geometric distribution with parameter p, show that
![]()
for m, ![]() .
.
We say that X has the ‘lack-of-memory property’ since, if we are given that ![]() , then the distribution of
, then the distribution of ![]() is the same as the original distribution of X. Show that the geometric distribution is the only distribution concentrated on the positive integers with the lack-of-memory property.
is the same as the original distribution of X. Show that the geometric distribution is the only distribution concentrated on the positive integers with the lack-of-memory property.
6. The random variable N takes non-negative integer values. Show that
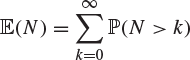
provided that the series on the right-hand side converges.
A fair die having two faces coloured blue, two red and two green, is thrown repeatedly. Find the probability that not all colours occur in the first k throws.
Deduce that, if N is the random variable which takes the value n if all three colours occur in the first n throws but only two of the colours in the first ![]() throws, then the expected value of N is
throws, then the expected value of N is ![]() . (Oxford 1979M)
. (Oxford 1979M)
7. Coupon-collecting problem. There are c different types of coupon, and each coupon obtained is equally likely to be any one of the c types. Find the probability that the first n coupons which you collect do not form a complete set, and deduce an expression for the mean number of coupons you will need to collect before you have a complete set.
*8. An ambidextrous student has a left and a right pocket, each initially containing n humbugs. Each time he feels hungry, he puts a hand into one of his pockets and, if it is not empty, he takes a humbug from it and eats it. On each occasion, he is equally likely to choose either the left or right pocket. When he first puts his hand into an empty pocket, the other pocket contains H humbugs.
Show that if ph is the probability that ![]() , then
, then
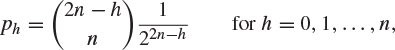
and find the expected value of H, by considering
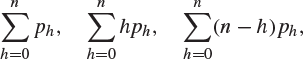
or otherwise. (Oxford 1982M)
9. The probability of obtaining a head when a certain coin is tossed is p. The coin is tossed repeatedly until n heads occur in a row. Let X be the total number of tosses required for this to happen. Find the expected value of X.
10. A population of N animals has had a certain number a of its members captured, marked, and then released. Show that the probability Pn that it is necessary to capture n animals in order to obtain m which have been marked is
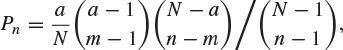
where ![]() . Hence, show that
. Hence, show that
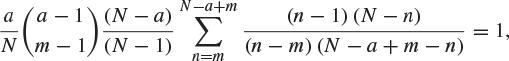
and that the expectation of n is ![]() . (Oxford 1972M)
. (Oxford 1972M)