Summary The branching process is a fundamental model for the random growth of populations. The method of generating functions, and in particular the random sum formula, provides the key to the study of this process. The criterion for the ultimate extinction of a branching process is stated and proved.

9.1 Random processes

Until now, we have been developing the basic terminology and results of probability theory, next, we turn our attention to simple applications. The passing of time plays an essential part in the world which we inhabit, and consequently many applications of probability involve quantities which develop randomly as time passes. Such randomly evolving processes are called random processes or stochastic processes, and there are many different types of these. Most real processes in nature, such as the pollen count in Phoenix or the position of Swansea City in the football league, develop according to rules which are too complicated to describe exactly, and good probabilistic models for these processes can be very complicated indeed. We shall stick to some of the simplest random processes, and the specific processes which we shall consider in some depth are

(a) branching processes: modelling the growth of a self-reproducing population (such as mankind),

(b) random walks: modelling the movement of a particle which moves erratically within a medium (a dust particle in the atmosphere, say),

(c) Poisson processes and related processes: modelling processes such as the emission of radioactive particles from a slowly decaying source, or the length of the queue at the supermarket cash register.

There is a fairly complete theory of each of these three types of process, of which the main features are described in Chapters 9–11, respectively. In contrast, the general theory of stochastic processes is much more challenging and is outside the range of this book. At one extreme, probabilists study ‘concrete’ processes such as those above, often designed to meet the needs of a particular application area, and at the other extreme there is an abstract theory of ‘general’ stochastic processes. Any tension between these two extremes is resolved through the identification of key properties which are shared by large families of processes and yet are sufficiently specific to allow the development of a useful theory. Probably the most important such property is the so-called ‘Markov property’. We do not discuss this here, but refer the reader to Chapter 12 for an account of Markov processes in discrete time.

9.2 A model for population growth

We define the term nomad to be a type of hypothetical object which is able to reproduce itself according to the following rules. At time , there exists a single nomad. This nomad lives for a unit of time and then, at time , it dies in the act of childbirth and is replaced by a family of offspring nomads. These nomads have similar biographies, each surviving only until time and then each dying and being replaced by a family of offspring. This death–birth process continues at all subsequent time points . If we know the sizes of all the individual nomad families, then we know everything about the development of the nomad population, and we might represent this in the usual way as a family tree (see Figure 9.1). The problem is that different nomads may have different numbers of offspring, and these numbers may not be entirely predictable in advance. We shall assume here that the family sizes are random variables which satisfy the following two conditions:

I. the family sizes are independent random variables each taking values in ,

II. the family sizes are identically distributed random variables with known mass function p, so that the number C of children of a typical nomad has mass function for .

Such a process is called a branching process and may be used as a simple model for bacterial growth or the spread of a family name (to give but two examples). Having established the model, the basic problem is to say something about how the development of the process depends on the family-size mass function p. In order to avoid trivialities, we shall suppose throughout this chapter that

(9.1)

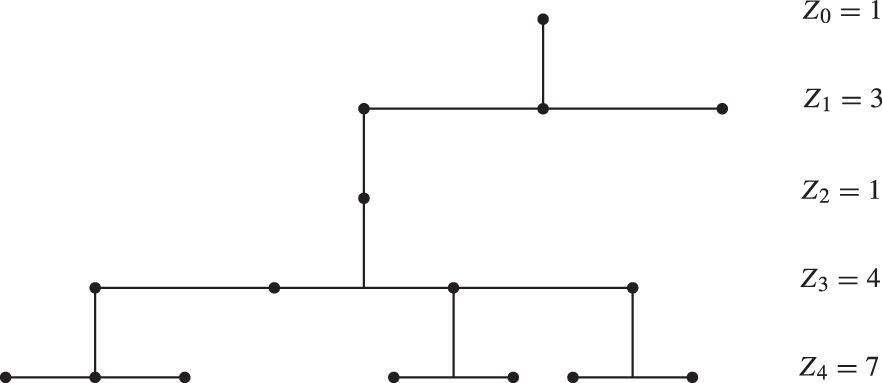
**Fig. 9.1** A typical nomad family tree, with generation sizes 1, 3, 1, 4, 7, .

We introduce some notation. The set of nomads born at time n is called the nth generation of the branching process, and we write Z_n for the number of such nomads. The evolution of the process is described by the sequence of random variables, and it is with this sequence that we work. Specific properties of the Z_n are given in the next section, and we close this section with a list of interesting questions.

(a) What is the mean and variance of Z_n?

(b) What is the mass function of Z_n?

(d) What is the probability that nomadkind ultimately becomes extinct?

9.3 The generating-function method

The first step in the study of this branching process is to explain how to find the distributions of the Z_i in terms of the family-size mass function p. Clearly, and

(9.2)

since Z₁ is the number of children of the founding nomad. It is not easy to give the mass function of Z₂ directly, since Z₂ is the sum of a random number Z₁ of random family sizes: writing C_i for the number of children of the ith nomad in the first generation, we have that

that is, Z₂ is the sum of the family sizes of the Z₁ nomads in the first generation. More generally, for

(9.3)

where are the numbers of children of the nomads in the th generation. The sum of a random number of random variables is treated better by using probability generating functions than by using mass functions. We write

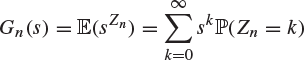
for the probability generating function of Z_n, and

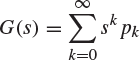
for the probability generating function of a typical family size. We wish to express G_n in terms of G, and we do this in the following theorem.

Theorem 9.4

The probability generating functions G, G₀, satisfy

(9.5)

and hence G_n is the nth iterate of G,

(9.6)

Proof

We have , and so . Equation (9.3) expresses Z_n as the sum of independent random variables, each having probability generating function G, and so the random sum formula, Theorem 4.36, may be applied with and to deduce that

(9.7)

By iteration,

where by (9.2).

Theorem 9.4 contains the information necessary for studying the development of the process. The next result is an immediate corollary.

Theorem 9.8

The mean value of Z_n is

(9.9)

where is the mean of the family-size distribution.

Proof

By the theory of probability generating functions,

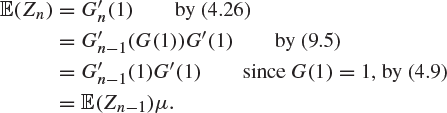
Therefore,

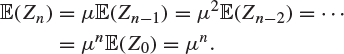
The variance of Z_n may be derived similarly in terms of the mean μ and the variance of the family-size distribution. See Exercise 9.12.

It follows by Theorem 9.8 that

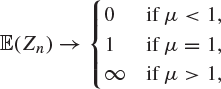
indicating that the behaviour of the process depends substantially on which of the three cases , , holds. We shall see this in more detail in the next two sections, where it is shown that if , the nomad population is bound to become extinct, whereas if , there is a strictly positive probability that the line of descent of nomads will continue forever. This dependence on the mean family-size μ is quite natural since ‘’ means that each nomad gives birth to (on average) strictly fewer nomads than are necessary to fill the gap caused by its death, whereas ‘’ means that each death results (on average) in an increase in the population. The case when is called critical since then the mean population-size equals 1 for all time; in this case, random fluctuations ensure that the population size will take the value 0 sooner or later, and henceforth nomadkind will be extinct.

Exercise 9.10

Show that, in the above branching process,

for any . This may be proved either directly from the conclusion of Theorem 9.4 or by adapting the method of proof of (9.7).

Exercise 9.11

Suppose that each family size of a branching process contains either one member only (with probability p) or is empty (with probability ). Find the probability that the process becomes extinct at or before the nth generation.

Exercise 9.12

Let μ and be the mean and variance of the family-size distribution. Adapt the proof of Theorem 9.8 to show that the variance of Z_n, the size of the nth generation of the branching process, is given by

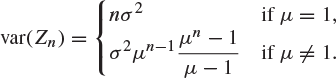
9.4 An example

The key to the analysis of branching processes is the functional equation

(9.13)

relating the probability generating functions of Z_n and and derived in Theorem 9.4. There are a few instances in which this equation may be solved in closed form, and we consider one of these cases here. Specifically, we suppose that the mass function of each family size is given by

so that each family size is one member smaller than a geometrically distributed random variable with parameter (remember (2.16)) and has probability generating function

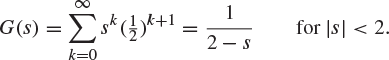
We proceed as follows in order to solve (9.13). First, if ,

Secondly, we apply (9.13) with to find that

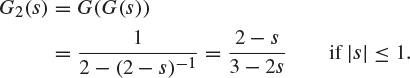
The next step gives

It is natural to guess that

(9.14)

for any , and this is proved easily from (9.13), by the method of induction.

The mass function of Z_n follows by expanding the right-hand side of (9.14) as a power series in s, to find that the coefficient of is

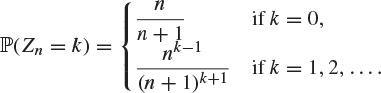
(9.15)

In particular,

so that this branching process becomes extinct sooner or later, with probability 1.

There is a more general case of greater interest. Suppose that the mass function of each family size is given by

where . The previous example is the case when , but we suppose here that so that . In this case,

and the solution to (9.13) is

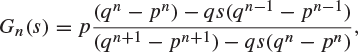
(9.16)

valid for and ; again, this can be proved from (9.13) by induction on n. The mass function of Z_n is rather more complicated than (9.15) but may be expressed in very much the same way. The probability of extinction is found to be

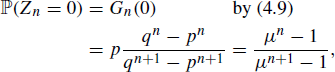
where is the mean family-size. Hence

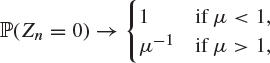
giving that ultimate extinction is certain if and less than certain if . Combined with the result when and , this shows that ultimate extinction is certain if and only if . We shall see in the next section that this is a special case of a general result.

Exercise 9.17

Find the mean and variance of Z_n when the family-size distribution is given by for and . Deduce that if and only if .

9.5 The probability of extinction

In the previous example, ultimate extinction of the branching process is certain if and only if the mean family-size μ satisfies . This conclusion is valid for all branching processes (except for the trivial branching process in which every family size equals 1 always), and we shall prove this. First, we define the extinction probability

Next, we show how to find e. Let be the event that the branching process is extinct (in that nomadkind has died out) by the nth generation, and let . Now,

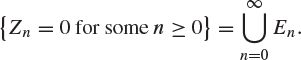
If , then necessarily , so that , and in particular . Since the sequence of events is increasing, we may use the continuity of probability measures, Theorem 1.54, to obtain that

(9.18)

How do we calculate e in practice? Clearly, if , then , since all families are non-empty. The next theorem deals with the general case.

Theorem 9.19 (Extinction probability theorem)

The probability e of ultimate extinction is the smallest non-negative root of the equation

(9.20)

Proof

Since , we have by (4.9) that . By (9.5) and (9.6),

Set to find that satisfies

(9.21)

with the boundary condition . Now take the limit as . By (9.18), . Furthermore, G is a power series with radius of convergence at least 1, giving that G is continuous on . It follows that e is a root of the equation , as required.

In order to show that e is the smallest non-negative root of (9.20), suppose that is any non-negative root of (9.20); we shall show that . First, G is non-decreasing on since it has non-negative coefficients, and hence

by (9.21). Similarly,

by (9.21), giving by induction that

Hence, .

The last theorem explains how to find the probability of ultimate extinction, the next tells us when extinction is bound to occur.

Theorem 9.22 (Extinction/survival theorem)

Assume that . The probability e of ultimate extinction satisfies if and only if the mean family-size μ satisfies .

We have eliminated the special case with , since in this trivial case all families have size 1, so that and .

Proof

We may suppose that , since otherwise and . We have seen that e is the smallest non-negative root of the equation . On the interval , G is

(a) continuous, since its radius of convergence is at least 1,

(b) non-decreasing, since ,

and so a sketch of G looks something like the curves in Figure 9.2. Generally speaking, there are either one or two intersections between the curve and the line in the interval . If the derivative satisfies , the geometry of Figure 9.2(a) indicates that there are two distinct intersections (and, in particular ). On the other hand, if , Figure 9.2(b) indicates that there is a unique such intersection, and in this case is the unique root in of the equation . However, , and in summary if and only if .

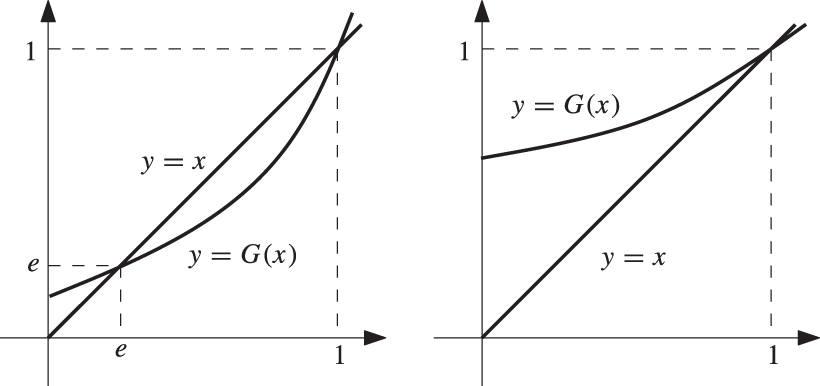
**Fig. 9.2** The curve 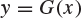and the line 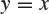, in the two cases (a) 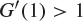and (b) .

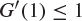Exercise 9.23

If the family-size distribution of a branching process has mass function for and , use Theorem 9.19 to show that the probability that the process becomes extinct ultimately is if .

Exercise 9.24

If each family size of a branching process has the binomial distribution with parameters 2 and p , show that the probability of ultimate extinction is

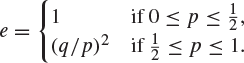
9.6 Problems

1. Let be independent random variables, each with mean μ and variance , and let N be a random variable which takes values in the positive integers and which is independent of the X_i. Show that the sum

has variance given by

If are the generation sizes of a branching process in which each family size has mean μ and variance , use the above fact to show that

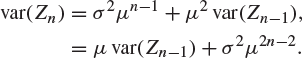
Deduce an expression for in terms of μ, , and n.

2. Use the result of Problem 9.6.1 to show that, if is a branching process whose family sizes have mean μ and variance , then as .

3. By using the partition theorem and conditioning on the value of Z_m, show that if is a branching process with mean family-size μ, then

4. If is a branching process in which and the size of the rth generation Z_r has the generating function , prove that

Suppose that the process is modified so that the initial generation Z₀ is Poisson with parameter λ, and the number of offspring of each individual is also Poisson with parameter λ. Find a function f such that if is the generating function of the total number of individuals , then

(Oxford 1977F)

5. A branching process has . Let the total number of individuals in the first n generations of the process be Z_n, with probability generating function Q_n. Prove that, for ,

where P₁ is the probability generating function of the family-size distribution. (Oxford 1974F)

6 (a) Explain what is meant by the term ‘branching process’.

(b) Let X_n be the size of the nth generation of a branching process in which each family size has probability generating function G, and assume that . Show that the probability generating function G_n of X_n satisfies for .

(c) Show that is the probability generating function of a non-negative integer-valued random variable when , and find G_n explicitly when G is thus given.

(d) Find the probability that , and show that it converges as to . Explain why this implies that the probability of ultimate extinction equals .

(Cambridge 2001)