The Physics Book

Robert Hooke (1635-1703)

Although microscopes had been available since about the late 1500s, English scientist Robert Hooke’s use of the compound microscope (a microscope with more than one lens) represents a particularly notable milestone, and his instrument can be considered as an important optical and mechanical forerunner of the modern microscope. For an optical microscope with two lenses, the overall magnification is the product of the powers of the ocular (eyepiece lens), usually about 10×, and the objective lens, which is closer to the specimen.

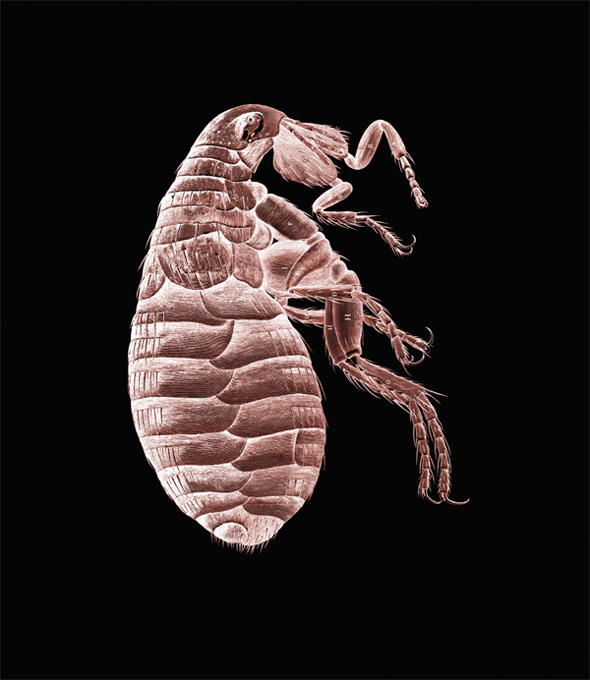
Hooke’s book Micrographia featured breathtaking microscopic observations and biological speculation on specimens that ranged from plants to fleas. The book also discussed planets, the wave theory of light, and the origin of fossils, while stimulating both public and scientific interest in the power of the microscope.

Hooke was first to discover biological cells and coined the word cell to describe the basic units of all living things. The word cell was motivated by his observations of plant cells that reminded him of “cellula,” which were the quarters in which monks lived. About this magnificent work, the historian of science Richard Westfall writes, “Robert Hooke’s Micrographia remains one of the masterpieces of seventeenth century science, [presenting] a bouquet of observations with courses from the mineral, animal and vegetable kingdoms.”

Hooke was the first person to use a microscope to study fossils, and he observed that the structures of petrified wood and fossil seashells bore a striking similarity to actual wood and the shells of living mollusks. In Micrographia, he compared petrified wood to rotten wood, and concluded that wood could be turned to stone by a gradual process. He also believed that many fossils represented extinct creatures, writing, “There have been many other Species of Creatures in former Ages, of which we can find none at present; and that ’tis not unlikely also but that there may be divers new kinds now, which have not been from the beginning.” More recent advances in microscopes are described in the entry “Seeing the Single Atom.”

full_image

Flea, from Robert Hooke’s Micrographia, published in 1665.

Amontons’ Friction

1669

Guillaume Amontons (1663–1705), Leonardo da Vinci (1452–1519), Charles-Augustin de Coulomb (1736–1806)

Friction is a force that resists the sliding of objects with respect to each other. Although it is responsible for the wearing of parts and the wasting of energy in engines, friction is beneficial in our everyday lives. Imagine a world without friction. How would one walk, drive a car, attach objects with nails and screws, or drill cavities in teeth?

In 1669, French physicist Guillaume Amontons showed that the frictional force between two objects is directly proportional to the applied load (i.e., the force perpendicular to the surfaces in contact), with a constant of proportionality (a frictional coefficient) that is independent of the size of the contact area. These relationships were first suggested by Leonardo da Vinci and rediscovered by Amontons. It may seem counterintuitive that the amount of friction is nearly independent of the apparent area of contact. However, if a brick is pushed along the floor, the resisting frictional force is the same whether the brick is sliding on its larger or smaller face.

Several studies have been conducted in the early years of the twenty-first century to determine the extent to which Amontons’ Law actually applies for materials at length scales from nanometers to millimeters—for example, in the area of MEMS (micro-electromechanical systems), which involves tiny devices such as those now used in inkjet printers and as accelerometers in car airbag systems. MEMS make use of microfabrication technology to integrate mechanical elements, sensors, and electronics on a silicon substrate. Amontons’ Law, which is often useful when studying traditional machines and moving parts, may not be applicable to machines the size of a pinhead.

In 1779, French physicist Charles-Augustin de Coulomb began his research into friction and found that for two surfaces in relative motion, the kinetic friction is almost independent of the relative speed of the surfaces. For an object at rest, the static frictional force is usually greater than the resisting force for the same object in motion.

full_image

Devices such as wheels and ball bearings are used to convert sliding friction into a decreased form of rolling friction, thus creating less resistance to motion.

Measuring the Solar System

1672

Giovanni Domenico Cassini (1625–1712)

Before astronomer Giovanni Cassini’s 1672 experiment to determine the size of the Solar System, there were some rather outlandish theories floating about. Aristarchus of Samos in 280 B.C. had said that the Sun was a mere 20 times farther from the Earth than the Moon. Some scientists around Cassini’s time suggested that stars were only a few million miles away. While in Paris, Cassini sent astronomer Jean Richer to the city of Cayenne on the northeast coast of South America. Cassini and Richer made simultaneous measurements of the angular position of Mars against the distant stars. Using simple geometrical methods (see the entry “Stellar Parallax”), and knowing the distance between Paris and Cayenne, Cassini determined the distance between the Earth and Mars. Once this distance was obtained, he employed Kepler’s Third Law to compute the distance between Mars and the Sun (see “Kepler’s Laws of Planetary Motion”). Using both pieces of information, Cassini determined that the distance between the Earth and the Sun was about 87 million miles (140 million kilometers), which is only seven percent less than the actual average distance. Author Kendall Haven writes, “Cassini’s discoveries of distance meant that the universe was millions of times bigger than anyone had dreamed.” Note that it would be difficult to make direct measurements of the Sun without risking his eyesight.

Cassini became famous for many other discoveries. For example, he discovered four moons of Saturn and discovered the major gap in the rings of Saturn, which, today, is called the Cassini Gap in his honor. Interestingly, he was among the earliest scientists to correctly suspect that light traveled at a finite speed, but he did not publish his evidence for this theory because, according to Kendall Haven, “He was a deeply religious man and believed that light was of God. Light therefore had to be perfect and infinite, and not limited by a finite speed of travel.”

Since the time of Cassini, our concept of the Solar System has grown, with the discovery, for example, of Uranus (1781), Neptune (1846), Pluto (1930), and Eris (2005).

full_image

Cassini calculated the distance from Earth to Mars, and then the distance from Earth to the Sun. Shown here is a size comparison between Mars and Earth; Mars has approximately half the radius of Earth.

Newton’s Prism

1672

Isaac Newton (1642–1727)

“Our modern understanding of light and color begins with Isaac Newton,” writes educator Michael Douma, “and a series of experiments that he publishes in 1672. Newton is the first to understand the rainbow—he refracts white light with a prism, resolving it into its component colors: red, orange, yellow, green, blue and violet.”

When Newton was experimenting with lights and colors in the late 1660s, many contemporaries thought that colors were a mixture of light and darkness, and that prisms colored light. Despite the prevailing view, he became convinced that white light was not the single entity that Aristotle believed it to be but rather a mixture of many different rays corresponding to different colors. The English physicist Robert Hooke criticized Newton’s work on the characteristics of light, which filled Newton with a rage that seemed out of proportion to the comments Hooke had made. As a result, Newton withheld publication of his monumental book Opticks until after Hooke’s death in 1703—so that Newton could have the last word on the subject of light and could avoid all arguments with Hooke. In 1704, Newton’s Opticks was finally published. In this work, Newton further discusses his investigations of colors and the diffraction of light.

Newton used triangular glass prisms in his experiments. Light enters one side of the prism and is refracted by the glass into various colors (since their degree of separation changes as a function of the wavelength of the color). Prisms work because light changes speed when it moves from air into the glass of the prism. Once the colors were separated, Newton used a second prism to refract them back together to form white light again. This experiment demonstrated that the prism was not simply adding colors to the light, as many believed. Newton also passed only the red color from one prism through a second prism and found the redness unchanged. This was further evidence that the prism did not create colors, but merely separated colors present in the original light beam.

full_image

Newton used prisms to show that white light was not the single entity that Aristotle believed it to be, but rather was a mixture of many different rays corresponding to different colors.

Tautochrone Ramp

1673

Christiaan Huygens (1629-1695)

Years ago, I wrote a tall tale of seven skateboarders who find a seemingly magical mountain road. Wherever on the road the skateboarders start their downhill coasting, they always reach the bottom in precisely the same amount of time. How could this be? In the 1600s, mathematicians and physicists sought a curve that specified the shape of a special kind of ramp or road. On this special ramp, objects must slide down to the very bottom in the same amount of time, regardless of the starting position. The objects are accelerated by gravity, and the ramp is considered to have no friction.

Dutch mathematician, astronomer, and physicist Christiaan Huygens discovered a solution in 1673 and published it in his Horologium Oscillatorium (The Pendulum Clock). Technically speaking, the tautochrone is a cycloid—that is, a curve defined by the path of a point on the edge of circle as the circle rolls along a straight line. The tautochrone is also called the brachistochrone when referring to the curve that gives a frictionless object the fastest rate of descent when the object slides down from one point to another.

Huygens attempted to use his discovery to design a more accurate pendulum clock. The clock made use of inverted cycloid arcs near where the pendulum string pivoted to ensure that the string followed the optimum curve, no matter where the pendulum started swinging. (Alas, the friction caused by the bending of the string along the arcs introduced more error than it corrected.)

The special property of the tautochrone is mentioned in Moby Dick in a discussion on a try-pot, a bowl used for rendering blubber to produce oil: “[The try-pot] is also a place for profound mathematical meditation. It was in the left-hand try-pot of the Pequod, with the soapstone diligently circling round me, that I was first indirectly struck by the remarkable fact, that in geometry all bodies gliding along a cycloid, my soapstone, for example, will descend from any point in precisely the same time.”

full_image

Christiaan Huygens, painted by Caspar Netscher (1639-1684).

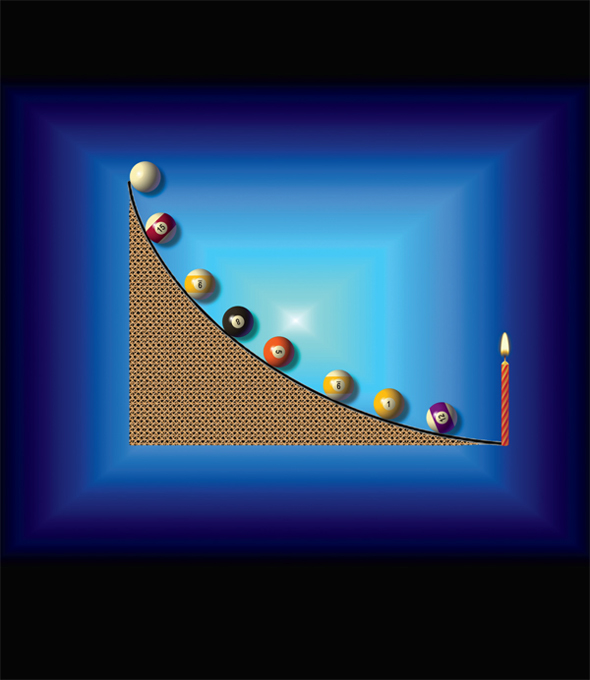
full_image

Under the influence of gravity, these billiard balls roll along the tautochrone ramp starting from different positions, yet the balls will arrive at the candle at the same time. The balls are placed on the ramp, one at a time.

Newton’s Laws of Motion and Gravitation

1687

Isaac Newton (1642–1727)

“God created everything by number, weight, and measure,” wrote Isaac Newton, the English mathematician, physicist, and astronomer who invented calculus, proved that white light was a mixture of colors, explained the rainbow, built the first reflecting telescope, discovered the binomial theorem, introduced polar coordinates, and showed the force causing objects to fall is the same kind of force that drives planetary motions and produces tides.

Newton’s Laws of Motion concern relations between forces acting on objects and the motion of these objects. His Law of Universal Gravitation states that objects attract one another with a force that varies as the product of the masses of the objects and inversely as the square of the distance between the objects. Newton’s First Law of Motion (Law of Inertia) states that bodies do not alter their motions unless forces are applied to them. A body at rest stays at rest. A moving body continues to travel with the same speed and direction unless acted upon by a net force. According to Newton’s Second Law of Motion, when a net force acts upon an object, the rate at which the momentum (mass × velocity) changes is proportional to the force applied. According to Newton’s Third Law of Motion, whenever one body exerts a force on a second body, the second body exerts a force on the first body that is equal in magnitude and opposite in direction. For example, the downward force of a spoon on the table is equal to the upward force of the table on the spoon.

Throughout his life, Newton is believed to have had bouts of manic depression. He had always hated his mother and stepfather, and as a teenager threatened to burn them alive in their house. Newton was also author of treatises on biblical subjects, including biblical prophecies. Few are aware that he devoted more time to the study of the Bible, theology, and alchemy than to science—and wrote more on religion than he did on natural science. Regardless, the English mathematician and physicist may well be the most influential scientist of all time.

full_image

Gravity affects the motions of bodies in outer space. Shown here is an artistic depiction of a massive collision of objects, perhaps as large as Pluto, that created the dust ring around the nearby star Vega.

Newton as Inspiration

1687

Isaac Newton (1642–1727)

The chemist William H. Cropper writes, “Newton was the greatest creative genius that physics has ever seen. None of the other candidates for the superlative (Einstein, Maxwell, Boltzmann, Gibbs, and Feynman) has matched Newton’s combined achievements as theoretician, experimentalist, and mathematician…. If you were to become a time traveler and meet Newton on a trip back to the seventeenth century, you might find him something like the performer who first exasperates everyone in sight and then goes on stage and sings like an angel….”

Perhaps more than any other scientist, Newton inspired the scientists who followed him with the idea that the universe could be understood in terms of mathematics. Journalist James Gleick writes, “Isaac Newton was born into a world of darkness, obscurity, and magic… veered at least once to the brink of madness… and yet discovered more of the essential core of human knowledge than anyone before or after. He was chief architect of the modern world…. He made knowledge a thing of substance: quantitative and exact. He established principles, and they are called his laws.”

Authors Richard Koch and Chris Smith note, “Some time between the 13th and 15th centuries, Europe pulled well ahead of the rest of the world in science and technology, a lead consolidated in the following 200 years. Then in 1687, Isaac Newton—foreshadowed by Copernicus, Kepler, and others—had his glorious insight that the universe is governed by a few physical, mechanical, and mathematical laws. This instilled tremendous confidence that everything made sense, everything fitted together, and everything could be improved by science.”

Inspired by Newton, astrophysicist Stephen Hawking writes, “I do not agree with the view that the universe is a mystery…. This view does not do justice to the scientific revolution that was started almost four hundred years ago by Galileo and carried on by Newton…. We now have mathematical laws that govern everything we normally experience.”

full_image

Photograph of Newton’s birthplace—Woolsthorpe Manor, England—along with an ancient apple tree. Newton performed many famous experiments on light and optics here. According to legend, Newton saw a falling apple here, which partly inspired his law of gravitation.

Tuning Fork

1711

John Shore (c. 1662–1752), Hermann von Helmholtz (1821–1894), Jules Antoine Lissajous (1822–1880), Rudolph Koenig (1832–1901)

Tuning forks—those Y-shaped metal devices that create a pure tone of constant frequency when struck—have played important roles in physics, medicine, art, and even literature. My favorite appearance in a novel occurs in The Great Gatsby, where Gatsby “knew that when he kissed this girl… his mind would never romp again like the mind of God. So he waited, listening for a moment longer to the tuning-fork that had been struck upon a star. Then he kissed her. At his lips’ touch she blossomed for him like a flower….”

The tuning fork was invented in 1711 by British musician John Shore. Its pure sinusoidal acoustic waveform makes it convenient for tuning musical instruments. The two prongs vibrate toward and away from one another, while the handle vibrates up and down. The handle motion is small, which means that the tuning fork can be held without significantly damping the sound. However, the handle can be used to amplify the sound by placing it in contact with a resonator, such as a hollow box. Simple formulas exist for computing the tuning-fork frequency based on parameters such as the density of the fork’s material, the radius and length of the prongs, and the Young’s modulus of the material, which is a measure of its stiffness.

In the 1850s, the mathematician Jules Lissajous studied waves produced by a tuning fork in contact with water by observing the ripples. He also obtained intricate Lissajous figures by successively reflecting light from one mirror attached to a vibrating tuning fork onto another mirror attached to a perpendicular vibrating tuning fork, then onto a wall. Around 1860, physicists Hermann von Helmholtz and Rudolph Koenig devised an electromagnetically driven tuning fork. In modern times, the tuning fork has been used by police departments to calibrate radar instruments for traffic speed control.

In medicine, these can be employed to assess a patient’s hearing and sense of vibration on the skin, as well as for identifying bone fractures, which sometimes diminish the sound produced by a vibrating turning fork when it is applied to the body near the injury and monitored with a stethoscope.

full_image

Tuning forks have played important roles in physics, music, medicine, and art.

Escape Velocity

1728

Isaac Newton (1642-1727)

Shoot an arrow straight up into the air, and it eventually comes down. Pull back the bow even farther, and the arrow takes longer to fall. The launch velocity at which the arrow would never return to the Earth is the escape velocity, v_e, and it can be computed with a simple formula: v_e = [(2GM)/r]^1/2, where G is the gravitational constant, and r is the distance of the bow and arrow from the center of the Earth, which has a mass of M. If we neglect air resistance and other forces and launch the arrow with some vertical component (along a radial line from the center of the Earth), then v_e = 6.96 miles per second (11.2 kilometers/second). This is surely one fast hypothetical arrow, which would have to be released at 34 times the speed of sound!

Notice that the mass of the projectile (e.g., whether it be an arrow or an elephant) does not affect its escape velocity, although it does affect the energy required to force the object to escape. The formula for v_e assumes a uniform spherical planet and a projectile mass that is much less than the planet’s mass. Also, v_e relative to the Earth’s surface is affected by the rotation of the Earth. For example, the arrow launched eastward while standing at the Earth’s equator has a v_e equal to about 6.6 miles/second (10.7 kilometers/ second) relative to the Earth.

Note that the v_e formula applies to a “one-time” vertical component of velocity for the projectile. An actual rocket ship does not have to achieve this speed because it may continue to fire its engines as it travels.

This entry is dated to 1728, the publication date for Isaac Newton’s A Treatise of the System of the World, in which he contemplates firing a cannonball at different high speeds and considers ball trajectories with respect to the Earth. The escape velocity formula may be computed in many ways, including from Newton’s Law of Universal Gravitation (1687), which states that objects attract one another with a force that varies as the product of the masses of the objects and inversely as the square of the distance between the objects.

full_image

Luna 1 was the first man-made object to reach the escape velocity of the Earth. Launched in 1959 by the Soviet Union, it was also the first spacecraft to reach the Moon.

Bernoulli’s Law of Fluid Dynamics

1738

Daniel Bernoulli (1700-1782)

Imagine water flowing steadily through a pipe that carries the liquid from the roof of a building to the grass below. The pressure of the liquid will change along the pipe. Mathematician and physicist Daniel Bernoulli discovered the law that relates pressure, flow speed, and height for a fluid flowing in a pipe. Today, we write Bernoulli’s Law as v²/2 + gz + p/ρ = C. Here, v is the fluid velocity, g the acceleration due to gravity, z the elevation (height) of a point in the fluid, p the pressure, ρ the fluid density, and C is a constant. Scientists prior to Bernoulli had understood that a moving body exchanges its kinetic energy for potential energy when the body gains height. Bernoulli realized that, in a similar way, changes in the kinetic energy of a moving fluid result in a change in pressure.

The formula assumes a steady (non-turbulent) fluid flow in a closed pipe. The fluid must be incompressible. Because most liquid fluids are only slightly compressible, Bernoulli’s Law is often a useful approximation. Additionally, the fluid should not be viscous, which means that the fluid should not have internal friction. Although no real fluid meets all these criteria, Bernoulli’s relationship is generally very accurate for free flowing regions of fluids that are away from the walls of pipes or containers, and it is especially useful for gases and light liquids.

Bernoulli’s Law often makes reference to a subset of the parameters in the above equation, namely that the decrease in pressure occurs simultaneously with an increase in velocity. The law is used when designing a venturi throat—a constricted region in the air passage of a carburetor that causes a reduction in pressure, which in turn causes fuel vapor to be drawn out of the carburetor bowl. The fluid increases speed in the smaller-diameter region, reducing its pressure and producing a partial vacuum via Bernoulli’s Law.

Bernoulli’s formula has numerous practical applications in the fields of aerodynamics, where it is considered when studying flow over airfoils, such as wings, propeller blades, and rudders.

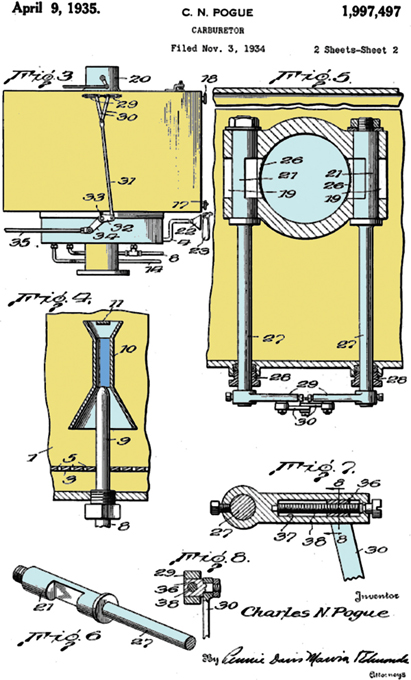
full_image

Many engine carburetors have contained a venturi with a narrow throat region that speeds the air and reduces the pressure to draw fuel via Bernoulli’s Law. The venture throat is labeled 10 in this 1935 carburetor patent.

Leyden Jar

1744

Pieter van Musschenbroek (1692–1761), Ewald Georg von Kleist (1700–1748), Jean-Antoine Nollet (1700–1770), Benjamin Franklin (1706–1790)

“The Leyden jar was electricity in a bottle, an ingenious way to store a static electric charge and release it at will,” writes author Tom McNichol. “Enterprising experimenters drew rapt crowds all over Europe… killing birds and small animals with a burst of stored electric charge…. In 1746, Jean-Antoine Nollet, a French clergyman and physicist, discharged a Leyden jar in the presence of King Louis XV, sending a current of static electricity rushing through a chain of 180 Royal Guards who were holding hands.” Nollet also connected a row of a several hundred robed Carthusian monks, giving them the shock of their lives.

The Leyden jar is a device that stores static electricity between an electrode on the outside of a jar and another electrode on the inside. An early version was invented in 1744 by Prussian researcher Ewald Georg von Kleist. A year later, Dutch scientist Pieter van Musschenbroek independently invented a similar device while in Leiden (also spelled Leyden). The Leyden jar was important in many early experiments in electricity. Today, a Leyden jar is thought of as an early version of the capacitor, an electronic component that consists of two conductors separated by a dielectric (insulator). When a potential difference (voltage) exists across the conductors, an electric field is created in the dielectric, which stores energy. The narrower the separation between the conductors, the larger the charge that may be stored.

A typical design consists of a glass jar with conducting metal foils lining part of the outside and inside of the jar. A metal rod penetrates the cap of the jar and is connected to the inner metal lining by a chain. The rod is charged with static electricity by some convenient means—for example, by touching it with a silk-rubbed glass rod. If a person touches the metal rod, that person will receive a shock. Several jars may be connected in parallel to increase the amount of possible stored charge.

full_image

British inventor James Wimshurst (1832–1903) invented the Wimshurst Machine, an electrostatic device for generating high voltages. A spark jumps across the gap formed by two metal spheres. Note the two Leyden jars for charge storage.

Ben Franklin’s Kite

1752

Benjamin Franklin (1706–1790)

Benjamin Franklin was an inventor, statesman, printer, philosopher, and scientist. Although he had many talents, historian Brooke Hindle writes, “The bulk of Franklin’s scientific activities related to lightning and other electrical matters. His connection of lightning with electricity, through the famous experiment with a kite in a thunderstorm, was a significant advance of scientific knowledge. It found wide application in constructions of lightning rods to protect buildings in both the United States and Europe.” Although perhaps not on par with many other physics milestones in this book, “Franklin’s Kite” has often been a symbol of the quest for scientific truth and has inspired generations of school children.

In 1750, in order to verify that lightning is electricity, Franklin suggested an experiment that involved the flying of a kite in a storm that seemed likely to become a lightning storm. Although some historians have disputed the specifics of the story, according to Franklin, his experiments were conducted on June 15, 1752 in Philadelphia in order to successfully extract electrical energy from a cloud. In some versions of the story, he held a silk ribbon tied to a key at the end of the kite string to insulate himself from the electrical current that traveled down the string to the key and into the Leyden jar (a device that stores electricity between two electrodes). Other researchers did not take such precautions and were electrocuted when performing similar experiments. Franklin wrote, “When rain has wet the kite twine so that it can conduct the electric fire freely, you will find it streams out plentifully from the key at the approach of your knuckle, and with this key a… Leiden jar may be charged….”

Historian Joyce Chaplin notes that the kite experiment was not the first to identify lighting with electricity, but the kite experiment verified this finding. Franklin was “trying to gauge whether the clouds were electrified and, if so, whether with a positive or a negative charge. He wanted to determine the presence of… electricity within nature, [and] it reduces his efforts considerably to describe them as resulting only in… the lightning rod.”

full_image

“Benjamin Franklin Drawing Electricity from the Sky” (c. 1816), by Anglo-American painter Benjamin West (1738–1820). A bright electrical current appears to drop from the key to the jar in his hand.

Black Drop Effect

1761

Torbern Olof Bergman (1735-1784), James Cook (1728-1779)

Albert Einstein once suggested that the most incomprehensible thing about the world is that it is comprehensible. Indeed, we appear to live in a cosmos that can be described or approximated by compact mathematical expressions and physical laws. Even the strangest of astrophysical phenomena are often explained by scientists and scientific laws, although it can take many years to provide a coherent explanation.

The mysterious black drop effect (BDE) refers to the apparent shape assumed by Venus as it transits across the Sun when observed from the Earth. In particular, Venus appears to assume the shape of a black teardrop when visually “touching” the inside edge of the Sun. The tapered, stretched part of the teardrop resembles a fat umbilical cord or dark bridge, which made it impossible for early physicists to determine Venus’ precise transit time across the Sun.

The first detailed description of the BDE came in 1761, when Swedish scientist Torbern Bergman described the BDE in terms of a “ligature” that joined the silhouette of Venus to the dark edge of the Sun. Many scientists provided similar reports in the years that followed. For example, British explorer James Cook made observations of the BDE during the 1769 transit of Venus.

full_image

British explorer James Cook observed the Black Drop Effect during the 1769 transit of Venus, as depicted in this sketch by the Australian astronomer Henry Chamberlain Russell (1836-1907).

Today, physicists continue to ponder the precise reason for the BDE. Astronomers Jay M. Pasachoff, Glenn Schneider, and Leon Golub suggest it is a “combination of instrumental effects and effects to some degree in the atmospheres of Earth, Venus, and Sun.” During the 2004 transit of Venus, some observers saw the BDE while others did not. Journalist David Shiga writes, “So the ‘black-drop effect’ remains as enigmatic in the 21st century as in the 19th. Debate is likely to continue over what constitutes a ‘true’ black drop…. And it remains to be seen whether the conditions for the appearance of black drop will be nailed down as observers compare notes… in time for the next transit….”

full_image

Venus transits the Sun in 2004, exhibiting the black-drop effect.

Bode’s Law of Planetary Distances

1766

Johann Elert Bode (1747–1826), Johann Daniel Titius (1729–1796)

Bode’s Law, also known as the Titius-Bode Law, is particularly fascinating because it seems like pseudo-scientific numerology and has intrigued both physicists and laypeople for centuries. The law expresses a relationship that describes the mean distances of the planets from the Sun. Consider the simple sequence 0, 3, 6, 12, 24, … in which each successive number is twice the previous number. Next, add 4 to each number and divide by 10 to form the sequence 0.4, 0.7, 1.0, 1.6, 2.8, 5.2, 10.0, 19.6, 38.8, 77.2, … Remarkably, Bode’s Law provides a sequence that lists the mean distances D of many planets from the Sun, expressed in astronomical units (AU). An AU is the mean distance between the Earth and Sun, which is approximately 92,960,000 miles (149,604,970 kilometers). For example, Mercury is approximately 0.4 of an AU from the Sun, and Pluto is about 39 AU from the Sun.

This law was discovered by the German astronomer Johann Titius of Wittenberg in 1766 and published by Johann Bode six years later, though the relationship between the planetary orbits had been approximated by Scottish mathematician David Gregory in the early eighteenth century. At the time, the law gave a remarkably good estimate for the mean distances of the planets that were then known—Mercury (0.39), Venus (0.72), Earth (1.0), Mars (1.52), Jupiter (5.2), and Saturn (9.55). Uranus, discovered in 1781, has a mean orbital distance of 19.2, which also agrees with the law.

Today scientists have major reservations about Bode’s Law, which is clearly not as universally applicable as other laws in this book. In fact, the relationship may be purely empirical and coincidental.

A phenomenon of “orbital resonances,” caused by orbiting bodies that gravitationally interact with other orbiting bodies, can create regions around the Sun that are free of long-term stable orbits and thus, to some degree, can account for the spacing of planets. Orbital resonances can occur when two orbiting bodies have periods of revolution that are related in a simple integer ratio, so that the bodies exert a regular gravitational influence on each other.

full_image

According to Bode’s Law, the mean distance of Jupiter to the Sun is 5.2 AU, and the actual measured value is 5.203 AU.

Lichtenberg Figures

1777

Georg Christoph Lichtenberg (1742–1799)

Among the most beautiful representations of natural phenomena are three-dimensional Lichtenberg figures, reminiscent of fossilized lightning trapped within a block of clear acrylic. These branching trails of electric discharges are named after German physicist Georg Lichtenberg, who originally studied similar electrical traces on surfaces. In the 1700s, Lichtenberg discharged electricity onto the surface of an insulator. Then, by sprinkling certain charged powders onto the surface, he was able to reveal curious tendrilous patterns.

Today, three-dimensional patterns can be created in acrylic, which is an insulator, or dielectric, meaning that it can hold a charge but that current cannot normally pass through it. First, the acrylic is exposed to a beam of high-speed electrons from an electron accelerator. The electrons penetrate the acrylic and are stored within. Since the acrylic is an insulator, the electrons are now trapped (think of a nest of wild hornets trying to break out of an acrylic prison). However, there comes a point where the electrical stress is greater than the dielectric strength of the acrylic, and some portions do suddenly become conductive. The escape of electrons can be triggered by piercing the acrylic with a metal point. As a result, some of the chemical bonds that hold the acrylic molecules together are torn apart. Within a fraction of a second, electrically conductive channels form within the acrylic as the electrical charge escapes from the acrylic, melting pathways along the way. Electrical engineer Bert Hickman speculates that these microcracks propagate faster than the speed of sound within the acrylic.

Lichtenberg figures are fractals, exhibiting branching self-similar structures at multiple magnifications. In fact, the fernlike discharge pattern may actually extend all the way down to the molecular level. Researchers have developed mathematical and physical models for the process that creates the dendritic patterns, which is of interest to physicists because such models may capture essential features of pattern formation in seemingly diverse physical phenomena. Such patterns may have medical applications as well. For example, researchers at Texas A&M University believe these feathery patterns may serve as templates for growing vascular tissue in artificial organs.

full_image

Bert Hickman’s Lichtenberg figure in acrylic, created by electron-beam irradiation, followed by manual discharge. The specimen’s internal potential prior to discharging was estimated to be around 2 million volts.

Black Eye Galaxy

1779

Edward Pigott (1753–1825), Johann Elert Bode (1747–1826), Charles Messier (1730–1817)

The Black Eye Galaxy resides in the constellation Coma Berenices and is about 24 million light years away from the Earth. Author and naturalist Stephen James O’Meara writes poetically of this famous galaxy with its “smooth silken arms [that] wrap gracefully around a porcelain core…. The galaxy resembles a closed human eye with a ‘shiner.’ The dark dust cloud looks as thick and dirty as tilled soil [but] a jar of its material would be difficult to distinguish from a perfect vacuum.”

Discovered in 1779 by English astronomer Edward Pigott, it was independently discovered just twelve days later by German astronomer Johann Elert Bode and about a year later by French astronomer Charles Messier. As mentioned in the entry “Explaining the Rainbow,” such nearly simultaneous discoveries are common in the history of science and mathematics. For example, British naturalists Charles Darwin and Alfred Wallace both developed the theory of evolution independently and simultaneously. Likewise, Isaac Newton and German mathematician Gottfried Wilhelm Leibniz developed calculus independently at about the same time. Simultaneity in science has led some philosophers to suggest that scientific discoveries are inevitable as they emerge from the common intellectual waters of a particular place and time.

Interestingly, recent discoveries indicate that the interstellar gas in the outer regions of the Black Eye Galaxy rotates in the opposite direction from the gas and stars in the inner regions. This differential rotation may arise from the Black Eye Galaxy having collided with another galaxy and having absorbed it over a billion years ago.

Author David Darling writes that the inner zone of the galaxy is about 3,000 light-years in radius and “rubs along the inner edge of an outer disk, which rotates in the opposite direction at about 300 km/s and extends out to at least 40,000 light-years. This rubbing may explain the vigorous burst of star formation that is currently taking place in the galaxy and is visible as blue knots embedded in the huge dust lane.”

full_image

The interstellar gas in the outer regions of the Black Eye Galaxy rotates in the opposite direction of the gas and stars in the inner regions. This differential rotation may arise from the galaxy having collided with another galaxy and having absorbed this galaxy over a billion years ago.

Black Holes

1783

John Michell (1724-1793), Karl Schwarzschild (1873-1916), John Archibald Wheeler (1911-2008), Stephen William Hawking (b. 1942)

Astronomers may not believe in Hell, but most believe in ravenous, black regions of space in front of which one would be advised to place a sign, “Abandon hope, all ye who enter here.” This was Italian poet Dante Alighieri’s warning when describing the entrance to the Inferno in his Divine Comedy, and, as astrophysicist Stephen Hawking has suggested, this would be the appropriate message for travelers approaching a black hole.

These cosmological hells truly exist in the centers of many galaxies. Such galactic black holes are collapsed objects having millions or even billions of times the mass of our Sun crammed into a space no larger than our Solar System. According to classical black hole theory, the gravitational field around such objects is so great that nothing—not even light—can escape from their tenacious grip. Anyone who falls into a black hole will plunge into a tiny central region of extremely high density and extremely small volume … and the end of time. When quantum theory is considered, black holes are thought to emit a form of radiation called Hawking radiation (see “Notes and Further Reading” and the entry “Stephen Hawking on Star Trek”).

Black holes can exist in many sizes. As some historical background, just a few weeks after Albert Einstein published his general relativity theory in 1915, German astronomer Karl Schwarzschild performed exact calculations of what is now called the Schwarzschild radius, or event horizon. This radius defines a sphere surrounding a body of a particular mass. In classical black-hole theory, within the sphere of a black hole, gravity is so strong that no light, matter, or signal can escape. For a mass equal to the mass of our Sun, the Schwarzschild radius is a few kilometers in length. A black hole with an event horizon the size of a walnut would have a mass equal to the mass of the Earth. The actual concept of an object so massive that light could not escape was first suggested in 1783 by the geologist John Michell. The term “black hole” was coined in 1967 by theoretical physicist John Wheeler.

full_image

Black holes and Hawking radiation are the stimulus for numerous impressionistic pieces by Slovenian artist Teja Krašek.

full_image

Artistic depiction of the warpage of space in the vicinity of a black hole.

Coulomb’s Law of Electrostatics

1785

Charles-Augustin Coulomb (1736–1806)

“We call that fire of the black thunder-cloud electricity,” wrote essayist Thomas Carlyle in the 1800s, “but what is it? What made it?” Early steps to understand electric charge were taken by French physicist Charles-Augustin Coulomb, the preeminent physicist who contributed to the fields of electricity, magnetism, and mechanics. His Law of Electrostatics states that the force of attraction or repulsion between two electric charges is proportional to the product of the magnitude of the charges and inversely proportional to the square of their separation distance r. If the charges have the same sign, the force is repulsive. If the charges have opposite signs, the force is attractive.

Today, experiments have demonstrated that Coulomb’s Law is valid over a remarkable range of separation distances, from as small as 10⁻¹⁶ meters (a tenth of the diameter of an atomic nucleus) to as large as 10⁶ meters (where 1 meter is equal to 3.28 feet). Coulomb’s Law is accurate only when the charged particles are stationary because movement produces magnetic fields that alter the forces on the charges.

Although other researchers before Coulomb had suggested the 1/r² law, we refer to this relationship as Coulomb’s Law in honor of Coulomb’s independent results gained through the evidence provided by his torsional measuring. In other words, Coulomb provided convincing quantitative results for what was, up to 1785, just a good guess.

One version of Coulomb’s torsion balance contains a metal and a non-metal ball attached to an insulating rod. The rod is suspended at its middle by a nonconducting filament or fiber. To measure the electrostatic force, the metal ball is charged. A third ball with similar charge is placed near the charged ball of the balance, causing the ball on the balance to be repelled. This repulsion causes the fiber to twist. If we measure how much force is required to twist the wire by the same angle of rotation, we can estimate the degree of force caused by the charged sphere. In other words, the fiber acts as a very sensitive spring that supplies a force proportional to the angle of twist.

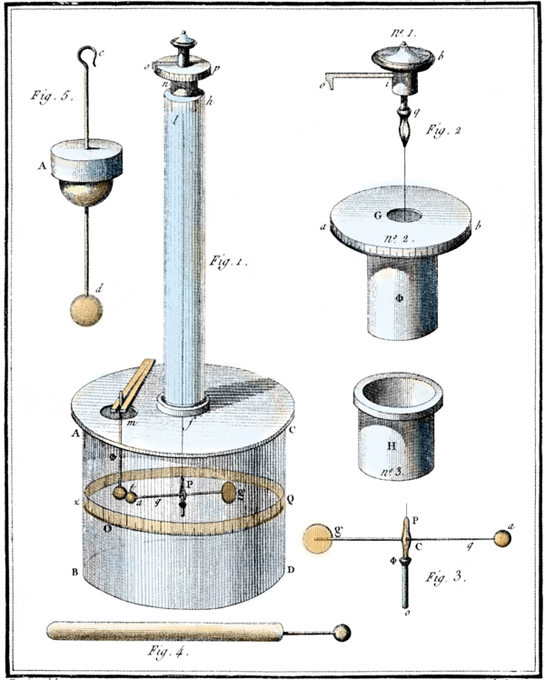
full_image

Charles-Augustin de Coulomb’s torsion balance, from his Mémoires sur l’électricité et le magnétisme (1785–1789).

Charles’ Gas Law

1787

Jacques Alexandre César Charles (1746-1823), Joseph Louis Gay-Lussac (1778-1850)

“It is our business to puncture gas bags and discover the seeds of truth,” wrote essayist Virginia Woolf. On the other hand, the French balloonist Jacques Charles knew how to make “gas bags” soar to find truths. The gas law named in his honor states that the volume occupied by a fixed amount of gas varies directly with the absolute temperature (i.e., the temperature in kelvins). The law can be expressed as V = kT where V is the volume at a constant pressure, T is the temperature, and k is a constant. Physicist Joseph Gay-Lussac first published the law in 1802, where he referenced unpublished work from around 1787 by Jacques Charles.

As the temperature of the gas increases, the gas molecules move more quickly and hit the walls of their container with more force—thus increasing the volume of gas, assuming that the container volume is able to expand. For a more specific example, consider warming the air within a balloon. As the temperature increases, the speed of the moving gas molecules increases inside the surface of the balloon. This in turn increases the rate at which the gas molecules bombard the interior surface. Because the balloon can stretch, the surface expands as a result of the increased internal bombardment. The volume of gas increases, and its density decreases. The act of cooling the gas inside a balloon will have the opposite effect, causing the pressure to be reduced and the balloon to shrink.

Charles was most famous to his contemporaries for his various exploits and inventions pertaining to the science of ballooning and other practical sciences. His first balloon journey took place in 1783, and an adoring audience of thousands watched as the balloon drifted by. The balloon ascended to a height of nearly 3,000 feet (914 meters) and seems to have finally landed in a field outside of Paris, where it was destroyed by terrified peasants. In fact, the locals believed that the balloon was some kind of evil spirit or beast from which they heard sighs and groans, accompanied by a noxious odor.

full_image

The first flight of Jacques Charles with co-pilot Nicolas-Louis Robert, 1783, who are seen waving flags to spectators. Versailles Palace is in the background. The engraving is likely created by Antoine François Sergent-Marceau, c. 1783.

Nebular Hypothesis

1796

Immanuel Kant (1724–1804), Pierre-Simon Laplace (1749–1827)

For centuries, scientists hypothesized that the Sun and planets were born from a rotating disk of cosmic gas and dust. The flat disk constrained the planets that formed from it to have orbits almost lying in the same plane. This nebular theory was developed in 1755 by the philosopher Immanuel Kant, and refined in 1796 by mathematician Pierre-Simon Laplace.

In short, stars and their disks form from the gravitational collapse of large volumes of sparse interstellar gas called solar nebulae. Sometimes a shock wave from a nearby supernova, or exploding star, may trigger the collapse. Gases in these protoplanetary disks (proplyds) of gas will be swirling more in one direction than the other, giving the gas cloud a net rotation.

Using the Hubble Space Telescope, astronomers have detected several proplyds in the Orion Nebula, a giant stellar nursery about 1,600 light-years away. The Orion proplyds are larger than the Sun’s solar system and contain sufficient gas and dust to provide the raw material for future planetary systems.

The violence of the early Solar System was tremendous as huge chunks of matter bombarded one another. In the inner Solar System, the Sun’s heat drove away the lighter-weight elements and materials, leaving Mercury, Venus, Earth, and Mars behind. In the colder outer part of the system, the solar nebula of gas and dust survived for some time and were accumulated by Jupiter, Saturn, Uranus, and Neptune.

Interestingly, Isaac Newton marveled at the fact that most of the objects that orbit the Sun are contained with an ecliptic plane offset by just a few degrees. He reasoned that natural processes could not create such behavior. This, he argued, was evidence of design by a benevolent and artistic creator. At one point, he thought of the Universe as “God’s Sensorium,” in which the objects in the Universe—their motions and their transformations—were the thoughts of God.

full_image

Protoplanetary disk. This artistic depiction features a small young star encircled by a disk of gas and dust, the raw materials from which rocky planets such as Earth may form.

Cavendish Weighs the Earth

1798

Henry Cavendish (1731–1810)

Henry Cavendish was perhaps the greatest of all eighteenth-century scientists, and one of the greatest scientists who ever lived. Yet his extreme shyness—a trait that made the vast extent of his scientific writings secret until after his death—caused some of his important discoveries to be associated with the names of subsequent researchers. The huge number of manuscripts uncovered after Cavendish’s death show that he conducted extensive research in literally all branches of physical sciences of his day.

The brilliant British chemist was so shy around women that he communicated with his housekeeper using only written notes. He ordered all his female housekeepers to keep out of sight. If they were unable to comply, he Fired them. Once when he saw a female servant, he was so mortified that he built a second staircase for the servants’ use so that he could avoid them.

In one of his most impressive experiments, Cavendish at the age of 70 “weighed” the world! In order to accomplish this feat, he didn’t transform into the Greek god Atlas, but rather determined the density of the Earth using highly sensitive balances. In particular, he used a torsional balance consisting of two lead balls on either end of a suspended beam. These mobile balls were attracted by a pair of larger stationary lead balls. To reduce air currents, he enclosed the device in a glass case and observed the motion of the balls from far away, by means of a telescope. Cavendish calculated the force of attraction between the balls by observing the balance’s oscillation period, and then computed the Earth’s density from the force. He found that the Earth was 5.4 times as dense as water, a value that is only 1.3% lower than the accepted value today. Cavendish was the first scientist able to detect minute gravitational forces between small objects. (The attractions were 1/500,000,000 times as great as the weight of the bodies.) By helping to quantify Newton’s Law of Universal Gravitation, he had made perhaps the most important addition to gravitational science since Newton.

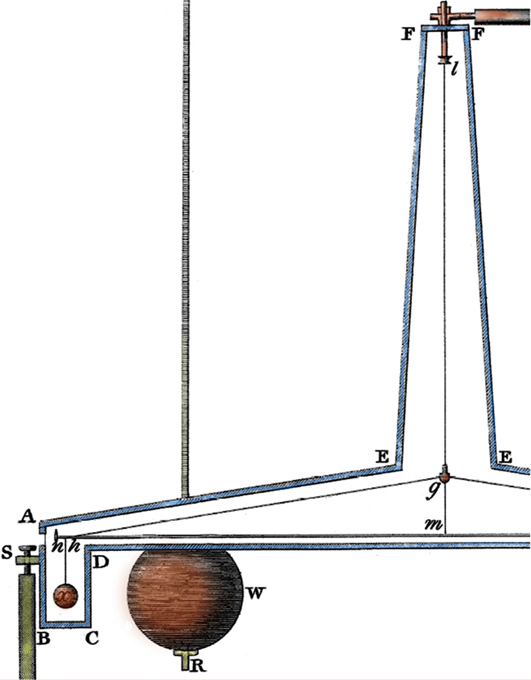
full_image

Close-up of a portion of the drawing of a torsion balance from Cavendish’s 1798 paper “Experiments to Determine the Density of the Earth.”

Battery

1800

Luigi Galvani (1737–1798), Alessandro Volta (1745–1827), Gaston Planté (1834–1889)

Batteries have played an invaluable role in the history of physics, chemistry, and industry. As batteries evolved in power and sophistication, they facilitated important advances in electrical applications, from the emergence of telegraph communication systems to their use in vehicles, cameras, computers, and phones.

Around 1780, physiologist Luigi Galvani experimented with frogs’ legs that he could cause to jerk when in contact with metal. Science-journalist Michael Guillen writes, “During his sensational public lectures, Galvani showed people how dozens of frogs’ legs twitched uncontrollably when hung on copper hooks from an iron wire, like so much wet laundry strung out on a clothesline. Orthodox science cringed at his theories, but the spectacle of that chorus line of flexing frog legs guaranteed Galvani sell-out crowds in auditoriums the world over.” Galvani ascribed the leg movement to “animal electricity.” However, Italian physicist and friend Alessandro Volta believed that the phenomenon had more to do with the different metals Galvani employed, which were joined by a moist connecting substance. In 1800, Volta invented what has been traditionally considered to be the first electric battery when he stacked several pairs of alternating copper and zinc discs separated by cloth soaked in salt water. When the top and bottom of this voltaic pile were connected by a wire, an electric current began to flow. To determine that current was flowing, Volta could touch its two terminals to his tongue and experience a tingly sensation.

“A battery is essentially a can full of chemicals that produce electrons,” write authors Marshall Brain and Charles Bryant. If a wire is connected between the negative and positive terminals, the electrons produced by chemical reactions flow from one terminal to the other.

In 1859, physicist Gaston Planté invented the rechargeable battery. By forcing a current through it “backwards,” he could recharge his lead-acid battery. In the 1880s, scientists invented commercially successful dry cell batteries, which made use of pastes instead of liquid electrolytes (substances containing free ions that make the substances electrically conductive).

full_image

As batteries evolved, they facilitated important advances in electrical applications, ranging from the emergence of telegraph communication systems to their use in vehicles, cameras, computers, and phones.

Wave Nature of Light

1801

Christiaan Huygens (1629–1695), Isaac Newton (1642–1727), Thomas Young (1773–1829)

“What is light?” is a question that has intrigued scientists for centuries. In 1675, the famous English scientist Isaac Newton proposed that light was a stream of tiny particles. His rival, the Dutch physicist Christiaan Huygens, suggested that light consisted of waves, but Newton’s theories often dominated, partly due to Newton’s prestige.

Around 1800, the English researcher Thomas Young—also famous for his work on deciphering the Rosetta Stone—began a series of experiments that provided support for Huygens’ wave theory. In a modern version of Young’s experiment, a laser equally illuminates two parallel slits in an opaque surface. The pattern that the light makes as it passes through the two slits is observed on a distant screen. Young used geometrical arguments to show that the superposition of light waves from the two slits explains the observed series of equally spaced bands (fringes) of light and dark regions, representing constructive and destructive interference, respectively. You can think of these patterns of light as being similar to the tossing of two stones into a lake and watching the waves running into one another and sometimes canceling each other out or building up to form even larger waves.

If we carry out the same experiment with a beam of electrons instead of light, the resulting interference pattern is similar. This observation is intriguing, because if the electrons behaved only as particles, one might expect to simply see two bright spots corresponding to the two slits.

Today, we know that the behavior of light and subatomic particles can be even more mysterious. When single electrons are sent through the slits one at a time, an interference pattern is produced that is similar to that produced for waves passing through both holes at once. This behavior applies to all subatomic particles, not just photons (light particles) and electrons, and suggests that light and other subatomic particles have a mysterious combination of particle and wavelike behavior, which is just one aspect of the quantum mechanics revolution in physics.

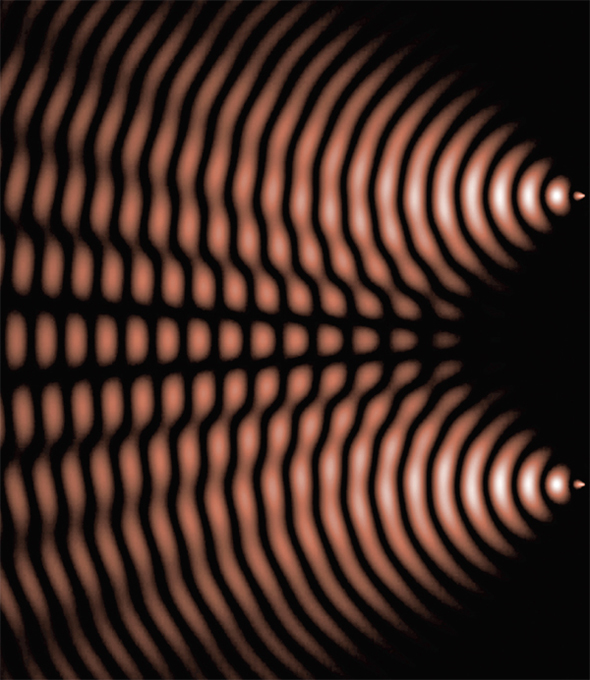
full_image

Simulation of the interference between two point sources. Young showed that the superposition of light waves from two slits explains the observed series of bands of light and dark regions, representing constructive and destructive interference, respectively.

Henry’s Gas Law

1803

William Henry (1775-1836)

Interesting physics is to be found even in the cracking of one’s knuckles. Henry’s Law, named after British chemist William Henry, states that the amount of a gas that is dissolved in a liquid is directly proportional to the pressure of the gas above the solution. It is assumed that the system under study has reached a state of equilibrium and that the gas does not chemically react with the liquid. A common formula used today for Henry’s Law is P = kC, where P is the partial pressure of the particular gas above the solution, C is the concentration of the dissolved gas, and k is the Henry’s Law constant.

We can visualize one aspect of Henry’s Law by considering a scenario in which the partial pressure of a gas above a liquid increases by a factor of two. As a result, on the average, twice as many molecules will collide with the liquid surface in a given time interval, and, thus, twice as many gas molecules may enter the solution. Note that different gases have different solubilities, and these differences also affect the process along with the value of Henry’s constant.

Henry’s Law has been used by researchers to better understand the noise associated with “cracking” of finger knuckles. Gases that are dissolved in the synovial fluid in joints rapidly come out of solution as the joint is stretched and pressure is decreased. This cavitation, which refers to the sudden formation and collapse of low-pressure bubbles in liquids by means of mechanical forces, produces a characteristic noise.

In scuba diving, the pressure of the air breathed is roughly the same as the pressure of the surrounding water. The deeper one dives, the higher the air pressure, and the more air dissolves in the blood. When a diver ascends rapidly, the dissolved air may come out of solution too quickly in the blood, and bubbles in the blood may cause a painful and dangerous disorder known as decompression sickness (“the bends”).

full_image

Cola in a glass. When a soda can is opened, the reduced pressure causes dissolved gas to come out of solution according to Henry’s Law. Carbon dioxide flows from the soda into the bubbles.

Fourier Analysis

1807

Jean Baptiste Joseph Fourier (1768-1830)

“The single most recurring theme of mathematical physics is Fourier analysis,” writes physicist Sadri Hassani. “It shows up, for example, in classical mechanics… in electromagnetic theory and the frequency analysis of waves, in noise considerations and thermal physics, and in quantum theory”—virtually any field in which a frequency analysis is important. Fourier series can help scientists characterize and better understand the chemical composition of stars and quantify signal transmission in electronic circuits.

Before French mathematician Joseph Fourier discovered his famous mathematical series, he accompanied Napoleon on his 1798 expedition to Egypt, where Fourier spent several years studying Egyptian artifacts. Fourier’s research on the mathematical theory of heat began around 1804 when he was back in France, and by 1807 he had completed his important memoir On the Propagation of Heat in Solid Bodies. One aspect of his fundamental work concerned heat diffusion in different shapes. For these problems, researchers are usually given the temperatures at points on the surface, as well as at its edges, at time t = 0. Fourier introduced a series with sine and cosine terms in order to find solutions to these kinds of problems. More generally, he found that any differentiable function can be represented to arbitrary accuracy by a sum of sine and cosine functions, no matter how bizarre the function may look when graphed.

Biographers Jerome Ravetz and I. Grattan-Guiness note, “Fourier’s achievement can be understood by [considering] the powerful mathematical tools he invented for the solutions of the equations, which yielded a long series of descendants and raised problems in mathematical analysis that motivated much of the leading work in that field for the rest of the century and beyond.” British physicist Sir James Jeans (1877-1946) remarked, “Fourier’s theorem tells us that every curve, no matter what its nature may be, or in what way it was originally obtained, can be exactly reproduced by superposing a sufficient number of simple harmonic curves—in brief, every curve can be built up by piling up waves.”

full_image

Portion of a jet engine. Fourier analysis methods are used to quantify and understand undesirable vibrations in numerous kinds of systems with moving parts.

Atomic Theory

1808

John Dalton (1766-1844)

John Dalton attained his professional success in spite of several hardships: He grew up in a family with little money; he was a poor speaker; he was severely color blind; and he was also considered to be a fairly crude or simple experimentalist. Perhaps some of these challenges would have presented an insurmountable barrier to any budding chemist of his time, but Dalton persevered and made exceptional contributions to the development of atomic theory, which states that all matter is composed of atoms of differing weights that combine in simple ratios in atomic compounds. During Dalton’s time, atomic theory also suggested that these atoms were indestructible and that, for a particular element, all atoms were alike and had the same atomic weight.

He also formulated the Law of Multiple Proportions, which stated that whenever two elements can combine to form different compounds, the masses of one element that combine with a fixed mass of the other are in a ratio of small integers, such as 1:2. These simple ratios provided evidence that atoms were the building blocks of compounds.

Dalton encountered resistance to atomic theory. For example, the British chemist Sir Henry Enfield Roscoe (1833-1915) mocked Dalton in 1887, saying, “Atoms are round bits of wood invented by Mr. Dalton.” Perhaps Roscoe was referring to the wood models that some scientists used in order to represent atoms of different sizes. Nonetheless, by 1850, the atomic theory of matter was accepted among a significant number of chemists, and most opposition disappeared.

The idea that matter was composed of tiny, indivisible particles was considered by the philosopher Democritus in Greece in the fifth century B.C., but this was not generally accepted until after Dalton’s 1808 publication of A New System of Chemical Philosophy. Today, we understand that atoms are divisible into smaller particles, such as protons, neutrons, and electrons. Quarks are even smaller particles that combine to form other subatomic particles such as protons and neutrons.

full_image

Engraving of John Dalton, by William Henry Worthington (c. 1795–c. 1839).

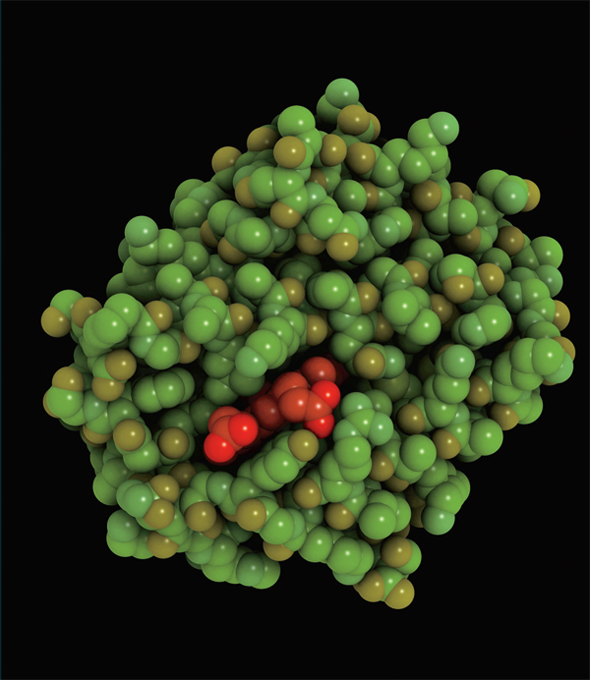
full_image

According to atomic theory, all matter is composed of atoms. Pictured here is a hemoglobin molecule with atoms represented as spheres. This protein is found in the red blood cell.

Avogadro’s Gas Law

1811

Amedeo Avogadro (1776-1856)

Avogadro’s Law, named after Italian physicist Amedeo Avogadro who proposed it in 1811, states that equal volumes of gases at the same temperature and pressure contain the same number of molecules, regardless of the molecular makeup of the gas. The law assumes that the gas particles are acting in an “ideal” manner, which is a valid assumption for most gases at pressures at or below a few atmospheres, near room temperature.

A variant of the law, also attributed to Avogadro, states that the volume of a gas is directly proportional to the number of molecules of the gas. This is represented by the formula V = a × N, where a is a constant, V is the volume of the gas, and N is the number of gas molecules. Other contemporary scientists believed that such a proportionality should be true, but Avogadro’s Law went further than competing theories because Avogadro essentially defined a molecule as the smallest characteristic particle of a substance—a particle that could be composed of several atoms. For example, he proposed that a water molecule consisted of two hydrogen atoms and one oxygen atom.

Avogadro’s number, 6.0221367 × 10²³, is the number of atoms found in one mole of an element. Today we define Avogadro’s number as the number of carbon-12 atoms in 12 grams of unbound carbon-12. A mole is the amount of an element that contains precisely the same number of grams as the value of the atomic weight of the substance. For example, nickel has an atomic weight of 58.6934, so there are 58.6934 grams in a mole of nickel.

Because atoms and molecules are so small, the magnitude of Avogadro’s number is difficult to visualize. If an alien were to descend from the sky to deposit an Avogadro’s number of unpopped popcorn kernels on the Earth, the alien could cover the United States of America with the kernels to a depth of over nine miles.

full_image

Place 24 numbered golden balls (numbered 1 through 24) in a bowl. If you randomly drew them out one at a time, the probability of removing them in numerical order is about 1 chance in Avogadro’s number—a very small chance!

Fraunhofer Lines

1814

Joseph von Fraunhofer (1787–1826)

A spectrum often shows the variation in the intensity of an object’s radiation at different wavelengths. Bright lines in atomic spectra occur when electrons fall from higher energy levels to lower energy levels. The color of the lines depends on the energy difference between the energy levels, and the particular values for the energy levels are identical for atoms of the same type. Dark absorption lines in spectra can occur when an atom absorbs light and the electron jumps to a higher energy level.

By examining absorption or emission spectra, we can determine which chemical elements produced the spectra. In the 1800s, various scientists noticed that the spectrum of the Sun’s electromagnetic radiation was not a smooth curve from one color to the next; rather, it contained numerous dark lines, suggesting that light was being absorbed at certain wavelengths. These dark lines are called Fraunhofer lines after the Bavarian physicist Joseph von Fraunhofer, who recorded them.

Some readers may find it easy to imagine how the Sun can produce a radiation spectrum but not how it can also produce dark lines. How can the Sun absorb its own light?

You can think of stars as fiery gas balls that contain many different atoms emitting light in a range of colors. Light from the surface of a star—the photosphere—has a continuous spectrum of colors, but as the light travels through the outer atmosphere of a star, some of the colors (i.e., light at different wavelengths) are absorbed. This absorption is what produces the dark lines. In stars, the missing colors, or dark absorption lines, tell us exactly which chemical elements are in the outer atmosphere of stars.

Scientists have catalogued numerous missing wavelengths in the spectrum of the Sun. By comparing the dark lines with spectral lines produced by chemical elements on the Earth, astronomers have found over seventy elements in the Sun. Note that, decades later, scientists Robert Bunsen and Gustav Kirchhoff studied emission spectra of heated elements and discovered cesium in 1860.

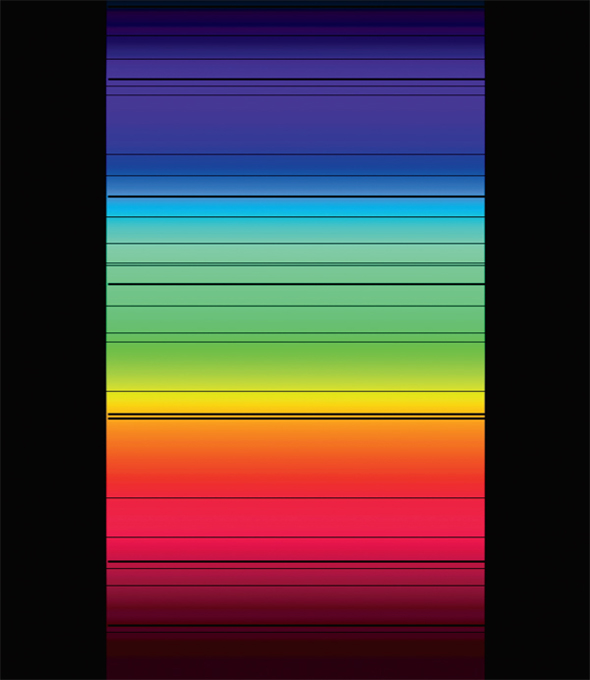
full_image

Visible solar spectrum with Fraunhofer lines. The y-axis represents the wavelength of light, starting from 380 nm at top and ending at 710 nm at bottom.

Laplace’s Demon

1814

Pierre-Simon, Marquis de Laplace (1749-1827)

In 1814, French mathematician Pierre-Simon Laplace described an entity, later called Laplace’s Demon, that was capable of calculating and determining all future events, provided that the demon was given the positions, masses, and velocities of every atom in the universe and the various known formulae of motion. “It follows from Laplace’s thinking,” writes scientist Mario Markus, “that if we were to include the particles in our brains, free will would become an illusion…. Indeed, Laplace’s God simply turns the pages of a book that is already written.”

During Laplace’s time, the idea made a certain sense. After all, if one could predict the position of billiard balls bouncing around a table, why not entities composed of atoms? In fact, Laplace has no need of God at all in his universe.

Laplace wrote, “We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, [it would embrace in] a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.”

Later, developments such as Heisenberg’s Uncertainty Principle (HUP) and Chaos Theory appear to make Laplace’s demon an impossibility. According to chaos theory, even minuscule inaccuracies in measurement at some initial time may lead to vast differences between a predicted outcome and an actual outcome. This means that Laplace’s demon would have to know the position and motion of every particle to infinite precision, thus making the demon more complex than the universe itself. Even if this demon existed outside the universe, the HUP tells us that infinitely precise measurements of the type required are impossible.

full_image

Pierre-Simon Laplace (posthumous portrait by Madame Feytaud [1842]).

full_image

In a universe with Laplace’s Demon, would free will be an illusion?

full_image

Artistic rendition of Laplace’s Demon observing the positions, masses, and velocities of every particle (represented here as bright specks) at a particular time.

Brewster’s Optics

1815

Sir David Brewster (1781-1868)

Light has fascinated scientists for centuries, but who would think that creepy cuttlefish might have something to teach us about the nature of light? A lightwave consists of an electric field and a magnetic field that oscillate perpendicular to each other and to the direction of travel. It is possible, however, to restrict the vibrations of the electric field to a particular plane by plane-polarizing the light beam. For example, one approach for obtaining plane-polarized light is via the reflection of light from a surface between two media, such as air and glass. The component of the electric field parallel to the surface is most strongly reflected. At one particular angle of incidence on the surface, called the Brewster’s angle after Scottish physicist David Brewster, the reflected beam consists entirely of light whose electric vector is parallel to the surface.

Polarization by light scattering in our atmosphere sometimes produces a glare in the skies. Photographers can reduce this partial polarization using special materials to prevent the glare from producing an image of a washed-out sky. Many animals, such as bees and cuttlefish, are quite capable of perceiving the polarization of light, and bees use polarization for navigation because the linear polarization of sunlight is perpendicular to the direction of the Sun.

Brewster’s experiments with light polarization led him to his 1816 invention of the kaleidoscope, which has often fascinated physics students and teachers who attempt to create ray diagrams in order to understand the kaleidoscope’s multiple reflections. Cozy Baker, founder of the Brewster Kaleidoscope Society, writes, “His kaleidoscope created unprecedented clamor…. A universal mania for the instrument seized all classes, from the lowest to the highest, from the most ignorant to the most learned, and every person not only felt, but expressed the feeling that a new pleasure had been added to their existence.” American inventor Edwin H. Land wrote “The kaleidoscope was the television of the 1850s….”

full_image

Using skin patterns that involve polarized light, cuttlefish can produce intricate “designs” as a means of communication. Such patterns are invisible to human eyes.

full_image

Brewster’s experiments with light polarization led him to his 1816 invention of the kaleidoscope.

Stethoscope

1816

René-Théophile-Hyacinthe Laennec (1781–1826)

Social historian Roy Porter writes, “By giving access to body noises—the sound of breathing, the blood gurgling around the heart—the stethoscope changed approaches to internal disease and hence doctor-patient relations. As last, the living body was no longer a closed book: pathology could now be done on the living.”

In 1816, French physician René Laennec invented the stethoscope, which consisted of a wooden tube with a trumpet-like end that made contact with the chest. The air-filled cavity transmitted sounds from the patient’s body to the physician’s ear. In the 1940s, stethoscopes with two-sided chest-pieces became standard. One side of the chest-piece is a diaphragm (e.g. a plastic disc that covers the opening), which vibrates when detecting body sounds and produces acoustic pressure waves that travel through the air cavity of the stethoscope. The other side contains a bell-shaped endpiece (e.g. a hollow cup) that is better at transmitting low-frequency sounds. The diaphragm side actually tunes out the low frequencies associated with heart sounds and is used to listen to the respiratory system. When using the bell side, the physician can vary the pressure of the bell on the skin and “tune” the skin vibration frequency in order to best reveal the heartbeat. Many other refinements occurred over the years that involved improved amplification, noise reduction, and other characteristics that were optimized by application of simple physical principles (see “Notes and Further Reading”).

In Laennec’s day, a physician often placed his ear directly on the patient’s chest or back. However, Laennec complained that this technique “is always inconvenient, both to the physician and the patient; in the case of females, it is not only indelicate but often impracticable.” Later, an extra-long stethoscope was used to treat the very poor when physicians wanted to be farther away from their flea-ridden patients. Aside from inventing the device, Laennec carefully recorded how specific physical diseases (e.g. pneumonia, tuberculosis, and bronchitis) corresponded to the sounds heard. Ironically, Laennec himself died at age 45 of tuberculosis, which his nephew diagnosed using a stethoscope.

full_image

Modern stethoscope. Various acoustic experiments have been conducted to determine the effect of chest-piece size and material on sound collection.

Fourier’s Law of Heat Conduction

1822

Jean Baptiste Joseph Fourier (1768-1830)

“Heat cannot be separated from fire, or beauty from the Eternal,” wrote Dante Alighieri. The nature of heat had also fascinated the French mathematician Joseph Fourier, well known for his formulas on the conduction of heat in solid materials. His Law of Heat Conduction suggests that the rate of heat flow between two points in a material is proportional to the difference in the temperatures of the points and inversely proportional to the distance between the two points.

If we place one end of an all-metal knife into a hot cup of cocoa, the temperature of the other end of the knife begins to rise. This heat transfer is caused by molecules at the hot end exchanging their kinetic and vibrational energies with adjacent regions of the knife through random motions. The rate of flow of energy, which might be thought of as a “heat current,” is proportional to the difference in temperatures at locations A and B, and inversely proportional to the distance between A and B. This means that the heat current is doubled if the temperature difference is doubled or if the length of the knife is halved.

If we let U be the conductance of the material—that is, the measure of the ability of a material to conduct heat—we may incorporate this variable into Fourier’s Law. Among the best thermal conductors, in order of thermal conductivity values, are diamond, carbon nanotubes, silver, copper, and gold. With the use of simple instruments, the high thermal conductivity of diamonds is sometimes employed to help experts distinguish real diamonds from fakes. Diamonds of any size are cool to the touch because of their high thermal conductivity, which may help explain why the word “ice” is often used when referring to diamonds.

Even though Fourier conducted foundational work on heat transfer, he was never good at regulating his own heat. He was always so cold, even in the summer, that he wore several large overcoats. During his last months, Fourier often spent his time in a box to support his weak body.

full_image

Raw copper ore. Copper is both an excellent thermal and electrical conductor.

full_image

The transfer of heat by various means plays a crucial role in the development of heat-sinks for computer chips. In this photo, the central object with a rectangular base is used to transfer heat away from the chip.

Olbers’ Paradox

1823

Heinrich Wilhelm Matthäus Olbers (1758–1840)

“Why is the sky dark at night?” In 1823, the German astronomer Heinrich Wilhelm Olbers presented a paper that discussed this question, and the problem subsequently became known as Olbers’ Paradox. Here is the puzzle. If the universe is infinite, as you follow a line of sight in any direction, that line must eventually intercept a star. This characteristic appears to imply that the night sky should be dazzlingly bright with starlight. Your first thought might be that the stars are far away and that their light dissipates as it travels such great distances. Starlight does dim as it travels, but by the square of the distance from the observer. However, the volume of the universe—and hence the total number of stars—would grow as the cube of the distance. Thus, even though the stars become dimmer the further away they are, this dimming is compensated by the increased number of stars. If we lived in an infinite visible universe, the night sky should indeed be very bright.

Here’s the solution to Olbers’ Paradox. We do not live in an infinite and static visible universe. The universe has a finite age and is expanding. Because only about 13.7 billion years have elapsed since the Big Bang, we can only observe stars out to a finite distance. This means that the number of stars that we can observe is finite. Because of the speed of light, there are portions of the universe we never see, and light from very distant stars has not had time to reach the Earth. Interestingly, the first person to suggest this resolution to Olbers’ Paradox was the writer Edgar Allan Poe.

Another factor to consider is that the expansion of the universe also acts to darken the night sky because starlight expands into a space that is ever more vast. Also, the Doppler Effect causes a red shift in the wavelengths of light emitted from the rapidly receding stars. Life as we know it would not have evolved without these factors because the night sky would have been extremely bright and hot.

full_image

If the universe is infinite, as you follow a line of sight in any direction, that line must eventually intercept a star. This characteristic appears to imply that the night sky should be dazzlingly bright with starlight.

Greenhouse Effect

1824

Joseph Fourier (1768–1830), Svante August Arrhenius (1859–1927), John Tyndall (1820–1893)

“Despite all its bad press,” write authors Joseph Gonzalez and Thomas Sherer, “the process known as the greenhouse effect is a very natural and necessary phenomenon…. The atmosphere contains gases that enable sunlight to pass through to the earth’s surface but hinder the escape of reradiated heat energy. Without this natural greenhouse effect, the earth would be much too cold to sustain life.” Or, as Carl Sagan once wrote, “A little greenhouse effect is a good thing.”

Generally speaking, the greenhouse effect is the heating of the surface of a planet as a result of atmospheric gases that absorb and emit infrared radiation, or heat energy. Some of the energy reradiated by the gases escapes into outer space; another portion is reradiated back toward the planet. Around 1824, mathematician Joseph Fourier wondered how the Earth stays sufficiently warm to support life. He proposed that although some heat does escape into space, the atmosphere acts a little like a translucent dome—a glass lid of a pot, perhaps—that absorbs some of the heat of the Sun and reradiates it downward to the Earth.

In 1863, British physicist and mountaineer John Tyndall reported on experiments that demonstrated that water vapor and carbon dioxide absorbed substantial amounts of heat. He concluded that water vapor and carbon dioxide must therefore play an important role in regulating the temperature at the Earth’s surface. In 1896, Swedish chemist Svante Arrhenius showed that carbon dioxide acts as a very strong “heat trap” and that halving the amount in the atmosphere might trigger an ice age. Today we use the term anthropogenic global warming to denote an enhanced greenhouse effect due to human contributions to greenhouse gases, such as the burning of fossil fuels.

Aside from water vapor and carbon dioxide, methane from cattle belching can also contribute to the greenhouse effect. “Cattle belching?” Thomas Friedman writes. “That’s right—the striking thing about greenhouse gases is the diversity of sources that emit them. A herd of cattle belching can be worse than a highway full of Hummers.”

full_image

“Coalbrookdale by Night” (1801), by Philip James de Loutherbourg (1740–1812), showing the Madeley Wood Furnaces, a common symbol of the early Industrial Revolution.

full_image

Large changes in manufacturing, mining, and other activities since the Industrial Revolution have increased the amount of greenhouse gases in the air. For example, steam engines, fuelled primarily by coal, helped to drive the Industrial Revolution.

Carnot Engine

1824

Nicolas Léonard Sadi Carnot (1796-1832)

Much of the initial work in thermodynamics—the study of the conversion of energy between work and heat—focused on the operation of engines and how fuel, such as coal, could be efficiently converted to useful work by an engine. Sadi Carnot is probably most often considered the “father” of thermodynamics, thanks to his 1824 work Réflexions sur la puissance motrice du feu (Reflections on the Motive Power of Fire).

Carnot worked tirelessly to understand heat flow in machines partly because he was disturbed that British steam engines seemed to be more efficient than French engines. During his day, steam engines usually burned wood or coal in order to convert water into steam. The high-pressure steam moved the pistons of the engine. When the steam was released through an exhaust port, the pistons returned to their original positions. A cool radiator converted the exhaust steam to water, so it could be heated again to steam in order to drive the pistons.

Carnot imagined an ideal engine, known today as the Carnot engine, that would theoretically have a work output equal to that of its heat input and not lose even a small amount of energy during the conversion. After experiments, Carnot realized that no device could perform in this ideal matter—some energy had to be lost to the environment. Energy in the form of heat could not be converted completely into mechanical energy. However, Carnot did help engine designers improve their engines so that the engines could work close to their peak efficiencies.

Carnot was interested in “cyclical devices” in which, at various parts of their cycles, the device absorbs or rejects heat; it is impossible to make such an engine that is 100 percent efficient. This impossibility is yet another way of stating the Second Law of Thermodynamics. Sadly, in 1832 Carnot contracted cholera and, by order of the health office, nearly all his books, papers, and other personal belongings had to be burned!

full_image

Sadi Carnot, by French photographer Pierre Petit (1832-1909).

full_image

Locomotive steam engine. Carnot worked to understand heat flow in machines, and his theories have relevance to this day. During his time, steam engines usually burned wood or coal.

Ampère’s Law of Electromagnetism

1825

André-Marie Ampère (1775-1836), Hans Christian Ørsted (1777-1851)

By 1825, French physicist André-Marie Ampère had established the foundation of electromagnetic theory. The connection between electricity and magnetism was largely unknown until 1820, when Danish physicist Hans Christian Ørsted discovered that a compass needle moves when an electric current is switched on or off in a nearby wire. Although not fully understood at the time, this simple demonstration suggested that electricity and magnetism were related phenomena, a finding that led to various applications of electromagnetism and eventually culminated in telegraphs, radios, TVs, and computers.

Subsequent experiments during a period from 1820 to 1825 by Ampère and others showed that any conductor that carries an electric current I produces a magnetic field around it. This basic finding, and its various consequences for conducting wires, is sometimes referred to as Ampère’s Law of Electromagnetism. For example, a current-carrying wire produces a magnetic field B that circles the wire. (The use of bold signifies a vector quantity.) B has a magnitude that is proportional to I, and points along the circumference of an imaginary circle of radius r centered on the axis of the long, straight wire. Ampère and others showed that electric currents attract small bits of iron, and Ampère proposed a theory that electric currents are the source of magnetism.

Readers who have experimented with electromagnets, which can be created by wrapping an insulated wire around a nail and connecting the ends of the wire to a battery, have experienced Ampère’s Law first hand. In short, Ampère’s Law expresses the relationship between the magnetic field and the electric current that produces it.

Additional connections between magnetism and electricity were demonstrated by the experiments of American scientist Joseph Henry (1797-1878), British scientist Michael Faraday (1791-1867), and James Clerk Maxwell. French physicists Jean-Baptiste Biot (1774-1862) and Félix Savart (1791-1841) also studied the relationship between electrical current in wires and magnetism. A religious man, Ampère believed that he had proven the existence of the soul and of God.

full_image

Engraving of André-Marie Ampère by A. Tardieu (1788-1841).

full_image

Electric motor with exposed rotor and coil. Electromagnets are widely used in motors, generators, loudspeakers, particle accelerators, and industrial lifting magnets.

Rogue Waves

1826

Jules Sébastien César Dumont d’Urville (1790–1842)

“From the time of the earliest civilizations,” writes marine physicist Susanne Lehner, “humankind has been fascinated with stories of giant waves—the ‘monsters’ of the seas… towers of water pounding down on a helpless boat. You can observe the wall of water coming… but you cannot run away and you cannot fight it…. Can we cope with [this nightmare] in the future? Predict extreme waves? Control them? Ride giant waves like surfers?”

It may seem surprising that in the twenty-first century, physicists do not have a complete understanding of the ocean surface, but the origin of rogue waves is not completely clear. In 1826, when French explorer and naval officer Captain Dumont d’Urville reported waves up to 98 feet (30 meters) in height—approximately the height of a 10-story building—he was ridiculed. However, after using satellite monitoring and many models that incorporate the relevant probability theory of wave distributions, we now know that waves this high are much more common than expected. Imagine the horrors of such a wall of water appearing without warning in mid-ocean, sometimes in clear weather, preceded by a trough so deep as to form a frightening “hole” in the ocean.

One theory is that ocean currents and seabed shapes act almost like optical lenses and focus wave actions. Perhaps high waves are generated by the superposition of crossing waves from two different storms. However, additional factors seem to play a role in creating such nonlinear wave effects that can produce the tall wall of water in a relatively calm sea. Before breaking, the rogue wave can have a crest four times higher than crests of neighbor waves. Many papers have been written that attempt to model formation of rogue waves using nonlinear Schrödinger equations. The effect of wind on the nonlinear evolution of waves has also been a productive area of research. Because rogue waves are responsible for the loss of ships and lives, scientists continue to search for ways to predict and avoid such waves.

full_image

Rogue waves can be terrifying, appearing without warning in mid-ocean, sometimes in clear weather, preceded by a trough so deep as to form a “hole” in the ocean. Rogue waves are responsible for the loss of ships and lives.

Ohm’s Law of Electricity

1827

Georg Ohm (1789-1854)

Although German physicist Georg Ohm discovered one of the most fundamental laws in the field of electricity, his work was ignored by his colleagues, and he lived in poverty for much of his life. His harsh critics called his work a “web of naked fancies.” Ohm’s Law of electricity states that the steady electric current I in a circuit is proportional to the constant voltage V (or total electromotive force) across a resistance and inversely proportional to the value R of the resistance: I = V/R.

Ohm’s experimental discovery of the law in 1827 suggested that the law held for a number of different materials. As made obvious from the equation, if the potential difference V (in units of volts) between the two ends of a wire is doubled, then the current I in amperes also doubles. For a given voltage, if the resistance doubles, the current is decreased by a factor of two.

Ohm’s Law has relevance in determining the dangers of electrical shocks on the human body. Generally, the higher the current flow, the more dangerous the shock is. The amount of current is equal to the voltage applied between two points on the body, divided by the electrical resistance of the body. Precisely how much voltage a person can experience and survive depends on the total resistance of the body, which varies from person to person and may depend on such parameters as body fat, fluid intake, skin sweatiness, and how and where contact is made with the skin.

Electrical resistance is used today to monitor corrosion and material loss in pipelines. For example, a net change in the resistance in a metal wall may be attributable to metal loss. A corrosion-detection device may be permanently installed to provide continuous information, or the device may be portable to gather information as needed. Note that without resistance, electric blankets, certain kettles, and Incandescent Light Bulbs would be useless.

full_image

Electric kettles rely on electrical resistance to create heat.

full_image

Circuit board with resistors (cylindrical objects with colored bands). The resistor has a voltage across its terminals that is proportional to the electric current passing through it, as given by Ohm’s Law. The colored bands indicate the resistance value.

Brownian Motion

1827

Robert Brown (1773–1858), Jean-Baptiste Perrin (1870–1942), Albert Einstein (1879–1955)

In 1827, Scottish botanist Robert Brown was using a microscope to study pollen grains suspended in water. Particles within the vacuoles of the pollen grains seemed to dance about in a random fashion. In 1905, Albert Einstein predicted the movement of such kinds of small particles by suggesting that they were constantly being buffeted by water molecules. At any instant in time, just by chance, more molecules would strike one side of the particle than another side, thereby causing the particle to momentarily move slightly in a particular direction. Using statistical rules, Einstein demonstrated that this Brownian motion could be explained by random fluctuations in such collisions. Moreover, from this motion, one could determine the dimensions of the hypothetical molecules that were bombarding the macroscopic particles.

In 1908, French physicist Jean-Baptiste Perrin confirmed Einstein’s explanation of Brownian motion. As a result of Einstein and Perrin’s work, physicists were finally compelled to accept the reality of atoms and molecules, a subject still ripe for debate even at the beginning of the twentieth century. In concluding his 1909 treatise on this subject, Perrin wrote, “I think that it will henceforth be difficult to defend by rational arguments a hostile attitude to molecular hypotheses.”

Brownian motion gives rise to diffusion of particles in various media and is so general a concept that it has wide applications in many fields, ranging from the dispersal of pollutants to the understanding of the relative sweetness of syrups on the surface of the tongue. Diffusion concepts help us understand the effect of pheromones on ants or the spread of muskrats in Europe following their accidental release in 1905. Diffusion laws have been used to model the concentration of smokestack contaminants and to simulate the displacement of hunter-gatherers by farmers in Neolithic times. Researchers have also used diffusion laws to study diffusion of radon in the open air and in soils contaminated with petroleum hydrocarbons.

full_image

Scientists used Brownian motion and diffusion concepts to model muskrat propagation. In 1905, five muskrats were introduced to Prague from the U.S. By 1914, their descendants had spread 90 miles in all directions. In 1927, they numbered over 100 million.

Graham’s Law of Effusion

1829

Thomas Graham (1805-1869)

Whenever I ponder Graham’s Law of Effusion, I cannot help but think of death and atomic weaponry. The law, named after Scottish scientist Thomas Graham, states that the rate of effusion of a gas is inversely proportional to the square root of the mass of its particles. This formula can be written as R₁/R₂ = (M₂/M₁)^1/2, where R₁ is the rate of effusion of gas 1, R₂ is the rate of effusion for gas 2, M₁ is the molar mass of gas 1, and M₂ is the molar mass of gas 2. This law works for both diffusion and effusion, the latter being a process in which individual molecules flow through very small holes without colliding with one another. The rate of effusion depends on the molecular weight of the gas. For example, gases like hydrogen with a low molecular weight effuse more quickly than heavier particles because the low-weight particles are generally moving at higher speeds.

Graham’s Law had a particularly ominous application in the 1940s when it was used in nuclear reactor technology to separate radioactive gases that had different diffusion rates due to the molecular weights of the gases. A long diffusion chamber was used to separate two isotopes of uranium, U-235 and U-238. These isotopes were allowed to chemically react with fluorine to produce the gas uranium hexafluoride. The less massive uranium hexafluoride molecules containing fissionable U-235 would travel down the chamber slightly faster than the more massive molecules containing the U-238.

During World War II, this separation process allowed the U.S. to develop an atomic bomb, which required the isolation of U-235 for the nuclear fission chain reaction. To separate U-235 and U-238, the government built a gaseous diffusion plant in Tennessee. The plant used diffusion through porous barriers and processed the uranium for the Manhattan Project, which yielded the atomic bomb dropped on Japan in 1945. In order to perform the isotope separation, the gaseous diffusion plant required 4,000 stages in a space that encompassed 43 acres.

full_image

Uranium ore.

full_image

K-52 gaseous diffusion site in Oak Ridge, Tennessee Manhattan Project. The main building was over half a mile long. (Photo taken by J. E. Westcott, official government photographer for the Manhattan Project.)

Faraday’s Laws of Induction

1831

Michael Faraday (1791-1867)

“Michael Faraday was born in the year that Mozart died,” Professor David Goodling writes. “Faraday’s achievement is a lot less accessible than Mozart’s [but …] Faraday’s contributions to modern life and culture are just as great…. His discoveries of … magnetic induction laid the foundations for modern electrical technology … and made a framework for unified field theories of electricity, magnetism, and light.”

English scientist Michael Faraday’s greatest discovery was that of electromagnetic induction. In 1831, he noticed that when he moved a magnet through a stationary coil of wire, he always produced an electric current in the wire. The induced electromotive force was equal to the rate of change of the magnetic flux. American scientist Joseph Henry (1797-1878) carried out similar experiments. Today, this induction phenomenon plays a crucial role in electric power plants.

Faraday also found that if he moved a wire loop near a stationary permanent magnet, a current flowed in the wire whenever it moved. When Faraday experimented with an electromagnet and caused the magnetic field surrounding the electromagnet to change, he then detected electric current flow in a nearby but separate wire.

Scottish physicist James Clerk Maxwell (1831-1879) later suggested that changing the magnetic flux produced an electric field that not only caused electrons to flow in a nearby wire, but that the field also existed in space—even in the absence of electric charges. Maxwell expressed the change in magnetic flux and its relation to the induced electromotive force (ε or emf) in what we call Faraday’s Law of Induction. The magnitude of the emf induced in a circuit is proportional to the rate of change of the magnetic flux impinging on the circuit.

Faraday believed that God sustained the universe and that he was doing God’s will to reveal truth through careful experiments and through his colleagues, who tested and built upon his results. He accepted every word of the Bible as literal truth, but meticulous experiments were essential in this world before any other kind of assertion could be accepted.

full_image

Photograph of Michael Faraday (c. 1861) by John Watkins (1823-1874).

full_image

A dynamo, or electrical generator, from G. W. de Tunzelmann’s Electricity in Modern Life, 1889. Power stations usually rely on a generator with rotating elements that convert mechanical energy into electrical energy through relative motions between a magnetic field and an electrical conductor.

Soliton

1834

John Scott Russell (1808–1882)

A soliton is a solitary wave that maintains its shape while it travels for long distances. The discovery of solitons is one of the most enjoyable tales of significant science arising from a casual observation. In August 1834, Scottish engineer John Scott Russell happened to be watching a horse-drawn barge move along a canal. When the cable broke and the barge suddenly stopped, Russell made a startling observation of a humplike water formation, which he described as follows: “a mass of water rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some 30 feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel.”

Russell subsequently performed experiments in a wave tank in his home to characterize these mysterious solitons (which he called a wave of translation), finding that the speed depends on the size of the soliton. Two solitons of different sizes (and hence velocities) can pass through each other, emerge, and continue their propagation. Soliton behavior has also been observed in other systems, such as plasmas and flowing sand. For example, barchan dunes, which involve arc-shaped sand ridges, have been seen “passing” through each other. The Great Red Spot of Jupiter may also be some kind of soliton.

Today, solitons are considered in a wide range of phenomena, ranging from nerve signal propagation to soliton-based communications in optical fibers. In 2008, the first known unchanging soliton in outer space was reported moving through the ionized gas surrounding the Earth at about 5 miles (8 kilometers) per second.

full_image

Barchan dunes on Mars. When two Earthly barchan ridges collide, they may form a compound ridge, and then reform their original shapes. (When one dune “crosses” another dune, sand particles do not actually travel through one another, but the ridge shapes may persist.)

Gauss and the Magnetic Monopole

1835

Carl Friedrich Gauss (1777-1855), Paul Dirac (1902-1984)

“One would think that monopoles should exist, because of the prettiness of the mathematics,” wrote British theoretical physicist Paul Dirac. Yet no physicist has ever found these strange particles. Gauss’ Law for Magnetism, named after German mathematician Carl Gauss, is one of the fundamental equations of electromagnetism and a formal way of stating that isolated magnetic poles (e.g. a magnet with a north pole and no south pole) do not exist. On the other hand, in electrostatics, isolated charges exist, and this lack of symmetry between electric and magnetic fields is a puzzle to scientists. In the 1900s, scientists often wondered precisely why it is possible to isolate positive and negative electric charges but not north and south magnetic poles.

In 1931, Paul Dirac was one of the first scientists to theorize about the possible existence of a magnetic monopole, and a number of efforts through the years have been made to detect magnetic monopole particles. However, thus far, physicists have never discovered an isolated magnetic pole. Note that if you were to cut a traditional magnet (with a north and south pole) in half, the resulting pieces are two magnets—each with its own north pole and south pole.

Some theories that seek to unify the electroweak and strong interactions in particle physics predict the existence of magnetic monopoles. However, if monopoles existed, they would be very difficult to produce using particle accelerators because the monopole would have a huge mass and energy (about 10¹⁶ giga-electron volts).

Gauss was often extremely secretive about his work. According to mathematical historian Eric Temple Bell, had Gauss published or revealed all of his discoveries when he made them, mathematics would have been advanced by fifty years. After Gauss proved a theorem, he sometimes said that the insight did not come from “painful effort but, so to speak, by the grace of God.”

full_image

Gauss on German postage stamp (1955).

full_image

Bar magnet, with north pole at one end and south pole at the other, along with iron filings showing the magnetic field pattern. Will physicists ever find a magnetic monopole particle?

Stellar Parallax

1838

Freidrich Wilhelm Bessel (1784–1846)

Humanity’s quest for determining the distance of stars from the Earth has had a long history. The Greek philosopher Aristotle and Polish astronomer Copernicus knew that if the Earth orbited our Sun, one would expect the stars to apparently shift back and forth each year. Unfortunately, Aristotle and Copernicus never observed the tiny parallaxes involved, and humans had to wait until the nineteenth century before parallaxes were actually discovered.

Stellar parallax refers to the apparent displacement of a star when viewed along two different lines of sight. Using simple geometry, this displacement angle can be used to determine the distance of the star to the observer. One way to calculate this distance is to determine the position of a star at a particular time of year. Half a year later, when the Earth has traveled halfway around the Sun, we again measure the star’s position. A nearby star will have appeared to move against the more distant stars. Stellar parallax is similar to effects you observe when closing one of your eyes. Look at your hand with one eye, then the other. Your hand seems to move. The larger the parallax angle, the closer the object is to your eye.

In the 1830s, there was an impassioned competition between astronomers to be the first person to accurately determine interstellar distances. It was not until 1838 that the first stellar parallax was measured. Using a telescope, German astronomer Freidrich Wilhelm Bessel studied the star 61 Cygni in the constellation of Cygnus the Swan. Cygni displayed significant apparent motion, and Bessel’s parallax calculations indicated that the star was 10.4 light-years (3.18 parsecs) away from the Earth. It is awe-inspiring that the early astronomers determined a way to compute vast interstellar distances without leaving the confines of their backyards.

Because the parallax angle is so small for stars, early astronomers could use this approach only for stars that are relatively close to the Earth. In modern times, astronomers have employed the European Hipparcos satellite to measure the distances of over 100,000 stars.

full_image

Researchers have measured parallaxes based on observations from NASA’s Spitzer Space Telescope and Earth-based telescopes to determine distances to objects that pass in front of stars in the Small Magellanic Cloud (upper left).

Fuel Cell

1839

William Robert Grove (1811-1896)

Some of you may recall the electrolysis of water performed in your high school chemistry class. An electrical current is applied between a pair of metal electrodes, which are immersed in the liquid, and hydrogen and oxygen gas are produced according to the chemical equation: electricity + 2H₂O (liquid) → 2H₂ (gas) + O₂ (gas). (In practice, pure water is a poor conductor of electricity, and one may add dilute sulfuric acid in order to establish a significant current flow.) The energy required to separate the ions is provided by an electrical power supply.

In 1839, lawyer and scientist William Grove created early fuel cells (FCs) by using a reverse process to produce electricity from hydrogen and oxygen in a fuel tank. Many combinations of fuels are possible. In a hydrogen FC, chemical reactions remove electrons from the hydrogen atoms, which creates hydrogen protons. The electrons travel through attached wires to provide a useful electrical current. Oxygen then combines with the electrons (which return from the electrical circuit) and hydrogen ions in the FC to produce water as a “waste product.” A hydrogen FC resembles a battery, but unlike a battery—which is eventually depleted and discarded or recharged—an FC can work indefinitely, as long as it has a supply of fuel in the form of oxygen from the air and hydrogen. A catalyst such as platinum is used to facilitate the reactions.

Some hope that FCs may one day be used more frequently in vehicles to replace the traditional combustion engine. However, obstacles to widespread use include cost, durability, temperature management, and hydrogen production and distribution. Nevertheless, FCs are very useful in backup systems and spacecraft; they were crucial in helping Americans travel to the moon. Benefits of FCs include zero carbon emissions and reduced dependence on oil.

Note that the hydrogen to power fuel cells is sometimes created by breaking down hydrocarbon-based fuels, which is counter to one desired goal of FCs: reducing greenhouse gases.

full_image

Photograph of a Direct Methanol Fuel Cell (DMFC), an electrochemical device that creates electricity using a methanol-water solution for fuel. The actual fuel cell is the layered cube shape toward the center of the image.

Poiseuille’s Law of Fluid Flow

1840

Jean Louis Marie Poiseuille (1797-1869)

Medical procedures for enlarging an occluded blood vessel can be very helpful because a small increase in the radius of a vessel can cause a dramatic improvement in blood flow. Here’s why. Poiseuille’s Law, named after French physician Jean Poiseuille, provides a precise mathematical relationship between the flow rate of a fluid in a pipe and the pipe width, fluid viscosity, and pressure change in the pipe. In particular, the law states that Q = [(πr⁴)/ (8μ)] × (ΔP/L). Here, Q is the fluid flow rate in the pipe, r is the internal radius of the pipe, full_image P is the pressure difference between two ends of the pipe, L is the pipe length, and μ is the viscosity of the fluid. The law assumes that the fluid under study is exhibiting laminar (i.e. smooth, non-turbulent) steady flow.

This principle has practical applications in medical fields; in particular, it applies to the study of flow in blood vessels. Note that the r⁴ term ensures that the radius of a tube plays a major role in determining the flow rate Q of the liquid. If all other parameters are the same, a doubling of the tube width leads to a sixteenfold increase in Q. Practically speaking, this means that we would need sixteen tubes to pass as much water as one tube twice their diameter. From a medical standpoint, Poiseuille’s Law can be used to show the dangers of atherosclerosis: If the radius of a coronary artery decreases twofold, the blood flow through it will decrease 16 times. It also explains why it is so much easier to sip a drink from a wide straw as compared to a slightly thinner straw. For the same amount of sipping effort, if you were to suck on a straw that is twice as wide, you would obtain 16 times as much liquid per unit time of sucking. When an enlarged prostate reduces the urethra’s radius, we can blame Poiseuille’s Law for why even a small constriction can have dramatic effects on the flow rate of urine.

full_image

Poiseuille’s Law explains why it so much more difficult to sip a drink using a narrow straw than a wider one.

full_image

Poiseuille’s Law can be used to show the dangers of atherosclerosis; for example, if the radius of an artery decreases twofold, the blood flow through it will decrease roughly sixteenfold.

Joule’s Law of Electric Heating

1840

James Prescott Joule (1818-1889)

Surgeons often rely on Joule’s Law of Electric Heating (named after British physicist James Joule), which states that the amount of heat H generated by a steady electric current flowing in a conductor may be calculated using H = K·R·I²·t. Here, R is the resistance of the conductor, I is the constant current flowing through the conductor, and t is the duration of current flow.

When electrons travel through a conductor with some resistance R, the electric kinetic energy that the electrons lose is transferred to the resistor as heat. A classical explanation of this heat production involves the lattice of atoms in a conductor. The collisions of the electrons with the lattice cause the amplitude of thermal vibration of the lattice to increase, thereby raising the temperature of the conductor. This process is known as Joule heating.

Joule’s Law and Joule heating play a role in modern electrosurgical techniques in which the heat at an electrical probe is determined by Joule’s Law. In such devices, current flows from an “active electrode” through the biological tissue to a neutral electrode. The ohmic resistance of the tissue is determined by the resistance of the area in contact with the active electrode (e.g. blood, muscle, or fatty tissue) and the resistance in the total path between the active and neutral electrode. In electrosurgery, the duration (t in Joule’s Law) is often controlled by a finger switch or foot pedal. The precise shape of the active electrode can be used to concentrate the heat so that it can be used for cutting (e.g., with a point-shaped electrode), or coagulation, which would result from diffuse heat that is produced by an electrode with a large surface area.

Today, Joule is also remembered for helping to establish that mechanical, electrical, and heat energy are all related and can be converted to one another. Thus, he provided experimental validations for many elements of the law of Conservation of Energy, also known as the First Law of Thermodynamics.

full_image

Photo of James Joule.

full_image

Joule’s Law and Joule heating play a role in modern liquid immersion heaters in which the heat is determined by Joule’s Law.

Anniversary Clock

1841

The first clocks had no minute hands, which gained importance only with the evolution of modern industrial societies. During the Industrial Revolution, trains began to run on schedules, factory work started and stopped at appointed times, and the tempo of life became more precise.

My favorite clocks are called torsion pendulum clocks, 400-day clocks, or anniversary clocks, because many versions only had to be wound once a year. I became intrigued with these clocks after reading about eccentric billionaire Howard Hughes, whose favorite room contained, according to biographer Richard Hack, “a world globe on a mahogany stand [and] a large fireplace on whose mantelpiece sat a French bronze 400-day clock that ‘was not to be over-wound for any reason’.”

The anniversary clock makes use of a weighted disk suspended on a thin wire or ribbon that functions as a torsion spring. The disk rotates back and forth around the vertical axis of the wire—a motion that replaces the swinging action of the traditional pendulum. Ordinary pendulum clocks date back at least to 1656, when Christiaan Huygens, inspired by drawings by Galileo, commissioned their construction. These clocks were more accurate than earlier clocks due to the nearly isochronous motion of the pendulum—the period of swing stays relatively constant, especially if the swings are small.

In the anniversary clock, the rotating disk winds and unwinds the spring slowly and efficiently, allowing the spring to continue powering the clock’s gears for long periods after a single initial winding. Early versions of the clock were not very accurate, partly because the spring force was temperature dependent. However, later versions made use of a spring that compensated for changes in temperature. The anniversary clock was patented by American inventor Aaron Crane in 1841. German clockmaker Anton Harder independently invented the clock around 1880. Anniversary clocks became popular wedding gifts at the end of World War II, when American soldiers brought them back to the United States.

full_image

Many versions of the anniversary clock only had to be wound about once a year. The anniversary clock makes use of a weighted disk suspended on a thin wire or ribbon that functions as a torsion spring.

Fiber Optics

1841

Jean-Daniel Colladon (1802–1893), Charles Kuen Kao (b. 1933), George Alfred Hockham (b. 1938)

The science of fiber optics has a long history, including such wonderful demonstrations as Swiss physicist Jean-Daniel Colladon’s light fountains in 1841, in which light traveled within an arcing stream of water from a tank. Modern fiber optics—discovered and independently refined many times through the 1900s—use flexible glass or plastic fibers to transmit light. In 1957, researchers patented the fiberoptic endoscope to allow physicians to view the upper part of the gastrointestinal tract. In 1966, electrical engineers Charles K. Kao and George A. Hockham suggested using fibers to transmit signals, in the form of light pulses, for telecommunications.

Through a process called total internal reflection (see entry on Snell’s Law), light is trapped within the fiber as a result of the higher refractive index of the core material of the fiber relative to that of the thin cladding that surrounds it. Once light enters the fiber’s core, it continually reflects off the core walls. The signal propagation can suffer some loss of intensity over very long distances, and thus it may be necessary to boost the light signals using optical regenerators. Today, optical fibers have many advantages over traditional copper wires for communications. Signals travel along relatively inexpensive and lightweight fibers with less attenuation, and they are not affected by electromagnetic interference. Also, fiber optics can be used for illumination or transferring images, thus allowing illumination or viewing of objects that are in tight, difficult-to-reach places.

In optical-fiber communications, each fiber can transmit many independent channels of information via different wavelengths of light. The signal may start as an electronic stream of bits that modulates lights from a tiny source, such as a light-emitting diode or laser diode. The resultant pulses of infrared light are then transmitted. In 1991, technologists developed photonic-crystal fibers that guide light by means of diffraction effects from a periodic structure such as an array of cylindrical holes that run through the fiber.

full_image

Optical fibers carry light along their lengths. Through a process called total internal reflection, light is trapped within the fiber until it reaches the end of the fiber.

Doppler Effect

1842

Christian Andreas Doppler (1803–1853), Christophorus Henricus Diedericus Buys Ballot (1817–1890)

“When a police officer zaps a car with a radar gun or a laser beam,” writes journalist Charles Seife, “he is really measuring how much the motion of the car is compressing the reflected radiation [via the Doppler Effect]. By measuring that squashing, he can figure out how fast the car is moving, and give the driver a $250 ticket. Isn’t science wonderful?”

The Doppler Effect, named after Austrian physicist Christian Doppler, refers to the change in frequency of a wave for an observer as the source of the wave moves relative to the observer. For example, if a car is moving while its horn is sounding, the frequency of the sound you hear is higher (compared to the actual emitted frequency) as the car approaches you, is identical at the instant that it passes you, and is lower as it moves away. Although we often think of the Doppler Effect with respect to sound, it applies to all waves, including light.

In 1845, Dutch meteorologist and physical chemist C. H. D. Buys Ballot performed one of the first experiments verifying Doppler’s idea for sound waves. In the experiment, a train carried trumpeters who played a constant note while other musicians listened on the side of the track. Using observers with “perfect pitch,” Buys Ballot thus proved the existence of the Doppler Effect, which he then reduced to a formula.

For many galaxies, their velocity away from us can be estimated from the red shift of a galaxy, which is an apparent increase in the wavelength (or decrease in frequency) of electromagnetic radiation received by an observer on the Earth compared to that emitted by the source. Such red shifts occur because galaxies are moving away from our own galaxy at high speeds as space expands. The change in the wavelength of light that results from the relative motion of the light source and the receiver is another example of the Doppler Effect.

full_image

Portrait of Christian Doppler, in the frontispiece to a reprint of his Über das farbige Licht der Doppelsterne (“Concerning the Colored Light of Double Stars”).

full_image

Imagine a sound or light source emitting a set of spherical waves. As the source moves right to left, an observer at left sees the waves as compressed. An approaching source is seen as blue-shifted (the wavelengths made shorter).

Conservation of Energy

1843

James Prescott Joule (1818-1889)

“The law of the conservation of energy offers … something to clutch at during those late-night moments of quiet terror, when you think of death and oblivion,” writes science-journalist Natalie Angier. “Your private sum of E, the energy in your atoms and the bonds between them, will not be annihilated…. The mass and energy of which you’re built will change form and location, but they will be here, in this loop of life and light, the permanent party that began with a Bang.”

Classically speaking, the principle of the conservation of energy states that the energy of interacting bodies may change forms but remains constant in a closed system. Energy takes many forms, including kinetic energy (energy of motion), potential energy (stored energy), chemical energy, and energy in the form of heat. Consider an archer who deforms, or strains, a bow. This potential energy of the bow is converted into kinetic energy of the arrow when the bow is released. The total energy of the bow and arrow, in principle, is the same before and after release. Similarly, chemical energy stored in a Battery can be converted into the kinetic energy of a turning motor. The gravitational potential energy of a falling ball is converted into kinetic energy as it falls. One key moment in the history of the conservation of energy was physicist James Joule’s 1843 discovery of how gravitational energy (lost by a falling weight that causes a water paddle to rotate) was equal to the thermal energy gained by water due to friction with the paddle. The First Law of Thermodynamics is often stated as: The increase in internal energy of a system due to heating is equal to the amount of energy added by heating, minus the work performed by the system on its surroundings.

Note that in our bow and arrow example, when the arrow hits the target, the kinetic energy is converted to heat. The Second Law of Thermodynamics limits the ways in which heat energy can be converted into work.

full_image

This potential energy of the strained bow is converted to kinetic energy of the arrow when the bow is released. When the arrow hits the target, the kinetic energy is converted to heat.

I-Beams

1844

Richard Turner (c. 1798–1881), Decimus Burton (1800–1881)

Have you ever wondered why so many steel girders used in construction have a cross-section shaped like the letter I? It turns out that this kind of beam is very efficient for resisting bending in response to a load applied perpendicular to the axis of the beam. For example, imagine a long I-beam supported on both ends, with a heavy elephant balancing in the middle. The upper layers of the beam will be compressed, and the bottom layers will be slightly lengthened, or stretched, by the tension force. Steel is expensive and heavy, so builders try to minimize the material used while preserving the structural strength. The I-beam is efficient and economical because more steel is placed in the top and bottom flanges, where its presence is most effective in resisting the bending. Steel I-beams may be formed by the rolling or extruding of steel, or by the creation of plate girders, which are formed by welding plates together. Note that other shapes are more effective than the I-beam if forces are applied side to side; the most efficient and economical shape for resisting bending in any direction is a hollow cylindrical shape.

Historic preservationist Charles Peterson writes of the importance of the I-beam: “The wrought-iron I-beam, perfected in the middle of the nineteenth century, was one of the great structural inventions of all time. The shape, first rolled in wrought-iron, was soon to be rolled in steel. When the Bessemer process made steel cheap, the I-beam came into use universally. It is the stuff of which skyscrapers and great bridges are made.”

Among the first-known I-beams introduced into buildings are the ones used in the Kew Gardens Palm House in London, built by Richard Turner and Decimus Burton between 1844 and 1848. In 1853, William Borrow of the Trenton Iron Company (TIC), in New Jersey approximated I-beams by bolting two component pieces back to back. In 1855, Peter Cooper, owner of TIC, rolled out I-beams from a single piece. This came to be known as the Cooper beam.

full_image

This massive I-beam was once part of the second sub-street level of the World Trade Center. It is now part of a 9/11 memorial at the California State Fair Memorial Plaza. These heavy beams were transported via railway from New York to Sacramento.

Kirchhoff’s Circuit Laws

1845

Gustav Robert Kirchhoff (1824–1887)

When Gustav Kirchhoff’s wife Clara died, the brilliant physicist was left alone to raise his four children. This task would have been difficult for any man, but it was made especially challenging by a foot injury that forced him to spend his life on crutches or in a wheelchair. Before the death of his wife, Kirchhoff became well known for his electrical circuit laws that focused on the relationships between currents at a circuit junction and the voltages around a circuit loop. Kirchhoff’s Current Law is a restatement of the principle of conservation of electrical charge in a system. In particular, at any point in an electrical circuit, the sum of currents flowing towards that point is equal to the sum of currents flowing away from that point. This law is often applied to the intersection of several wires to form a junction—i.e., junctions shaped like a + or a T—in which current travels toward the junction for some wires and away in other wires.

Kirchhoff’s Voltage Law is a restatement of the Conversation of Energy law for a system: The sums of the electrical potential differences around a circuit must be zero. Imagine that we have a circuit with junctions. If we start at any junction and follow a succession of circuit elements that form a closed path back to the starting point, the sum of the changes in potential encountered in the loop is equal to zero. (Elements include conductors, resistors, and batteries.) As an example, voltage rises may occur when we follow the circuit across a Battery (traversing from the − to + ends of a typical battery symbol in a circuit drawing). As we continue to trace the circuit in the same direction away from the battery, voltage drops may occur, for example, as a result of the presence of resistors in a circuit.

full_image

Gustav Kirchhoff.

full_image

Kirchhoff’s electrical circuit laws have been used by engineers for many decades to understand the relationships between currents and voltages in circuits, as represented by circuit diagrams such as in this noise reduction circuit diagram (U.S. Patent 3,818,362, 1974).

Discovery of Neptune

1846

John Couch Adams (1819–1892), Urbain Jean Joseph Le Verrier (1811–1877), Johann Gottfried Galle (1812–1910)

“The problem of tracking the planets with the highest precision is an immensely complex one,” writes astronomer James Kaler. “For two bodies, we have a beautifully simple set of rules. For just three bodies mutually pulling on one another, it is mathematically proven that no such rules exist…. The triumph of this mathematical science [called perturbation theory], and indeed of Newtonian mechanics itself, was in the discovery of Neptune.”

Neptune is the only planet in our Solar System whose existence and location was mathematically predicted before the planet was actually observed. Astronomers had noted that Uranus, discovered in 1781, exhibited certain irregularities in its orbit around the Sun. Astronomers wondered if perhaps this meant that Newton’s Laws did not apply far out in the Solar System, or that perhaps a large unseen object was perturbing the orbit of Uranus. French astronomer Urbain Le Verrier and British astronomer John Couch Adams both performed calculations to locate a possible new planet. In 1846, Le Verrier told German astronomer Johann Galle where to point Galle’s telescope based on Le Verrier’s calculations, and in about half an hour Galle found Neptune within one degree of the predicted position—a dramatic confirmation of Newton’s Law of Universal Gravitation. Galle wrote to Le Verrier on September 25, “Monsieur, the planet of which you indicated the position really exists.” Le Verrier replied, “I thank you for the alacrity with which you applied my instructions. We are thereby, thanks to you, definitely in possession of a new world.”

British scientists argued that Adams had also discovered Neptune at the same time, and a dispute arose as to whom was the true discoverer of the planet. Interestingly, for centuries, a number of astronomers before Adams and Le Verrier had observed Neptune but simply thought it to be a star rather than a planet.

Neptune is invisible to the naked eye. It orbits the Sun once every 164.7 years and has the fastest winds of any planet in our solar system.

full_image

Neptune, the eighth planet from the Sun, and its moon Proteus. Neptune has 13 known moons, and its equatorial radius is nearly four times that of the Earth’s.

Second Law of Thermodynamics

1850

Rudolf Clausius (1822–1888), Ludwig Boltzmann (1844–1906)

Whenever I see my sand castles on the beach fall apart, I think of the Second Law of Thermodynamics (SLT). The SLT, in one of its early formulations, states that the total entropy, or disorder, of an isolated system tends to increase as it approaches a maximum value. For a closed thermodynamic system, entropy can be thought of as a measure of the amount of thermal energy unavailable to do work. German physicist Rudolf Clausius stated the First and Second Laws of Thermodynamics in the following form: The energy of the universe is constant, and the entropy of the universe tends to a maximum.

Thermodynamics is the study of heat, and more generally the study of transformations of energy. The SLT implies that all energy in the universe tends to evolve toward a state of uniform distribution. We also indirectly invoke the SLT when we consider that a house, body, or car—without maintenance—deteriorates over time. Or, as novelist William Somerset Maugham wrote, “It’s no use crying over spilt milk, because all of the forces of the universe were bent on spilling it.”

Early in his career, Clausius stated, “Heat does not transfer spontaneously from a cool body to a hotter body.” Austrian physicist Ludwig Boltzmann expanded upon the definition for entropy and the SLT when he interpreted entropy as a measure of the disorder of a system due to the thermal motion of molecules.

From another perspective, the SLT says that two adjacent systems in contact with each other tend to equalize their temperatures, pressures, and densities. For example, when a hot piece of metal is lowered into a tank of cool water, the metal cools and the water warms until each is at the same temperature. An isolated system that is finally at equilibrium can do no useful work without energy applied from outside the system, which helps explain how the SLT prevents us from building many classes of Perpetual Motion Machines.

full_image

Rudolph Clausius.

full_image

Microbes build their “improbable structures” from ambient disordered materials, but they do this at the expense of increasing the entropy around them. The overall entropy of closed systems increases, but the entropy of individual components of a closed system may decrease.

Ice Slipperiness

1850

Michael Faraday (1791–1867), Gabor A. Somorjai (b. 1935)

“Black ice” generally refers to clear water that has frozen on dark roadways and which poses a particular danger to motorists who are often unable to see it. Interestingly, black ice sometimes forms without the presence of rain, snow, or sleet, because condensation from dew, mist, and fog on roadways can freeze. The frozen water of black ice is transparent because relatively few air bubbles are trapped in the ice.

Over the centuries, scientists have wondered why black ice, or any form of ice, is slippery. On June 7, 1850, English scientist Michael Faraday suggested to the Royal Institution that ice has a hidden layer of liquid water on its surface, which makes the surface slippery. To test his hypotheses, he simply pressed two ice cubes together and they stuck. He then argued that these extremely thin liquid layers froze when they were no longer at the surface.

Why are ice skaters able to skate on ice? For many years, the textbook answer was that the skate blades exerted a pressure that lowers the melting temperature of the ice, thus causing a thin layer of water to form. Although this answer is no longer believed to be valid, the friction between the skate blade and the ice may generate heat and cause some liquid water to temporarily form. Another recent explanation suggests that the water molecules on the surface vibrate more because no water molecules exist on top of them. This creates a very thin layer of liquid water on the surface, even if the temperature is below the freezing point of water. In 1996, chemist Gabor Somorjai used low-energy electron diffraction methods to prove that a thin layer of liquid water exists at the surface of ice. Faraday’s 1850 theory seems to be vindicated. Today, scientists are not quite sure whether this intrinsic layer of liquid water or the liquid water caused by friction plays a greater role in the slipperiness of ice.

full_image

Molecular structure of ice crystal.

full_image

Why are ice skaters able to skate on ice? Due to molecular vibrations, a very thin layer of liquid water exists on the surface, even if the temperature is below the freezing point of water.

Foucault’s Pendulum

1851

Jean Bernard Léon Foucault (1819–1868)

“The motion of the pendulum is not due to any transcendental or mysterious forces from without,” writes author Harold T. Davis, “but is due simply to the fact that the earth turns under the swinging weight. And yet perhaps the explanation is not so simple since the experiment was performed for the first time in 1851 by Jean Foucault. Simple facts have not usually remained undiscovered for so many years…. The principle for which Bruno died and for which Galileo suffered was vindicated. The earth moved!”

In 1851, French physicist Léon Foucault (pronounced “Foo-koh”) demonstrated his experiment in the Panthéon, a neoclassical domed building in Paris. An iron ball the size of a pumpkin swung from 220 feet (67 meters) of steel wire. As the pendulum swung, its direction of motions gradually changed, rotating clockwise at a rate of 11 degrees per hour, thus proving that the Earth rotated. To visualize this proof, let us imagine transporting the Panthéon to the North Pole. Once the pendulum is swinging, its plane of oscillation is independent of the Earth’s movement, and the Earth simply rotates beneath it. Thus, at the North Pole, the pendulum’s plane of oscillation rotates clockwise through 360 degrees every 24 hours. The rate at which the pendulum’s plane of oscillation rotates depends on its latitude: At the equator, it does not change at all. At Paris, the pendulum makes a full circle in roughly 32.7 hours.

Of course, by 1851, scientists knew that the Earth rotated, but Foucault’s pendulum provided dramatic and dynamic evidence for such rotation in an easily interpreted fashion. Foucault described his pendulum: “The phenomenon develops calmly, but it is inevitable, unstoppable…. Any person, brought into the presence of this fact, stops for a few moments and remains pensive and silent; and then generally leaves, carrying with him forever a sharper, keener sense of our incessant motion through space.”

Early in his life, Foucault studied medicine, a field that he left for physics when he discovered his fear of blood.

full_image

Foucault’s pendulum in the Panthéon, Paris.

Stokes’ Law of Viscosity

1851

George Gabriel Stokes (1819-1903)

Whenever I think of Stokes’ Law, I think of shampoo. Consider a solid sphere of radius r moving with a velocity v through a fluid of viscosity µ. Irish physicist George Stokes determined that the frictional force F that resists the motion of the sphere can be determined with the equation F = 6πrµv. Note that this drag force F is directly proportional to the sphere radius. This was not intuitively obvious because some researchers supposed that the frictional force would be proportional to the cross-section area, which erroneously suggests an r² dependence.

Consider a scenario in which a particle in a fluid is subject to the forces of gravity. For example, some older readers may recall the popular Prell shampoo TV commercial that shows a pearl dropping through a container of the green shampoo. The pearl starts off with zero speed and then initially accelerates, but the motion of the pearl quickly generates a frictional resistance counter to the acceleration. Thus, the pearl rapidly reaches a condition of zero acceleration (Terminal Velocity) when the force of gravity is balanced by the force of friction.

Stokes’ Law is considered in industry when studying sedimentation that occurs during the separation of a suspension of solid particles in a liquid. In these applications, scientists are often interested in the resistance exerted by the liquid to the motion of the descending particle. For example, a sedimentation process is sometimes used in the food industry for separating dirt and debris from useful materials, separating crystals from the liquid in which they are suspended, or separating dust from air streams. Researchers use the law to study aerosol particles in order to optimize drug delivery to the lungs.

In the late 1990s, Stokes’ Law was used to provide a possible explanation of how micrometer-sized uranium particles can remain airborne for many hours and traverse great distances—and thus possibly have contaminated Persian Gulf War soldiers. Cannon rounds often contained depleted-uranium penetrators, and this uranium becomes aerosolized when the rounds impact hard targets, such as tanks.

full_image

George Stokes.

full_image

Informally, viscosity is related to the fluid’s “thickness” and resistance to flow. Honey, for example, has a higher viscosity than water. Viscosity varies with temperature, and honey flows more readily when heated.

Gyroscope

1852

Jean Bernard Léon Foucault (1819–1868), Johann Gottlieb Friedrich von Bohnenberger (1765–1831)

According to the 1897 Every Boy’s Book of Sport and Pastime, “The gyroscope has been called the paradox of mechanics: when the disk is not spinning, the apparatus is an inert mass; but with the disc in rapid rotation, it seems to set gravity at defiance, or when held in the hand, a peculiar sensation is felt by the tendency of the thing to move some other way to that in which you wish to turn it, as if it were something alive.”

In 1852, the term gyroscope was first used by Léon Foucault, the French physicist who conducted many experiments with the device and who is sometimes credited with its invention. In fact, German mathematician Johann Bohnenberger invented the device using a rotating sphere. A mechanical gyroscope is traditionally in the form of a heavy spinning disc suspended within supporting rings called gimbals. When the disc spins, the gyroscope exhibits amazing stability and maintains the direction of the axis of rotation thanks to the principle of conservation of angular momentum. (The direction of the angular momentum vector of a spinning object is parallel to the axis of spin.) As an example, imagine that the gyroscope is pointed toward a particular direction and set spinning within a gimbal mount. The gimbals will reorient, but the axis of the wheel maintains the same position in space, no matter how the frame is moved. Because of this property, gyroscopes are sometime used for navigational purposes when magnetic compasses would be ineffective (in the Hubble Telescope, for example) or when they would be insufficiently precise, as in intercontinental ballistic missiles. Airplanes have several gyroscopes associated with navigational systems. The gyroscope’s resistance to external motion also makes it useful aboard spacecraft to help them maintain a desired direction. This tendency to continue to point in a particular direction is also found in spinning tops, the wheels of bicycles, and even the rotation of the Earth.

full_image

Gyroscope invented by Léon Foucault and built by Dumoulin-Froment, 1852. Photo taken at National Conservatory of Arts and Crafts museum, Paris.

Stokes’ Fluorescence

1852

George Gabriel Stokes (1819-1903)

As a child, I collected green fluorescent minerals that reminded me of the Land of Oz. Fluorescence usually refers to the glow of an object caused by visible light that is emitted when the object is stimulated via electromagnetic radiation. In 1852, physicist George Stokes observed phenomena that behaved according to Stokes’ Law of Fluorescence, which states that the wavelength of emitted fluorescent light is always greater than the wavelength of the exciting radiation. Stokes published his finding in his 1852 treatise “On the Change of Refrangibility of Light.” Today, we sometimes refer to the reemission of longer wavelength (lower frequency) photons by an atom that has absorbed photons of shorter wavelengths (higher frequency) as Stokes’ fluorescence. The precise details of the process depend on the characteristics of a particular atom involved. Light is generally absorbed by atoms in about 10⁻¹⁵ seconds, and this absorption causes electrons to become excited and jump to a higher energy state. The electrons remain in the excited state for about 10⁻⁸ seconds, and then the electron may emit energy as it returns to the ground state. The phrase Stokes’ shift usually refers to the difference in wavelength or frequency between absorbed and emitted quanta.

Stokes coined the term fluorescence after fluorite, a strongly fluorescent mineral. He was the first to adequately explain the phenomenon in which fluorescence can be induced in some materials through stimulation with ultraviolet (UV) light. Today, we know that these kinds of materials can be made to fluoresce by stimulation with numerous forms of electromagnetic radiation, including visible light, infrared radiation, X-rays, and radio waves.

Applications of fluorescence are many and varied. An electrical discharge in a fluorescent light causes the mercury atoms to emit ultraviolet light, which is then absorbed by a fluorescent material coating the tube that reemits visible light. In biology, fluorescent dyes are used as labels for tracking molecules. Phosphorescent materials do not re-emit the absorbed radiation as quickly as fluorescent materials.

full_image

Compact fluorescent light.

full_image

Collection of various fluorescent minerals under UV-A, UV-B, and UV-C light. Photo has been rotated to better fit the space.

Buys-Ballot’s Weather Law

1857

Christophorus Henricus Diedericus Buys Ballot (1817–1890)

You can impress your friends, as I do, by going outside into windy weather with the apparently mystical ability of being able to point toward the direction of lower pressure. Buys-Ballot’s Law, named after Dutch meteorologist Christoph Buys Ballot, asserts that in the Northern Hemisphere, if a person stands with his back to the wind, the low pressure area will be to his left. This means that wind travels counterclockwise around low pressure zones in the Northern Hemisphere. (In the Southern Hemisphere, wind travels clockwise.) The law also states that the wind and the pressure gradient are at right angles if measured sufficiently far above the surface of the Earth in order to avoid frictional effects between the air and the Earth’s surface.

The weather patterns of the Earth are affected by several planetary features such as the Earth’s roughly spherical shape and the Coriolis Effect, which is the tendency for any moving body on or above the surface of the Earth, such as an ocean current, to drift sideways from its course due to the rotation of the Earth. Air that is closer to the equator is generally traveling faster than air farther away because equatorial air is farther from the Earth’s axis of rotation. To help visualize this, consider that air farther from the axis must travel faster in a day than air at higher latitudes, which are closer to the axis of the Earth. Thus, if a low pressure system in the north exists, it will draw air from the south that can move faster than the ground below it because the more northerly part of the Earth’s surface has a slower eastward motion than the southerly surface. This means that the air from the south will move east as a result of its higher speed. The net effect of air movement from north and south is a counterclockwise swirl around a low pressure area in the Northern Hemisphere.

full_image

Christophorus Buys Ballot.

full_image

Hurricane Katrina, August 28, 2005. Buys-Ballot’s Law can be used on the ground by people trying to determine the approximate location of the center and direction of travel of a hurricane.

Kinetic Theory

1859

James Clerk Maxwell (1831–1879), Ludwig Eduard Boltzmann (1844–1906)

Imagine a thin plastic bag filled with buzzing bees, all bouncing randomly against one another and the surface of the bag. As the bees bounce around with greater velocity, their hard bodies impact the wall with greater force, causing it to expand. The bees are a metaphor for atoms or molecules in a gas. The kinetic theory of gases attempts to explain the macroscopic properties of gases—such as pressure, volume, and temperature—in terms of the constant movements of such particles.

According to kinetic theory, temperature depends on the speed of the particles in a container, and pressure results from the collisions of the particles with the walls of the container. The simplest version of kinetic theory is most accurate when certain assumptions are fulfilled. For example, the gas should be composed of a large number of small, identical particles moving in random directions. The particles should experience elastic collisions with themselves and the container walls but have no other kinds of forces among them. Also, the average separation between particles should be large.

Around 1859, physicist James Clerk Maxwell developed a statistical treatment to express the range of velocities of gas particles in a container as a function of temperature. For example, molecules in a gas will increase speed as the temperature rises. Maxwell also considered how the viscosity and diffusion of a gas depend on the characteristics of the molecules’ motion. Physicist Ludwig Boltzmann generalized Maxwell’s theory in 1868, resulting in the Maxwell-Boltzmann distribution law, which describes a probability distribution of particle speeds as a function of temperature. Interestingly, scientists still debated the existence of atoms at this time.

We see the kinetic theory in action in our daily lives. For example, when we inflate a tire or balloon, we add more air molecules to the enclosed space, which results in more collisions of the molecules on the inside of the enclosed space than there are on the outside. As a result, the enclosure expands.

full_image

According to kinetic theory, when we blow a soap bubble, we add more air molecules to the enclosed space, leading to more molecular collisions on the bubble’s inside than on the outside, causing the bubble to expand.

Maxwell’s Equations

1861

James Clerk Maxwell (1831-1879)

“From a long view of the history of mankind,” writes physicist Richard Feynman, “seen from, say, ten thousand years from now—there can be no doubt that the most significant event of the 19th century will be judged as Maxwell’s discovery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade.”

In general, Maxwell’s Equations are the set of four famous formulas that describe the behavior of the electric and magnetic fields. In particular, they express how electric charges produce electric fields and the fact that magnetic charges cannot exist. They also show how currents produce magnetic fields and how changing magnetic fields produce electric fields. If you let E represent the electric field, B represent the magnetic field, ε₀ represent the electric constant, μ₀ represent the magnetic constant, and J represent the current density, you can express Maxwell’s equations thus:

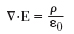		Gauss’ Law for Electricity
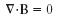		Gauss’ Law for Magnetism (no magnetic monopoles)
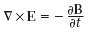		Faraday’s Law of Induction
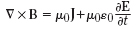		Ampère’s Law with Maxwell’s extension

Note the utter compactness of expression, which led Einstein to rate Maxwell’s achievement on a par with that of Isaac Newton’s. Moreover, the equations predicted the existence of electromagnetic waves.

Philosopher Robert P. Crease writes of the importance of Maxwell’s equations: “Although Maxwell’s equations are relatively simple, they daringly reorganize our perception of nature, unifying electricity and magnetism and linking geometry, topology and physics. They are essential to understanding the surrounding world. And as the first field equations, they not only showed scientists a new way of approaching physics but also took them on the first step towards a unification of the fundamental forces of nature.”

full_image

Mr. and Mrs. James Clerk Maxwell, 1869.

full_image

Computer core memory of the 1960s can be partly understood using Ampere’s Law in Maxwell’s Equations, which describes how a current-carrying wire produces a magnetic field that circles the wire and, thus, can cause the core (doughnut shape) to change its magnetic polarity.

Electromagnetic Spectrum

1864

Frederick William Herschel (1738-1822), Johann Wilhelm Ritter (1776-1810), James Clerk Maxwell (1831-1879), Heinrich Rudolf Hertz (1857-1894)

The electromagnetic spectrum refers to the vast range of frequencies of electromagnetic (EM) radiation. It is composed of waves of energy that can propagate through a vacuum and that contain electric and magnetic field components that oscillate perpendicular to each other. Different portions of the spectrum are identified according to the frequency of the waves. In order of increasing frequency (and decreasing wavelength), we have radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.

We can see light with wavelengths between 4,000 and 7,000 angstroms, where an angstrom is equal to 10⁻¹⁰ meters. Radio waves may be generated by electrons that move back and forth in transmission towers and have wavelengths ranging from several feet to many miles. If we represent the electromagnetic spectrum as a 30-octave piano, in which the wavelength of radiation doubles with each octave, visible light occupies only part of an octave. If we wanted to represent the entire spectrum of radiation that has been detected by our instruments, we would need to add at least 20 octaves to the piano.

Extraterrestrials may have senses beyond our own. Even on the Earth, we find examples of creatures with increased sensitivities. For example, rattlesnakes have infrared detectors that give them “heat pictures” of their surroundings. To our eyes, both the male and female Indian luna moths are light green and indistinguishable from each other, but the luna moths themselves perceive the ultraviolet range of light. Therefore, to them, the female looks quite different from the male. Other creatures have difficulty seeing the moths when they rest on green leaves, but luna moths are not camouflaged to one another; rather, they see each other as brilliantly colored. Bees can also detect ultraviolet light. In fact, many flowers have beautiful patterns that bees can see to guide them to the flower. These attractive and intricate patterns are totally hidden from human perception.

The physicists listed at the top of this entry played key research roles with respect to the electromagnetic spectrum.

full_image

To our eyes, male and female luna moths are light green and indistinguishable from each other. But the luna moths themselves perceive in the ultraviolet range of light, and to them the female looks quite different from the male.

Surface Tension

1866

Loránd von Eötvös (1848-1919)

The physicist Loránd Eötvös once wrote, “Poets can penetrate deeper into the realm of secrets than scientists,” yet Eötvös used the tools of science to understand the intricacies of surface tension, which plays a role in numerous aspects of nature. At the surface of a liquid, the molecules are pulled inward by intermolecular forces. Eötvös determined an interesting relationship between the surface tension of a liquid and the temperature of a liquid: full_image . Here, the surface tension of a liquid is related to its temperature T, the critical temperature of the liquid (T₀), and its density ρ. The constant k is approximately the same for many common liquids, including water. T₀ is the temperature at which the surface tension disappears or becomes zero.

The term surface tension usually refers to a property of liquids that arises from unbalanced molecular forces at or near the surface of a liquid. As a result of these attractive forces, the surface tends to contract and exhibits properties similar to those of a stretched elastic membrane. Interestingly, the surface tension, which may be considered a molecular surface energy, changes in response to temperature essentially in a manner that is independent of the nature of the liquid.

During his experiments, Eötvös had to take special care that the surface of his fluids had no contamination of any kind, so he worked with glass vessels that had been closed by melting. He also used optical methods for determining the surface tension. These sensitive methods were based on optical reflection in order to characterize the local geometry of the liquid surface.

Water strider insects can walk on water because the surface tension causes the surface to behave like an elastic membrane. In 2007, Carnegie Mellon University researchers created robotic striders and found that “optimal” robotic wire legs coated with Teflon were about 2 inches (5 centimeters) long. Furthermore, twelve legs attached to the 0.03-ounce (1-gram) body can support up to 0.3 ounces (9.3 grams).

full_image

Water strider.

full_image

Photograph of two red paper clips floating on water, with projected colored stripes indicating water surface contours. Surface tension prevents the paper clips from submerging.

Dynamite

1866

Alfred Bernhard Nobel (1833–1896)

“Humanity’s quest to harness the destructive capacity of fire is a saga that extends back to the dawn of civilization,” writes author Stephen Bown. “Although gunpowder did bring about social change, toppling feudalism and ushering in a new military structure …, the true great era of explosives, when they radically and irrevocably changed the world, began in the 1860s with the remarkable intuition of a sallow Swedish chemist named Alfred Nobel.”

Nitroglycerin had been invented around 1846 and was a powerful explosive that could easily detonate and cause loss of life. In fact, Nobel’s own Swedish factory for manufacturing nitroglycerin exploded in 1864, killing five people, including his younger brother Emil. The Swedish government prohibited Nobel from rebuilding his factory. In 1866, Nobel discovered that by mixing nitroglycerin with a kind of mud composed of finely ground rock known as kieselguhr (and sometimes referred to as diatomaceous earth), he could create an explosive material that had much greater stability than nitroglycerine. Nobel patented the material a year later, calling it dynamite. Dynamite has been used primarily in mining and construction industries, but it has also been used in war. Consider the many British soldiers based in Gallipoli during World War I who made bombs out of jam tins (literally, cans that had contained jam) packed with dynamite and pieces of scrap metal. A fuse was used for detonation.

Nobel never intended for his material to be used in war. In fact, his main goal was to make nitroglycerin safer. A pacifist, he believed that dynamite could end wars quickly, or that the power of dynamite would make war unthinkable—too horrifying to carry out.

Today, Nobel is famous for his founding of the Nobel Prize. The Bookrags staff write, “Many have observed the irony in the fact that he left his multimillion dollar fortune, made by the patenting and manufacture of dynamite and other inventions, to establish prizes awarded ‘to those, who during the preceding year, shall have conferred the greatest benefit on mankind’.”

SEE ALSO Little Boy Atomic Bomb (1945).

full_image

Dynamite is sometimes used in open-pit mining. Open-pit mines that produce building materials and related stones are often referred to as quarries.

Maxwell’s Demon

1867

James Clerk Maxwell (1831–1879), Léon Nicolas Brillouin (1889–1969)

“Maxwell’s demon is no more than a simple idea,” write physicists Harvey Leff and Andrew Rex. “Yet it has challenged some of the best scientific minds, and its extensive literature spans thermodynamics, statistical physics, quantum mechanics, information theory, cybernetics, the limits of computing, biological sciences, and the history and philosophy of science.”

Maxwell’s demon is a hypothetical intelligent entity—first envisioned by Scottish physicist James Clerk Maxwell—that has been used to suggest that the Second Law of Thermodynamics might be violated. In one of its early formulations, this law states that the total entropy, or disorder, of an isolated system tends to increase over time as it approaches a maximum value. Moreover, it maintains that heat does not naturally flow from a cool body to a warmer body.

To visualize Maxwell’s demon, imagine two vessels, A and B, connected by a small hole and containing gas at equal temperatures. Maxwell’s demon could, in principle, open and close this hole to allow individual gas molecules to pass between the vessels. Additionally, the demon allows only fast-moving molecules to pass from vessel A to B, and only slow-moving molecules to go from B to A. In doing so, the demon creates greater kinetic energy (and heat) in B, which could be used as a source of power for devices. This appears to provide a loophole in the Second Law of Thermodynamics. The little creature—whether alive or mere machine—exploits the random, statistical features of molecular motions to decrease entropy. If some mad scientist could create such an entity, the world would have an endless source of energy.

One “solution” to the problem of Maxwell’s demon came from French physicist Léon Brillouin around 1950. Brillouin and others banished the demon by showing that the decrease in entropy resulting from the demon’s careful observations and actions would be exceeded by the increase in entropy needed to actually choose between the slow and fast molecules. The demon requires energy to operate.

full_image

Maxwell’s Demon is able to segregate collections of hot and cold particles, depicted here in red and blue colors. Could Maxwell’s Demon provide us with an endless source of energy?

full_image

Artistic depiction of Maxwell’s Demon, allowing fast-moving molecules (orange) to accumulate in one region and slow-moving molecules (blue-green) in another.

Discovery of Helium

1868

Pierre Jules César Janssen (1824–1907), Joseph Norman Lockyer (1836–1920), William Ramsay (1852–1916)

“It may seem surprising now,” write authors David and Richard Garfinkle, “when helium-filled balloons are at every child’s birthday party, but [in 1868] helium was a mystery in much the same way dark matter is today. Here was a substance that had never been seen on the Earth, was only seen in the Sun, and was only known indirectly through the presence of its spectral line.”

Indeed, the discovery of helium is notable because it represents the first example of a chemical element discovered on an extraterrestrial body before being found on the Earth. Even though helium is abundant in the universe, it was completely unknown for most of human history.

Helium is inert, colorless, and odorless and has boiling and melting points that are the lowest among all elements. After hydrogen, it is the second most abundant element in the universe, making up about 24 percent of the galactic stellar mass. Helium was discovered in 1868 by astronomers Pierre Janssen and Norman Lockyer after observing an unknown spectral line signature in sunlight. However, it wasn’t until 1895 that British chemist Sir William Ramsay discovered helium on the Earth in a radioactive, uranium-rich mineral. In 1903, large reservoirs of helium were found in U.S. natural gas fields.

Because of its extremely low boiling temperature, liquid helium is the standard coolant for superconducting magnets used in MRI (magnetic resonance imaging) devices and particle accelerators. At very low temperatures, liquid helium exhibits the peculiar properties of a Superfluid. Helium is also important for deep-sea divers (to prevent too much oxygen from entering the brain) and for welders (to reduce oxidation during the application of high temperatures). It is also used for rocket launches, lasers, weather balloons, and leak detection.

Most helium in the universe is the helium-4 isotope—containing two protons, two neutrons, and two electrons—formed during the Big Bang. A smaller portion is formed in stars through nuclear fusion of hydrogen. Helium is relatively rare above ground on the Earth because, as demonstrated by an untethered helium-filled balloon that rises into the atmosphere, it is so light that most has escaped into space.

full_image

USS Shenandoah (ZR-1), flying in the vicinity of New York City, c. 1923. The Shenandoah is notable in that it was the first rigid airship to use helium gas rather than flammable hydrogen gas.

Baseball Curveball

1870

Fredrick Ernest Goldsmith (1856–1939), Heinrich Gustav Magnus (1802–1870)

Robert Adair, author of The Physics of Baseball, writes, “The pitcher’s action up to the release of the ball is part of the art of pitching; the action of the ball after release … is addressed by physics.” For years, arguments raged in popular magazines as to whether the curveballs pitched in baseball really curved, or whether they were simply some kind of optical illusion.

While it may be impossible to definitively say which baseball player first developed the curveball, professional pitcher Fred Goldsmith is often credited with giving the first publicly recorded demonstration of a curveball on August 16, 1870, in Brooklyn, New York. Many years later, research into the physics of curveballs showed that, for example, when a topspin was placed on the ball—so that the top of the ball rotated in the direction of the pitch—a significant deviation from the ball’s ordinary course of travel took place. In particular, a layer of air rotates with the ball, like a whirlpool, and the air layer near the bottom of the ball travels faster than near the top—the top of the whirlpool travels against the direction of ball travel. According to Bernoulli’s principle, when air or liquid flows, it creates a region of low air pressure that is related to the flow velocity (see Bernoulli’s Law of Fluid Dynamics). This pressure difference between the top and the bottom of the ball causes it to have a curving trajectory, dropping as it nears the batter. This drop or “break” may be a deviation of as many as 20 inches off the course of a ball that has no spin. German physicist Heinrich Magnus described this effect in 1852.

In 1949, engineer Ralph Lightfoot used a wind tunnel to prove that the curveball actually curves. However, an optical illusion enhances the effect of the curveball because, as the ball nears the plate and shifts from the batter’s direct vision to his peripheral vision, the spinning motion distorts the batter’s perception of the ball’s trajectory so that it appears to drop suddenly.

full_image

A layer of air rotates with the curveball, creating a pressure difference between the top and the bottom of the ball. This difference can cause the ball to have a curving trajectory so that it drops as it nears the batter.

Rayleigh Scattering

1871

John William Strutt, 3rd Baron Rayleigh (1842–1919)

In 1868, the Scottish poet George MacDonald wrote, “When I look into the blue sky, it seems so deep, so peaceful, so full of a mysterious tenderness that I could lie for centuries, and wait for the dawning of the face of God out of the awful loving-kindness.” For many years, both scientists and laypeople have wondered what made the sky blue and the sunsets a fiery red. Finally, in 1871, Lord Rayleigh published a paper providing the answers. Recall that the “white light” from the Sun is actually composed of a range of hidden colors, which you can reveal with a simple glass prism. Rayleigh scattering refers to the scattering of sunlight by the gas molecules and microscopic density fluctuations in the atmosphere. In particular, the angle through which sunlight scatters varies inversely as the fourth power of the color wavelength. This means that blue light scatters much more than other colors, such as red, because the wavelength of blue light is shorter than the wavelength of red light. Blue light scatters strongly across much of the sky, and thus someone on the Earth observes a blue sky. Interestingly, the sky does not look violet (even though this color has a shorter wavelength than blue light), partly because there is more blue light than violet light in the spectrum of sunlight and because our eyes are more sensitive to blue than to violet light.

When the Sun is near the horizon, such as during sunset, the amount of air through which sunlight passes to an observer is greater than when the Sun is higher in the sky. Thus, more of the blue light is scattered away from the observer, leaving longer wavelength colors to dominate the view of the sunset.

Note that Rayleigh scattering applies to particles in the air having a radius of less than about a tenth of the wavelength of radiation, such as gas molecules. Other laws of physics apply when a significant amount of larger particles is in the air.

full_image

For centuries, both scientists and laypeople have wondered what made the sky blue and the sunsets a fiery red. Finally, in 1871 Lord Rayleigh published a paper providing the answers.

Crookes Radiometer

1873

William Crookes (1832–1919)

As a child, I had three “light mills” lined up on the window sill, with their paddles all spinning, as if by magic. The explanation of the movement has generated much debate through the decades, and even the brilliant physicist James Maxwell was initially confounded by the mill’s mode of operation.

The Crookes radiometer, also called the light mill, was invented in 1873 by English physicist William Crookes. It consists of a glass bulb that is partially evacuated and, within it, four vanes mounted on a spindle. Each vane is black on one side and shiny or white on the other. When exposed to light, the black sides of the paddles absorb photons and become warmer than the light sides, causing the paddles to turn so that the black sides move away from the light source, as explained below. The brighter the light, the faster the rotation speed. The paddles will not turn if the vacuum is too extreme within the bulb, and this suggests that movement of the gas molecules inside the bulb is the cause of the motion. Additionally, if the bulb is not evacuated at all, too much air resistance prevents rotation of the paddles.

At first, Crookes suggested that the force turning the paddles resulted from the actual pressure of the light upon the blades, and Maxwell originally agreed with this hypothesis. However, it became clear that this theory was insufficient, given that the paddles did not turn in a strong vacuum. Also, light pressure would be expected to cause the shiny, reflective side of the paddles to move away from the light. In fact, the light mill’s rotation can be attributed to the motions of gas molecules as a result of the difference in temperature between the sides of the paddle. The precise mechanism appears to make use of a process called thermal transpiration, which involves the motion of gas molecules from the cooler sides to the warmer sides near the edges of the blades, creating a pressure difference.

full_image

Sir William Crookes, from J. Arthur Thomson’s The Outline of Science, 1922.

full_image

The Crookes radiometer, also called the light mill, consists of a glass bulb that is partially evacuated. Inside are four vanes, mounted on a spindle. When light is shined on the radiometer, the blades rotate.

Boltzmann’s Entropy Equation

1875

Ludwig Eduard Boltzmann (1844-1906)

“One drop of ink may make a million think,” says an old proverb. Austrian physicist Ludwig Boltzmann was fascinated by statistical thermodynamics, which focuses on the mathematical properties of large numbers of particles in a system, including ink molecules in water. In 1875, he formulated a mathematical relationship between entropy S (roughly, the disorder of a system) and the number of possible states of the system W in a compact expression: S = k·log W. Here, k is Boltzmann’s constant.

Consider a drop of ink in water. According to Kinetic Theory, the molecules are in constant random motion and always rearranging themselves. We assume that all possible arrangements are equally probable. Because most of the arrangements of ink molecules do not correspond to a drop of clustered ink molecules, most of the time we will not observe a drop. Mixing occurs spontaneously simply because so many more arrangements exist that are mixed than that are not. A spontaneous process occurs because it produces the most probable final state. Using the formula S = k·log W, we can calculate the entropy and can understand why the more states that exist, the greater the entropy. A state with a high probability (e.g. a mixed ink state) has a large value for the entropy, and a spontaneous process produces the final state of greatest entropy, which is another way of stating the Second Law of Thermodynamics. Using the terminology of thermodynamics, we can say that there are a number of ways W (number of microstates) that exist to create a particular macrostate—in our case, a mixed state of ink in a glass of water.

Although Boltzmann’s idea of deriving thermodynamics by visualizing molecules in a system seems obvious to us today, many physicists of his time criticized the concept of atoms. Repeated clashes with other physicists, combined with an apparent lifelong struggle with bipolar disorder, may have contributed to the physicist’s suicide in 1906 while on vacation with his wife and daughter. His famous entropy equation is engraved on his tombstone in Vienna.

full_image

Ludwig Eduard Boltzmann.

full_image

Imagine that all possible arrangements of ink and water molecules are equally probable. Because most of the arrangements do not correspond to a drop of clustered ink molecules, most of the time we will not observe a droplet once the ink drop is added.

Incandescent Light Bulb

1878

Joseph Wilson Swan (1828–1914), Thomas Alva Edison (1847–1931)

The American inventor Thomas Edison, best known for his development of the light bulb, once wrote, “To invent you need a good imagination and a pile of junk.” Edison was not the only person to have invented a version of the incandescent light bulb—that is, a light source that makes use of heat-driven light emissions. Other equally notable inventors include Joseph Swan of England. However Edison is best remembered because of the combination of factors he helped to promote—a long-lasting filament, the use of a higher vacuum within the bulb than others were able to produce, and a power distribution system that would make the light bulb of practical value in buildings, streets, and communities.

In an incandescent light bulb, an electric current passes through the filament, heating it to produce light. A glass enclosure prevents oxygen in the air from oxidizing and destroying the hot filament. One of the greatest challenges was to find the most effective material for the filament. Edison’s carbonized filament of bamboo could emit light for more than 1,200 hours. Today, a filament made of tungsten wire is often used, and the bulb is filled with an inert gas such as argon to reduce evaporation of material from the filament. Coiled wires increase the efficiency, and the filament within a typical 60-watt, 120-volt bulb is actually 22.8 inches (580 millimeters) in length.

If a bulb is operated at low voltages, it can be surprisingly long lasting. For example, the “Centennial Light” in a California fire station has been burning almost continually since 1901. Generally, incandescent lights are inefficient in the sense that about 90% of the power consumed is converted to heat rather than visible light. Although today more efficient forms of light bulbs (e.g. compact fluorescent lamps) are starting to replace the incandescent light bulbs, the simple incandescent bulb once replaced the soot-producing and more dangerous lamps and candles, changing the world forever.

full_image

Edison light bulb with a looping carbon filament.

Plasma

1879

William Crookes (1832–1919)

A plasma is a gas that has become ionized, which means that the gas contains a collection of free-moving electrons and ions (atoms that have lost electrons). The creation of a plasma requires energy, which may be supplied in a variety of forms, including thermal, radiant, and electrical. For example, when a gas is sufficiently heated so that the atoms collide with one another and knock their electrons off, a plasma can be formed. Like a gas, a plasma does not have a definite shape unless enclosed in a container. Unlike ordinary gases, magnetic fields may cause a plasma to form a tapestry of unusual structures, such as filaments, cells, layers, and other patterns of startling complexity. Plasmas can exhibit a rich variety of waves not present in ordinary gases.

British physicist William Crookes first identified plasmas in 1879 while experimenting with a partially evacuated electrical discharge tube called a Crookes tube. Interestingly, a plasma is the most common state of matter—far more common than solids, liquids, and gases. Shining stars are made of this “fourth state of matter.” On the Earth, common examples of plasma producers include fluorescent lights, plasma TVs, neon signs, and lightning. The ionosphere—the upper atmosphere of the Earth—is a plasma produced by solar radiation that has a practical importance because it influences radio communication around the world.

Plasma studies employ a large range of plasma gases, temperatures, and densities in fields that range from astrophysics to fusion power. The charged particles in plasmas are sufficiently close so that each particle influences many nearby charged particles. In plasma TVs, xenon and neon atoms release photons of light when they are excited. Some of these photons are ultraviolet photons (which we can’t see) that interact with phosphor materials, causing them, in turn, to emit visible light. Each pixel in the display is made up of smaller subpixels that have different phosphors for green, red, and blue colors.

full_image

Plasma lamp, exhibiting complex phenomena such as filamentation. The beautiful colors result from the relaxation of electrons in excited states to lower energy states.

Hall Effect

1879

Edwin Herbert Hall (1855-1938), Klaus von Klitzing (b. 1943)

In 1879, American physicist Edwin Hall placed a thin gold rectangle in a strong magnetic field that was perpendicular to the rectangle. Let us imagine that x and x are two parallel sides of the rectangle and that y and y′ are the other parallel sides. Hall then connected battery terminals to sides x and x′ to produce a current flow in the x direction along the rectangle. He discovered that this produced a tiny voltage difference from y to y′, which was proportional to the strength of an applied magnetic field, B_z, multiplied by the current. For many years, the voltage produced by the Hall Effect was not used in practical applications because it was small. However, in the second half of the twentieth century, the Hall Effect blossomed into countless areas of research and development. Note that Hall discovered his tiny voltage 18 years before the electron was actually discovered. The Hall coefficient R_H is the ratio of the induced electric field E_y to the current density j_x multiplied by B_z: R_H = E_y/(j_xB_z). The ratio of the created voltage in the y direction to the amount of current is known as the Hall resistance. Both the Hall coefficient and resistance are characteristics of the material under study. The Hall Effect turned out to be very useful for measuring either the magnetic field or the carrier density. Here, we use the term carrier instead of the more familiar term electron because, in principle, an electrical current may be carried by charged particles other than electrons (e.g. positively charged carriers referred to as holes).

Today, the Hall Effect is used in many kinds of magnetic field sensors within applications that range from fluid flow sensors, to pressure sensors, to automobile ignition timing systems. In 1980, German physicist Klaus von Klitzing discovered the quantum Hall Effect when, using a large magnetic field strength and low temperatures, he noticed discrete steps in the Hall resistance.

full_image

High-end paintball guns make use of Hall Effect sensors to provide a very short throw, allowing a high rate of fire. The throw is the distance that the trigger travels before actuating.

Piezoelectric Effect

1880

Paul-Jacques Curie (1856–1941), Pierre Curie (1859–1906)

“Every [scientific] discovery, however small, is a permanent gain,” French physicist Pierre Curie wrote to Marie, a year before they married, urging her to join him in “our scientific dream.”As a young teenager, Pierre Curie had a love of mathematics—spatial geometry, in particular—which would later be of value to him in his work on crystallography. In 1880, Pierre and his brother Paul-Jacques demonstrated that electricity was produced when certain crystals were compressed—a phenomenon now called piezoelectricity. Their demonstrations involved crystals such as tourmaline, quartz, and topaz. In 1881, the brothers demonstrated the reverse effect: that electric fields could cause some crystals to deform. Although this deformation is small, it was later found to have applications in the production and detection of sound and the focusing of optical components. Piezoelectric applications have been used in the design of phonograph cartridges, microphones, and ultrasonic submarine detectors. Today, electric cigarette lighters use a piezoelectric crystal to produce a voltage in order to ignite the gas from the lighter. The U.S. military has explored the possible use of piezoelectric materials in soldiers’ boots for generating power in the battlefield. In piezoelectric microphones, sound waves impinge on the piezoelectric material and create a change in voltage.

Science-journalist Wil McCarthy explains the molecular mechanism of the piezoelectric effect, which “occurs when pressure on a material creates slight dipoles within it, by deforming neutral molecules or particles so that they become positively charged on one side and negatively charged on the other, which in turn increase an electrical voltage across the material.” In an old-fashioned phonograph, the needle glides within the wiggly grooves of the record, which deform the needle tip made of Rochelle salt and create voltages that are converted to sound.

Interestingly, the material of bone exhibits the piezoelectric effect, and piezoelectric voltages may play a role in bone formation, nourishment, and the effect that mechanical loads have on bone.

full_image

An electric cigarette lighter employs a piezoelectric crystal. Pressing a button causes a hammer to hit the crystal, which produces an electric current that flows across a spark gap and ignites the gas.

War Tubas

1880

War tuba is the informal name given to a large variety of huge acoustic locators—many of which had an almost-comical appearance—that played a crucial role in the history of warfare. These devices were primarily used to locate aircraft and guns from World War I to the early years of World War II. Once radar (detection systems using electromagnetic waves) was introduced in the 1930s, the amazing war tubas were mostly rendered obsolete, but they were sometimes used either for misinformation (e.g. to mislead the Germans into thinking that radar was not being used) or if radar-jamming methods were deployed. Even as late as 1941, Americans used acoustic locators to detect the first Japanese attack on Corregidor in the Philippines.

Through the years, the acoustic locators have taken many forms, ranging from personal devices that resemble horns strapped to the shoulders, such as the topophone of the 1880s, to huge multi-horn protuberances mounted on carriages and operated by multiple users. The German version—a Ringtrichterrichtungshoerer (“ring-horn acoustic direction detector”)—was used in World War II to assist with the initial nighttime aiming of searchlights at airplanes.

The December 1918 Popular Science described how 63 German guns were detected by acoustic location in a single day. Microphones concealed beneath rocks across a landscape were connected by wires to a central location. The central station recorded the precise moment at which every sound was received. When used to locate guns, the station recorded the sound of the flying shell passing overhead, the boom of the gun, and shell explosion sounds. Corrections were made to adjust for variations in the speed of sound waves due to atmospheric conditions. Finally, the difference in times at which the same sound was recorded from the receiving stations was compared with the known distances among stations. British and French military observers then directed airplane bombers to destroy the German guns, some of which were camouflaged and nearly undiscoverable without the acoustic locators.

full_image

A huge two-horn system at Bolling Field, Washington DC (1921).

SEE ALSO Tuning Fork (1711), Stethoscope (1816).

full_image

Photograph (mirrored) of Japanese Emperor Hirohito inspecting an array of acoustic locators, also known today as war tubas, that were used to locate aircraft before the invention of radar.

Galvanometer

1882

Hans Christian Oersted (1777–1851), Johann Carl Friedrich Gauss (1777–1855), Jacques-Arsène d’Arsonval (1851–1940)

A galvanometer is a device for measuring electric currents using a needle, or pointer, that rotates in response to electrical current. In the mid-1800s, the Scottish scientist George Wilson spoke with awe of the galvanometer’s dancing needle, writing that a similar compass needle was the “guide of Columbus to the New World [and] was the precursor and pioneer of the telegraph. Silently … it led the explorers across the waste of waters to the new homes of the world; but when these were largely filled, and houses … longed to exchange affectionate greetings, it … broke silence. The quivering magnetic needle which lies in the coil of the galvanometer is the tongue of the electric telegraph, and already engineers talk of it as speaking.”

One of the earliest forms of galvanometers emerged from the 1820 work of Hans Christian Oersted, who discovered that electric current flowing through a wire created a surrounding magnetic field that deflected a magnetized needle. In 1832, Carl Friedrich Gauss built a telegraph that made use of signals that deflected a magnetic needle. This older kind of galvanometer made use of a moving magnet, which had the disadvantage of being affected by any nearby magnets or iron masses, and its deflection was not linearly proportional to the current. In 1882, Jacques-Arsène d’Arsonval developed a galvanometer that used a stationary permanent magnet. Mounted between the magnet’s poles was a coil of wire that generated a magnetic field and rotated when electric current flowed through the coil. The coil was attached to a pointer, and the angle of deflection was proportional to the current flow. A small torsion spring returned the coil and pointer to the zero position when no current was present.

Today, galvanometer needles are typically replaced by digital readouts. Nevertheless, modern galvanometer-like mechanisms have had a variety of uses, ranging from positioning pens in analog strip chart recorders to positioning heads in hard-disk drives.

full_image

Hans Christian Oersted.

full_image

An antique ammeter with binding posts and a dial with scale for DC milliamperes. (This is original physics laboratory equipment at the State University of New York College at Brockport.) The D’Arsonval galvanometer is a moving-coil ammeter.

Green Flash

1882

Jules Gabriel Verne (1828–1905), Daniel Joseph Kelly O’Connell (1896–1982)

Interest in the mysterious green flashes that are sometimes glimpsed above the setting or rising sun was kindled in the West by Jules Verne’s romantic novel The Green Ray (1882). The novel describes the quest for the eerie green flash, “a green which no artist could ever obtain on his palette, a green of which neither the varied tints of vegetation nor the shades of the most limpid sea could ever produce the like! If there is a green in Paradise, it cannot be but of this shade, which most surely is the true green of Hope…. He who has been fortunate enough once to behold it is enabled to see closely into his own heart and to read the thoughts of others.”

Green flashes result from several optical phenomena and are usually easier to see over an unobstructed ocean horizon. Consider a setting sun. The Earth’s atmosphere, with its layers of varying density, acts like a prism, causing different colors of light to bend at different angles. Higher-frequency light, such as green and blue light, bends more than lower-frequency light, such as red and orange. As the Sun dips below the horizon, the lower-frequency reddish image of the Sun is obstructed by the Earth, but the higher-frequency green portion can be briefly seen. Green flashes are enhanced by mirage effects, which can create distorted images (including magnified images) of distant objects because of differences in air densities. For example, cold air is denser than warm air and thus has a greater refractive index than warm air. Note that the color blue is usually not seen during the green flash because blue light is scattered beyond view (see Rayleigh Scattering).

For years, scientists often believed that reports of green flashes were optical illusions induced by staring too long at the setting sun. However, in 1954, the Vatican priest Daniel O’Connell took color photographs of a green flash as the Sun was setting over the Mediterranean Sea, thus “proving” the existence of the unusual phenomenon.

full_image

Green flash, photographed in San Francisco, 2006.

Michelson-Morley Experiment

1887

Albert Abraham Michelson (1852–1931) and Edward Williams Morley (1838–1923)

“It is hard to imagine nothing,” physicist James Trefil writes. “The human mind seems to want to fill empty space with some kind of material, and for most of history that material was called the aether. The idea was that the emptiness between celestial objects was filled with a kind of tenuous Jell-O.”

In 1887, physicists Albert Michelson and Edward Morley conducted pioneering experiments in order to detect the luminiferous aether thought to be pervading space. The aether idea was not too crazy—after all, water waves travel through water and sound travels through air. Didn’t light also require a medium through which to propagate, even in an apparent vacuum? In order to detect aether, the researchers split a light beam into two beams that traveled at right angles to each other. Both beams were reflected back and recombined to produce a striped interference pattern that depended on the time spent traveling in both directions. If the Earth moved through an aether, this should be detectable as a change in the interference pattern produced when one of the light beams (which had to travel into the aether “wind”) was slowed relative to the other beam. Michelson explained the idea to his daughter, “Two beams of light race against each other, like two swimmers, one struggling upstream and back, while the other, covering the same distance just crosses and returns. The second swimmer will always win if there is any current in the river.”

In order to make such fine measurements, vibrations were minimized by floating the apparatus on a pool of mercury, and the apparatus could be rotated relative to the motion of the Earth. No significant change in the interference patterns was found, suggesting that the Earth did not move through an “aether wind”—making the experiment the most famous “failed” experiment in physics. This finding helped to persuade other physicists to accept Einstein’s Special Theory of Relativity.

full_image

The Michelson-Morley Experiment demonstrated that the earth did not move through an aether wind. In the late 1800s, a luminiferous aether (the light-bearing substance artistically depicted here) was thought to be a medium for the propagation of light.

Birth of the Kilogram

1889

Louis Lefèvre-Gineau (1751-1829)

Since 1889, the year the Eiffel Tower opened, a kilogram has been defined by a platinum-iridium cylinder the size of a salt shaker, carefully sequestered from the world within a jar within a jar within a jar in a temperature- and humidity-controlled vault in the basement of the International Bureau of Weights and Measures near Paris. Three keys are required to open the vault. Various nations have official copies of this mass to serve as their national standards. The physicist Richard Steiner once remarked, partly in humor, “If somebody sneezed on that kilogram standard, all the weights in the world would be instantly wrong.”

Today, the kilogram is the only base unit of measurement that is still defined by a physical artifact. For example, the meter is now equal to the distance traveled by light in vacuum during a time interval of 1/299,792,458 of a second—rather than by marks on a physical bar. The kilogram is a unit of mass, which is a fundamental measure of the amount of matter in the object. As can be understood from Newton’s F = ma (where F is force, m is mass, and a is acceleration), the greater an object’s mass, the less the object accelerates under a given force.

Researchers are so nervous about scratching or contaminating the Paris cylinder that it has been removed from its secure location only in 1889, 1946, and 1989. Scientists have discovered that the masses of the entire worldwide collection of kilogram prototypes have been mysteriously diverging from the Paris cylinder. Perhaps the copies grew heavier by absorbing air molecules, or perhaps the Paris cylinder has become lighter. These deviations have led physicists on the quest to redefine the kilogram in terms of a fundamental unchanging constant, independent of a specific hunk of metal. In 1799, French chemist Louis Lefèvre-Gineau defined the kilogram with respect to a mass of 1000 cubic centimeters of water, but measurements of the mass and volume were inconvenient and imprecise.

full_image

Industries have often used reference masses for standards. Accuracies varied as the references became scraped and suffered other deteriorations. Here, the label dkg stands for decagram (or dekagram)—a metric unit of mass equal to 10 grams.

Birth of the Meter

1889

In 1889, the basic unit of length known as the meter was in the form of a special one-meter bar made of platinum and iridium, measured at the melting point of ice. Physicist and historian Peter Galison writes, “When gloved hands lowered this polished standard meter M into the vaults of Paris, the French, literally, held the keys to a universal system of weights and measures. Diplomacy and science, nationalism and internationalism, specificity and universality converged in the secular sanctity of that vault.”

Standardized lengths were probably among the earliest “tools” invented by humans for constructing dwellings or for bartering. The word meter comes from the Greek métron, meaning “a measure,” and the French mètre. In 1791, the French Academy of Sciences suggested that the meter be set equal to one ten-millionth of the distance from the Equator to the North Pole, passing through Paris. In fact, a multi-year French expedition took place in an effort to determine this distance.

The history of the meter is both long and fascinating. In 1799, the French created a bar made from platinum with the appropriate length. In 1889, a more definitive platinum-iridium bar was accepted as the international standard. In 1960, the meter was defined as being equal to the impressive-sounding 1,650,763.73 wavelengths in vacuum of the radiation corresponding to the transition between the 2p10 and 5d5 quantum levels of the krypton-86 atom! No longer did the meter have a direct correspondence to a measurement of the Earth. Finally, in 1983, the world agreed that the meter was equal to the distance traveled by light in vacuum during a time interval of 1/299,792,458 of a second.

Interestingly, the first prototype bar was short by a fifth of a millimeter because the French did not take into account that the Earth is not precisely spherical but flattened closer to the poles. However, despite this error, the actual length has not changed; rather, the definition has changed in order to increase the possible precision of the measurement.

full_image

For centuries, engineers have been interested in making increasingly fine measurements of length. For example, calipers can be used to measure and compare the distances between two points on an object.

Eötvös’ Gravitational Gradiometry

1890

Loránd von Eötvös (1848-1919)

Hungarian physicist and world-renowned mountain-climber Loránd Eötvös was not the first to use a torsion balance (an apparatus that twists in order to measure very weak forces) to study the gravitational attraction between masses, but Eötvös refined his balance to gain added sensitivity. In fact, the Eötvös balance became one of the best instruments for measuring gravitational fields at the surface of the Earth and for predicting the existence of certain structures beneath the surface. Although Eötvös focused on basic theory and research, his instruments later proved important for prospecting for oil and natural gas.

This device was essentially the first instrument useful for gravitational gradiometry—that is, for the measurement of very local gravitational properties. For example, Eötvös’ early measurements involved his mapping changes of the gravitational potential at different locations in his office and, shortly after, the entire building. Local masses in the rooms influence the values he obtained. The Eötvös balance could also be used to study the gravitational changes due to slow motions of massive bodies or fluids. According to physicist Péter Király, “changes in the water level of the Danube could allegedly be detected from a cellar 100 meters away with a centimeter precision, but that measurement was not well documented.”

Eötvös’ measurements also showed that gravitational mass (the mass m in Newton’s Law of Gravitation, F = Gm₁m₂/r²) and inertial mass (the constant mass m responsible for inertia in Newton’s Second Law, which we often write as F = ma) were the same—at least to an accuracy of about five parts in 10⁹. In other words, Eötvös showed that the inertial mass (the measure of the resistance of an object to acceleration by an applied force) is the same as gravitational mass (the factor determining the weight of an object) to within a great level of accuracy. This information later proved useful for Einstein when he formulated the General Theory of Relativity. Einstein cited Eötvös’ work in Einstein’s 1916 paper, “The Foundation of the General Theory of Relativity.”

full_image

Loránd Eötvös, 1889.

full_image

Visualization of gravity, created with data from NASA’s Gravity Recovery and Climate Experiment (GRACE). Variations in the gravity field are shown across the Americas. Red shows the areas where gravity is stronger.

Tesla Coil

1891

Nikola Tesla (1856–1943)

The Tesla coil (TC) has played a significant role in stimulating generations of students to become interested in the wonders of science and electrical phenomena. On the wilder side, it is sometimes used in horror movies by mad scientists to create impressive lightning effects, and paranormal researchers creatively suggest that “heightened supernatural activity has been reported when they are in use!”

Developed around 1891 by the inventor Nikola Tesla, the TC can be used to produce high-voltage, low-current, high-frequency, alternating-current electricity. Tesla used the TCs to conduct experiments involving the transmission of electrical energy without wires to extend the limits of our understanding of electrical phenomena. “None of the circuit’s typical components were unknown at the time,” writes the Public Broadcasting Service (PBS), “but its design and operation together achieved unique results—not the least because of Tesla’s masterful refinements in construction of key elements, most particularly of a special transformer, or coil, which is at the heart of the circuit’s performance.”

Generally speaking, an electrical transformer transfers electrical energy from one circuit to another through the transformer’s coils. A varying current in the primary coil winding creates a varying magnetic flux in the transformer’s core, which then creates a varying magnetic field through the secondary winding that induces a voltage in the secondary winding. In the TC, a high-voltage capacitor and spark gap are used to periodically excite a primary coil with bursts of current. The secondary coil is excited through resonant inductive coupling. The more turns the secondary winding has in relation to the primary winding, the larger the increase in voltage. Millions of volts can be produced in this fashion.

Often, the TC has a large metal ball (or other shape) on top from which streams of electricity chaotically shoot. In practice, Tesla had constructed a powerful radio transmitter, and he also used the device to investigate phosphorescence (a process in which energy absorbed by an object is released in the form of light) and X-rays.

full_image

High-voltage arcs of a Tesla coil discharging to a piece of copper wire. The voltage is approximately 100,000 volts.

Thermos

1892

James Dewar (1842–1923), Reinhold Burger (1866–1954)

Invented by Scottish physicist James Dewar in 1892, the thermos (also called the Dewar flask or vacuum flask) is a double-walled container with a vacuum space between the walls that enables the flask to keep its contents hotter or colder than the surroundings for a significant period of time. After it was commercialized by German glass-blower Reinhold Burger, the thermos “was an instant success and a worldwide bestseller,” writes author Joel Levy, “thanks in part to the free publicity it gained from the day’s leading explorers and pioneers. Thermos vacuum flasks were carried to the South Pole by Ernest Shackleton, the North Pole by William Parry, the Congo by Colonel Roosevelt and Richard Harding Davis, Mount Everest by Sir Edmund Hillary, and into the skies by both the Wright brothers and Count von Zeppelin.”

The flask works by reducing the three principal ways in which objects exchange heat with the environment: conduction (e.g. the way heat spreads from the hot end of an iron bar to the colder end), radiation (e.g. the heat one feels radiating from bricks in a fireplace after the fires have burned out), and convection (e.g. circulation of soup in a pot that is heated from below). The narrow, hollow region between the inner and outer walls of the thermos, which is evacuated of air, reduces loss by conduction and convection, while the reflective coating on the glass reduces loss by infrared radiation.

The thermos has important uses beyond keeping a beverage hot or cold; its insulating properties have allowed for the transport of vaccines, blood plasma, insulin, rare tropical fish, and much more. During World War II, the British military produced around 10,000 thermoses that were taken by bomber crews on their nighttime raids over Europe. Today, in laboratories all over the world, thermoses are used to store ultra-cold liquids such as liquid nitrogen or liquid oxygen.

In 2009, researchers at Stanford University showed how a stack of photonic crystals (periodic structures known for blocking narrow-frequency ranges of light) layered within a vacuum could provide significantly better suppression of thermal radiation than a vacuum alone.

full_image

Beyond keeping a beverage hot or cold, thermoses have been used to carry vaccines, blood plasma, rare tropical fish, and more. In laboratories, vacuum flasks are used to store ultracold liquids, such as liquid nitrogen or liquid oxygen.

X-rays

1895

Wilhelm Conrad Röntgen (1845–1923), Max von Laue (1879–1960)

Upon seeing her husband’s X-ray image of her hand, Wilhelm Röntgen’s wife “shrieked in terror and thought that the rays were evil harbingers of death,” writes author Kendall Haven. “Within a month, Wilhelm Röntgen’s X-rays were the talk of the world. Skeptics called them death rays that would destroy the human race. Eager dreamers called them miracle rays that could make the blind see again and could beam … diagrams straight into a student’s brains.” However, for physicians, X-rays marked a turning point in the treatment of the sick and wounded.

On November 8, 1895, the German physicist Wilhelm Röntgen was experimenting with a cathode-ray tube when he found that a discarded fluorescent screen lit up over a meter away when he switched on the tube, even though the tube was covered with a heavy cardboard. He realized that some form of invisible ray was coming from the tube, and he soon found that they could penetrate various materials, including wood, glass, and rubber. When he placed his hand in the path of the invisible rays, he saw a shadowy image of his bones. He called the rays X-rays because they were unknown and mysterious at that time, and he continued his experiments in secrecy in order to better understand the phenomena before discussing them with other professionals. For his systematic study of X-rays, Röntgen would win the first Nobel Prize.

Physicians quickly made use of X-rays for diagnoses, but the precise nature of X-rays was not fully elucidated until around 1912, when Max von Laue used X-rays to create a diffraction pattern of a crystal, which verified that X-rays were electromagnetic waves, like light, but of a higher energy and a shorter wavelength that was comparable to the distance between atoms in molecules. Today, X-rays are used in countless fields, ranging from X-ray crystallography (to reveal the structure of molecules) to X-ray astronomy (e.g., the use of X-ray detectors on satellites to study X-ray emissions from sources in outer space).

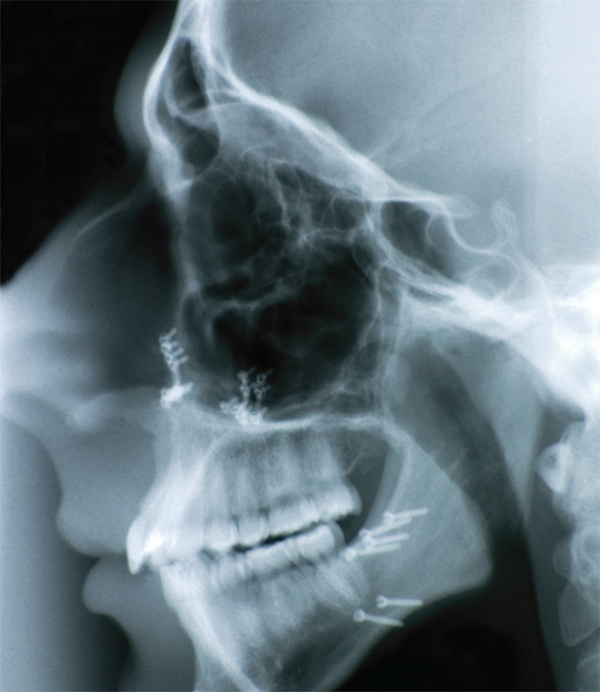
full_image

X-ray of the side view of a human head, showing screws used to reconstruct the jaw bones.

Curie’s Magnetism Law

1895

Pierre Curie (1859-1906)

French physical chemist Pierre Curie considered himself to have a feeble mind and never went to elementary school. Ironically, he later shared the Nobel Prize with his wife Marie for their work on radioactivity. In 1895, he illuminated an interesting relationship between the magnetization of certain kinds of materials and the applied magnetic field and temperature T: M = C × (B_ext/T). Here, M is the resulting magnetization, and B_ext is the magnetic flux density of the applied (external) field. C is the Curie point, a constant that depends on the material. According to Curie’s Law, if one increases the applied magnetic field, one tends to increase the magnetization of a material in that field. As one increases the temperature while holding the magnetic field constant, the magnetization decreases.

Curie’s Law is applicable to paramagnetic materials, such as aluminum and copper, whose tiny atomic magnetic dipoles have a tendency to align with an external magnetic field. These materials can become very weak magnets. In particular, when subject to a magnetic field, paramagnetic materials suddenly attract and repel like standard magnets. When there is no external magnetic field, the magnetic moments of particles in a paramagnetic material are randomly oriented and the paramagnet no longer behaves as a magnet. When placed in a magnetic field, the moments generally align parallel to the field, but this alignment may be counteracted by the tendency for the moments to be randomly oriented due to thermal motion.

Paramagnetic behavior can also be observed in ferromagnetic materials—e.g., iron and nickel—that are above their Curie temperatures, T_c. The Curie temperature is a temperature above which the materials lose their ferromagnetic ability—that is, the ability to possess a net (spontaneous) magnetization even when no external magnetic field is nearby. Ferromagnetism is responsible for most of the magnets you encounter at home, such as permanent magnets that may be sticking to your refrigerator door or the horseshoe magnet you played with as a child.

full_image

Photograph of Pierre Curie and his wife Marie, with whom he shared the Nobel Prize.

full_image

Platinum is an example of a paramagnetic material at room temperature. This platinum nugget is from Konder mine, Yakutia, Russia.

Radioactivity

1896

Abel Niépce de Saint-Victor (1805-1870), Antoine Henri Becquerel (1852-1908), Pierre Curie (1859-1906), Marie Skłodowska Curie (1867-1934), Ernest Rutherford (1871-1937), Frederick Soddy (1877-1956)

To understand the behavior of radioactive nuclei (the central regions of atoms), picture popcorn popping on your stove. Kernels appear to pop at random over several minutes, and a few don’t seem to pop at all. Similarly, most familiar nuclei are stable and are essentially the same now as they were centuries ago. However, other kinds of nuclei are unstable and spew fragments as the nuclei disintegrate. Radioactivity is the emission of such particles.

The discovery of radioactivity is usually associated with French scientist Henri Becquerel’s 1896 observations of phosphorescence in uranium salts. Roughly a year before Becquerel’s discovery, German physicist Wilhelm Röntgen discovered X-rays while experimenting with electrical discharge tubes, and Becquerel was curious to see if phosphorescent compounds (compounds that emit visible light after being stimulated by sunlight or other excitation waves) might also produce X-rays. Becquerel placed uranium potassium sulfate on a photographic plate that was wrapped in black paper. He wanted to see if this compound would phosphoresce and produce X-rays when stimulated by light.

To Becquerel’s surprise, the uranium compound darkened the photographic plate even when the packet was in a drawer. Uranium seemed to be emitting some kind of penetrating “rays.” In 1898, physicists Marie and Pierre Curie discovered two new radioactive elements, polonium and radium. Sadly, the dangers of radioactivity were not immediately recognized, and some physicians began to provide radium enema treatments among other dangerous remedies. Later, Ernest Rutherford and Frederick Soddy discovered that these kinds of elements were actually transforming into other elements in the radioactive process.

Scientists were able to identify three common forms of radioactivity: alpha particles (bare helium nuclei), beta rays (high-energy electrons), and gamma rays (high-energy electromagnetic rays). Author Stephen Battersby notes that, today, radioactivity is used for medical imaging, killing tumors, dating ancient artifacts, and preserving food.

full_image

During the late 1950s, fallout shelters grew in number across the US. These spaces were designed to protect people from radioactive debris from a nuclear explosion. In principle, people might remain in the shelters until the radioactivity had decayed to a safer level outside.

Electron

1897

Joseph John “J. J.” Thomson (1856–1940)

“The physicist J. J. Thomson loved to laugh,” writes author Josepha Sherman. “But he was also clumsy. Test tubes broke in his hands, and experiments refused to work.” Nevertheless, we are lucky that Thomson persisted and revealed what Benjamin Franklin and other physicists had suspected—that electrical effects were produced by minuscule units of electrical charge. In 1897, J. J. Thomson identified the electron as a distinct particle with a mass much smaller than the atom. His experiments employed a cathode ray tube: an evacuated tube in which a beam of energy travels between a positive and negative terminal. Although no one was sure what cathode rays actually were at the time, Thompson was able to bend the rays using a magnetic field. By observing how the cathode rays moved through electric and magnetic fields, he determined that the particles were identical and did not depend on the metal that emitted them. Also, the particles all had the same ratio of electric charge to mass. Others had made similar observations, but Thomson was among the first to suggest that these “corpuscles” were the carriers of all forms of electricity and a basic component of matter.

Discussions of the various properties of electrons are presented in many sections of this book. Today, we know that the electron is a subatomic particle with negative electric charge and a mass that is 1/1,836 of the mass of a proton. An electron in motion generates a magnetic field. An attractive force, known as the Coulomb force, between the positive proton and the negative electron causes electrons to be bound to atoms. Chemical bonds between atoms may result when two or more electrons are shared between atoms.

According to the American Institute of Physics, “Modern ideas and technologies based on the electron, leading to the television and the computer and much else, evolved through many difficult steps. Thomson’s careful experiments and adventurous hypotheses were followed by crucial experimental and theoretical work by many others [who] opened for us new perspective—a view from inside the atom.”

full_image

A lightning discharge involves a flow of electrons. The leading edge of a bolt of lightning can travel at speeds of 130,000 miles per hour (60,000 meters/second) and can reach temperatures approaching 54,000 °F (30,000 °C).

Mass Spectrometer

1898

Wilhelm Wien (1864–1928), Joseph John “J. J.” Thomson (1856–1940)

“One of the pieces of equipment that has contributed most to the advancement in scientific knowledge in the twentieth century is undoubtedly the mass spectrometer,” writes author Simon Davies. The mass spectrometer (MS) is used to measure the masses and relative concentrations of atoms and molecules in a sample. The basic principle involves the generation of ions from a chemical compound, then separating these ions according to their mass-to-charge ratio (m/z), and finally detecting the ions and characterizing them according to their m/z and abundance in the sample. The specimen may be ionized by many methods, including by bombarding it with energetic electrons. The resulting ions can be charged atoms, molecules, or molecular fragments. For example, the specimen may be bombarded with an electron beam, which forms positively charged ions when it strikes a molecule and knocks an electron out of the molecule. Sometimes, molecular bonds are broken, creating charged fragments. In a MS, the speed of a charged particle may change while passing through an electric field, and its travel direction altered by a magnetic field. The amount of ion deflection is affected by m/z (e.g., the magnetic force deflects lighter ions more than heavier ions). The detector records the relative abundance of each ion type.

When identifying the fragments detected in a sample, the resulting mass spectrum is often compared against spectra of known chemicals. MS can be used for many applications, including determining different isotopes in a sample (i.e. elements that have a different number of neutrons), protein characterization (e.g. using an ionization method called electrospray ionization), and exploring outer space. For example, MS devices were taken on space probes used to study atmospheres of other planets and moons.

Physicist Wilhelm Wien established the foundation of mass spectrometry in 1898, when he found that beams of charged particles were deflected by electric and magnetic fields according to their m/z. J. J. Thomson and others refined the spectrometry apparatus through the years.

full_image

A mass spectrometer on the Cassini–Huygens spacecraft was used to analyze particles in the atmospheres of Saturn and its moons and rings. Launched in 1997, the craft was part of a joint mission of NASA, the European Space Agency, and the Italian Space Agency.

Blackbody Radiation Law

1900

Max Karl Ernst Ludwig Planck (1858–1947), Gustav Robert Kirchhoff (1824–1887)

“Quantum mechanics is magic,” writes quantum physicist Daniel Greenberger. Quantum theory, which suggests that matter and energy have the properties of both particles and waves, had its origin in pioneering research concerning hot objects that emit radiation. For example, imagine the coil on an electric heater that glows brown and then red as it gets hotter. The Blackbody Radiation Law, proposed by German physicist Max Planck in 1900, quantifies the amount of energy emitted by blackbodies at a particular wavelength. Blackbodies are objects that emit and absorb the maximum possible amount of radiation at any given wavelength and at any given temperature.

The amount of thermal radiation emitted by a blackbody changes with frequency and temperature, and many of the objects that we encounter in our daily lives emit a large portion of their radiation spectrum in the infrared, or far-infrared, portion of the spectrum, which is not visible to our eyes. However, as the temperature of a body increases, the dominant portion of its spectrum shifts so that we can see a glow from the object.

In the laboratory, a blackbody can be approximated using a large, hollow, rigid object such as a sphere, with a hole poked in its side. Radiation entering the hole reflects off the inner walls, dissipating with each reflection as the walls absorb the radiation. By the time the radiation exits through the same hole, its intensity is negligible. Thus, this hole acts as a blackbody. Plank modeled the cavity walls of blackbodies as a collection of tiny electromagnetic oscillators. He posited that the energy of oscillators is discrete and could assume only certain values. These oscillators both emit energy into the cavity and absorb energy from it via discrete jumps, or in packages called quanta. Planck’s quantum approach involving discrete oscillator energies for theoretically deriving his Radiation Law led to his 1918 Nobel Prize. Today, we know that the universe was a near-perfect blackbody right after the Big Bang. German physicist Gustav Kirchhoff introduced the actual term blackbody in 1860.

full_image

Max Planck, 1878.

full_image

Molten glowing lava is an approximation of blackbody radiation, and the temperature of the lava can be estimated from the color.