CHAPTER XIII

MANY-VALUED FUNCTIONS OF A COMPLEX VARIABLE

Logarithms of Complex Numbers. Definition. If w = exp (z), then z is called a natural logarithm of w, and we write z = Log w.

 

We have seen that to any value of z, ≡ x + iy, there corresponds one and only one value of w, =exp (z) ≡ exp (x+iy), viz. e^x cis y ; see p. 194. We shall now show that to a given value of w there correspond an unlimited number of values of z, =Log w.

Values of Log w, where w = ρ(cos φ + i sin φ).

Let z, ≡ x + iy, be a natural logarithm of w.

By definition,

 

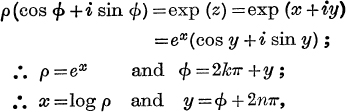
where log ρ is the unique logarithm of ρ as defined in Ch. IV;

 

Thus the natural logarithm of a complex number, as defined above, is an infinitely many-valued function.

If ϕ₁ is the principal value of the amplitude of w, so that

 

we define the principal value, log w, of Log w, by the relation

 

By using the results of Ex. VIII. f, No. 8, we may express the relation (3) as follows :

 

Functional Law for Log w.

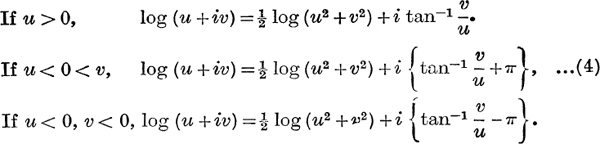
Let w₁ = ρ₁(cos ϕ₁ + i sin ϕ₁) and w₂ = ρ₂(cos ϕ₂ + i sin ϕ₂), then, by equation (2),

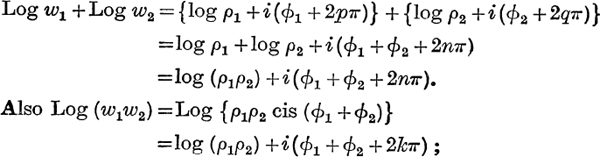
every value of Log w1 + Log w2 is equal to some value of Log (w₁w₂), and conversely.

We therefore write

 

In the same way it may be proved that

 

and in particular

 

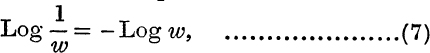
where every value of either side is equal to some value of the other side.

Further, if n is an integer,

 

But, in contrast with (5) and (6) it is not true to say that every value of Log wⁿ is one of the values of n Log w ; for example,

 

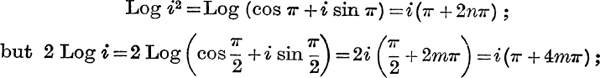
thus only some of the values of Log i2 are values of 2 Log i; the rest are values of 2 Log ( -i).

It should be noted that (5) and (6) are not necessarily true for principal values, i.e. if Log is replaced by log. Thus, in (5), am w₁ + am w₂ may be outside the limits, – π to +π ; for example,

 

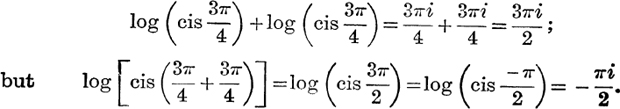
Example 1. Find the results corresponding to those in equation (4), p. 241, for log(u+iv), when (i) u = 0, (ii) u 0, v=0.

 

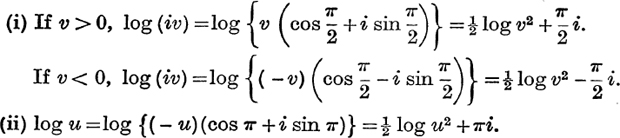
It should be noticed that, in (i), log v² may be replaced by log | v \; it cannot be replaced by log v unless v > 0.

Example 2. Are the functions (i) exp (Log w), (ii) exp (i Log w), one-valued or many-valued ?

 

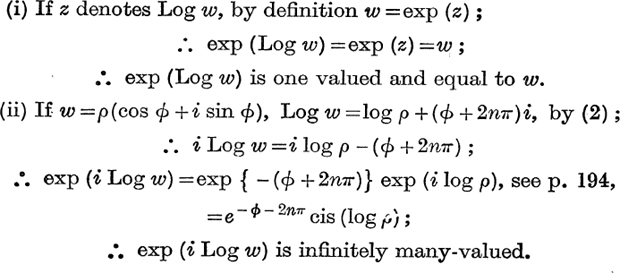
Example 3. If a; is real, prove that

 

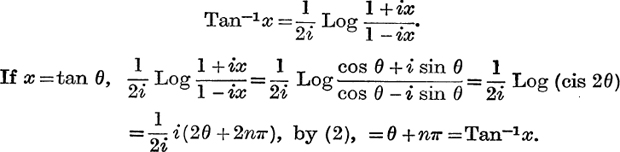
This result holds in the sense that any value of either function is equal to some value of the other.

EXERCISE XIII. a.

1. Find (i) the general value, (ii) the principal value, of

(a) Log 1 ; (b) Log i ; (c) Log ( - 2) ; (d) Log ( - 2i).

2. Find (i) the general value, (ii) the principal value, of

(a) Log (1 +i) ; (b) Log (√) ; (c) Log ( - 3 + 4i); (d) Log ( - 3 - 4i).

3. What is the general value of Log ( -e) ?

4. Find (i) the general value, (ii) the principal value, of

Log (cos α+i sin α), where (2n - 1)π < α ≤ (2n + 1)π.

5. What are the values of a and b if log (a+ib) =2 –

6. Express log (1 +cos θ +i sin 2θ) in the form a+ib, given that .

7. Find the general values of (i) i Log i ; (ii) Log (1 +i √3).

8. Express log (1 +i tan α) in the form a+ib, when

9. What are the values of a and b if log

10. If a < 0 < b and where find the values of

 

11. Express Log (1 - cos θ -i sin θ) in the form a+ib, giving rules for determining its principal value.

12. If (a+bi) log (c+di) =f + gi, express c and d in terms of a, b, f, g.

13. If , in what sense is Log 1=3 Log ω? Express some other values of Log 1 in a similar form.

14. If log z=a+bi and z log z =p +qi, prove that

 

15. What is the general value of exp when b=0?

16. What are the values of

(i) exp {(1 +i) Log i} ; (ii) exp {(1 +i) Log (1 +i)} ?

17. What is the value of exp {i Log (cos α+i sin α)} ?

18. Express Log {Log (cos θ+i sin θ)} in the form a +ib.

19. If z≡x+iy and x ≠ 1, prove that

 

and give the values of k for different positions of the point P which represents z in the Argand Diagram.

20. Give an expression corresponding to that in No. 19 for log (z + 1), and answer the same question about k.

21. Answer the same question as in No. 19 for considering the cases when P is (i) inside, (ii) outside, the circle |z| =1.

22. Find the value of log , when z=cos θ+ i sin θ.

23. If 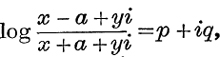and if p is constant, find the locus of the point P representing x + iy. Also find the locus when q is constant.

24. If and if the point P representing z moves round the circle |z| = a, discuss the behaviour of q. Also state what happens when P moves on an arbitrary circle through (a, 0) and ( – a, 0).

25. If where z≡x+iy, prove that x is positive or zero, or else x < 0 and y ≥1 or y<–1.

The Logarithmic Series. It has been proved on pp. 84, 85 that, if – 1 < x ≤ 1,

 

We now proceed to consider the corresponding series

 

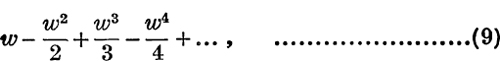
where w is a complex number equal to ρ( cos ϕ+i sin ϕ).

 

is convergent for 0 ≤ ρ< 1, it follows that the series (9) is absolutely convergent, and therefore convergent, for |w|<1. The series (9) may be written,

 

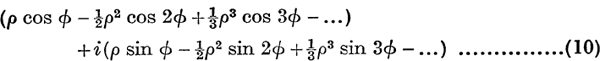
We proceed to evaluate separately the two parts of this function.

(i) From Ch. IX., equation (8), p. 175, we have, writing –x for x,

 

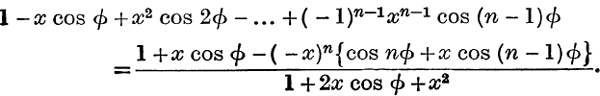
Subtract each side from unity and divide by x, then

 

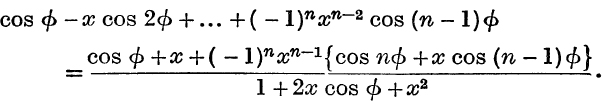
Integrate w.r.t. x both sides of this identity from x =0 to x =p, then

 

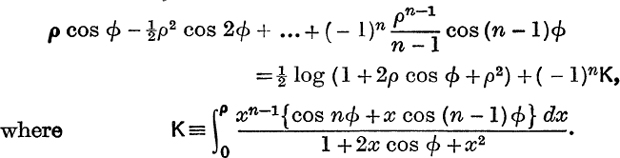
We shall suppose that 0 ≤ ρ < 1. It follows that, within the limits of integration,

 

 

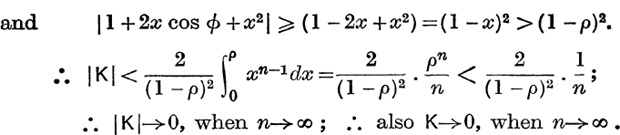
Therefore for 0 ≤ ρ< 1, the first series of (10) is convergent and

 

(ii) Again from Ch. IX, equation (9), we have, writing -x for x,

 

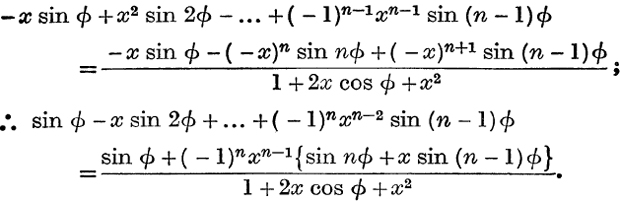
Integrate w.r.t. x from x = 0 to x = ρ, as before, then

 

 

 

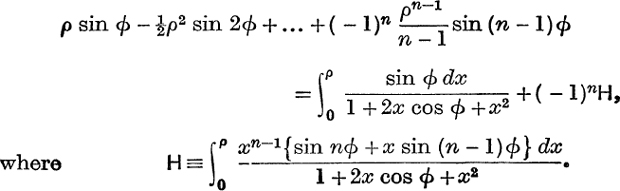
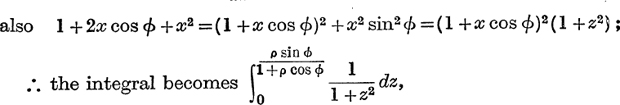
and this, see Ex. IV. a, No. 17, p. 57, is the principal value of

 

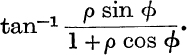
Also, by the same argument as before, it follows that, for 0 ≤ ρ< 1, H→0 when n→∞.

Therefore, for 0 ≤ ρ< 1, the second series of (10) is convergent and

 

From (11) and (12) it follows that, if |w|<1,

 

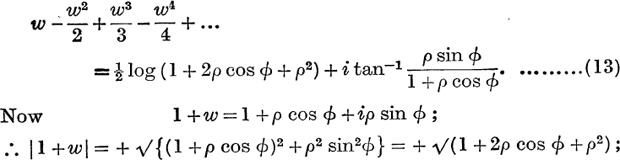
also, since 1 + ρ cos ϕ> 0, the principal value of the amplitude of 1 +w is 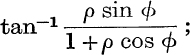therefore the principal value, log (1 +w), of Log (1 +w) is equal to the sum to infinity of (9) ; we therefore write

 

The Circle of Convergence. The series (9) is not convergent when |w| > 1. If w is represented by a point P in the Argand Diagram, the series (9) is convergent if P lies inside the circle |w| = 1, and is not convergent if P lies outside the circle |w| = 1. We therefore call this circle the circle of convergence for the power series. It is usually easy to determine the circle of convergence for a given power series, but in general it is difficult to discover how the series behaves when P lies on the circle itself. Here, we know from Ch. V., p. 84, that (14) holds for w = 1, i.e. when P is at the point (1, 0) and that the series is divergent when w = – 1, i.e. when P is at the point ( – 1, 0). It can be proved that (14) holds for all values of w for which |w| = 1, except w = – 1, i.e. for all positions of P on the circle of convergence except the point ( – 1, 0). Although a rigorous proof of this result is beyond the scope of this book, we shall state here some of the results which follow when this fact is assumed.

In (14), put w = cos α + i sin α, where α ≠ (2n + 1)π, then

 

But log (1 + cos α + i sin α)

 

 

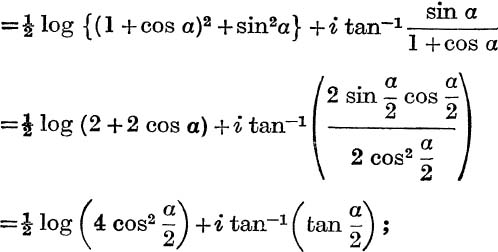
and

 

provided that α ≠ (2n + 1)π.

The sum to infinity of the series in (16₁) is the principal value of Tan^{– 1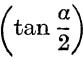} ; this may be expressed as follows :

 

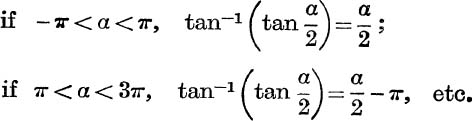
In general,

 

 

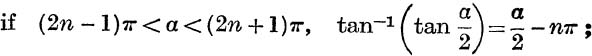
Also, in the excluded case, α = (2n + l)π, the sum of the series (16₂) is obviously zero.

Using these results, the reader should draw the graph of

 

which, he will find, is discontinuous at the points x = (2n + 1)π.

For example, if x→ π from above, y→> – , but, if x→π from below y→ + , while at x = π, y = 0.

Example 4. Find the sum to infinity of

 

From equation (14),

 

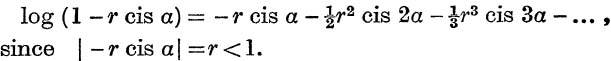
But log (1 – r cis α) = log (1 – r cos α – ir sin α)

 

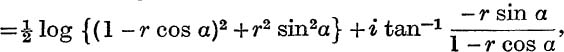
since 1 –r cos α > 0, (see p. 241);

 

Example 5. Find a series in powers of x, involving α, whose sum to infinity is one of the values of θ satisfying the equation,

 

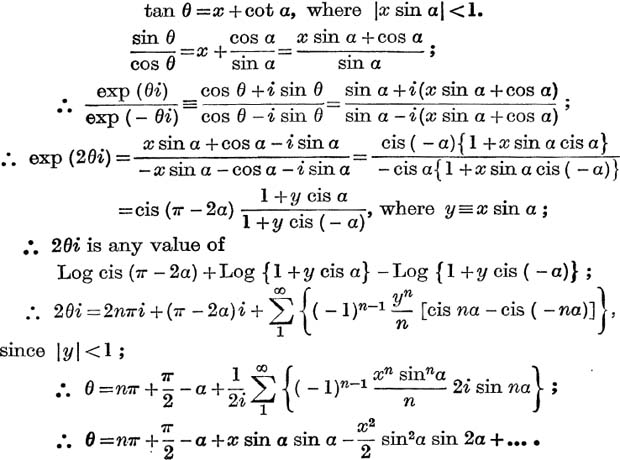
Note. It follows from p. 247 that the value of the series

 

Thus the value of θ given by taking n = 0 is that solution of

 

EXERCISE XIII. b.

1. If |z| < 1, express as a series of powers of z:

 

Is log always equal to log (1 + z) – log (1 – z), excluding z = ± 1 ?

2. If |r| < 1, sum to infinity : r cos α + r² cos 2α + r³ cos 3α + … .

3. If α ≠ nπ, sum to infinity:

 

4. ABC is a triangle such that b < c; prove that is the sum to infinity of the series, sin A + sin 2A + sin 3A + … .

5. ABC is a triangle, prove that C is the sum to infinity of the series :

 

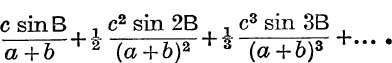
6. Find the sum to infinity of

 

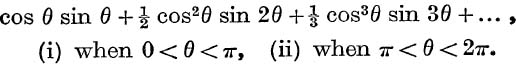
7. If , prove that

 

What is the sum to infinity of this series, if ?

8. Find the range of values of x, if the sum to infinity of the series, sin 2x – sin 4x + sin 6x – …, is (i) x, (ii) x – π.

9. If nπ < θ < (n + 1)π, find the sum to infinity of the series,

 

10. ABC is a triangle; prove that log is the sum to infinity of

 

11. Find the sum to infinity of the series,

 

where neither α + β nor α – β is an odd multiple of π.

12. If x ≠ nπ, find the sum to infinity of the series,

 

13. If y = x sin α + x² sin 2α + x³ sin 3α + … , where |x| < 1, provo that sin y = x sin (y + α).

14. If y = x – t sin 2x + t² sin 4x – t³ sin 6x + … , where

 

15. If |x| < 1, find the sum to infinity of the series,

 

16. If , prove that

 

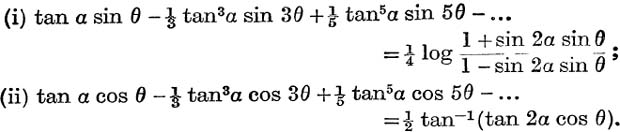
17. If (1 + x) tan θ = (1 – x)tan ϕ, and if |x| < 1, expand θ in ascending powers of x.

18. If tan α = cos 2ω tan λ, and tan²ω < 1, expand λ in ascending powers of tan²ω.

19. If 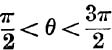, find the sum to infinity of the series

 

20. If |x| < 1, expand in ascending powers of x.

Generalised Indices. If α is positive and n is rational, it has been proved in Ch. IV, (see p. 65), that

 

If z is complex and equal to r(cos θ + i sin θ), where r ≠ 0, and if n is rational and equal to , where p, q are co-prime integers, it has been proved in Ch. IX, (see p. 165), that

 

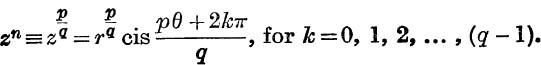
We shall now show that this is the same as exp (n Log z);

 

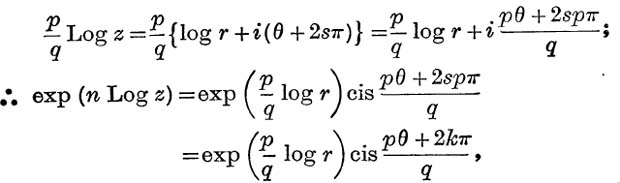
since 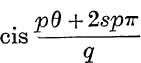for s = 0, 1, 2,… (q – 1) is the same as 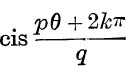for k = 0, 1, 2, … (q – 1) when p and q are co-prime.

But, by (17), ;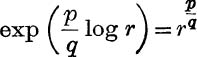

 

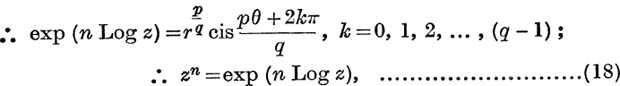
where n is any rational number, and z ≠ 0.

Definition. If z is any complex number except 0, and if w is any complex number, the function z^w is defined by the relation

 

The relations (17), (18) show that the definitions of Ch. IV and Ch. IX for aⁿ and zⁿ are consistent with, and in fact suggest, the definition (19).

Modulus and Amplitude of z^w. If z = r(cos θ + i sin θ), r ≠ 0, and w = u + iv, by (19),

 

 

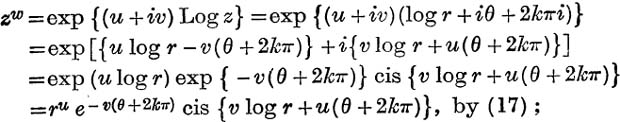
Thus z^w is an infinitely many-valued function, unless v = 0 and u is rational.

If v = 0 and w = u = , we have already seen that z^w is q-valued.

The principal value of z^w is defined to be exp (w log z); with the notation just used, this may be written

 

One special case of (20) should be noted :

 

 

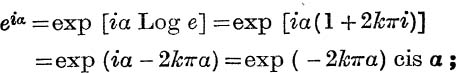
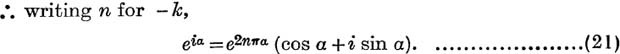
Thus e^iα is an infinitely many-valued function, and cos α + i sin α is merely its principal value. It is best, therefore, to avoid writing e^iα for the sum of the series 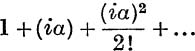; the sum of this series is exp (iα) or cis α and is, like these functions, one-valued.

The Binomial Series. The investigation of the binomial series

 

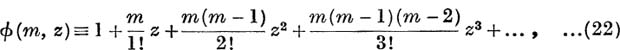
lies outside the scope of this book. We shall merely state the facts, and give some applications of them in Ex. XIII. c.

(i) If m is a positive integer or zero, the number of terms in the series is finite and the sum is the one-valued function (1 + z)^m, for all values of z.

(ii) If m is not a positive integer or zero, suppose that m = α + iβ.

(a) If |z| < 1, the series is absolutely convergent, and its sum to infinis the principal value of (1 + z)^m, that is to say,

 

(b) If |z| = 1, z ≠ – 1, the series is absolutely convergent if α > 0, and is convergent, but not absolutely, if – 1 < α ≤ 0, and in either case its sum to infinity is exp {m log(1 + z)}. If α ≤ – 1, the series is divergent.

(c) If z = – 1, the series is absolutely conyergent if α > 0, and its sum to infinity is 0. If α = 0, β ≠ 0, or if α < 0, the series is divergent.

(d) If |z| > 1, the series is divergent.

Note. Although the complete statement is necessarily elaborate, there is one simple fact that covers the vast majority of cases that occur: namely, on the circle of convergence, excluding z = – 1, the series is convergent if α > – 1.

Logarithms to an Arbitrary Base. Definition. If ζ is any one of the values given by z^w = ζ, we say that w is a logarithm of ζ to the base z, and we write

 

By definition (19), exp {w Log z} = z^w = ζ;

by definition (1), p. 241, w Log z = Log ζ;

 

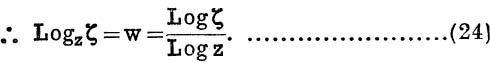
If ζ = ρ(cos ψ + i sin ψ) and z = r(cos θ + i sin θ), then

 

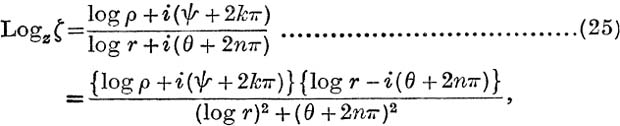
which shows that Log_zζ is a doubly infinitely many-valued function.

The principal value of Log_zζ is defined by the relation,

 

Note. Sometimes a more restricted definition is given for Log_zζ as follows : If ζ is the principal value of z^w, then w is called a logarithm of ζ to the base z.

In this case, w = Log_zζ is equivalent to ζ = exp (w log z);

by definition (1), p. 241, w log z = Log ζ;

 

And, in particular, .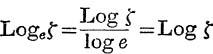

With this definition, Log_zζ is a singly infinitely many-valued function and becomes identical with Log ζ when z = e.

EXERCISE XIII. c.

Express the general values of the following in the form a + ib or in the modulus-amplitude form:

1. 2ⁱ.

2. l^{1 + i}.

3. iⁱ.

4. (l – i)ⁱ.

5. (l + i)^{– i}.

6. (– i)^{– i}.

7. e^πi.

8. e^πi.

9. e^nπi.

10. e^{x – yi}.

11. i^{– π}.

12. π^{– i}.

Write the following in a form which shows their many-valuedness:

13. Log₁₀².

14. Log₁³.

15. Log_iⁱ.

16. Log₉³.

17. Log e^{u + iv}.

18. (cos θ – sin θ)ⁱ.

19. What value does the definition z^w = exp (w Log z) give for i².

20. What is the condition for the principal value of e^{u + iv} to be of the form a + 0i ?

21. Prove that the principal value of i ^{log(1 + i)} is cis .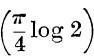

22. Find the modulus and amplitude of the principal value of x^x, if x is a negative number.

23. Find the general value of e^exp(θi) × e^{exp(– θi)}.

24. If p + 0i is the principal value of (x + yi)^{a + bi}, where x > 0, prove that b log (x² + y²) + a tan^–1 is a multiple of π.

How is this affected if x < 0 and y < 0 ?

25. Prove that the ratio of the principal values of (1 + i)^{1 – i} and (1 – i)^{1 + i} is sin (log 2) + i cos (log 2).

26. Find the values of z for which i^z = cis απ.

27. (i) Is every value of z^w₁ × z^w₂ a value of z^{w₁ + w₂}?
  (ii) Is every value of z^{w₁ + w₂} a value of z^w₁ × z^w₂?
  (iii) Are the principal values of z^w₁ × z^w₂ and z^{w₁ + w₂} equal ?

28. Prove that the points in the Argand Diagram which represent the values of e^{cos α + isin α} lie on the equiangular spiral whose polar equation is r = ce^{– θtan α}, where log c = sec α.

29. If |x| < 1, prove that the sum to infinity of the series,

 

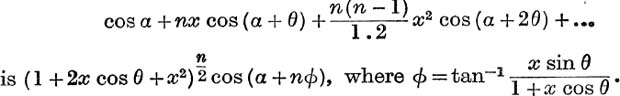
30. If, in the triangle ABC, a < b, prove that cos nA is the sum to infinity of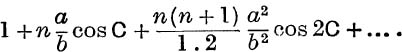

31. If n is real, state the conditions for convergence of the series:

 

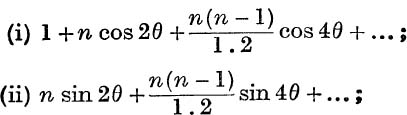
and find the sums to infinity if

 

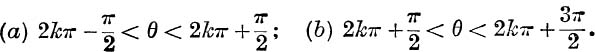
32. If n < 1, find the sum to infinity of the series,

 

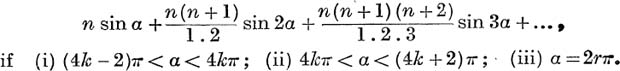
33. Prove that, if 0 < θ < π, the sum to infinity of the series,

 

is . Find the sum to infinity if π < θ < 2π.

34. If , prove that cos nθ cosⁿ θ is the sum to infinity of the series,

 

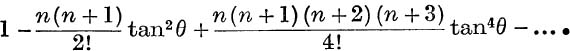
Find the sum to infinity if .

35. If |x| < 1, find the sum to infinity of the series,

 

The Generalised Inverse Circular and Hyperbolic Functions. The function Tan^{– 1}z is defined to be any value of w which satisfies the equation, z = tan w. The other inverse functions are defined in a similar manner ; all of them are many-valued. Thus

 

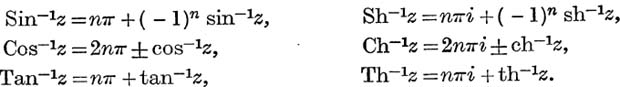
The inverse hyperbolic functions can be expressed as logarithmic functions. For example,

 

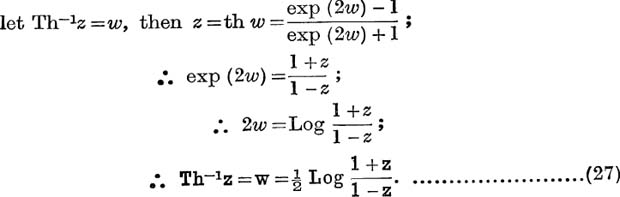
In expressing the inverse functions in the form α + iβ, care is required. The work for Tan^{– 1}(x + iy) is given in full below, and the other results are stated in Ex. XIII. d, Nos. 15, 16.

Expression of Tan^{– 1}(X + iy) in the form α + iβ. From the relation,

 

 

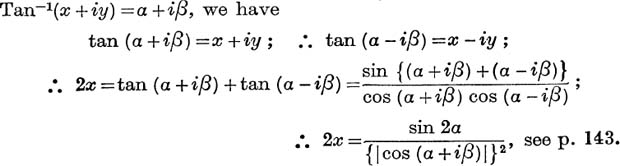
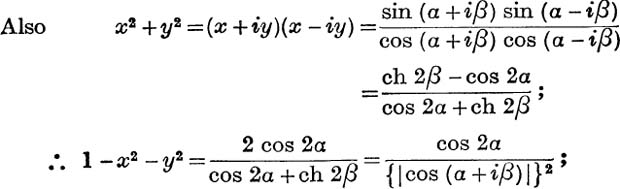
sin 2α has the same sign as 2x, and cos 2α has the same sign as 1 – x² – y²;

 

Unless both x and 1 – x² – y² are zero, that is unless x = 0 and y = ± 1, equation (28) gives one, and only one, value of 2α, say 2α₀, such that – π < 2α₀ ≤ π, and the general value is given by

 

where .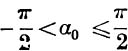

 

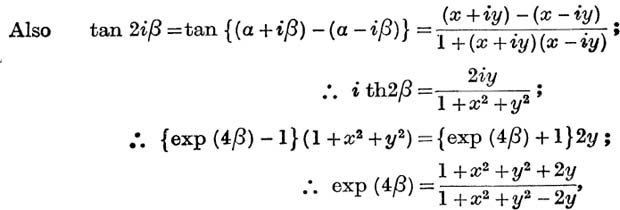
which gives a unique (real) value of β, namely

 

 

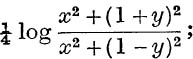
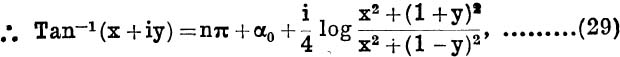
where α₀ is the unique angle satisfying equation (28), such that 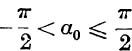. For the principal value, we have

 

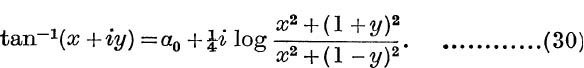
The function Tan^{– 1}(x + iy) is not defined for either of the pairs of values, x = 0, y = 1, or x = 0, y = – 1.

Note. The reader should observe the necessity for determining the sign of sin 2α and cos 2α. It might seem to him quicker to say

 

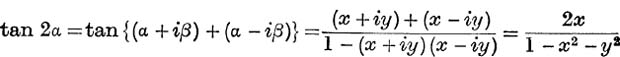
and to deduce that 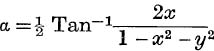, but this gives two values of α between – and + , and it is evident from the previous work that one of these is incorrect.

Also equation (28) is written in a proportion form to avoid considering separately the special cases 1 – x² – y² = 0, x = 0.

EXERCISE XIII. d.

1. Prove that, in equation (29), if x² + y² ≠ 1, α₀ may be replaced by 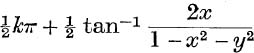, where

(i) k = 0, if x² + y² < 1;

(ii) k = 1, if x² + y² > 1 and x > 0;

(iii) k = – 1, if x² + y² > 1 and x < 0.

2. Prove that Ch^–1z = 2nπi ± i cos^–1z; find similar expressions for Sh^–1z and Th^–1z.

3. Prove that Sh^–1z = inπ + (– 1)ⁿ log {z + (1 + z²)}.

4. Prove that Ch^–1z = 2inπ ± log {z + (z² – 1)}.

5. If cos^–1(α + iβ) = u + iv, prove that

(i) α2 sec²u – β² cosec²u = 1;

(ii) α² sech²v + β² cosech²v = 1;

(iii) cos²u and ch²v are the roots of the equation

 

6. If sin^–1 (α + iβ) = u + iv, prove that sin²u and ch²v are the roots of the equation μ² – μ(l + α² + β²) + α² = 0.

7. Prove that one value of 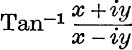, where x > y > 0, is

 

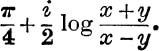
8. If ch^–1 (x + iy) + ch^–1 (x – iy) = ch^–1α, prove that

 

9. If Sin^–12 = u + iv, prove that u = 2nπ + and v = ±log(2 + 3).

10. Solve cos z = 1.

11. Solve sin z = 1.

12. Evaluate Cos^–1(–2·6).

13. Evaluate Sin^–1i.

14. Express tan^–1(cos θ + i sin θ) in the form u + iv, if

 

15. If Cos^–1(x + iy) = u + iv, where x > 0 and y > 0, prove that

(i) cos²u and ch²v are the roots of λ² – (1 + x² + y²)λ + x² = 0 ;

(ii) ch v = t₁ + t₂ and cos u = t₁ – t₂, where t₁ = and ;

(iii) sin u and sh v are of opposite sign.

Deduce that ,

 

16. If Sin^–1 (x + iy) = u + iv, where x > 0 and y > 0, prove that, with fche notation of No. 15,

 

 

17. If tan (α + iβ) = tan ϕ + i sec ϕ, prove that, for 0 < ϕ < ,

 

Find the values of 2α and β for – < ϕ < 0.

18. Prove that, for real values of θ,

 

19. If sin^–1 (cos x + i sin x) = u + iv, prove that, for principal values.

 

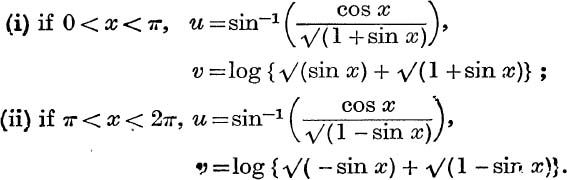
EASY MISCELLANEOUS EXAMPLES

EXERCISE XIII. e.

Express in the form a + bi:

1. .

2. e^{(x + yi)2}

3. (sin θ + i cos θ)ⁱ.

4. Log {Log (cos θ + i sin θ)}.

5. .

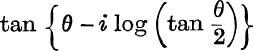6. Find all the values of (1 + i)^{1 + i}.

7. Prove that, for 0 < x < π,

 

Find a similar expression for log sin (x + iy), if and y > 0.

8. If log , Prove that θ = i Log cot .

9. Sum to infinity:

 

10. If sin θ = th and if cos θ > 0, prove that one value of

 

11. If tan tan , and if 0 < α < π, 0 < β < π, prove that

 

12. If (1 – c) tan x = (1 + c) tan (x – y), and |c| < l, express y as a series of powers of c, involving x.

13. If 2π < θ < 4π, find the sum to infinity of the series,

 

14. If 0 < θ < 2π, find the sum to infinity of the series,

 

15. If n < 1 and – π < θ < π, prove that cos is the sum to infinity of

 

Find the sum if π < θ < 3π.

16. Find the sum to infinity of the series,

 

17. Find all real values of x, y, such that log cos (x + iy) = i tan^–1.

18. Find all the values of z, if i^z = e(cos α + i sin α).

19. If , find the sum to infinity of

 

20. Prove that, if Th^–1(tan x) = a + ib and i Sec^–1 (cos 2x) = c + id, then a = ± c.

HARDER MISCELLANEOUS EXAMPLES

EXERCISE XIII. f.

1. If log sin (x + iy) = α + iβ, prove that 2e^2α = ch 2y – cos 2x.

2. If |h| < 1, expand log (1 + 2h cos θ + h²) in powers of h.

3. If tan^–1(ξ + iη) = sin^–1 (x + iy), prove that

 

4. Simplify sin (Log iⁱ).

5. Prove that, for a > 0, one value of (a + bi)^{α + βi} is of the form vi, if β log (a² + b²) + α tan^–1 is an odd multiple of .

6. If tan log (a + ib) = x + iy, where x² + y² ≠ 1, prove that

 

7. If ch (x + iy) = sec(u + iv), prove that

 

8. Prove that 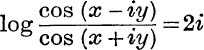tan^–1 (tan x th y).

9. If 3 tan (θ – α) = tan θ, prove that one value of α is the sum to infinity of

 

10. If , find the sum to infinity of the series,

 

11. If 0 < θ < π, find the sum to infinity of the series,

 

12. If the principal value of 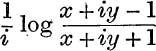is u + iv, prove that, when y tends to zero through positive values, u tends to π or zero according as x does or does not lie between – 1 and + 1.

13. If 0 < x < π, express sini(x + yi) in the modulus-amplitude form.

14. If tan (x + iy) = cot θ – i cosec θ, find the principal values of x and y in terms of θ, (i) if 0 < θ < ; (ii) if – < θ < 0.

15. Prove that one value of is log 2.

16. If x > 0, y > 0, express Ch^–1(x + iy) in the form a + ib.

17. If n > – 1, find the sum to infinity of the series,

 

18. Find the sum to infinity of the series,

 

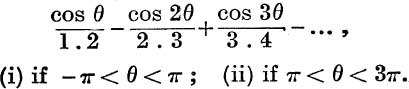
19. If y = log tan 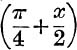, prove that x = –i Log tan .

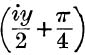If y is expressed as a convergent series in powers of x,

 

if x can be expressed as a convergent series in powers of y, find the expansion for x in powers of y.

20. Prove that 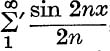, where ∑′ denotes that terms for which n is a multiple of 3 are omitted, is

 

21. Determine the conditions under which

 

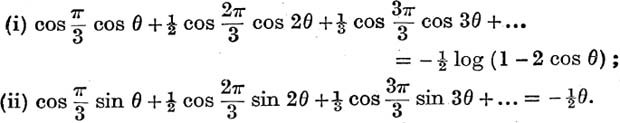
22. If P, P₁, P₂ represent the complex numbers z, z₁, z₂, and if the half-line from P parallel to Ox either cuts P₁P₂ externally or does not cut P₁P₂ at all, prove that .