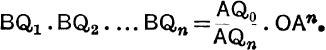
CHAPTER VII

PROJECTION AND FINITE SERIES

Projection.  The projection of a point on a straight line is the foot of the perpendicular from the point to the line.

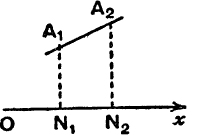
If, in Fig. 45, N₁, N₂ are the projections of A₁, A₂ on Ox, then N₁N₂ is called the projection of A₁A₂ on Ox.

If O is the origin, Ox the x-axis and (x₁, y₁), (x₂ , y₂) the coordinates of A₁ A₂, then

 

FIG. 45.

 

This relation is true for all positions of A₁ and A₂, provided that the usual sign-conventions of coordinate geometry are observed.

The coordinates of a point are directed (i.e. positive or negative) numbers ; N₁N₂ represents the displacement from N₁ to N₂ and is measured by a positive number if N₁ → N₂ and O → x he have the same sense, and by a negative number if they have opposite senses. (See also M.G., p. 37.)

If A₁, A₂, A₃ are any three points in a plane and if all the projections are taken on the same line Ox, then

 

If N₁, N₂, N₃ are the projections, and (x₁, y₁), (x₂, y₂), (x₃, y₃) are the coordinates, of A₁, A₂, A₃, then

 

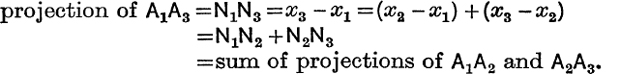
A similar argument shows that, for any number of points in a plane, the projection of AC is the sum of the projections of AB₁, B₁B₂, B₂B₃, …, B_n–1B_n, B_nC. (See M.G. Ch. V.)

The following results are evident from Fig. 46.

 

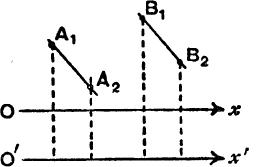
FIG. 46.

(i) If O′x′ is parallel to and in the same sense as Ox, the projections of A₁A₂ on Ox and O′x′ are equal.

(ii) If two lines A₁A₂, B₁B₂ are equal and parallel and in the same sense, their projections on any line Ox are equal.

(iii) The projection of A₁A₂ on any line Ox is equal in magnitude and opposite in sign to that of A₂A₁ on Ox. For, if A₁ is (x₁, y₁) and A₂ is (x₂, y₂), the projections are x₂ – x₁ and x₁ – x₂ respectively.

Measurement of Angles.  An angle from a directed line Ox to a directed line A₁A₂ is defined as follows, (see Fig. 47). Through A₁ draw A₁x₁ parallel to Ox and in the same sense ; then if a rotation through an angle θ in the anti-clockwise direction will bring A₁x₁ into the position A₁A₂, the angle θ is called an angle from Ox to A₁A₂. This is sometimes written

 

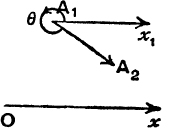
FIG. 47.

 

The following facts deserve notice :

(i) If θ is an angle from Ox to A₁A₂, then θ + 2nπ is also an angle from Ox to A₁A₂, n being any positive or negative integer.

(ii) The angles from Ox to A₂A₁ are not the same as those from Ox to A₁A₂. If one value of (A₁A₂, Ox) is θ, then one value of (A₂A₁, Ox) is θ + π.

(iii) With the notation of (ii), one value of (Ox, A₁A₂) is – θ, and the general value is 2nπ – θ.

The equality sign in equation (3) is in fact the sign of congruence (mod 27r) ; and the order of the elements in the symbol, (A₁A₂, Ox), is relevant.

Evaluation of Projections. If the length of A₁P is l units, and if (A₁P, Ox) = θ the projection of A₁P on

 

This is a direct consequence of the definition of the cosine of the general angle (E.T., Ch. VII, p. 99). For, if A₁x₁ is parallel to and in the same sense as Ox, (A₁P, A₁x₁) = (A₁P,Ox) = θ,

 

FIG. 48.

 

Here, l is a signless number and the statement is true for all values of θ; l cos θ may, of course, be either positive or negative.

Position of a point on a directed line. On a directed line A₁A₂, there are two positions of P such that the length of A₁P is l units see Fig. 49 (a) and Fig. 49 (b).

This ambiguity can be removed by a natural use of a sign-convention.

If the sense of A₁P is the same as that of A₁A₂, we write A₁P = + l, and if it is opposite to the sense of A₁A₂ we write A₁P = – l. By means of this convention, the position of a point P on a directed line is fixed

 

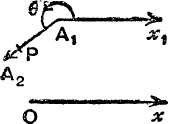
FIG. 49 (a).

 

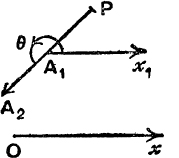
FIG. 49 (b).

uniquely by the directed(positive or negative) number which is the measure of A₁P. It is often convenient to represent this directed number by A₁P.

We can now replace equation (4) by the following :

If the directed line A₁A₂ makes an angle θ with Ox, and if the position of P on A₁A₂ is given by the directed number A₁P, then

 

For, in Fig. 49(a), (A₁P, Ox) = (A₁A₂, Ox) = θ and A₁P = + l, where l units is the length of A₁P;

by (4), projection of A₁P on Ox = l cos θ = A₁P. cos θ.

In Figs. 49 (a), 49 (b), the projections of A₁P on Ox are equal in magnitude and opposite in sign ;

in Fig. 49 (b), the projection of A₁P on Ox = –l cos θ; but in Fig. 49 (b), A₁P = – l;

the projection is A₁P cos θ, as before.

Projection on the axis of y. The axis of y is the directed line through O, which makes + with Ox, and the y-coordinate of any point P is the projection of OP on Oy.

It follows, by the same argument as before, from the definition of the sine of the general angle, that if (A₁A₂, Ox) = θ, and if P is any point on the directed line A₁A₂, given by the directed number A₁P, then

 

Example 1.  Find, with the data of Fig. 50, the projections of OB on Ox and Oy.

(OA, Ox) = a; but the directed line AB is ahead of OA ;

 

the projections of OA, AB on Ox are ;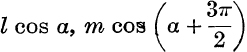

projection of OB on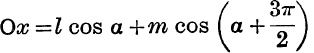

 

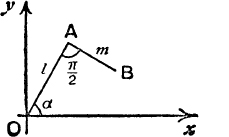
FIG. 50.

 

Note.  It saves time in working examples to adjust the signs of the terms by inspection of the figure ; a glance at Fig. 50 shows that the projection of OB on OY is l sin α – m cos α, not l sin α + m cos α.

EXERCISE VII. a.

1. In Fig. 51, ABC is equilateral and (AB, Ox) = θ; find expressions for (i) (BC, Ox) ; (ii) (CA, Ox); (iii) (BA, Ox); (iv) (Ox, AC).

 

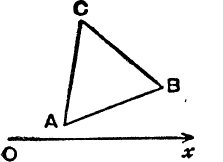
FIG. 51.

 

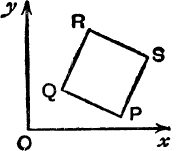
FIG. 52.

2. In Fig. 52, PQRS is a square and (PQ, Ox) = ϕ; find expressions for (i) (PS, Ox); (ii) (RS, Ox); (iii) (SQ, Ox); (iv) (RP, Ox).

3. With the data of No. 1, name a directed line such that the angle from Ox to it equals .

4. With the data of No. 2, name a directed line such that the angle from Ox to it equals .

5. With the data of Fig. 53, find the projections of the direction line AB, CD, EF, (i) on Ox, (ii) on Oy.

 

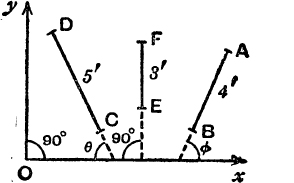
FIG. 53.

6. With the data of No. 2, if the length of PQ is c units, find the projections of the directed lines RQ, QP, QS, (i) on Ox, (ii) on Oy.

7. In Fig. 54, ABCDEF is a regular hexagon; the length of AB is a umts; find the projections on AK of the directed lines AB, BC, AC, AD, CF.

 

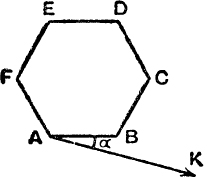
FIG. 54.

 

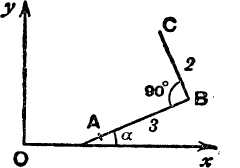
FIG. 55.

8. With the data of Fig. 55, find the projections of AC, (i) on Ox; (ii) on Oy.

9. With the data of Fig. 56, find the coordinates of C and D.

 

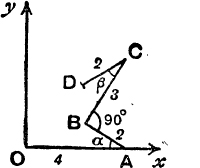
FIG. 56.

 

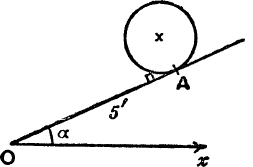
FIG. 57.

10. Fig. 57 represents a wheel of radius 1 ft. on an inclined plane; OA = 5 ft. Find the height of its centre above the horizontal Ox.

11. If from the point (h, k) a line of length r is drawn in a direction making an angle θ with Ox, what are the coordinates of its other extremity ?

12. If the directed line AB is of length s, and if (AB, Ox) = ϕ, and if B is the point (h, k), what are the coordinates of A ?

13. If AB, BC are of lengths r₁, r₂ and make angles θ₁, θ₂ with Ox, what is the length of AC ?

14. In Fig. 58, OD and PR are perpendiculars to AB, the length of OD is p, and the coordinates of P are (h, k); find the length of RP by taking the projections of RD, DO, ON, NP on OD.

 

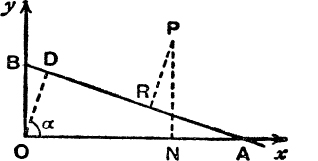
FIG. 58.

Addition Theorems. To prove that

 

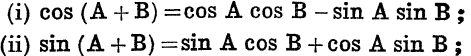
for angles of any magnitude.

Let the directed lines Oξ, OP, Oη make angles A, A +B, A + with

Ox ; and let the projections of P on Oξ, Oη be N, M. Suppose that OP contains l units of length.

The positions of N, M on the directed lines Oξ, Oη are given by the directed numbers which measure ON, OM, and these are, by the definitions of the cosine and sine of the general angle, l cos B, l sin B.

by equation (5), p. 120,

 

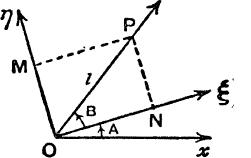
FIG. 59.

 

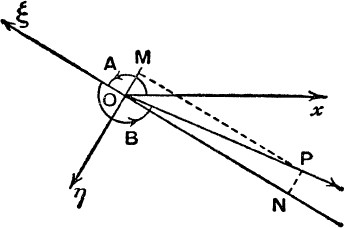
FIG. 60.

 

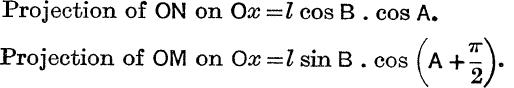
Also the projection of OP on Ox = l cos (A +B).

But the projection of OP on Ox is equal to the sum of the projections of ON, NP, i.e. to the sum of the projections of ON, OM, on Ox.

 

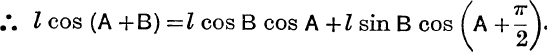
But , see E.T., pp. 199, 200;

 

Further, if the directed line Oy makes + with Ox, the projections of ON, OM, OP on Oy are

 

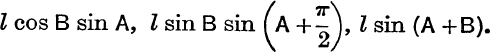
as before,

 

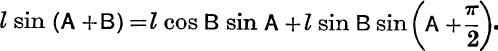
But 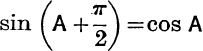, see E.T., pp. 199, 200;

 

This proof holds good for values of A and B of any magnitude, positive or negative. Figs. 59, 60 show two possible cases; the

 

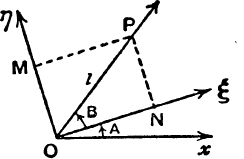
FIG. 59.

 

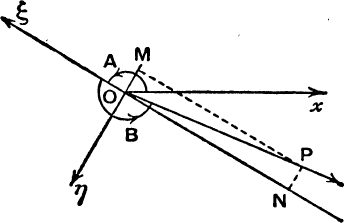
FIG. 60.

reader should draw other figures (e.g. A = 100°, B = 50° or A = 220°, B = 160°) and satisfy himself that the proof applies to them, without any modification.

Since the results of this chapter and their proofs hold for negative angles (see E.T., Ch. XIV, p. 198), we may write –B for B in (7) and (8). This gives

 

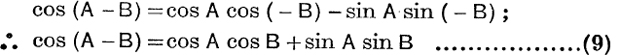
and

 

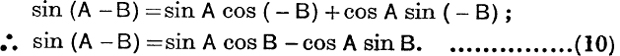
Application of Projection to the Summation of Certain Series.

Sum to n terms the series

 

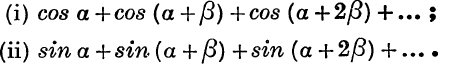
In Fig. 61, OA₁, A₁A2, …, A_n–1A_n are equal chords of a circle of radius R, forming an open polygon with exterior angles β.

 

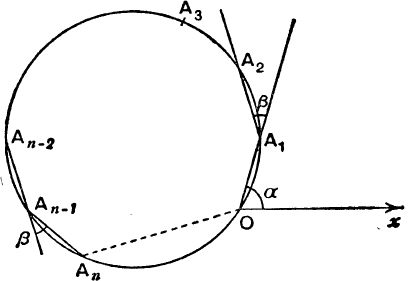
FIG. 61.

Each chord subtends an angle at the circumference and

from the formula , its length is ; also OA_n subtends an angle at the circumference, therefore .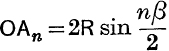

Draw Ox so that (OA₁, Ox) = a.

Then

 

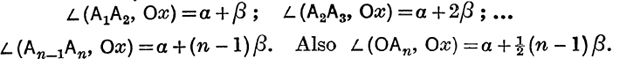
Now the projection of OA_n on Ox is the sum of the projections on Ox of OA₁, A₁A₂, … A_n–1A_n;

 

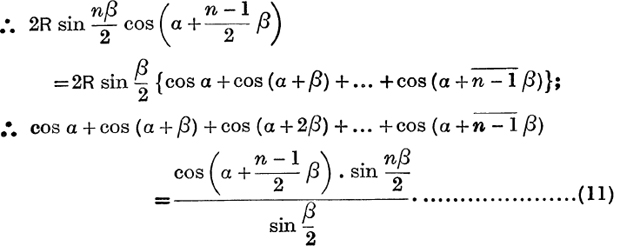
Similarly, taking the projections on Oy,

 

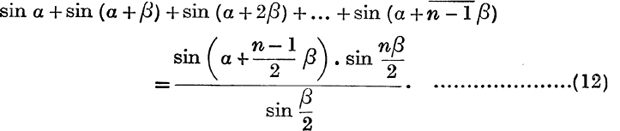
Relation (12) may be deduced from relation (11) by writing α – for α.

EXERCISE VII. b.

1. Examine the proof on pp. 123, 124 for the expansion of cos (A + B), drawing appropriate figures, in the following cases:

 

2. If in Fig. 59 the coordinates of P referred to Ox and the line Oy which makes + with Ox as axes, are x and y, what are the coordinates of P referred to Oξ and Oη ?

3. Answer the same question as in No. 2 for Fig. 60.

4. Write out in full the proof by the method of pp. 123, 124, that

 

 

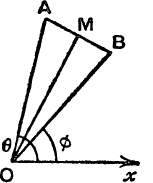
FIG. 62.

5. In Fig. 62, OA = OB, AM = MB, xOA = θ, xOB = ϕ; express the projections of OA, OB in terms of those of OM, MA, MB, and, by adding, prove that

 

6. With the data of No. 5, by subtracting, prove the corresponding formulae for cos θ – cos ϕ and sin θ – sin ϕ.

7. By projecting the sides of a regular pentagon on suitable lines, prove that

 

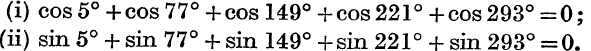
8. Prove the results of No. 7 by formulae (11) and (12).

9. Prove by projection that

 

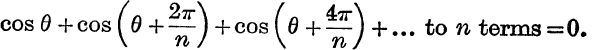
Is a similar result true for sines ?

10. Use formulae (11) and (12) to verify the results of No. 9.

11. By means of the identity

 

Prove this

 

Prove this also by formula (II)

12. By means of the identity

 

find the sum of the series sinθ +sin 3θ +sin 5θ + … to n terms. Check your result by formula (12).

Series. The formulae (11), (12) give the sums of series of sines or cosines of angles which are in A.P. Their utility justifies the addition of an analytical proof, which also illustrates an important method of summation.

Sum to n terms the series

 

Multiply each term by 2 sin .

 

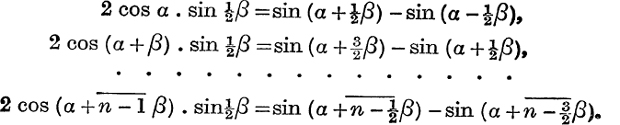
By addition,

 

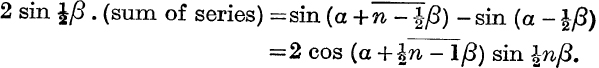
This gives for the sum of the series the same expression as was obtained in relation (11), p. 125.

The sum can be expressed in words as follows :

 

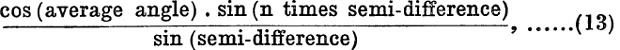
and it is best to remember it in this form.

The reader should show that the series

 

can be summed by multiplying each term by the same factor as before, 2 sin 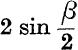and that the sum may be written

 

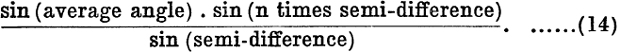
The fact that the second series can be deduced from the first by writing for α shows that the multiplier 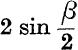required for the first must equally suit the second series.

If π + β is written for β in the two series, we obtain

 

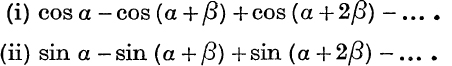
These could be summed directly by using the multiplier,

 

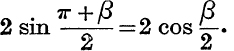
The sums of the sine and cosine series are deducible from one another by differentiation with respect to α.

The application of differentiation or integration to deduce the sum of one series from that of another is frequently useful.

It is justified by the identities :

 

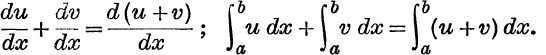
But this argument does not apply to an infinite series, because the sum of an infinite series is not the sum of its terms, and term-by-term differentiation or integration of an infinite series need not in fact give the differential coefficient or integral of the sum to infinity, unless special conditions are satisfied.

Example 2. Sum to n terms

 

The series

 

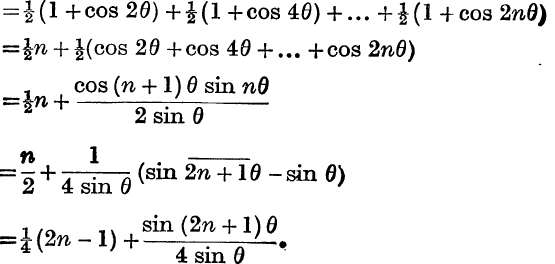
Example 3. Sum to n terms :

 

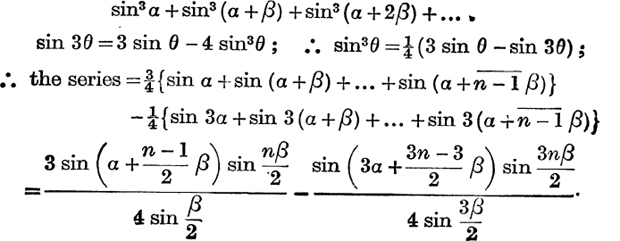
EXERCISE VII. c.

1. Sum ton terms: .

2. Prove that .

3. Prove that .

4. If n – 1 is a positive integer, prove that and , for r = 1 to n, are both zero.

5. Prove that , for r = 1 to n, is –.

6. Prove that .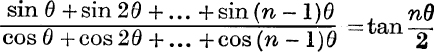

7. Sum: cos α – cos (α + β) + cos (α + 2β) – cos (α + 3β) + …

(i) to 2n terms; (ii) to (2n + 1) terms; (iii) to m terms.

Sum to n terms the series in Nos. 8-17.

8. sin α – sin (α + β) + sin (α + 2β) – … .

9. cos θ – cos 2θ + cos 3θ – ….

10. sin²θ + sin²2θ +sin²3θ + … .

11. cos (2n – 1)θ + cos (2n – 3)θ + cos (2n – 5)θ ….

12. cos θ sin 2θ + cos 2θ sin 3θ + cos 3θ sin 4θ + …

13. cosθ – sin 2θ – cos 3θ + sin 4θ + cos 5θ – sin 6θ – ….

14. cos²θ + cos²(θ + ϕ) + cos²(θ + 2ϕ) + ….

15. sin ²θ sin 2θ +sin²2θ sin 3θ +sin²3θ sin4θ + ….

16. cos³θ + cos³2θ + cos³3θ + ….

17. cos⁴θ + cos⁴2θ + cos⁴3θ + ….

18. Find the sum to n terms of sin θ +sin 2θ + sin 3θ + … and deduce the sum to n terms of cos θ + 2 cos 2θ + 3 cos 3θ + ….

19. Prove that sin θ + 3 sin 3θ + 5 sin 5θ + … to n terms

 

20. If , for r = 1 to n, prove that

 

21. If , prove that (i) the sum of any number of terms of the series cos θ – cos 3θ + cos 5θ – cos 7θ + … is positive or zero and less than and that (ii) the sum of n terms of the series

 

The Difference Method. The series on p. 127 were summed by expressing each term as a difference. No rule can be given which shows exactly when or how to apply the method. Considerable experience and ingenuity are sometimes required.

The essence of the method consists in expressing the general (rth) term, u_r, in the form f(r + 1) – f(r).

Then

 

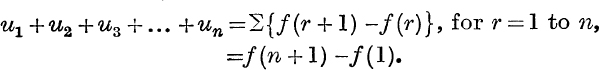
The difficulty disappears if the reader is asked to prove that the sum to any number of terms, say r terms, is ϕ(r), that is to say, if he knows what the answer is to be.

For

 

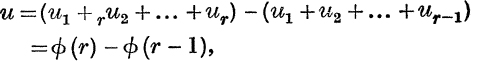
and the known form of the answer therefore supplies the form of the difference which he must obtain. In such cases, the work is substantially equivalent to the method of induction.

Example 4. Prove that the sum to n terms of

 

If this form for the sum is correct, the 1st term, tan θ, must equal cot θ – 2 cot 2θ; we therefore start by proving that this is so.

Now

 

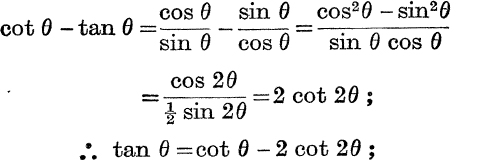
writing 2θ for θ and multiplying by 2,

 

Similarly,

 

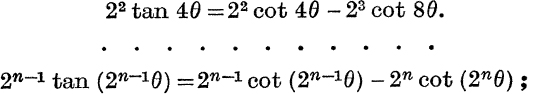
by addition, the sum to n terms of the given series is

 

Example 5. Sum to n terms :

(i)  cosec 2θ + cosec 4θ + cosec 8θ + … ;

(ii) 2 cosec 2θ cot 2θ + 4 cosec 4θ cot 4θ + 8 cosec 8θ cot 8θ + … .

(i) We have ;

 

Similarly, writing 2θ for θ,

 

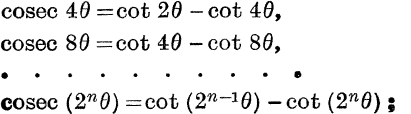
by addition, the sum to n terms of the given series is

 

(ii) Since , it follows at once that the sum of the second series is

 

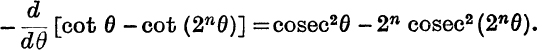
If a series such as (ii) occurred apart from the series (i) which has here served as a guide, the method would become apparent by using integration. Thus

 

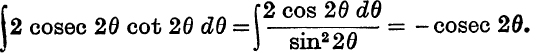
EXERCISE VII. d.

1. Prove that tan θ sec 2θ = tan 2θ – tan θ; hence find the sum to n terms of tan θ sec 2θ + tan 2θ sec 4θ + tan 4θ sec 8θ + … .

2. Prove that tan θ = cot θ – 2 cot 2θ ; hence find the sum to n terms of .

3. Prove that 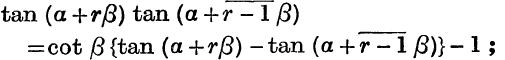; use this result to sum to n terms a certain series.

4. Prove that tan 2θ – 2 tan θ = tan²θ tan 2θ ; use this result to sum to n terms a certain series.

5. Prove that ; use this result to sum to n terms a certain series.

6. (i) Prove that .

  (ii) Sum to n terms, cosec θ cosec 2θ + cosec 2θ cosec 3θ + … .

7. Prove that the sum to n terms of

 

equals .

8. Prove that the sum to n terms of

 

equals .

Sum to n terms the series in Nos. 9-15.

9. sec θ sec 2θ + sec 2θ sec 3θ + sec 3θ sec 4θ + … .

10. tan θ tan 2θ + tan 2θ tan 3θ + tan 3θ tan 4θ + … .

11. cot θ cot 2θ + cot 2θ cot 3θ + cot 3θ cot 4θ + … .

12. .

13. sin θ sec 3θ + sin 3θ sec 9θ +sin 9θ sec 27θ + … .

14. .

15. .

16. Prove that . Hence sum the series, .

Sum to n terms the following series :

17. .

18. .

19. .

20. .

EASY MISCELLANEOUS EXAMPLES.

EXERCISE VII. e.

1. In Fig. 63, AB, BC are of unit length ; prove by projection that

 

What is the maximum value of cos α – sin α ?

 

FIG. 63.

2. Use the method of No. 1 to find the maximum value of

 

3. AD is an altitude of ∆ ABC, and Z is the middle point of AB. Prove that the projection of ZC on AD is c sin B.

4. If a and b are given numbers, express a cos θ + b sin θ in the form r sin(θ + α). Give geometrical interpretations of r and α. What are the maximum and minimum values of a cos α + b sin θ, and for what values of θ do they occur ?

5. Prove that , for r = 1 to n, is zero.

6. Prove that , for r = 1 to n, is .

7. Find , for r = 1 to n.

8. Find , for r = 1 to n.

9. Sum to n terms :

 

10. Prove that

 

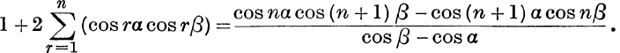
11. Prove that ∑(r sinr θ), for r = 1 to n, is

 

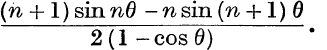
12. Evaluate ∑(r²cos rθ), for r = 1 to n.

13. Prove that , and deduce the values of , for r = 1 to n.

14. Sum the series log cos θ + log cos 2θ + log cos 4θ + log cos 8θ + … to n terms.

15. Evaluate when s_n is equal to the sum to n terms of .

16. If s_n = ∑sin rθ, for r = 1 to n, and if θ ≠ 2rπ, prove that

 

Also find the same limit for ∑ cos (2r – 1) θ, for r = 1 to n, when θ ≠ kπ

17. Sum to n terms tanθ + 2 tan 2θ + 4 tan 4θ + ….

18. Sum to n terms tan² θ + 2² tan² 2θ + 4²tan² 4θ +….

19. Prove that 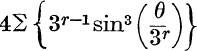to n, is equal to . Deduce another result by differentiation.

20. In attempting to draw a regular polygon A₁A₂ … A_n a person draws the sides A₁A₂, A₂A₃, … in order each of length c, but makes each interior angle of the figure too great by a. Prove that the final vertex, A_n+1, will be at distance front A₁.

21. If O is the circumcentre of the regular polygon A₁A₂ … A_n, prove that the sum of the projections of OA_l, OA₂, … OA_n on any line is zero.

22. In No. 21, if P is any point, and R is the circumradius, prove that .

23. If P is any point on the minor arc A₁A_2n+1 of the circumcircle of a regular polygon A₁A₂ … A_2n+1, prove that

 

24. If O is the centre of the in–circle, radius a, of a regular polygon A₁A₂ … A_n and if P is any point, prove that the sum of the squares of the perpendiculars from P to A₁A₂, A₂A₃, …, A_n–1A_n, A_nA₁ is

 

HARDER MISCELLANEOUS EXAMPLES

EXERCISE VII. f.

1. ABC is a triangle, whose side BC is divided at K in the ratio of p : q. If the projections of AB, AC, AK on any given line Ox are denoted by , prove that .

Obtain a special result by taking Ox to be the side BC ; and deduce that (p + q) cot AKC = q[cot B – p cot C.

2. OA, OB, OC are concurrent edges and OD is a diagonal of a rectangular box. If OP makes angles α, β, γ and θ with OA, OB, OC and OD, prove that

(i)  OD cos θ = OA cosα + OB cosβ + OC cos γ;

(ii) cos²α + cos²β + cos²γ = 1.

3. In any quadrilateral ABCD, prove that

 

4. In any pentagon ABCDE, where AB = a, BC = b, etc., prove that a² + b² – c₂ – d² – e² = 2ab cos B – 2cd cos D – 2de cos E + 2ce cos (D + E).

Sum to n terms the series whose rth terms are :

5. sin rx sin ry sin rz.

6. cos²rθ sin³rθ.

7. cos⁵rθ.

8. (n – r + 1) cos (r – 1)θ.

9. r cos (n – r)θ.

10. (n – r + 1) cos²(r – 1)θ.

11. Prove that .

12. Evaluate ..

13. What is the product of

14. What is the product of

15. Prove that .

16. Prove that .

Sum to n terms the series whose rth terms are:

17. .

18. .

19. sin 4rθ cosec rθ.

20. .

21. Sum to infinity the series :

 

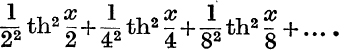
22. A₁A₂ … A_n is a regular polygon, prove that

 

23. A₁A₂ … A_n is a regular polygon inscribed in a circle centre O, radius R ; P is a point near O. Prove that

 

24. A regular polygon of n sides is inscribed in a circle centre O, radius R ; P is a point at distance c from O. Perpendiculars are drawn from P to the sides of the polygon. Prove that the sum of the squares of the sides of the new polygon formed by the feet of these perpendiculars is .

25. AB is a diameter of a circle centre O; Q₀ is any point on the circumference; Q₁, Q₂, Q₃, … Q_n are the middle points of the arcs AQ₀, AQ₁, … AQ_n–1 respectively. Prove that