The first intention of the painter is to make a flat surface display a body as if modeled and separated from this plane.… This accomplishment … arises from light and shade.… Perspective, with respect to painting, is divided into three parts … the first is the diminution in the size of bodies at various distances; the second part is that which deals with the diminishing in color of these bodies; the third is the diminution in distinctness of the shapes and boundaries which the bodies exhibit at various distances.1
—Leonardo da Vinci
ccording to physics, with receding distance the intensity of light from the scene (the source) drops off as the inverse square of the distance. There is additional attenuation of this intensity from the absorption and scattering of light by the atmosphere interposed between the subject and the viewer. This scattering or dispersion of light by the atmosphere also causes degradation in the resolution of the image as well as dilution or smearing of the wavelengths defining colors—a process that also leads to the blue appearance of the sky. Since the rays of light, traveling in straight lines, are all received by the eye at a point, the size of the image must drop off linearly with distance.
Leonardo’s observations in that opening quote are entirely compatible with the principles established by science. Dust particles, microscopic pollen, and water molecules suspended in the air cause light to scatter and change frequencies. The effect is to add “white light,” washing out the vividness of the spectrum of colors from the source. As for the “blue of the sky,” it can be explained by the Rayleigh scattering phenomenon, demonstrated mathematically almost four hundred years after Leonardo made the pronouncement.
A property of light that is crucial to the scientist, but inconsequential to the artist, is its finite speed, rendering the scene viewed a composite image in time. It is essential for the astronomer to take into account that in the image of the night sky some stars lie a few light-years away, while others are hundreds, thousands, or millions of light-years away. It may be interesting, although, entirely irrelevant for the portrait painter, that in the image of his subject, light from the sitter’s cheeks and ears may be “older” by a fraction of a nanosecond than light from the tip of his nose (depending on how the subject is turned). And it is also irrelevant that in the image viewed by the landscape painter, light from the distant mountains and valleys is older by a few microseconds than light from objects in the foreground.
The theory of linear perspective is of central importance as a tool for the painter to create an illusion of depth—the appearance of three dimensions on a two-dimensional plane. It was already present in the works of Agatharchus, scene painter for the great tragic dramatist, Aeschylus, in the fifth century B.C. Indeed, so effective were Agatharchus’s scrims (backdrops) that they gained Plato’s enthusiastic praise of the illusion of reality presented. Although no perspective paintings from classical Greece have survived, Pompeii, that veritable time capsule from A.D. 79, offers a window onto Roman architectural drawing and most likely a window onto the earlier Greek as well. Neuroscientist Christopher Tyler, an authority on human vision and separately on the theory of perspective in painting, suggests that it may even have been Greek artists who painted those architectural murals in Pompeii in which a measure of perspective is displayed.2
Euclid (325–270 B.C.) formalized geometry, but the use of perspective in ancient art was based on the artist’s intuition rather than on any mathematical authority. In the architectural drawings in Pompeii, for example, there are unrelated vanishing points along a pair of parallel horizon lines, whereas the correct picture in the one-point perspective scheme calls for a single horizon line and a single vanishing point. Medieval and even early Renaissance artists had been content to represent their subjects symbolically. Since their subjects were usually religious, the backgrounds were generally flat gold leaf, as far removed from reality and perspective design as heaven is from earth.
Projective geometry, the mathematics underlying the rules of perspective, was born in the Renaissance and indeed may have ushered in the art of the High Renaissance. One-point perspective appeared first in the works of Masaccio and Masolino in the first half of the fifteenth century, coming to full fruition in the works of Leonardo da Vinci in the second half of the century. Although the scheme was firmly established with Leonardo, it saw further refinement in subsequent centuries with the introduction of two-point perspective a century later and three-point perspective much later—after cameras with tiltable lenses for architectural renditions were invented in the twentieth century.
The actual timeline of the development of projective geometry so closely parallels the development of the rules of perspective in art that it strongly suggests an all-pervasive interaction, the interdynamics between art and science. It was the Renaissance artist who insisted on the need to represent nature as it actually appeared, not as it was thought to appear. This vision turned out to be a transcendent gift of the artist to the scientist. The role of Leonardo in this context cannot be overstated. One of the most significant drivers in the development of the theory of perspective was Leonardo, the paragon of the artist-scientist: a consummate artist doing science, a consummate scientist doing art. Later we will see three portraits of women that Leonardo painted at fifteen-year intervals. With each portrait Leonardo returned to painting having done little art in between, but each time showing astonishing growth as an artist, not just starting where he left off, but at an astoundingly higher level. In the time between paintings he did everything else—the mental inventions, the sketches, the anatomical studies, designs of bridges, spring driven vehicles, thoughts of human flight and experiments with optics. Painting alone was simply too easy, and slavishly producing canvas after canvas without substantial experimentation was the lazy way out. He berated and cajoled other artists: “Those who fall in love with practice without science,” he wrote, “are like pilots who board a ship without rudder or compass.”3 Leonardo was bridging the two fields of art and science, and creating as he went along. Raphael, on the other hand, superb draftsman, practiced exquisite, flawless composition and perspective, but was not “a driver” in the same sense.4 He applied established rules but did not discover any new ones.
If one is to seek an answer to why the artist in the Renaissance became aware of issues of perspective, one has to look no further than the extraordinary serendipity that saw the artist as an architect and engineer. The image of the Renaissance man as one frequently preoccupied with philosophy, literature, poetry, music, mathematics and natural philosophy (science), as well as with the skills of the artist-architect, is not just an empty metaphor. The cross-semination of the variety of interests he brought to his work and the presence of enlightened patrons willing to listen served as key ingredients in the remarkable intellectual and artistic blossoming of the period.
In a number of instances there are opportunities to see how the artist started the work and how a painting was thought out or abstracted. In some cases detailed studies for a final painting have survived as cartoons. In others, a sketch can be seen on the canvas of the unfinished work. Modern technologies such as stereoscopic microscopy, infrared reflectography, or x-radiography can be applied to the finished works, making overpainted details visible. Before painting the Adoration of the Magi the twenty-nine-year-old Leonardo produced intricate perspective and compositional studies for his design. The painting itself was left unfinished, but it became one of the gems of the Uffizi in Florence. This is a work we shall revisit in Chapter 9.
Meanwhile, Leonardo’s northern contemporary, Albrecht Dürer, was so preoccupied with understanding the issues of perspective that in his works of art he adhered strictly to the system he was developing independently, but he also created works of art, mostly woodcuts, demonstrating actual techniques for achieving error-free perspective. In one woodcut the artist is seen observing his subject from a fixed point of perspective through a frame onto which a grid has been scored. As he observes his subject through the scored frame defining his plane of view, he painstakingly maps out the image on the drawing board on his table, similarly scored. In another woodcut we see mounted within the frame a pane of glass (with a scored grid). The pane of glass is hinged in the style of a window that can swing outward, so that the angle it makes with the plane of view can be adjusted (Figure 7.1). The artist seeks to correlate the intersection of rays of light from his subject with the angled pane and the visual plane defined by the frame itself.
The quest of the Renaissance artist was to formulate theorems that would assist in precisely mapping a three-dimensional scene observed (or imagined) onto an imaginary pane of glass, or specifying exactly how a scene would appear on the two-dimensional pane. Obviously, the canvas itself is not transparent, but the scene, properly visualized on that imaginary pane, would then be recreated on the canvas. The questions that the Renaissance artist raised and the theorems he deduced became seminal issues for a new branch of mathematics, projective geometry.5 In the hands of the professional mathematicians the field blossomed into an elegant, general, and powerful geometry, with applications to physics, crystallography, and chemistry.
A square at a distance will have different appearances depending on the vantage point of the observer—an intuitively obvious result, and one that can be proven by ordinary Euclidean geometry. What assists the artist in deducing the proper shape is that transparent plane interposed between the observer’s eye and the subject, the square. A single square floor tile viewed directly from above will have a square appearance with the normal 90-degree vertices and sides of equal length. But observed at an oblique angle, an array of square tiles will have the shapes of quadrilateral figures, with parallel lines, defined by the edges of the tiles, appearing to converge at vanishing points. Nonetheless, the impression they create will be precisely that of square tiling.
The Dutch genre artists of the seventeenth century, especially Pieter de Hooch and Johannes Vermeer, are known for those impeccable lines of perspective with floor tiles, doorways, and walls all defining lines of one-point and two-point perspective. Vermeer’s magnum opus, The Art of Painting (Plate 7), shows that the appearance of the individual tiles on the flat space of the painting is anything but square, but the pattern conveyed is clearly that of square tiling. Parallel lines extrapolated from opposite edges of the tiles lead off into infinity, where they converge at a pair of vanishing points on the horizon line, thus demonstrating two-point perspective.
Vermeer created tantalizingly few paintings—approximately three dozen, only two dozen of which have survived—half a painting for each year of his short lifetime, and half as many as Rembrandt’s self-portraits alone. He created some of the most compelling works in the history of art, yet his personal life is shrouded in mystery. Common to nearly all his paintings are the unerring perspective and the nature of the scene—set in his studio with a female subject. After his father died when the artist was twenty, he was left to live with his mother and sister. When he took a wife, Catharina Thins, he moved into a rent-free house provided by his mother-in-law, again making his immediate companions women. When Catharina had children, a business at which she was beyond prolific—bearing fifteen children, eleven of whom survived—there was again a preponderance of girls. This sea of females that surrounded him may have colored his choice of subjects for his paintings. In all but two of his single subject paintings the subject is a woman. Yet he has portrayed these women so sensitively, in works that still confound and amaze us, works described as “serene and unnerving, sensuous and disembodied.”6 They appear mellifluous, placid, and always timeless.
Figure 7.1. Albrecht Dürer, De Symmetria Partium Humanorum Corporum (Draftsman Doing Perspective Drawings of a Woman), 1532. The Metropolitan Museum of Art, Gift of Felix M. Warburg, 1918. (Courtesy The Metropolitan Museum of Art, New York)
As a favorite son of the Dutch school Vermeer is second only to Rembrandt, who had a prodigious output. Although some of Vermeer’s Dutch contemporaries, especially Rembrandt and even Franz Hals, may have painted more forceful and dramatic psychological characters, their subjects are distinctly seventeenth-century Dutch contemporaries of the artists. With Vermeer’s subjects there is a timeless character to their visage; they could be our contemporaries. Except for a few resplendent outdoor scenes of Delft, the background is almost always the same: the artist’s studio, simple props chosen for the occasion, subdued light from a window at the left.
Phillip Steadman, an architect by training, who analyzed Vermeer’s paintings painstakingly for two decades and tracked down the few houses in which Vermeer lived, recently published a theory about Vermeer’s use of a camera obscura, or a type of “perspective box” similar to the one used by Samuel van Hoogstraten, in planning out his composition and achieving impeccable perspective (the simple optics involved consists of a pair of double convex lenses mounted in the aperture of the box).7 Steadman’s theory is vigorously disputed by art historian Walter Liedtke. Focusing on one painting, The Milkmaid, Liedtke writes, “It is not photographic, nor even materialistic effect, but an illusionistic device that works splendidly in that small, intensely colored picture.… Vermeer achieved an effect similar to that seen in a camera obscura (or a photographic reconstruction of how they work), but he was also enhancing effects of light that had been described by Dutch artists a few decades earlier (for example, Franz Hals).” Moreover, according to Liedtke, Vermeer may be unusual in his talent but is not really apart from the prevailing Delft school in technique, and “extraordinary talents can only come into being if they have the blood of such a community in them.”8 Without jumping headlong into the fray, I believe from my personal perspective as a scientist-artist there is most likely some truth to Steadman’s claim as well as Liedtke’s counter. Vermeer was indeed extraordinarily talented, and the fascination with new instruments was part and parcel of the Dutch Golden Age.
The controversy regarding whether and to what extent Vermeer may have used optical artifices to achieve the beguiling effects in his paintings may never be resolved. One undisputed fact, however, is that Vermeer did have access to the finest lens makers of the time. His closest friend was Antonie van Leeuwenhoek, inventor of the microscope. The refracting telescope was invented in Holland, and the exceedingly successful wave theory of light still used in elementary physics was developed by another Dutch compatriot, Christian Huygens. The inarguable fact is that there was evolving around Vermeer optical theory, and applications for art and science, and he was both a generous contributor to and a grateful benefactor of them.
While Vermeer and the Dutch masters were plying their trade in Holland, a self-taught French architect-engineer, Girard Desargues, formulated a powerful theorem in projective geometry, still known as “Desargues’s theorem.” The theorem—complicated conceptually and difficult to prove mathematically—pertains to points of convergence for lines in a geometric construction. In a number of works by acknowledged masters, including those serene and sublime indoor scenes of Vermeer and perhaps in the trademark Venetian panoramas of Canaletto, there appears intuitive compliance with the tenets of Desargues’s theorem. And much earlier still, Leonardo, in composing the Last Supper, had displayed thorough understanding of the derived perspective of the theorem. The perspective underlying the Last Supper is seen in the upper left inset of Plate 8.
Rather than getting mired further in the mathematical aspects of perspective, I shall examine the notions of one-point, two-point, three-point, and four-point perspective graphically with my own work, some of it created for the my book of lithographs, Oxford and the English Countryside.9 In one-point perspective a convenient artifice an artist might use is a perfectly clear cube, with minimal refraction, or light bending. The opposing faces of the cube are parallel to each other; the edges can be extrapolated to a vanishing point on the horizon line. Depending on whether the cube is viewed from above or from below, the horizon line will descend or ascend accordingly—but each time with the lines of perspective converging on the horizon line. The cube can represent a model for the interior of a room or, just as effectively, a street scene with the fronts of facing buildings parallel to each other (Figure 7.2).
Among the finest treasures of the Vatican are the series of monumental frescos Raphael executed between 1509 and 1511. In one, the School of Athens, Raphael integrates three elements of interest to us here. First is the breathtaking demonstration of one-point perspective, which had come into full fruition at the turn of the sixteenth century (Plate 9). Then we have a group portrait of the great natural philosophers of antiquity, a historical composite spanning approximately eighteen centuries—from Heraclitus (active sixth century B.C.) to Averroes (active twelfth century A.D.) And finally there are Raphael’s contemporaries—other artists, who serve as models for the philosophers. The mural offers an extraordinary real-life group portrait.
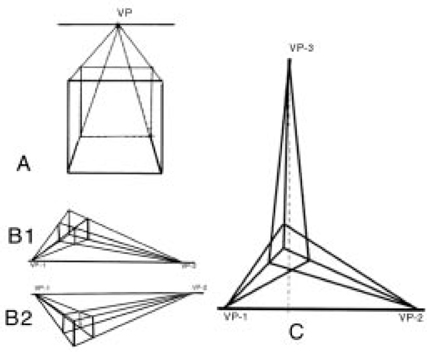
Figure 7.2. Diagrams of (A) one-point perspective; (B1, B2) two-point perspective; (C) three-point perspective
The sprawling character in the light blue toga in the lower center is Diogenes (c. 412–323 B.C.). In the lower left the man scrawling mathematics on a tablet, with two observers looking over his shoulder, is Pythagoras (c. 560–480 B.C.). At the bottom right, engaged in a geometric construction with a compass, while four young men watch intently, is the figure of Euclid, the geometer (c. 325–270 B.C.). At the top of the stairs and just below the colossal statue of Athena is the likeness of Socrates (479–399 B.C.). For the foregoing philosophers the artist-models are not known, although the model for Euclid is thought to be the architect Bramante. The brooding, dark, lonely character near the bottom of the mural, leaning on his elbow and seemingly in deep concentration, is meant to be Heraclitus, for whom the model is Michelangelo (1475–1564). The orthogonals (radial lines) of the one-point perspective employed converge on the two central characters seen at the top of the stairs: on the right, Aristotle (384–322 B.C.), and on the left, Plato (427–347 B.C.), for whom the model was Leonardo da Vinci. In the extreme lower right a cluster of four men engages in conversation, one representing Zoroaster (fifth century B.C.) and another, Ptolemy, each holding a globe. The second man from the right in that group, serving as host for the viewer, is the artist himself, Raphael. Historically the Renaissance artist, especially in the unique persona of Leonardo da Vinci, artist-scientist, preceded the Renaissance scientist in learning to observe nature, and especially how to ask the right questions, not just to hypothesize and introspect.
In two-point perspective there exist two vanishing points, and generally the subject, perhaps a building, is seen edge on. The center of gravity of each scene is the cube in the foreground. The upper and lower horizontal edges are extrapolated into the distance where they converge on a horizon line. The lines of perspective from four of the parallel edges of the cube converge at one of the two vanishing points, and the lines of perspective from four other edges (perpendicular to the first set) converge at the other vanishing point. In one instance the observer is above the top surface of the cube (Figure 7.2 B2); in the other the observer is below, looking upward at the bottom surface of the cube (Figure 7.2 B1). It is readily seen that if the cube is rotated about a vertical axis passing through the center of the cube, the vanishing points move horizontally along the line of sight, the horizon line.
An example of two-point perspective is seen in my own ink sketch (Figure 7.3). The scene is the northwest corner of the Supreme Court Building in Washington, D.C., where columns with ornate Corinthian capitals stand below the pediment. It is apparent that by rotating the subject around a vertical axis, one of the two vanishing points can be rotated to a point behind the cube, but then the other vanishing point will recede further into the distance on one side or the other. In the drawing, if the lines of perspective (drawn along the edges of the building) are extrapolated far enough, they would be found to converge at two separate vanishing points. These vanishing points VP-1 and VP-2 are located on the horizon line.
Figure 7.3. Two-point perspective illustrated in the detail of the United States Supreme Court Building, Washington, D.C. (ink sketch by the author)
Figure 7.4. Three-point perspective illustrated in a view of Tom Tower, Christ Church, Oxford (lithograph by the author)
In three-point perspective three separate vanishing points are utilized in giving the scene depth, while emphasizing the height of a subject. The scene depicted is either looking down from a great height (such as an aerial perspective of skyscrapers), or looking up to a considerable height from ground level. As in the preceding cases the “center of gravity” of the scene is the cube. A normal, or perpendicular vector is constructed at the center of the bottom surface of the cube (dotted line) in order to define the direction of the third vanishing point, or where the lines extrapolated from the vertical edges of the cube all converge (Figure 7.4). The three vanishing points are VP-1, VP-2, and VP-3.
Finally, in four-point perspective, there are four vanishing points: two converge on the horizon line, and the other two, at a pair of points far above and far below the subject. A simple scenario can be invoked in order to visualize the vanishing points at the top and bottom: an observer is placed at the fifty-first floor of a building across the street from the 102-story Empire State Building. As the observer views the building, the top will appear to converge at a vanishing point far above the building, and so too the bottom of the building, which will appear to converge at a point far below ground level. (Four-point perspective has not been illustrated among these figures.)
So far, we have seen the golden rectangle and the law of divine proportion first as geometric constructions and subsequently as the generator of the logarithmic spiral, the pentagram, and the pentagon. In the last chapter we noted that many of the patterns and regularities encountered in nature were seen to parallel those mathematical constructs. The pyramids and the Parthenon were found to be related to the golden ratio. In the context of graphic art, the golden rectangle becomes an artifice to organize artistic composition. And indeed there is evidence that, whether consciously or unwittingly, artists often imbue their works of art with this proportion, select their vantage points accordingly, and wherever possible site their subjects so that certain lines emerge as especially natural. Many of these lines coincide with the geometric construction lines partitioning the rectangle, and many of these lines also coincide with the lines of perspective.
Figure 7.5. The composition of the author’s lithograph Church Lane, Ledbury, England, is based on the subdivision of the golden rectangle seen in the inset figure, the “sweet spot” located in the lower portion of the rectangle.
Initially a canvas with length-to-width ratio approximating the proportion of the golden rectangle is selected: a pair of sequential numbers of the Fibonacci series, for example, 21 by 34 inches on the imperial system or perhaps 100 by 162 centimeters (about 40 by 66½ in.). Although this scheme can be used equally effectively with the canvas configured horizontally or vertically, only the latter case will be demonstrated. The canvas positioned vertically has a full-width square delineated either in the upper part of the rectangle or in the lower part. The former is especially conducive to portrait composition, the latter to street scenes. The quadrilateral area formed by the intersection of the diagonals defines the “sweet spot” (akin to that on the face of a tennis racket), inviting placement of an especially salient part of the scene.
I used this scheme when I did my ink drawing Church Lane at Ledbury, England (Figure 7.5). The scene has considerable bilateral symmetry, one side virtually mirroring the other. The simple network of diagonals of the golden rectangle closely resembles the intricate lacework of perspective lines in the one-point perspective scheme examined earlier. The representational artist has artistic freedom—to select the angle, pick the correct time of day for proper lighting, lower or raise branches of trees, add people, and subtract people, but not to redesign a building. The use, at least by the author, of the technique described above, reflects a belief that doing so will optimize the chance of rendering justice to the scene depicted and to the abstract requirements of art.
H. E. Huntley, writing about experimental aesthetics, reported studies by a number of German psychologists of the late nineteenth and early twentieth century regarding preferences for rectangles of different proportions.10 In 1876 Gustav Fechner made an inventory of thousands of common rectangular shapes—from windows to playing cards, from book covers to writing pads—and found an unusually high occurrence of rectangles reflecting the shape of the golden rectangle. Subsequently, he canvassed large groups of people and tabulated their preferences for rectangles of different length-to-width ratios: 1:1, 6:5, 5:4, 4:3, 10:7, 3:2, ϕ = 1.618, 23:13, 2:1 and 5:2. The results Fechner tabulated are presented as a table for ten different rectangles as 1, 2, 3, 4, … 10, respectively, and the associated histogram plotted as a bar chart (Figure 7.6). In the chart there appear bars at each ratio to indicate the actual preference in percentage of the individuals surveyed. As the bar chart shows quite clearly, the golden rectangle with length-to-width ratio of ϕ, is the overwhelming favorite among all the rectangles, having garnered 35 percent of the vote.
The results of similar studies by a number of other late nineteenth- and early-twentieth-century researchers—among them Adolf Zeising in Der Goldene Schnitt (1884), Witmar (1894), Lalo (1908) and Thorndike (1917), according to Huntley point unambiguously to a popular preference for rectangles approximating the golden rectangle.11 Helen Hedian reported an analysis—within the framework of the golden ratio—on four hundred paintings “of accepted excellence.”12 According to Hedian, all but a few of the artworks yielded to such an analysis, with the majority of the works yielding ϕ = 1.618 and a variation the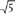 
-rectangle, i.e., 1:2.236 066. These and other values associated with the golden ratio and tabulated earlier (see Chapter 3) were found among the works she analyzed.
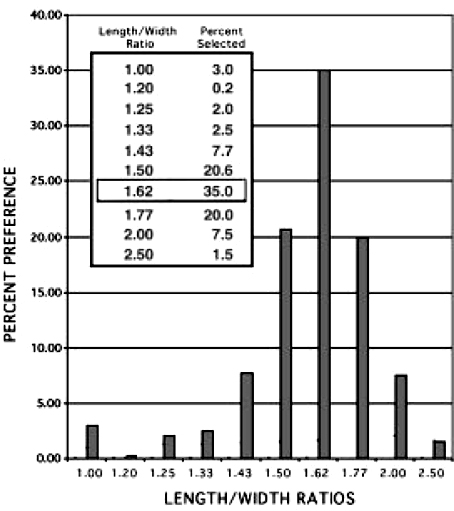
Figure 7.6. Chart of Gustav Fechner’s 1876 study revealing human affinity for the golden rectangle
Hedian’s inventory includes from the early Renaissance Giotto’s Ognissanti Madonna (c. 1310) in the Uffizi. This painting displays lines of perspective and divisions of the golden rectangle highly reminiscent of some of the geometric constructions encountered in Chapter 3. From the eighteenth and nineteenth centuries, she cites J.M.W. Turner’s Bay of Baise (Tate Gallery, London) and George Romney’s Lady de la Pole (1786; Museum of Fine Arts, Boston) as being susceptible to analyses in terms of the golden rectangle and its subdivisions. Among the paintings that she cites as having ratios close to 1:2.236 are Cézanne’s Still Life with Peppermint Bottle of 1894 (National Gallery of Art, Washington, D.C.); Seurat’s Fishing Fleet (c. 1885, The Museum of Modern Art, New York); Picasso’s Lady with a Fan (1905; Harriman Collection, National Gallery of Art, Washington, D.C.); and Matisse’s Variation on de Heem (1915). Finally, she cites a number of ancient works, among them an Egyptian stele (c. 2150 B.C.), an Assyrian winged demigod from the ninth century B.C., and the Dying Lioness from Nineveh, seventh century B.C., for inviting analyses in terms of the golden rectangle.
In the following pages I shall present my own sampling of masterworks incorporating geometric figures—polygons, polyhedra, the golden rectangle, logarithmic spiral, and others. The creators of these works have all been dominant figures of their respective times.
Spain can boast among its favorite sons El Greco, Diego Velázquez, Francisco Goya, Pablo Picasso, and Salvador Dali, some of the most influential artists in the history of art. Diego Velázquez’s Adoration of the Magi (see Plate 7, left), displays a height-to-width ratio very close to ϕ. Moreover, as a near golden rectangle it can be neatly subdivided, delineating a square in the lower portion, with the upper portion again forming a golden rectangle. The rectangle in the upper portion is subdivided again, creating a square in the upper left and another golden rectangle on the upper right. The intersection of these lines, defining the golden point, is at the place between the infant Christ’s eyes.
Until the late eighteenth and early nineteenth centuries creative artists saw themselves as having an abiding task—to reflect nature. That was the message in Leonardo’s words: “The most praiseworthy form of painting is the one that most resembles what it imitates.” And a century later that sentiment was echoed by Shakespeare in Hamlet III: ii, “the purpose of playing … was and is, to hold as ’twere the mirror up to nature.” In the Romantic period in England—in the poetry, first of Wordsworth and Coleridge, then Keats, Shelley, and Byron—the artist began to illuminate nature rather than to reflect it. (A similar transformation took place in music with the emergence of the Romantic composers—Beethoven, Schubert, and Chopin.) Impressionist and Post-Impressionist art would not have burst forth without this metamorphosis in outlook, nor Cubism a little later.
The postimpressionist artist Georges Seurat attempted to render the effects of artificial light at night using Pointillism, a technique that he personally invented. Inspired by a French translation of a lecture on artificial light by American artist James Whistler, Seurat formulated a scientific theory paralleling the ideas of Charles Henry (1859–1926), in which he cobbled together aesthetics and the physiology and psychology of the senses. Seurat, in describing his thoughts, wrote: “Art is Harmony. Harmony is the analogy of contrary and similar elements of tone, of color, and of line, considered according to their dominants and under the influence of light, in gay, calm, or sad combinations.… Gaiety of tone is given by the luminous dominant; of color, by the warm dominant; of line, by lines above the horizontal.”
Seurat’s works frequently incorporated the golden ratio, but none as prominently as Circus Side Show (La Parade) (Figure 7.7).13 Created near the end of his brief life, the painting describes the scene at the entrance to a traveling theater—free entertainment offered for the purpose of attracting audiences to attend the main event. Demarcations in color and texture offer clues to subdividing the canvas with vertical and horizontal lines, such as NE, CI, LG, etc. The rectangle defined by NEHK in the painting displays the ratio of length-to-width of approximately ϕ, making this portion of the canvas a golden rectangle. NCIK defines a square, rendering CEHI another golden rectangle. ϕ, in fact, is found at a minimum in the following four ratios:
Figure 7.7. Geometric diagram overlaying Georges Seurat, Circus Sideshow (La Parade), 1887–88. Oil on canvas, 39¼ × 59 in. The Metropolitan Museum of Art, Bequest of Stephen C. Clark, 1960.(Courtesy Metropolitan Museum of Art, New York)
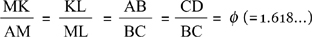
The multiple occurrence of the ratio is most likely a product of Seurat’s artistic intuition, a reflection of Fechner’s findings. If he had been formally applying the law of divine proportion, he would most likely not have remained mute in describing the process, after all, he had not been shy in articulating his “scientific theory.”
In Europe of the Middle Ages the circle had been regarded as a symbol for the divine or for heaven (as it was also regarded, for centuries, by Chinese philosophers). The reason for this may be that the circle is seen as an infinite-sided polygon with no beginning and no end. The earth, represented by a square with its sharply defined features, was symbolically subordinated to heaven by having the square circumscribed by the circle. The square, in turn, helps in generating equilateral triangles of angles 60°—60°—60° or isosceles triangles of angles 45°—90°—45°. By the time of the Renaissance the earth had risen to greater prominence, and man was the measure of all things. A triangular organization of composition circumscribed by a circular boundary was often used in the High Renaissance, for example in two prominent paintings: Michelangelo’s Holy Family and Raphael’s Alba Madonna (Plate 10).14
In Michelangelo’s tondo, the artist’s only known work to have been executed on canvas or panel, a geometric construction is found in a pair of interlocking triangles, evocative of the Star of David. (The horizon line defines one side of the star’s lower triangle.) An intriguing feature of the painting is that the figures exhibit a porcelain-like translucent quality. But then Michelangelo, by his own claim, was first and foremost a sculptor. The figure of the Virgin Mary exhibits a helical shape used to produce depth and dynamism, first introduced by Leonardo. As for Raphael’s Alba Madonna, embodying one of the finest pictorial compositions of the Renaissance, the painting was part of a collection purchased from the Hermitage in the early 1930s—the seller being the cash-strapped Stalin, who never had much use for art. The three figures in the painting are organized in a triangular scheme—of a right isosceles triangle with the 90-degree angle at the top. An even more precise organizational structure that the trio exhibits, however, is three-dimensional pyramidal form, again influenced by Leonardo. Finally a helical twist in the Virgin’s body, also a Leonardo influence, produces a sense of dynamism.
Dynamic symmetry was employed in antiquity—in the Egyptian pyramids 4,700 years ago, in the temples of Karnak and Luxor 3,300 years ago, in the Greek temples of the Age of Pericles 2,400 years ago and in Roman buildings a few centuries later—and persisted for several hundred years.15 In great art and architecture in disparate times the scheme seemed to be reinvented—developed independently (notwithstanding the Greek influence on the Romans). The defining Byzantine architectural gem, the Hagia Sophia, was built in the mid-sixth century on a model of an interlocking hemisphere and regular polyhedra. Five hundred years later still the great Gothic cathedrals in western Europe were constructed, in some instances incorporating dynamic symmetry. In the Renaissance dynamic symmetry was rejuvenated as an accompaniment to interest in the scholarship and art of the classical world. In the following section we examine a pair of edifices—the cathedral of Notre-Dame in Paris, a masterpiece of medieval architecture, and the pair or Petronas Towers in Kuala Lumpur, a cathedral to commerce—both reaching upward toward heaven, built nine hundred years apart.
The years 1163 to 1250, virtually coinciding with Leonardo Fibonacci’s lifetime, saw the erection of the most famous Gothic cathedral in all of Christendom—the cathedral of Notre-Dame in Paris. Architectural historians offer elegant artistic and structural explanations for virtually all aspects of the remarkable edifice, rising so high toward heaven, with flying buttresses seemingly introduced as adornment instead of for the critical purpose of supporting immense walls weakened by colossal windows. But one can only speculate about how the architect chose the proportions of the various external sections—was it by chance, the aesthetic judgment of the artistic eye, or the application of the Fibonacci series? We may never know. The Fibonacci series was, however, just being formulated in Pisa, although the divine proportion derived from ϕ had long been known. What is clear is that the facade of Notre-Dame features the proportions embodied in the golden ratio (Figure 7.8, left). The various segments indicated as adjacent pairs of lines exhibit ratios close to that magic ratio, 1:1.618. Specifically, the following proportions are surprisingly accurate for the great medieval cathedral:
Figure 7.8. Two prominent works of architecture, built almost a millennium apart, both illustrating the recursive use of the golden ratio: (left) Notre-Dame-de-Paris; (right) Petronas Towers, Kuala Lumpur
The surface abfe defines a square. With the rectangle bcjf added to it, the resulting surface has the shape of the golden rectangle. Similarly cdqh forms a square, but with the rectangle bcjf added to it, the resulting surface becomes a golden rectangle. Of course, bcgf itself is a golden rectangle. In the second course ijml forms a square, and with the golden rectangle jknm added to it, the resulting figure becomes a golden rectangle. The mirror reflection of these figures on the right hand side also satisfies the divine proportion. In the lower course rspo forms a square, but with the golden rectangle stqp added to the square, the resulting figure becomes a golden rectangle. The mirror reflection on the right also satisfies the divine proportion. Finally the entire west facade including the towers, displays proportions very close to those of the golden rectangle.
Applying the principle to new structures became a driving force behind Le Corbusier’s architecture in the first half of the twentieth century. Other modern architects have also invoked elements of dynamic symmetry in their own creations. In the Halliburton Tower, at Rhodes College in Memphis, Tennessee, architect H. Clinton Parrent has used the proportions given by sequential terms of the Fibonacci series to arrive at the heights of the various courses. In the closing years of the twentieth century a far more imposing edifice than that tower—indeed a pair of towers connected by a bridge—was erected in Kuala Lumpur (Figure 7.8, right). The national oil company of Malaysia, Petronas, commissioned the twin towers that exceed the height the Sears Tower in Chicago, the previous holder of the title of the world’s tallest building. The Petronas Towers (1998), designed by Cesar Pelli and Associates, rise 1,470 feet to proclaim Malaysia as a rising economic world power. In its structural design the base of each building is an octagon—a shape formed by an interlocking pair of squares, emblematic of the union of heaven and the earth. Massive columns of high-performance concrete and steel rise from each point of intersection of the squares in order to give structural integrity to the massive edifices, which are, on the surfaces, clad in stainless steel and glass. Then new sections appear to rise, reminiscent of the sections in a telescope, with a semblance of a mathematical pattern. A measurement of the segments reveals their proportions to fall into the scheme
reflecting the law of divine proportion.
In physics one proceeds by describing microscopic and macroscopic reality in terms of models at a tangible scale and writing equations for these models. By solving these equations one can hope to comprehend how and why nature behaves as it does. Physics can handle collisions of galaxies and collisions of individual atoms. But including all of the interactions extant may make the equations insoluble, or mathematically intractable. Ignoring some of the interactions and parameters may allow the equations to be solved. However, neglecting certain crucial interactions—such as gravitation in a problem at the cosmic scale or electromagnetic forces in a problem at the atomic scale—may make the mathematics relatively simple, but the associated physical description will no longer reflect reality. One may end up describing a soap bubble instead of a boulder. A number of models exist to describe one phenomenon or another associated with the atomic nucleus—the liquid drop model, optical model, unified model, single-particle shell model, etc.—but no single model hitherto developed has been able to explain all the phenomena, all the processes. Moreover, such models are rarely the sources of revolutionary change in our fundamental understanding of the nucleus.
In contradistinction, truly transformative changes in science most often follow from inspiration received from unlikely sources and from viewing reality from different and original vantage points. Viewing nature in an entirely different manner may lead to radical syntheses. Einstein, by considering the speed of light as absolute while relegating the notions of length, mass, and time to relative status, launched the special theory of relativity. A generation later Louis de Broglie’s suggestion that particles—molecules, atoms, nucleons—display a dual particle/wave nature turned out to be a pivotal hypothesis in launching quantum mechanics, the most successful picture of the world at the atomic scale.
So it is in art. When nature is observed in entirely different ways, and the description takes on entirely distinct styles, the possibility exists for a transformative revolution. The discovery of linear perspective launched the Renaissance in art, and in a much broader sense—by observing and pondering nature rather than idealizing it—planted the seeds of modern science. These were revolutionary in outlook and result. The impressionist movement in art was launched when the artist/observer in late-nineteenth-century France saw a need to capture the essence of the subject, rather than merely to reflect it. These movements in art compare in their significance in radical reductionism to the relativistic and quantum mechanical revolutions in physics. They showed the seminal and enduring qualities necessary to qualify as transformative revolutions.
Ultimately, the scientist and the artist, both in the business of describing nature, are receptive to shapes and patterns—to real images, static or fleeting, as well as to optical illusions. In the following pages we shall consider a few instances of how nature might have presented itself to the artist, and the bold manner in which the artist has dealt with the subject. The works are those of M. C. Escher, Bev Doolittle, and Frederick Hart. Their work is not revolutionary or transformative. Rather they each exemplify a single, even a narrow and confined manner, of modeling and representing nature. And like the physicist’s models of the nucleus, each method of representation is by no means all-inclusive or all-embracing. They successfully show us, in a way similar to the physicist’s tangible scale models, how some, but not all, of the phenomena of perception work on us. This short catalogue also presents some minor musings by Leonardo da Vinci, and the techniques that these ruminations appear to have inspired.
M. C. Escher wrote about having received inspiration for his graphic art in part from viewing the tile work of Islamic artists in Spain, but reflected, “What a pity it is that Islam did not permit them to make graven images.” Unencumbered himself by such religious interdicts, he utilized animate as well as inanimate, realistic as well as mythical figures with abandon. Many of Escher’s symmetrical musings were tantamount to mathematical mosaics. In his well-known woodcut Horsemen we see figures on horseback in white appearing to travel to the right, and similar figures reflected and darkened, heading leftward. In a different period of his career Escher unveiled graphic art in which the figures undergo gradual evolution, a style he dubbed “metamorphosis.”
I think that to find meanings you have to look at things from different directions.17
—Bev Doolittle
Bev Doolittle’s pronouncement is as pertinent for the scientist as it is for the artist. This contemporary Western artist displays a distinctive style—seamlessly blending animate life in the foreground with the inanimate background. White pintos with brown blotches are set against patches of clay amidst pristine snow, other horses with native riders astride are seen through clumps of aspen trees, or a grizzly bear is barely visible, camouflaged by dense thicket. Gestalt psychology, the subject of which is shape recognition, describes how the human mind is able to process an image with little difficulty and to distinguish the foreground from the background (Plate 11, bottom). Computers, programmed to scan the scene for color differences and shapes, would have a virtually impossible task identifying the horses. This is mimicry in nature celebrated in art. Doolittle’s work displays simultaneously a realistic and abstract quality, and rarely is it clear whether to classify it as one or the other. What is evident, however, is that it always engages the viewer, forcing him to take a second and a third look, and indeed to become a participant in the scene. Doolittle’s works radiate an unequivocal message that things are rarely what they seem—an unfaltering missive also for scientists practicing their art.
Mimicry in nature manifests itself in physical characteristics developed by animals to camouflage them against the background—the predator to become more effective as a hunter, and the prey to blunt the effectiveness of the predator. The mighty polar bear, unchallenged in its position at the top of the food chain, nonetheless optimizes its hunting prowess by virtually fading into the ice and snow of its background. On a different scale the praying mantis similarly dissolves into its background—blades of grass or green twigs on which it perches in wait for its food. The viceroy, a butterfly that is a delicacy to some birds, has evolved to resemble closely the monarch, a butterfly entirely unpalatable to the same birds. Unwilling to take a chance, birds steer clear of the viceroy. But then there is the puzzling case of the zebra. The bold black and white stripes make the zebra as inconspicuous as a lavender hippopotamus or, worst still, a zebra. Has nature blundered in this instance? Not at all! A herd of agitated zebras melds into a vast terrifying monolith, generating clouds of dust and galloping thunder, the individual animals virtually indistinguishable in the maelstrom, thereby confusing predators.
Even in the category of hidden images we recognize a Leonardo connection. A man of great personal charm and humor, and eager to interject some irony in his works, Leonardo planted hidden ironies and double entendres in his paintings and drawings. The portrait of Ginevra de’ Benci at the National Gallery of Art in Washington (which we will take up further in Chapter 9) is a double-sided painting—the portrait of the young woman on the recto and flora on the verso—a laurel and palm framing a juniper twig. In Italian the word for juniper is ginepro, clearly a play on the subject’s name. Among the anatomical drawings in the Codex Windsor is the detailed drawing of a cow embryo. Leonardo must have had a smile on his face when he invoked some subtle “cryptotechne,” inserting the inverted image of a cow in the drawing. The image is unmistakable once it is pointed out, but subtle it is. Meanwhile, prepossessed by the exquisite shapes of nature, perhaps even cognizant of their mathematical connection, Leonardo must have noticed the smoothly arched, ever-widening curve of the logarithmic spiral describing the shape of the embryo itself. It has a similar shape to the human embryo at about six weeks.
Perspective, as we saw in the last chapter, helps to project a three-dimensional image onto a two-dimensional plane. It assists in rationalizing the relationship of the objects within the scene, and simultaneously the relationship between the viewer and the scene. One-point perspective had its birth among artists in the Renaissance, and in subsequent centuries developed in the hands of artists and mathematicians. The mathematical formalism underlying perspective is found in projective geometry.
Having opened this chapter with an examination of perspective, we shall close it with a discussion of perspective carried to an extreme, the artist observing his subject from an altogether unusual vantage point, sometimes a well-defined peephole. The result is anamorphoses. The etymology is not entirely clear—the word may have its roots in ana (again) and morphe (shape), suggesting that the viewer has to take an active part in the realization of the image, or it could be derived from an (meaning absence of or without) and morphe, thus “shapeless.” Although the root of the word is not unequivocal, the description of the work itself is correct in both senses. The image certainly appears “shapeless,” and it clearly requires the active participation of the viewer, looking again and again
The first known work utilizing anamorphic art dates from 1485. At first glance it looks like a puerile drawing depicting an infant (Figure 7.9). An infant the subject is, but puerile this artist is not. The slit of the eye is much shorter and the slope of the chin more pronounced on the right, with the distortion increasing gradually as one moves to the left. That asymmetry offers a clue—the picture is meant to be viewed from a grazing angle, from the right edge of the sheet. The sketch is introduced unobtrusively and without explanation among the pages of Leonardo da Vinci’s Codex Atlanticus.18 Having invented anamorphic art, Leonardo most likely produced other examples. Francesco Melzi, Leonardo’s assistant and heir to the Leonardo manuscripts, described having seen a drawing of a “[D]ragon and lion in combat … a wonder to behold”—the illusion created by this graphic distortion. This work, however, has not survived.
Figure 7.9. Leonardo’s anamorphic art. The image of the face appears to “float” above the page.
In the sixteenth and seventeenth centuries other prominent artists, including Caravaggio and Annibale Carracci in Italy and Hans Holbein in the north, experimented with anamorphic art. The Venetian Giovanni Battista Tiepolo, known for his magically illusionistic ceiling and dome paintings, became an unrivaled master of the style, but then the technique seemed to lose its appeal, except as a source of fascination for scientists examining optical themes or experimenting with virtual reality. Often this art is seen in the form of a swirl of color, entirely unrecognizable in form and perspective. But when the proper reflector—the one specifically used in creating the painting in the first place—is placed in the designated spot, the painting regains proper perspective and springs to life.
In Chapter 5 we encountered the remarkable lengths to which the builders of the Parthenon—Phidias, Callicrates, and Ictinus—went in order to obviate detracting optical illusions. Among various tricks employed was the convex curvature that the base of the building was given as an artifice to eliminate the “sagging” look that a straight horizontal base would normally present when viewed against the convex curvature of the horizon. They had also aimed the axes of the columns to converge far above the building, partly to negate the splayed appearance of the columns rising from a convex base and partly perhaps to create an illusion of great height. This is reminiscent of three-point perspective—which would not appear formally for another two-and-a-half millennia.
During the classical period of Greece, along with the notion of the divine proportion, optical tricks were skillfully applied. The Greeks knew a good deal about detracting optical illusions and how to counterbalance them, and they are believed to have known about perspective, at least intuitively. Optical illusions were most likely recognized, however, long before the classical Greek period. With optical illusions our senses deceive us, and we can only confirm that this is so if we make measurements. The effect of lines or colors judiciously arranged throws off one’s perspective.
A rectangle ABCD and a parallelogram A′ B′ C′ D′ have been constructed, each with the convenient long-side to short-side ratios of 1.618:1 (Figure 7.10). Indeed, the former is a golden rectangle; the latter is reminiscent of a golden rectangle seemingly distorted by a pair of horizontal shearing forces. In the rectangle the segment MN bisects the segment AD, and the diagonals AN and ND help to generate the isosceles triangle AND. These diagonals are of equal length. In the case of the parallelogram, the segment M′N′ certainly does not bisect A′D′ and the segment A′M′ certainly does not equal the segment M′D′. And at first glance the diagonals A′N′ appears to be shorter than the diagonal N′D′. In reality, however, A′N′D′ also defines an isosceles triangle as did AND. Thus A′N′ does in fact equal N′D′, as a measurement would immediately confirm. Indeed, it is an optical illusion that makes A′N′ appear to be shorter than N′D′. In distinction to optical illusions there are Gestalts, which are the visual perceptions of shapes and patterns of natural formations—permanent or ephemeral—and their inadvertent association with familiar phenomena.
It is unusual that a pattern as frequently seen in nature as the logarithmic spiral has not found more frequent application by artists. Earlier we saw how the logarithmic spiral was generated geometrically from the golden rectangle, and subsequently the ubiquitous quality of the spiral was seen in patterns in nature, “accidentally” in man’s creations, or in an entirely different phenomenon, in the trajectory of the malfunctioning Trident missile (see Plate 4).
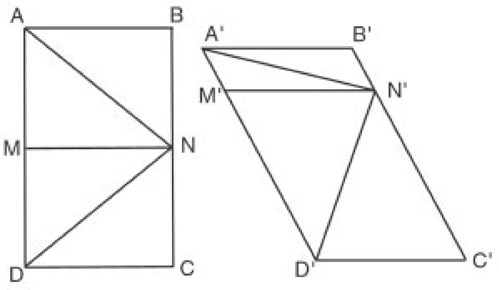
Figure 7.10. Example of an optical illusion. The segment A′N′ appears to be shorter than the segment N′D′, although they are precisely the same length.
In classical antiquity the shape inspired the basic designs of Ionic capitals, and, emulating the horns of rams, it was used in women’s jewelry. I have personally encountered only two modern works prominently featuring the spiral, and both created within a few years of each other, both in the National Cathedral in Washington, D.C. The first, a window created in 1973 by stained-glass artist Rodney Winfield, commemorates NASA’s Apollo XI, which in 1969 made its way to the moon and returned with lunar samples. In the Space Window an elongated figure 8 embodies simultaneously a double connotation—the trajectory of the spacecraft and the symbol for infinity. Indeed, the work, according to its creator, is rife with symbolism: a melding of the infinitesimal and the infinite scales of space, and the fleeting and the eternal scales of time. The lower circle on the right is at once the earth and the moon (seen in total eclipse); the lower circle on the left alludes to vast galaxies (including the Milky Way) and to star-gobbling black holes. In the mode of many abstract works, it invites subjective interpretation. There is the obvious allusion to manned space exploration. The space engineer gazing at the image might see the lunar-lander separating from the spacecraft, leaving the lunar-orbiter aloft, and spiraling onto the lunar surface; the physicist would recognize representations of escape velocity and orbital velocity—subjects of Newtonian mechanics. Ultimately, it is art celebrating cutting-edge science and technology. Aside from that aspect, there is for me one additional intriguing element in the window: the occurrence of a perfect logarithmic spiral—not Archimedean, nor hyperbolic, nor any other kind. It is in the upper circle that the logarithmic spiral is seen, converging on a piece of moon rock—3.5 billion years old—embedded in the window, and creating a virtual eyepiece to the mysterious (see Plate 2, right).
The second example—subtle and exuding extraordinary power—is Ex Nihilo (see Plate 5, bottom) by Frederick Hart, who employed the logarithmic spiral intuitively in organizing his composition. In 1974 the sculptor, then thirty-one years old, was awarded the commission for three friezes in the cathedral’s west facade—it is perhaps the most significant religious sculpture of the twentieth century. In architectural terms, the description of the sculptural program comprises the three portal tympana, each supported by a central column figure—one of Saint Peter, another of Adam, and a third of Saint Paul. A carving representing the creation of humans, Ex Nihilo, was to be located in the central portal and the creation of day and night, respectively, in the two flanking portals.
Hart’s friend, the author Tom Wolfe, described the frieze as “depicting mankind emerging from the swirling rush of chaos.”19 “Swirling rush” is indeed an appropriate description for that maelstrom of eight bodies seemingly issuing forth spontaneously from bedrock. But perhaps the inspiration for the composition was in the subliminal messages we receive from nature and its patterns in sunflowers, hurricanes, and chambered nautiluses. The inset (see Plate 5, bottom) presents the mathematical logarithmic spiral, the cross-section of the chambered nautilus, digitally overlaid on Ex Nihilo, Hart’s masterpiece.20 In organizing the composition a “best fit” can be made with the curve passing through the elbows of at least five of the figures.
Born in 1943, Hart, at just fifty-four, suffered a stroke in the right hemisphere of his brain, leaving him partially paralyzed on the left side, and at least temporarily curtailing his prodigious pace. Even though he was a right-handed sculptor the damage to the emoting, nonverbal side of the brain had put limitations on his ability to perceive objects in space, although “he was still able to conceptualize, formulate ideas, process the sensual underpinnings of those ideas, and create an expression of those ideas in a newly created image.”21 With heroic will and intensive physical therapy he regained some of the use of his left arm. Overcoming the reduction in spatial perception—the ability to perceive (not just to see) both his subject and his rendering required additional effort. He made progress in this area by concentrating harder and using mirrors as well as a specially modified camera.
Eighteen months after his stroke, in August 1999, Hart was diagnosed with cancer, and just three days later succumbed to the ravages of the disease. He was two months shy of his fifty-sixth birthday. Although I knew and admired him immensely, I never got the chance to discuss with him the logarithmic spiral that appears to organize the composition of the frieze. But I am convinced it was decidedly not a conscious exercise; in his own words he once explained, “I saw Ex Nihilo (‘out of nothing’) as a single expression of creation, as the metamorphosis of divine spirit and energy. The figures emerge from the nothingness of chaos, caught in the moment of eternal transformation—the majesty and mystery of divine force in a state of becoming.” His widow, Lindy Hart, explained that it had been a swirling pattern “in a formation of clouds” that inspired her husband, but added, “Rick would have been captivated to see the [logarithmic] spiral superimposed.” Tradition has it that Michelangelo similarly received his vision of the Creation scene for the Sistine Chapel from an ephemeral cloud formation.
As for the episode of Hart’s stroke, it parallels the effect of a similar stroke that the left-handed Leonardo suffered in the left hemisphere of his brain, partially paralyzing his right arm, and, in his case, effectively ending his career as a painter. For artistic creativity to thrive, the conjoining of both hemispheres of the brain appears to be important, or perhaps the various functions are not altogether the exclusive domain of one side or the other—at least in the examples of these two artists.
Regarding the significance of ϕ in works of art there are both unbridled enthusiasts and outspoken detractors, each group ready to offer uncontestable evidence to corroborate its views. Each, to me, is correct on one level, and incorrect at another. Among the enthusiasts ϕ is attributed to successful schemes in virtually every creative enterprise—in art, musical composition, poetry, even investing in the market. And indeed, if we look hard enough, we are bound to find an unlimited number of examples among man’s creations in which the golden ratio occurs. One has to assess each piece separately, and guard against reading between the lines. Among detractors (especially among a number of mathematicians) there is strident protest: the Parthenon’s end facades do not display exactly 1:1.618, but rather 1:1.71; the outline of the Great Pyramid, makes a length-to-width ratio of 8:5 (translating to 1.60). Both buildings are, nonetheless, close to 1.618 in their proportions. And in the case of the Great Pyramid rising at 52°, it is not the ratio of length-to-width that is unusually intriguing, but rather the ratios of the areas of the sides. (The analysis indeed suggested that it was a happy accident, a result of the convenient scheme of taking the pyramid’s perimeter to be 2π times its height that produced the recurrent ratio 1.618 in the variety of area measurements.)
As a scientist and artist, however, I am convinced that there is a subliminal message that the artist picks up from nature that provides the basis for a sense of proportion, and it is this sense of proportion that manifests itself in so many artists’ works. That is the simplest and most likely explanation of the ratio’s appearance in paintings by Velázquez, Dali, and Seurat. The evidence of our affinity for the ratio is unmistakable in Fechner’s data. The codification occurs formally only in a limited number of “systems” such as in the music of Bartók, Debussy, and Schillinger,23 in the architecture of Vitruvius, Bramante, and Le Corbusier, in the paintings of Mondrian, possibly also those of Seurat. But the single artist that most likely cobbled together mathematical form and artistic design consciously is the scientist-artist Leonardo, and even he does not speak explicitly about the subject. The evidence is in the grand mélange of the mathematical musings, studies in perspective, formal drawings, illustrations in De divina proportione, quick sketches, and the finished paintings—all forming pieces of an elaborate puzzle.
