1. C. P. Snow, The Two Cultures and the Scientific Revolution (Cambridge: Cambridge University Press, 1959).
1. Printing by movable type had been introduced in China and Korea long before Gutenberg, however it was made of awkward ceramic pieces, existed as a cumbersome number of characters, and was used for printing posters rather than books. Before Gutenberg, printers in Europe had to use wood engravings; each was created to print an entire page, thus only capable of producing a limited number of copies.
2. By the time the first university was established in Europe (Bologna in 1088), there already existed two universities in North Africa—al-Qarawiyin in Fez, Morocco (879) and al-Azhar in Cairo (970). In Salerno in the mid-eleventh century there was actually a university that predated Bologna’s; it was a specialized medical school.
3. Roger Bacon (1220–1292) and William of Ockham (c. 1300–1349), both connected with the University of Oxford, put reason above religious doctrine and were regarded as pariahs by the Church. Their brand of philosophy flourished in northern Europe and would be entirely hospitable to modern science, but Bacon and Ockham would have been in deep trouble had they been operating in Italian universities. Of the Italian universities, Bologna, founded as a law school, was unusually free of clerical pressures against unfettered intellectual dialogue. Two other institutions—Padua, especially famous for its medical and law schools, and Pavia, for its medical school—both accommodated anatomical studies.
4. Dino De Paoli, “Leonardo da Vinci’s Geology and the Simultaneity of Time,” 21st-Century Science and Technology, summer 2001, pp. 17–33.
5. Martin Kemp, ed. Leonardo on Painting.
6. Marco Rosci, The Hidden Leonardo, English trans. John Gilbert (Chicago: Rand McNally, 1977).
1. This description of the tools of the artist versus those of the mathematician was introduced by Leonard Shlain.
2. Richard Feynman, Character of Physical Law (Cambridge, Mass.: MIT Press, 1964), p. 34.
3. Eugene P. Wigner, Symmetries and Reflections: Scientific Essays (Cambridge, Mass.: MIT Press, 1967), pp. 222–37.
4. Eugene Wigner (1902–1995) was one of the modern heirs to the spirit of intellectual diversity. Around 1930 he and a half-dozen other young Hungarians emigrated abroad—five to the United States, one to Canada, and one to England. All had finished high school in Budapest (several were members of the class of 1920 at the Evangélicus Gimnázium); all had earned bachelor’s degrees from the University of Budapest; and all doctorates from German universities. Along with Wigner, the unprecedented brain drain included his classmates, Leo Szilard, instrumental in launching the Manhattan Project that developed the atom bomb; Edward Teller, the “Father of the H-bomb”; and Janesh “Johnny” von Neumann, one of the most important mathematicians in history and a colleague of Einstein’s at the Institute for Advanced Study in Princeton. The brain trust also included Denis Gabor, winner of the Nobel Prize in Physics for developing holography; Albert Szent-Gyorgi, winner of a Nobel Prize in Physiology and Medicine; and Eugene Ormandy, conductor of the Philadelphia Symphony Orchestra in its heyday.
5. In antiquity, the Romans regarded the Alps merely as barriers keeping out the barbarians. Nowhere in Shakespeare is there a romantic allusion to mountains. As late as the seventeenth and eighteenth centuries the Alps were regarded as aberrations on an otherwise smooth, spherical earth. Beginning with the romantic period, mountains become places of beauty and spiritual significance.
6. Jacob Bronowski, “The Creative Process,” Scientific American 199, no. 8 (September 1958), pp. 5–11.
7. A recent book in its very title heralds the notion of Leonardo initiating scientific methodology: Michael White, Leonardo: The First Scientist (New York: Saint Martin’s Press, 2000).
8. Jacob Bronowski, The Ascent of Man (New York: Little, Brown, 1973), p. 113.
9. Ibid.
10. Princeton University’s preeminence in physics is a legacy of Joseph Henry (1797–1878), rather than of Albert Einstein, who was actually a member of the Institute for Advanced Study, also located in Princeton. Henry, a professor of physics at Princeton from 1832 to 1846, discovered the law underlying the electric generator independently of Michael Faraday in 1830, but did not publish it. Introducing insulated wires into coils, he amplified the strength of his electromagnets. Henry also designed the electric motor, variations of which we still use.
11. Stephen Jay Gould, Rocks of Ages (New York: Ballantine, 1999), p. 6.
1. Suggested by Christopher Tyler (private communication).
2. Carl Boyer, A History of Mathematics, rev. by U. Merzbach, 2d ed. (New York: Wiley, 1991), p. 4.
3. Robert Kaplan, The Nothing That Is (Oxford and New York: Oxford University Press, 1999).
4.Seyyed Hossein Nasr, Islamic Science: An Illustrated Study (Westerham, Kent, England: World of Islam Festival Publishing Company, 1976).
5. Quatrain 24 from Edward Fitzgerald, The Rubaiyyat of Omar Khayyám 5th ed., quoted in M. H. Abrams, ed., The Norton Anthology of English Literature, 7th ed, vol. 2 (New York: W. W. Norton, 2000), p. 1308.
6. For a short and entertaining account, see Dennis Overbye, “How Islam Won, and Lost, the Lead in Science,” New York Times, “Science Times,” October 30, 2001, D, pp. 1, 3.
7. An irrational number is a number that cannot be expressed as an integer or as the ratio of two integers. 
=1.414 213 56 … and π (=3.141 592 65 …) are a pair of common irrational numbers expressed here accurately to eight places beyond the decimal. But this is not to say that one cannot specify them to a desired degree of accuracy by a ratio of integers, e.g., in the case of π the ratio 22/7, often taught to school children, equals 3.142 857 14 …, and is correct to just three places. An approximation correct to six places is 355/113=3.141 592 9 … A useful mnemonic for remembering π to fifteen places exists: “How I need a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.” The number of letters in each word corresponds to the successive place values in π: “How,” 3; “I,” 1; “need,” 4; etc.
8. The Fibonacci series has as its basis three statements:
u1, u2, u3, … un
u1 = u2 = 1,
un = un–1 + un–2
with n=1, 2, 3, …
Thus 1, 1, 2, 3, 5, 8,13, 21, 34, 55, 89,144, 233, 377, 610, 987, … Now if the ratio Rn is defined by
Rn = un+1/un
one finds for R1, R2, R3, …
the values are 1, 2, 1.5, 1.67, 1.60, 1.63, 1.615, … converging in the limit:
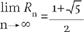
which to six places after the decimal equals 1618 034, a number denoted by ϕ.
The terms of the series can be computed with a recursion relation. The nth term can be computed directly from
The derivation of the nth term of the Fibonacci series:
Let an+2=an+1 + an’ so that an+2–an+1 – an = 0. The characteristic equation ϕ2 - ϕ - 1 = 0, a quadratic, has characteristic solutions ϕ = (1±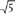 
)/2.
From (2) we have c1 + c2 = 1. Substituting c2 = 1 - c1 into (3), we obtain
c1 = (1+5)/(2+5) and c2 = (5–1)/()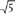
and (1) can then be written
The terms u1, u2, u3 … in the text above, are related to a0, a, a2, … in this derivation by un+1 = an.
Thus
which is just the expression cited earlier.
9. Table of common values associated with the golden section: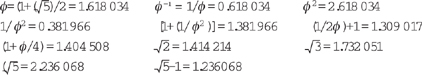
10. The logarithmic spiral can be written mathematically as an exponential equation in polar coordinates. On the x-axis one marks off a unit distance. Then one proceeds in a counterclockwise direction, contracting this distance by a factor of ϕ–1 = 1/ϕ = 0.618 0 34 upon reaching 90° (or π/2 radians), by a factor of ϕ–2 = 1/ϕ2 =0.381966 at 180° (or π radians), by a factor of ϕ–3 = 1/ϕ3 =0 236 069 at 270°, and a factor of ϕ–4 = 1/ϕ4 = 0 145 898 at 360° (i.e., a full circle), the resulting curve will define a logarithmic spiral
The evaluation is entirely evocative of the expression for the exponential decay of a radioactive nuclide,
The dependent variable N is the number of nuclei remaining at time t
when the original number at t=0 was No; the 2 in the natural log (In) comes from the inverse of 1/2; Tl/2 is the half life of the radioactive nuclide (e.g., 5,715 years for C14); the independent variable is the time t.
11. H.F.R. Adams, The Si-Metric Units, rev. ed. (Montreal: McGraw-Hill Ryerson, 1974), pp. 9–10.
1. We have only the fragments of Protagoras’s doctrine, but they seem to question the existence of the gods. The impiety and atheistic pronouncements may have been the reason he was banished from Athens.
2. Reviel Netz, “The Origins of Mathematical Physics: New Light on an Old Question,” Physics Today, June 2000, pp. 43–37. Until very recently mathematicians believed that the concept of infinity became a subject of interest for mathematics only in recent times. Modern classical scholars, however, in deciphering the recently discovered Archimedes palimpsest, produced a thousand years ago from Archimedes’ original writings, found his claims of comparing a pair of infinite sets. A palimpsest is a book white-washed and over-written.
1. A. P. McMahon, Treatise on Painting. Codex Urbinus Latinus 1270 (Princeton, N. J.: Princeton University Press, 1956).
2. Kurt Mendelssohn, “A Scientist Looks at the Pyramids,” American Scientist 89 (March–April 1971), pp. 210–20; Kurt Mendelssohn, The Riddle of the Pyramids (New York: Praeger, 1974).
3. Kurt Mendelssohn, private communication.
4. Isaac Asimov, Asimov’s Biographical Encyclopedia of Science and Technology, 2d rev. ed. (New York: Doubleday, 1982).
5. Mendelssohn, private communication.
6. David H. Koch, “Dating the Pyramids,” Archaeology 52, no. 5 (September–October 1999), pp. 26–33.
7. Farouk El-Baz, “Gifts of the Desert,” Archaeology 54, no. 2 (March–April 2001), pp. 42–45.
8. My friend, the dean, has since passed away. I would rather not divulge his name, although for years after the incident took place he continued to joke and laugh about it.
9. Jay Hambidge, Dynamic Symmetry in the Greek Vase (New Haven, Conn.: Yale University Press, 1920); Jay Hambidge, The Elements of Dynamic Symmetry (New York: Dover, 1967).
10. As a freshman at Georgetown University in 1959–60, I was invited to a dinner by my classmate Anil Nehru, the son of B. K. Nehru, the Indian financial ambassador to Washington, D.C., and the nephew of Prime Minister Jahawarlal Nehru. The guest of honor at the dinner was Salvador Dali. Unhappily, I did not know then of the Pythagoreans’s fascination with the dodecahedron and could not ask Dali whether he had that notion in mind when he created his painting.
1. Christopher Tyler, who made this observation in a private communication, is the discoverer of the center-line principle that figures prominently in portraits.
2. Stephen Jay Gould, Ever Since Darwin: Reflections in Natural History (New York: W. W. Norton, 1977), p. 201.
3. Leonard Shlain, Art and Physics: Parallel Visions in Space, Time, and Light (New York: William Morrow, 1991). Shlain is a surgeon who practices in San Francisco.
4. Most intellectual endeavors benefit when they conjoin complementary objective and subjective aspects. Form and feeling is one such pair. Essayist Samuel Johnson (1709–1784), captured another nuance of this principle, “Integrity without knowledge,” he wrote, “is weak and useless, and knowledge without integrity is dangerous and dreadful.”
5. This is the title of a book by the seventeenth-century Swiss mathematician Jacob Bernoulli, who investigated the logarithmic spiral extensively. See Mario Livio, The Golden Ratio (New York, Broadway Books, 2002), pp. 116–17.
6. D. Harel, R. Unger, J. L. Sussman, “Beauty is in the Genes of the Beholder,” Trends in Biological Sciences 11 (April 4, 1986).
7. Peter S. Stevens, Patterns in Nature (Boston: Atlantic Monthly Press, 1974), pp. 136–66.
8. Ibid., pp. 160–61.
9. Ibid., p. 164.
10. Livio, The Golden Ratio, p. 120. Livio’s explanation is based on the discovery by Vance Tucker et al., “Curved Flight Path and Sideways Vision in Peregrine Falcons,” Journal of Experimental Biology 203, no. 24 (December 15, 2000), pp. 3755–63.
11. Kemp, ed., Leonardo on Painting, pp. 123–29.
12. Robert Ricketts, professor emeritus of Occlusion at the University of Southern California and professor emeritus of Orthodontics at Loma Linda University, California. “Divine Proportion in Facial Esthetics,” Clinics in Plastic Surgery 9, no. 4 (October 1982). There is also his compendious work, Provocation and Perception in Cranio-Facial Orthopedics (1989). Of the nine books available in three volumes, the section of special interest to us is “Facial Art, the Divine Proportion and Esthetics,” part I, section 1, chapter 6, pp. 169–202.
13. The pencil sketch depicts a longtime friend and former student, Rochele Hc Hirsch, née Elizabeth Stansell, at Mary Washington College of the University of Virginia.
14. For the aesthetic dentist’s formula for the “beautiful smile,” I am grateful to Dr. Arthur Sitrin of Miami, Florida.
15. Marquardt, private communication.
16. Marquardt’s Web page is http://goldennumber.net/beauty.html. The actor John Cleese and actress Elizabeth Hurley collaborated on a television program aired on the Discovery Channel in August 2001. The episode has its own Web page: http://tlc.discovery.com/convergence/humanface/humanface.html.
1. Kemp, ed., Leonardo on Painting, pp. 17, 52.
2. Tyler was the first to point out the attempt at achieving proper perspective in the paintings in Pompeii. The scheme in Pompeii failed because of the existence of more than one horizon line. Personal communication plus the following Web sites: http://www.ski.org/CWTyler_lab/CWT;yler/PrePublications/index.html and http://www.ski.org/CWTyler/Art%20Investigations/PerspectiveHistory/Perspective.BriefHistory.html.
3. A. P. McMahon, Treatise on Painting. Codex Urbinus Latinus 1270 (Princeton, N. J.: Princeton University Press, 1956).
4. A compelling argument is made to this effect in Kemp, The Science of Art, pp. 44–52.
5. Morris Kline, “Projective Geometry,” Scientific American, January 1955, reprinted in Science and the Arts (New York: Scientific American, 1995), pp. 30–35.
6. Sanford Schwarts, “Camera Work,” New York Review of Books 48, no. 9 (May 31, 2001), pp. 6–12.
7. Van Hoogstraten’s perspective box is discussed in Lisa Jardin’s excellent book, Ingenious Pursuits: Building the Scientific Revolution (New York: Doubleday, 1999), pp. 107–11.
8. Walter Liedtke, curator of European art and a specialist in Dutch and Flemish paintings at the Metropolitan Museum of Art, is primary author of the exhibition catalogue Vermeer and the Delft School (New Haven, Conn.: Yale University Press, 2001), p. 156.
9. Bülent Atalay, Oxford and the English Countryside: Impressions in Ink (London: Eton House, 1974).
10. H. E. Huntley, The Divine Proportion (New York: Dover, 1970), pp. 60–69.
11. Ibid., pp. 62–65. Along with Fechner, Huntley cites Adolf Zeising, Der Goldene Schnitt (1884), Witmar (1894), and Thorndike (1917).
12. Helen Hedian, “The Golden Section and the Artist,” Fibonacci Quarterly 14, no. 5 (1976), pp. 406–18.
13. Two books in which Seurat’s Circus Side Show is presented in connection with the golden ratio are David Bergamini, Mathematics (New York: Life Science Library, 1963), and Livio, Golden Ratio.
14. Another example of a circular painting with similar shapes and symmetries is Raphael’s Madonna della Seggiola (Madonna of the Chair) of 1514 (Florence, Galleria Palatino and a second version, Dubrovnik Cathedral, Croatia).
15. Physicists among the readers should know that the expression “dynamic symmetry” as used here has nothing to do with the usual dynamical symmetry groups in physics.
16. Crypto means “hidden” or “secret,” and techne means “skill” or “art,” that is, something manufactured.
17. Elise Maclay, The Art of Bev Doolittle (New York: Bantam Books, 1990). For permission to reproduce the artist’s works, I am grateful to Doolittle and her representative, The Greenwich Workshop, http://www.greenwichworkshop.com.
18. Fred Leeman, Hidden Images (New York: Harry N. Abrams, 1976); p. 10. (Codex Atlanticus, fol. 35 verso a. c. 1485), Biblioteca Ambrosiana, Milan.
19. Tom Wolfe et al., Frederick Hart: Sculptor (New York: Hudson Hills, 1994). This magnificent book featuring the artist’s work contains essays by prominent literati and art critics, including J. Carter Brown, the late director of the National Gallery. My own cherished copy was a present in 1998 from the artist, with whom I shared an affinity for the classical style in art. The book is a must for any collector of art books who also prefers a confluence of truth and beauty in art, and not just truth alone (as evinced by the modern art establishment). I must admit to empathizing with the pronouncements of a pair of prominent English writers: foreign correspondent Alistair Cooke, who found in some modern works of art “decadence in the name of originality,” and British playwright Tom Stoppard, who quipped, “Contemporary art is imagination without skill.”
20. I first noticed the logarithmic spiral in Ex Nihilo around 1984, and subsequently discussed it in lectures in the 1980s and 1990s. Indeed, I had planned to surprise Hart during a lecture I gave at the Smithsonian in October 1998 by projecting the image seen in Plate 5, but he was unable to attend the lecture. It was only after writing about it for this book during 2000–3 that I came across another author’s reference to the spiral. In an incisive essay, “Evolution out of Chaos: The Creation Sculptures,” Frederick Turner mentions the spiral, as well as the Fibonacci series and the nautilus, indeed, making many of the same connections I make in this book (see Frederick Hart: Sculptor, p. 60).
21. Lindy Hart, a good personal friend, has served as the source for much of the information regarding the sculptor’s experience.
22. Among papers by detractors is mathematician George Markowksy, “Misconceptions about the Golden Ratio,” College Mathematics Journal 23, no. 1 (January 1992), pp. 2–19.
23. That Joseph Schillinger (1895–1943) had employed the golden ratio in his musical compositions was unknown to me until recently when I came across Livio, Golden Ratio.
1. This also appears to be a cut-off age to begin to learn a foreign language without a trace of an accent; see Betty Edwards, Drawing on the Right Side of the Brain (New York: Houghton Mifflin, 1979).
2. Ibid.
3. This is the title of a small exhibition held in the National Portrait Gallery, London, April–June, 1999.
4. Alan Riding, “Hypothesis: The Artist Does See Things Differently.” New York Times, May 4, 1999, B, p. 1.
5. Ibid.
6. Robert L. Solso, “The Cognitive Neuroscience of Art: A Preliminary fMRI Observation,” Journal of Consciousness Studies 7, no. 8–9 (August–September 2000), pp. 75–85.
7. Robert L. Solso, private communication.
8. The five portraits by Humphrey Ocean hanging in the National Portrait Gallery include a 1983 portrait of Sir Paul McCartney.
9. Riding, “Hypothesis.”
10. Sonnet XVIII: 5–8.
11. Guy Gugliotta, “Why Art Connects with a Left,” Washington Post, October 18, 1999, A, p. 9. Raphael, born in 1483, would have been at least twenty-three when Leonardo painted the Mona Lisa. He may have seen Leonardo creating the portrait, musicians creating the proper mood for the subject and the artist, but it would be a stretch to have Raphael sitting at Leonardo’s knee.
12. C. W. Tyler, “The Human Expression of Symmetry: Art and Neuroscience,” International Conference on the Unity of the Sciences; Session: Symmetry in Its Various Aspects: Search for Order in the Universe. Seoul, Korea (February 2000). See also Web sites: http://www.ski.org/CWTyler_lab/CWTyler/PrePublications/ARVO/1998/
Portraits/index.html and http://www.ski.org/CWTyler_lab/CWTyler/Art%20investigations/Symmetry/Symmetry.html.
13. In a number of other portraits painted by Wyeth the center-line is found to coincide with an eye, and in many other cases simply to reflect the gaussian distribution formed by Tyler’s data.
14. Private communication with the author.
15. I. C. McManus, N. K. Humphrey, “Turning the Left Cheek,” Nature 243 (1973), pp. 271–72.
16. I. E. Gordon, “Left and Right in Goya’s Portraits,” Nature 249 (1974), pp. 197–98.
17. N. H. Robinson, The Royal Society Catalogue of Portraits (London: Royal Society, 1980).
18. P. R. Coles, “Profile Orientations and Social Distance in Portrait Painting,” Perception 3 (1974), pp. 303–8; O. Grüsser, et al., “Cerebral Lateralisation and Some Implications for Art, Aesthetics, Perception and Artistic Creativity.” Beauty and the Brain: Biological Aspects of Aesthetics, ed. Ingo Rentschler, et al. (Basel: Birkhäuser, 1988), pp. 257–93.
19. Michael E. R. Nicholls, “Asymmetries in Portraits: Insight from Neuropsychology,” in Side Bias: A Neuropsychological Perspective, ed. M. Mandal, et al. (Dordreckt: Kluwer, 2000), pp. 313–29. Michael E. R. Nicholls et al., “Laterality of Expression in Portraiture: Putting Your Best Cheek Forward,” Proceedings of the Royal Society London B 266 (1999), pp. 1517–22.
20. The remaining eight portraits were eliminated, having violated the center-line principle.
1. Kemp, ed. Leonardo on Painting, pp. 13–46.
2. Ibid., pp. 268, 270.
3. David Alan Brown, curator of Italian Renaissance Art at the National Gallery of Art, offers an excellent history and artistic analysis of this work in his Leonardo da Vinci: Origins of Genius. See also the video “The Story of Ginevra” (produced by the National Gallery of Art), for which Brown collaborated with National Gallery conservator David Bull and Oxford art historian Martin Kemp.
4. Bull also found Leonardo’s fingerprints on the Ginevra de’ Benci. Based on his studies he claims Leonardo was the first artist to soften edges and achieve subtle blending by dabbing his finger in the paint. Following Leonardo, many others, including Bellini and Titian, were dabbing the freshly laid paint with their fingers.
5. Daniel Glick, “The Case of the Polish Leonardo,” Washington Post Magazine, March 15, 1992, pp. 16–29.
6. M. J. Gelb, “Lessons in Thinking From the Inspiring Leonardo da Vinci,” Bottom Line (January 1, 1999), p. 13; M. J. Gelb, How to Think Like Leonardo da Vinci (New York: Delacorte, 1998).
1. Michael White, Leonardo: The First Scientist (New York: Saint Martin’s Press, 2000).
2. Nuland, Leonardo da Vinci, p. 114.
3. Evangelista Torricelli (1608–1647) was an Italian physicist and Daniel Bernoulli (1700–1782), a Swiss mathematician. The Bernoulli family of Basel included a dozen eminent mathematicians; perhaps the most prominent of them were the brothers Jacob and Jean, who developed the calculus of variation and the mathematical description of the curve known as the lemniscate and the formalism of differential equations.
4. Archimedes, educated in Alexandria, may have seen it used there, or he may have invented it. It is still used on the banks of the Nile. The simplicity and efficiency of the device explains its enduring power.
5. Ladislao Reti, ed., The Unknown Leonardo (New York: McGraw-Hill, 1974), p. 181.
6. Stillman Drake and James MacLachlan, “Galileo’s Discovery of the Parabolic Trajectory,” Scientific American, March 1975, pp. 102–10.
7. Vernard Folley, “Leonardo and the Invention of the Wheellock,” Scientific American 278 (January 1998), pp. 74–79.
8. Ladislao Reti, The Unknown Leonardo, pp. 291–92.
9. In the case of the Leonardo bicycle, however, there is considerable controversy. A number of scholars claim that the Leonardo design is a modern forgery. The drawing certainly lacks the usual quality of draftsmanship of Leonardo, but others suggest that it is a drawing by an apprentice, based on a lost drawing by Leonardo.
10. Among trees that sow seeds by way of samaras are the maple, the ailanthus, and the tulip poplar, all indigenous to Italy. The twisted foil shape and the eccentrically located seed makes the shape a natural helicopter.
11. Communication between the Turkish heads of state and Italian painters continued on to a third generation, with Yavuz Sultan Selim, the son of Bayezid, inviting Michelangelo in 1517 to visit the Turkish capital and to undertake some projects of an artistic and engineering nature. Selim, an enlightened monarch emulating more his grandfather than his father, had seen the opportunity to infuse Ottoman culture with the energy of the Italian High Renaissance. Michelangelo, however, busy painting the ceiling of the Sistine Chapel, showed no interest in the commission and the offer was withdrawn.
12. Nuland, Leonardo da Vinci, p. 148.
13. Ibid.
14. Ibid., p. 131.
15. J. J. O’Connor and E. F. Robertson, http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Bernoulli_Jacob.html
1. Some of his teachings on science are even more preposterous. He claimed men had more teeth than women. He taught spontaneous generation for the origin of life. He also claimed that a man reached his peak at fifty-two—to which “peak” he was referring is not clear, but he was fifty-two years old when he made the statement.
2. The expression “falling body” to the physicist is any object that has been dropped, and “free-fall” refers to dropping in a medium devoid of drag. In the world of Leonardo, when Niccolò Machiavelli and Cesare Borgia flourished, the expression “falling bodies” could just as easily have conjured up images of cadavers, or soon-to-become cadavers.
3. Copernicus was evidently familiar with Aristarchus’s work and mentioned it in the introduction of the manuscript of his great book De revolutionibus orbeum coelestium (1543), but decided to drop it in the published edition.
4. A simple mnemonic—Bode’s law—exists to remember the distances of the first six planets. Although called a “law,” it is neither a physical law nor was it Bode who discovered it. Start by taking the series 0, 3, 6, 12, 24, 48, 96 (i.e., after 0 for the first term, and 3 for the second term, double 3 to get the next term, double the next term to get the following, etc.) Then add 4 to each term of the series that has just been generated: thus 4, 7, 10, 16, 28, 52, 100. Finally, divide each term by 10, in order to obtain 0.4, 0.7, 1.0, 1.6, 2.8, 5.2, and 10. These are the distances in AU of the planets, except for the anomaly that occurs at 2.8. There is no planet there. But there is the Asteroid Belt!
5. The tables are named after King Alphonse of Portugal, who commissioned them.
6. Hermeticism was purportedly based on the mystical teachings of Hermes Trismegistus (“triple-divine”), a contemporary of Moses. It was believed to be handed down through a number of ancient philosophers, including Pythagoras and Plato, and the teachings were formally written out in the second and third centuries A.D. by a band of Neoplatonists. The “sorcerer’s stone” (known in the United States as the “philosopher’s stone”) that alchemists believed would convert base metals into gold, had been created by Hermes Trismegistus. Of course, alchemy had a salutary effect in leading to the birth of chemistry. The expression “hermetically sealed” alludes to the enigmatic character Hermes.
7. In order to compute Jupiter’s period, one can use Kepler’s third law:
8. Galileo’s equations describing free-fall are given by
s(t)=1/2gt2+vot+so
v(t)=gt+vo
a(t)=g
s(t) represents the height or altitude of the body at a specified time t;
v(t), the velocity of the body at time t; and a(t), the acceleration—which is clearly independent of time and mass—a constant!
9. Dava Sobel, Galileo’s Daughter (New York: Walker and Co., 1999). This book portrays Galileo as a father deeply devoted to his eldest daughter, whom he had placed in a nunnery while she was still a young teenager. An unusually intelligent young woman, Sister Marie Celeste—born the love child “Virginia”—spent most of her life as a nun. She corresponded regularly with her father, and although his letters to her no longer exist, her letters to him have survived; and it was these letters Sobel pieced together in creating her endearing account.
10. Richard Feynman, the legendary twentieth-century physicist, was no slouch himself. He served on the faculty of Caltech for the better part of forty years. While still a Ph.D. student at Princeton he took a leave and worked in the Manhattan Project on the theoretical physics team creating the first atomic bomb. In the 1940s he formulated quantum electrodynamics (QED) and won a Nobel Prize for this work in 1965.
11. The universal law of gravitation reads F = Gm m r2. The symbols m and m’ represent the masses of the bodies, r is the d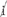
stance between the masses (measured center to center), and G is the universal gravitational constant.
12. The “projectile” is launched from a point (xo, yo) with an initial speed of vo and at an angle θoπ (measured relative to the horizon); the gravitational acceleration g = −9.8m/sec2 (–32 ft./sec.2). Classical mechanics yields, with air resistance ignored, the trajectory of the projectile to be given in terms of the coordinates x, y, and θ0 by
The first equation describes a downward-turned parabola, or one that “spills water.” For the same initial speed v0 the highest point for a trajectory, the apogee, occurs when the projectile is launched at an initial angle of 90°. The second equation reveals that the horizontal distance, the range, is maximized when the initial angle θ0 = 45° a fact that football quarterbacks and punters know intuitively.
13. The list of Cambridge University’s graduates who have won the Nobel Prize is available through the Web site http://www.damtp.cam.ac.uk/user/smb1001/camnobel.html.
1. Shlain, L., Art and Physics, p. 306.
2. As a sampling I suggest the following four books: Richard Feynman, The Character of Physical Law (Cambridge, Mass.: MIT Press, 1965); Steven Weinberg, First Three Minutes (New York: Basic Books, 1977); Leon Lederman, The God Particle (Houghton Mifflin 1993); and Brian Greene, The Elegant Universe (New York: W. W. Norton, 1999).
3. French press clipping, April 7, 1922, reporting on an address to the French Philosophical Society at the Sorbonne. Einstein Archive 35–378; and Berliner Tageblatt, April 8, 1922, Einstein Archive 79–535. See Alice Calaprice, ed., The Quotable Einstein (Princeton, N. J.: Princeton University Press, 1996), pp. 7–8.
4. The analogue in two dimensions of curved space derives from the difference in “predicted” and “measured” (or actual) values of a distance. For example, one can “predict” the radius by constructing a circle with a compass; measuring the circumference of the circle; then dividing the circumference by 2π. On a flat plane, the “excess radius,” defined by the measured value minus the predicted value, is zero. This is the case for Euclidean or plane geometry. Yet on curved surfaces there will exist a difference between the measured and predicted radii. On the surface of a sphere the excess radius turns out to be a positive value—there is more measured radius than the predicted. On a saddle-shaped surface the excess radius turns out to be negative (or there is less measured radius than the predicted). In four dimensions general relativity gives a mathematical expression to compute the excess radius:
where G is the universal
gravitational constant in Newton’s expression for the universal law of gravitation; M is the mass of the body causing the warping in space, and c represents the speed of light.
5. The Mössbauer effect discovered in the late 1950s allowed Harvard physicists Robert Vivian Pound and Hans Rebka to demonstrate that clocks do run at different rates at different heights in a gravitational field. The “clocks” were a pair of identical radioactive samples of the element iron. The frequency in the radioactive emission of the sample located at the upper part of the tower, but measured at the base of the tower, was ever so much greater than that of the sample located at the base of the tower. This difference in the passage of time is an effect of the general theory of relativity. The special theory of relativity also predicts timedilation, a slowing down of time, in frames of references moving uniformly at relativistic speeds. In the early 1970s two physicists from the Naval Research Lab in Washington, D.C., took a flight on Pan American Flight 1, traveling around the world, accompanied by an atomic clock, then on Flight 2, traveling around the world in the opposite direction. In comparing the times elapsed on eastward and westward flights, and correlating their data with an identical atomic clock left back in the laboratory, they were able to confirm time dilation.
6. The optical region is the part of the electromagnetic spectrum where we can see with ordinary vision. Other regions are radio, gamma ray, x-ray, ultraviolet, and infrared.
7. The full quotation is found in Shlain, Art and Physics, p. 306.
8. Frank Wilczek, Physics Today(June 2000), p. 11. Wilczek, previously the J. Robert Oppenheimer Professor in the School of Natural Sciences at the Institute for Advanced Study in Princeton, New Jersey, and now at MIT.
9. LASER is the acronym of Light Amplification by Stimulated Emission of Radiation; and MASER, Microwave Amplification by Stimulated Emission of Radiation. Although it is in the ground state that most atoms reside, the atoms of some elements possess an affinity to have excited levels populated, or “optically pumped,” with mediation from an external energy source. When this population inversion is achieved, irradiating the atoms with photons of just the right energy results in “stimulated emission”—many times more photons emitted as absorbed—with the emitted photons all in phase. It is, however, modern quantum mechanics rather than “old quantum theory” that must be invoked in order to explain the absorption and emission process fully.
10. The time-dependent and time-independent forms of Schrödinger’s equation are
The symbol H represents the Hamiltonian or total energy operator; the upper case Ψ in the first equation represents the state function; the lower case Ψ in the second equation, the eigenfunction. In the time-dependent and time-independent versions of Schrödinger’s equation the symbol H represents the Hamiltonian or total energy operator E, the energy eigenvalue; i is the imaginary number, square root of –1; and
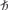=h/2π
where h is Planck’s constant 6.63 × 10–34 joule • sec (and “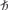” = 1.05 × 10–34 joule • sec).
11. Louis de Broglie (1892–1987) received the Nobel Prize for Physics in 1929. Heisenberg (1901–1976) was awarded the Nobel Prize in 1932; Schrödinger (1887–1961) and Dirac (1902–1984) were awarded the prize jointly in 1933.
12. The metaphor comes from Dennis Overbye, “Science Times,” New York Times, October 28, 2002, D, pp. 1, 4.
13. Calaprice, The Quotable Einstein.
14. Flexner, one of the great innovators of American education, was recently featured in a definitive new biography: Thomas N. Bonner, Iconoclast: Abraham Flexner and a Life in Learning (Baltimore: Johns Hopkins University Press, 2002).
15. Landon Y. Jones, Jr., “Bad Days on Mount Olympus,” Atlantic 233 (February 1974), pp. 37–46. This is an excellent article recounting the founding of the Institute for Advanced Study.
16. Banesh Hoffman, collaborated with Helen Dukas, Einstein: Creator and Rebel (New York: Viking Press, 1972).
17. See Brewster’s Memoirs of Newton 2: 27 (1885). http://www.quotationspage.com/quotes/Issac_Newton/
1. Alan Turing, educated at Cambridge University, formulated the mathematical basis of the computer—the Turing machine. During the Second World War, Turing was a member of Enigma Project at Blechley Hall, England, commissioned to decipher secret German codes. With a machine called “Colossus,” utilizing the logic of the Turing machine, the mathematicians of Blechley Hall indeed succeeded in deciphering the secret code. A few years after the war, however, the immensely gifted but altogether tormented mathematician committed suicide.
2. ENIAC is the acronym for the Electronic Numerical Integrator and Calculator; UNIVAC, for Universal Automatic Computer; FORTRAN (FORmula TRANslation); COBOL (Common Business Oriented Language); ALGOL (ALGOrithmic Language).
3. Hillary M. Sheets, “Portrait of Leonardo,” ARTnews (January 2003), pp. 100–107. Leonardo da Vinci: Master Draftsman, exh. cat. (Metropolitan Museum of Art, January 22–March 30, 2003) is the definitive exhibition and catalogue of Leonardo’s drawings.
4. James Gleick, Genius: The Life and Science of Richard Feynman (New York: Pantheon, 1992), pp. 10–11. This book uses the expression “magician” (introduced by Kac) to distinguish the extraordinarily intuitive and prescient intellectuals from the less intuitive, and perhaps more plodding “ordinary geniuses.”
5. Archimedes, Bach, Mozart, Einstein.
6. This statement paraphrases a prominent Newton biographer’s characterization of his subject.
7. After Einstein died in Princeton in 1955, the young pathologist performing the postmortem on the great physicist rescued the brain. It was stored in formaldehyde for about four decades before brain physiologists began to do rigorous examinations on the brain’s structure. Canadian brain physiologist Sandra F. Witelson and her co-authors reported in Lancet 9191 (November 20, 1999) that they had discovered the peculiar abnormality in Einstein’s brain.
8. Nuland, Leonardo da Vinci, p. 11.
9. This was also the resonating message of Wordsworth in his ruminations on Isaac Newton’s statue in the antechapel of Trinity College (see Chapter 11).
10. Although he was using photography for documentation by the early 1850s, art critic John Ruskin made a plea for people to make sketches.