1
Complex Numbers
You, have you really understood all that stuff?
What?
The story of imaginary numbers?
Robert Musil, The Confusions of Young Törless (1907)1
Complex numbers lie at the very core of quantum mechanics and are therefore absolutely essential to a basic understanding of quantum computation. In this chapter we present this important system of numbers from both the algebraic and the geometric standpoints. Section 1.1 presents some motivation and the basic definitions. The algebraic structure and operations on complex numbers are given in Section 1.2. The chapter concludes with Section 1.3, where complex numbers are presented from a geometric point of view and advanced topics are discussed. Our hope is that this chapter will help you get a little closer to what Sir Roger Penrose has very aptly called the “magic of complex numbers” (Penrose, 2005).
Reader Tip. Many readers will find that they are already familiar with some of the material presented in this chapter. The reader who feels confident in her comprehension of the fundamental knowledge of complex numbers, the basic operations, and their properties can safely move on to later chapters. We suggest, though, that you at least skim through the following pages to see what topics are covered. Return to Chapter 1 as a reference when needed (using the index to find specific topics). 
1.1 BASIC DEFINITIONS
The original motivation for the introduction of complex numbers was the theory of algebraic equations, the part of algebra that seeks solutions of polynomial equations. It became readily apparent that there are plenty of cases in which no solution among familiar numbers can be found. Here is the simplest example:
Indeed, any possible x2 would be positive or zero. Adding 1 ends up with some quantity to the left that is strictly positive; hence, no solution exists.
Exercise 1.1.1 Verify that the equation x4 + 2x2 + 1 = 0 has no solution among the real numbers. (Hint: Factor the polynomial.)
The aforementioned argument seems to dash any hope of solving Equation (1.1). But does it?
Before building any new number system, it pays to remind ourselves of other sets of numbers that we usually work with
positive numbers, 
;
natural numbers, 
;
integers (or whole numbers), 
;
rational numbers, 
;
real numbers, 
;
In none of these familiar number systems can a valid solution to Equation (1.1) be found. Mathematics often works around difficulties by simply postulating that such a solution, albeit unknown, is available somewhere. Let us thus boldly assume that this enigmatic solution does indeed exist and determine what it looks like: Equation (1.1) is equivalent to
What does this state? That the solution of Equation (1.1) is a number such that its square is −1, i.e., a number i such that
Of course we know that no such number exists among known (i.e., real) numbers, but we have already stated that this is not going to deter us. We will simply allow this new creature into the realm of well-established numbers and use it as it pleases us. Because it is imaginary, it is denoted i. We will impose on ourselves an important restriction: aside from its weird behavior when squared, i will behave just like an ordinary number.
Example 1.1.1 What is the value of i3? We shall treat i as a legitimate number, so
Exercise 1.1.2 Find the value of i15. (Hint: Calculate i, i2, i3, i4, and i5. Find a pattern.)
In opening the door to our new friend i, we are now flooded with an entire universe of new numbers: to begin with, all the multiples of i by a real number, like 2 × i. These fellows, being akin to i, are known as imaginary numbers. But there is more: add a real number and an imaginary number, for instance, 3 + 5 × i, and you get a number that is neither a real nor an imaginary. Such a number, being a hybrid entity, is rightfully called a complex number.
Definition 1.1.1 A complex number is an expression
where a, b are two real numbers; a is called the real part of c, whereas b is its imaginary part. The set of all complex numbers will be denoted as 
. When the × is understood, we shall omit it.
Complex numbers can be added and multiplied, as shown next.
Example 1.1.2 Let c1 = 3 − i and c2 = 1 + 4i. We want to compute c1 + c2 and c1 × c2.
Multiplying is not as easy. We must remember to multiply each term of the first complex number with each term of the second complex number. Also, remember that i2 = − 1.
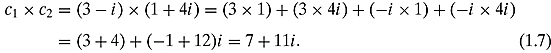
Exercise 1.1.3 Let c1 = − 3 + i and c2 = 2 − 4i. Calculate c1 + c2 and c1 × c2.
With addition and multiplication we can get all polynomials. We set out to find a solution for Equation (1.1); it turns out that complex numbers are enough to provide solutions for all polynomial equations.
Proposition 1.1.1 (Fundamental Theorem of Algebra). Every polynomial equation of one variable with complex coefficients has a complex solution.
Exercise 1.1.4 Verify that the complex number − 1 + i is a solution for the polynomial equation x2 + 2x + 2 = 0.
This nontrivial result shows that complex numbers are well worth our attention. In the next two sections, we explore the complex kingdom a little further.
Programming Drill 1.1.1 Write a program that accepts two complex numbers and outputs their sum and their product.
1.2 THE ALGEBRA OF COMPLEX NUMBERS
Admittedly, the fact that we know how to handle them does not explain away the oddity of complex numbers. What are they? What does it mean that i squared is equal to − 1?
In the next section, we see that the geometrical viewpoint greatly aids our intuition. Meanwhile, we would like to convert complex numbers into more familiar objects by carefully looking at how they are built.
Definition 1.1.1 tells us two real numbers correspond to each complex number: its real and imaginary parts. A complex number is thus a two-pronged entity, carrying its two components along. How about defining a complex number as an ordered pair of reals?
Ordinary real numbers can be identified with pairs (a, 0)
whereas imaginary numbers will be pairs (0, b). In particular,
Addition is rather obvious – it adds pairs componentwise:
Multiplication is a little trickier:
Does this work? Multiplying i by itself gives
which is what we wanted.
Using addition and multiplication, we can write any complex number in the usual form:
We have traded one oddity for another: i was previously quite mysterious, whereas now it is just (0, 1). A complex number is nothing more than an ordered pair of ordinary real numbers. Multiplication, though, is rather strange: perhaps the reader would have expected a componentwise multiplication, just like addition. We shall see later that by viewing complex numbers through yet another looking glass the strangeness linked to their multiplication rule will fade away.
Example 1.2.1 Let c1 = (3, −2) and c2 = (1, 2). Let us multiply them using the aforementioned rule:
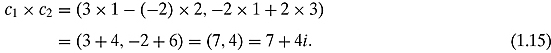
Exercise 1.2.1 Let c1 = (−3, −1) and c2 = (1, −2). Calculate their product.
So far, we have a set of numbers and two operations: addition and multiplication. Both operations are commutative, meaning that for arbitrary complex numbers c1 and c2,
and
Both operations are also associative:
and
Exercise 1.2.2 Verify that multiplication of complex numbers is associative.
Moreover, multiplication distributes over addition: for all c1, c2, c3, we have
Let us verify this property: first we write the complex numbers as pairs c1 = (a1, b1), c2 = (a2, b2), and c3 = (a3, b3). Now, let us expand the left side
Turning to the right side of Equation (1.20) one piece at a time gives
summing them up we obtain
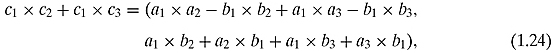
which is precisely what we got in Equation (1.21).
Having addition and multiplication, we need their complementary operations: subtraction and division.
Subtraction is straightforward:
in other words, subtraction is defined componentwise, as expected.
As for division, we have to work a little: If
then by definition of division as the inverse of multiplication
or
So we end up with
To determine the answer, we must solve this pair of equations for x and y. Multiply both sides of (1) by a2 and both sides of (2) by b2. We end up with
Now, let us add (1′) and (2′) to get
Solving for x gives us
We can perform the same trick for y by multiplying (1) and (2) by b2 and −a2, respectively, and then summing. We obtain
In more compact notation, we can express this equation as
Notice that both x and y are calculated using the same denominator, namely, 
. We are going to see what this quantity means presently. In the meantime, here is a concrete example.
Example 1.2.2 Let c1 = −2 + i and c2 = 1 + 2i. We will compute 
. In this case, a1 = −2, b1 = 1, a2 = 1, and b2 = 2. Therefore,
The answer is thus 
.
Exercise 1.2.3 Let c1 = 3i and c2 = −1 − i. Calculate .
Now, let us go back to the mysterious denominator in the quotient formula in Equation (1.36). Real numbers have a unary operation, the absolute value, given by
We can define a generalization of this operation2 to the complex domain by letting
This quantity is known as the modulus of a complex number.
Example 1.2.3 What is the modulus of c = 1 − i?
The geometric meaning of the modulus is discussed in the next section. For now, we remark that the quantity in the denominator of the quotient of two complex numbers is nothing more than the modulus squared of the divisor:
This modulus must be different from zero, which always happens unless the divisor is itself zero.
Exercise 1.2.4 Calculate the modulus of c = 4 − 3i.
Exercise 1.2.5 Verify that given two arbitrary complex numbers c1 and c2, the following equality always holds:
Exercise 1.2.6 Prove that
When are they, in fact, equal? (Hint: Square both sides.)
Exercise 1.2.7 Show that for all 
, we have c + (0, 0) = (0, 0) + c = c. That is, (0, 0) is an additive identity.
Exercise 1.2.8 Show that for all we have c× (1, 0) = (1, 0) × c = c. That is, (1, 0) is a multiplicative identity.
In summation, we have defined a new set of numbers, , endowed with four operations, verifying the following properties:
(i) Addition is commutative and associative.
(ii) Multiplication is commutative and associative.
(iii) Addition has an identity: (0, 0).
(iv) Multiplication has an identity: (1, 0).
(v) Multiplication distributes with respect to addition.
(vi) Subtraction (i.e., the inverse of addition) is defined everywhere.
(vii) Division (i.e., the inverse of multiplication) is defined everywhere except when the divisor is zero.
A set with operations satisfying all these properties is called a field. is a field, just like 
, the field of real numbers. In fact, via the identification that associates a real number to a complex number with 0 as the imaginary component, we can think of as a subset3 of . sits inside ; but is a vast field, so vast, indeed, that all polynomial equations with coefficients in have a solution in itself. is also a roomy field, but not enough to enjoy this last property (remember Equation (1.1)). A field that contains all solutions for any of its polynomial equations is said to be algebraically complete. is an algebraically complete field, whereas is not.
There is a unary operation that plays a crucial role in the complex domain. The reader is familiar with “changing signs” of real numbers. Here, however, there are two real numbers attached to a complex number. Therefore, there are three ways of changing sign: either change the sign of the real part or change the sign of the imaginary part, or both. Let us analyze them one by one.
Changing both signs of the complex number is done by multiplying by the number − 1 = (−1, 0).
Exercise 1.2.9 Verify that multiplication by (−1, 0) changes the sign of the real and imaginary components of a complex number.
Changing the sign of the imaginary part only is known as conjugation.4 If c = a + bi is an arbitrary complex number, then the conjugate of c is 
. Two numbers related by conjugation are said to be complex conjugates of each other.
Changing the sign of the real part 
has no particular name, at least in the algebraic context.5
The following exercises will guide you through conjugation’s most important properties.
Exercise 1.2.10 Show that conjugation respects addition, i.e.,
Exercise 1.2.11 Show that conjugation respects multiplication, i.e.,
Notice that the function
given by conjugation is bijective, i.e., is one-to-one and onto. Indeed, two different complex numbers are never sent to the same number by conjugation. Moreover, every number is the complex conjugate of some number. A function from a field to a field that is bijective and that respects addition and multiplication is known as a field isomorphism. Conjugation is thus a field isomorphism of to .
Exercise 1.2.12 Consider the operation given by flipping the sign of the real part. Is this a field isomorphism of ? If yes, prove it. Otherwise, show where it fails.
We cannot continue without mentioning another property of conjugation:
In words, the modulus squared of a complex number is obtained by multiplying the number with its conjugate. For example,
We have covered what we need from the algebraic perspective. We see in the next section that the geometric approach sheds some light on virtually all topics touched on here.
Programming Drill 1.2.1 Take the program that you wrote in the last programming drill and make it also perform subtraction and division of complex numbers. In addition, let the user enter a complex number and have the computer return its modulus and conjugate.
1.3 THE GEOMETRY OF COMPLEX NUMBERS
As far as algebra is concerned, complex numbers are an algebraically complete field, as we have described them in Section 1.2. That alone would render them invaluable as a mathematical tool. It turns out that their significance extends far beyond the algebraic domain and makes them equally useful in geometry and hence in physics. To see why this is so, we need to look at a complex number in yet another way. At the beginning of Section 1.2, we learned that a complex number is a pair of real numbers. This suggests a natural means of representation: real numbers are placed on the line, so pairs of reals correspond to points on the plane, or, equivalently, correspond to vectors starting from the origin and pointing to that point (as shown in Figure 1.1).
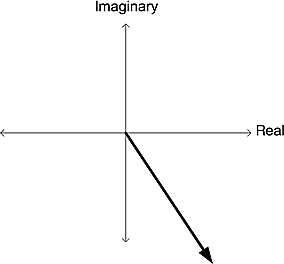
Figure 1.1. Complex plane.
In this representation, real numbers (i.e., complex numbers with no imaginary part) sit on the horizontal axis and imaginary numbers sit on the vertical axis. This plane is known as the complex plane or the Argand plane.
Through this representation, the algebraic properties of the complex numbers can be seen in a new light. Let us start with the modulus: it is nothing more than the length of the vector. Indeed, the length of a vector, via Pythagoras’ theorem, is the square root of the sum of the squares of its edges, which is precisely the modulus, as defined in the previous section.
Example 1.3.1 Consider the complex numbers c = 3 + 4i depicted in Figure 1.2. The length of the vector is the hypotenuse of the right triangle whose edges have length 3 and 4, respectively. Pythagoras’ theorem gives us the length as
This is exactly the modulus of c.
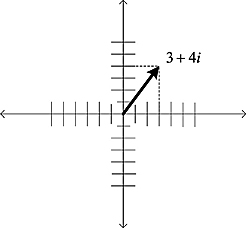
Figure 1.2. Vector 3 + 4i.
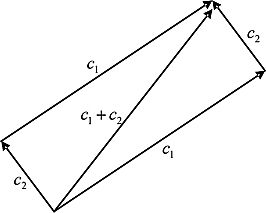
Figure 1.3. Parallelogram rule.
Next comes addition: vectors can be added using the so-called parallelogram rule illustrated by Figure 1.3. In words, draw the parallelogram whose parallel edges are the two vectors to be added; their sum is the diagonal.
Exercise 1.3.1 Draw the complex numbers c1 = 2 − i and c2 = 1 + i in the complex plane, and add them using the parallelogram rule. Verify that you would get the same result as adding them algebraically (the way we learned in Section 1.2).
Subtraction too has a clear geometric meaning: subtracting c2 from c1 is the same as adding the negation of c2, i.e., −c2, to c1. But what is the negation of a vector? It is just the vector of the same length pointed in the opposite direction (see Figure 1.4).
Exercise 1.3.2 Let c1 = 2 − i and c2 = 1 + i. Subtract c2 from c1 by first drawing −c2 and then adding it to c1 using the parallelogram rule.
To give a simple geometrical meaning to multiplication, we need to develop yet another characterization of complex numbers. We saw a moment ago that for every complex number we can draw a right triangle, whose edges’ lengths are the real and imaginary parts of the number and whose hypotenuse’s length is the modulus. Now, suppose someone tells us the modulus of the number what else do we need to know to draw the triangle? The answer is the angle at the origin.
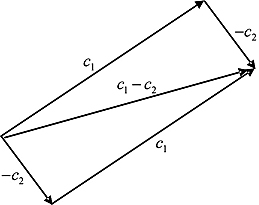
Figure 1.4. Subtraction.
The modulus ρ and the angle θ (notice: two real numbers, as before) are enough to uniquely determine the complex number.
We know how to compute ρ from a, b:
θ is also easy, via trigonometry:
The (a, b) representation is known as the Cartesian representation of a complex number, whereas (ρ, θ) is the polar representation.
We can go back from polar to Cartesian representation, again using trigonometry:
Example 1.3.2 Let c = 1 + i. What is its polar representation?
c is the vector of length 
from the origin at an angle of 
radians, or 45º.
Exercise 1.3.3 Draw the complex number given by the polar coordinates ρ =3 and 
. Compute its Cartesian coordinates.
Programming Drill 1.3.1 Write a program that converts a complex number from its Cartesian representation to its polar representation and vice versa.
Before moving on, let us meditate a little: what kind of insight does the polar representation give us? Instead of providing a ready-made answer, let us begin with a question: how many complex numbers share exactly the same modulus? A moment’s thought will tell us that for a fixed modulus, say, ρ = 1, there is an entire circle centered at the origin (as shown in Figure 1.5).
Figure 1.5. Phase θ.
Figure 1.6. Points on a line with the same phase.
So, here comes the angle: imagine the circle as your watch, and the complex number as the needle. Angle θ tells us the “time.” The “time” is known in physics and engineering as the phase, whereas the length of the “needle” (i.e., the modulus) is the magnitude of the number.
Definition 1.3.1 A complex number is a magnitude and a phase.
The ordinary positive reals are just complex numbers such that their phase is zero. The negative reals have phase π. By the same token, imaginary numbers are numbers with constant phase equal to 
(positive imaginary) or 
(negative imaginary).
Given a constant phase, there is an entire line of complex numbers having that phase as depicted in Figure 1.6.
Observe that a complex number has a unique polar representation only if we confine the phase between 0 and 2π:
(and the ρ ≥ 0). If we restrict θ in this fashion, though, we cannot in general add angles (the sum may be bigger than 2π). A better course is to let the angle be anything and reduce it modulo 2π:
Two complex numbers in polar representations will be identical if their magnitude is the same and if the angles are the same modulo 2π, as shown by the following example.
Example 1.3.3 Are the numbers (3, −π) and (3, π) the same? Indeed they are: their magnitude is the same and their phases differ by (−π) − π = −2π = (−1)2π.
We are now ready for multiplication: given two complex numbers in polar coordinates, (ρ1, θ1) and (ρ2, θ2), their product can be obtained by simply multiplying their magnitude and adding their phase:
Example 1.3.4 Let c1 = 1 + i and c2 = −1 + i. Their product, according to the algebraic rule, is
Now, let us take their polar representation
(Carry out the calculations!) Therefore, their product using the rule described earlier is
If we revert to its Cartesian coordinates, we get
which is precisely the answer we arrived at with the algebraic calculation in Equation (1.61).
Figure 1.7 is the graphical representation of the two numbers and their product.
As you can see, we simply rotated the first vector by an angle equal to the phase of the second vector and multiplied its length by the length of the second vector.
Exercise 1.3.4 Multiply c1 = −2 −i and c2 = −1 −2i using both the algebraic and the geometric method; verify that the results are identical.
Reader Tip. Most of the rest of this chapter are basic ideas in complex numbers; however, they will not really be used in the text. The part on roots of unity will arise in our discussion of Shor’s algorithm (Section 6.5). The rest is included for the sake of completeness. The restless reader can safely skim the rest of this chapter on the first reading.
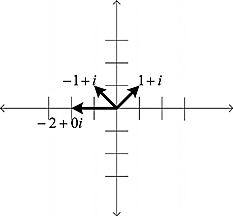
Figure 1.7. Two complex numbers and their product.
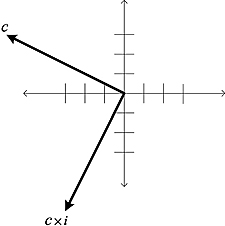
Figure 1.8. Multiplication by i.
We have implicitly learned an important fact: multiplication in the complex domain has something to do with rotations of the complex plane. Indeed, observe just what happens by left or right multiplication by i:
i has modulus 1, so the magnitude of the result is exactly equal to that of the starting point. The phase of i is 
, so multiplying by i has the net result of rotating the original complex number by 90º, a right angle. The same happens when we multiply any complex number; so we can safely conclude that multiplication by i is a right-angle counterclockwise rotation of the complex plane, as shown in Figure 1.8.
Exercise 1.3.5 Describe the geometric effect on the plane obtained by multiplying by a real number, i.e., the function
where r0 is a fixed real number.
Exercise 1.3.6 Describe the geometric effect on the plane obtained by multiplying by a generic complex number, i.e., the function
where c0 is a fixed complex number.
Programming Drill 1.3.2 If you like graphics, write a program that accepts a small drawing around the origin of the complex plane and a complex number. The program should change the drawing by multiplying every point of the diagram by a complex number.
Now that we are armed with a geometric way of looking at multiplication, we can tackle division as well. After all, division is nothing more than the inverse operation of multiplication. Assume that
are two complex numbers in polar form; what is the polar form of 
? A moment’s thought tells us that it is the number
In words, we divide the magnitudes and subtract the angles.
Example 1.3.5 Let c1 = −1 + 3i and c2 = −1 − 4i. Let us calculate their polar coordinates first:
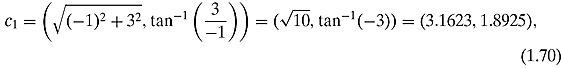
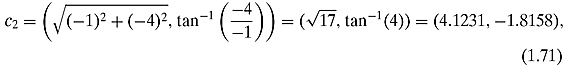
therefore, in polar coordinates the quotient is
Exercise 1.3.7 Divide 2 + 2i by 1 − i using both the algebraic and the geometrical method and verify that the results are the same.
You may have noticed that in Section 1.2, we have left out two important operations: powers and roots. The reason was that it is much easier to deal with them in the present geometric setting than from the algebraic viewpoint.
Let us begin with powers. If c = (ρ, θ) is a complex number in polar form and n a positive integer, its nth power is just
because raising to the nth power is multiplying n times. Figure 1.9 shows a complex number and its first, second, and third powers.
Exercise 1.3.8 Let c = 1 − i. Convert it to polar coordinates, calculate its fifth power, and revert the answers to Cartesian coordinates.
What happens when the base is a number of magnitude 1? Its powers will also have magnitude 1; thus, they will stay on the same unit circle. You can think of the various powers 1, 2,… as time units, and a needle moving counterclockwise at constant speed (it covers exactly θ radians per time unit, where θ is the phase of the base).
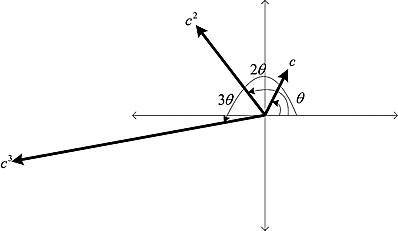
Figure 1.9. A complex number and its square and cube.
Let us move on to roots. As you know already from high-school algebra, a root is a fractional power. For instance, the square root means raising the base to the power of one-half; the cube root is raising to the power of one-third; and so forth. The same holds true here, so we may take roots of complex numbers: if c = (ρ, θ)is a complex in polar form, its nth root is
However, things get a bit more complicated. Remember, the phase is defined only up to multiples of 2π. Therefore, we must rewrite Equation (1.74) as
It appears that there are several roots of the same number. This fact should not surprise us: in fact, even among real numbers, roots are not always unique. Take, for instance, the number 2 and notice that there are two square roots, and 
.
How many nth roots are there? There are precisely nth roots for a complex number. Why? Let us go back to Equation (1.75).
How many different solutions can we generate by varying k? Here they are:
That is all: when k = n, we obtain the first solution; when k = n + 1, we obtain the second solution; and so forth. (Verify this statement!)
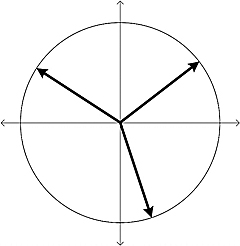
Figure 1.10. The three cube roots of unity.
To see what is happening, let us assume that ρ = 1; in other words, let us find nth roots of a complex number c = (1, θ) on the unit circle. The n solutions in Equation (1.77) can be interpreted in the following way: Draw the unit circle, and the vectors whose phase is 
plus an angle equal to 
of the entire circle, where k = 1,…, n. We get precisely the vertices of a regular polygon with n edges. Figure 1.10 is an example when n = 3.
Exercise 1.3.9 Find all the cube roots of c = 1 + i.
By now we should feel pretty comfortable with the polar representation: we know that any complex number, via the polar-to-Cartesian function, can be written as
Let us introduce yet another notation that will prove to be very handy in many situations. The starting point is the following formula, known as Euler’s formula:
The full justification of the remarkable formula of Euler lies outside the scope of this book.6 However, we can at least provide some evidence that substantiates its validity. First of all, if θ = 0, we get what we expected, namely, 1. Secondly,
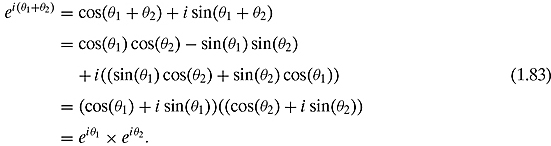
In other words, the exponential function takes sums into products as it does in the real case.
Exercise 1.3.10 Prove De Moivre’s formula:
(Hint: The trigonometric identities used earlier, with induction on n, will do the work.)
Now that we know how to take the exponential of an imaginary number, there is no problem in defining the exponential of an arbitrary complex number:
Euler’s formula enables us to rewrite Equation (1.78) in a more compact form:
We shall refer to Equation (1.86) as the exponential form of a complex number.
Exercise 1.3.11 Write the number c = 3 − 4i in exponential form.
The exponential notation simplifies matters when we perform multiplication:
Exercise 1.3.12 Rewrite the law for dividing complex numbers in exponential form.
With this notation, we can look at the roots of the complex number 1 = (1, 0) = 1 + 0i. Let n be a fixed number. There are n different roots of unity. Setting c = (1, 0). in Equation (1.75), we get
By permitting k = 0, 1, 2,…, n− 1, we get n different roots of unity. Notice that if we set k = n, we get back to the first one. The kth root of unity in exponential form is e2πik/n. We denote these n different roots of unity by
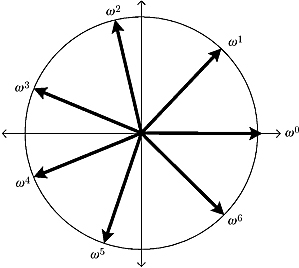
Figure 1.11. The seventh root of unity and its powers.
Geometrically these n roots of unity correspond to splitting up the unit circle into n parts where the first partition is (1, 0). Figure 1.11 is a picture of the seventh root of unity and all its powers.
If we multiply two roots of unity, we get
Notice also that
and hence
Exercise 1.3.13 Draw all the fifth roots of unity.
We are now in a position to characterize geometrically any function on complex numbers. The simplest functions one can think of beyond the elementary operations are polynomials. An arbitrary polynomial with complex coefficients looks like
where c0, c1,…, cn−1 are in . P(x) can be seen as a function from to
To build some geometric intuition on polynomials, you can try your hand at the following two exercises.
Exercise 1.3.14 Describe the geometric meaning of the function
from to .
Exercise 1.3.15 Describe the geometric meaning of the function
from to .
After polynomials, the next set of functions are rational functions, or quotients of polynomials:
In general, describing the action on the plane provided by a rational function is no simple matter. The simplest case, though, is relatively easy and a very important one:
where a, b, c, d are in and ad− bc≠ 0 is known as the Möbius transformation. The following set of exercises introduce some of the basic properties of Möbius transformations. (In particular, we show that the set of Möbius transformations form a group.)7
Exercise 1.3.16 When a = d = 0 and b = c = 1, we get 
. Describe the geometrical effect of this transformation. (Hint: See what happens to the points inside and outside the circle of radius 1.)
Exercise 1.3.17 Prove that the composition of two Möbius transformations is a Möbius transformation. In other words, if Ra,b,c,d and Ra′,b′,c′,d′ are two Möbius transformations, the transformation Ra′,b′,c′,d′ 
Ra,b,c,d given by
is also a Möbius transformation.
Exercise 1.3.18 Show that the identity transformation, i.e., the transformation that leaves every point fixed, is a Möbius transformation.
Exercise 1.3.19 Show that each Möbius transformation has an inverse that is also a Möbius transformation, i.e., for each Ra,b,c,d you can find Ra′,b′,c′,d′ such that
There are many more functions in the complex domain, but to introduce them one needs tools from complex analysis, i.e., calculus over the complex numbers. The main idea is quite simple: replace polynomials with a power series, i.e., polynomials with an infinite number of terms. The functions one studies are the so-called analytic functions, which are functions that can be coherently pieced together from small parts, each of which is represented by a series.
Programming Drill 1.3.3 Expand your program. Add functions for multiplication, division, and returning the polar coordinates of a number.
We have covered the basic language of complex numbers. Before we embark on our quantum journey, we need another tool: vector spaces over the complex field.
References: Most of the material found in this chapter can be found in any calculus or linear algebra textbook. References for some of the more advanced material presented at the end of the chapter can be found in, e.g., Bak and Newman (1996), Needham (1999), Schwerdtfeger (1980), and Silverman (1984).
The history of complex numbers goes back to the mid-sixteenth century during the Italian Renaissance. The story of Tartaglia, Cardano, Bombelli and their effort to solve algebraic equations is well worth reading. Some of this fascinating tale is in Nahin (1998), Mazur (2002), and several wonderful sections in Penrose (1994).
1 For the German-speaking reader, here is the original text (the translation at the beginning is ours):
Du, hast du das vorhin ganz verstanden?
Was?
Die Geschichte mit den imaginären Zahlen?
Musil’s Törless is a remarkable book. A substantial part is dedicated to the struggle of young Törless to come to grips with mathematics, as well as with his own life. Definitely recommended!
2 The definition given in Equation (1.40) is entirely equivalent to the more familiar one: |a| = a if a ≥ 0, and |a| = − a if a < 0.
3 A subset of a field that is a field in its own right is called a subfield: is a subfield of .
4 Its “geometric” name is real-axis reflection. The name becomes obvious in the next section.
5 In the geometric viewpoint, it is known as imaginary-axis reflection. After reading Section 1.3, we invite you to investigate this operation a bit further.
6 For the calculus-savvy reader: Use the well-known Taylor expansions.
Assume that they hold for complex values of x. Now, formally multiply sin(x) by i and add componentwise cos(x) to obtain Euler’s formula.
7 Möbius transformations are a truly fascinating topic, and perhaps the best entrance door to the geometry of complex numbers. We invite you to find out more about them in Schwerdtfeger (1980).